数值模拟方法和反演
水文模拟中的参数反演方法研究

水文模拟中的参数反演方法研究水文模拟是一种重要的水文学研究方法,它通过对水文过程的模拟,来研究水文系统的运行规律和演化趋势。
在水文模拟中,参数反演是一个重要的环节,它通过对水文模型中的参数进行调节,使其能够更好地模拟实际水文过程。
本文将从参数反演的基本概念、常用方法以及应用前景等方面,探讨水文模拟中的参数反演方法研究。
一、参数反演的基本概念水文模型是一种描述水文过程的数学模型,它由一组方程和参数组成。
其中,方程是描述水文变量之间关系的数学表达式,参数则是指这些关系中所涉及的常数或系数。
在实际应用中,水文模型中的参数往往需要进行反演调节,以达到更加精确的模拟效果。
参数反演是指通过对水文过程的数据观测,来估算出水文模型中的参数值。
在反演过程中,需要根据实际情况选择适宜的反演方法,以保证精度和可靠性。
二、常用的参数反演方法1. 基于参数梯度的反演方法这种方法是基于一阶和二阶参数敏感性分析理论,通过分析模型输出与参数的变化关系,来反演出最优的参数组合。
其中,一阶参数敏感度反映了模型输出与参数值之间的线性关系,而二阶参数敏感度则反映了模型输出与参数变化率之间的非线性关系。
这种方法具有计算简便、准确性高的优点,但需要进行多次模型计算,计算量比较大。
2. 基于遗传算法的反演方法这种方法是一种常用的优化算法,通过模拟自然进化过程,来不断寻找模型的最优参数组合。
具体来说,首先建立一个适应度函数,用来评价模型输出与观测结果之间的差异。
然后,对于每个种群中的个体,随机选择若干个参数进行变异、交叉等操作,以产生新的个体,并根据适应度函数进行选择。
经过多次迭代选择后,最终找到最优参数组合。
这种方法可以较好地处理多参数问题,但需要进行大量迭代计算,计算效率较低。
3. 基于马尔科夫链蒙特卡罗法的反演方法这种方法是利用蒙特卡罗法计算模型参数的先验分布,并通过马尔科夫链进行参数搜索,最终得到最优的参数组合。
具体来说,首先利用先验分布随机生成一些参数组合,然后根据模型输出与观测结果之间的差异,计算出这些参数组合的后验概率分布。
金塘水道悬沙场遥感反演及数值模拟

金塘水道悬沙场遥感反演及数值模拟蒯宇;陶建峰;康彦彦【摘要】Based on the data from the GOCI(Geostationary Ocean Color Imager), three different remote sensing models were compared and the neural network model with a relative higher accuracy was chosen to interpret the SSC (Suspended Sediment Concentration) field during the spring tide in June 2015. A 2D tidal current and suspended sediment model was adopted to carry out numerical simulation of suspended sediment movement during the same period. Comparison results between the remote sensing interpretation and the numerical model show that the SSC is higher in the north part of the Jintang Channel than it in the south part, and it has a periodic characteristic that the SSC increases during the flood period and decreases during the ebb tide. The remote sensing results and deduced numerical model results are relatively similar in both water surface SSC distribution and magnitude, which provides a method for areas with large horizontal scales lacking SSC data.%基于GOCI遥感数据,通过三种遥感模型的比较,选择了精度较高的神经网络模型,对2015年6月大潮时期的悬沙场进行解译,并建立了二维潮流泥沙数学模型对同时段的悬沙场进行了模拟.比较遥感解译与数模的结果得到:金塘水道悬沙场呈现北高南低的分布特征,时间上具有明显的周期性,涨潮时悬沙量逐渐减小,落潮时逐渐增大;遥感解译与数模模拟推算得到的水体表面的悬沙场在分布趋势和量值上较为一致,为大范围水域缺少泥沙分布资料的情况提供了一种可借鉴的研究方法.【期刊名称】《水道港口》【年(卷),期】2017(038)003【总页数】7页(P228-234)【关键词】金塘水道;遥感解译;数值模拟;悬沙输移【作者】蒯宇;陶建峰;康彦彦【作者单位】河海大学水文水资源与水利工程科学国家重点实验室, 南京 210098;河海大学港口海岸与近海工程学院, 南京 210098;河海大学水文水资源与水利工程科学国家重点实验室, 南京 210098;河海大学港口海岸与近海工程学院, 南京210098;河海大学港口海岸与近海工程学院, 南京 210098【正文语种】中文【中图分类】P748;O242.1金塘水道是一条由潮流长期冲蚀作用形成的峡道型潮汐通道[1],是连接杭州湾南岸海域与外海的潮汐通道之一(图1)。
地震模型正演
地震模型正演与反演简介一、地震模型正演(seismic forward modeling)的概念如果我们已知地下的地质模型,它的地震响应如何?地震模型正演就是通过室内模拟得到地质模型对于地震波的响应。
地震模型正演包括物理模拟和数值模拟,数值模拟就是应用相应的地球物理方程和数值计算求解已知的地质模型在假定激发源的作用下的地震相应。
通常,我们针对特定的勘探区块,应用期望或实际的采集参数通过地震正演模拟野外地震采集,得到单炮记录,再通过速度分析、动校正、叠加、偏移等处理得到成像数据。
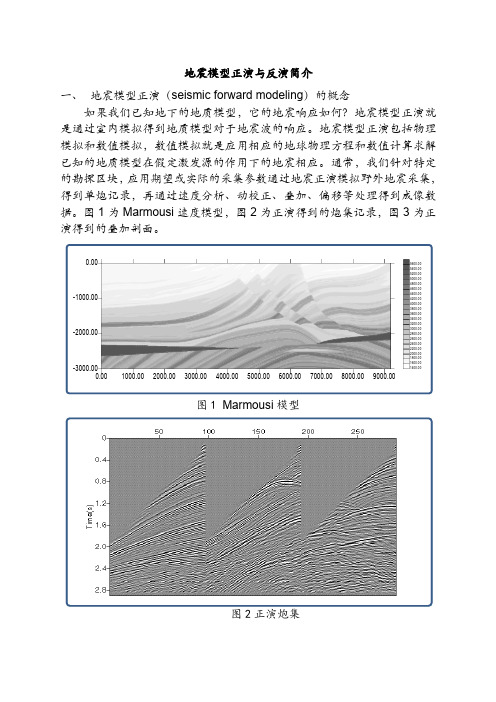
图1为Marmousi速度模型,图2为正演得到的炮集记录,图3为正演得到的叠加剖面。
图1 Marmousi模型图2正演炮集图3 正演叠加剖面二、数值模型正演方法通常,我们提到的模型正演为数值模拟的模型正演,目前常用的数值模拟地震模型正演方法包括基于射线原理的射线追踪法,以及基于波动方程的有限差分法、有限元法、积分方程法、快速傅里叶变换法和拟谱法等。
射线追踪法主要反映地震波的运动学特征,有限差分、有限元法则适合复杂地质构造的正演模拟,积分方程法涉及复杂的数学推导,快速傅里叶变换法在频率域计算得到正演数据。
三、数值模型正演的步骤数值模拟求解地震模型正演问题的步骤主要包括以下三个方面:1) 地质建模,根据研究对象和问题建立地球物理或地质模型;2) 数学建模,根据应用的物理手段和地球物理模型建立相应的数学模型;3) 模拟计算,选择正演计算方法,编写计算程序进行数值模拟计算。
四、什么是地震反演地震反演技术就是充分利用测井、钻井、地质资料提供的丰富的构造、层位、岩性等信息,从常规的地震剖面推导出地下地层的波阻抗、密度、速度、孔隙度、渗透率、沙泥岩百分比、压力等地球物理信息。
反演就是由地震数据得到地质模型,进行储层、油藏研究。
地震资料反演可分为两部分:1)通过有井(绝对)、无井(相对)波阻抗反演得到波阻抗、速度数据体。
2)利用测井、测试资料结合波阻抗、速度数据进行岩性反演,得到孔隙度、渗透率、砂泥百分比、压力等物理数据。
数值模拟方法

式中bi,j为位置(i,j)处的水底高程,i,j为自由面的高度,kmax为垂直方向上网格单元的最 大数目。本手册中其它向量也运用类似的定义。
4.2动量的半隐式格式
速度场的基本半隐式化演进可被离散到n*的解空间,类似TRIM中的方法,即得:
式中G是一显式源项向量,1表示自由水面的“隐性度”(隐性度一般的取值范围为0.5 < 1 < 1.0已在ELCOM版本1中编码,但未经全面测试)。ELCOM中默认的半隐格式是对从形 式上看为时间上一阶精确的自由水面演进采用后向欧拉离散法(即1=1)。 经证明(Casulli和Cattani,1994),求解流体静力学方程组使用的后向欧拉法可被扩展为 方程4.2和4.3的一般二层格式,从形式来看为二阶精确(当1 =1时)。然而在粗网格模拟中, 数值离散精度的增加不一定导致模型技巧的提高。通常,在对许多湖泊和河口进行模拟时,正 压模态是通过CFL条件来求解的,CFL取值可能为5到10之间或大于10。在这种情况下,半隐式 离散化或许稳定,但水流物理过程表达“准确程度”的决定因素为现研究的流态类型。截断误 差的性质对于了解该方法性能至关重要。若采用一阶方法,导程误差为二阶,且在自由水面上 产生阻尼波。若采用二阶方法,导程误差扩散,且在自由水面产生在水域上传播的数值波;通 常使得线性正压波演化为陡峭前沿涌潮,使得受地形影响的表面波产生局地高速流。因此,一 阶方法可以较好描述自由水面形态和局部正压流速,但显示出自由水面惯性响应的多余阻尼。 相比之下,二阶方法以最低的数值耗散将能量保持为表面波的形式,但对于波的形态描述较 差。在静水力学求解中,弥散波将导致贯穿水柱的人工局部加压的产生,这对于求解技术是不 利的。相比之下,表面波的多余阻尼在风速减弱的时候将导致与正压响应相关的大规模运动的 减弱(即正压模式的“震荡”是衰减的)。总体上,高强度增压系统采用后向欧拉格式模拟较 好,因为两、三个周期以前的波能通常与一阶的物理过程不相关。 采用二层隐式离散化(Casulli和Cheng, 1992)或其它显式离散化技术,矩阵A可以表示
数值模拟估算低低卫-卫跟踪观测技术反演地球重力场的空间分辨率

数值模拟估算低低卫-卫跟踪观测技术反演地球重力场的空间分辨率周旭华;吴斌;许厚泽;彭碧波【期刊名称】《地球物理学报》【年(卷),期】2005(048)002【摘要】从两个方面模拟研究了低低卫-卫跟踪观测技术恢复地球重力场的空间分辨率.利用重力位系数作为扰动量,积分30天的轨道,研究重力位系数变化引起低低卫-卫跟踪星间距离和速率变化,结果表明,对于地球重力场模型EGM96的前120阶,99.8%和97%的位系数扰动引起星间距离和速率变化的均方差大于1×10-5m 和1×10-7m/s,并且星间距离观测值对地球重力场的反应更为敏感.不考虑非保守力误差的影响,用随机误差为1×10-5m和1×10-6m/s的星间距离和速率变化作模拟观测量,恢复了78阶地球重力场位系数,结果表明,采用随机误差为1×10-5m 的星间距离恢复地球重力场的精度明显高于1×10-6m/s的星间速率结果,但是如果考虑非保守力误差影响,则星间测速的优越性大大增强.【总页数】6页(P282-287)【作者】周旭华;吴斌;许厚泽;彭碧波【作者单位】中国科学院测量与地球物理研究所,动力大地测量重点实验室,武汉,430077;中国科学院测量与地球物理研究所,动力大地测量重点实验室,武汉,430077;中国科学院测量与地球物理研究所,动力大地测量重点实验室,武汉,430077;中国科学院测量与地球物理研究所,动力大地测量重点实验室,武汉,430077【正文语种】中文【中图分类】P223【相关文献】1.低低卫-卫跟踪重力测量物理模型及部分姿轨控技术需求 [J], 唐富荣;薛大同;达道安2.由GOCE高低卫卫跟踪数据反演地球重力场的模拟研究 [J], 刘晓刚;孙文;李新星;周睿3.基于卫-卫跟踪观测技术利用能量守恒法恢复地球重力场的数值模拟研究 [J], 郑伟;邵成刚;罗俊;许厚泽4.低低卫-卫跟踪模式中卫星轨道高度和星间距离的指标设计论证 [J], 刘晓刚;肖云;李婧;李迎春;庞振兴5.基于轨道扰动引力谱分析的方法确定低低观测重力卫星反演重力场的空间分辨率[J], 庞振兴;肖云;赵润因版权原因,仅展示原文概要,查看原文内容请购买。
地球物理反演总结

地球物理反演总结一、名词解释(30)二、简答(30)三、综述(40)第一章正问题:给定一个问题,寻找答案反问题:给定一个答案,寻找问题适定性问题:解一定存在;解的唯一性;问题发生一些小的变动仅导致问题的解发生小的变动非适定性问题:解不一定存在;解可能不唯一;问题中小的变动导致问题解较大变动正演问题(正问题):已知模型m,求解数据d的过程反演问题(反问题):已知数据d,求解模型参数m的过程地震反演(SeismicInversion):把常规的界面型反射剖面转换成岩层型的测井剖面,将地震资料变成可与测井资料直接对比的形式,实现这种转换的处理过程叫地震反演。
地震反演在石油勘探开发中的应用:1、微构造识别;2、岩性预测;3、储层参数评价4、流体识别(烃类检测)地球物理反演:根据各种位场、地震波、地球自由振荡、交变电磁场、以及热学的地球物理观测数据去推测地球内部的结构形态及物质成分,定量计算各种有关的物理参数地震勘探中应用最广的反演问题是地震波阻抗反演,地震波阻抗反演是储层地球物理研究的最基本的处理技术之一,通过地震波阻抗反演把常规的界面型地震反射剖面转换成岩层型的伪测井剖面,因而使地震资料转变成可以与钻井资料直接对比的剖面形式,可以说波阻抗反演是地震资料处理的最终处理结果。
地震反演的目的:根据地震资料,反推出地下介质的波阻抗、速度和密度等岩石地球物理参数的分布,估算储层参数,并进行储层预测,以便为油气田的勘探和开发提供可靠的基础资料。
第二章地震正演定义:地震正演是根据设计的地质模型,选择速度、密度、波松比等地层参数,用某种方法求得地震响应,通过与实际剖面对比,合理解释复杂的地质现象。
地质模型:物理模型、数值模型算法原理:褶积模型、绕射迭加模型、射线追踪模型、波动方程模型地震物理模拟:在实验室内将野外的地质构造和地质体按照一定的模拟相似比制作成物理模型,并用超声波或激光超声波等方法对野外地震勘探方法进行模拟的一种地震模拟方法。
反演问题的数值解法研究

反演问题的数值解法研究第一章引言反演问题是指通过观测数据得到模型参数或物理参数的过程。
在许多领域中,反演问题都是非常重要的,如地球物理学、医学成像、无损检测等。
由此带来的数值计算问题也是非常重要的,因为反演问题涉及到从离散的观测数据中推断出连续的参数,需要依赖数值方法来求解。
本文主要呈现了一些常用的反演问题的数值解法的研究,包括线性反演问题和非线性反演问题。
我们将对各种反演问题的数值解法进行介绍,包括正则化方法、Bayesian方法、梯度下降等。
第二章线性反演问题线性反演问题是指观测数据与模型参数之间的函数关系是线性的反演问题。
我们通常将这种问题表示为$A\mathbf{x}=\mathbf{b}$,其中$A$是线性算子,$\mathbf{x}$是模型参数,$\mathbf{b}$是观测数据。
线性反演问题的数值解法可以使用奇异值分解(SVD)或者正则化方法。
其中,SVD可以将线性反演问题转换为一个完全指定和完全可逆的问题,可以得到唯一的解。
但是,由于数值算法的限制和观测数据误差的影响,SVD不一定是最好的解决方案。
为了解决这个问题,我们可以使用正则化方法。
正则化方法是一种通过增加稳定性约束条件来处理不适定反演问题的技术。
这些约束条件可以有效地减少反演问题的不确定性。
常用的正则化方法包括Tikhonov正则化和阻尼最小二乘法。
Tikhonov正则化是通过加入二次惩罚项来限制解的大小,从而使得解更加平滑。
阻尼最小二乘法是通过同时加入观测数据误差和模型误差的项来解决线性反演问题。
这两种方法都可以通过基于SVD的方法求解。
需要注意的是,对于线性反演问题,只有当观测数据是无误的时候才能得到正确的解。
这是因为线性反演问题的解非常敏感,即使存在微小的误差,也会导致解的失真。
第三章非线性反演问题与线性反演问题不同,非线性反演问题的观测数据与模型参数之间具有非线性关系。
常见的非线性反演问题包括逆时偏移(RTM)、全波形反演(FWI)和电磁成像等。
地球物理反演方法及应用领域分析

地球物理反演方法及应用领域分析一、引言地球物理反演是一种通过观测地球上的物理场,并利用物理定律和数学模型,对地下结构和地球内部特征进行分析的方法。
地球物理反演方法在地质勘探、地震研究、资源勘探等领域具有重要应用价值。
本文将围绕地球物理反演方法展开讨论,并分析其在不同应用领域的具体应用。
二、地球物理反演方法1. 重力反演法:重力反演法是通过测量不同地点的重力场强度,利用物理模型和解析方法,进行地下密度结构的反演。
它在石油勘探、地质构造研究和火山活动监测等领域都有广泛应用。
2. 电磁反演法:电磁反演法通过测量电磁场数据,包括电磁地震、磁力计和电磁感应仪等,来推断地下岩石的电性性质。
电磁反演法在矿产资源勘探、地下水资源评价和环境地球物理研究等领域具有重要作用。
3. 地震反演法:地震反演法是通过地震波在地下传播的速度以及反射和折射现象,推断地下介质的物理特性。
它在地震勘探、地震监测和地震预测等领域发挥着重要作用。
4. 磁法反演法:磁法反演法是通过测量地磁场的强度和方向,推断地下岩石的磁性特征。
它在矿产勘探、石油勘探和矿床研究等领域中得到广泛应用。
三、地球物理反演方法的应用领域1. 地质勘探:地球物理反演方法在地质勘探领域中极为重要。
通过研究地球物理场的各种参数,例如重力场、磁场和电磁场,可以获得地下岩石的构造、性质和分布情况。
这对于石油勘探、矿产资源探测和地质灾害预警具有重要意义。
2. 地震研究:地球物理反演方法在地震研究中起到关键作用。
地震波的传播速度和反射、折射现象可以帮助科学家了解地震震源的位置、深度和强度,进而预测地震活动趋势和地震风险区域。
3. 矿产资源勘探:地球物理反演方法在矿产资源勘探中有广泛应用。
通过测量地下电磁场、地震波速度和重力场等物理参数,可以判断地下矿床的位置、形态和含量。
这对于矿产勘探和矿石储量评估具有重要意义。
4. 环境地球物理研究:地球物理反演方法在环境地球物理研究中也扮演着重要角色。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三篇数值模拟方法和反演引言已知场源分布和地下介质的物性分布,要求计算地表或地下场的分布,这就是地球物理勘探的正演问题,它是地球物理勘探资料解释的基础。
反过来根据所测到的地表或地下场的分布以及场的分布,来推断地下介质的特性分布,就是地球物理勘探中的反演问题,它就是对地球物理勘探资料的解释。
地球物理的正演问题,除了少数简单物性分布可用场论中的经典方法解析求解外,极大部分都需要用数值模拟方法求解。
这些方法包括有限单元法、有限差分法和边界元法。
有限差分法(Finite Difference Method—FDM)是从地球物理场所满足的偏微分方程和边界条件出发,将微分方程转变为差分方程。
其研究步骤是:首先将研究区域按一定方式离散化,例如对二维断面可以将研究范围划分为一系列小的长方形单元,然后在每个单元内假设物性均匀,地球物理位、场呈线性变化,因而微分方程中的微分就可用差分来代替,于是就可以建立一组线性差分方程,最后求解此线性方程组即得到相应的位、场分布。
有限单元法(Finite Element Method—FEM)也是从地球物理场所满足的偏微分方程和边界条件出发,根据微分方程的解与泛函极小问题的等价性,将微分方程和其边界条件转化为相应泛函的变分问题。
其研究步骤仍然是将研究的区域按一定方式划分离散化,例如对二维情况,可以将断面分割成一系列小的长方形单元或三角形单元,同样设单元内位、场呈线性变化,物性参数均匀,这是泛函是各节点位、场的二次函数,利用求极小的必要条件,即泛函对各节点位、场的变分为零,二次函数的变分为一次函数,由此可得到一个线性方程组,解此线性方程组便可求得各节点的位、场值。
有限元法由于可采用三角形网络划分研究区域,所以能比较容易弯曲的物性界面和起伏地形,这是它比有限差分法优越之处。
当然有限差分法也可通过较密的网格剖分来近似地模拟弯曲的物性界面和起伏地形,但这时要增加计算工作量。
边界单元法(Boundary Element Method-BEM)是在有限单元法以后发展起来的一种数值方法。
在边界单元法以前,就有所谓的边界积分方程法,它通过格林公式,将由偏微分方程表示的边值问题,转变成区域边界上的积分方程,然后,将场值集中在边界的若干点上(即用边界单元法中的所谓零次插值),求解积分方程。
有限单元法发展起来以后,其中的单元划分和插值函数的概念,被用来解边界积分方程法,发展成为边界单元法。
可以说,边界单元法是解边界积分方程的有限单元法。
地球物理反演问题求解方法可分为线性反演方法与非线性反演方法两类。
地球物理线性反演方法有最小二乘(最小方差)法、线性规划法、L 范数解以及广义线性反演法等。
非线性反演方法有:梯度法、尝试法、蒙特卡洛法、人工神经网络法、模拟退火法、遗传算法等。
第一章 地球物理模拟的有限差分法有限差分法是近似求解偏微分方程边值问题最常用的方法。
有限差分法解椭圆型偏微分方程的基本思想,是用离散的、只含有限个未知数的差分方程去近似代替连续变量的微分方程及边界条件,并把相应的差分方程的解作为边值问题的数值近似值。
有限差分法将连续问题离散化的步骤是首先对求解区域作网格剖分,用有限个网格节点代替连续区域,用数值微商代替微分,或以数值积分代替积分进行离散,从而把微分方程的定解问题化为线性代数方程组的求解问题。
本章将通过介绍二维均匀直流电场的有限差分法模拟来介绍有限差分法的具体作法。
一、差分方程的导出如图(3-1-1),均匀二维直流电场的边值问题可由下式表示BCnuAD n uAB E n uCD E n uΩz u z x u x ∈=∂∂∈=∂∂∈=∂∂∈-=∂∂∈=⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂ 0 0000σσ ( 3-1-1)图4-1-1 均匀二维电场有限差分模拟区域及网格上式中假设y 轴平行地质体走向,E 0为已知的x 方向上均匀电场强度,故方程中没有y 变量。
u 为待求的电位。
有限差分法求解(3-1-1)式的作法是,首先将给定的二维地电断面离散化,通常采用平行于x轴和平行于z轴的直线划分断面成许多小长方形,每个小长方形称为单元,两平行线组的交点称为节点。
可将x 方向节点编号为i=1,2,…,N ;z 方向节点编号为j=1,2,…,M 。
将研究区域离散以后,由中心差商公式1121---∆-=⎪⎭⎫⎝⎛∂∂i i i i x u u x u ,i i i i x u u x u ∆-=⎪⎭⎫ ⎝⎛∂∂++121(3-1-2)则()⎥⎦⎤⎢⎣⎡∆-+∆-∆+∆=∆+∆⎪⎭⎫⎝⎛∂∂-⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫⎝⎛∂∂+-----+i i i i i i i i i i i i ix u u x u u x x x x x u x u x u 11111212122221(3-1-3)式中各量的意义及其相应位置见图3-1-2。
图4-1-2 计算差分时的网格点位示意图相应于(3-1-1)式左端各项的差分形式为][2)(11111ii i i i i i i i i i x u u x u u x x x u x ∆-+∆-∆+∆=∂∂∂∂+----σσσ ][2)(11111jj j j j j j j j j j z u u z u u z z z u z ∆-+∆-∆+∆=∂∂∂∂+----σσσ 由此可得与(3-1-1)式对应的差分方程为0,1,1,,1,1=+++++-+-j i ijP j i ij B j i ij T j i ij R j i ij L u u u u u c c c c c(3-1-4)式中⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫+++-=∆∆+∆=∆∆+∆=∆∆+∆=∆∆+∆=--------)()(2,)(2)(2,)(21,111,1,11,1c c c c c c c c c ijB ij T ij R ij L ij P j j j j i ij B j j j j i ij T i i i ji ijR i i i ji ijL z z z z z z x x x x x x σσσσ (3-1-5)这里c ij L,c ij R,c ijT,cijB为相邻节点的连接系数,cij P为自身连接系数。
从上式可见,节点(i,j )的电位u i,j 值只与(i-1,j ),(i+1,j ),(i,j-1)和(i,j+1)周围四个节点的u 值有关,其连接系数仅与网格形状大小和位置以及相应的介质导电率σ值有关。
二、边界条件的处理对于边界节点,考虑到各种边界条件,式(3-1-3)可进一步简化。
(1)对于地面节点即j =1行,满足诺依曼条件,即可设空中虚行j =0,j =0行的各节点为j =2行各节点对地面的镜象,设对应的u 值和σ值均相等,故有10z z ∆=∆ 2,0,i i σσ=2,0,i i u u =(3-1-6)(2)对地下边界节点j=M 行,同样满足诺依曼条件,此时可直接令1,,-=M i M i u u(3-1-7)(3)对左面和右面边界,由一阶中心差商(3-1-2)公式,可得1,1,1,2,1 --∆-=-∆=-N j N j N j j x E u u x E u u (3-1-8) 利用上面各式,可以建立每个节点的差分方程,于是可得到线性方程组,其矩阵形式为S CU = (3-1-9)式中C 为连接系数所组成的矩阵,U 为待求的各节点电位值组成的向量,S 为与源有关的右端项向量。
求解线性方程组(3-1-9),可得网格各节点电位值。
第二章 有限元法有限单元法是50年代从弹性力学中发展起来的方法。
主要优点是适用于物性参数复杂分布区域的数值模拟。
它的解题步骤如下:(1)给出地球物理边值问题;(2)将边值问题转化为变分问题;(3)用有限元方法解泛函极值问题;(4)解线性方程组。
下面将通过对于直流线源二维地电问题的有限元数值模拟来介绍有限元方法。
一、直流线源二维地电断面的边值问题设线源方向和地质体走向相同,并与y 轴并行,这样电位仅是x,z 的函数。
若线源位于地面P 点,则可得到电位满足下列微分方程Ω∈-=∇⋅∇ )(2)(p I u δσ(3-2-1)为简单计,假设计算区域Ω很大,从而边界处电位满足如下边界条件:Γ∈=∂∂ 0nu(3-2-2) (3-2-1)(3-2-2)就是直流线源的边值问题。
二、直流线源二维地电断面的变分问题方程(3-2-1)两边同乘以变分u δ后在区域Ω内积分:)(2)(Ω-=Ω∇⋅∇⎰⎰⎰ΩΩud p I ud u δδδσ(3-2-3)由于:)()()(u u u u u u δσδσδσ∇⋅∇+∇⋅∇=∇⋅∇用积分公式,并注意到边界条件(3-2-2)可得Ω∇⋅∇-=Ω∇⋅∇-Γ∂∂=Ω∇⋅∇-Ω∇⋅∇=Ω∇⋅∇⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ΩΩΓΩΩΩd u u d u u d nuu d u u d u u ud u )( )( )( )()(δσδσσδδσδσδσ (3-2-4) 将(3-2-4)代入(3-2-3),并将变分号提出,可得:0])(2[2=Ω-∇⎰⎰Ωd u p I u δσδ也即边值问题(3-2-1)(3-2-2)与下面的变分问题等价⎪⎩⎪⎨⎧=Ω-∇=⎰⎰Ω0)(])(21[)(2u I d u p I u u I δδσ (3-2-5)三、有限元法第1步:区域剖分将积分区域剖分成许多三角单元,总节点数为N (图3-2-1),则(3-2-5)式中对区域Ω的积分可分界为对各三角单元△积分之和。
⎰∑∆ΩΩ-∂∂+∂∂=d u z x I zu x u u I p p })()(2])()[({21)(22δδσ (3-2-6)(a) (b)图3-2-1 区域Ω有限元网格剖分(a )及三角单元(b )示意图第2步:线性插值假设三角单元内电导率为σ,电位u 线性变化,即在每个三角单元△ ∆=++=U N T 332211u N u N u N u(3-2-7)这里,下标1、2和3是三角单元的三角节点号(参见图3-2-1b ); T U ),,(321u u u =∆ 是三角单元节点上的电位;)(21,),(3,21l l l l c z b x a N N N N ++∆==TN 是x 和z 的线性函数),3,2,1(=l 其中⎩⎨⎧=个节点上时)位于三角单元另外二当(上时)位于三角单元节点当(x,z l x,z z x N l 01),( )(1221b a b a -=∆是三角单元的面积。
可以得出:122133113223321123312231213132321,,,,,,z x z x c z x z x c z x z x c x x b x x b x x b z z a z z a z z a -=-=-=-=-=-=-=-=-=式中))(,(2,211z x z x 和)(3,3z x 是三角单元三角节点的x 和z 坐标。
