贝叶斯分类讲解

统计分析实验 Bayes 分类器设计

研究目的：

理解贝叶斯分类器，能够根据自己的设计对贝叶斯决策理论算法有一个深刻地认识，理解二类分类器的设计原理。

实验材料：

假定某个局部区域细胞识别中正常（1ω）和非正常（2ω）两类先验概率分别为

正常状态：P （1ω）=0.9；

异常状态：P （2ω）=0.1。

现有一系列待观察的细胞，其观察值为x ：

-3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531

-2.7605 -3.7287 -3.5414 -2.2692 -3.4549 -3.0752

-3.9934 2.8792 -0.9780 0.7932 1.1882 3.0682

-1.5799 -1.4885 -0.7431 -0.4221 -1.1186 4.2532

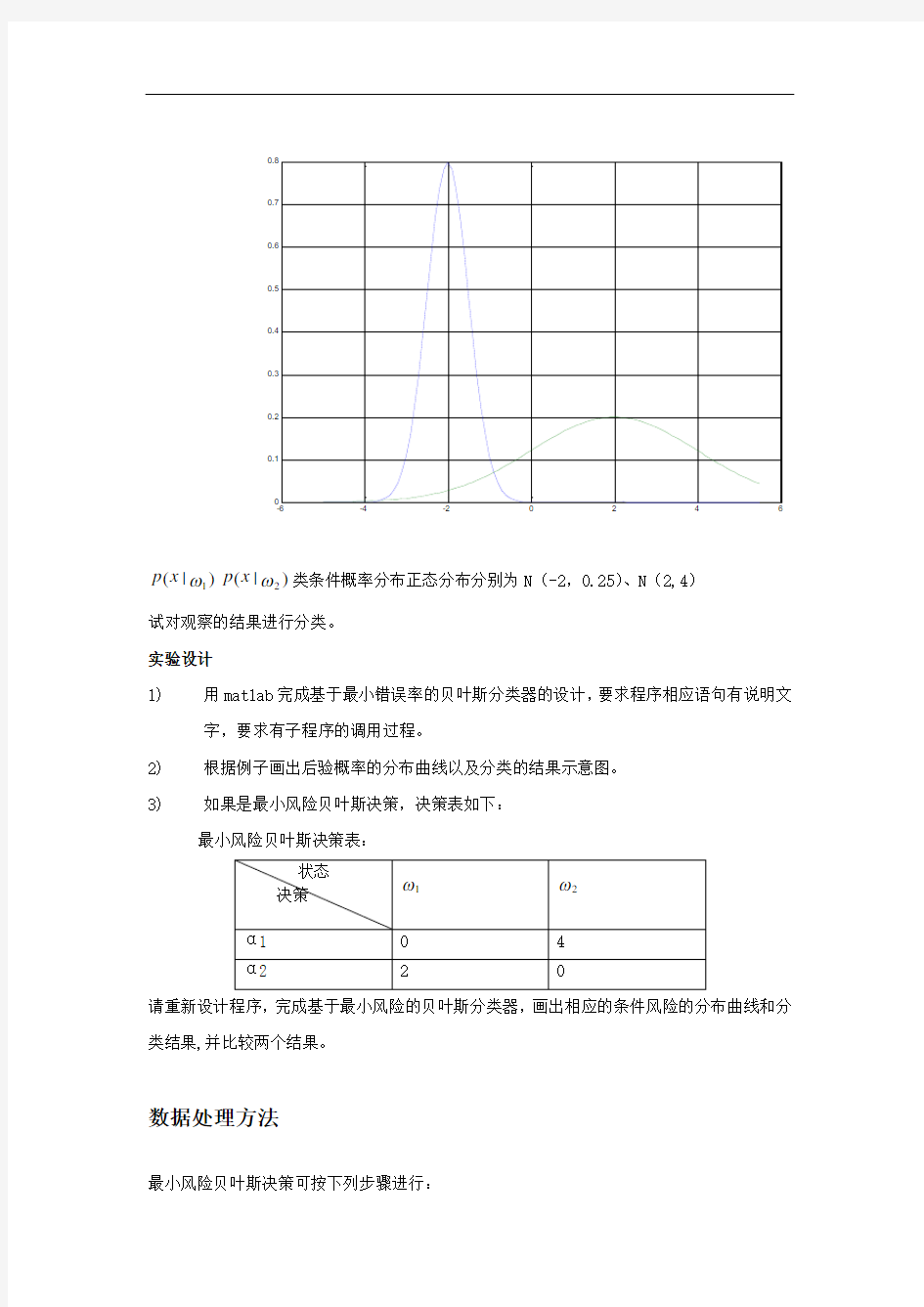
已知类条件概率是的曲线如下图：

)|(1ωx p )|(2ωx p 类条件概率分布正态分布分别为N （-2，0.25）、N （2,4）

试对观察的结果进行分类。

实验设计

1) 用matlab 完成基于最小错误率的贝叶斯分类器的设计，要求程序相应语句有说明文

字，要求有子程序的调用过程。

根据例子画出后验概率的分布曲线以及分类的结果示意图。 3) 如果是最小风险贝叶斯决策，决策表如下：

最小风险贝叶斯决策表：

请重新设计程序，完成基于最小风险的贝叶斯分类器，画出相应的条件风险的分布曲线和分类结果,并比较两个结果。

数据处理方法

最小风险贝叶斯决策可按下列步骤进行：

(1)在已知)(i P ω，)(i X P ω，i=1,…，c 及给出待识别的X 的情况下，根据贝叶斯公式计算出后验概率：

j=1,…，x

(2)利用计算出的后验概率及决策表，按下面的公式计算出采取i a ,i=1,…，a 的条件风险

∑==c j j j i

i X P a X a R 1)(),()(ωωλ,i=1,2,…,a

(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…，a 进行比较，找出使其条件风险最小的决策k a ，即

（1） ()()

1,min k i i a R a x R a x == （2）则k a 就是最小风险贝叶斯决策。

◆ 最小错误率贝叶斯决策

? 分类器设计

x=[-3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531 -2.7605 -3.7287

-3.5414 -2.2692 -3.4549 -3.0752 -3.9934 2.8792 -0.9780 0.7932

1.1882 3.0682 -1.5799 -1.4885 -0.7431 -0.4221 -1.1186 4.2532 ] pw1=0.9 ; pw2=0.1

e1=-2; a1=0.5

e2=2;a2=2

m=numel(x) %得到待测细胞个数

pw1_x=zeros(1,m) %存放对w1的后验概率矩阵

pw2_x=zeros(1,m) %存放对w2的后验概率矩阵

results=zeros(1,m) %存放比较结果矩阵

for i = 1:m

%计算在w1下的后验概率

pw1_x(i)=(pw1*normpdf(x(i),e1,a1))/(pw1*normpdf(x(i),e1,a1)+pw2*normpdf(x(i),e2,a2))

%计算在w2下的后验概率

pw2_x(i)=(pw2*normpdf(x(i),e2,a2))/(pw1*normpdf(x(i),e1,a1)+pw2*normpdf(x(i),e2,a2))

end

for i = 1:m

∑==c j i

i i i i P X P P X P X P 1)()()

()()(ωωωωω

if pw1_x(i)>pw2_x(i) %比较两类后验概率

result(i)=0 %正常细胞

else

result(i)=1 %异常细胞

end

a=[-5:0.05:5] %取样本点以画图

n=numel(a)

pw1_plot=zeros(1,n)

pw2_plot=zeros(1,n)

for j=1:n

pw1_plot(j)=(pw1*normpdf(a(j),e1,a1))/(pw1*normpdf(a(j),e1,a1)+pw2*normpdf(a(j),e2,a2))

%计算每个样本点对w1的后验概率以画图

pw2_plot(j)=(pw2*normpdf(a(j),e2,a2))/(pw1*normpdf(a(j),e1,a1)+pw2*normpdf(a(j),e2,a2))

end

figure(1)

hold on

plot(a,pw1_plot,'k-',a,pw2_plot,'r-.')

for k=1:m

if result(k)==0

plot(x(k),-0.1,'b*') %正常细胞用*表示

else

plot(x(k),-0.1,'rp') %异常细胞用五角星表示

end;

legend('正常细胞后验概率曲线','异常细胞后验概率曲线','正常细胞','异常细胞')

xlabel('样本细胞的观察值')

ylabel('后验概率')

title('后验概率分布曲线')

grid on

return ;

?实验内容仿真

x = [-3.9847 , -3.5549 , -1.2401 , -0.9780 , -0.7932 , -2.8531 ,-2.7605 , -3.7287 , -3.5414 , -2.2692 , -3.4549 , -3.0752 , -3.9934 , 2.8792 , -

0.9780 , 0.7932 , 1.1882 , 3.0682, -1.5799 , -1.4885 , -0.7431 , -0.4221 , -1.1186 , 4.2532 ]

disp(x)

pw1=0.9

pw2=0.1

[result]=bayes(x,pw1,pw2)

◆最小风险贝叶斯决策

分类器设计

function [R1_x,R2_x,result]=danger(x,pw1,pw2)

m=numel(x) %得到待测细胞个数

R1_x=zeros(1,m) %存放把样本X判为正常细胞所造成的整体损失

R2_x=zeros(1,m) %存放把样本X判为异常细胞所造成的整体损失

result=zeros(1,m) %存放比较结果

e1=-2

a1=0.5

e2=2

a2=2

%类条件概率分布px_w1:（-2，0.25） px_w2（2,4）

r11=0

r12=2

r21=4

r22=0

%风险决策表

for i=1:m %计算两类风险值

R1_x(i)=r11*pw1*normpdf(x(i),e1,a1)/(pw1*normpdf(x(i),e1,a1)+pw2*normpdf(x(i),e 2,a2))+r21*pw2*normpdf(x(i),e2,a2)/(pw1*normpdf(x(i),e1,a1)+pw2*normpdf(x(i),e2 ,a2))

R2_x(i)=r12*pw1*normpdf(x(i),e1,a1)/(pw1*normpdf(x(i),e1,a1)+pw2*normpdf(x(i),e 2,a2))+r22*pw2*normpdf(x(i),e2,a2)/(pw1*normpdf(x(i),e1,a1)+pw2*normpdf(x(i),e2 ,a2))

end

for i=1:m

if R2_x(i)>R1_x(i)%第二类比第一类风险大

result(i)=0 %判为正常细胞（损失较小），用0表示

else

result(i)=1 %判为异常细胞，用1表示

end

a=[-5:0.05:5] %取样本点以画图

n=numel(a)

R1_plot=zeros(1,n)

R2_plot=zeros(1,n)

for j=1:n

R1_plot(j)=r11*pw1*normpdf(a(j),e1,a1)/(pw1*normpdf(a(j),e1,a1)+pw2*normpdf(a(j ),e2,a2))+r21*pw2*normpdf(a(j),e2,a2)/(pw1*normpdf(a(j),e1,a1)+pw2*normpdf(a(j) ,e2,a2))

R2_plot(j)=r12*pw1*normpdf(a(j),e1,a1)/(pw1*normpdf(a(j),e1,a1)+pw2*normpdf(a(j ),e2,a2))+r22*pw2*normpdf(a(j),e2,a2)/(pw1*normpdf(a(j),e1,a1)+pw2*normpdf(a(j) ,e2,a2))

%计算各样本点的风险以画图

end

figure(1)

hold on

plot(a,R1_plot,'b-',a,R2_plot,'g*-')

for k=1:m

if result(k)==0

plot(x(k),-0.1,'b^')%正常细胞用上三角表示

else

plot(x(k),-0.1,'go')%异常细胞用圆表示

end;

legend('正常细胞','异常细胞','Location','Best')

xlabel('细胞分类结果')

ylabel('条件风险')

title('风险判决曲线')

grid on

return

?实验内容仿真

x = [-3.9847 , -3.5549 , -1.2401 , -0.9780 , -0.7932 , -2.8531 ,-2.7605 , -3.7287 , -3.5414 , -2.2692 , -3.4549 , -3.0752 , -3.9934 , 2.8792 , -0.9780 , 0.7932 , 1.1882 , 3.0682, -1.5799 , -1.4885 , -0.7431 , -0.4221 , -1.1186 , 4.2532 ]

disp(x)

pw1=0.9

pw2=0.1

[R1_x,R2_x,result]=danger(x,pw1,pw2)

结果：

◆最小错误率贝叶斯决策

后验概率曲线与判决结果在一张图上：后验概率曲线如图所示，带*的绿色曲线为判决成异常细胞的后验概率曲线；另一条平滑的蓝色曲线为判为正常细胞的后验概率曲线。根据最小错误概率准则，判决结果见曲线下方，其中“上三角”代表判决为正常细胞，“圆圈”

代表异常细胞。

各细胞分类结果：

0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 1 0 0 0 1 0 1 0为判成正常细胞，1为判成异常细胞

图1 基于最小错误率的贝叶斯判决

最小风险贝叶斯决策

风险判决曲线如图2所示，其中带*的绿色曲线代表异常细胞的条件风险曲线；另一条光滑的蓝色曲线为判为正常细胞的条件风险曲线。根据贝叶斯最小风险判决准则，判决结果见曲线下方，其中“上三角”代表判决为正常细胞，“圆圈“代表异常细胞。

各细胞分类结果：

1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 0 0 0 1 0 1 其中，0为判成正常细胞，1为判成异常细胞

-5-4-3-2-1

012345

细胞的观察值后验概率后验概率分布曲线

朴素贝叶斯分类算法及其MapReduce实现

最近发现很多公司招聘数据挖掘的职位都提到贝叶斯分类，其实我不太清楚他们是要求理解贝叶斯分类算法，还是要求只需要通过工具（SPSS，SAS，Mahout）使用贝叶斯分类算法进行分类。反正不管是需求什么都最好是了解其原理，才能知其然，还知其所以然。我尽量简单的描述贝叶斯定义和分类算法，复杂而有全面的描述参考“数据挖掘：概念与技术”。贝叶斯是一个人，叫（Thomas Bayes），下面这哥们就是。本文介绍了贝叶斯定理，朴素贝叶斯分类算法及其使用MapReduce实现。贝叶斯定理首先了解下贝叶斯定理 P X H P(H) P H X= 是不是有感觉都是符号看起来真复杂，我们根据下图理解贝叶斯定理。这里D是所有顾客（全集），H是购买H商品的顾客，X是购买X商品的顾客。自然X∩H是即购买X又购买H的顾客。 P(X) 指先验概率，指所有顾客中购买X的概率。同理P(H)指的是所有顾客中购买H 的概率，见下式。

X P X= H P H= P(H|X) 指后验概率，在购买X商品的顾客，购买H的概率。同理P(X|H)指的是购买H商品的顾客购买X的概率，见下式。 X∩H P H|X= X∩H P X|H= 将这些公式带入上面贝叶斯定理自然就成立了。朴素贝叶斯分类分类算法有很多，基本上决策树，贝叶斯分类和神经网络是齐名的。朴素贝叶斯分类假定一个属性值对给定分类的影响独立于其他属性值。描述：这里有个例子假定我们有一个顾客X（age = middle，income=high，sex =man）：?年龄（age）取值可以是：小（young），中（middle），大（old） ?收入（income）取值可以是：低（low），中（average），高（high） ?性别（sex）取值可以是：男（man），女（woman）其选择电脑颜色的分类标号H：白色（white），蓝色（blue），粉色（pink）问题：用朴素贝叶斯分类法预测顾客X，选择哪个颜色的分类标号，也就是预测X属于具有最高后验概率的分类。解答： Step 1 也就是说我们要分别计算X选择分类标号为白色（white），蓝色（blue），粉色（pink）的后验概率，然后进行比较取其中最大值。根据贝叶斯定理

贝叶斯分类器的matlab实现

贝叶斯分类器的matlab实现贝叶斯分类原理： 1)在已知P(Wi)，P(X|Wi)(i=1,2)及给出待识别的X的情况下，根据贝叶斯公式计算出后验概率P(Wi|X) ; 2)根据1)中计算的后验概率值，找到最大的后验概率，则样本X属于该类举例：解决方案：但对于两类来说，因为分母相同，所以可采取如下分类标准：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%% %By Shelley from NCUT，April 14th 2011 %Email:just_for_h264@https://www.360docs.net/doc/f316339671.html, %此程序利用贝叶斯分类算法，首先对两类样本进行训练， %进而可在屏幕上任意取点，程序可输出属于第一类，还是第二类%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%% clear; close all %读入两类训练样本数据 load data %求两类训练样本的均值和方差 u1=mean(Sample1); u2=mean(Sample2); sigm1=cov(Sample1); sigm2=cov(Sample2); %计算两个样本的密度函数并显示 x=-20:0.5:40; y= -20:0.5:20; [X,Y] = meshgrid(x,y); F1 = mvnpdf([X(:),Y(:)],u1,sigm1); F2 = mvnpdf([X(:),Y(:)],u2,sigm2); P1=reshape(F1,size(X)); P2=reshape(F2,size(X)); figure(2) surf(X,Y,P1) hold on surf(X,Y,P2) shading interp colorbar title('条件概率密度函数曲线'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% %以下为测试部分 %利用ginput随机选取屏幕上的点（可连续取10个点）

大数据挖掘(8)：朴素贝叶斯分类算法原理与实践

数据挖掘（8）：朴素贝叶斯分类算法原理与实践隔了很久没有写数据挖掘系列的文章了，今天介绍一下朴素贝叶斯分类算法，讲一下基本原理，再以文本分类实践。一个简单的例子朴素贝叶斯算法是一个典型的统计学习方法，主要理论基础就是一个贝叶斯公式，贝叶斯公式的基本定义如下：这个公式虽然看上去简单，但它却能总结历史，预知未来。公式的右边是总结历史，公式的左边是预知未来，如果把Y看出类别，X看出特征，P(Yk|X)就是在已知特征X的情况下求Yk类别的概率，而对P(Yk|X)的计算又全部转化到类别Yk的特征分布上来。举个例子，大学的时候，某男生经常去图书室晚自习，发现他喜欢的那个女生也常去那个自习室，心中窃喜，于是每天买点好吃点在那个自习室蹲点等她来，可是人家女生不一定每天都来，眼看天气渐渐炎热，图书馆又不开空调，如果那个女生没有去自修室，该男生也就不去，每次男生鼓足勇气说：“嘿，你明天还来不？”,“啊，不知道，看情况”。然后该男生每天就把她去自习室与否以及一些其他情况做一下记录，用Y表示该女生是否去自习室，即Y={去，不去}，X是跟去自修室有关联的一系列条件，比如当天上了哪门主课，蹲点统计了一段时间后，该男生打算今天不再蹲点，而是先预测一下她会不会去，现在已经知道了今天上了常微分方法这么主课，于是计算P(Y=去|常微分方

程)与P(Y=不去|常微分方程)，看哪个概率大，如果P(Y=去|常微分方程) >P(Y=不去|常微分方程)，那这个男生不管多热都屁颠屁颠去自习室了，否则不就去自习室受罪了。P(Y=去|常微分方程)的计算可以转为计算以前她去的情况下，那天主课是常微分的概率P(常微分方程|Y=去)，注意公式右边的分母对每个类别（去/不去）都是一样的，所以计算的时候忽略掉分母，这样虽然得到的概率值已经不再是0~1之间，但是其大小还是能选择类别。后来他发现还有一些其他条件可以挖，比如当天星期几、当天的天气，以及上一次与她在自修室的气氛，统计了一段时间后，该男子一计算，发现不好算了，因为总结历史的公式：这里n=3，x(1)表示主课，x(2)表示天气，x(3)表示星期几，x(4)表示气氛，Y仍然是{去，不去}，现在主课有8门，天气有晴、雨、阴三种、气氛有A+,A,B+,B，C五种，那么总共需要估计的参数有8*3*7*5*2=1680个，每天只能收集到一条数据，那么等凑齐1 680条数据大学都毕业了，男生打呼不妙，于是做了一个独立性假设，假设这些影响她去自习室的原因是独立互不相关的，于是有了这个独立假设后，需要估计的参数就变为，(8+3+7+5)*2 = 46个了，而且每天收集的一条数据，可以提供4个参数，这样该男生就预测越来越准了。

Bayes分类器原理

贝叶斯分类器一、朴素贝叶斯分类器原理目标：计算(|)j P C t 。注：t 是一个多维的文本向量分析：由于数据t 是一个新的数据，(|)j P C t 无法在训练数据集中统计出来。因此需要转换。根据概率论中的贝叶斯定理 (|)()(|)() P B A P A P A B P B = 将(|)j P C t 的计算转换为： (|)() (|)()j j j P t C P C P C t P t = （1）其中，()j P C 表示类C j 在整个数据空间中的出现概率，可以在训练集中统计出来（即用C j 在训练数据集中出现的频率()j F C 来作为概率()j P C 。但(|)j P t C 和()P t 仍然不能统计出来。首先，对于(|)j P t C ，它表示在类j C 中出现数据t 的概率。根据“属性独立性假设”，即对于属于类j C 的所有数据，它们个各属性出现某个值的概率是相互独立的。如，判断一个干部是否是“好干部”（分类）时，其属性“生活作风＝好”的概率（P(生活作风＝好|好干部)）与“工作态度＝好”的概率（P(工作态度＝好|好干部)）是独立的，没有潜在的相互关联。换句话说，一个好干部，其生活作风的好坏与其工作态度的好坏完全无关。我们知道这并不能反映真实的情况，因而说是一种“假设”。使用该假设来分类的方法称为“朴素贝叶斯分类”。根据上述假设，类j C 中出现数据t 的概率等于其中出现t 中各属性值的概率的乘积。即： (|)(|)j k j k P t C P t C =∏ （2）其中，k t 是数据t 的第k 个属性值。

贝叶斯分类作业题

作业：在下列条件下，求待定样本x=(2,0)T的类别，画出分界线，编程上机。 1、二类协方差不等 Matlab程序如下： >> x1=[mean([1,1,2]),mean([1,0,-1])]',x2=[mean([-1,-1,-2]),mean([1,0,-1])]' x1 = 1.3333 x2 = -1.3333 >> m=cov([1,1;1,0;2,-1]),n=cov([-1,1;-1,0;-2,-1]) m = 0.3333 -0.5000 -0.5000 1.0000 n = 0.3333 0.5000 0.5000 1.0000 >> m1=inv(m),n1=inv(n) m1 = 12.0000 6.0000 6.0000 4.0000

n1 = 12.0000 -6.0000 -6.0000 4.0000 >> p=log((det(m))/(det(n))) p = >> q=log(1) q = >> x=[2,0]' x = 2 >> g=0.5*(x-x1)'*m1*(x-x1)-0.5*(x-x2)'*n1*(x-x2)+0.5*p-q g = -64 （说明：g<0,则判定x=[2,0]T属于ω1类）（化简矩阵多项式0.5*(x-x1)'*m1*(x-x1)-0.5*(x-x2)'*n1*(x-x2)+0.5*p-q，其中x1,x2已知，x 设为x=[ x1,x2]T,化简到(12x1-16+6x2）(x1-4/3)+(6x1-8+4x2) -(12x1+16-6x2)(x1+4/3)-(-6x1-8+4x2)x2，下面用matlab化简，程序如下） >> syms x2; >> syms x1; >> w=(12*x1-16+6*x2)*(x1-4/3)+(6*x1-8+4*x2)*x2-(12*x1+16-6*x2)*(x1+4/3)-(-6*x1-8+4*x2)*x 2,simplify(w) w =

贝叶斯分类多实例分析总结

用于运动识别的聚类特征融合方法和装置提供了一种用于运动识别的聚类特征融合方法和装置，所述方法包括：将从被采集者的加速度信号中提取的时频域特征集的子集内的时频域特征表示成以聚类中心为基向量的线性方程组；通过求解线性方程组来确定每组聚类中心基向量的系数；使用聚类中心基向量的系数计算聚类中心基向量对子集的方差贡献率；基于方差贡献率计算子集的聚类中心的融合权重；以及基于融合权重来获得融合后的时频域特征集。加速度信号 →时频域特征 →以聚类中心为基向量的线性方程组 →基向量的系数 →方差贡献率 →融合权重基于特征组合的步态行为识别方法本发明公开了一种基于特征组合的步态行为识别方法，包括以下步骤：通过加速度传感器获取用户在行为状态下身体的运动加速度信息；从上述运动加速度信息中计算各轴的峰值、频率、步态周期和四分位差及不同轴之间的互相关系数；采用聚合法选取参数组成特征向量；以样本集和步态加速度信号的特征向量作为训练集，对分类器进行训练，使的分类器具有分类步态行为的能力；将待识别的步态加速度信号的所有特征向量输入到训练后的分类器中，并分别赋予所属类别，统计所有特征向量的所属类别，并将出现次数最多的类别赋予待识别的步态加速度信号。实现简化计算过程，降低特征向量的维数并具有良好的有效性的目的。传感器 →样本及和步态加速度信号的特征向量作为训练集 →分类器具有分类步态行为的能力基于贝叶斯网络的核心网故障诊断方法及系统本发明公开了一种基于贝叶斯网络的核心网故障诊断方法及系统，该方法从核心网的故障受理中心采集包含有告警信息和故障类型的原始数据并生成样本数据，之后存储到后备训练数据集中进行积累，达到设定的阈值后放入训练数据集中；运用贝叶斯网络算法对训练数据集中的样本数据进行计算，构造贝叶斯网络分类器；从核心网的网络管理系统采集含有告警信息的原始数据，经贝叶斯网络分类器计算获得告警信息对应的故障类型。本发明，利用贝叶斯网络分类器构建故障诊断系统，实现了对错综复杂的核心网故障进行智能化的系统诊断功能，提高了诊断的准确性和灵活性，并且该系统构建于网络管理系统之上，易于实施，对核心网综合信息处理具有广泛的适应性。告警信息和故障类型 →训练集 —>贝叶斯网络分类器

五种贝叶斯网分类器的分析与比较

五种贝叶斯网分类器的分析与比较摘要：对五种典型的贝叶斯网分类器进行了分析与比较。在总结各种分类器的基础上，对它们进行了实验比较，讨论了各自的特点，提出了一种针对不同应用对象挑选贝叶斯网分类器的方法。关键词：贝叶斯网；分类器；数据挖掘；机器学习故障诊断、模式识别、预测、文本分类、文本过滤等许多工作均可看作是分类问题，即对一给定的对象（这一对象往往可由一组特征描述），识别其所属的类别。完成这种分类工作的系统，称之为分类器。如何从已分类的样本数据中学习构造出一个合适的分类器是机器学习、数据挖掘研究中的一个重要课题，研究得较多的分类器有基于决策树和基于人工神经元网络等方法。贝叶斯网（Ｂａｙｅｓｉａｎｎｅｔｗｏｒｋｓ，ＢＮｓ）在ＡＩ应用中一直作为一种不确定知识表达和推理的工具，从九十年代开始也作为一种分类器得到研究。本文先简单介绍了贝叶斯网的基本概念，然后对五种典型的贝叶斯网分类器进行了总结分析，并进行了实验比较，讨论了它们的特点，并提出了一种针对不同应用对象挑选贝叶斯分类器的方法。１贝叶斯网和贝叶斯网分类器贝叶斯网是一种表达了概率分布的有向无环图，在该图中的每一节点表示一随机变量，图中两节点间若存在着一条弧，则表示这两节点相对应的随机变量是概率相依的，两节点间若没有弧，则说明这两个随机变量是相对独立的。按照贝叶斯网的这种结构，显然网中的任一节点ｘ均和非ｘ的父节点的后裔节点的各节点相对独立。网中任一节点Ｘ均有一相应的条件概率表（ＣｏｎｄｉｔｉｏｎａｌＰｒｏｂａｂｉｌｉｔｙＴａｂｌｅ，ＣＰＴ），用以表示节点ｘ在其父节点取各可能值时的条件概率。若节点ｘ无父节点，则ｘ的ＣＰＴ为其先验概率分布。贝叶斯网的结构及各节点的ＣＰＴ定义了网中各变量的概率分布。贝叶斯网分类器即是用于分类工作的贝叶斯网。该网中应包含一表示分类的节点Ｃ，变量Ｃ的取值来自于类别集合｛Ｃ，Ｃ，．．．．，Ｃ｝。另外还有一组节点ｘ＝（ｘ，ｘ，．．．．，ｘ）反映用于分类的特征，一个贝叶斯网分类器的结构可如图１所示。对于这样的一贝叶斯网分类器，若某一待分类的样本Ｄ，其分类特征值为ｘ＝（ｘ，ｘ，．．．．，ｘ），则样本Ｄ属于类别Ｃ的概率为Ｐ（Ｃ＝Ｃ｜Ｘ＝ｘ），因而样本Ｄ属于类别Ｃ的条件是满足（１）式：Ｐ（Ｃ＝Ｃ｜Ｘ＝ｘ）＝Ｍａｘ｛Ｐ（Ｃ＝Ｃ｜Ｘ＝ｘ），Ｐ（Ｃ＝Ｃ｜Ｘ＝ｘ），．．．，Ｐ（Ｃ＝Ｃ｜Ｘ＝ｘ）｝（１）而由贝叶斯公式Ｐ（Ｃ＝Ｃ｜Ｘ＝ｘ）＝（２）其中Ｐ（Ｃ＝Ｃｋ）可由领域专家的经验得到，而Ｐ（Ｘ＝ｘ｜Ｃ＝Ｃｋ）和Ｐ（Ｘ＝ｘ）的计算则较困难。应用贝叶斯网分类器分成两阶段。一是贝叶斯网分类器的学习（训练），即从样本数据中构造分类器，包括结构（特征间的依赖关系）学习和ＣＰＴ表的学习。二是贝叶斯网分类器的推理，即计算类结点的条件概率，对待分类数据进行分类。这两者的时间复杂性均取决于特征间的依赖程度，甚至可以是ＮＰ完全问题。因而在实际应用中，往往需

贝叶斯分类实验报告doc

贝叶斯分类实验报告篇一：贝叶斯分类实验报告实验报告实验课程名称数据挖掘实验项目名称贝叶斯分类年级 XX级专业信息与计算科学学生姓名学号 1207010220 理学院实验时间： XX 年 12 月 2 日学生实验室守则一、按教学安排准时到实验室上实验课，不得迟到、早退和旷课。二、进入实验室必须遵守实验室的各项规章制度，保持室内安静、整洁，不准在室内打闹、喧哗、吸烟、吃食物、随地吐痰、乱扔杂物，不准做与实验内容无关的事，非实验用品一律不准带进实验室。三、实验前必须做好预习（或按要求写好预习报告），未做预习者不准参加实验。四、实验必须服从教师的安排和指导，认真按规程操作，未经教师允许不得擅自动用仪器设备，特别是与本实验无关的仪器设备和设施，如擅自动用

或违反操作规程造成损坏，应按规定赔偿，严重者给予纪律处分。五、实验中要节约水、电、气及其它消耗材料。六、细心观察、如实记录实验现象和结果，不得抄袭或随意更改原始记录和数据，不得擅离操作岗位和干扰他人实验。七、使用易燃、易爆、腐蚀性、有毒有害物品或接触带电设备进行实验，应特别注意规范操作，注意防护；若发生意外，要保持冷静，并及时向指导教师和管理人员报告，不得自行处理。仪器设备发生故障和损坏，应立即停止实验，并主动向指导教师报告，不得自行拆卸查看和拼装。八、实验完毕，应清理好实验仪器设备并放回原位，清扫好实验现场，经指导教师检查认可并将实验记录交指导教师检查签字后方可离去。九、无故不参加实验者，应写出检查，提出申请并缴纳相应的实验费及材料消耗费，经批准后，方可补做。十、自选实验，应事先预约，拟订出实验方案，经实验室主任同意后，在指导教师或实验技术人员的指导下进行。十一、实验室内一切物品未经允许严禁带出室外，确需带出，必须经过批准并办理手续。学生所在学院：理学院专业：信息与计算科学班级：信计121

贝叶斯分类算法

最近在面试中，除了基础& 算法& 项目之外，经常被问到或被要求介绍和描述下自己所知道的几种分类或聚类算法，而我向来恨对一个东西只知其皮毛而不得深入，故写一个有关聚类& 分类算法的系列文章以作为自己备试之用(尽管貌似已无多大必要，但还是觉得应该写下以备将来常常回顾思考)。行文杂乱，但侥幸若能对读者也起到一定帮助，则幸甚至哉。本分类& 聚类算法系列借鉴和参考了两本书，一本是Tom M.Mitchhell所著的机器学习，一本是数据挖掘导论，这两本书皆分别是机器学习& 数据挖掘领域的开山or杠鼎之作，读者有继续深入下去的兴趣的话，不妨在阅读本文之后，课后细细研读这两本书。除此之外，还参考了网上不少牛人的作品(文末已注明参考文献或链接)，在此，皆一一表示感谢。本分类& 聚类算法系列暂称之为Top 10 Algorithms in Data Mining，其中，各篇分别有以下具体内容： 1. 开篇：决策树学习Decision Tree，与贝叶斯分类算法(含隐马可夫模型HMM)； 2. 第二篇：支持向量机SVM(support vector machine)，与神经网络ANN； 3. 第三篇：待定... 说白了，一年多以前，我在本blog内写过一篇文章，叫做：数据挖掘领域十大经典算法初探(题外话：最初有个出版社的朋友便是因此文找到的我，尽管现在看来，我离出书日期仍是遥遥无期)。现在，我抽取其中几个最值得一写的几个算法每一个都写一遍，以期对其有个大致通透的了解。 OK，全系列任何一篇文章若有任何错误，漏洞，或不妥之处，还请读者们一定要随时不吝赐教& 指正，谢谢各位。基础储备：分类与聚类在讲具体的分类和聚类算法之前，有必要讲一下什么是分类，什么是聚类，都包含哪些具体算法或问题。常见的分类与聚类算法简单来说，自然语言处理中，我们经常提到的文本分类便就是一个分类问题，一般的模式分类方法都可用于文本分类研究。常用的分类算法包括：朴素的贝叶斯分类算法(native Bayesian classifier)、基于支持向量机(SVM)的分类器，k-最近邻法(k-nearest neighbor，

贝叶斯分类器工作原理

贝叶斯分类器工作原理原理贝叶斯分类器是一种比较有潜力的数据挖掘工具，它本质上是一种分类手段，但是它的优势不仅仅在于高分类准确率，更重要的是，它会通过训练集学习一个因果关系图（有向无环图）。如在医学领域，贝叶斯分类器可以辅助医生判断病情，并给出各症状影响关系，这样医生就可以有重点的分析病情给出更全面的诊断。进一步来说，在面对未知问题的情况下，可以从该因果关系图入手分析，而贝叶斯分类器此时充当的是一种辅助分析问题领域的工具。如果我们能够提出一种准确率很高的分类模型，那么无论是辅助诊疗还是辅助分析的作用都会非常大甚至起主导作用，可见贝叶斯分类器的研究是非常有意义的。与五花八门的贝叶斯分类器构造方法相比，其工作原理就相对简单很多。我们甚至可以把它归结为一个如下所示的公式：其中实例用T{X0，X1，…，Xn-1}表示，类别用C 表示，AXi 表示Xi 的父节点集合。选取其中后验概率最大的c ，即分类结果，可用如下公式表示 () ()()() ()( ) 0011111 00011111 0|,, ,|,,, ,C c |,i i n n n i i X i n n n i i X i P C c X x X x X x P C c P X x A C c P X x X x X x P P X x A C c ---=---========= ===∝===∏∏()() 1 0arg max |A ,i n c C i i X i c P C c P X x C c -∈=====∏

上述公式本质上是由两部分构成的：贝叶斯分类模型和贝叶斯公式。下面介绍贝叶斯分类器工作流程： 1．学习训练集，存储计算条件概率所需的属性组合个数。 2．使用1中存储的数据，计算构造模型所需的互信息和条件互信息。 3．使用2种计算的互信息和条件互信息，按照定义的构造规则，逐步构建出贝叶斯分类模型。 4．传入测试实例 5．根据贝叶斯分类模型的结构和贝叶斯公式计算后验概率分布。6．选取其中后验概率最大的类c，即预测结果。其流程图如下所示：

作业1-贝叶斯分类器

作业1、BAYES分类器算法1. %绘图，从多个视角观察上述3维2类训练样本 clear all; close all; N1=440; x1(1,:)=-1.7+0.9*randn(1,N1); % 1 类440 个训练样本,3 维正态分布 x1(2,:)= 1.6+0.7*randn(1,N1); x1(3,:)=-1.5+0.8*randn(1,N1); N2=400; x2(1,:)= 1.3+1.2*randn(1,N2); % 2 类400 个训练样本,3 维正态分布 x2(2,:)=-1.5+1.3*randn(1,N2); x2(3,:)= 1.4+1.1*randn(1,N2); plot3(x1(1,:),x1(2,:),x1(3,:),'*',x2(1,:),x2(2,:),x2(3,:),'o'); grid on; axis equal; axis([-5 5 -5 5 -5 5]); xlabel('x ');ylabel('y ');zlabel('z '); %假定2类的类条件概率分布皆为正态分布，分别估计2类的先验概率、均值向量、协方差矩阵 p1=N1/(N1+N2); % 1 类的先验概率 p2=N2/(N1+N2); % 2 类的先验概率 u1=sum(x1')/N1; % 1 类均值估计 u1=u1' for i=1:N1 xu1(:,i)=x1(:,i)-u1;end; e1=(xu1*xu1')/(N1-1) % 1 类协方差矩阵估计 u2=sum(x2')/N2; % 2 类均值估计 u2=u2' for i=1:N2 xu2(:,i)=x2(:,i)-u2;end; e2=(xu2*xu2')/(N2-1) % 2 类协方差矩阵估计 %求解2类的BAYES分类器的决策（曲）面，并绘图、从多个视角观察决策面 %bayse 概率概率分布函数 w10=-(1/2)*u1'*(inv(e1))*u1-0.5*log(det(e1))+log(0.52); w20=-(1/2)*u2'*(inv(e2))*u2-0.5*log(det(e2))+log(0.48); W1=-(0.5)*inv(e1); W2=-(0.5)*inv(e2); w1=inv(e1)*u1; w2=inv(e2)*u2; temp=-5:0.1:5; [x1,y1,z1]=meshgrid(temp,temp,temp); val=zeros(size(x1)); for k=1:(size(x1,1)^3) X=[x1(k),y1(k),z1(k)]';

iris数据集的贝叶斯分类

IRIS 数据集的Bayes 分类实验一、实验原理 1) 概述模式识别中的分类问题是根据对象特征的观察值将对象分到某个类别中去。统计决策理论是处理模式分类问题的基本理论之一，它对模式分析和分类器的设计有着实际的指导意义。贝叶斯（Bayes ）决策理论方法是统计模式识别的一个基本方法，用这个方法进行分类时需要具备以下条件：各类别总体的分布情况是已知的。要决策分类的类别数是一定的。其基本思想是：以Bayes 公式为基础，利用测量到的对象特征配合必要的先验信息，求出各种可能决策情况（分类情况）的后验概率，选取后验概率最大的,或者决策风险最小的决策方式(分类方式)作为决策（分类）的结果。也就是说选取最有可能使得对象具有现在所测得特性的那种假设，作为判别的结果。常用的Bayes 判别决策准则有最大后验概率准则（MAP ），极大似然比准则（ML ），最小风险Bayes 准则，Neyman-Pearson 准则（N-P ）等。 2) 分类器的设计对于一个一般的c 类分类问题，其分类空间： {}c w w w ,,,21 =Ω 表特性的向量为： ()T d x x x x ,,,21 = 其判别函数有以下几种等价形式： a) ()()i j i w w i j c j w w x w P x w P ∈→≠=∈→>，且，,,2,11 ， b) ()()() ()i j j i w w i j c j w P w x p w P w x p ∈→≠=>，且，,,2,1i c) ()() () ()()i i j j i w w i j c j w P w P w x p w x p x l ∈→≠=>=，且，,,2,1 d) ()()() ()i j j i i w w i j c j w P w x np w P w x p ∈→≠=+>+，且，,,2,1ln ln ln 3) IRIS 数据分类实验的设计

模式识别大作业

作业1 用身高和/或体重数据进行性别分类（一）基本要求：用FAMALE.TXT和MALE.TXT的数据作为训练样本集，建立Bayes分类器，用测试样本数据对该分类器进行测试。调整特征、分类器等方面的一些因素，考察它们对分类器性能的影响，从而加深对所学内容的理解和感性认识。具体做法： 1．应用单个特征进行实验：以（a）身高或者（b）体重数据作为特征，在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数，建立最小错误率Bayes分类器，写出得到的决策规则，将该分类器应用到测试样本，考察测试错误情况。在分类器设计时可以考察采用不同先验概率（如0.5对0.5, 0.75对0.25, 0.9对0.1等）进行实验，考察对决策规则和错误率的影响。图1-先验概率0.5:0.5分布曲线图2-先验概率0.75:0.25分布曲线图3--先验概率0.9:0.1分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。程序：bayesflq1.m和bayeszcx.m

关（在正态分布下一定独立），在正态分布假设下估计概率密度，建立最小错误率Bayes 分类器，写出得到的决策规则，将该分类器应用到训练/测试样本，考察训练/测试错误情况。比较相关假设和不相关假设下结果的差异。在分类器设计时可以考察采用不同先验概率（如0.5 vs. 0.5, 0.75 vs. 0.25, 0.9 vs. 0.1等）进行实验，考察对决策和错误率的影响。训练样本female来测试图1先验概率0.5 vs. 0.5 图2先验概率0.75 vs. 0.25 图3先验概率0.9 vs. 0.1 图4不同先验概率对测试样本1进行试验得图

朴素贝叶斯分类算法代码实现

朴素贝叶斯分类算法一．贝叶斯分类的原理贝叶斯分类器的分类原理是通过某对象的先验概率，利用贝叶斯公式计算出其后验概率，即该对象属于某一类的概率，选择具有最大后验概率的类作为该对象所属的类。也就是说，贝叶斯分类器是最小错误率意义上的优化。贝叶斯分类器是用于分类的贝叶斯网络。该网络中应包含类结点C，其中C 的取值来自于类集合( c1 , c2 , ... , cm)，还包含一组结点X = ( X1 , X2 , ... , Xn)，表示用于分类的特征。对于贝叶斯网络分类器，若某一待分类的样本D，其分类特征值为x = ( x1 , x2 , ... , x n) ，则样本D 属于类别ci 的概率P( C = ci | X1 = x1 , X2 = x 2 , ... , Xn = x n) ，( i = 1 ,2 , ... , m) 应满足下式： P( C = ci | X = x) = Max{ P( C = c1 | X = x) , P( C = c2 | X = x ) , ... , P( C = cm | X = x ) } 贝叶斯公式： P( C = ci | X = x) = P( X = x | C = ci) * P( C = ci) / P( X = x) 其中，P( C = ci) 可由领域专家的经验得到,而P( X = x | C = ci) 和P( X = x) 的计算则较困难。二．贝叶斯伪代码整个算法可以分为两个部分，“建立模型”与“进行预测”，其建立模型的伪代码如下： numAttrValues 等简单的数据从本地数据结构中直接读取构建几个关键的计数表 for(为每一个实例) { for( 每个属性 ){ 为 numClassAndAttr 中当前类，当前属性，当前取值的单元加 1 为 attFrequencies 中当前取值单元加 1 } } 预测的伪代码如下： for(每一个类别){ for(对每个属性 xj){ for(对每个属性 xi){

朴素贝叶斯分类器

朴素贝叶斯分类器 Naive Bayesian Classifier C语言实现信息电气工程学院计算本1102班 20112212465 马振磊

1.贝叶斯公式通过贝叶斯公式，我们可以的知在属性F1-Fn成立的情况下，该样本属于分类C的概率。而概率越大，说明样本属于分类C的可能性越大。若某样本可以分为2种分类A，B。要比较P(A | F1,F2......) 与P(B | F1,F2......)的大小只需比较，P(A)P(F1,F2......| A) ,与P(B)P(F1,F2......| B) 。因为两式分母一致。而P(A)P(F1,F2......| A)可以采用缩放为P(A)P(F1|A)P(F2|A).......(Fn|A) 因此，在分类时，只需比较每个属性在分类下的概率累乘，再乘该分类的概率即可。分类属性outlook 属性temperature 属性humidity 属性wind no sunny hot high weak no sunny hot high strong yes overcast hot high weak yes rain mild high weak yes rain cool normal weak no rain cool normal strong yes overcast cool normal strong no sunny mild high weak yes sunny cool normal weak yes rain mild normal weak yes sunny mild normal strong yes overcast mild high strong yes overcast hot normal weak no rain mild high strong 以上是根据天气的4种属性，某人外出活动的记录。若要根据以上信息判断 (Outlook = sunny,Temprature = cool,Humidity = high,Wind = strong) 所属分类。 P(yes| sunny ,cool ,high ,strong )=P(yes)P(sunny|yes)P(cool |yes)P(high|yes)P(strong|yes)/K P(no| sunny ,cool ,high ,strong )=P(no)P(sunny|no)P(cool |no)P(high|no)P(strong|no)/K K为缩放因子，我们只需要知道两个概率哪个大，所以可以忽略K。 P(yes)=9/14 P(no)=5/14 P(sunny|yes)=2/9 P(cool|yes)=1/3 P(high|yes)=1/3 P(strong|yes)=1/3 P(sunny|no)=3/5 P(cool|no)=1/5 P(high|no)=4/5 P(strong|no)=3/5 P(yes| sunny ,cool ,high ,strong)=9/14*2/9*1/3*1/3*1/3=0.00529 P(no| sunny ,cool ,high ,strong )=5/14*3/5*1/5*4/5*3/5=0.20571 No的概率大，所以该样本实例属于no分类。

算法杂货铺——分类算法之贝叶斯网络(Bayesian networks)

算法杂货铺——分类算法之贝叶斯网络(Bayesian networks) 2010-09-18 22:50 by EricZhang(T2噬菌体), 2561 visits, 网摘, 收藏, 编辑 2.1、摘要在上一篇文章中我们讨论了朴素贝叶斯分类。朴素贝叶斯分类有一个限制条件，就是特征属性必须有条件独立或基本独立（实际上在现实应用中几乎不可能做到完全独立）。当这个条件成立时，朴素贝叶斯分类法的准确率是最高的，但不幸的是，现实中各个特征属性间往往并不条件独立，而是具有较强的相关性，这样就限制了朴素贝叶斯分类的能力。这一篇文章中，我们接着上一篇文章的例子，讨论贝叶斯分类中更高级、应用范围更广的一种算法——贝叶斯网络（又称贝叶斯信念网络或信念网络）。 2.2、重新考虑上一篇的例子上一篇文章我们使用朴素贝叶斯分类实现了SNS社区中不真实账号的检测。在那个解决方案中，我做了如下假设： i、真实账号比非真实账号平均具有更大的日志密度、各大的好友密度以及更多的使用真实头像。 ii、日志密度、好友密度和是否使用真实头像在账号真实性给定的条件下是独立的。但是，上述第二条假设很可能并不成立。一般来说，好友密度除了与账号是否真实有关，还与是否有真实头像有关，因为真实的头像会吸引更多人加其为好友。因此，我们为了获取更准确的分类，可以将假设修改如下： i、真实账号比非真实账号平均具有更大的日志密度、各大的好友密度以及更多的使用真实头像。 ii、日志密度与好友密度、日志密度与是否使用真实头像在账号真实性给定的条件下是独立的。 iii、使用真实头像的用户比使用非真实头像的用户平均有更大的好友密度。

贝叶斯分类器

实验报告一．实验目的 1、掌握密度函数监督参数估计方法； 2、掌握贝叶斯最小错误概率分类器设计方法。二．实验内容对于一个两类分类问题，设两类的先验概率相同，（12()()P P ωω=），两类的类条件概率密度函数服从二维正态分布，即 11(|)~(,)P N ω1x μΣ2(|)~(,)P N ω22x μΣ 其中，=[3,6]T 1μ，0.50=02???? ?? 1Σ，=[3,-2]T 2μ，20=02??????2Σ。 1）随机产生两类样本； 2）设计最大似然估计算法对两类类条件概率密度函数进行估计； 3）用2）中估计的类条件概率密度函数设计最小错误概率贝叶斯分类器，实现对两类样本的分类。三．实验原理最大似然估计 1．作用

在已知试验结果（即是样本）的情况下，用来估计满足这些样本分布的参数，把可能性最大的那个参数θ作为真实* θ的参数估计。 2. 离散型设X 为离散型随机变量， 12=(,,...,)k θθθθ为多维参数向量，如果随机变量 1,...,n X X 相互独立且概率计算式为 {}1(;,...) i i i k P x p x θθX ==，则可得概率函数为 {}1111,...,(;,...)n n n i k i P x x p x θθ=X =X ==∏，在 12=(,,...,)k θθθθ固定时，上式表示11,...,n n x x X =X =的概率；当 11,...,n n x x X =X =已知的时候，它又变成 12=(,,...,)k θθθθ的函数，可以把它记为12111(,,...,)(;,...,)n k k i L p x θθθθθ==∏，称此函数为似然函数。似然函数值的大小意味着该样本值出现的可能性的大小，既然已经得到了样本值 11,...,n n x x X =X =，那么它出现的可能性应该是较大的，即似然函数的值也应该是比较大的，因而最大似然估计就是选择使12(,,...,) k L θθθ达到最大值的那个θ作为真实* θ的估计。 3. 连续型设X 为连续型随机变量，其概率密度函数为1(;,...) i k f x θθ， 1,...n x x 为从该总体中抽出的样本，同样的如果 1,...n x x 相互独立且同分布，于是样本的联合概率密度为12111(,,...,)(;,...,) n k k i L f x θθθθθ==∏。大致过程同离散型一样。最大后验概率判决准则先验概率 1() P ω和 2() P ω，类条件概率密度 1(|) P X ω和 2(|) P X ω，根据贝叶斯公式1 (|)() (|)(|)() i i i c j j j p x P P X p X P ωωωωω== ∑，当 12(|)(|) P P ωω>x x 则可以下结论，在x 条件下，事件 1ω出现的可能性大，将x 判定为1ω类。

基于贝叶斯的文本分类

南京理工大学经济管理学院课程作业课程名称：本文信息处理作业题目：基于朴素贝叶斯实现文本分类姓名：赵华学号： 114107000778 成绩：

基于朴素贝叶斯实现文本分类摘要贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。本文作为分类算法的第一篇，将首先介绍分类问题，对分类问题进行一个正式的定义。然后，介绍贝叶斯分类算法的基础——贝叶斯定理。最后，通过实例讨论贝叶斯分类中最简单的一种：朴素贝叶斯分类。关键词社区发现标签传播算法社会网络分析社区结构 1引言数据挖掘在上个世纪末在数据的智能分析技术上得到了广泛的应用。分类作为数据挖掘中一项非常重要的任务，目前在商业上应用很多。分类的目的是学会一个分类函数或分类模型(也常常称作分类器)，该分类器可以将数据集合中的数据项映射到给定类别中的某一个，从而可以用于后续数据的预测和状态决策。目前，分类方法的研究成果较多，判别方法的好坏可以从三个方面进行：1）预测准确度，对非样本数据的判别准确度；2）计算复杂度，方法实现时对时间和空间的复杂度；3）模式的简洁度，在同样效果情况下，希望决策树小或规则少。分类是数据分析和机器学习领域的基本问题。没有一个分类方法在对所有数据集上进行分类学习均是最优的。从数据中学习高精度的分类器近年来一直是研究的热点。各种不同的方法都可以用来学习分类器。例如，人工神经元网络[1]、决策树[2]、非参数学习算法[3]等等。与其他精心设计的分类器相比，朴素贝叶斯分类器[4]是学习效率和分类效果较好的分类器之一。朴素贝叶斯方法，是目前公认的一种简单有效的分类方法，它是一种基于概率的分类方法，被广泛地应用于模式识别、自然语言处理、机器人导航、规划、机器学习以及利用贝叶斯网络技术构建和分析软件系统。 2贝叶斯分类 2.1分类问题综述对于分类问题，其实谁都不会陌生，说我们每个人每天都在执行分类操作一点都不夸张，只是我们没有意识到罢了。例如，当你看到一个陌生人，你的脑子下意识判断TA是男是女；你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱、那边有个非主流”之类的话，其实这就是一种分类操作。从数学角度来说，分类问题可做如下定义：已知集合：和，确定映射规则，使得任意有且仅有一个使得成立。（不考虑模糊数学里的模糊集情况）其中C叫做类别集合，其中每一个元素是一个类别，而I叫做项集合，其中每一个元素是一个待分类项，f叫做分类器。分类算法的任务就是构造分类器f。

《模式识别》实验报告-贝叶斯分类

《模式识别》实验报告 ---最小错误率贝叶斯决策分类一、实验原理对于具有多个特征参数的样本（如本实验的iris 数据样本有4d =个参数），其正态分布的概率密度函数可定义为 11 22 11()exp ()()2(2)T d p π-??=--∑-???? ∑x x μx μ 式中，12,,,d x x x ????=x 是d 维行向量，12,,,d μμμ????=μ 是d 维行向量，∑是d d ?维协方差矩阵，1-∑是∑的逆矩阵，∑是∑的行列式。本实验我们采用最小错误率的贝叶斯决策，使用如下的函数作为判别函数 ()(|)(), 1,2,3i i i g p P i ωω==x x （3个类别）其中()i P ω为类别i ω发生的先验概率，(|)i p ωx 为类别i ω的类条件概率密度函数。由其判决规则，如果使()()i j g g >x x 对一切j i ≠成立，则将x 归为i ω类。我们根据假设：类别i ω，i=1,2,……,N 的类条件概率密度函数(|)i p ωx ，i=1,2,……,N 服从正态分布，即有(|)i p ωx ~(,)i i N ∑μ，那么上式就可以写为 112 2 ()1()exp ()(),1,2,32(2)T i i d P g i ωπ-?? = -∑=???? ∑ x x -μx -μ 对上式右端取对数，可得 111()()()ln ()ln ln(2)222 T i i i i d g P ωπ-=-∑+-∑-i i x x -μx -μ 上式中的第二项与样本所属类别无关，将其从判别函数中消去，不会改变分类结果。则判别函数()i g x 可简化为以下形式 111 ()()()ln ()ln 22 T i i i i g P ω-=-∑+-∑i i x x -μx -μ