18各种全息图及衍射效率
合集下载
全息术(光栅、照相)

简介全息的意义是记录物光波的全部信息。
自从20世纪60年代激光出现以来得到了全面的发展和广泛的应用。
它包含全息照相和全息干涉计量两大内容。
全息照相的种类很多,按一定分类法有:同轴全息图、离轴全息图、菲涅耳全息图和傅里叶变换全息图等等。
本实验主要包括两项基本全息照相实验:(一)全息光栅:可以看成基元全息图,当参考光波和物光波都是点光源且与全息干板对称放置时可以在干板上形成平行直条纹图形,采用线性曝光可以得到正弦振幅型全息光栅。
(二)三维全息:通过干涉将漫反射物体的三维信息记录在全息干板上,再通过原光路衍射得到与原物体完全相似的物光波。
本实验的意义是让学生通过这两个实验,掌握全息照相的基本技术,更深刻地认识光的相干条件的物理意义,初步了解全息术的基本理论。
全息光栅光路图全息照相光路图教学重点1.使学生学会全息照相的干涉记录和衍射再现的技术手段。
2.使学生较深刻理解全息照相的本质。
3.使学生了解全息照相的应用。
教学难点1.拍摄高质量的全息图的技术关键。
2.全息图的衍射效率。
自测题1.(1)全息照相通过条纹的对比度记录了物体的强度分布信息。
(2)全息照相通过条纹的深浅记录了物体的强度分布信息。
2.(1)拍摄物体的三维全息图时分束板的透过率为50%(2)拍摄物体的三维全息图时分束板的透过率为5%。
3.在拍摄全息图时所用的扩束镜为(1)长焦距透镜(2)短焦距透镜。
4.如果全息图被打坏了,取一小块再现看到(1)不完整的像(2)较小的像。
思考题1.用细激光束垂直照射拍好的全息光栅,如能在垂直的白墙上看到五个亮点,说明什么问题?2.如果想拍摄一个100线/mm的全息光栅应如何布置光路?3.怎样测量全息光栅的衍射效率?4.为什么拍摄物体的三维全息图要求干板的分辨率在1500线/mm以上?。
[课件]光学全息PPT
![[课件]光学全息PPT](https://img.taocdn.com/s3/m/96dd38aea0116c175f0e482f.png)
(t0和都是常数)
若假定参考光强在H表面上是均匀的,则
* * t x , yt O O R O R b 2
2、波前记录与再现
2.2 波前再现
用参考波照明
用共轭参考波照明
2、波前记录与再现 用相干光波照射全息图,假定它在全息图平面上的复振幅分布为C(x,y),
波前记录
UU 2 UU 4 1 3
其中,=sin/,参考波的空间频率。
波前再现
3、同轴全息图与离轴全息图
从频率域的角度考虑离轴全息图。假定物体最高空间频率为fM周/mm,则 如下图:U3和U4的频谱G3和G4分别位于(0,)和(0,-)处。
为使成像光波和晕轮光U2有效分离,G2、G3和G4之间不能重叠,则必须满 足条件: i n 3 fM 3 fM 或 s
d x d y z z 0 M i i 2 i 1 d x d y z z 0 0 1 0 r z 0 1 z 2 c
1
5、几种不同类型的全息图
全息图的种类繁多,有很多不同的分类方法:
根据记录介质的相对厚度,可分为平面全息图和体全息图; 根据对照明光波的调制作用,可分为振幅全息图和位相全息图; 根据物光和参考光的相对方位,可分为同轴全息图和离轴全息图; 根据再现时照明光源和观察者在全息图的两侧还是同一侧,可分为透射全息图
和反射全息图;
根据记录物体与照相干板的相对距离,分为菲涅耳全息图和夫朗和费全息图; 根据制作时使用光源的性质,可分为连续波激光全息图和脉冲激光全息图。
5、几种不同类型的全息图
5.1 傅里叶变换全息图
利用透镜的傅里叶变换性质产生物体的频谱,并引入参考波与之 干涉,就得到了傅里叶变换全息图,其记录光路如下图所示。
18-2 夫琅禾费单缝衍射
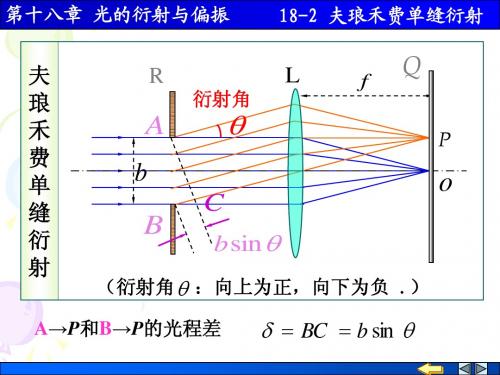
第一暗纹的衍射角 θ 1 = arcsin
λ
λ 一定
θ b 减小, 1增大 b ⇒λ,θ1 ⇒
b λ b增大, 1减小 ⇒ 0, θ1 ⇒ 0 光直线传播 θ b π
一定, 越大, 越大,衍射效应越明显。 θ b 一定,λ越大, 1越大,衍射效应越明显。 的两暗纹间) (2)中央明纹 )中央明纹(k=1的两暗纹间 的两暗纹间 角范围 −
入射波长变化, 入射波长变化,衍射效应如何变化 ?
越大, 越大,衍射效应越明显. λ 越大,θ1越大,衍射效应越明显.
第十八章 光的衍射与偏振
18-2 夫琅禾费单缝衍射 18-
(3)条纹宽度(相邻条纹间距) )条纹宽度(相邻条纹间距)
2 λ b sin θ = ± (2k + 1) 2
b sin θ = ± 2 k
第十八章 光的衍射与偏振
18-2 夫琅禾费单缝衍射 18-
补例1 设有一单色平面波斜射到宽度为b的单缝 补例 设有一单色平面波斜射到宽度为 的单缝 上(如图),求各级暗纹的衍射角θ. 如图),求各级暗纹的衍射角 ), 解:
∆ = AD − BC
= b(sin θ − sin α )
b
由暗纹条件
α
C
2
衍射最大
λ
b
< sinθ <
λ
b
线范围 −
λ
b
f <x<
λ
b
f
中央明纹的宽度 l 0 = 2 x1 ≈ 2
λ
b
f
第十八章 光的衍射与偏振
18-2 夫琅禾费单缝衍射 18-
单缝宽度变化,中央明纹宽度如何变化? 单缝宽度变化,中央明纹宽度如何变化?
20-全息2-平面全息图、体积全息图
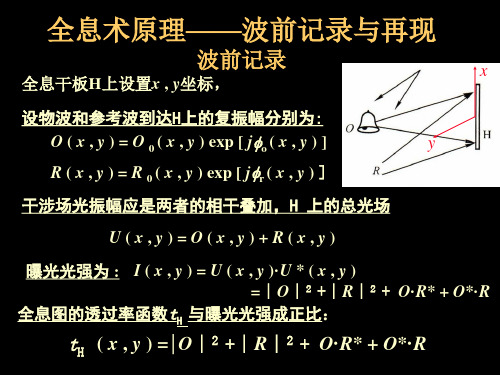
傅里叶全息 1: 它所记录的是物的频谱 图两大特点 2: 全息图的条纹结构有序,呈多族余弦光栅按一 定规律线性重叠而成。
§5-4 平面全息图
2、傅里叶变换全息图
再 现 光 路
平行光垂直入射: C ( x , y ) = Co exp ( jφc ) = 1 全息图后的光振幅为: UH’ = C · tH ≈ tH = | O | 2 + Ro2 包含物的频谱 共轭频谱
Uf2 = ℱ–1 { R02 } 是d 函数,形成焦点处的亮点,称为零级
§5-4 平面全息图
2、傅里叶变换全息图
再 现 光 路
Uf3 ℱ 第三项:
1
R O f
0 x
x
, f y exp j 2f x b
R O f
o
, f y exp- j 2f x bexp j 2 f x x'o f y y 'o dfx df y , f y expj 2 f x ( x'o b) f y y 'o dfx df y
§5-4 平面全息图
2、傅里叶变换全息图
物光波:O ( xo , yo ) = O0 ( xo , yo ) exp [ jfo ( xo , yo ) ] 参考光: 可利用置于前焦面上的点光源产生,设其位置坐标为 (-b,0),数学表述为δ 函数: R( x , y ) = R δ ( x + b , y )
用照明光波 C ( x , y ) = C 0 ( x , y ) exp [ jfc ( x , y ) ] 照射全息图 透过H后的光场复振幅 U’( x , y ) = C ( x , y )· tH ( x , y )
第2章体积全息原理1

分析体光栅衍射特性的最基本、最经典的理论模型是 1969年Bell实验室Kogelnik建立的一维平面波耦合波 理论。
2.5.1 体光栅与布拉格衍射
1) 介质的相对介电常数r与空间坐标无关,即
常数时,为均匀介质,否则为非均匀介质。
2) r与电场强度无关的介质称为线性介质,否
则为非线性介质。
3) 如果r的大小与电场在介质中的方向无关,
由右图可知:
kr xˆkD sin r zˆkD cosr ks xˆks sin s zˆks coss
(29) (30)
体全息图中的耦合波方程(续)
在所以体任全一息图点中的,电任场一E点是都再有现再光现和光衍和射衍光射复光振相幅叠之加和,,
即
E
yˆ[Er
(z)
exp(
jkr
体全息图的分类
体全息图主要可分为透射和反射两种,其主要 区别在于记录时物光和参考光的传播方向不同 而造成体全息图内部干涉层面的不同趋向,从 而使两者在再现特性上有所区别。
透射体全息图
物光和参考光从介质的同侧入射,介质内干涉 面几乎与介质表面垂直,并且再现时表现为较 强的角度选择性。当用白光再现时,入射角度 的改变将引起再现像波长的改变。
(8)
根据方程(7)、(8),对于角频率为的光场
的复振幅满足的波动方程为
2E ( 200r j0 )E ( E) 0
(9)
方程(9)被称为矢量波动方程。这是因为方程 (9)包含了 xˆ、yˆ、zˆ 分量。当然方程(9)在一 定的条件下可以进一步简化为标量波动方程。
体全息图中的波动方程(续)
耦合波理论的研究现状
➢ 1969年,Kogelnik,一维的无限大平面波 耦合波理论
2.5.1 体光栅与布拉格衍射
1) 介质的相对介电常数r与空间坐标无关,即
常数时,为均匀介质,否则为非均匀介质。
2) r与电场强度无关的介质称为线性介质,否
则为非线性介质。
3) 如果r的大小与电场在介质中的方向无关,
由右图可知:
kr xˆkD sin r zˆkD cosr ks xˆks sin s zˆks coss
(29) (30)
体全息图中的耦合波方程(续)
在所以体任全一息图点中的,电任场一E点是都再有现再光现和光衍和射衍光射复光振相幅叠之加和,,
即
E
yˆ[Er
(z)
exp(
jkr
体全息图的分类
体全息图主要可分为透射和反射两种,其主要 区别在于记录时物光和参考光的传播方向不同 而造成体全息图内部干涉层面的不同趋向,从 而使两者在再现特性上有所区别。
透射体全息图
物光和参考光从介质的同侧入射,介质内干涉 面几乎与介质表面垂直,并且再现时表现为较 强的角度选择性。当用白光再现时,入射角度 的改变将引起再现像波长的改变。
(8)
根据方程(7)、(8),对于角频率为的光场
的复振幅满足的波动方程为
2E ( 200r j0 )E ( E) 0
(9)
方程(9)被称为矢量波动方程。这是因为方程 (9)包含了 xˆ、yˆ、zˆ 分量。当然方程(9)在一 定的条件下可以进一步简化为标量波动方程。
体全息图中的波动方程(续)
耦合波理论的研究现状
➢ 1969年,Kogelnik,一维的无限大平面波 耦合波理论
物理光学18 光衍射基本理论

7
2、惠更斯-菲涅耳原理
“波前上任何一个未受阻挡的点都可以看作是一个频率 (或波长)与入射波相同的子波源;在其后任何一地点的光 振动,就是所有这些子波叠加的结果”。 可见,惠更斯-菲涅耳原理实际上认为惠更斯子波是频率 (波长)相同的相干光波,这些子波的传播服从光干涉叠加 原理。 根据惠更斯-菲涅耳原理,我们可以建立一个定量计算衍 射问题的公式,来描述单色光波在传播途中任意两个面,
P2 P4 Π
(a)
S
Σ
惠更斯-菲涅耳
索末菲(A. Sommerfeld)的定义:
P1 P3 P4 P2
Π
(b)
所谓衍射就是“不能用反射或折射来
衍射现象图
解释的光线对直线光路的任何偏离”。
2
衍射的要素及衍射问题
衍射现象中的有三项基本的要素。
(1)、由光源S发射的光波。其性质可以用光波的波长组成、 波面形状、复振幅分布等参量定量描述;
E(P)
1
4
E
S[ n
exp( jkr') r'
E
n
(exp( jkr'))d '
r'
(3)
公式(3)表明的规律称为“亥姆霍茨-基尔霍夫定理”。
E(P)是P点的电场; k是简谐波的传播数。 S是包围P点的封闭曲面。
S
P r'
E 是面元d '处电场沿
n 法线方向的变化率。
n
d '
r '是面元d '到P点的距离。
'
r0
r'
是光栏开口允许通过的波面部分。 d '是'上的面元
r '是'上的点M '到P点的距离。
2、惠更斯-菲涅耳原理
“波前上任何一个未受阻挡的点都可以看作是一个频率 (或波长)与入射波相同的子波源;在其后任何一地点的光 振动,就是所有这些子波叠加的结果”。 可见,惠更斯-菲涅耳原理实际上认为惠更斯子波是频率 (波长)相同的相干光波,这些子波的传播服从光干涉叠加 原理。 根据惠更斯-菲涅耳原理,我们可以建立一个定量计算衍 射问题的公式,来描述单色光波在传播途中任意两个面,
P2 P4 Π
(a)
S
Σ
惠更斯-菲涅耳
索末菲(A. Sommerfeld)的定义:
P1 P3 P4 P2
Π
(b)
所谓衍射就是“不能用反射或折射来
衍射现象图
解释的光线对直线光路的任何偏离”。
2
衍射的要素及衍射问题
衍射现象中的有三项基本的要素。
(1)、由光源S发射的光波。其性质可以用光波的波长组成、 波面形状、复振幅分布等参量定量描述;
E(P)
1
4
E
S[ n
exp( jkr') r'
E
n
(exp( jkr'))d '
r'
(3)
公式(3)表明的规律称为“亥姆霍茨-基尔霍夫定理”。
E(P)是P点的电场; k是简谐波的传播数。 S是包围P点的封闭曲面。
S
P r'
E 是面元d '处电场沿
n 法线方向的变化率。
n
d '
r '是面元d '到P点的距离。
'
r0
r'
是光栏开口允许通过的波面部分。 d '是'上的面元
r '是'上的点M '到P点的距离。
全息技术第七辑体光栅的衍射效率和选择性51页PPT
全息技术第七辑体光栅的衍射效率和 选择性
1、战鼓一响,法律无声。——英国 2、任何法律的根本;不,不成文法本 身就是 讲道理 ……法 律,也 ----即 明示道 理。— —爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正,其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等,但是在法律 面前人 人是平 等的。 ——波 洛克
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
51
1、战鼓一响,法律无声。——英国 2、任何法律的根本;不,不成文法本 身就是 讲道理 ……法 律,也 ----即 明示道 理。— —爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正,其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等,但是在法律 面前人 人是平 等的。 ——波 洛克
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
51
大学物理第十八讲 光栅衍射、晶体的X射线衍射
衍射角
a: 透光部分的宽度 b: 不透光部分宽度
L
相邻两缝间的光程差
G
P
d sin
●屏上某一衍射 方向的光强由光 栅常数决定。
d d sin
o
f
2
光栅衍射图样的定性分析
●各单缝衍射的光强 相同且位置分布全同. ●受单缝衍射 光强调制的各 a d 缝之间再产生 多缝干涉,形 成光栅衍射条 纹。
N 5
光栅衍射主 极大
(综合结果)
6 3 0
d / a 3 I N 2 I ( ) k a
3 6
a
sin
5
2.光栅方程(明纹公式)
(主极大)
2
sin N sin sin N I I0 I a ( ) sin sin d 2 I N I a ( ) 主极大 sin k
§11-6
光栅衍射
一、光栅 在透光或反光性能上具有周期性空间结构的光学元件.
平面光栅—在透明平面玻璃上刻成若干等间距的刻痕, 或在镀铬板上用光刻的办法刻出若干条刻痕做成的器 件。 透射光栅
反射光栅
d d
1
二、光栅常数、衍射原理
光栅常数: d a b
通常d 值: 105 ~ 106 m (每厘米103~104条刻痕)
劳厄实验
劳厄斑点
1912年劳厄进 行了晶片的X 射线衍射实验
铅板 X射线
单晶片
照 像 底 片
18
二、布拉格公式
1913年英国布拉格父子用一种简便计算方法定量地解 释了X射线衍射的规律。1915年父子双双荣获诺贝尔 物理学奖。 :掠射角 d:晶格常数 上下层散射光光程差: a
a: 透光部分的宽度 b: 不透光部分宽度
L
相邻两缝间的光程差
G
P
d sin
●屏上某一衍射 方向的光强由光 栅常数决定。
d d sin
o
f
2
光栅衍射图样的定性分析
●各单缝衍射的光强 相同且位置分布全同. ●受单缝衍射 光强调制的各 a d 缝之间再产生 多缝干涉,形 成光栅衍射条 纹。
N 5
光栅衍射主 极大
(综合结果)
6 3 0
d / a 3 I N 2 I ( ) k a
3 6
a
sin
5
2.光栅方程(明纹公式)
(主极大)
2
sin N sin sin N I I0 I a ( ) sin sin d 2 I N I a ( ) 主极大 sin k
§11-6
光栅衍射
一、光栅 在透光或反光性能上具有周期性空间结构的光学元件.
平面光栅—在透明平面玻璃上刻成若干等间距的刻痕, 或在镀铬板上用光刻的办法刻出若干条刻痕做成的器 件。 透射光栅
反射光栅
d d
1
二、光栅常数、衍射原理
光栅常数: d a b
通常d 值: 105 ~ 106 m (每厘米103~104条刻痕)
劳厄实验
劳厄斑点
1912年劳厄进 行了晶片的X 射线衍射实验
铅板 X射线
单晶片
照 像 底 片
18
二、布拉格公式
1913年英国布拉格父子用一种简便计算方法定量地解 释了X射线衍射的规律。1915年父子双双荣获诺贝尔 物理学奖。 :掠射角 d:晶格常数 上下层散射光光程差: a
全息技术第七辑体光栅的衍射效率和选择性51页PPT
术第七辑体光栅的衍射效率和 选择性
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
36、“不可能”这个字(法语是一个字 ),只 在愚人 的字典 中找得 到。--拿 破仑。 37、不要生气要争气,不要看破要突 破,不 要嫉妒 要欣赏 ,不要 托延要 积极, 不要心 动要行 动。 38、勤奋,机会,乐观是成功的三要 素。(注 意:传 统观念 认为勤 奋和机 会是成 功的要 素,但 是经过 统计学 和成功 人士的 分析得 出,乐 观是成 功的第 三要素 。
39、没有不老的誓言,没有不变的承 诺,踏 上旅途 ,义无 反顾。 40、对时间的价值没有没有深切认识 的人, 决不会 坚韧勤 勉。
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
k-fst-光学信息处理第十四讲
傅里叶变换全息图统计原理
傅里叶变换全息图旳某些性质特点及应用
(1)衍射像分离旳条件:要使再现时各衍射项能分离开,则统计时参照点源位置与物旳尺寸要选择合适,一般来说,b必须不小于物体尺寸旳3/2倍 (2)统计介质旳辨别率:取决于全息图中最精细旳光栅构造,因而应该满足 再现像旳辨别率:再现像旳辨别率取决于全息图旳宽度 (3)再现时产生旳像旳线模糊和色模糊会影响辨别率,因而对统计时点源旳尺寸及再现光源线宽要严格限制 (4)傅里叶全息图统计旳是频谱,对于大部分低频物来说,其频谱直径仅1mm左右,尤其合用于高密度全息存储(5)傅里叶全息图旳光能集中在原点附近
R ( xo , yo ) = R0 δ ( xo + b , yo )
参照光: 可利用置于前焦面上旳点光源产生,设其位置坐标为(-b,0),数学表述为δ函数:
fx = xf / ( λf )、fy = yf / ( λf ),xf﹑yf为透镜后焦面旳空间坐标,f为透镜焦距
傅里叶变换全息图统计原理图
无透镜傅里叶变换全息图统计光路
无透镜傅里叶变换全息图在统计和再现时都不用透镜,用平行光照明物,参照点源置于物平面(-b,0)处,经过菲涅耳衍射照射到干板上,统计光路如下图示
无透镜傅里叶变换全息图统计原理
物光波: 参照光波:曝光光强:进行线性处理后,透射率 tH ∝ I 。由上式能够看出,物光波和参照光波中旳二次位相因子在曝光光强体现式中相互抵消。这就是能够省去透镜统计傅里叶变换全息图旳原因。
像全息图
用物光再现全息“翻译器”输出
用物光波再现也出现四项: U1+U2 = ( O ☆ O + R ☆ R ) * O 是物旳几何像 U3 = (O * O ) * R*(-xo’,-yo’) *δ(xo’- b,yo’) 表达在(b,0)处得到参照波旳共轭像,是个模糊像 U4 = (O ☆ O ) * R(xo’,yo’)*δ(xo’+ b,yo’) = (O ☆ O ) * R(xo’+ b,yo’) ≈ R(xo’+ b,yo’) 表达在(- b,0)位置得到参照波旳原始像。
傅里叶变换全息图旳某些性质特点及应用
(1)衍射像分离旳条件:要使再现时各衍射项能分离开,则统计时参照点源位置与物旳尺寸要选择合适,一般来说,b必须不小于物体尺寸旳3/2倍 (2)统计介质旳辨别率:取决于全息图中最精细旳光栅构造,因而应该满足 再现像旳辨别率:再现像旳辨别率取决于全息图旳宽度 (3)再现时产生旳像旳线模糊和色模糊会影响辨别率,因而对统计时点源旳尺寸及再现光源线宽要严格限制 (4)傅里叶全息图统计旳是频谱,对于大部分低频物来说,其频谱直径仅1mm左右,尤其合用于高密度全息存储(5)傅里叶全息图旳光能集中在原点附近
R ( xo , yo ) = R0 δ ( xo + b , yo )
参照光: 可利用置于前焦面上旳点光源产生,设其位置坐标为(-b,0),数学表述为δ函数:
fx = xf / ( λf )、fy = yf / ( λf ),xf﹑yf为透镜后焦面旳空间坐标,f为透镜焦距
傅里叶变换全息图统计原理图
无透镜傅里叶变换全息图统计光路
无透镜傅里叶变换全息图在统计和再现时都不用透镜,用平行光照明物,参照点源置于物平面(-b,0)处,经过菲涅耳衍射照射到干板上,统计光路如下图示
无透镜傅里叶变换全息图统计原理
物光波: 参照光波:曝光光强:进行线性处理后,透射率 tH ∝ I 。由上式能够看出,物光波和参照光波中旳二次位相因子在曝光光强体现式中相互抵消。这就是能够省去透镜统计傅里叶变换全息图旳原因。
像全息图
用物光再现全息“翻译器”输出
用物光波再现也出现四项: U1+U2 = ( O ☆ O + R ☆ R ) * O 是物旳几何像 U3 = (O * O ) * R*(-xo’,-yo’) *δ(xo’- b,yo’) 表达在(b,0)处得到参照波旳共轭像,是个模糊像 U4 = (O ☆ O ) * R(xo’,yo’)*δ(xo’+ b,yo’) = (O ☆ O ) * R(xo’+ b,yo’) ≈ R(xo’+ b,yo’) 表达在(- b,0)位置得到参照波旳原始像。
