初中奥数系列:12.1.3旋转类全等问题(5).讲义学生版
初中数学专题复习:旋转(类型全面)

旋转旋转:在平面内,将一个图形绕一个定点沿某个方向转动一个角度成为与原来相等的图形,这样的图形运动叫做图形的旋转,这个定点叫做旋转中心,图形转动的角叫做旋转角.旋转特征:图形旋转时,图形中的每一点旋转的角都相等,都等于图形的旋转角。
(一)正三角形类型在正ΔABC中,P为ΔABC内一点,将ΔABP绕A点按逆时针方向旋转600,使得AB与AC重合。
经过这样旋转变化,将图(1-1-a)中的PA、PB、PC三条线段集中于图(1-1-b)中的一个ΔP'CP中,此时ΔP'AP也为正三角形。
例1. 如图:(1-1):设P是等边ΔABC内的一点,PA=3,PB=4,PC=5,∠APB的度数是________.(二)正方形类型在正方形ABCD中,P为正方形ABCD内一点,将ΔABP绕B点按顺时针方向旋转900,使得BA与BC重合。
经过旋转变化,将图(2-1-a)中的PA、PB、PC三条线段集中于图(2-1-b)中的ΔCPP'中,此时ΔBPP'为等腰直角三角形。
例2. 如图(2-1):P是正方形ABCD内一点,点P到正方形的三个顶点A、B、C的距离分别为PA=1,PB=2,PC=3。
求此正方形ABCD面积。
(三)等腰直角三角形类型在等腰直角三角形ΔABC中,∠C=90°, P为ΔABC内一点,将ΔAPC绕C点按逆时针方向旋转900,使得AC与BC重合。
经过这样旋转变化,在图(3-1-b)中的一个ΔP'CP为等腰直角三角形。
例3.如图,在ΔABC中,∠ACB =900,BC=AC,P为ΔABC内一点,且PA=3,PB=1,PC=2。
求∠BPC的度数。
旋转实际上是一种全等变换,由于具有可操作性,因而是考查同学们动手能力、观察能力的好素材,也就成了近几年中考试题中频繁出现的内容。
题型多以填空题、计算题呈现。
在解答此类问题时,我们通常将其转换成全等求解。
根据变换的特征,找到对应的全等形,通过线段、角的转换达到求解的目的。
初中奥数系列:12.1.2平移类全等问题.题库学生版
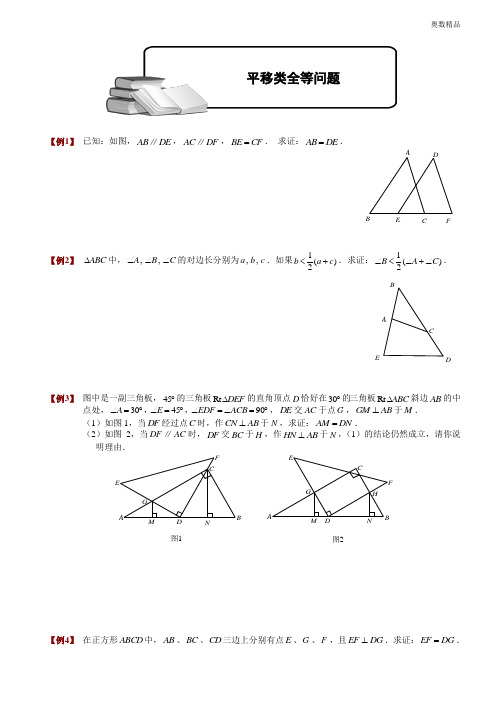
【例1】 已知:如图,AB DE ∥,AC DF ∥,BE CF =. 求证:AB DE =.FEDC B A【例2】 ABC ∆中,,,A B C ∠∠∠的对边长分别为,,a b c .如果1()2b a c <+.求证:1()2B AC ∠<∠+∠.EDCBA【例3】 图中是一副三角板,45︒的三角板Rt DEF ∆的直角顶点D 恰好在30︒的三角板Rt ABC ∆斜边AB 的中点处,304590A E EDF ACB ∠=︒∠=︒∠=∠=︒,,,DE 交AC 于点G ,GM AB ⊥于M . (1)如图1,当DF 经过点C 时,作CN AB ⊥于N ,求证:AM DN =. (2)如图2,当DF AC ∥时,DF 交BC 于H ,作HN AB ⊥于N ,(1)的结论仍然成立,请你说明理由.图2图1EHABCD FGMN NMGF ED CBA【例4】 在正方形ABCD 中,AB 、BC 、CD 三边上分别有点E 、G 、F ,且EF DG ⊥.求证:EF DG =.平移类全等问题GFEDCBA【例5】 在正方形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边上的点,且EG FH ⊥,求证:EG FH =.HGF ED CB A【例6】 如图所示,在ABC ∆的边BC 上取两点D 、E ,且BD CE =,求证:AB AC AD AE +>+.AB CD E【例7】 如图,已知ABC ∆⑴请你在BC 边上分别取两点D 、E (BC 的中点除外),连结AD 、AE ,写出使此图中只存在两对.....面积相等的三角形的相应条件,并表示出面积相等的三角形; ⑵请你根据使⑴成立的相应条件,证明AB AC AD AE +>+.CBA⑴DE CBA【例8】 ABC ∆中,90B ∠=︒,M 为AB 上一点,使得AM BC =,N 为BC 上一点,使得CN BM =,连AN 、CM 交于P 点.试求APM ∠的度数,并写出你的推理证明的过程.N MPCB A【例9】 如图所示,设ABCD 是矩形,K 为矩形所在平面上的一点,连接KA 与KD 均与BC 相交.由点B 向直线DK 引垂线,由点C 向直线AK 引垂线,二垂线相交于M ,求证M K AD ⊥.DMBFEKCA【例10】 如图,梯形ABCD 中,AD BC ∥,以两腰AB ,CD 为一边分别向两边作正方形ABGE 和DCHF ,连接AD 的垂直平分线l 交线段EF 于点M .求证:点M 为EF 的中点.MlHFDCEGBA【例11】 已知线段OA 、OB 、OC 、OD 、OE 、OF .AOB BOC ∠=∠COD =∠DOE =∠EOF =∠60=︒.且2AD BE CF ===.求证:OAB OCD OEF S S S ∆∆∆++.F【例12】 如图所示,在六边形ABCDEF 中,AB ED ∥,AF CD ∥,BC FE ∥,AB ED =,AF CD =,BC FE =.又知对角线FD BD ⊥,24FD =厘米,18BD =厘米.请你回答:六边形ABCDEF 的面积是多少平方厘米?。
初中旋转课件ppt

旋转的对称性
中心对称
面对称
当一个图形绕着某一点旋转180度后 ,它与自身重合,这种性质称为中心 对称。
当一个图形绕着垂直于平面的轴旋转 180度后与自身重合,这种性质称为 面对称。
轴对称
如果一个图形绕着一条直线旋转180 度后与自身重合,这种性质称为轴对 称。
旋转的几何意义
旋转的向量表示
在二维空间中,一个向量绕着原 点旋转一定角度后可以用一个新 的向量表示,该向量由原始向量
旋转木马的转动原理
旋转木马的转动原理主要基于机械和电力驱动。每个木马 或其他座位的支撑结构都装有一个转轴,转轴通过轴承与 中心轴相连。
当中心轴转动时,通过轴承带动转轴,从而使每个座位围 绕中心轴进行旋转。为了保持旋转的平稳和均匀,通常会 使用减速器和电机等传动装置进行驱动和控制。
旋转磁场的产生原理
旋转在日常生活中的应用
旋转机械
旋转机械是日常生活中常见的机械装置,如电动机、发电机、涡 轮机等,通过旋转来传递能量和动力。
旋转运动
旋转运动是许多体育项目中的基本动作,如滑冰、自行车赛、篮球 等,通过旋转可以改变运动方向和速度。
旋转门
旋转门是建筑入口的一种常见设计,通过旋转门可以控制人流的进 出,同时具有美观和节能的效果。
和旋转角度决定。
旋转的矩阵表示
在二维空间中,旋转也可以用一 个2x2的旋转矩阵来表示,该矩 阵描述了旋转的方向和大小。
旋转的性质
在二维空间中,旋转具有一些重 要的性质,如旋转不改变向量的 长度和方向、不改变图形的形状
和大小等。
2023
PART 03
旋转的应用
REPORTING
旋转在几何图形中的应用
2023
初中数学旋转的六大模型题

初中数学旋转的六大模型题旋转是数学中的一个重要概念,也是初中数学中经常会遇到的一个题型。
通过旋转,我们可以改变图形的朝向和位置,从而帮助我们更好地理解几何形状和解决问题。
下面是初中数学中常见的六大旋转模型题,帮助学生更好地理解旋转的概念和运用。
1. 点的旋转:题目给出一个点的坐标和旋转角度,要求求出旋转后的点的坐标。
这种题目可以帮助学生理解点的旋转规律和计算方法。
2. 图形的旋转:题目给出一个图形的坐标或者边长,要求将图形按照给定的角度进行旋转,然后求出旋转后的图形的坐标或者边长。
这种题目可以帮助学生理解图形的旋转规律和变化。
3. 对称图形的旋转:题目给出一个对称图形和旋转角度,要求求出旋转后的图形。
这种题目可以帮助学生理解对称图形的旋转规律和变化。
4. 旋转体的表面积和体积:题目给出一个旋转体的形状和旋转轴的位置,要求求出旋转体的表面积和体积。
这种题目可以帮助学生理解旋转体的形成过程和计算方法。
5. 旋转体的截面图形:题目给出一个旋转体的形状和旋转轴的位置,要求求出旋转体在某一截面上的图形。
这种题目可以帮助学生理解旋转体的截面变化和图形特征。
6. 旋转体的切面面积:题目给出一个旋转体的形状和旋转轴的位置,要求求出旋转体在某一位置上的切面面积。
这种题目可以帮助学生应用切线和面积计算,理解旋转体的切面特征。
通过这六大旋转模型题,学生可以更好地掌握旋转的概念和运用,提高解决数学问题的能力。
在解题过程中,学生需要善于利用旋转的几何性质和计算方法,灵活运用数学知识,加深对数学的理解和认识。
同时,这些题目也能够培养学生的逻辑思维能力和推理能力,提高解决问题的能力和思维水平。
数学活动--旋转 初中九年级数学教学课件PPT 人教版

平移
直角三角形 求线段长,线段平方和最小时点坐标, 线段和最小时点坐标
折叠 矩形
求点坐标,线段间关系式,折叠时坐标
2011
旋转 直角三角形 求点坐标,角度间关系,直线解析式
2010 点的运动 矩形
三角形周长最小,四边形周长最小时动 点坐标
天津市第二十中学
2
考察内容
以平面直角坐标系为背景,以平 移、轴对称、旋转为解题的条件 或手段,考察学生对初中常见规 律性平面几何图形的掌握,同时 也考察学生对代数工具的综合运 用能力,以及对转化思想的运用 能力。
天津市第二十中学
5
3. 在(2)的条件下,边OA上 的一点P旋转后的对应 点为P′,当O′P+BP′取得最小值时,求点P′的坐标 (直接写出结果即可)
天津市第二十中学
6
2.(2014•天津)在平面直角坐标系中,O为原点,点 A(﹣2,0),B(0,2),点E,点F分别为OA,OB的中点. 若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′ 记旋转角为α. 1. 如图①,当α=90°时,求AE′,BF′的长; 2. 如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
上,且,连接交于点,作于点.试问当点,在移动过程中,线
段的长度是否发生变化?若变化,说明理由;若不变,求出线 段的长度(直接写出结果即可).
y D
PC
y D
PC
A
E
M
F
O
Bx O
B
Nx
图①
x
图②
x
复习建议:回归课本,梳理基本知识原理
16
探究 平面直角坐标系中的动点最短路径问题
例 3 如图 Z8-3,在平面直角坐标系中,矩形 OACB
初中数学竞赛中考讲义之几何三大变换之旋转

第32讲几何三大变换之旋转旋转的性质【例题讲解】例题1.如图所示,将一副三角板的直角顶点重合摆放在桌面上,若145AOD ∠=︒,则BOC ∠=度.【解答】解:由图145AOD ∠=︒ ,1459055AOC AOD COD ∴∠=∠-∠=︒-︒=︒,则905535BOC ∠=︒-︒=度.故答案为:35.例题2.如图,ABC ∆中,90ACB ∠=︒,30A ∠=︒,将ABC ∆绕C 点按逆时针方向旋转α角(090)α︒<<︒得到DEC ∆,设CD 交AB 于F ,连接AD ,当旋转角α度数为,ADF ∆是等腰三角形.旋转中心:O旋转角:∠AOA'=∠BOB'=∠COC'性质:OA=OA'、OB=OB'、OC=OC'旋转中心:B旋转角:∠ABA'=∠CBC'性质:AB=A'B 、CB=C'B 连接AA'、CC'△ABA'∽△CBC',且均为等腰三角形【解答】解:ABC ∆ 绕C 点按逆时针方向旋转α角(090)α︒<<︒得到DEC ∆,DCA α∴∠=,CD CA =,11(180)9022CDA CAD αα∴∠=∠=︒-=︒-,ADF ∆ 是等腰三角形,30DFA α∠=︒+,①CD CA =,则CDA CAD ∠=∠,当FD FA =,则FDA FAD ∠=∠,这不合题意舍去,②当AF AD =,ADF AFD ∴∠=∠,190302αα∴︒-=︒+,解得40α=︒;③当DF DA =,DFA DAF ∴∠=∠,13090302αα∴︒+=︒--︒,解得20α=︒.故答案为40︒或20︒.【旋转60°】得等边例题3.如图,在直角坐标系中,点A 在y 轴上,△AOE 是等边三角形,点P 为x 轴正半轴上任意一点,连接AP ,将线段AP 绕点A 逆时针60°得到线段AQ ,连接QE 并延长交x 轴于点F .(1)问∠QFP 角度是否发生变化,若不变,请说明理由;(2)若AO =,OP =x ,请表示出点Q 的坐标(用含x 的代数式表示)【解答】(1)不变(2)【旋转90°】构造全等例题4.如图,在平面直角坐标系中,点(,)A a b 为第一象限内一点,且a b <.连结OA ,并以点A 为旋转中心把OA 逆时针转90︒后得线段BA .若点A 、B 恰好都在同一反比例函数的图象上,则b a的值等于多少?【解答】解:过A 作AE x ⊥轴,过B 作BD AE ⊥,90OAB ∠=︒ ,90OAE BAD ∴∠+∠=︒,90AOE OAE ∠+∠=︒ ,BAD AOE ∴∠=∠,在AOE ∆和BAD ∆中,90AOE BAD AEO BDA AO BA ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,()AOE BAD AAS ∴∆≅∆,AE BD b ∴==,OE AD a ==,DE AE AD b a ∴=-=-,OE BD a b +=+,则(,)B a b b a +-;A 与B 都在反比例图象上,得到()()ab a b b a =+-,整理得:22b a ab -=,即2(10b b a a--=, △145=+=,∴152b a ±=, 点(,)A a b 为第一象限内一点,0a ∴>,0b >,则152b a +=.故答案为152+.【旋转180°】由中心对称得平行四边形例题5.如图所示,抛物线2:(0,0)m y ax b a b =+<>与x 轴于点A 、B (点A 在点B 的左侧),与y 轴交于点C .将抛物线m 绕点B 旋转180︒,得到新的抛物线n ,它的顶点为1C ,与x 轴的另一个交点为1A .(1)四边形11AC A C 是什么特殊四边形,请写出结果并说明理由;(2)若四边形11AC A C 为矩形,请求出a ,b 应满足的关系式.【解答】解:(1)当1a =-,1b =时,抛物线m 的解析式为:21y x =-+.令0x =,得:1y =.(0,1)C ∴.令0y =,得:1x =±.(1,0)A ∴-,(1,0)B ,C 与1C 关于点B 中心对称,∴抛物线n 的解析式为:22(2)143y x x x =--=-+;四边形11AC A C 是平行四边形.理由:连接AC ,1AC ,11A C ,C 与1C 、A 与1A 都关于点B 中心对称,1AB BA ∴=,1BC BC =,∴四边形11AC A C 是平行四边形.(2)令0x =,得:y b =.(0,)C b ∴.令0y =,得:20ax b +=,∴x =∴(A B ,∴AB BC ===.要使平行四边形11AC A C 是矩形,必须满足AB BC =,∴=,∴24(b b b a a⨯-=-,3ab ∴=-.a ∴,b 应满足关系式3ab =-.例题6.如图1,抛物线23y ax ax b =-+经过(1,0)A -,(3,2)C 两点,与y 轴交于点D ,与x 轴交于另一点B .(1)求此抛物线的解析式;(2)如图2,过点(1,1)E -作EF x ⊥轴于点F ,将AEF ∆绕平面内某点旋转180︒后得MNQ ∆(点M ,N ,Q 分别与点A ,E ,F 对应),使点M ,N 在抛物线上,求点M ,N 的坐标.【解答】解:(1) 抛物线23y ax ax b =-+过(1,0)A -、(3,2)C ,03a a b ∴=++,299a a b =-+.解得12a =-,2b =,∴抛物线解析式213222y x x =-++.(2)如图2,由题意知,AEF ∆ 绕平面内某点旋转180︒后得MNQ ∆,∴设绕点I 旋转,联结AI ,NI ,MI ,EI ,AI MI = ,NI EI =,∴四边形AEMN 为平行四边形,//AN EM ∴且AN EM =.(1,1)E - 、(1,0)A -,∴设(,)M m n ,则(2,1)N m n -+M 、N 在抛物线上,213222n m m ∴=-++,2131(2)(2)222n m m +=--+-+,解得3m =,2n =.(3,2)M ∴,(1,3)N .【旋转过后落点问题】例题7.如图,Rt ABC ∆中,已知90C ∠=︒,48B ∠=︒,点D 在边BC 上,2BD CD =,把Rt ABC ∆绕点D 逆时针旋转(0180)m m ︒<<︒度后,如果点B 恰好落在初始Rt ABC ∆的边上,那么m =.【解答】解:当旋转后点B 的对应点B '落在AB 边上,如图1,Rt ABC ∆ 绕点D 逆时针旋转(0180)m m ︒<<︒度得到Rt △A B C ''',DB DB ∴'=,B DB m ∠'=,48DB B B ∴∠'=∠=︒,18084B DB DB B B ∴∠'=︒-∠'-∠=︒,即84m =︒;当点B 的对应点B '落在AB 边上,如图2,Rt ABC ∆ 绕点D 逆时针旋转(0180)m m ︒<<︒度得到Rt △A B C ''',DB DB ∴'=,B DB m ∠'=,2BD CD = ,2DB CD ∴'=,90C ∠=︒ ,30CB D ∴∠'=︒,60CDB ∴∠'=︒,18060120B DB ∴∠'=︒-︒=︒,即120m =︒,综上所述,m 的值为84︒或120︒.故答案为84︒或120︒.例题8.如图,在Rt ACB ∆中,90ACB ∠=︒,点O 在AB 上,且6CA CO ==,1cos 3CAB ∠=,若将ACB ∆绕点A 顺时针旋转得到Rt △AC B '',且C '落在CO 的延长线上,连接BB '交CO 的延长线于点F ,则BF =.【解答】解:过C 作CD AB ⊥于点D ,CA CO = ,AD DO ∴=,在Rt ACB ∆中,16cos 3AC CAB AB AB∠===,318AB AC ∴==,在Rt ADC ∆中:1cos 3AD CAB AC ∠==,123AD AC ∴==,24AO AD ∴==,18414BO AB AO ∴=-=-=,△AC B ''是由ACB ∆旋转得到,AC AC ∴=',AB AB =',CAC BAB ∠'=∠',1(180)2ACC CAC ∠'=︒-∠' ,1(180)2ABB BAB ∠'=︒-∠',ABB ACC ∴∠'=∠',∴在CAO ∆和BFO ∆中,BFO CAO ∠=∠,CA CO = ,COA CAO ∴∠=∠,又COA BOF ∠=∠ (对顶角相等),BOF BFO ∴∠=∠,14BF BO ∴==.故答案为:14.例题9.在平面直角坐标系xOy 中,抛物线26(0)y mx mx n m =++>与x 轴交于A ,B 两点(点A 在点B 左侧),顶点为C ,抛物线与y 轴交于点D ,直线BC 交y 轴于E ,且ABC ∆与AEC ∆这两个三角形的面积之比为2:3.(1)求点A 的坐标;(2)将ACO ∆绕点C 顺时针旋转一定角度后,点A 与B 重合,此时点O 的对应点O '恰好也在y 轴上,求抛物线的解析式.【解答】解:(1)如图1,抛物线26(0)y mx mx n m =++>∴对称轴3x =-,当:2:3ABC AEC S S ∆∆=时,:2:1ABC AEB S S ∆∆∴=,过点C 作CF x ⊥轴于F ,:2:1CF OE ∴=易知,BFC BOE ∆∆∽,::2:1BF OB CF OE ∴==,1OB ∴=,2BF =,5OA ∴=,(5,0)A ∴-,(1,0)B -;(2)(1,0)B - ,06m m n ∴=-+,5n m ∴=,(3,4)C m ∴--,如图2,作CF AB ⊥于F ,CP OD ⊥于P ,则四边形CFOP 是矩形,4OP CF m ∴==,3CP OF ==,OP O P '=,28OO OP m'∴==由旋转知,5OA BO '==,在Rt BOO '∆中,1OB =,根据勾股定理得,2285126m =-=,64m ∴=263656424y x x ∴=++【旋转+“恰好”问题】例题10.如图,在直角坐标系中,直线4y =+分别与x 轴、y 轴交于点M 、N ,点A 、B 分别在y 轴、x 轴上,且30B ∠=︒,4AB =,将ABO ∆绕原点O 顺时针转动一周,当AB 与直线MN 平行时点A 的坐标.【另外再可思考,当“AB 所在直线与MN 垂直时点A 的坐标”】【解答】解:①4AB = ,30ABO ∠=︒,122OA AB ∴==,903060BAO ∠=︒-︒=︒,120OAD ∴∠=︒,直线MN 的解析式为43y x =-+,30NMO ∴∠=︒,//AB MN ,30ADO NMD ∴∠=∠=︒,30AOC ∴∠=︒,112AC OA ∴==,OC ∴==∴点A 的坐标为,1);② 图②中的点A 与图①中的点A 关于原点对称,∴点A 的坐标为:(,1)-,故答案为:,1)、(1)-.例题11.在平面直角坐标系中,已知O 为坐标原点,点(3,0)A ,(0,4)B ,以点A 为旋转中心,把ABO ∆顺时针旋转,得ACD ∆.记旋转角为α.ABO ∠为β.(Ⅰ)如图①,当旋转后点D 恰好落在AB 边上时,求点D 的坐标;(Ⅱ)如图②,当旋转后满足//BC x 轴时,求α与β之间的数量关系:(Ⅲ)当旋转后满足AOD β∠=时,求直线CD 的解析式(直接写出结果即可).【解答】解:(1) 点(3,0)A ,(0,4)B ,得3OA =,4OB =,∴在Rt AOB ∆中,由勾股定理,得225AB OA OB =+=,根据题意,有3DA OA ==.如图①,过点D 作DM x ⊥轴于点M ,则//MD OB ,ADM ABO ∴∆∆∽.有AD AM DM AB AO BO==,得39355AD AM AO AB ==⨯= ,65OM ∴=,∴125MD =,∴点D 的坐标为6(5,12)5.(2)如图②,由已知,得CAB α∠=,AC AB =,ABC ACB ∴∠=∠,∴在ABC ∆中,1802ABC α∴=︒-∠,//BC x 轴,得90OBC ∠=︒,9090ABC ABO β∴∠=︒-∠=︒-,2αβ∴=;(3)若顺时针旋转,如图,过点D 作DE OA ⊥于E ,过点C 作CF OA ⊥于F ,AOD ABO β∠=∠= ,3tan 4DE AOD OE ∴∠==,设3DE x =,4OE x =,则43AE x =-,在Rt ADE ∆中,222AD AE DE =+,2299(43)x x ∴=+-,2425x ∴=,96(25D ∴,72)25,∴直线AD 的解析式为:247277y x =-, 直线CD 与直线AD 垂直,且过点D ,∴设724y x b =-+,把96(25D ,72)25代入得,72796252425b =-⨯+,解得4b =,互相垂直的两条直线的斜率的积等于1-,∴直线CD 的解析式为7424y x =-+.同理可得直线CD的另一个解析式为7424y x=-.【巩固练习】1.如图,在等边ABC ∆中,D 是边AC 上一点,连接BD .将BCD ∆绕点B 逆时针旋转60︒得到BAE ∆,连接ED .若10BC =,9BD =,则AED ∆的周长是.2.如图一段抛物线:(3)(03)y x x x =--,记为1C ,它与x 轴交于点O 和1A ;将1C 绕1A 旋转180︒得到2C ,交x 轴于2A ;将2C 绕2A 旋转180︒得到3C ,交x 轴于3A ,如此进行下去,直至得到10C ,若点(28,)P m 在第10段抛物线10C 上,则m 的值为.3.如图,Rt ABC ∆中,90C ∠=︒,30ABC ∠=︒,2AC =,ABC ∆绕点C 顺时针旋转得△11A B C ,当1A 落在AB 边上时,连接1B B ,取1BB 的中点D ,连接1A D ,则1A D 的长度是.4.如图,AOB ∆中,90AOB ∠=︒,3AO =,6BO =,AOB ∆绕点O 逆时针旋转到△A OB ''处,此时线段A B ''与BO 的交点E 为BO 的中点,求线段B E '的值.5.如图,在直角坐标系中,直线14:83l y x =+与y 轴交于点A ,与x 轴交于点B ,将直线1l 绕着点A 顺时针旋转45︒得到2l .求2l 的函数表达式.6.如图,四边形ABCO 是平行四边形,2OA =,6AB =,点C 在x 轴的负半轴上,将ABCO 绕点A 逆时针旋转得到ADEF ,AD 经过点O ,点F 恰好落在x 轴的正半轴上,若点D 在反比例函数(0)k y x x =<的图象上,则k 的值为.7.在平面直角坐标系中,O 为坐标原点,点A 的坐标为(8,0)-,直线BC 经过点(8,6)B -,(0,6)C ,将四边形OABC 绕点O 按顺时针方向旋转a 度得到四边形OA B C ''',此时直线OA '、直线B C ''分别与直线BC 相交于点P 、Q .在四边形OABC 旋转过程中,若使12BP BQ =?则点P 的坐标为.8.如图,在BDE ∆中,90BDE ∠=︒,BD =,点D 的坐标为(5,0),15BDO ∠=︒,将BDE∆旋转到ABC ∆的位置,点C 在BD 上,则旋转中心的坐标为.9.已知正方形ABCD 的边长为5,E 在BC 边上运动,DE 的中点G ,EG 绕E 顺时针旋转90︒得EF ,问CE =时,A 、C 、F 在一条直线上.10.如图,一次函数1(0)2y x m m =-+>的图象与x 轴、y 轴分别交于点A 、B ,点C 在线段OA 上,点C 的横坐标为n ,点D 在线段AB 上,且2AD BD =,将ACD ∆绕点D 旋转180︒后得到△11A C D .(1)若点1C 恰好落在y 轴上,试求n m的值;(2)当4n =时,若△11A C D 被y 轴分得两部分图形的面积比为3:5,求该一次函数的解析式.11.在ABC ∆中,5AB AC ==,3cos 5ABC ∠=,将ABC ∆绕点C 顺时针旋转,得到△11A B C .(1)如图①,当点1B 在线段BA 延长线上时.①求证:11//BB CA ;②求△1AB C 的面积;(2)如图②,点E 是BC 边的中点,点F 为线段AB 上的动点,在ABC 绕点C 顺时针旋转过程中,点F 的对应点是1F ,求线段1EF 长度的最大值与最小值的差.12.如图(1),在ABC=,动点P在线段AC上以5/cm s的速度从=,3BC cmAB cmC∆中,90∠=︒,5点A运动到点C,过点P作PD AB',设点P的⊥于点D,将APD∆绕PD的中点旋转180︒得到△A DP 运动时间为()x s.(1)当点A'落在边BC上时,求x的值;(2)在动点P从点A运动到点C过程中,当x为何值时,△A BC'是以A B'为腰的等腰三角形;(3)如图(2),另有一动点Q与点P同时出发,在线段BC上以5/cm s的速度从点B运动到点C,过点Q 作QE AB⊥于点E,将BQE',连结A B'',当直线A B''与ABC∆绕QE的中点旋转180︒得到△B EQ∆的一边垂直时,求线段A B''的长.13.如图,(0,2)A ,(1,0)B ,点C 为线段AB 的中点,将线段BA 绕点B 按顺时针方向旋转90︒得到线段BD ,抛物线2(0)y ax bx c a =++≠经过点D .(1)若该抛物线经过原点O ,且13a =-,求该抛物线的解析式;(2)在(1)的条件下,点(,)P m n 在抛物线上,且POB ∠锐角,满足90POB BCD ∠+∠<︒,求m 的取值范围.14.如图1,抛物线210y ax ax c =-+经过ABC ∆的三个顶点,已知//BC x 轴,点A 在x 轴上,点C 在y 轴上35OA BC =,且AC BC =.(1)求抛物线的解析式;(2)如图2,将AOC ∆沿x 轴对折得到1AOC ∆,再将1AOC ∆绕平面内某点旋转180︒后得△112(A O C A ,O ,1C 分别与点1A ,1O ,2C 对应)使点1A 、2C 在抛物线_P 上,求点1A 、2C 的坐标;15.点P为图①中抛物线22m>上任一点,将抛物线绕顶点G逆时针旋转90︒=-+为常数,0)y x mx m m2(后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.(1)若点Q的坐标为(-,求该抛物线的函数关系式;(2)如图②,若原抛物线恰好也经过A点,点Q在第一象限内,是否存在这样的点P使得AGQ∆是以AG 为底的等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.参考答案1.【解答】解:ABC ∆ 是等边三角形,10AC AB BC ∴===,BAE ∆ 由BCD ∆逆时针旋旋转60︒得出,AE CD ∴=,BD BE =,60EBD ∠=︒,10AE AD AD CD AC ∴+=+==,60EBD ∠=︒ ,BE BD =,BDE ∴∆是等边三角形,9DE BD ∴==,AED ∴∆的周长19AE AD DE AC BD =++=+=.故答案为:19.2.【解答】解:令0y =,则(3)0x x --=,解得10x =,23x =,1(3,0)A ∴,由图可知,抛物线10C 在x 轴下方,相当于抛物线1C 向右平移3927⨯=个单位,再沿x 轴翻折得到,∴抛物线10C 的解析式为(27)(273)(27)(30)y x x x x =---=--,(28,)P m 在第10段抛物线10C 上,(2827)(2830)2m ∴=--=-.3.【解答】解:90ACB ∠=︒ ,30ABC ∠=︒,2AC =,9060A ABC ∴∠=︒-∠=︒,4AB =,BC =,1CA CA = ,1ACA ∴∆是等边三角形,112AA AC BA ===,1160BCB ACA ∴∠=∠=︒,1CB CB = ,1BCB ∴∆是等边三角形,1BB ∴=,12BA =,1190A BB ∠=︒,1BD DB ∴==,1A D ∴==,.4.【解答】解:90AOB ∠=︒ ,3AO =,6BO =,AB ∴==AOB ∆ 绕顶点O 逆时针旋转到△A OB ''处,3AO A O ∴='=,A B AB ''==,点E 为BO 的中点,116322OE BO ∴==⨯=,OE A O ∴=',过点O 作OF A B ⊥''于F ,1362A OB S OF ''=⨯=⨯⨯ ,解得655OF =,在Rt EOF ∆中,5EF ==,OE A O =' ,OF A B ⊥'',22A E EF ∴'==(等腰三角形三线合一),B E A B A E ∴'=''-'=5.【解答】解: 直线483y x =+与y 轴交于点A ,与x 轴交于点B ,(0,8)A ∴、(6,0)B -,如图2,过点B 做BC AB ⊥交直线2l 于点C ,过点C 作CD x ⊥轴,在BDC ∆和AOB ∆中,CBD BAO CDB AOB BC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩()BDC AOB AAS ∴∆≅∆,6CD BO ∴==,8BD AO ==,6814OD OB BD ∴=+=+=,C ∴点坐标为(14,6)-,设2l 的解析式为y kx b =+,将A ,C 点坐标代入,得1468k b b -+=⎧⎨=⎩,解得178k b ⎧=⎪⎨⎪=⎩,2l ∴的函数表达式为187y x =+;6.【解答】解:如图所示:过点D 作DM x ⊥轴于点M ,由题意可得:BAO OAF ∠=∠,AO AF =,//AB OC ,则BAO AOF AFO OAF ∠=∠=∠=∠,故60AOF DOM ∠=︒=∠,624OD AD OA AB OA =-=-=-= ,2MO ∴=,MD =,(2,D ∴--,2(k ∴=-⨯-=.故答案为:.7.【解答】解:存在这样的点P 和点Q ,使12BP BQ =.理由如下:过点Q 画QH OA ⊥'于H ,连接OQ ,则QH OC OC ='=,12POQ S PQ OC ∆= ,12POQ S OP QH ∆= ,PQ OP ∴=.设BP x =,12BP BQ =,2BQ x ∴=,如图4,当点P 在点B 左侧时,3OP PQ BQ BP x ==+=,在Rt PCO ∆中,222(8)6(3)x x ++=,解得13612x =+,23612x =-,(不符实际,舍去).3692PC BC BP ∴=+=+,1(92P ∴--,6),如图5,当点P 在点B 右侧时,OP PQ BQ BP x ∴==-=,8PC x =-.在Rt PCO ∆中,222(8)6x x -+=,解得254x =,257844PC BC BP ∴=-=-=,27(4P ∴-,6),综上可知,存在点136(92P --,6),27(4P -,6)使12BP BQ =.8.【解答】解:如图,AB 与BD 的垂直平分线的交点即为旋转中心P ,连接PD ,过P 作PF x ⊥轴于F .点C 在BD 上,∴点P 到AB 、BD 的距离相等,都是12BD ,即12⨯=45PDB ∴∠=︒,4PD ==,15BDO ∠=︒ ,451560PDO ∴∠=︒+︒=︒,30DPF ∴∠=︒,114222DF PD ∴==⨯=, 点D 的坐标是(5,0),523OF OD DF ∴=-=-=,由勾股定理得,PF ===∴旋转中心的坐标为(3,.故答案为:(3,.9.【解答】解:过F 作FN BC ⊥,交BC 延长线于N 点,连接AC ,90DCE ENF ∠=∠=︒ ,90DEC NEF ∠+∠=︒,90NEF EFN ∠+∠=︒,DEC EFN ∴∠=∠,Rt FNE Rt ECD ∴∆∆∽,DE 的中点G ,EG 绕E 顺时针旋转90︒得EF ,:2:1DE EF ∴=,:::2:1CE FN DE EF DC NE ∴===,2CE NF ∴=,1522NE CD ==.45ACB ∠=︒ ,∴当45NCF ∠=︒时,A 、C 、F 在一条直线上.则CNF ∆是等腰直角三角形,CN NF ∴=,2CE CN ∴=,22553323CE NE ∴==⨯=.53CE ∴=时,A 、C 、F 在一条直线上.故答案为:53.10.【解答】解:(1)由题意,得(0,)B m ,(2,0)A m ,如图,过点D 作x 轴的垂线,交x 轴于点E ,交直线11A C 于点F ,易知:23DE m =,2(3D m ,2)3m ,14(3C m n -,4)3m ,∴403m n -=,∴43n m =;(2)由(1)得,当3m >时,点1C 在y 轴右侧;当23m <<时,点1C 在y 轴左侧.①当3m >时,设11A C 与y 轴交于点P ,连接1C B ,由△11A C D 被y 轴分得两部分图形的面积比为3:5,S ∴△1:BA P S △13:1BC P =,11:3A P C P ∴=,∴,185m ∴=,11825y x ∴=-+;②当23m <<时,同理可得:11827y x =-+;综上所述,11827y x =-+或11825y x =-+.11.【解答】解:(1)①证明:AB AC = ,1B C BC =,1AB C B ∴∠=∠,B ACB ∠=∠,1AB C ACB ∠=∠ (旋转角相等),111B CA AB C ∴∠=∠,11//BB CA ∴;②过A 作AF BC ⊥于F ,过C 作CE AB ⊥于E ,如图①:AB AC = ,AF BC ⊥,BF CF ∴=,3cos 5ABC ∠=,5AB =,3BF ∴=,6BC ∴=,16B C BC ∴==,1318655BE B E ∴==⨯=,1365BB ∴=,424655CE =⨯=,13611555AB ∴=-=,∴△1AB C 的面积为:1112413225525⨯⨯=;(2)如图2,过C 作CF AB ⊥于F ,以C 为圆心CF 为半径画圆交BC 于1F ,1EF 有最小值,此时在Rt BFC ∆中,245CF =,1245CF ∴=,1EF ∴的最小值为249355-=;如图,以C 为圆心BC 为半径画圆交BC 的延长线于1F ,1EF 有最大值;此时11369EF EC CF =+=+=,∴线段1EF 的最大值与最小值的差为936955-=.12.【解答】解:(1)如图1, 在ABC ∆中,90C ∠=︒,5AB cm =,3BC cm =,4AC cm ∴=,当点A '落在边BC 上时,由题意得,四边形APA D '为平行四边形,PD AB ⊥ ,90ADP C ∴∠=∠=︒,APD ABC ∴∆∆∽,5AP x = ,4A P AD x ∴'==,45PC x =-,A PD ADP ∠'=∠ ,//A P AB ∴',∴△A PC ABC '∆∽,∴PC A P AC AB '=,即45445x x -=,解得:2041x =,∴当点A '落在边BC 上时,2041x =;(2)当A B BC '=时,222(58)(3)3x x -+=,解得:4012373x ±=.45x ,∴4073x -=;当A B A C '='时,58x =.(3)Ⅰ、当A B AB ''⊥时,如图6,DH PA AD '∴==,HE B Q EB ='=,2224235AB AD EB x x =+=⨯+⨯= ,514x ∴=,514A B QE PD x ∴''=-==;Ⅱ、当A B BC ''⊥时,如图7,5B E x ∴'=,57DE x =-,53cos 575x B x ∴==-,1546x ∴=,2523A B B D A D ∴''='-'=;Ⅲ、当A B AC ''⊥时,如图8,由(1)有,2041x =,12sin 41A B PA A ∴''='=;当A B AB ''⊥时,514x =,514A B ''=;当A B BC ''⊥时,1546x =,2546A B ''=;当A B AC ''⊥时,2053x =,2553A B ''=.13.【解答】解:(1)过点D 作DF x ⊥轴,垂足为F .90ABD ∠=︒ ,90DBF ABO ∴∠+∠=︒.又90OAB ABO ∠+∠=︒ ,DBF OAB ∴∠=∠.由旋转的性质可知AB BD =.在AOB ∆和BFD ∆中DBF OAB AOB BFD AB BD ∠=∠⎧⎪∠=∠⎨⎪=⎩,AOB BFD ∴∆≅∆.1DF OB ∴==,2AO BF ==.(3,1)D ∴.把点D 和点O 的坐标代入213y x bx c =-++得:1300b c c -++=⎧⎨=⎩,解得:43b =,0c =.∴抛物线的解析式为21433y x x =-+.(2)如图2所示:点(0,2)A ,(1,0)B ,C 为线段AB 的中点,1(2C ∴,1).C 、D 两点的纵坐标为1,//CD x ∴轴.BCD ABD ∴∠=∠.∴当POB BAO ∠=∠时,恰好90POB BCD ∠+∠=︒.设点P 的坐标为214(,)33m m m -+.当点P 在x 轴上且POB BAO ∠=∠时,则1tan tan 2POB BAO ∠=∠=,即2141332m m m -+=,解得:52m =或0m =(舍去).当点P 位于x 轴的下方,点P '处时,且POB BAO ∠=∠时,则1tan tan 2POB BAO ∠=∠=,即2141332m m m -=,解得:112m =或0m =(舍去).POB ∠ 为锐角,4m ∴≠.由图形可知:当点P 在抛物线上P 与P '之间移动时,90POB BCD ∠+∠<︒.m ∴的取值范围是:51122m <<且4m ≠.14.【解答】解:(1)35OA BC = ,AC BC =∴设3OA k =,5(0)AC BC k k ==>4OC k∴= 当0x =时,210y ax ax c c=-+=(0,)C c ∴,即4OC c k==4c k ∴=3(4c A ∴-,50)(4c B ,)c 抛物线经过点A 、B ∴2233()10()04455(1044c c a a c c c a a c c ⎧---+=⎪⎪⎨⎪-+=⎪⎩解得:1128a c ⎧=-⎪⎨⎪=⎩∴抛物线解析式为:2158126y x x =-++(2)如图1,1AOC ∆旋转后得到△112A O C 的位置如图所示116O A OA ∴==,128O C OC ==,11//O A x 轴,12O C x ⊥轴设2C 坐标为215(,8)126t t t -++,则2115(6,)126A t t t +-+221515(6)(6)8126126t t t t ∴-++++=-+解得:10t =1A ∴坐标为(16,0),2C 坐标为(10,8).15.【解答】解:(1) 对于222y x mx m =-+,当0y =时,x m =,OG m ∴=,点Q 为点P 绕顶点G 逆时针旋转90︒后的对应点,P m ∴,2)m +,把P m +,2)m +代入222y x mx m =-+中,得222)2)m m m m m +=-+,4m ∴=,∴该抛物线的函数关系式为;2816y x x =-+;(2)存在,点Q 在第一象限内,AQ GQ =,如图2中,由题意可知OA OG =,∴m =,1m ∴=,∴点(0,1)A ,点A 的对应点(2,1)C ,(1,0)G ,∴直线CG 解析式为1y x =-,线段CG 的中垂线MN 解析式为2y x =-+,由2221y x y x x =-+⎧⎨=-+⎩解得15232x y ⎧=⎪⎪⎨⎪=⎪⎩或15232x y ⎧=⎪⎪⎨⎪=⎪⎩, 点P 在第一象限,∴点P坐标1(2+,32-.。
奥数天天练——旋转与轨迹(学生版)
奥数天天练——旋转与轨迹(学⽣版)【例 1】正三⾓形ABC 的边长是6厘⽶,在⼀条直线上将它翻滚⼏次,使A 点再次落在这条直线上,那么A点在翻滚过程中经过的路线总长度是多少厘⽶?如果三⾓形⾯积是15平⽅厘⽶,那么三⾓形在滚动过程中扫过的⾯积是多少平⽅厘⽶?(结果保留π)【巩固】直⾓三⾓形ABC 放在⼀条直线上,斜边AC 长20厘⽶,直⾓边BC 长10厘⽶.如下图所⽰,三⾓形由位置Ⅰ绕A 点转动,到达位置Ⅱ,此时B ,C 点分别到达1B ,1C 点;再绕1B 点转动,到达位置Ⅲ,此时A ,1C 点分别到达2A ,2C 点.求C 点经1C 到2C ⾛过的路径的长.60?30?B 1C 1C 2A 2CB AⅢⅡⅠ【巩固】如图,⼀条直线上放着⼀个长和宽分别为4cm 和3cm 的长⽅形Ⅰ.它的对⾓线长恰好是5cm .让这个长⽅形绕顶点B 顺时针旋转90°后到达长⽅形Ⅱ的位置,这样连续做三次,点A 到达点E 的位置.求点A ⾛过的路程的长.ⅣⅢⅡⅠEDCBA【例 2】草场上有⼀个长20⽶、宽10⽶的关闭着的⽺圈,在⽺圈的⼀⾓⽤长30⽶的绳⼦拴着⼀只⽺(见如图).问:这只⽺能够活动的范围有多⼤?(圆周率取3.14)【巩固】⼀只狗被拴在底座为边长3m的等边三⾓形建筑物的墙⾓上(如图),绳长是4m,求狗所能到的地⽅的总⾯积.(圆周率按3.14计算)3【例3】如图是⼀个直径为3cm的半圆,让这个半圆以A点为轴沿逆时针⽅向旋转60?,此时B点移动到'B 点,求阴影部分的⾯积.(图中长度单位为cm,圆周率按3计算).BA【例4】如图所⽰,直⾓三⾓形ABC的斜边AB长为10厘⽶,60∠=?,此时BC长5厘⽶.以点B为ABC中⼼,将ABC顺时针旋转120?,点A、C分别到达点E、D的位置.求AC边扫过的图形即图中阴影部分的⾯积.(π取3)E【巩固】如右图,以OA 为斜边的直⾓三⾓形的⾯积是24平⽅厘⽶,斜边长10厘⽶,将它以O 点为中⼼旋转90?,问:三⾓形扫过的⾯积是多少?(π取3)【巩固】(2008年“学⽽思杯”数学试题)如图,直⾓三⾓形ABC 中,B ∠为直⾓,且2BC =厘⽶,4AC = 厘⽶,则在将ABC ?绕C 点顺时针旋转120?的过程中,AB 边扫过图形的⾯积为.(π 3.14=)CB AB'A'C B A【例 5】如图,ABC ?是⼀个等腰直⾓三⾓形,直⾓边的长度是1⽶.现在以C 点为圆⼼,把三⾓形ABC 顺时针转90度,那么,AB 边在旋转时所扫过的⾯积是平⽅⽶.(π 3.14=)ABC(B')A B【例 6】 (祖冲之杯竞赛试题)如图,ABCD 是⼀个长为4,宽为3,对⾓线长为5的正⽅形,它绕C 点按顺时针⽅向旋转90 ,分别求出四边扫过图形的⾯积.CBD A【例 7】 (2004年第九届华杯赛初赛)半径为25厘⽶的⼩铁环沿着半径为50厘⽶的⼤铁环的内侧作⽆滑动的滚动,当⼩铁环沿⼤铁环滚动⼀周回到原位时,问⼩铁环⾃⾝转了⼏圈?【巩固】如果半径为25厘⽶的⼩铁环沿着半径为50厘⽶的⼤铁环的外侧作⽆滑动的滚动,当⼩铁环沿⼤铁环滚动⼀周回到原位时,问⼩铁环⾃⾝转了⼏圈?【巩固】如图所⽰,⼤圆周长是⼩圆周长的n(1n )倍,当⼩圆在⼤圆内侧(外侧)作⽆滑动的滚动⼀圈后⼜回到原来的位置,⼩圆绕⾃⼰的圆⼼转动了⼏周?【例8】如图,15枚相同的硬币排成⼀个长⽅形,⼀个同样⼤⼩的硬币沿着外圈滚动⼀周,回到起始位置.问:这枚硬币⾃⾝转动了多少圈?【巩固】12个相同的硬币可以排成下⾯的4种正多边形(圆⼼的连线).⽤⼀个同样⼤⼩的硬币,分别沿着四个正多边形的外圈⽆滑动地滚动⼀周.问:在哪个图中这枚硬币⾃⾝转动的圈数最多,最多转动了多少圈?【例 9】⼀枚半径为1cm 的圆形硬币相互紧靠着平放在桌⾯上,让⼀枚硬币沿着它们的外轮廓滚过后回到原来的位置,那么与原A 点重合的点是______.硬币⾃⼰转动______,硬币圆⼼的运动轨迹周长为_______.【例 10】先做⼀个边长为2cm 的等边三⾓形,再以三个顶点为圆⼼,2cm 为半径作弧,形成曲边三⾓形(如左图).再准备两个这样的图形,把⼀个固定住(右图中的阴影),另⼀个围绕着它滚动,如右图那样,从顶点相接的状态下开始滚动.请问此图形滚动时经过的⾯积是多少平⽅厘⽶?(π 3.14 )CBA 222【练1】取⼋个⼤⼩相同的硬币,摆成右图形状。
初中数学专题:旋转问题
1 My*学习要点与方法点拨:
出题位置:选择、填空最后一道题和倒数第二道题,压轴题最后两道
“旋转”在苏教版中是一个独立章节,在中考和平时的考试张经常出现,结合三角形, 对旋转的应用。同时,旋转对解决动点问题有极大的帮助。
」、基本图形一: 将/ AOB旋转至/ A'OB',图①、②分别可以得到结论?
旋转点会有一组对角相等( 考题规律,如果已知条件为较小的角度相等,则题目一定需要较大的角相等;如果 条件给出较大的角相等,则一定需要较小的角相等 )
、基本图形二: 将厶AOB旋转至△ A OB连接AA与BB',分别在图①、②中证明△ OAA^fA OBB相似。
旋转后连接得到的两个三角形相似。 因为旋转的两个三角形全等,连接后出现等腰三角形,顶角相等;则底角亦相等;或根据夹角成比例证明相似。
三、解题步骤 (1) 第一步:找旋转点,角相等; (2) 第二步:证全等、相似; (3) 第三步:利用全等、相似得到边、角条件。
专题二旋转
② 四边形等基本图形考察学生 2 $模块精讲 例1.在锐角△ ABC中,AB=4, BC=5 / ACB=45,将△ ABC绕点B按逆时针方向旋转,得到△ ABG.
(1)当点Ci在线段CA的延长线上时,如图 1,求/ CGA的度数;
(2)如图2,A ABC绕点B按逆时针方向旋转,连接 AAi,。6,若厶ABA的面积为4,求厶CBG的面积;
(3)点E为线段AB中点,点P是线段AC上的动点,在厶ABC绕点B按逆时针方向旋转过程中, 点P的对应点是点 Pi, 求线段EP长度的最大值与最小值.
例2.已知△ ABC是等边三角形
(1)将厶ABC绕点A逆时针旋转角(0 °v日V 180°),得到△ ADE BD和EC所在直线相交于点 O ①如图a,当=20。时,△ ABD与△ ACE是否全等? (填“是”或“否”), / BOE= 度; ②当△ ABC旋转到如图b所在位置时,求/ BOE的度数; ⑵如图c,在AB和AC上分别截取点B'和C',使AB=AB ,AC=AC'J2连接B'。’,将厶AB C'绕点A逆时 针旋转角(0° V V 180°),得到△ ADE BD和EC所在直线相交于点 O,请利用图c探索/ BOE的度数,直接写出结果,不必说明理由 3 例4.【2016 •扬州】已知正方形ABCD的边长为4, 一个以点A为顶点的45°角绕点A旋转,角的两边分别与 边BC DC的
(完整版)九年级上圆与旋转专题期末复习讲义
期末复习2(圆与旋转)学生/课程年级学科授课教师日期时段核心内容旋转、中心对称、圆课型一对一教学目标1.掌握旋转的性质2.掌握中心对称图形3.掌握垂径定理、圆周角定理,以及圆的切线等知识重、难点重点:旋转与圆的性质难点:旋转与圆的综合应用知识梳理旋转1、概念:把一个图形绕着某一点O转动一个角度的图形变换叫做旋转,点O叫做旋转中心,转动的角叫做旋转角.旋转三要素:旋转中心、旋转方向、旋转角2、旋转的性质:(1)旋转前后的两个图形是全等形;(2)两个对应点到旋转中心的距离相等(3)两个对应点与旋转中心的连线段的夹角等于旋转角3、中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.4、中心对称的性质:(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.(2)关于中心对称的两个图形是全等图形. 5、中心对称图形:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.6、坐标系中的中心对称:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点P′(-x,-y).圆1、垂径定理及论:2、如图:有五个元素,“知二可推三”;需记忆其中四个推论.3、圆周角定理及推论:(1)圆周角的度数等于它所对的弧的度数的一半;(2)一条弧所对的圆周角等于它所对的圆心角的一半;(如图)(3)“等弧对等角”“等角对等弧”;(4)“直径对直角”“直角对直径”;(如图)(5)如三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(如图)(6)圆内接四边形,对角互补4、切线的判定与性质定理:如图:有三个元素,“知二可推一”;需记忆其中四个定理.5、有关的计算:导学一:图形的旋转例 1. 如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=度.我爱展示1. [单选题] 如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=;⑤S△AOC+S△AOB=.其中正确的结论是().A.①②③⑤B.①②③④C.①②③④⑤D.①②③导学二:旋转的综合应用例 1. 已知边长为1cm的正方形ABCD和正方形AEFG如图1放置,点B,D分别在AE,AG上,将正方形ABCD绕点A顺时针旋转,设旋转角为α(0°<α<90°).(1)连接BE,DG,如图2所示,求证:BE=DG;(2)当0°<α<45°时,在图2中,连接AF交BC于点P,CD交AG于Q,连接PQ,求证:旋转过程中△PCQ的周长等于定值2m;(3)如图3,连接CF,取CF的中点O,连接BO,GO,试判断△BOG的形状,并说明理由.【学有所获】(1)遇到线段和差的问题,可以通过截长补短来构造辅助线 (2)当遇到等腰三角形、正方形,或者两条相等线段有公共顶点的时候,可以考虑使用旋转的方法来构造辅助线。
中考数学专题模型—【专题12】几何图形的旋转模型研究(学生版+教师版)
【专题12】几何图形的旋转模型研究【回归概念】旋转变换是由一个图形改变为另一个图形,在改变过程中,原图上所有的点都绕一个固定的点换同一方向,转动同一个角度。
旋转模型主要体现在以下几个情况:【规律探寻】1.共顶点旋转模型(证明基本思想“SAS”)2.利用旋转思想构造辅助线(1)根据相等的边先找出被旋转的三角形(2)根据对应边找出旋转角度(3)根据旋转角度画出对应的旋转的三角形3.旋转变换前后具有以下性质:(1)对应线段相等,对应角相等(2)对应点位置的排列次序相同(3)任意两条对应线段所在直线的夹角都等于旋转角 .4.旋转变换还用于处理:①几何最值问题:几何最值两个重要公理依据是:两点之间线段最短和垂线段最短;②有关线段的不等关系;③自己构造绕某点旋转某角度(特别是60度),把共顶点的几条线段变为首尾相接的几条线段,再变为共线取得最小值问题,计算中常用到等腰三角形或勾股定理等知识。
【典例解析】【例题1】(2019•湖北省随州市•3分)如图,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为______.【例题2】(2019•浙江绍兴•12分)如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.(1)在旋转过程中,①当A,D,M三点在同一直线上时,求AM的长.②当A,D,M三点为同一直角三角形的顶点时,求AM的长.(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2,此时∠AD2C=135°,CD2=60,求BD2的长.【例题3】(2018•自贡)如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.【达标检测】1. (2018海南)(3.00分)如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为()A.6 B.8 C.10 D.122. (2017山东泰安)如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为()A.30°B.60° C.90° D.120°3. (2019•湖北省荆门市•3分)如图,Rt△OCB的斜边在y轴上,OC=3,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B',则B点的对应点B′的坐标是()A3,﹣1)B.(13)C.(2,0)D3,0)4. 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF 中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=()A.5 B.4 C. D.5.(2019浙江丽水3分)将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM,GN是折痕.若正方形EFGH与五边形MCNGF的面积相等,则的值是()A.522B.2﹣1 C.D.226. (2019•湖南常德•3分)如图,已知△ABC是等腰三角形,AB=AC,∠BAC=45°,点D在AC边上,将△ABD绕点A逆时针旋转45°得到△ACD′,且点D′、D、B三点在同一条直线上,则∠ABD的度数是.7. (2019•湖南益阳•4分)在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是.8. (2019•海南省•4分)如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连结EF.若AB=3,AC=2,且α+β=∠B,则EF=.9. (2019,山西,3分)如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE 交AC于点F,则CF的长为 cm.10. (2019•广西北部湾•8分)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,-1)、B(1,-2)、C(3,-3).(1)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1;(2)请画出△ABC关于y轴对称的△A2B2C2;(3)请写出A1、A2的坐标.11. (2018•宁波)如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.(1)求证:△ACD≌△BCE;(2)当AD=BF时,求∠BEF的度数.14,点D,E分别在边12. (2019•浙江丽水•12分)如图,在等腰Rt△ABC中,∠ACB=90°,AB=2AB,BC上,将线段ED绕点E按逆时针方向旋转90°得到EF.(1)如图1,若AD=BD,点E与点C重合,AF与DC相交于点O.求证:BD=2DO.(2)已知点G为AF的中点.①如图2,若AD=BD,CE=2,求DG的长.②若AD=6BD,是否存在点E,使得△DEG是直角三角形?若存在,求CE的长;若不存在,试说明理由.【参考答案】【典例解析】【例题1】(2019•湖北省随州市•3分)如图,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为______.【答案】(-2,2)【解析】解:∵点C的坐标为(1,0),AC=2,∴点A的坐标为(3,0),如图所示,将Rt△ABC先绕点C逆时针旋转90°,则点A′的坐标为(1,2),再向左平移3个单位长度,则变换后点A′的对应点坐标为(-2,2),故答案为:(-2,2).根据旋转变换的性质得到旋转变换后点A的对应点坐标,根据平移的性质解答即可.本题考查的是坐标与图形变化旋转和平移,掌握旋转变换、平移变换的性质是解题的关键.【例题2】(2019•浙江绍兴•12分)如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.(1)在旋转过程中,①当A,D,M三点在同一直线上时,求AM的长.②当A,D,M三点为同一直角三角形的顶点时,求AM的长.(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2,此时∠AD2C=135°,CD2=60,求BD2的长.【分析】(1)①分两种情形分别求解即可.②显然∠MAD不能为直角.当∠AMD为直角时,根据AM2=AD2﹣DM2,计算即可,当∠ADM=90°时,根据AM2=AD2+DM2,计算即可.(2)连接CD.首先利用勾股定理求出CD1,再利用全等三角形的性质证明BD2=CD1即可.【解答】解:(1)①AM=AD+DM=40,或AM=AD﹣DM=20.②显然∠MAD不能为直角.当∠AMD为直角时,AM2=AD2﹣DM2=302﹣102=800,∴AM=202或(﹣202舍弃).当∠ADM=90°时,AM2=AD2+DM2=302+102=1000,∴AM=1010或(﹣1010舍弃).综上所述,满足条件的AM的值为202或1010.(2)如图2中,连接CD.由题意:∠D1AD2=90°,AD1=AD2=30,∴∠AD2D1=45°,D1D2=302,∵∠AD2C=135°,∴∠CD2D1=90°,∴CD1==6,∵∠BAC=∠A1AD2=90°,∴∠BAC﹣∠CAD2=∠D2AD1﹣∠CAD2,∴∠BAD1=∠CAD2,∵AB=AC,AD2=AD1,∴△BAD2≌△CAD1(SAS),∴BD2=CD1=6.【点评】本题属于四边形综合题,考查了等腰直角三角形的性质,勾股定理,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.【例题3】(2018•自贡)如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.【分析】(1)先判断出∠OCE=60°,再利用特殊角的三角函数得出OD=OC,同OE=OC,即可得出结论;(2)同(1)的方法得OF+OG=OC,再判断出△CFD≌△CGE,得出DF=EG,最后等量代换即可得出结论;(3)同(2)的方法即可得出结论.【解答】解:(1)∵OM是∠AOB的角平分线,∴∠AOC=∠BOC=∠AOB=30°,∵CD⊥OA,∴∠ODC=90°,∴∠OCD=60°,∴∠OCE=∠DCE﹣∠OCD=60°,在Rt△OCD中,OD=OC•cos30°=OC,同理:OE=OC,∴OD+OE=OC;(2)(1)中结论仍然成立,理由:过点C作CF⊥OA于F,CG⊥OB于G,∴∠OFC=∠OGC=90°,∵∠AOB=60°,∴∠FCG=120°,同(1)的方法得,OF=OC,OG=OC,∴OF+OG=OC,∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,∴OF=OD+DF=OD+EG,OG=OE﹣EG,∴OF+OG=OD+EG+OE﹣EG=OD+OE,∴OD+OE=OC;(3)(1)中结论不成立,结论为:OE﹣OD=OC,理由:过点C作CF⊥OA于F,CG⊥OB于G,∴∠OFC=∠OGC=90°,∵∠AOB=60°,∴∠FCG=120°,同(1)的方法得,OF=OC,OG=OC,∴OF+OG=OC,∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,∴OF=DF﹣OD=EG﹣OD,OG=OE﹣EG,∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD,∴OE﹣OD=OC.【达标检测】1. (2018海南)(3.00分)如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为()A.6 B.8 C.10 D.12【分析】根据旋转的性质得出AC=AC1,∠BAC1=90°,进而利用勾股定理解答即可.【解答】解:∵将△ABC绕点A逆时针旋转60°得到△AB1C1,∴AC=AC1,∠CAC1=90°,∵AB=8,AC=6,∠BAC=30°,∴∠BAC1=90°,AB=8,AC1=6,∴在Rt△BAC1中,BC1的长=,故选:C.2. (2017山东泰安)如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为()A.30° B.60° C.90° D.120°【分析】根据题意确定旋转中心后即可确定旋转角的大小.【解答】解:如图:显然,旋转角为90°,故选C.3. (2019•湖北省荆门市•3分)如图,Rt△OCB的斜边在y轴上,OC3,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B',则B点的对应点B′的坐标是()A.(3,﹣1)B.(1,﹣3)C.(2,0)D.(3,0)【分析】如图,利用含30度的直角三角形三边的关系得到BC=1,再利用旋转的性质得到OC′=OC =3,B′C′=BC=1,∠B′C′O=∠BCO=90°,然后利用第四象限点的坐标特征写出点B′的坐标.【解答】解:如图,在Rt△OCB中,∵∠BOC=30°,∴BC=33OC=33×3=1,∵Rt△OCB绕原点顺时针旋转120°后得到△OC′B',∴OC′=OC=3,B′C′=BC=1,∠B′C′O=∠BCO=90°,∴点B′的坐标为(3,﹣1).故选:A.【点评】本题考查了坐标与图形变化﹣旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.4. 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF 中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=()A.5 B.4 C.D.【分析】由△DQF∽△FQE,推出===,由此求出EQ、FQ即可解决问题.【解答】解:如图,在等腰直角三角形△DEF中,∠EDF=90°,DE=DF,∠1=∠2=∠3,∵∠1+∠QEF=∠3+∠DFQ=45°,∴∠QEF=∠DFQ,∵∠2=∠3,∴△DQF∽△FQE,∴===,∵DQ=1,∴FQ=,EQ=2,∴EQ+FQ=2+,故选D【点评】1.应用旋转解决几何问题时:(1)抓住旋转中的“变”与“不变”;(2)找准旋转前后的对应点和对应线段、旋转角等;(3)充分利用旋转过程中线段、角之间的关系.2.当旋转方向没有确定时,需要分类,即分逆时针和顺时针两种情况讨论.5. (2019浙江丽水3分)将一张正方形纸片按如图步骤,通过折叠得到图④,再沿虚线剪去一个角,展开铺平后得到图⑤,其中FM,GN是折痕.若正方形EFGH与五边形MCNGF的面积相等,则的值是()A.522- B .2﹣1 C . D .22【分析】连接HF ,设直线MH 与AD 边的交点为P ,根据剪纸的过程以及折叠的性质得PH =MF 且正方形EFGH 的面积=×正方形ABCD 的面积,从而用a 分别表示出线段GF 和线段MF 的长即可求解.【解答】解:连接HF ,设直线MH 与AD 边的交点为P ,如图:由折叠可知点P 、H 、F 、M 四点共线,且PH =MF ,设正方形ABCD 的边长为2a ,则正方形ABCD 的面积为4a 2,∵若正方形EFGH 与五边形MCNGF 的面积相等∴由折叠可知正方形EFGH 的面积=15×正方形ABCD 的面积=245a , ∴正方形EFGH 的边长GF =245a =255a ∴HF=2GF =2105a ∴MF=PH =210252a a -=5105a - ∴510-2552- 故选:A .【点评】本题主要考查了剪纸问题、正方形的性质以及折叠的性质,由剪纸的过程得到图形中边的关系是解题关键.6. (2019•湖南常德•3分)如图,已知△ABC 是等腰三角形,AB =AC ,∠BAC=45°,点D 在AC 边上,将△ABD 绕点A 逆时针旋转45°得到△ACD′,且点D′、D 、B 三点在同一条直线上,则∠ABD 的度数是 .【考点】旋转.【分析】由旋转的性质可得∠BAC=∠CAD'=45°,AD=AD',由等腰三角形的性质可得∠AD'D=67.5°,∠D'AB=90°,即可求∠ABD的度数.【解答】解:∵将△ABD绕点A逆时针旋转45°得到△ACD′,∴∠BAC=∠CAD'=45°,AD=AD',∴∠AD'D=67.5°,∠D'AB=90°,∴∠ABD=22.5°.故答案为22.5°.【点评】本题考查了旋转的性质,等腰三角形的性质,熟练运用旋转的性质是本题的关键.7. (2019•湖南益阳•4分)在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是.【考点】旋转.【分析】根据旋转角的概念找到∠BOB′是旋转角,从图形中可求出其度数.【解答】解:根据旋转角的概念:对应点与旋转中心连线的夹角,可知∠BOB′是旋转角,且∠BOB′=90°,故答案为90°.【点评】本题主要考查了旋转角的概念,解题的关键是根据旋转角的概念找到旋转角.8. (2019•海南省•4分)如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连结EF.若AB=3,AC=2,且α+β=∠B,则EF=.【分析】由旋转的性质可得AE =AB =3,AC =AF =2,由勾股定理可求EF 的长.【解答】解:由旋转的性质可得AE =AB =3,AC =AF =2,∵∠B+∠BAC =90°,且α+β=∠B ,∴∠BAC+α+β=90°∴∠EAF =90°∴EF == 故答案为: 【点评】本题考查了旋转的性质,勾股定理,灵活运用旋转的性质是本题的关键.9. (2019,山西,3分)如图,在△ABC 中,∠BAC=90°,AB=AC=10cm ,点D 为△ABC 内一点,∠BAD=15°,AD=6cm ,连接BD ,将△ABD 绕点A 逆时针方向旋转,使AB 与AC 重合,点D 的对应点E ,连接DE ,DE 交AC 于点F ,则CF 的长为 cm.【解析】过点A 作AG⊥DE 于点G ,由旋转可知:AD=AE ,∠DAE=90°,∠CAE=∠BAD=15° ∴∠AED=45°;在△AEF 中:∠AFD=∠AED+∠CAE=60°在Rt△ADG 中:AG=DG=232=AD 在Rt△AF G 中:622,63====FG AF AG GF ∴6210-=-=AF AC CF故答案为:6210-10. (2019•广西北部湾•8分)如图,在平面直角坐标系中,已知△ABC 的三个顶点坐标分别是A (2,-1)、B (1,-2)、C (3,-3).(1)将△ABC 向上平移4个单位长度得到△A 1B 1C 1,请画出△A 1B 1C 1;(2)请画出△ABC关于y轴对称的△A2B2C2;(3)请写出A1、A2的坐标.【答案】解:(1)如图所示:△A1B1C1,即为所求;(2)如图所示:△A2B2C2,即为所求;(3)A1(2,3),A2(-2,-1).【解析】(1)直接利用平移的性质得出对应点位置进而得出答案;(2)直接利用轴对称的性质得出对应点位置进而得出答案;(3)利用所画图象得出对应点坐标.此题主要考查了轴对称变换以及平移变换,正确得出对应点位置是解题关键.11. (2018•宁波)如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.(1)求证:△ACD≌△BCE;(2)当AD=BF时,求∠BEF的度数.【分析】(1)由题意可知:CD=CE,∠DCE=90°,由于∠ACB=90°,所以∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,所以∠ACD=∠BCE,从而可证明△ACD≌△BCE(SAS)(2)由△ACD≌△BCE(SAS)可知:∠A=∠CBE=45°,BE=BF,从而可求出∠BEF的度数.【解答】解:(1)由题意可知:CD=CE,∠DCE=90°,∵∠ACB=90°,∴∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,∴∠ACD=∠BCE,在△ACD与△BCE中,∴△ACD≌△BCE(SAS)(2)∵∠ACB=90°,AC=BC,∴∠A=45°,由(1)可知:∠A=∠CBE=45°,∵AD=BF,∴BE=BF,∴∠BEF=67.5°【点评】图形在旋转过程中,图中的每一个点与旋转中心的连线都绕着旋转中心转动了相同的角度,对应线段相等,对应角相等.在利用此性质解决问题时,应充分寻找对应线段、对应角.14,点D,E分别在边12. (2019•浙江丽水•12分)如图,在等腰Rt△ABC中,∠ACB=90°,AB=2AB,BC上,将线段ED绕点E按逆时针方向旋转90°得到EF.(1)如图1,若AD=BD,点E与点C重合,AF与DC相交于点O.求证:BD=2DO.(2)已知点G为AF的中点.①如图2,若AD=BD,CE=2,求DG的长.②若AD=6BD,是否存在点E,使得△DEG是直角三角形?若存在,求CE的长;若不存在,试说明理由.【考点】三角形综合.【分析】(1)如图1中,首先证明CD=BD=AD,再证明四边形ADFC是平行四边形即可解决问题.(2)①作DT⊥BC于点T,FH⊥BC于H.证明DG是△ABF的中位线,想办法求出BF即可解决问题.②分三种情形情形:如图3﹣1中,当∠DEG=90°时,F,E,G,A共线,作DT⊥BC于点T,FH⊥BC 于H.设EC=x.构建方程解决问题即可.如图3﹣2中,当∠EDG=90°时,取AB的中点O,连接OG.作EH⊥AB于H.构建方程解决问题即可.如图3﹣3中,当∠DGE=90°时,构造相似三角形,利用相似三角形的性质构建方程解决问题即可.【解答】(1)证明:如图1,∵CA=CB,∠ACB=90°,BD=AD,∴CD⊥AB,CD=AD=BD,∵CD=CF,∴AD=CF,∵∠ADC=∠DCF=90°,∴AD∥CF,∴四边形ADFC是平行四边形,∴OD=OC,∴BD=2OD.(2)①解:如图2,作DT⊥BC于点T,FH⊥BC于H.由题意:BD=AD=CD=2,BC2BD=14,∵DT⊥BC,∴BT=TC=7,∵EC=2,∴TE=5,∵∠DTE=∠EHF=∠DEF=90°,∴∠DET+∠TDE=90°,∠DET+∠FEH=90°,∴∠TDE=∠FEH,∵ED=EF ,∴△DTE≌△EHF(AAS),∴FH=ET =5,∵∠DDBE=∠DFE=45°,∴B,D ,E ,F 四点共圆,∴∠DBF+∠DEF=90°,∴∠DBF=90°,∵∠DBE=45°,∴∠FBH=45°,∵∠BHF=90°,∴∠HBF=∠HFB=45°,∴BH=FH =5,∴BF=52, ∵∠ADC=∠ABF=90°,∴DG∥BF, ∵AD=DB ,∴AG=GF ,∴DG=12BF =522. ②解:如图3﹣1中,当∠DEG=90°时,F ,E ,G ,A 共线,作DT⊥BC 于点T ,FH⊥BC 于H .设EC =x .∵AD=6BD ,∴BD=AB =22,∵DT⊥BC,∠DBT=45°,∴DT=BT =2,∵△DTE≌△EHF,∴EH=DT =2,∴BH=FH =12-x ,∵FH∥AC,∴=,∴14122x x -=, 整理得:x 2-12x+28=0,解得x 2. 如图3﹣2中,当∠EDG=90°时,取AB 的中点O ,连接OG .作EH⊥AB 于H .设EC =x ,由2①可知BF 2 (12-x),OG =12BF 2 (12-x),∵∠EHD=∠EDG=∠DOG=90°,∴∠ODG+∠OGD=90°,∠ODG+∠EDH=90°,∴∠DGO=∠HDE,∴△EHD∽△DOG,∴=,∴=,整理得:x2-36x+268=0,解得x=18-2或18+2(舍弃),如图3﹣3中,当∠DGE=90°时,取AB的中点O,连接OG,CG,作DT⊥BC于T,FH⊥BC于H,EK⊥CG 于K.设EC=x.∵∠DBE=∠DFE=45°,∴D,B,F,E四点共圆,∴∠DBF+∠DEF=90°,∵∠DEF=90°,∴∠DBF=90°,∵AO=OB,AG=GF,∴OG∥BF,∴∠AOG=∠ABF=90°,∴OG⊥AB,∵OG垂直平分线段AB,∵CA=CB,∴O,G,C共线,由△DTE≌△EHF,可得EH=DT=BT=2,ET=FH=12-x,BF=2 (12-x),OG=BF=22(12-x),CK=EK=22x,GK=72-22(12-x)-22x,由△OGD∽△KEG,可得=,∴=,解得x=2.综上所述,满足条件的EC的值为2或18-142.【点评】本题属于几何变换综合题,考查了等腰直角三角形的性质,平行四边形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奥数精品
【例1】 如图,正方形ABCD内一点P,15PADPDA,连结PB、PC,请问:PBC是等边三角形
吗?为什么?
P
D
C
B
A
【例2】 在ABC中,ABAC,P是ABC内任意一点,已知APCAPB,求证:PBPC.
A
P
CB
【例3】 如图,O是等边三角形ABC内一点,已知:115AOB,125BOC,则以线段OAOBOC,,为
边构成三角形的各角度数是多少?
O
C
B
A
【巩固】在等边ABC中,P为BC边上一点,则以AP、BP、CP为边组成的新三角形的最大内角为1,
则( )
A.90 B.120
C.120 D.135
【巩固】已知,如图,P是正方形ABCD内一点,且::1:2:3PAPBPC,求APB∠的度数.
例题精讲
旋转类全等问题
奥数精品
P
DC
BA
【巩固】如图所示:ABC中,90ACB,ACBC,P是ABC内的一点,且3AP,2CP,1BP,
求BPC的度数.
1
23
P
C
B
A
【例4】 如图,P为正方形ABCD内一点,123PAPDPC,,,将PDC绕着D点按逆时针旋转90到
PQD
的位置。
(1)求:PQPD的值;(2)求APD的度数。
Q
P
D
C
B
A
【例5】 如图,P是等边ABC内一点,若3AP,4PB,5PC,求APB的度数.
P
C
B
A
54
3
【巩固】如图所示,P是等边ABC内部一点,3PC,4PA,5PB,求ABC的边长.
P
CBA
【巩固】如图所示,P是等边ABC中的一点,2PA,23PB,4PC,试求ABC的边长.
