初中奥数讲义_完美的正方形附答案
非常完美正方形

OO G AB E HG ABHF A B 非常完美正方形【知识必备】1、正方形的相关性质,对角线把正方形分成四个全等的等腰直角三角形;2、“角平分线、平行线、等腰三角形”模型: “角平分线、垂线、等腰三角形”模型:4、“十字架”模型:即垂直必相等,但相等不一定垂直5、“半角”模型:正方形ABCD 中,∠EAF=450,则:(1)BE+DF=EF ;(2)222BG DH GH +=(3)∠AEB=∠AEF ;……【思想方法】1、 正方形具有轴对称、旋转不变性(绕顶点转或对角线交点转90度),一般总是与解直角三角形分不开;2、正方形的性质与轴对称(翻折)、旋转等图形变换结合;与线段垂直平分线、角平分线的结合;与三角形全等、相似的结合;【练习】1、如图,边长为2的正方形ABCD 中,AE 平分∠DAC ,AE 交CD 于点F ,C E ⊥AE ,垂足为E ,EG ⊥CD ,垂足为G ,点H 在BC 边上,BH=DF ,连接AH 、FH ,FH 与AC 交于点M ,则以下结论:①FH=2BH ;②AC ⊥FH ;③S △ACF =1;④CE=12AF ;⑤EG 2=FG•DG, 其中正确结论的个数为( )A .2个B .3个C .4个D .5个2、正方形ABCD 中,对角线AC 、BD 交于点O ,DE 平分∠ADO 交AC 于点E ,把△ADE 沿AD 翻折,得到得到△ADE′,点F 是DE 的中点,连接AF ,BF ,E′F .若AE=√2.则四边形ABFE′的面积是_______3、如图,在正方形ABCD 中,AB=6,点E 在CD 边上,DE=13DC ,连接AE ,将△ADE 沿AE 翻折,点D 落在点F 处,点O 是对角线BD 的中点,连接OF 并延长OF 交CD 于点G ,连接BF ,BG ,则△BFG 的周长是________.4、如图,正方形ABCD的边长为AC,BD相交于点O,E是OC的中点,连接BE,过点A作A M⊥BE于点M,交BD于点F,则FM的长为_________5、如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的是_______6、如图,正方形ABCD的边长为1,AC、BD是对角线,将△DCB绕点D顺时针旋转45度得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG,则下列结论:①四边形AEGF是菱形②△AED≌△GED ③∠DFG=112.5°④BC+FG=1.5,其中正确的结论是__________7、如图,边长为1的正方形ABCD 的对角线AC ,BD 相交于点O ,有直角∠MPN ,使直角顶点P 与点O 重合,直角边PM ,PN 分别与OA ,OB 重合,然后逆时针旋转∠MPN , 旋转角为θ(0°<θ<90°),PM 、PN 分别交AB 、BC 于E 、F 两点,连接EF 交OB 于点G ,则下列结论中正确的是___.8、如图,在边长为a 正方形ABCD中,把边BC 绕点B 逆时针旋转60°,得到线段BM ,连接AM 并延长交CD 于N ,连接MC ,则⊿MNC 的面积为 ( )A.2B.21a 2C.2aD.2a。
word完整版正方形2知识点及同步练习含答案推荐文档

学科:数学教学内容:正方形【学习目标】1. 探索并掌握正方形的概念及特征,并学会识别正方形.2•能正确理解平行四边形、矩形、菱形、正方形的区别与联系.【基础知识概述】1. 正方形定义:(1) 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.(2) 正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.(3) 既是矩形又是菱形的四边形是正方形.2. 正方形的特征:正方形具有四边形、平行四边形、矩形、菱形的一切特征.(1) 边一一四边相等、邻边垂直、对边平行.(2) 角——四角都是直角.(3) 对角线一一①相等;②互相垂直平分;③每条对角线平分一组对角.(4) 是轴对称图形,有4条对称轴.3. 正方形的识别方法:(1) 一组邻边相等的矩形是正方形.(2) —个角是直角的菱形是正方形.4. 正方形与矩形、菱形、平行四边形的关系:矩形、菱形、正方形都是特殊的平行四边形,它们的包含关系如图图12-2-135. 正方形的面积:正方形的面积等于边长的平方或者等于两条对角线乘积的一半.【例题精讲】例1 如图12-2-14,已知过正方形ABCD对角线BD上一点P,作PE丄BC于E,作PF丄CD于F.试说明AP = EF.12-2-13 .分析:由PE 丄BC , PF 丄CD 知,四边形PECF 为矩形,故有 EF = PC ,这时只需证 AP =CP ,由正方形对角线互相垂直平分知AP = CP .解:连结AC 、PC ,•••四边形ABCD 为正方形, ••• BD 垂直平分AC , ••• AP = CP .•/ PE 丄 BC , PF 丄 CD ,/ BCD = 90°, •四边形PECF 为矩形,• PC = EF , • AP = EF .注意:①在正方形中,常利用对角线互相垂直平分证明线段相等.②无论是正方形还是矩形经常通过连结对角线证题,这样可以使分散条件集中. 思考:由上述条件是否可以得到 AP 丄EF .提示:可以,延长 AP 交EF 于N ,由PE // AB ,有/ NPE =Z BAN . 又/ BAN =Z BCP ,而/ BCP = Z PFE ,故/ NPE =Z PFE ,而/ PFE +Z PEF = 90°,所以/ NPE +Z PEF = 90°,贝U AP 丄 EF .例 2 如图 12-2-15 ,△ ABC 中,Z ABC = 90°, BD 平分Z ABC , DE 丄 BC , DF 丄 AB , 试说明四边形 BEDF 是正方形.解:T Z ABC = 90°, DE 丄 BC ,• DE // AB ,同理,DF // BC , • BEDF 是平行四边形.•/ BD 平分Z ABC , DE 丄 BC , DF 丄 AB ,• DE = DF .又•••/ ABC = 90°, BEDF 是平行四边形, •四边形BEDF 是正方形. 思考:还有没有其他方法?提示:(有一种方法可以证四边形 DFBE 为矩形,然后证 BE = DE ,可得.另一种方法, 可证四边形DFBE 为菱形,后证一个角为 90°可得)注意:灵活选择正方形的识别方法.甘 E.V■ 12-2U4例3 如图12-2-16所示,四边形ABCD是正方形,△ ADE是等边三角形,求/ BEC 的大小.(D (2)图12-2-16分析:等边三角形和正方形都能提供大量的线段相等和角相等,常能产生一些等腰三角形,十分便于计算.在本题中,必须注意等边三角形与正方形不同的位置关系.在(1)图中,△ ABE和厶DCE都是等腰三角形,顶角都是150°,可得底角/ AEB与/ DEC都是15°,则/ BEC为30°.而在(2)图中,等边三角形在正方形内部,△ABE和厶DCE是等腰三角形,顶角是30°,可得底角/ AEB和/ DEC为75。
完美正方形

完美正方形完美正方形「完美正方形」是指在一正方形内切割出大小都相异的小正方形.而我们的研究,则放宽条件,允许同样大小的正方形不超过三个.我们先估算出正方形中可切割的最大正方形边长范围,再以方格纸手画的方式找出边长1至25的解,在过程中,我们发现可用放大的方式解决边长为合数的正方形.因此我们将重点放在边长为质数的正方形,我们将正方形分割成两个连续整数边长的正方形,则剩下少一单位的缺角正方形区域.我们探讨缺角正方形区域的解,再讨论分析回原来的正方形.最后解出了边长1至100中全部有解的正方形.对於更大边长的正方形,我们的方法也可行.所以我们以流程图来表示解决问题的过程,并用电脑试算边长1至1000的完美正方形.研究动机在暑假专书研读:名人趣题妙解书中,我们看到了塔尔塔利亚的巧分格纸,觉得很感兴趣,所以我们将完美正方形与巧分格纸两个融合,当作我们科展的题目.研究目的「完美正方形」是指,在一正方形内切割成不同大小,边长为整数的正方形,且这些切割出的正方形,均不能全等,这个主题在文献上有不错的研究成果.而我们的研究,则放宽条件,允许每一种同样大小的正方形不超过三个,希望可以探讨边长1~100中哪些正方形有解,哪些正方形无解如果有解如何切割文献探讨1926年,苏联数学家鲁金对"完美正方形"的存在提出了猜想.到1938年,他们终于找到了一个由63个大小不同的正方形组成的大正方形,人们称它为63阶的完美正方形.次年有人给出了一个39阶的完美正方形.1964年,塔特的学生,滑铁卢大学的威尔逊博士找到了一个25阶的完美正方形.1948年,威尔科克斯提出了一个24阶的完美正方形,在往后的30年中,人们一度以为24就是完美正方形的最小阶.1978年,荷兰特温特技术大学的杜依维斯蒂尤,用大型电子电脑算出了一个21阶的完美正方形.这是完美正方形的最终目标了.因为鲁金曾证明,小於21阶的完美正方形是不存在的.。
初三数学完美正方巧妙构造
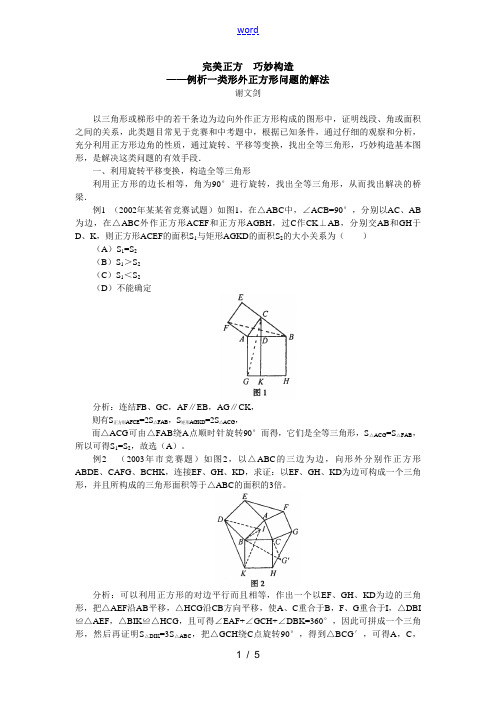
完美正方巧妙构造——例析一类形外正方形问题的解法谢文剑以三角形或梯形中的若干条边为边向外作正方形构成的图形中,证明线段、角或面积之间的关系,此类题目常见于竞赛和中考题中,根据已知条件,通过仔细的观察和分析,充分利用正方形边角的性质,通过旋转、平移等变换,找出全等三角形,巧妙构造基本图形,是解决这类问题的有效手段.一、利用旋转平移变换,构造全等三角形利用正方形的边长相等,角为90°进行旋转,找出全等三角形,从而找出解决的桥梁.例1 (2002年某某省竞赛试题)如图1,在△ABC中,∠ACB=90°,分别以AC、AB 为边,在△ABC外作正方形ACEF和正方形AGBH,过C作CK⊥AB,分别交AB和GH于D、K,则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系为()(A)S1=S2(B)S1>S2(C)S1<S2(D)不能确定分析:连结FB、GC,AF∥EB,AG∥CK,则有S正方形AFCE=2S△FAB,S矩形AGKD=2S△ACG,而△ACG可由△FAB绕A点顺时针旋转90°而得,它们是全等三角形,S△ACG=S△FAB,所以可得S1=S2,故选(A)。
例2 (2003年市竞赛题)如图2,以△ABC的三边为边,向形外分别作正方形ABDE、CAFG、BCHK,连接EF、GH、KD,求证:以EF、GH、KD为边可构成一个三角形,并且所构成的三角形面积等于△ABC的面积的3倍。
分析:可以利用正方形的对边平行而且相等,作出一个以EF、GH、KD为边的三角形,把△AEF沿AB平移,△HCG沿CB方向平移,使A、C重合于B,F、G重合于I,△DBI ≌△AEF,△BIK≌△HCG,且可得∠EAF+∠GCH+∠DBK=360°,因此可拼成一个三角形,然后再证明S△DIK=3S△ABC,把△GCH绕C点旋转90°,得到△BCG′,可得A,C,G ′在一条直线上,且C 为AG ′的中点。
初中数学竞赛第十六讲完美的正方形(含答案)

第十六讲完美的正方形有一组邻边相等并且有一个角是直角的平行四边形是正方形,换句话说:正方形是各边都相等的矩形,正方形是各角都相等的菱形,正方形既是矩形又是菱形,它具有矩形和菱形的一切性质.矩形、菱形,正方形都是特殊的四边形,它们的概念交错,关系复杂,性质有许多相似之处,一些判定和性质定理又是可逆的,所以在学习中注重概念的理解,着眼于概念间的区别与联系.连正方形的对角线,能得到特殊三角形、全等三角形,由于正方形常常与直角三角形联系在一起,所以在解有关正方形问题时要用到直角三角形性质,具有代数风格,体现数形结合思想.熟悉以下基本图形,基本结论:例题求解【例1】如图,若四边形ABCD是正方形,△CDE是等边三角形,则∠EAB的度数为.(2001年北京市竞赛题)思路点拨图中还有等腰三角形,利用等腰三角形性质计算.注可以证明,在所有用长相等的四边形中,正方形的面积最大.我们熟悉的“七巧板”,那是把一块正方形板切分成三角形、正方形、平行四边形的7块,用它可以拼出许多巧妙的图形,“七巧板”是我国古代人民智慧的结晶.【例2】如图,在正方形ABCD中,O是对角线AC、BD的交点,过O作OC⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的长为( )A.7 B.5 C.4 D.3. (2001年江苏省泰州市中考题)思路点拨AE、CF、EF不在同一个三角形中,运用全等三角形寻找相等的线段,使分散的条件集中到同一个三角形中.【例3】如图,正方形ABCD中,E、F是AB、BC边上两点,且EF=AC+FC,DG⊥EF于G,求证:DC=DA.(重庆市竞赛题)思路点拨构造AE+FC的线段是解本例的关键.【例4】已知正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN⊥DM 且交∠CBZ的平分线于N(如图甲).(1)求证:MD=MN(2)若将上述条件中的“M是AB中点”改为“M是AB上的任意一点”,其余条件不变(如图乙),则结论“MD=MN”还成立吗?如果成立,请证明:如果不成立,请说明理由.(上海市闽行区中考题)思路点拨对于图甲,取AD中点F,通过构造全等三角形证明MD=MN;这种证法能否迁移到图乙情景中去?从而作出正确的判断.注探索是学习的生命线,深入探究、学会探索是时代提出的新要求.数学解题中的探索活动可从以下几个方面进行:(1)在题设条件不变情况下,发现挖掘更多的结论;(2)通过强化或弱化来改变条件,考查结论是否改变或寻求新的结论;(3)构造逆命题.对于例3,请读者思考,在不改变题设条件的前提下,(1)∠EDF等于多少度?(2)怎样证明明逆命题?例4改变点的位置,赋以运动,从特殊到一般,(1)的结果为(2)的猜想提供了借鉴的依据,又为猜想设置了障碍,前面的证明思路是后面的证明模式.【例5】操作:将一把三角尺放在边长为l的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.探究:设A,P两点间的距离为x(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由(图1、图2、图3的形状大小相同,图1供操作、实验用,图2、图3备用).思路点拨 本例是探究式的操作型试题,第(1)问需抓住滑动中∠BPQ 是直角这一不变量,画出滑动中一般情形的图形,通过观察提出猜想,再给予论证,第(3)问需要在操作中观察出使△PCQ 是等腰三角形的两种情形.注 数学学习是一个生动活泼的过程,动手实践,自主探索是学习数学的重要形式,它说明了存在的事实是怎样被发现和被发现的现象又是怎样获得证实的,解这类问题,需边操作,边观察、边思考,综合运用相关知识方法探究结论.学历训练1.如图,P 是正方形ABCD 内一点,将△ABP 绕点B 顺时针方向旋转能与△CBP ′重合,若PB=3,则PP ′= . (2002年河南省中考题)2.如图,正方形ABCD 中,E 为CD 边上一点,F 为BC 延长线上一点,CE=CF ,若∠BEC=60°,则∠EFD 的度数为 . (2000年苏州市中考题)(第1题) (第2题) (第3题) (第4题)3.如图,∠POQ=90°,边长为2㎝的正方形ABCD 的顶点B 在OP 上,C 在OQ 上,且∠OBC=30°,则A 、D 到OP 的距离分别为 . (2003年南京市中考题)4.如图,正方形ABCD 中,CE ⊥MN ,若∠MCE =35°,则∠ANM 的度数是 .(第5题) (第6题) (第7题) (第8题)5.如图,E 是边长为l 的正方形ABCD 的对角线BD 上一点,且BE=BC ,P 为CE 上任意一点,PQ ⊥BC 于点Q ,PR ⊥BE 于点R ,则PQ+PR 的值为( )(2003年河北省中考题)A .22B .21C .23D .32 6.如图,在四边形ABCD 中,AB=BC ,∠ABC=∠CDA=90°,BE ⊥AD 于E ,8 ABCD S 四边形,则BC的长为( )A.2 B.3 C.3D.22(2003年武汉市选拔赛试题)7.如图,在正方形ABCD中,C为CD上的一点,延长月C至F,使CF=CE,连结DF,BE与DF相交于G,则下面结论错误的是( )A.BE=DF B.BG⊥DF C.∠F+∠CEB=90°D.∠FDC+∠ABG=90°(2001年山东省临沂市中考题)8.如图,已知正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF的面积为200,则BE的值是( )A.15 B.12 C .11 D.109.(1)如图甲,若点P为正方形ABCD边AB上一点,以PA为一边作正方形AEFP,连BE、DP,并延长DP交BE于点H,求证:DH⊥BF;(2)如图乙,若点P为正方形ABCD内任一点,其余条件不变,(1)的结论是否成立?若成立,请给出证明;若不成立,请说明理由.(2002年泰州市中考题)10.如图,P为正方形ABCD的对角线BD上任一点,PF⊥CD,PE⊥BC,C、F分别为垂足,探索AP与EF的关系.11.如图,正方形ABCD中,AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,求△AEF的面积.(第1l届“希望杯”邀请赛试题)12.如图,已知E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD相交于M、N,若∠EAF=50°,则∠CME+∠CNF= .(第12题) (第13题) (第14题)13.如图,在Rt △ABC 中,∠C =90°,AC=3,以AB 为一边向三角形外作正方形ABEF ,正方形的中心为O ,OC=24,则BC 边的长为 .(第13 “希望杯”邀请赛试题)14.如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为7㎝2和11㎝2,则 △CDE 的面积等于 cm 2.(武汉市选拔赛试题)15.如图,将边长为12cm 的正方形ABCD 折叠,使得A 点落在边CD 上的E 点,然后压平得折痕FG ,若GF 的长为13cm ,则线段CE 的长为 . (2002年北京市竞赛题)(第15题) (第17题) (第18题)16.将一个正方形分割成n 个小正方形(n>1),则n 不可能取( )A .4B .5C .8D .9. (第16届江苏省竞赛题)17.如图,正方形ABCD 中,P 、Q 分别是BC 、CD 上的点,若∠PAQ=45°,∠BAP=20°,则∠AQP=( )A .65°B . 60°C .35°D .70°18.如图,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE=a ,AF=b ,若S EFGH =32,则a b 等于( ) A .22 B .32 C .23 D .33 (第12届“希望杯”邀请赛试题) 19.如图,BF 平行于正方形ADCD 的对角线AC ,点E 在BF 上,且AE=AC ,CF ∥AC ,则∠BCF 等于( )A .150°B .135°C . 105°D .120°(第19题) (第20题)20.图甲中,正方形ABDE、CDFI、EFGH的面积分别为17,10,13,图乙中,DPQR为矩形,对照图乙,计算图甲中六边形ABCIGH的面积.(第15届江苏省竞赛题)21.如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.22.如图,有4个动点P、Q、E、F分别从正方形ABCD的4个顶点出发,沿着AB、BC、CD、DA以同样的速度向B、C、D、A各点移动.(1)判定四边形PQEF的形状;(2)PE是否总是经过某一定点,井说明理由;(3)四边形PQEF的顶点位于何处时,其面积最小、最大?各是多少?23.如图a,D为线段AE上任一点,分别以AD、DE为边作正方形ABCD和正方形DEFG,连结BF、AG、CE、BG、BE、BG、BE分别交AD,DC于P、Q两点.(1)①找出图中三对相等的线段(正方形边长相等除外);②找出图中三对相等的钝角;③找出图中一对面积相等的钝角三角形,这两个三角形全等吗?(2)如图b,当正方形ABCD和正方形DEFG都变为菱形,且∠GDE=∠ADC时,(1)中的结论哪些成立,哪些不成立?请对不成立的情况说明理由.(3)如图“当正方形ABCD和正方形DEFG都变为矩形,且DA>DC,DE>DG,△ABD ∽△EFD时,(1)中的结论哪些不成立,哪些成立?.如果成立,请证明.(2003年郴州市中考题)24.如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.(北京市竞赛题)。
完美正方形

完美正方形「完美正方形」是指在一正方形内切割出大小都相异的小正方形.最早由莫伦提出.数学家们一度花了很大精力都无任何结果,以至于1930年苏联著名数学家鲁金猜想,不可能把一个正方形分割成有限个大小不同的正方形.莫伦对此猜想提出了挑战,并提供了一个解决思路:如果同一个矩形有两个不同的正方形剖分,且其中一个剖分的每个正方形都不同于另一个剖分的每个正方形,那么,这两个剖分再添上两个正方形(它异于两个剖分中的任何一个正方形),便可构造出一个完美正方形,而在此之前,完美矩形已经有了比较丰富的成果.1939年,斯普拉格按照莫伦的构想成功地构造出一个55阶的完美正方形,其边长为4205.几个月后,阶数更小(28阶)、边长更短(1015)的完美正方形由剑桥大学三一学院的四位大学生构造出来.1948年,威尔科克斯构造出24阶完美正方形,但其中含有一个完美矩形(此类正方形称为混完美正方形,完全由正方形构造成的正方形称为纯完美正方形),一直到1978年,这个纪录才被打破.1967年,威尔森构造成功25阶、26阶完美正方形.1962年,荷兰特温特技术大学的杜伊维斯廷证明:不存在20阶以下的完美正方形.1978年,杜伊维斯廷借助计算机技术,成功地构造出一个21阶的完美正方形,它是唯一的,且它不仅阶数最低,同时数字也更简单,此外构造上它也有许多优美的特点,比如2的某些次幂恰好位于一条对角线上,等等.杜伊维斯廷同时还证明了:低于21阶的完美正方形不存在.1982年,杜伊维斯廷又证明了:不存在低于24阶的混完美正方形.1992年,布卡姆和杜伊维斯廷给出了21~25阶全部207个纯完美正方形:阶数21 22 23 24 25个数 1 8 12 26 160至此,完美正方形的讨论暂时画上一个句号.但数学家的研究并没有停止,他们又研究了不同大小正方形是否可以填充整个平面的问题,此外他们还将完美剖分的问题推广到莫比乌斯带、圆柱面、环面和克莱茵瓶上,也取得了许多有趣的成果.但是立方体填充被证明是没有的.。
人教版八年级数学第24讲完美的正方形
人教版八年级第24讲完美的正方形姓名:________ 班级:________ 成绩:________一、单选题1 . 如图,在正方形ABCD中,点E,F分别在CD,BC上,且AF=BE,BE与AF相交于点G,则下列结论中错误的是()A.BF=CE B.∠DAF=∠BECC.AF⊥BE D.∠AFB+∠BEC=90°2 . 已知四边形是平行四边形,下列结论中不正确的是()A.当时,它是菱形B.当时,它是菱形C.当时,它是矩形D.当时,它是正方形3 . △ABC中,∠C=90°,∠BAC的平分线交BC于D,且CD=15,AC=30,则AB的长为()A.30B.40C.50D.604 . 如图,圆P的半径为10,A、B是圆上任意两点,且AB=12,以AB为边作正方ABCD(点D、P在直线AB的两侧),若AB边绕点P旋转一周,则CD边扫过的面积为().A.0B.36πC.D.6π5 . 一块竹条编织物,先将其按如图所示绕直线MN翻转旋转180°,再将它按照逆时针方向旋转90°,所得的竹条编织物是()A.B.C.D.二、填空题6 . 对角线长为的正方形的周长为________,面积为________.7 . 如图,已知正方形ABCD的边长为2,连接AC、BD,CE平分∠ACD交BD于点E,则DE=____.三、解答题8 . 综合与实践--------图形变换中的数学问题问题情境:如图1,已知矩形中,点是的中点,连接.将矩形沿剪开,得到四边形和四边形.(1)求证:四边形是矩形;操作探究:保持矩形位置不变,将矩形从图1的位置开始,绕点按逆时针方向旋转,设旋转角为().操作中,提出了如下向题,请你解答:(2)如图2,当矩形旋转到点落在线段上时,线段恰好经过点,设与相交于点.判断四边形的形状,并说明理由;(3)请从两题中任选一题作答.A.在矩形旋转过程中,连接线段和.当时,直接写出旋转角的度数.B.已知矩形中,.在矩形旋转过程中,连接线段和,当时,直接写出的长.9 . 在数学兴趣小组活动中,小亮进行数学探究活动.△ABC是边长为2的等边形,E是AC上一点,小亮以BE 为边向BE的右侧作等边三角形BEF,连接CF.(1)如图1,当点E在线段AC上时,EF、BC相交于点D,小亮发现有两个三角形全等,请你找出来,并证明.(2)当点E在线段上运动时,点F也随着运动,若四边形ABFC的面积为,求AE的长.(3)如图2,当点E在AC的延长线上运动时,CF、BE相交于点D,请你探求△ECD的面积S1与△DBF的面积S2之间的数量关系.并说明理由.(4)如图2,当△ECD的面积S1=时,求AE的长.10 . 已知:如图,在中,,是的边的中点,,,垂足分别是、.求证:;只添加一个条件,使四边形是正方形,并给出证明.11 . 如图1,在△ABC和△MNB中,∠ACB=∠MBN=90°,AC=BC=4,MB=NB=2,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG.(1)判断四边形EFDG的形状,并证明;(2)求FD的长;(3)如图2,将图1中的△MBN绕点B逆时针旋转90°,其他条件不变,猜想此时四边形EFDG的形状,并证明.12 . 如图,在正方形ABCD中,点E是AB边上一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM 交GF于点H,EF与CB交于点N,连接CG.(1)求证:CD⊥CG;(2)若tan∠MEN=,求的值;(3)已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为?请说明理由.13 . 如图所示的方角铁皮,要求用一条直线将其分成面积相等的两部分,请你设计两种不同的分割方案(用铅笔画图,不写画法,保留作图痕迹或简要的文字说明).参考答案一、单选题1、2、3、4、5、二、填空题1、2、三、解答题1、2、3、4、5、6、。
浙教版数学八年级下册_知识拓展:完美正方形
完美正方形
我们能不能将一个大正方形分割为一些彼此互不相同的小正方形?或者反过来说,我们能不能用一些大小各不相同的小正方形拼合成一个大正方形?答案是可以的。
这样的一个大正方形,叫做完美正方形(又称完全正方形)。
第一个完美正方形是由英国剑桥大学的四位数学家组成的研究小组于1938年发现的。
这个完美正方形可分为69个小正方形,因此称为69阶完美正方形。
此后,又有许多其他阶的完美正方形被发现。
于是,人们试图寻找一个由个数最少的小正方形拼合而成的(即最低阶的)完美正方形。
利用电子计算机已经证明:不存在20阶或20阶以下的完美正方形。
1978年,荷兰数学家杜伊杰斯廷发现了21阶的完美正
方形,边长为112,如图(图中数字为小正方形边长)。
更加奇妙的是,它还是一个简单完美正方形,即其中的小正方形不构成任何矩形。
杜伊杰斯廷的发现很可能是独一无二的,也就是说,很可能再也没有与此不同的21阶完美正方形了。
正方形性质及判定口诀
(1)
正方形,好应用,边相等,角相同.
菱形性质全具备,外加对角线相等.
各角均是九十度,矩形性质也适用.
(2)
怎么判定正方形,方法可以有多种.
实质不过有两条,你可千万要记清:
矩形还要等边长,菱形尚须四角同.。
完美的正方形 公开课课件 八年级下册人教版
18.2.3完美的正方形
一、童年的回忆---折纸
• 为什么折纸的纸张常用正方形的?
边? 角? 对角线? 对称性?
你能用恰当的方式表示出平行四边形、矩形、菱形、
正方形之间的包含关系吗?
能
平行四边形
矩形
正 菱形 方
形
正方形是轴对称图 形,它的对称轴是 什么?
对角线所在直线和 对边中点所确定的
G A
⑤
①
O
E
②
⑥
B
D
⑧
④
F
③⑦
C H
五、以正方形为背景的三角形全等
如图所示的运动:正方形ABCD和正方 形AKCM中,将正方形AKLM绕点A向 左旋转某个角度.连线段MD、KB,它 们能相等吗?请证明你的结论.
六、求以正方形为背景的最短距离和
• 如图,在边长为4的正方形ABCD中,E是AB边
直线
二、展示一下你的折纸才艺
2017年安顺旧州山里江南风车节
三、求正方形的面积
• 1、正方形的边长为5其面积等于 25 • 2、正方形的对角线长为5其面积等于 12.5
正方形具有菱形的性质,对角线 互相垂直,其面积还等于对角线 之积的一半。
四、王老汉分地
王老汉4个孝顺的孩子想让他们勤劳一生的父亲安享晚 年,王老汉有一块正方形的土地,他想修建两条笔直的 小路使得两条笔直的小路将土地平均分成面积相等的四 部分分给他的四个孩子(不考虑道路的宽度).你能帮王 老汉想到几种方法?
上的一点,且AE=3,点Q为对角线AC上的动点,
则△BEQ周长的最小值为
.
【解析】由正方形的对称性,
得Bቤተ መጻሕፍቲ ባይዱD两点关于AC对称,连接
完美的正方形 经典讲义
完美的正方形正方形是四边形中最特殊的一种,它是中心对称图形也是轴对称图形,在分析有关条件与结论之间的关系时,可以利用这种性质进行分析,把图形(主要是三角形)进行旋转实现线段与角的位置的转化,在解题过程中综合中心对称、轴对称及等腰三角形、线段的垂直平分线、角的平分线的知识来解决问题。
例1:如图:四边形ABCD 为正方形,以AB 为边向正方形外作等边三角形ABE ,CE 与DB 相交于点F ,则∠AFD= 度.AECDBF例2:如图:将边长为12cm 的正方形ABCD 折叠,使得A 点落在CD 上的E 点,然后压平得折痕FG ,若FG=13cm ,求线段CE 之长.例3:如图:已知E、F分别是正方形ABCD 的边BC 、CD 上的点,AE 、AF 分别与对角线BD 相交于点M 、N .若∠EAF=050,求∠CME +∠CNF 的度数.CMA NDF E例4:如图:正方形ABCD 中,E、F是AB 、BC 边上两点,且EF=AE+FC ,D G ⊥EF 于G . 说明:DG=DA例5:如图,操作:把正方形CGEF 的对角形CE 放在正方形ABCD 的边BC 的延长线上(C G ﹥BC ),取线段AE 的中点M .探索:线段MD 、MF 的关系,并加以说明.FA DB C GEEG上题中,若将正方形CGEF绕点C旋转任意角度(如图),其它条件不变.探究:线段MD、MF的关系,并加以证明.ADBFMCEG课后作业:1.如图,在四边形ABCD 中,AB=BC ,∠ABC =∠CDA=090,BE ⊥AD 于E ,四边形ABCD 的面积为8,则BE 的长为( )A .2 B.3 C.3 D.222.如图,正方形ABCD 的面积为256,点F 在AD 上,点E 在AB 的延长线上,直角三角形CEF 的面积为200,则BE= . 3.如图,A在线段B G上,四边形ABCD 和DEFG 都是正方形,面积分别为7平方厘米和11平方厘米,则△CDE 的面积等于 平方厘米.4.如图,正方形ABCD 的边长为a ,点E 、F 、G 、H 分别在正方形的四条边上,已知E F ∥GH ,EF=GH .(1)若AE=AH=a 31,求四边形EFGH 的周长和面积;(2)求四边形EFGH 的周长的最小值.BCDAEFADBCECD EB AFGADHBEGFC5.如图,已知正方形ABEF 和ACGH 在三角形BAC 的外侧,M 是BC 边的中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完美的正方形有一组邻边相等并且有一个角是直角的平行四边形是正方形,换句话说:正方形是各边都相等的矩形,正方形是各角都相等的菱形,正方形既是矩形又是菱形,它具有矩形和菱形的一切性质.矩形、菱形,正方形都是特殊的四边形,它们的概念交错,关系复杂,性质有许多相似之处,一些判定和性质定理又是可逆的,所以在学习中注重概念的理解,着眼于概念间的区别与联系.连正方形的对角线,能得到特殊三角形、全等三角形,由于正方形常常与直角三角形联系在一起,所以在解有关正方形问题时要用到直角三角形性质,具有代数风格,体现数形结合思想.熟悉以下基本图形,基本结论:例题求解【例1】如图,若四边形ABCD是正方形,△CDE是等边三角形,则∠EA B的度数为.(北京市竞赛题)思路点拨图中还有等腰三角形,利用等腰三角形性质计算.注可以证明,在所有用长相等的四边形中,正方形的面积最大.我们熟悉的“七巧板”,那是把一块正方形板切分成三角形、正方形、平行四边形的7块,用它可以拼出许多巧妙的图形,“七巧板”是我国古代人民智慧的结晶.【例2】如图,在正方形ABCD中,O是对角线AC、BD的交点,过O作OC⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的长为( )A.7 B.5 C.4 D.3(江苏省泰州市中考题)思路点拨 AE、CF、EF不在同一个三角形中,运用全等三角形寻找相等的线段,使分散的条件集中到同一个三角形中.【例3】如图,正方形ABCD中,E、F是AB、BC边上两点,且EF=AC+FC,DG⊥EF于G,求证:DC=DA.(重庆市竞赛题)思路点拨构造AE+FC的线段是解本例的关键.【例4】已知正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN⊥DM且交∠CBZ的平分线于N(如图甲).(1)求证:MD=MN(2)若将上述条件中的“M是AB中点”改为“M是AB上的任意一点”,其余条件不变(如图乙),则结论“MD=MN”还成立吗?如果成立,请证明:如果不成立,请说明理由.(上海市闽行区中考题)思路点拨对于图甲,取AD中点F,通过构造全等三角形证明MD=MN;这种证法能否迁移到图乙情景中去?从而作出正确的判断.注探索是学习的生命线,深入探究、学会探索是时代提出的新要求.数学解题中的探索活动可从以下几个方面进行:(1)在题设条件不变情况下,发现挖掘更多的结论;(2)通过强化或弱化来改变条件,考查结论是否改变或寻求新的结论;(3)构造逆命题.对于例3,请读者思考,在不改变题设条件的前提下,(1)∠EDF等于多少度?(2)怎样证明明逆命题?例4改变点的位置,赋以运动,从特殊到一般,(1)的结果为(2)的猜想提供了借鉴的依据,又为猜想设置了障碍,前面的证明思路是后面的证明模式.【例5】操作:将一把三角尺放在边长为l的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.探究:设A,P两点间的距离为x(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的关系式,并写出x的取值范围;(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由(图1、图2、图3的形状大小相同,图1供操作、实验用,图2、图3备用).思路点拨本例是探究式的操作型试题,第(1)问需抓住滑动中∠BPQ是直角这一不变量,画出滑动中一般情形的图形,通过观察提出猜想,再给予论证,第(3)问需要在操作中观察出使△PCQ是等腰三角形的两种情形.注数学学习是一个生动活泼的过程,动手实践,自主探索是学习数学的重要形式,它说明了存在的事实是怎样被发现和被发现的现象又是怎样获得证实的,解这类问题,需边操作,边观察、边思考,综合运用相关知识方法探究结论.学力训练1.如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若PB=3,则PP′= .河南省中考题)2.如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF,若∠BEC=60°,则∠EFD的度数为. (苏州市中考题)3.如图,∠POQ=90°,边长为2㎝的正方形ABCD 的顶点B 在OP 上,C 在OQ 上,且∠OBC=30°,则A 、D 到OP 的距离分别为 . (南京市中考题)4.如图,正方形ABCD 中,CE ⊥MN ,若∠MCE =35°,则∠ANM 的度数是 .5.如图,E 是边长为l 的正方形ABCD 的对角线BD 上一点,且BE=BC ,P 为CE 上任意一点,PQ ⊥BC 于点Q ,PR ⊥BE 于点R ,则PQ+PR 的值为( ) (河北省中考题) A .22 B .21 C .23 D .326.如图,在四边形ABCD 中,AB=BC ,∠ABC=∠CDA=90°,BE ⊥AD 于E ,8 ABCD S 四边形,则BC 的长为( ) A .2 B .3 C .3 D .22 (武汉市选拔赛试题)7.如图,在正方形ABCD 中,C 为CD 上的一点,延长月C 至F ,使CF=CE ,连结DF ,BE 与DF 相交于G ,则下面结论错误的是( )A .BE=DFB .BG ⊥DFC .∠F+∠CEB=90°D .∠FDC+∠ABG =90°(山东省临沂市中考题)8.如图,已知正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF的面积为200,则BE的值是( )A.15 B.12 C .11 D.109.(1)如图甲,若点P为正方形ABCD边AB上一点,以PA为一边作正方形AEFP,连BE、DP,并延长DP 交BE于点H,求证:DH⊥BF;(2)如图乙,若点P为正方形ABCD内任一点,其余条件不变,(1)的结论是否成立?若成立,请给出证明;若不成立,请说明理由.(泰州市中考题)10.如图,P为正方形ABCD的对角线BD上任一点,PF⊥CD,PE⊥BC,C、F分别为垂足,探索AP与EF的关系.11.如图,正方形ABCD中,AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,求△AEF的面积.( “希望杯”邀请赛试题)12.如图,已知E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD相交于M、N,若∠EAF=50°,则∠CME+∠CNF= .13.如图,在Rt △ABC 中,∠C =90°,AC=3,以AB 为一边向三角形外作正方形ABEF ,正方形的中心为O ,OC=24,则BC 边的长为 . ( “希望杯”邀请赛试题)14.如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为7㎝2和11㎝2,则△CDE 的面积等于 cm 2.(武汉市选拔赛试题)15.如图,将边长为12cm 的正方形ABCD 折叠,使得A 点落在边CD 上的E 点,然后压平得折痕FG ,若GF 的长为13cm ,则线段CE 的长为 . (北京市竞赛题) 16.将一个正方形分割成n 个小正方形(n>1),则n 不可能取( ) A .4 B .5 C .8 D .9 (江苏省竞赛题)17.如图,正方形ABCD 中,P 、Q 分别是BC 、CD 上的点,若∠PAQ=45°,∠BAP=20°,则∠AQP=( )A .65°B . 60°C .35°D .70°18.如图,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE=a ,AF=b ,若S EFGH =32,则a b 等于( ) A .22 B .32 C .23 D .33 ( “希望杯”邀请赛试题) 19.如图,BF 平行于正方形ADCD 的对角线AC ,点E 在BF 上,且AE=AC ,CF ∥AC ,则∠BCF 等于( ) A .150° B .135° C . 105° D .120°20.图甲中,正方形ABDE、CDFI、EFGH的面积分别为17,10,13,图乙中,DPQR为矩形,对照图乙,计算图甲中六边形ABCIGH的面积.(江苏省竞赛题)21.如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.22.如图,有4个动点P、Q、E、F分别从正方形ABCD的4个顶点出发,沿着AB、BC、CD、DA以同样的速度向B、C、D、A各点移动.(1)判定四边形PQEF的形状;(2)PE是否总是经过某一定点,井说明理由;(3)四边形PQEF的顶点位于何处时,其面积最小、最大?各是多少?23.如图a,D为线段AE上任一点,分别以AD、DE为边作正方形ABCD和正方形DEFG,连结BF、AG、CE、BG、BE、BG、BE分别交AD,DC于P、Q两点.(1)①找出图中三对相等的线段(正方形边长相等除外);②找出图中三对相等的钝角;③找出图中一对面积相等的钝角三角形,这两个三角形全等吗?(2)如图b,当正方形ABCD和正方形DEFG都变为菱形,且∠GDE=∠ADC时,(1)中的结论哪些成立,哪些不成立?请对不成立的情况说明理由.(3)如图“当正方形ABCD和正方形DEFG都变为矩形,且DA>DC,DE>DG,△ABD∽△EFD时,(1)中的结论哪些不成立,哪些成立?.如果成立,请证明.(郴州市中考题)24.如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.(北京市竞赛题)。
