【最新】浙教版九年级上册同步测试:4.7 图形的位似
九年级数学上册 4.7 图形的位似课后练习 (新版)浙教版

4.7 图形的位似1. 下列说法正确的是(C )A. 若两个图形是相似图形,则这个图形一定是位似图形B. 两个正方形是位似图形C. 位似图形是相似图形D. 两个全等图形是位似图形2.如图,点O 是等边三角形PQR 的中心,P ′,Q ′,R ′分别是OP ,OQ ,OR 的中点,则△P ′Q ′R ′与△PQR 是位似三角形.此时,△P ′Q ′R ′与△PQR 的位似比、位似中心分别为(D )A .2,点P B.12,点PC .2,点O D.12,点O,(第2题)),(第3题))3.如图,已知△ABC 与△DEF 是位似图形,位似比为2∶3.若AB =4,则DE 的长为(C )A.83B .5C .6D .9 4.在平面直角坐标系中,已知点E (-4,2),F (-2,-2),以原点O 为位似中心,相似比为12,把△EFO 缩小,则点E 的对应点E ′的坐标是(D )A .(-2,1)B .(-8,4)C .(-8,4)或(8,-4)D .(-2,1)或(2,-1)5. 如图,在平面直角坐标系中,正方形ABCD 的两边BC ,AB 分别在x 轴、y 轴的正半轴上,正方形A ′B ′C ′D ′与正方形ABCD 是以AC 的中点O ′为位似中心的位似图形.已知AC =3 2,若点A ′的坐标为(1,2),则正方形A ′B ′C ′D ′与正方形ABCD 的位似比是__13__.,(第5题)) ,(第6题))6.如图,已知矩形ABCD 与矩形EFGH 是以点O 为位似中心的位似图形,OB ∶OF =3∶5,则矩形ABCD 的面积和矩形EFGH 的面积之比为__9∶25__.7. 利用位似作图的方法,可以将一个图形放大或缩小,位似中心可选在任意位置.8.已知△ABC 与△A ′B ′C ′是位似图形,△A ′B ′C ′的面积为6cm 2,周长是△ABC 的一半.若AB =8cm ,则AB 边上高等于__6__cm.9.如图,已知四边形ABCD ,用尺规作图将它放大,使放大前后的图形对应线段的比为1∶2(不写作法,但要求保留作图痕迹).,(第9题))【解】 如解图.,(第9题解))(第10题)10. 如图,点O 是△ABC 外的一点,分别在射线OA ,OB ,OC 上取点A ′,B ′,C ′,使得OA ′OA =OB ′OB =OC ′OC ,连结A′B′,B ′C ′,C ′A ′,所得△A′B′C′与△ABC 是否是位似图形?并说明理由.【解】 △A′B′C′与△ABC 是位似图形.理由如下:∵OA ′OA =OB ′OB,∠AOB =∠A′OB′, ∴△OA ′B ′∽△OAB,∴A ′B ′AB =OA ′OA .同理,B ′C ′BC =OB ′OB ,A ′C ′AC =OA ′OA .∴A ′B ′AB =B ′C ′BC =A ′C ′AC, ∴△A ′B ′C ′∽△ABC.又∵A′A,C ′C ,B ′B 都经过点O , ∴△A ′B ′C ′和△ABC 是位似图形.(第11题)11.如图,在平面直角坐标系中,连结点A(0,2),B(2,0),C(5,3)构成△ABC,请以原点O为位似中心,1∶2为位似比,在第一象限内作出△ABC的位似图形△A′B′C′,并写出△A′B′C′各顶点的坐标.【解】分别在OA,OB,OC的延长线上取OA′=2OA,OB′=2OB,OC′=2OC.连结A′B′,B′C′,C′A′,则△A′B′C′就是所求作的位似图形.∵A(0,2),B(2,0),C(5,3),∴A′(0,4),B′(4,0),C′(10,6).12.已知△A BC三个顶点的坐标如下表:(1)将下表补充完整,并在直角坐标系中画出△A′B′C′;(第12题)(2)观察△ABC与△A′B′C′,写出一个有关这两个三角形关系的正确结论.【解】(1)如图,△A′B′C′即为所求.(2)△ABC与△A′B′C′是以点O为位似中心,1∶2为位似比的位似图形.13.如图,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).(第13题)(1)以原点O为位似中心,在y轴的左侧作图,将△OBC放大到两倍(即新三角形与原三角形的相似比为2∶1);(2)分别写出B,C两点的对应点B′,C′的坐标;(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.【解】(1)如图,△OB′C′即为所求.(2)B′(-6,2),C′(-4,-2).(3)M′(-2x,-2y).14. 在检查视力时,规定人与视力表之间的距离应为 5 m,如图①.现因房间两面墙的距离为3 m ,因此,使用平面镜来解决房间小的问题,如图②,若使墙面镜子能呈现完整的视力表,由平面镜成像的原理,作出了光路图,其中视力表AB 的上下边沿A ,B 发出的光线经平面镜MM ′的上下边沿反射后射入人眼C 处.如果视力表的全长为0.8 m ,请计算:镜长至少应为多少米?,(第14题))【解】 过点C 作CD⊥MM′,垂足为D ,延长CD 交A′B′于点E. ∵AB ∥MM ′∥A ′B′,∴CE ⊥A ′B ′,△CMM ′∽△CA ′B ′,∴MM ′A ′B ′=CDCE .又∵CD=5-3=2(m),CE =5 m ,A ′B ′=AB =0.8 m ,∴MM ′0.8=25, ∴MM ′=0.32 m.∴镜长至少为0.32 m.15.如图,在平面直角坐标系中,已知△ABC 三个顶点的坐标分别为A (-1,2),B (-3,4),C (-2,6).(1)画出△ABC 绕点A 顺时针旋转90°后得到的△A 1B 1C 1;(2)以原点O 为位似中心,画出将△A 1B 1C 1三条边放大到原来的2倍后的△A 2B 2C 2.,(第15题))【解】 (1)如图,△A 1B 1C 1即为所求. (2)如图,△A 2B 2C 2即为所求.。
浙教版数学九年级上册4.7 图形的位似.docx

4.7 图形的位似1.对于平面图形上的任意两点P ,Q ,如果经过某种变换得到新图形上的对应点P ′,Q ′,保持PQ =P ′Q ′,那么我们把这种变换称为“等距变换”,下列变换中,不一定是等距变换的是(D )A. 平移B. 旋转C. 轴对称D. 位似2.如图,△ABC 和△DEF 是以点O 为位似中心的位似图形,且D 是OA 的中点,则EFBC等于(A ) A. 12 B. 13 C. 14 D. 23(第2题) (第3题)3.如图,以点O 为位似中心,将△ABC 缩小后得到△A ′B ′C ′.已知OB =3OB ′,则△A ′B ′C ′与△ABC 的面积比为(D )A. 1∶3B. 1∶4C. 1∶5D. 1∶94.在平面直角坐标系中,已知点E (-4,2),F (-2,-2),以原点O 为位似中心,位似比为12,把△EFO 缩小,则点E 的对应点E ′的坐标是(D )A. (-2,1)B. (-8,4)C. (-8,4)或(8,-4)D. (-2,1)或(2,-1)5.如图,△OAB 与△OCD 是以点O 为位似中心的位似图形,位似比为1∶2,∠OCD =90°,CO =C D.若点B (1,0),则点C 的坐标为(1,1).(第5题) (第6题)6.如图,E ,F ,G ,H 分别是OA ,OB ,OC ,OD 的中点,四边形EFGH 的面积是3,则四边形ABCD 的面积=__12__.(第7题)7.如图,正方形OEFG 和正方形ABCD 是位似图形,点F 的坐标为(-1,1),点C 的坐标为(-4,2),则这两个正方形的位似中心的坐标是(2,0).(第8题)8.如图,在平面直角坐标系中,已知点A (-3,6),B (-9,-3),以原点O 为位似中心,相似比为3∶1,把△ABO 缩小,求点A 的对应点A ′的坐标.【解】 ∵点A (-3,6),且相似比为3∶1, ∴OA ′=13OA ,∴易得点A ′的坐标为⎝ ⎛⎭⎪⎫-3×13,6×13或⎝ ⎛⎭⎪⎫3×13,-6×13,即点A ′的坐标为(-1,2)或(1,-2).9.如图,在平面直角坐标系中,正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形,且相似比为13,点A ,B ,E 在x 轴上.若正方形BEFG 的边长为6,则点C 的坐标为(A )(第9题)A. (3,2)B. (3,1)C. (2,2)D. (4,2)【解】 ∵正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形,且相似比为13,∴AD BG =13. ∵BG =6,∴BC =AD =2. 易得AD ∥BG ,∴△OAD ∽△OBG ,∴OA OB =AD BG =13,∴OA 2+OA =13,解得OA =1. ∴OB =3.∴点C 的坐标为(3,2).10.如图,△OAB 与△OCD 是以点O 为位似中心的位似图形,相似比为1∶2,∠OCD =90°,CO =C D.若点B (1,0),则点C 的坐标为(1,1).(第10题)【解】 ∵△OAB 与△OCD 是以点O 为位似中心的位似图形,CO =CD , ∴AO =AB ,∠OAB =∠OCD =90°, ∴△OAB 为等腰直角三角形.∵点B (1,0),∴易得点A ⎝ ⎛⎭⎪⎫12,12.∵△OAB 与△OCD 的相似比为1∶2, ∴点C 的坐标为(1,1).11.如图,在△ABC 的内部任取一点O ,连结AO ,BO ,CO ,并在AO ,BO ,CO 这三条线段的延长线上分别取点D ,E ,F ,使OD OA =OE OB =OF OC =12,连结DE ,EF ,FD ,于是得到△DEF .你认为△DEF 与△ABC 相似吗?为什么?你认为它们也具有位似图形的特征吗?(第11题)【解】 △DEF ∽△AB C.理由如下:∵OD OA =OE OB =OF OC,∠EOF =∠BOC ,∠DOE =∠AOB ,∠FOD =∠COA , ∴△DOE ∽△AOB ,△EOF ∽△BOC ,△FOD ∽△COA , ∴DE AB =OE OB =EF BC =OF OC =FDCA,∴△DEF ∽△ABC .它们具有位似图形的特征,且它们是以点O 为位似中心的位似图形.12.数学课上,老师要求同学们在扇形纸片OAB 上画出一个正方形,使得正方形的四个顶点分别落在扇形半径OA ,OB 和AB ︵上,有一部分同学是过样画的,如图①,若在扇形OAB 内画出正方形CDEF ,使得点C ,D 在OA 上,点F 在OB 上,连结OE 并延长,交AB ︵于点G ,过点G 作GJ ⊥OA 于点J ,作GH ⊥GJ 交OB 于点H ,再过点H 作HI ⊥OA 于点I .(1)请问他们画出的四边形GHIJ 是正方形吗?如果是,请给出证明;如果不是,请说明理由. (2)还有一部分同学是用另外一种不同于图①的方法画出的,请你参照图①的画法,在图②上画出这个正方形(保留痕迹,不要求证明).(第12题)【解】 (1)四边形GHIJ 是正方形.证明如下: ∵GJ ⊥OA ,GH ⊥GJ ,HI ⊥OA , ∴∠GJI =∠JIH =∠JGH =90°, ∴四边形GHIJ 是矩形. 易知FC ∥HI ,EF ∥GH ,∴△FOC ∽△HOI ,△EFO ∽△GHO , ∴OF OH =FC HI ,OF OH =EFGH ,∴FC HI =EF GH. 又∵FC =EF ,∴HI=GH.∴矩形GHIJ是正方形.(2)如图②,正方形MNGH即为所求.初中数学试卷。
2020年浙教版数学九年级上册 4.7 图形的位似(含答案)

拓展训练2020年浙教版数学九年级上册 4.7 图形的位似基础闯关全练1.如图,在正方形网格中,△ABC和△DEF相似,则关于位似中心与相似比的叙述正确的是( )A.位似中心是点B,相似比是2:1B.位似中心是点D,相似比是2:1C.位似中心在点G,H之间,相似比为2:1D.位似中心在点G,H之间,相似比为1:22.如图,△DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC 的中点,若△ABC的面积是8,则△DEF的面积是( )A.2B.4C.6D.83.在平面直角坐标系中,有两点A(4,2),B(3,0),以原点为位似中心,A’B’与AB的相似比为,得到线段A'B'.则正确的画法是()A. B.C. D.能力提升全练如图,A是反比例函数图象上一点,点B、D在y轴正半轴上,△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3,△ABD的面积为1,则该反比例函数的解析式为_________.三年模拟全练一、选择题1.(2019浙江杭州期中,6,★☆☆)如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD= 90°,,若B(2,0),则点C的坐标为( )A.(4,0)B.(3,1)C.(3,3)D.(3,3)二、解答题2.(2018浙江金华第五中学期末,24,★☆☆)如图,在网格图中的△ABC与△DEF是否成位似图形?说明理由.如果是,请画出它们的位似中心.五年中考全练1.(2018山东潍坊中考,8,★★☆)在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心把△AOB放大到原来的两倍,则点P的对应点的坐标为( ) A.( 2m,2n)B.(2m,2n)或(-2m,-2n)C.D.或二、填空题2.(2018广西百色中考,17,★☆☆)如图,已知△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,且,若点A(-1,0),点,则A'C'=________.三、解答题3.(2018四川巴中中考,25,★☆☆)在如图所示的平面直角坐标系中,已知点A(-3,-3),点B(-1,-3),点C(-1,-1).(1)画出△ABC;(2)画出△ABC关于x轴对称的△A₁B₁C₁,并写出A₁点的坐标:____;(3)以O为位似中心,在第一象限内把△ABC扩大到原来的两倍,得到△A₂B₂C₂,并写出A₂点的坐标:____________.核心素养全练如果将一个三角形绕着它一个角的顶点旋转后使这个角的一边与另一边重叠,再将旋转后的三角形位似缩放,使重叠的两边重合,我们称这样的图形变换为三角形转似,这个角的顶点称为转似中心,所得的三角形称为原三角形的转似三角形.如图,在△ABC中,AB=5,BC=6,AC=4,△A₁B₁C是△ABC以点C为转似中心的一个转似三角形,此时A₁B₁的长度为_________;那么以点C为转似中心的一个转似三角形(点分别与A、B对应)的边的长为____________.4.7 图形的位似基础闯关全练1.C如图,连结AF,CE,DB,则交点即为位似中心.∴位似中心在点G,H之间,又∵AC= 2EF,∴△ABC和△DEF的相似比为2:1,故选C.2.A ∵点D,E,F分别是OA,OB,OC的中点,∴,∴△DEF与△ABC的相似比是1:2,∴,即,∴,故选A.3.D分两种情况画出满足题意的线段,故选D.能力提升全练答案解析过A作AE⊥x轴,垂足为E,∵△ABD是△COD关于点D的位似图形,且△ABD与△COD的位似比是1:3.∴,∵OE=AB,OD∥AE,∴,设BD=a,AB=b,∴DO=3a,∴AE=4a,∵,∴,∴ab=2,∴AB·AE= 4ab=8,∴反比例函数的解析式为.三年模拟全练一、选择题1.C ∵∠OAB=∠OCD= 90°,CO= CD,Rt△OAB与Rt△OCD是位似图形,点B的坐标为(2,0),∴BO=2,AO=AB=,∴,∵Rt△OAB与Rt△OCD的相似比为1:2,∴点C的坐标为(3,).故选C.二、解答题2.解析是位似图形,位似中心为图中的点P.理由:由图易知△ABC∽△DEF,又经过各对应两点的直线都经过点P.所以△ABC与△DEF是位似图形,且位似中心是点P.五年中考全练一、选择题1.B当放大后的△A'OB'与△AOB在原点O同侧时,点P的对应点的坐标为( 2m,2n);当放大后的△A'OB'与△AOB在原点O两侧时,点P的对应点的坐标为(-2m,- 2n),故选B.二、填空题2.答案解析过C'作C'D⊥x轴于点D,∵△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,且,点A(-1,0),点,∴A’(-2,0),C’(1,2),∴OA’=2,DC’=2,OD=1,∴A’D=1+2=3,∴.三、解答题3.解析(1)△ABC如图所示.(2)△A₁B₁C₁如图所示,A₁(-3,3).(3)△A₂B₂C₂如图所示,A₂(6,6).核心素养全练答案 310;n⎪⎭⎫ ⎝⎛⨯325 解析 由题意知△ABC ∽△A ₁B ₁C ,∴,∴,∴.如图所示,将△A ₁B ₁C 绕点C 顺时针旋转,使A ₁C 与B ₂C 重叠,再将三角形位似缩放使A ₁C=B ₂C ,则易知,故以点C 为转似中心的一个转似三角形(点分别与A 、B 对应)的边的长为.。
2019秋浙教版数学九年级上册同步测试题:4.7 图形的位似
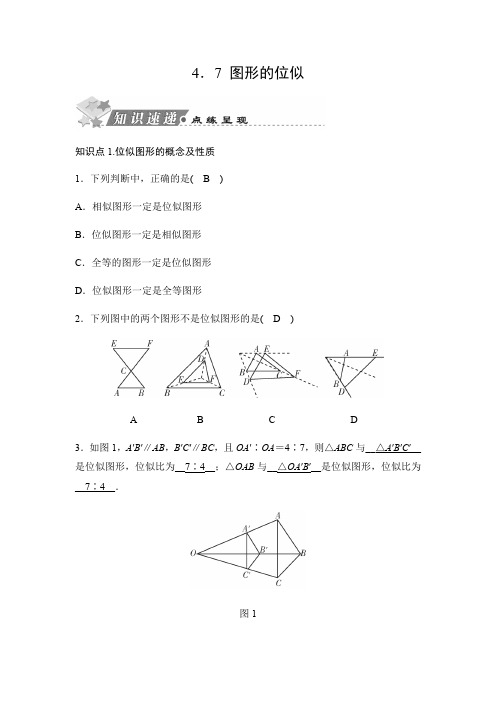
4.7 图形的位似知识点1.位似图形的概念及性质1.下列判断中,正确的是(B)A.相似图形一定是位似图形B.位似图形一定是相似图形C.全等的图形一定是位似图形D.位似图形一定是全等图形2.下列图中的两个图形不是位似图形的是(D)A B C D3.如图1,A′B′∥AB,B′C′∥BC,且OA′∶OA=4∶7,则△ABC与__△A′B′C′__是位似图形,位似比为__7∶4__;△OAB与__△OA′B′__是位似图形,位似比为__7∶4__.图14.如图2,已知五边形ABCDE,O点是五边形ABCDE内一点,A1,B1,C1,D1,E1分别是OA,OB,OC,OD,OE上的点,且A1B1∥AB,B1C1∥BC,C1D1∥CD,D1E1∥DE,A1E1∥AE.若OD=2OD1,S五边形ABCDE=100,求五边形A1B1C1D1E1的面积.图2解:∵A1B1∥AB,B1C1∥BC,C1D1∥CD,D1E1∥DE,A1E1∥AE,∴五边形ABCDE与五边形A1B1C1D1E1位似,∵OD=2OD1,∴S五边形A1B1C1D1E1S五边形ABCDE=14,∵S五边形ABCDE=100,∴五边形A1B1C1D1E1的面积为25.知识点2.位似作图5.如图3,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.(1)在图中画出四边形AB′C′D′;(2)填空:△AC′D′是__等腰直角__三角形.图3 第5题答图解:(1)如答图.知识点3.以原点为位似中心的位似图形6.如图4,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1∶2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为(B)A.(1,2) B.(1,1)C.(2,2) D.(2,1)图4 第6题答图【解析】如答图,连结BC,∵∠OCD=90°,CO=CD,∴△OCD是等腰直角三角形,∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为1∶2,∴点B是OD的中点,且BC⊥OD,∴OB=BC,∵B(1,0),∴C(1,1).7.已知在平面直角坐标系中,点A(-3,-1),B(-2,-4),C(-6,-5),以原点为位似中心将△ABC缩小,位似比为1∶2,则点B的对应点的坐标为__(1,2)或(-1,-2)__.8.如图5,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(2,0),B(2,1),C(0,1),以坐标原点O为位似中心,将矩形OABC放大为原图形的2倍,记所得矩形为OA1B1C1,B的对应点为B1,且B1在OB的延长线上,则B1的坐标为__(4,2)__.图5易错点:关于坐标原点为位似中心的坐标问题,容易出现漏解情况.9.如图6,A(2,1),B(1,-1),以O为位似中心,按比例尺1∶2,把△AOB 放大,则点A的对应点A′的坐标为__(4,2)或(-4,-2)__.图6。
4.7 图形的位似 浙教版数学九年级上册同步课件

动时,画笔A′画出图形F′,图形F′将图形F放大了.反之,
图形F是图形F′的缩小图形.位似比可通过调节点B,D
的位置来确定.
例1 如图,请以坐标原
点O为位似中心,作平行
四边形ABCD的位似图形,
并把平行四边形ABCD的
边长放大3倍.
【解析】把平行四
边形ABCD的边长放
大3倍,即画一个与
平行四边形ABCD的
叫做位似图形,经过各对应两点的直线的交点叫做
位似中心.位似中心到两个对应点的距离之比叫做位
似比.
利用图形的位似可以把一个图形放大或缩小.
若所画图形与原图形的位似比大于1,则将图形放
大;若所画图形与原图形的位似比小于1,则将原
图形缩小.
放缩尺是将图形进行放大或缩小的工具.如图,点O位
置固定不变,在A,A′处装有画笔.当画笔A沿图形F运
4.7 图形的位似
这一组蝴蝶图案除彼此相似外,还有什么特点?
如果两个图形不仅形状相同,而且每组对应点所在
的直线都经过同一点,那么这样的两个图形叫做位似
图形, 这个点叫做位似中心.
显然,位似图形是相似图形的特殊情形,其相似比又
叫做它们的位似比.
如图,O是四边形ABCD所在平面内任意一点.连结OA,
位似比为3:1的平
行四边形.
作法:
1.连结OA,OB,OC,
G
F
OD.
2.分别延长OA,OB,
E
OC,OD到G,C,E,
F,使
=3.
=
=
=
G
F
3.依次连结GC,
CE ,EF,FG.
浙教版九年级数学上册习题课件:课时训练 4.7 图形的位似(共25张PPT)

∵ADBE=ADCF=BECF=2
5 .∴△ABC∽△DEF. 2
(2)存在,共有 6 个三角形.△P2P5D,△P4P5F,△P2P4D,△P4P5D,△P2P4P5,
△P1FD.
(3)存在. △P2P4P5,位似比为 1∶1,位似中心为 P2P4 的中点.
10.如图,在平面直角坐标中,正方形 ABCD 与正方形 BEFG 是以原点 O 为
5.对于平面图形上的任意两点 P,Q,如果经过某种变换得到新图形上的对应 点 P′,Q′,保持 PQ=P′Q′,我们把这种变换称为“等距变换”,下列变换中不一 定是等距变换的是( D )
A.平移 B.旋转 C.轴对称 D.位似
6.如图,△ABC 和△DEF 是位似三角形,且 AC=2DF,那么 OE∶OB
BAD=120°,其中 AD=4.
(1)点 D 坐标为
,点 E 坐标为
;
(2)固定图①中的菱形 ABCD,将菱形 EFCH 绕 O 点顺时针方向旋转 α 度角
(0°<α<90°),并延长 OE 交 AD 于 P,延长 OH 交 CD 于 Q,如图②所示,
①当 α=30°时,求点 P 的坐标;
②试探究:在旋转的过程中是否存在某一角度 α,使得四边形 AFEP 是平行
四边形?若存在,请推断出 α 的值;若不存在,说明理由.
解:(1)(2 3,0),(0,1); (1) 由(1)知,OA=2,OD=2 3,∠OAD=60°.
∵菱形 EFGH 与菱形 ABCD 的相似比为 1∶2,AD=4, ∴EF=12AB=12AD=2.
① 当 α=30°时,∠APO=90°,则 AP=12OA=1.作 PM⊥OA 于点 M. 则 AM=12AP=12,PM= 23,∵OM=OA-AM=32, ∴点 P 的坐标是( 23,32);
浙教版九年级上册数学第4章 相似三角形 图形的位似

9.如图,在平面直角坐标系中,正方形ABCD与正方形 BEFG是以原点O为位似中心的位似图形,且位似比为 1∶3,点A,B,E在x轴上,若正方形BEFG的边长为 6,则点C的坐标为____________. (3 , 2)
ZJ版九年级上
第4章相似三角形
4.7 图形的位似
提示:点击 进入习题
1D
2D
3B
4C
5A
答案显示
62 5
7B
8 见习题
提示:点击 进入习题
9 (3,2)
答案显示
13 见习题
10 (4,-2)
14 见习题
11 见习题
15 见习题
12 见习题
1.图中两个四边形是位似图形,它们的位似中心是( D ) A.点M B.点N C.点O D.点P
∵FE∥AB,∴∠OEF=∠OAB. 同理∠OEH=∠OAD, ∴ ∠ HEF = ∠ DAB , 同 理 , ∠ EFG = ∠ ABC , ∠ FGH = ∠ BCD , ∠ GHE = ∠ CDA , ∴▱EFGH∽▱ABCD.
又∵各对应点的连线相交于点O, ∴▱ABCD与四边形EFGH是位似图形, O为位似中心.
解:是. 理由如下:∵E,F 分别是 OA,OB 的中 点,∴FE=12AB,FE∥AB. ∵G,H 分别是 OC,OD 的中点, ∴HG=12CD,HG∥CD.
同理 FG=12BC,EH=12AD,
EAFB=FBGC=GCHD=HADE=12.
九年级数学上册第四章相似三角形4.7图形的位似随堂练习含解析新版浙教版

4.7__图形的位似1.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.其中正确命题的序号是( A )A.②③B.①②C.③④D.②③④2.如图4-7-1中两个四边形是位似图形,它们的位似中心是( D )图4-7-1A.点M B.点NC.点O D.点P【解析】根据位似图形的定义:对应点的连线交于一点,交点就是位似中心.即位似中心一定在对应点的连线上.点P在对应点M和点N所在直线上,再连结另两个对应点,即可得出P为两图形的位似中心.故选D.3.[xx·绥化]如图4-7-2,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4∶9,则OB′∶OB为( A )图4-7-2A.2∶3 B.3∶2C .4∶5D .4∶9【解析】 由位似变换的性质可知△A ′B ′C ′∽△ABC .∵△A ′B ′C ′与△ABC 的面积的比是4∶9,△A ′B ′C ′与△ABC 的相似比为2∶3,∴OB ′OB =23. 4.如图4-7-3,在平面直角坐标系中,以原点O 为位似中心,将△ABO 的边长扩大到原来的2倍,得到△A ′B ′O .若点A 的坐标是(1,2),则点A ′的坐标是( C )图4-7-3A .(2,4)B .(-1,-2)C .(-2,-4)D .(-2,-1)5.[xx·烟台]如图4-7-4,在平面直角坐标系中,正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形,且位似比为13,点A ,B ,E 在x 轴上,若正方形BEFG 的边长为6,则点C 的坐标为( A )图4-7-4A .(3,2)B .(3,1)C .(2,2)D .(4,2)6.在平面直角坐标系中,已知点E 的坐标为(-4,2),点F 的坐标为(-2,-2),以原点O 为位似中心,位似比为12,把△EFO 缩小,则点E 的对应点E ′的坐标是( D )A .(-2,1)B .(-8,4)C .(-8,4)或(8,-4)D .(-2,1)或(2,-1)【解析】 根据题意画出相应的图形,找出点E 的对应点E ′的坐标即可.第6题答图∴点E 的对应点E ′的坐标是(-2,1)或(2,-1).故选D.7.如图4-7-5,以O 为位似中心,将△ABC 放大得到△DEF ,若AD =OA ,则△ABC 与△DEF 的面积之比为( B )图4-7-5A .1∶2B .1∶4C .1∶5D .1∶6【解析】 ∵AD =OA ,∴OA ∶OD =1∶2,∴S △ABC ∶S △DEF =(OA ∶OD )2=1∶4.故选B. 8.如图4-7-6,以O 为位似中心,将五边形ABCDE 放大后得到五边形A ′B ′C ′D ′E ′,已知OA =10 cm ,OA ′=20 cm ,则五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比值是__1∶2__.图4-7-6【解析】 ∵五边形ABCDE 与五边形A ′B ′C ′D ′E ′位似,OA =10 cm ,OA ′=20 cm , ∴五边形ABCDE ∽五边形A ′B ′C ′D ′E ′,且相似比为OA ∶OA ′=10∶20=1∶2, ∴五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比值是1∶2.9.[xx·长沙]如图4-7-7,△ABO 三个顶点的坐标分别为A (2,4),B (6,0),O (0,0),以原点O 为位似中心,把这个三角形缩小为原来的12,可以得到△A ′B ′O ,已知点B ′的坐标是(3,0),则点A ′的坐标是__(1,2)__.图4-7-7【解析】 ∵点A 的坐标为(2,4),以原点O 为位似中心,把这个三角形缩小为原来的12,∴点A ′的坐标是⎝ ⎛⎭⎪⎫2×12,4×12,即(1,2).10.[xx·柳州]如图4-7-8,以原点O 为位似中心,把△OAB 放大后得到△OCD ,求△OAB 与△OCD 的位似比.图4-7-8解:∵点B 的坐标是(4,0),点D 的坐标是(6,0), ∴OB =4,OD =6, ∴OB OD =46=23, ∵△OAB 与△OCD 关于点O 位似, ∴△OAB 与△OCD 的位似比为23.11.[xx·枣庄改编]如图4-7-9,在平面直角坐标系中,已知△ABC 三个顶点的坐标分别是A (2,2),B (4,0),C (4,-4).(1)请在图中,画出△ABC 向左平移6个单位长度后得到的△A 1B 1C 1;图4-7-9(2)以点O 为位似中心,将△ABC 缩小为原来的12,得到△A 2B 2C 2,请在图中y 轴的右侧画出△A 2B 2C 2.解: (1)画出△ABC 向左平移6个单位长度后得到的△A 1B 1C 1,如答图所示;第11题答图(2)以点O 为位似中心,将△ABC 缩小为原来的12,得到在y 轴右侧的△A 2B 2C 2,如答图所示.12.如图4-7-10,在△ABC 中,A ,B 两个顶点在x 轴的上方,点C 的坐标是(-1,0).以C 为位似中心,在x 轴的下方作△ABC 的位似图形,并把△ABC 的边长放大到原来的2倍,记所得的图形是△A ′B ′C .设点B 的对应点B ′的横坐标是a ,则点B 的横坐标是( D ) A .-12aB .-12(a -1)C .-12(a -1)D .-12(a +3)图4-7-10第12题答图【解析】 如答图,过点B 和点B ′作x 轴的垂线,垂足分别是D 和E . ∵点B ′的横坐标是a ,点C 的坐标是(-1,0). ∴EC =a +1.又∵△A ′B ′C 与△ABC 的位似比为2∶1, ∴DC =12(a +1),∴DO =12(a +3),∴点B 的横坐标是-12(a +3).故选D.13.[xx·滨州]在平面直角坐标系中,点C ,D 的坐标分别为C (2,3),D (1,0).现以原点为位似中心,将线段CD 放大得到线段AB ,若点D 的对应点B 在x 轴上且OB =2,则点C 的对应点A 的坐标为__(4,6)或(-4,-6)__. 【解析】 依题意作答图:第13题答图由题意,得位似中心是O ,位似比为2∶1, ∴OA =2OC ,∵C (2,3),∴A (4,6)或(-4,-6).14.如图4-7-11,分别按下列要求作出四边形ABCD 以O 为位似中心的位似四边形. (1)沿AO 方向放大为原图的2倍; (2)沿OA 方向放大为原图的2倍.图4-7-11解:(1)如答图所示,四边形A′B′C′D′即为所求;(2)如答图所示,四边形A″B″C″D″即为所求.第14题答图15.[xx·凉山州]如图4-7-12,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC 三个顶点分别为A(-1,2),B(2,1),C(4,5).(1)画出△ABC关于x轴对称的△A1B1C1;(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.图4-7-12解:(1)如答图所示,△A1B1C1就是所求三角形;(2)如答图所示,△A2B2C2就是所求三角形.第15题答图如答图,分别过点A 2,C 2作y 轴的平行线,过点B 2作x 轴的平行线,交点分别为E ,F , ∵A (-1,2),B (2,1),C (4,5),△A 2B 2C 2与△ABC 位似,且位似比为2, ∴A 2(-2,4),B 2(4,2),C 2(8,10),∴A 2E =2,C 2F =8,EF =10,B 2E =6,B 2F =4, ∴S △A 2B 2C 2=12×(2+8)×10-12×2×6-12×4×8=28.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页(共10页) 新浙教版九年级上册同步测试:4.7 图形的位似 一、选择题 1.如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一
象限内将线段AB缩小为原来的后得到线段CD,则端点C的坐标为( )
A.(3,3) B.(4,3) C.(3,1) D.(4,1) 2.如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′
均在图
中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
A.(,n) B.(m,n) C.(m,) D.() 3.如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
A.(2,5) B.(2.5,5) C.(3,5) D.(3,6) 第2页(共10页)
4.如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),
点D(3,1),则点D的对应点B的坐标是( )
A.(4,2) B.(4,1) C.(5,2) D.(5,1) 5.如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,则△ABC与△DEF的面积
之比为( )
A.1:2 B.1:4 C.1:5 D.1:6 6.在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为
,把△ABO缩小,则点A的对应点A′的坐标是( ) A.(﹣2,1) B.(﹣8,4) C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1) 7.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若
B(1,0),则点C的坐标为( )
A.(1,2) B.(1,1) C.(,) D.(2,1) 8.如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一
象限内将线段AB缩小为原来的后得到线段CD,则端点C和D的坐标分别为( ) 第3页(共10页)
A.(2,2),(3,2) B.(2,4),(3,1) C.(2,2),(3,1) D.(3,1),
(2,2) 9.下列说法正确的是( ) A.相等的圆心角所对的弧相等 B.无限小数是无理数 C.阴天会下雨是必然事件 D.在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标
的比等于k或﹣k 10.△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,
则△A′B′C′的面积是( ) A.3 B.6 C.9 D.12 11.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为
,把△EFO缩小,则点E的对应点E′的坐标是( ) A.(﹣2,1) B.(﹣8,4) C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1) 12.已知两点A(5,6)、B(7,2),先将线段AB向左平移一个单位,再以原点O为位似中心,
在第一象限内将其缩小为原来的得到线段CD,则点A的对应点C的坐标为( ) A.(2,3) B.(3,1) C.(2,1) D.(3,3) 13.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′
是以点
P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
A.(0,0) B.(0,1) C.(﹣3,2) D.(3,﹣2) 第4页(共10页)
14.如图,在直角坐标系中,有两点A(6,3),B(6,0),以原点O位似中心,相似比为,
在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1) 15.下列关于位似图形的表述: ①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形
是位似图形; ④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( ) A.②③ B.①② C.③④ D.②③④ 16.如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′
与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点, =k.已知关于x,y的二元一次方程(m,n是实数)无解,在以m,n为坐标(记为(m,n))的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则k•t的值等于( )
A. B.1 C. D. 二、填空题 第5页(共10页)
17.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AB:
DE= .
18.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:,点A的坐标为(0,1),则点E的坐标是 .
19.如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正
方形OA1B1C1,其边长OA1缩小为OA的,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n= .
20.如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′
是△
ABO关于点A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为 . 第6页(共10页)
三、解答题 21.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形
AB′C′D′,使它与四边形ABCD位似,且相似比为2. (1)在图中画出四边形AB′C′D′; (2)填空:△AC′D′是 三角形.
22.如图,在边长为1个单位长度的小正方形网格中: (1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1. (2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2. (3)求△CC1C2的面积.
23.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3). (1)画出△ABC关于x轴对称的△A1B1C1; (2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1
的相似比为2:1. 第7页(共10页)
24.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)
(正方形网格中每个小正方形的边长是一个单位长度). (1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ; (2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ; (3)△A2B2C2的面积是 平方单位.
25.在13×13的网格图中,已知△ABC和点M(1,2). (1)以点M为位似中心,位似比为2,画出△ABC的位似图形△A′B′C′; (2)写出△A′B′C′的各顶点坐标. 第8页(共10页)
26.如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变
换和平移变换后得到△A3B3C3. (1)△ABC与△A1B1C1的位似比等于 ; (2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2; (3)请写出△A3B3C3是由△A2B2C2怎样平移得到的? (4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
27.如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(﹣2,4),B(﹣2,1),
C(﹣5,2). (1)请画出△ABC关于x轴对称的△A1B1C1. (2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2,得到对应的点A2,B2,C2,请画出△A2B2C2. (3)求△A1B1C1与△A2B2C2的面积比,即: = (不写解答过程,直接写出结果). 第9页(共10页)
28.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4)C(﹣2,6) (1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1 (2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2.
29.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2). (1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标; (2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标; (3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.
