2014年瓶窑一中初三数学余高自主招生考试辅导材料—反比例之填空题
2014年中考数学试题分类汇编-反比例函数
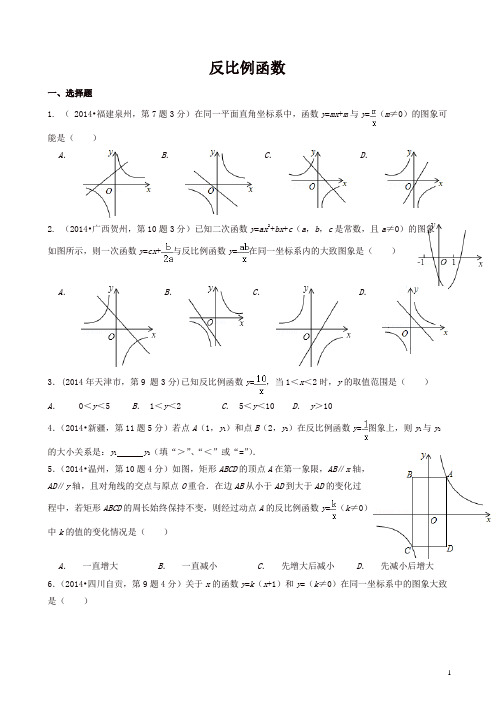
反比例函数一、选择题1. ( 2014•福建泉州,第7题3分)在同一平面直角坐标系中,函数y =mx +m 与y =(m ≠0)的图象可能是( )如图所示,则一次函数y =cx +与反比例函数y =在同一坐标系内的大致图象是( )A .B .C .D .3.(2014年天津市,第9 题3分)已知反比例函数y =,当1<x <2时,y 的取值范围是( )A . 0<y <5B . 1<y <2C . 5<y <10D . y >104.(2014•新疆,第11题5分)若点A (1,y 1)和点B (2,y 2)在反比例函数y =图象上,则y 1与y 2的大小关系是:y 1 y 2(填“>”、“<”或“=”).5.(2014•温州,第10题4分)如图,矩形ABCD 的顶点A 在第一象限,AB ∥x 轴,AD ∥y 轴,且对角线的交点与原点O 重合.在边AB 从小于AD 到大于AD 的变化过程中,若矩形ABCD 的周长始终保持不变,则经过动点A 的反比例函数y =(k ≠0) 中k 的值的变化情况是( )是( )7.(2014·云南昆明,第8题3分)左下图是反比例函数)0(≠=k k xy 为常数,的图像,则一次函数kkx y -=的图像大致是( )8. (2014•湘潭,第8题,3分)如图,A 、B 两点在双曲线y =上,分别经过A 、B 两点向轴作垂线段,已知S 阴影=1,则S 1+S 2=( )A 、3 B 、 4 C 、5 D 、69. (2014•益阳,第6题,4分)正比例函数y =6x 的图象与反比例函数y =的图象的交点位于( ) 10. (2014•株洲,第4题,3分)已知反比例函数y =的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )1. ( 2014•广西玉林市、防城港市,第18题3分)如图,OABC 是平行四边形,对角线OB 在轴正半轴上,位于第一象限的点A和第二象限的点C 分别在双曲线y =和y =的一支上,分别过点A 、C 作x轴的垂线,垂足分别为M 和N ,则有以下的结论: ①=;C BA②阴影部分面积是(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是(把所有正确的结论的序号都填上).2.(2014年天津市,第14题3分)已知反比例函数y=(k为常数,k≠0)的图象位于第一、第三象限,写出一个符合条件的k的值为.3.(2014•武汉,第15题3分)如图,若双曲线y=与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且OC=3BD,则实数k的值为4.(2014•邵阳,第13题3分)若反比例函数的图象经过点(﹣1,2),则k的值是.5.(2014•孝感,第17题3分)如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为 6 .6.(2014•浙江湖州,第15题4分)如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD ∽△ACO,则直线OA的解析式为.7.(2014年江苏南京,第11题,2分)已知反比例函数y=的图象经过点A(﹣2,3),则当x=﹣3时,y= .8.(2014•滨州,第17题4分)如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为﹣6 .9.(2014•菏泽,第13题3分)如图,Rt△ABO中,∠AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:,若点A(x0,y0)的坐标x0,y0满足y0=,则点B(x,y)的坐标x,y所满足的关系式为y=﹣2x.10.(14•济宁,第14题3分)如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=的图象上,OA=1,OC=6,则正方形ADEF的边长为.三.解答题1. ( 2014•福建泉州,第26题14分)如图,直线y=﹣x+3与x,y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).(1)求该反比例函数的关系式;(2)设PC⊥y轴于点C,点A关于y轴的对称点为A′;①求△A′BC的周长和sin∠BA′C的值;②对大于1的常数m,求x轴上的点M的坐标,使得sin∠BMC=.2. ( 2014•广东,第23题9分)如图,已知A(﹣4,),B(﹣1,2)是一次函数y=kx+b与反比例函数y=(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?(2)求一次函数解析式及m的值;(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.3. ( 2014•珠海,第19题7分)如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边在AD在x轴上,点B在第四象限,直线BD与反比例函数y=的图象交于点B、E.(1)求反比例函数及直线BD的解析式;(2)求点E的坐标.4.(2014年四川资阳,第20题8分)如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.(1)求一次函数和反比例函数的解析式;(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?5.(2014年云南省,第17题6分)将油箱注满k升油后,轿车科行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?6.(2014•舟山,第22题10分)实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=(k>0)刻画(如图所示).(1)根据上述数学模型计算:①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?②当x=5时,y=45,求k的值.(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.8.(2014•四川自贡,第22题12分)如图,一次函数y=kx+b与反比例函数的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;(2)根据图象直接写出的x的取值范围;(3)求△AOB的面积.9.(2014•浙江湖州,第20题分)如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=的图象上,过点A的直线y=x+b交x轴于点B.(1)求k和b的值;(2)求△OAB的面积.10.(2014•浙江宁波,第22题10分)如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=,反比例函数y=(k>0)的图象过CD的中点E.(1)求证:△AOB≌△DCA;(2)求k的值;(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,判断点G是否在反比例函数的图象上,说明理由.11. (2014•泰州,第26题,14分)平面直角坐标系xOy中,点A、B分别在函数y1=(x>0)与y2=﹣(x<0)的图象上,A、B的横坐标分别为a、b.(第1题图)(1)若AB∥x轴,求△OAB的面积;(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1=(x>0)的图象都有交点,请说明理由.12.(2014•呼和浩特,第23题8分)如图,已知反比例函数y=(x>0,k是常数)的图象经过点A(1,4),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.(1)写出反比例函数解析式;(2)求证:△ACB∽△NOM;(3)若△ACB与△NOM的相似比为2,求出B点的坐标及AB所在直线的解析式.13.(2014•德州,第21题10分)如图,双曲线y=(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).(1)确定k的值;(2)若点D(3,m)在双曲线上,求直线AD的解析式;(3)计算△OAB的面积.14.(2014•菏泽,第17题7分)(2)如图,在平面直角坐标系xOy中,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数y=(x>0)的图象相交于点B(2,1).①求m的值和一次函数的解析式;②结合图象直接写出:当x>0时,不等式kx+b>的解集.15.(2014年山东泰安,第26题)如图①,△OAB中,A(0,2),B(4,0),将△AOB向右平移m个单位,得到△O′A′B′.(1)当m=4时,如图②.若反比例函数y=的图象经过点A′,一次函数y=ax+b的图象经过A′、B′两点.求反比例函数及一次函数的表达式;(2)若反比例函数y=的图象经过点A′及A′B′的中点M,求m的值.。
2014年泉港一中高中自主招生(数学及答案)

2014年泉港一中高中自主招生加试数学试卷2014.5.10(总分:120分 请将答案或解答填到答题卷上)一、填空题(本大题共10小题;每小题5分,共50分)1.某同学在使用计算器求30个数的平均值的时候,错将99误输入为9,那么由此求出的平均数与实际平均数的差的绝对值为 . 2.已知1=x 是关于x 不等式组⎩⎨⎧>≤a x x 2的一个解,那么实数a 的取值范围是 . 3. 如果130=⎪⎪⎭⎫⎝⎛-m m ,则实数m 的取值范围为____________ 4.已知:2110,2110+=-=y x , 则xyx y y xy x ---22的值为__________. 5.一个圆锥的侧面展开图是半径为4的半圆,则该圆锥的底面半径是_______.6.(如图)随机地在如图所示的等边三角形及内区域投针,则针扎到其内切圆(阴影)区域的概率为 .7.一束光线从y 轴上的点A (0 ,m )出发,经过x 轴上的点M ⎪⎭⎫⎝⎛0,43反射后恰好经过点B (3,3),则=m .8.设点P 是半径为5的⊙O 内一定点,且OP =4,则过点P 的所有弦中,弦长可能取到的所有整数值之和为 .9.如图,已知⊙O 过正方形ABCD 的顶点A 、D ,且与BC 边相切,若⊙O 的半径为1,则正方形的边长为 .10.将1,-2,3,-4,5,-6……按一定规律排列如下图,则第10行从左到右第9个数是__________.二、解答题(本大题共6小题;共70分)11. (本题满分10分)如图,A 、B 、C 、D 、E 是⊙O 上的五个等分点,连接AC 、BE 相交于点F. (1)求证:AC AF AB ⋅=2(2)设n CF m AF ==,,求n m :的值.12.(本题满分10分)已知函数2x y -=的图象向右平移2个单位,再向上平移n )0(>n 个单位后得到的抛物线C 恰好与直线82+-=x y 相切与点A. (1)求抛物线C 得解析式 (2)若抛物线C 的顶点为B ,交y 轴与点D ,∆ABD 的外接圆交x 轴与M 、N 两点,求MN 的长13. (本题满分12分)为了探索代数式()168422+-++x x 的最小值,小李同学运用了“数形结合”思想.具体方法是这样的:如图,C 为线段BD 上一动点,分别过点B 、D 作,AB BD ED BD ⊥⊥,连结AC 、EC .已知AB=2,DE=4,BD=8,设BC=x .则42+=x AC ,()1682+-=x CE , 则问题即转化成求AC+CE 的最小值.(1)我们知道当A 、C 、E 在同一直线上时, AC+CE 的值最小,于是可求得()168422+-++x x 的最小值等于 ,此时x= ;(2)请你根据上述的方法和结论,若代数式()222121x m x -+++(其中)0>m 的最小值等于13,求m 值.14. (本题满分12分)已知关于x 的方程0)3)(1(2=+--m x x x ,m 为实数. (1)当4=m 时,求方程的根;(2)若方程的三个实根中恰好有两个实根相等,求m 的值;(3)若方程的三个实根恰好能成为一个三角形的三边长,求m 的取值范围.15. (本题满分14分)在等腰三角形中,建立边角之间的联系.我们定义:等腰三角形中底边与腰长的比叫做顶角的正对(符号为sad ).如图1,在∆ABC 中,AB=AC ,顶角A 的正对记作sad A ,这时sad A=底边÷腰=ABBC.容易知道一个角的大小,与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解决下列问题:(1)计算:sad 060= ________;sad 090= ________;sad 0120= ________; (2)对于00<A <0180,则∠A 的正对值sad A 的取值范围是_____________. (3)如图2在直角三角形ABC 中BC AC ⊥,已知sin A=53,试求sad A 的值.16.( 本题满分14分)当11x -≤≤时,函数2221y x mx n =--++的最小值是4-,最大值是0,求m 、n 的值.2014年泉港一中高中自主招生数学参考答案及评分标准一、填空题(本大题共10小题;每小题5分,共50分)1. 32. 1<a 3.0>m 且31≠m 4. 9104 5.2 67.1 8. 40 9.5810. -90 二、解答题(本大题共6小题;共70分)11.(本小题满分10分)(1)证明:A 、B 、C 、D 、E 是⊙O 上的五个等分点,∴五边形ABCDE 为⊙O 的内接正五边形,其每个内角为()108518025=⨯-,∠ABF=∠BAF=∠ACB= 36,∠CBF=∠CFB= 72, ∴∆AB F ∽∆ACB, AB=BC=CF, 则ABAF AC AB =得AC AF AB ⋅=2…………………5分(2)解:由(1)有AB=CF=n, 由AC AF AB ⋅=2=()CF AF AF +⋅∴)(2n m m n +=,化为022=-+n mn m012=-⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛n m n m ,而0>n m 解得215-=n m 符合题意 . ..…………………10分 12.(本小题满分10分)解:(1)抛物线C:())0(22>+--=n n x y联立()⎩⎨⎧+--=+-=nx y x y 2282化为01262=-+-n x x直线与抛物线相切∴0)12(436=--=∆n 得3=n∴抛物线C 的解析式为()322+--=x y …………………5分(2)令0=x 得1-=y ,∴ D(0,-1), 抛物线的顶点B(2,3) 由(1)n=3时0962=+-x x 得3=x∴切点A(3,2)则2,52,23===AB BD AD ,满足222AB AD BD +=∴ABD ∆为斜边BD 的直角三角形,其外接圆圆心E 为BD 中点E(1,1),半径为521==BD r , ∴MN 的长度为4152222=-=-d r …………………10分13.(本小题满分12分)解: (1)最小值10,此时38=x …………………6分(2)由(1)设A B ⊥BD,ED ⊥DB,AB=1,DE=m ,BC=x 则()22212,1m x CE x AC +-=+=∴()222121x m x -+++的最小值=AC+CE 的最小值AC+C E ≥AE=13∴()22213121=++m 且0>m∴4=m ,此时由x x -=1241得512=x …………………12分 14.(本小题满分12分)解: (1)m=4时方程为0)43)(1(2=+--x x x 得01=-x 或0432=+-x x 由01=-x 得1=x由0432=+-x x 得07169<-=-=∆,该方程无实数解∴方程的实根为1=x …………………3分(2)由由01=-x 得11=x由032=+-m x x 得049≥-=∆m 两根为32,x x若12=x ,则031=+-m 得2=m ,方程为0232=+-x x 得2,132==x x 符合题意若32x x =时049=-=∆m 得49=m 方程为04932=+-x x 得2332==x x 符合题意综上知2=m 或49=m …………………8分(3)方程的三个实根满足11=x ,032=+-m x x 得049≥-=∆m 两根为32,x x 且,332=+x x m x x =⋅32方程的三个实根恰好能成为一个三角形的三边长,则⎪⎩⎪⎨⎧<-≥-=∆>1||049032x x m m 由()1494||3222232<-=-+=-m x x x x x x 得2>m492≤<∴m …………………12分 15.(本小题满分14分)解:(1)sad 060= ____1_; sad 090= 2; sad 0120= 3;…………………4分 (2)20<<sadA …………………8分 (3)不妨设BC=3,AB=5则AC=4,在AB 上取点D ,使得AD=4,故ACD ∆为腰长4的等腰三角形,作CE ⊥AB 于E 点。
中考复习数学真题汇编14:反比例函数(含答案)

一、选择题1. )若点(1x ,1y ),(2x ,2y ),(3x ,3y )都是反比例函数y =1x-图象上的点,并且1y <0<2y <3y ,则下列各式中正确的是 ·············································································· ( ) A .1x <2x <3x B .1x <3x <2xC .2x <1x <3xD .2x <3x <1x【答案】D2. 知点A (-2,y 1),B (3,y 2)是反比例函数(0)ky k x=< 图象上的两点,则有 ( ) A .120y y << B .210y y << C .120y y << D .210y y << 【答案】B【解析】解:(1)(0)ky k x=<的大致图像如下图所示,由图像可得:210y y <<;(2) 根据反比例函数(0)ky k x=<,可得xy =k (k <0),即横纵坐标乘积为负数,∵ x A = -2<0, ∴ y 1>0;同理可得:y 2<0;∴ y 2<0<y 1,故选B .xyBAy 2y 13-2O3. )如图,正比例函数11y k x =的图象与反比例函数22k y x=的图象相交于A 、B 两点,其中点A 的横坐标为2,当12y y >时,x 的取值范围是( )A.x <-2或x >2B. x <-2或0<x <2C. -2<x <0或0<x <2D. -2<x <0或x >2【答案】D4.x12题图A4.如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,,反比例函数kyx=的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k 的值是A.B.-C.D.-【答案】D【解析】解:利用三角函数求出D点坐标:D(-6,,把D点坐标(-6,代入kyx=得:k=-故选D.5. (2015浙江台州,4,4分)若反比例函数kyx=的象限经过点(2,-1),则该反比例函数的图像在()A.第一、二象限B.第一、三象限C.第二、三象限D.第二、四象限【答案】D6.4分)以正方形ABCD 两条对角线的交点O 为坐标原点,建 立如图所示的平面直角坐标系,双曲线3y x=经过点D ,则正方形ABCD 的面积是 ( ) A.10B.11C.12D.13【答案】C.【解析】由双曲线的几何意义可知四边形ABCD 的面积=4×3=12,故选C.7. 若反比例函数ky x=的图像经过(2,-1),则该反比例函数的图像在( ) A .第一、二象限 B .第一、三象限 C .第二、三象限 D .第二、四象限 【答案】D【解答】 解:将(2,-1)代入解析式得k =-2,根据反比例函数的图像性质,k <0,图像在二、四象限, 故选D8. )如图,点A 的坐标是(2,0),△ABO 是等边三角形,点B 在第一象限,若反比例函数ky x=的图象经过点B ,则k 的值是( )A.1B.2C.D. 【答案】C9.反比例函数y=x6,当1<x <3时,y 的取值范围是( ) A.0<y <1 B.1<y <2 C.2<y <6 D.y >6 【答案】C.10. 若点A (3,-4)、B (-2,m )在同一个反比例函数的图像上,则m 值为( )A.6 B.-6 C.12 D.-12【答案】A【解答】解:因为A、B两点都在同一反比例函数图像上,满足xy=k,故3×(-4)=-2×m,解得m=6,选A11.)若点A(a,b)在反比例函数2yx=的图像上,则代数式ab-4的值为()A.0 B.-2 C.2 D.-6 【答案】B【解析】将A点的坐标代入解析式,得ab=2,则ab-4=-2.12.比例函数2yx=-的图象上有两点P1(x1,y1),p2(x2,y2),若x1<0<x2,则下列结论正确的是()A .y1<y2<0 B. y1<0<y2 C .y1>y2>0 D y1>0>y2【答案】D【解析】解:k=-2<0,函数图象位于二、四象限,∵x1<0<x2点P1(x1,y1)位于第二象限,y1>0,点p2(x2,y2)位于第四象限y2<0,故y1>0>y2二、填空题1.分)如图,反比例函数y=kx的图象经过点(-1,-,点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.(1)k的值为________;(2)在点A运动过程中,当BP平分∠ABC时,点C的坐标是________.【答案】(1)(2)(2,-2.分)把一个长、宽、高分别为3cm、2cm、1cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S(cm2)与高h(cm)之间的函数关系式为.【答案】6 Sh =3. 分)如图,在平面直角坐标系中,菱形OBCD 的边OB 在x 轴正半轴上,反比例函数ky x=(x >0)的图象经过菱形对角线的交点A ,且与边BC 交于点F.若点D 的坐标为(6,8),则点F 的坐标是___________.【答案】8123(,)4. 分)如图,过原点O 的直线与反比例函数y 1,y 2的图象在第一象限内分别交于点A 、B ,且A 为OB 的中点,若函数11y x=,则y 2与x 的函数表达式是 ▲ . y 2y 1=1x【答案】24y x= 【解析】由1112442ACO BOD kS S ∆∆===⋅ ,得k=45. 如图7,在平面直角坐标系中,点M 为x 轴正半轴上一点,过点M 的直线l ∥y 轴,且直线l 分别与反比例函数8y x =(x >0)和ky x=(x >0)的图象交于P 、Q 两点,若S △POQ =14,则k 的值为__________.【答案】-206.分)已知A (-1,m )与B (2,m -3)是反比例函数ky x=图象上的两个点,则m 的值为 . 【答案】 27. 比例函数()10y mx m =>的图象与反比例函数()20ky k x=≠的图象交于点(),4A n 和点B ,AM y ⊥轴,垂足为M ,若△AMB 的面积为8,则满足12y y >的实数x 的取值范围是_____________. 【答案】20x -<<或2x >8. 分)在平面直角坐标系中,O 为坐标原点,设点P (1,t )在反比例函数y =x2的图象上,过点P 作直线l 与x 轴平行,点Q 在直线l 上,满足QP =OP .若反比例函数y =xk的图象经过点Q ,则k = . 【答案】2+25,2-25.9.点(a -1,y 1)、(a +1,y 2)在反比例函数xky =(k >0)的图像上,若y 1<y 2,则a 的取值范围是 . 【答案】−1<a <110. 如图,等边三角形AOB 的顶点A 的坐标为(﹣4,0),顶点B 在反比例函数()ky x x=<0的图象上,则k= .【答案】-【解析】过B 作BD ⊥AO 于D ,所以D (﹣2,0)因为△AOB 是等边三角形,所以∠OBD=30° ∴BD=B (﹣2,k=2-⨯--11. 如图,已知点A ,C 在反比例函数a y x =(a > 0)的图象上,点B ,D 在反比例函数by x=(b <0)的图象上,AB ∥CD ∥x 轴,AB ,CD 在x 轴的两侧,AB = 3,CD = 2,AB 与CD 的距离为5,则a -b 的值是.【答案】612. 如图,矩形OABC 的顶点A ,C 的坐标分别是(4,0)和(0,2),反比例函数y =kx(x >0)的图象过对角线的交点P 并且与AB ,BC 分别交于D ,E 两点. 连接OD ,OE ,DE , 则△ODE 的面积为 .【答案】15413. 分)已知y 是x 的反比例函数,当x > 0时,y 随x 的增大而减小.请写出一个..满足以上条件的函数表达式 .【答案】(答案不唯一)【解析】∵当x > 0时,y 随x 的增大而减小∴反比例函数图像在一,三象限;故14. 分)一个反比例函数图象过点A (-2,-3),则这个反比例函数的解析式是 . 【答案】6y x=15. )如右图,在平面直角坐标系中,四边形ODEF 和四边形ABCD 都是正方形,点F在x 轴的正半轴上,点C在边DE上,反比例函数()0,ky k x x=≠>0的图象过点B、E ,若AB=2,则k 的值为【答案】6+【解析】解:反比例函数()0,ky k x x=≠>0设E(a 、a ),若AB=2, ∵四边形ODEF 和四边形ABCD 都是正方形, ∴B (2,a +2),∴22k a a ka ⎧=⎪⎪⎨⎪+=⎪⎩,()222a a =+,2240a a --=,1a ==±a >1a =22(16k a ===+16. (2015浙江省绍兴市,15,5分)在平面直角坐标系的第一象限内,边长为1的正方形ABCD 的边均平行于坐标轴,A 点的坐标为(a ,a)。
初三数学总复习──一次函数、正比例及反比例函数

初三数学总复习──一次函数、正比例及反比例函数一、填空题:1. 已知函数32)2(3--+=mx m y 是一次函数,则m= ;此图象经过第 象限。
2. 一束光线从y 轴上点A (0,1)出发, 经过x 轴上点C 反射后经过点 B (3,3),则光线从A 点到B 点经过的路线长是 ; 直线BC 的解析式为 。
3. 如图,一个矩形推拉窗,窗高1.5米,则活动窗扇的通风面积A (平方米)与拉开长度b (米)的关系式是: ;4. 已知一次函数2+=kx y ,请你补充一个条件: ,使y 随x5. 如果直线y =ax +b 经过一、二、三象限,那么ab0 (填上“<”或“>”或“=”). 6. 如图:表示长沙市2003年6月份某一天的气温随时间变化的情况,请观察此图,回答下列问题:(1)这天的最高气温是 度?(2)这天共有 小时的气温在31度以上; (3)这天有 (时间)范围内温度在上升?(4)请你预测一下,次日凌晨1点的气温是多少度? 答:。
7. 用火柴棒按如图的方式搭一行三角形,搭一个三角形需3支火柴棒,搭2个三角形需5支火柴棒,搭3个 三角形需7支火柴棒,照这样的规律搭下去,搭n 个 三角形需要S 支火柴棒,那么S 关于n 的函数关系式 是 (n 为正整数)∙∙ ∙ ∙ ∙∙ ∙∙ ∙30DC BA8. 如图是反比例函数xky =上的图象,那么k 与0的大小关系是k 0. 9. 一个函数的图象过点(1,2),且y 随x 的增大而增大,则这个函数的解析式是(任写一个).10. 已知反比例函数的图象过(-2,-3),则它的解析式为 .11. 在平面直角坐标系内,从反比例函数xk y =(k >0)的图象上的一点分别作x 、y 轴的垂线段,与x 、y 轴所围成的矩形面积是12,那么该函数解析式是 。
12. 若正比例函数x m y )21(-=的图像经过点A (1x ,1y )和点B (2x ,2y ),当1x <2x 时1y >2y ,则m 的取值范围是 .13. 已知函数m x y +-=与4-=mx y 的图像的交点在x 轴的负半轴上,那么m 的值为 .14. 函数y = kx + 1与函数x y =在同一坐标系中的大致图象是( )30OO时间/小时3333333332222222224211812963二、解答题:15. 已知y -1与x 成正比例,且x =2时,y =5,写出y 与x 之间的函数关系式;当x =-1时,求y 的值;当y =0时,求x 的值。
2014年河北省中考数学试题及答案解析版

2014年河北省中考数学试卷参考答案与试题解析一、选择题(共16小题,1~6小题,每小题2分;7~16小题,每小题2分,共42分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2分)(2014•河北)﹣2是2的()A.倒数B.相反数C.绝对值D.平方根考点:相反数.分析:根据只有符号不同的两个数互为相反数,可得一个数的相反数.解答:解:﹣2是2的相反数,故选:B.点评:本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.2.(2分)(2014•河北)如图,△ABC中,D,E分别是边AB,AC的中点.若DE=2,则BC=()A.2B.3C.4D.5考点:三角形中位线定理.分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得BC=2DE.解答:解:∵D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∴BC=2DE=2×2=4.故选C.点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,熟记定理是解题的关键.3.(2分)(2014•河北)计算:852﹣152=()A.70 B.700 C.4900 D.7000考点:因式分解—运用公式法.分析:直接利用平方差进行分解,再计算即可.解答:解:原式=(85+15)(85﹣15)=100×70=7000.故选:D.点评:此题主要考查了公式法分解因式,关键是掌握平方差公式:a2﹣b2=(a+b)(a﹣b).4.(2分)(2014•河北)如图,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角是()A.20°B.30°C.70°D.80°考点:三角形的外角性质.分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.解答:解:a,b相交所成的锐角=100°﹣70°=30°.故选B.点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.5.(2分)(2014•河北)a,b是两个连续整数,若a<<b,则a,b分别是()A.2,3 B.3,2 C.3,4 D.6,8考点:估算无理数的大小.分析:根据,可得答案.解答:解:,故选:A.点评:本题考查了估算无理数的大小,是解题关键.6.(2分)(2014•河北)如图,直线l经过第二、三、四象限,l的解析式是y=(m﹣2)x+n,则m的取值范围在数轴上表示为()A.B.C.D.考点: 一次函数图象与系数的关系;在数轴上表示不等式的解集.专题: 数形结合.分析:根据一次函数图象与系数的关系得到m﹣2<0且n<0,解得m<2,然后根据数轴表示不等式的方法进行判断.解答:解:∵直线y=(m﹣2)x+n经过第二、三、四象限,∴m﹣2<0且n<0,∴m<2且n<0.故选C.点评:本题考查了一次函数图象与系数的关系:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).也考查了在数轴上表示不等式的解集.7.(3分)(2014•河北)化简:﹣=()A.0B.1C.x D.考点:分式的加减法.专题: 计算题.分析:原式利用同分母分式的减法法则计算,约分即可得到结果.解答:解:原式==x.故选C点评:此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.8.(3分)(2014•河北)如图,将长为2、宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n≠()A.2B.3C.4D.5考点:图形的剪拼.分析:利用矩形的性质以及正方形的性质,结合勾股定理得出分割方法即可.解答:解:如图所示:将长为2、宽为1的矩形纸片分割成n个三角形后,拼成面积为2的正方形,则n可以为:3,4,5,故n≠2.故选:A.点评:此题主要考查了图形的剪拼,得出正方形的边长是解题关键.9.(3分)(2014•河北)某种正方形合金板材的成本y(元)与它的面积成正比,设边长为x厘米.当x=3时,y=18,那么当成本为72元时,边长为()A.6厘米B.12厘米C.24厘米D.36厘米考点:一次函数的应用.分析:设y与x之间的函数关系式为y=kx2,由待定系数法就可以求出解析式,当y=72时代入函数解析式就可以求出结论.解答:解:设y与x之间的函数关系式为y=kx2,由题意,得18=9k,解得:k=2,∴y=2x2,当y=72时,72=2x2,∴x=6.故选A.点评:本题考查了待定系数法求函数的解析式的运用,根据解析式由函数值求自变量的值的运用,解答时求出函数的解析式是关键.10.(3分)(2014•河北)如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A,B围成的正方体上的距离是()A.0B.1C.D.考点:展开图折叠成几何体.分析:根据展开图折叠成几何体,可得正方体,根据勾股定理,可得答案.解答:解;AB是正方体的边长,AB=1,故选:B.点评:本题考查了展开图折叠成几何体,勾股定理是解题关键.11.(3分)(2014•河北)某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是()A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球D.掷一个质地均匀的正六面体骰子,向上的面点数是4考点:利用频率估计概率;折线统计图.分析:根据统计图可知,试验结果在0.17附近波动,即其概率P≈0.17,计算四个选项的概率,约为0。
2014年全国各地中考数学真题分类解析汇编:12 反比例函数(2)

反比例函数一、选择题1. (2014•福建泉州,第7题3分)在同一平面直角坐标系中,函数与(m≠0)的图象可能是()A.B.C.D.考点:反比例函数的图象;一次函数的图象.分析:先根据一次函数的性质判断出m取值,再根据反比例函数的性质判断出m的取值,二者一致的即为正确答案.解答:解:A、由函数的图象可知m>0,由函数的图象可知m>0,故本选项正确;B、由函数的图象可知m<0,由函数的图象可知m>0,相矛盾,故本选项错误;C、由函数的图象y随x的增大而减小,则m<0,而该直线与y轴交于正半轴,则m>0,相矛盾,故本选项错误;D、由函数的图象y随x的增大而增大,则m>0,而该直线与y轴交于负半轴,则m<0,相矛盾,故本选项错误;故选:A.点评:本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.2. (2014•广西贺州,第10题3分)已知二次函数2(a,b,c是常数,且a≠0)的图象如图所示,则一次函数与反比例函数在同一坐标系内的大致图象是()A.B.C.D.考点:二次函数的图象;一次函数的图象;反比例函数的图象.分析:先根据二次函数的图象得到a>0,b<0,c<0,再根据一次函数图象与系数的关系和反比例函数图象与系数的关系判断它们的位置.解答:解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线﹣>0,∴b<0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴一次函数的图象过第二、三、四象限,反比例函数分布在第二、四象限.故选B.点评:本题考查了二次函数的图象:二次函数2(a、b、c为常数,a≠0)的图象为抛物线,当a>0,抛物线开口向上;当a<0,抛物线开口向下.对称轴为直线﹣;与y轴的交点坐标为(0,c).也考查了一次函数图象和反比例函数的图象.[来源:学§科§网Z§X§X§K]3.(2014年天津市,第9 题3分)已知反比例函数,当1<x<2时,y的取值范围是()A.0<y <5 B.1<y<2 C.5<y<10 D.y>10考点:反比例函数的性质.分析:将1和2分别代入反比例函数即可确定函数值的取值范围.解答:解:∵反比例函数中当1时10,当2时,5,∴当1<x<2时,y的取值范围是5<y<10,故选C.点评:本题考查了反比例函数的性质:(1)反比例函数(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.4.(2014•新疆,第11题5分)若点A(1,y1)和点B(2,y2)在反比例函数图象上,则y1与y2的大小关系是:y1y2(填“>”、“<”或“=”).考点:反比例函数图象上点的坐标特征.分析:直接把点A(1,y)和点B(2,y2)代入反比例函数,求出点y1,y2的值,再比较出其大小即1可.解答:解:∵点A(1,y)和点B(2,y2)在反比例函数的图象上,1∴y11,y2=,∵1>,∴y1>y2.故答案为:>.点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.5.(2014•温州,第10题4分)如图,矩形的顶点A在第一象限,∥x轴,∥y轴,且对角线的交点与原点O重合.在边从小于到大于的变化过程中,若矩形的周长始终保持不变,则经过动点A的反比例函数(k≠0)中k的值的变化情况是()A.一直增大B.一直减小C.先增大后减小D.先减小后增大考点:反比例函数图象上点的坐标特征;矩形的性质.分析:设矩形中,2a,2b,由于矩形的周长始终保持不变,则为定值.根据矩形对角线的交点与原点O重合及反比例函数比例系数k的几何意义可知•,再根据一定时,当时,最大可知在边从小于到大于的变化过程中,k的值先增大后减小.解答:解:设矩形中,2a,2b.∵矩形的周长始终保持不变,∴2(22b)=4()为定值,∴为定值.∵矩形对角线的交点与原点O重合∴•,又∵为定值时,当时,最大,∴在边从小于到大于的变化过程中,k的值先增大后减小.故选C.点评:本题考查了矩形的性质,反比例函数比例系数k的几何意义及不等式的性质,有一定难度.根据题意得出•是解题的关键.6.(2014•四川自贡,第9题4分)关于x的函数(1)和(k≠0)在同一坐标系中的图象大致是()A.B.C.D.考点:反比例函数的图象;一次函数的图象分析:根据反比例函数的比例系数可得经过的象限,一次函数的比例系数和常数项可得一次函数图象经过的象限.解答:解:若k>0时,反比例函数图象经过一三象限;一次函数图象经过一二三象限,所给各选项没有此种图形;若k<0时,反比例函数经过二四象限;一次函数经过二三四象限,D答案符合;故选D.点评:考查反比例函数和一次函数图象的性质;若反比例函数的比例系数大于0,图象过一三象限;若小于0则过二四象限;若一次函数的比例系数大于0,常数项大于0,图象过一二三象限;若一次函数的比例系数小于0,常数项小于0,图象过二三四象限.关于x的函数(1)和(k≠0)在同一坐标系中的图象大致是()A.B.C.D.考点:反比例函数的图象;一次函数的图象分析:根据反比例函数的比例系数可得经过的象限,一次函数的比例系数和常数项可得一次函数图象经过的象限.解答:解:若k>0时,反比例函数图象经过一三象限;一次函数图象经过一二三象限,所给各选项没有此种图形;若k<0时,反比例函数经过二四象限;一次函数经过二三四象限,D答案符合;故选D.点评:考查反比例函数和一次函数图象的性质;若反比例函数的比例系数大于0,图象过一三象限;若小于0则过二四象限;若一次函数的比例系数大于0,常数项大于0,图象过一二三象限;若一次函数的比例系数小于0,常数项小于0,图象过二三四象限.7.(2014·云南昆明,第8题3分)左下图是反比例函数)0 (≠=kkxky为常数,的图像,则一次函数kkxy-=的图像大致是()考点:反比例函数的图象;一次函数的图象.分析:根据反比例函数的图象,可知0>k,结合一次函数的图象性质进行判断即可.解答:解:根据反比例函数的图象经过一、三象限,可知0>k,由一次函数kkxy-=,可知:0>k时,图象从左至右呈上升趋势,),0(k-是图象与y轴的交点,0<-k所以交点在y轴负半轴上.故选B.点评:本题考查了反比例函数的图象性质和一次函数函数的图象性质,要掌握它们的性质才能灵活解题.8. (2014•湘潭,第8题,3分)如图,A、B两点在双曲线上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S12=()(第1题图)A.3B.4C.5D.6考点:反比例函数系数k的几何意义.分析:欲求S12,只要求出过A、B两点向x轴、y轴作垂线段求出与坐标轴所形成的矩形的面积即可,而矩形面积为双曲线的系数k,由此即可求出S12.解答:解:∵点A、B是双曲线上的点,分别经过A、B两点向x轴、y轴作垂线段,则根据反比例函数的图象的性质得两个矩形的面积都等于4,∴S12=4+4﹣1×2=6.故选D.点评:本题主要考查了反比例函数的图象和性质及任一点坐标的意义,有一定的难度.DCBAOO OOO xxx xy y yyyxxky=9. (2014•益阳,第6题,4分)正比例函数6x的图象与反比例函数的图象的交点位于()A.第一象限B.第二象限C.第三象限D.第一、三象限考点:反比例函数与一次函数的交点问题.[来源:学*科*网]分析:根据反比例函数与一次函数的交点问题解方程组即可得到两函数的交点坐标,然后根据交点坐标进行判断.解答:解:解方程组得或,所以正比例函数6x的图象与反比例函数的图象的交点坐标为(1,6),(﹣1,﹣6).故选D.点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.10. (2014•株洲,第4题,3分)已知反比例函数的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是()A.(﹣6,1)B.(1,6)C.(2,﹣3)D.(3,﹣2)考点:反比例函数图象上点的坐标特征.分析:先根据点(2,3),在反比例函数的图象上求出k的值,再根据的特点对各选项进行逐一判断.解答:解:∵反比例函数的图象经过点(2,3),∴2×3=6,A、∵(﹣6)×1=﹣6≠6,∴此点不在反比例函数图象上;B、∵1×6=6,∴此点在反比例函数图象上;C、∵2×(﹣3)=﹣6≠6,∴此点不在反比例函数图象上;D、∵3×(﹣2)=﹣6≠6,∴此点不在反比例函数图象上.故选B.点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数中的特点是解答此题的关键.11. (2014•扬州,第3题,3分)若反比例函数(k≠0)的图象经过点P(﹣2,3),则该函数的图象的点是()A.(3,﹣2)B.(1,﹣6)C.(﹣1,6)D.(﹣1,﹣6)考点:反比例函数图象上点的坐标特征分析:先把P(﹣2,3)代入反比例函数的解析式求出﹣6,再把所给点的横纵坐标相乘,结果不是﹣6的,该函数的图象就不经过此点.解答:解:∵反比例函数(k≠0)的图象经过点P(﹣2,3),∴﹣2×3=﹣6,∴只需把各点横纵坐标相乘,不是﹣6的,该函数的图象就不经过此点,四个选项中只有D不符合.故选D.点评:本题主要考查反比例函数图象上点的坐标特征,所有在反比例函数上的点的横纵坐标的积应等于比例系数.二.填空题1. (2014•广西玉林市、防城港市,第18题3分)如图,是平行四边形,对角线在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线和的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①=;②阴影部分面积是(k12);③当∠90°时,12|;④若是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是①④(把所有正确的结论的序号都填上).考点:反比例函数综合题.专题:综合题.分析:作⊥y轴于E,⊥y轴于F,根据平行四边形的性质得S△△,利用三角形面积公式得到,则有,再利用反比例函数k的几何意义和三角形面积公式得到S△1•,S△2•,所以有=;由S△|,S△2|,得到S阴影部分△△(12|)=(k1﹣k2);当∠90°,得到四边形是矩形,由于不能确定与相1等,则不能判断△≌△,所以不能判断,则不能确定12|;若是菱形,根据菱形的性质得,可判断△≌△,则,所以12|,即k1=﹣k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.解答:解:作⊥y轴于E,⊥y轴于F,如图,∵四边形是平行四边形,∴S△△,∴,∴,∵S△1•,S△2•,∴=,所以①正确;∵S△1|,S△2|,∴S阴影部分△△(12|),而k1>0,k2<0,∴S阴影部分=(k1﹣k2),所以②错误;当∠90°,∴四边形是矩形,∴不能确定与相等,而,∴不能判断△≌△,∴不能判断,∴不能确定12|,所以③错误;若是菱形,则,而,∴△≌△,∴,∴12|,∴k1=﹣k2,∴两双曲线既关于x轴对称,也关于y轴对称,所以④正确.故答案为①④.点评:本题考查了反比例函数的综合题:熟练掌握反比例函数的图象、反比例函数k的几何意义、平行四边形的性质、矩形的性质和菱形的性质.2.(2014年天津市,第14题3分)已知反比例函数(k为常数,k≠0)的图象位于第一、第三象限,写出一个符合条件的k的值为1.考点:反比例函数的性质.专题:开放型.分析:反比例函数(k为常数,k≠0)的图象在第一,三象限,则k>0,符合上述条件的k的一个值可以是1.(正数即可,答案不唯一)解答:解:∵反比例函数的图象在一、三象限,∴k>0,只要是大于0的所有实数都可以.例如:1.故答案为:1.点评:此题主要考查反比例函数图象的性质:(1)k>0时,图象是位于一、三象限;(2)k<0时,图象是位于二、四象限.3.(2014•武汉,第15题3分)如图,若双曲线与边长为5的等边△的边,分别相交于C,D两点,且3,则实数k的值为.考点:反比例函数图象上点的坐标特征;等边三角形的性质分析:过点C作⊥x轴于点E,过点D作⊥x轴于点F,设3x,则,分别表示出点C、点D的坐标,代入函数解析式求出k,继而可建立方程,解出x的值后即可得出k的值.解答:解:过点C作⊥x轴于点E,过点D作⊥x轴于点F,设3x,则,在△中,∠60°,则,,则点C坐标为(x,x),在△中,,∠60°,则,,则点D的坐标为(5﹣x,x),将点C的坐标代入反比例函数解析式可得:2,将点D的坐标代入反比例函数解析式可得:﹣x2,则x2﹣x2,解得:x1=1,x2=0(舍去),故×12=.故答案为:.点评:本题考查了反比例函数图象上点的坐标特征,解答本题关键是利用k的值相同建立方程,有一定难度.4.(2014•邵阳,第13题3分)若反比例函数的图象经过点(﹣1,2),则k的值是﹣2 .考点:待定系数法求反比例函数解析式分析:因为(﹣1,2)在函数图象上,,从而可确定k的值.解答:解:∵图象经过点(﹣1,2),∴﹣1×2=﹣2.故答案为:﹣2.点评:[来源:学§科§网Z§X§X§K]本题考查待定系数法求反比例函数解析式,关键知道反比例函数式的形式,从而得解.5.(2014•孝感,第17题3分)如图,△的一条直角边在x轴上,双曲线经过斜边的中点C,与另一直角边交于点D.若S△9,则S△的值为6.考点:反比例函数系数k的几何意义.分析:过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即.解答:解:如图,过C点作⊥x轴,垂足为E.∵△中,∠90°,∴∥,∵C为△斜边的中点C,∴为△的中位线,∵△∽△,∴=.∵双曲线的解析式是,∴S△△,∴S△4S△2k ,由S△﹣S△△2S △18,得2k﹣18,12,S△△6,故答案为:6.点评:本题考查了反比函数k的几何意义,过图象上的任意一点作x轴、y轴的垂线,所得三角形的面积是,是经常考查的知识点,也体现了数形结合的思想.6.(2014•浙江湖州,第15题4分)如图,已知在△中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数(k≠0)在第一象限的图象经过的中点B,交于点D,连接.若△∽△,则直线的解析式为.分析:设,根据点D在反比例函数图象上表示出,再根据相似三角形对应边成比例列式求出,然后根据中点的定义表示出点B的坐标,再根据点B在反比例函数图象上表示出a、k的关系,然后用a表示出点B的坐标,再利用待定系数法求一次函数解析式解答.解:设,∵点D在上,∴,∵△∽△,∴=,∴,∴点A(a,),∵点B是的中点,∴点B的坐标为(,),∵点B在反比例函数图象上,∴=,解得,a2=2k,∴点B的坐标为(,a),设直线的解析式为,则m•,解得2,所以,直线的解析式为2x.故答案为:2x.点评:本题考查了相似三角形的性质,反比例函数图象上点的坐标特征,用的长度表示出点B的坐标是解题的关键,也是本题的难点.7.(2014年江苏南京,第11题,2分)已知反比例函数的图象经过点A(﹣2,3),则当﹣3时,.考点:反比例函数分析:先把点A(﹣2,3)代入求得k的值,然后将﹣3代入,即可求出y的值.[来源§§]解答:∵反比例函数的图象经过点A(﹣2,3),∴﹣2×3=﹣6,∴反比例函数解析式为﹣,∴当﹣3时,﹣=2.故答案是:2.点评:本题考查了反比例函数图象上点的坐标特征.利用待定系数法求得反比例函数解析式是解题的关键.8.(2014•滨州,第17题4分)如图,菱形的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为﹣6 .考点:反比例函数图象上点的坐标特征;菱形的性质专题:探究型.分析:先根据菱形的性质求出C点坐标,再把C点坐标代入反比例函数的解析式即可得出k的值.解答:解:∵菱形的两条对角线的长分别是6和4,∴C(﹣3,2),∵点C在反比例函数的图象上,∴2=,解得﹣6.故答案为:﹣6.点评:本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式.9.(2014•菏泽,第13题3分)如图,△中,∠90°,点A在第一象限、点B在第四象限,且:1:,若点A(x0,y0)的坐标x0,y0满足y0=,则点B(x,y)的坐标x,y所满足的关系式为﹣2x.考点:反比例函数图象上点的坐标特征;相似三角形的判定与性质.分析:设点B在反比例函数(k<0)上,分别过点A、B作,分别垂直y轴于点C、D,由相似三角形的判定定理得出△∽△,再由相似三角形的性质得出△的面积,进而可得出结论.解答:解:设点B在反比例函数(k<0)上,分别过点A、B作,分别垂直y轴于点C、D,∵∠∠90°,∠∠90°,∠∠90°,∴∠∠,∴△∽△,∴=()2=()2=,∵点A(x0,y0)的坐标x0,y0满足y0=,∴S△,∴S△1,∴﹣2,∴点B(x,y)的坐标x,y所满足的关系式为﹣2x.故答案为:﹣2x.点评:此题考查了反比例函数图象上点的坐标特点,此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.10.(2014•济宁,第14题3分)如图,四边形是矩形,是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在上,点B、E在反比例函数的图象上,1,6,则正方形的边长为2.。
中考数学反比例函数及其应用专题训练(含答案)
中考数学反比例函数及其应用专题训练一、选择题1. 姜老师给出一个函数表达式,甲、乙、丙三位同学分别正确指出了这个函数的一个性质.甲:函数图象经过第一象限;乙:函数图象经过第三象限;丙:在每一个象限内,y值随x值的增大而减小.根据他们的叙述,姜老师给出的这个函数表达式可能是()A. y=3xB. y=3 xC. y=-1x D. y=x22.若点(1,y1),(2,y2),(3,y3)在反比例函数y=kx(k<0)的图象上,则y1,y2,y3的大小关系是A.y1>y2>y3B.y3>y2>y1 C.y1>y3>y2D.y2>y3>y13.反比例函数y=kx经过点(2,1) ,则下列说法错误..的是()A. k=2B.函数图象分布在第一、三象限C.当x>0时,随x的增大而增大D.当x>0时,y随x的增大而减小4. 如图,过反比例函数y=kx(k>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为() A. 2 B. 3 C. 4 D. 55.如图,函数(0)y kx b k =+≠与my (m 0)x=≠的图象相交于点(2,3),(1,6)A B --两点,则不等式mkx b x+>的解集为( )A. 2x >-B. 20x -<<或1x >C. 1x >D. 2x <-或01x <<6. 如图,O 为坐标原点,四边形OACB 是菱形,OB 在x 轴的正半轴上,sin ∠AOB=45,反比例函数y =48x 在第一象限内的图象经过点A ,与BC 交于点F ,则△AOF 的面积等于( )A. 60B. 80C. 30D. 407.如图,在平面直角坐标系中,△OAB的边OA 在x 轴正半轴上,其中∠OAB =90°,AO =AB ,点C 为斜边OB 的中点,反比例函数y =kx(k >0,x >0)的图象过点C ,且交线段AB 于点D ,连结CD ,OD ,若S △OCD =32,则k 的值为( )D CBAxyOA .3B .52C .2D .18.如图,函数y =1(0)1(0)x xx x⎧>⎪⎪⎨⎪-<⎪⎩的图象所在坐标系的原点是( )A .点MB .点NC .点PD .点Q二、填空题9. 若点(3,5)在反比例函数y=(k ≠0)的图象上,则k= .10. 已知函数y =-1x ,当自变量的取值为-1<x <0或x ≥2,函数值y 的取值____________.11. 我们把直角坐标系中横坐标与纵坐标都是整数的点称为整点.反比例函数y=-3x 的图象上有一些整点,请写出其中一个整点的坐标________.12. 已知反比例函数y =kx (k ≠0)的图象如图所示,则k 的值可能是________(写一个即可).13. 如图,过原点O 的直线与反比例函数y 1、y 2的图象在第一象限内分别交于点A 、B ,且A 为OB 的中点.若函数y 1=1x ,则y 2与x 的函数表达式是________.14. 双曲线y =m -1x 在每个象限内,函数值y 随x 的增大而增大,则m 的取值范围是________.15. 如图,直线y 1=kx (k ≠0)与双曲线y 2=2x (x >0)交于点A (1,a ),则y 1>y 2的解集为________.16. 如图,直线l ⊥x 轴于点P ,且与反比例函数y 1=k 1x (x >0)及y 2=k 2x (x >0)的图象分别交于点A ,B ,连接OA ,OB ,已知△OAB 的面积为2,则k 1-k 2=__________.三、解答题17. 如图,已知反比例函数y=(x>0)的图象与一次函数y=-x+4的图象交于A和B(6,n)两点.(1)求k和n的值;(2)若点C(x,y)也在反比例函数y=(x>0)的图象上,求当2≤x≤6时,函数值y的取值范围.18. 如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A在x轴的正半轴上,顶点C的坐标为(1,3).(1)求图象过点B的反比例函数的解析式;(2)求图象过点A、B的一次函数的解析式;(3)在第一象限内,当以上所求一次函数的图象在所求反比例函数的图象下方时,请直接写出自变量x的取值范围.19. 如图,在直角坐标系中,直线y=-12x与反比例函数y=kx的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.(1)求反比例函数的表达式;(2)将直线y=-12x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.20. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=35.(1)求反比例函数的解析式;(2)连接OB,求△AOB的面积.21.如图,在直角坐标系中,已知点B(4,0),等边三角形OAB的顶点A在反比例函数y k的图象上.x(1)求反比例函数的表达式.(2)把△OAB向右平移a个单位长度,对应得到△O'A'B',当这个函数图象经过△O'A'B'一边的中点时,求a的值.答案一、选择题1. 【答案】B【解析】图象经过一,三象限,则它可能是正比例函数或反比例函数;在每一个象限内,y随x的增大而减小,则它是反比例函数,并且反比例函数中的比例系数大于0,故本题选B.2. 【答案】C【解析】∵k<0,∴在每个象限内,y随x值的增大而增大,∴当x=–1时,y1>0,∵2<3,∴y2<y3<y1,故选C.3. 【答案】C【解析】本题考查了反比例函数图象上点的坐标特征与反比例函数的性质,因为反比例函数y=kx经过点(2,1) ,∴1=2k,∴k=2,故A选项正确;∵反比例函数的解析式为y=2x,k=2>0,∴图象分布在第一、三象限,故B选项正确;∵k=2>0,∴当x>0时,y随x的增大而减小,故C选项错误;∵k=2>0,∴当x<0时,y 随x的增大而减小,故D选项正确,故选C.4. 【答案】C【解析】∵点A在反比例函数y=kx的图象上,且AB⊥x轴于点B,设点A坐标为(x,y),∴k=xy,∵点A在第一象限,∴x、y都是正数,∴S△AOB=12OB·AB=12xy,∵S△AOB=2,∴k=xy=4.5. 【答案】【答案】D【解析】本题是数形结合题,通过观察反比例函数与一次函数的图像解决问题.通过图像观察,可知,当2x<-或01x<<时,一次函数的图像在反比例函数图像的上方.故选D.6. 【答案】D【解析】如解图所示,过点A作AG⊥OB,垂足为G,设A点纵坐标为4m,∵sin∠AOB=45,∴OA=5m,根据勾股定理可得OG=3m,又∵点A在反比例函数y=48x上,∴3m×4m=48,∴m1=2,m2=-2(不合题意,舍去),∴AG=8,OG=6,OA=OB=10,∵四边形OBCA是菱形,∴BC∥OA,∴S△AOF=12S菱形OBCA=12×AG×OB=12×8×10=40.故选D.7. 【答案】C【解析】如图,作CE⊥x轴于点E,∵点C,D均在反比例函数y=kx的图象上,∴S △COE= S △AOD=2k,∵S 四边形OADC=S △COE +S 梯形ADCE=S △AOD+S △OCD ,∴S 梯形ADCE= S △OCD=32,不妨设OA=AB=a ,∵∠OAB=90°,∴点A (a ,0),B (a ,a ),∵点C 为斜边OB 的中点,∴C (12a ,12a )∴k =12a ×12a =14a 2,∵点D 的横坐标是a ,∴点D 的纵坐标是14a ,即D (a ,14a ).∵S 梯形ADCE=12(AD+CE )·AE=32,∴12×(14a +12a )×(a -12a )=32,得:a 2=8,∴k =14a 2=14×8=2.ED CBAxyO8. 【答案】A【解析】由已知可知函数y =1(0)1(0)x xx x⎧>⎪⎪⎨⎪-<⎪⎩关于y 轴对称,所以点M 是原点;故选A .二、填空题9. 【答案】15[解析]把点(3,5)的坐标代入反比例函数y=,得k=3×5=15,故答案为15.10. 【答案】y >1或-12≤y <0 【解析】∵函数y =-1x ,∴该反比例函数图象在二、四象限,且在二、四象限都随x 的增大而增大,画出草图如解图,当-1<x <0时,y >1;当x≥2时,-12≤y <0,∴函数值y 的取值为y >1或-12≤y <0.11. 【答案】(1,-3)(答案不唯一,合理即可)【解析】对于y =-3x ,依题意,说明只要x 是3的约数即可,如(1,-3),(-1,3).12. 【答案】-2(答案不唯一)【解析】根据反比例函数的图象在二、四象限,则k <0,如k =-2(答案不唯一).13. 【答案】y 2=4x 【解析】设y 2与x 的函数关系式为y 2=k x ,A 点坐标为(a ,b),则ab =1.又A 点为OB 的中点,因此,点B 的坐标为(2a ,2b),则k =2a·2b =4ab =4,所以y 2与x 的函数关系式为y 2=4x .14. 【答案】m <1【解析】∵在每个象限内,函数值y 随x 的增大而增大,∴双曲线在二、四象限内,∴在函数y =m -1x 中,m -1<0,即m <1.15. 【答案】x >1【解析】当x >1时,直线的图象在双曲线图象的上方,即y 1>y 2.因此,y 1>y 2的解集为x >1.16. 【答案】4【解析】∵反比例函数y 1=k 1x (x >0)及y 2=k 2x (x >0)的图象均在第一象限内,∴k 1>0,k 2>0,∵AP ⊥x 轴,∴S △OAP =12k 1,S △OBP =12k 2,∴S △OAB =S △OAP -S △OBP=12(k1-k2)=2,解得k1-k2=4.三、解答题17. 【答案】解:(1)把B(6,n)代入一次函数y=-x+4中,可得n=-×6+4=1,所以B点的坐标为(6,1).又B在反比例函数y=(x>0)的图象上,所以k=xy=1×6=6,所以k的值为6,n的值为1.(2)由(1)知反比例函数的解析式为y=.当x=2时,y==3;当x=6时,y==1,由函数图象可知,当2≤x≤6时函数值y的取值范围是1≤y≤3.18. 【答案】(1)如解图,过点C作CD⊥OA于点D,则OD=1,CD=3,在Rt△OCD中,由勾股定理得OC=OD2+CD2=2,∵四边形OABC为菱形,∴BC=AB=OA=OC=2,则点B的坐标为(3,3),设反比例函数的解析式为y=kx(k≠0),∵其图象经过点B,∴将B(3,3)代入,得3=k3,解得k =33, ∴该反比例函数的解析式为y =33x ;(2)∵OA =2,∴点A 的坐标为(2,0),由(1)得B (3,3),设图象经过点A 、B 的一次函数的解析式为y =k ′x +b (k ′≠0),将A (2,0),B (3,3)分别代入,得⎩⎪⎨⎪⎧2k ′+b =03k ′+b =3,解得⎩⎪⎨⎪⎧k ′=3b =-23, ∴该一次函数的解析式为y =3x -23;(3)由图象可得,满足条件的自变量x 的取值范围是2<x <3.19. 【答案】解:(1)∵点A 的纵坐标是3,当y =3时,3=-12x, 解得x =-6,∴点A 的坐标为(-6,3),(1分)把A(-6,3)代入y =k x ,得3=k -6, 解得k =-18,∴反比例函数的解析式为y =-18x .(3分)解图(2)如解图,连接CO ,∵A ,B 关于原点对称,∴AO =BO ,∴S △AOC =12S △ABC =24.(4分)作CF ⊥x 轴于点F ,AE ⊥x 轴于点E ,则S △CFO =S △AEO =12AE·EO =12×3×6=9,S △AOC =S 梯形AEFC =24.设C(x ,-18x ),则有(3-18x )(x +6)2=24,(5分) 整理得x 2-16x -36=0,∴x 1=-2,x 2=18(舍去),∴C(-2,9),(7分)设y =-12x 平移后的解析式为y =-12x +b ,把C(-2,9)代入上式得,9=1+b ,解得b =8,∴平移后的直线的函数表达式为y =-12x +8.(8分)20. 【答案】(1)【思路分析】如解图,过点A 作AE ⊥x 轴于点E ,由三角函数求出点A 坐标,再用待定系数法求出反比例函数的解析式便可.解:如解图过点A 作AE ⊥x 轴于点E ,∵OA =5,sin ∠AOC =35,∴AE =OA·sin ∠AOC =5×35=3,OE =OA 2-AE 2=4,∴A(-4,3),(3分)设反比例函数的解析式为y =k x (k≠0),把A(-4,3)代入解析式,得k =-12,∴反比例函数的解析式为y =-12x .(5分)(2)【思路分析】先把B 点坐标代入所求出的反比例函数解析式,求出m 的值,进而求出直线AB 的解析式,再求出点D 的坐标,便可求△AOD 与△BOD 的面积之和,即△AOB 的面积.解:把B(m ,-4)代入y =-12x 中,得m =3,∴B(3,-4).设直线AB 的解析式为y =kx +b ,把A(-4,3)和B(3,-4)代入得, ⎩⎪⎨⎪⎧-4k +b =33k +b =-4, 解得⎩⎪⎨⎪⎧k =-1b =-1,(7分) ∴直线AB 的解析式为y =-x -1,(8分)则AB 与y 轴的交点D(0,-1),∴S △AOB =S △AOD +S △BOD =12×1×4+12×1×3=3.5.(10分)21. 【答案】(1)反比例函数的解析式为y =;(2)a 的值为1或3. 【解析】(1)如图1,过点A 作AC ⊥OB 于点C ,∵△OAB 是等边三角形,∴∠AOB =60°,OC 12=OB , ∵B (4,0),∴OB =OA =4,∴OC=2,AC=23.把点A(2,23)代入y kx=,解得k=43.∴反比例函数的解析式为y43x =;(2)分两种情况讨论:①当点D是A′B′的中点,如图2,过点D作DE⊥x轴于点E.由题意得A′B′=4,∠A′B′E=60°,在Rt△DEB′中,B′D=2,DE=3,B′E=1.∴O′E=3,把y3=代入y43=,得x=4,∴OE=4,∴a=OO′=1;②如图3,点F是A′O′的中点,过点F作FH⊥x轴于点H.由题意得A′O′=4,∠A′O′B′=60°,在Rt△FO′H中,FH3=O′H=1.把y=y=,得x=4,x∴OH=4,∴a=OO′=3,综上所述,a的值为1或3.。
浙江新中考2014届中考数学总复习课件(11)反比例函数
6 6. (2013· 宁波)已知一个函数的图象与 y= 的图象 x 6 关于 y 轴成轴对称,则该函数的解析式为 y=- . x 7. (2013· 绍兴)在平面直角坐标系中,O 是原点, A 是 x 轴上的点,将射线 OA 绕点 O 旋转,使点 A 与 3 双曲线 y= 上的点 B 重合.若点 B 的纵坐标是 1, x 则点 A 的横坐标是 2 或-2.
考点一
反比例函数的定义
k -1 一般地,函数 y= (或写成 y=kx )(k 是常数, x k≠0)叫做反比例函数. 反比例函数的解析式可以写成 xy= k(k≠ 0),它 表明在反比例函数中自变量 x 与其对应函数值 y 之积, 总等于已知常数 k.
考点二
反比例函数的图象和性质
k 1.反比例函数 y= (k 是常数, k≠ 0)的图象是 x 双曲线. 因为 x≠ 0,k≠0,相应地 y 值也不能为 0,所以 反比例函数的图象无限接近 x 轴和 y 轴,但永不与 x 轴、 y 轴相交.
11. (2013· 丽水 )如图,科技小组准备用材料围建 一个面积为 60 m 的矩形科技园 ABCD,其中一边 AB 靠墙,墙长为 12 m.设 AD 的长为 x m, DC 的长为 y m.
2
(1)求 y 与 x 之间的函数关系式; (2)若围成矩形科技园 ABCD 的三边材料总长不超 过 26 m,材料 AD 和 DC 的长都是整米数,求出满足 条件的所有围建方案. 60 解:(1)由题意,得 xy= 60,即 y= . x 60 ∴所求的函数关系式为 y= . x
如图①和②,S 矩形 PAOB=PA· PB= |y|· |x|= |xy|= |k|, 1 1 同理可得 S△ OPA= S△ OPB= |xy|= |k|. 2 2 温馨提示 根据图象描述性质、根据性质大致画出图象及求 解析式是一个难点,要逐步理解和掌握.
2014年全国中考数学试题分类汇编12_反比例函数(含解析)
反比例函数一、选择题1. (2014•福建泉州)在同一平面直角坐标系中,函数y=mx+m与y =(m≠0)的图象可能是()2. (2014•广西贺州)已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+与反比例函数y=在同一坐标系内的大致图象是()A.B.C.D.3.(2014年天津市)已知反比例函数y =,当1<x<2时,y的取值范围是()A.0<y<5 B.1<y<2 C.5<y<10 D.y>104.(2014•新疆)若点A(1,y1)和点B(2,y2)在反比例函数y=图象上,则y 1与y2的大小关系是:y1y2(填“>”、“<”或“=”).5.(2014•温州)如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=(k≠0)中k的值的变化情况是()6.(2014•四川自贡)关于x 的函数y =k (x +1)和y =(k ≠0)在同一坐标系中的图象大致是( ). . . D . 关于x 的函数y =k (x +1)和y =(k ≠0)在同一坐标系中的图象大致是( ) . . . D .7.(2014·云南昆明)左下图是反比例函数)0(≠=k k x y 为常数,的图像,则一次函数k kx y -=的图像大致是( )8. (2014•湘潭)如图,A 、B 两点在双曲线y =上,分别经过A 、B 两点向轴作垂线段,已知S 阴影=1,则S 1+S 2=()9. (2014•益阳)正比例函数y =6x 的图象与反比例函数y=的图象的交点位于( )DC B A10. (2014•株洲)已知反比例函数y=的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是()11. (2014•扬州)若反比例函数y=(k≠0)的图象经过点P(﹣2,3),则该函数的图象的点是()二.填空题1.(2014•武汉)如图,若双曲线y=与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且OC=3BD,则实数k的值为.2.(2014•邵阳)若反比例函数的图象经过点(﹣1,2),则k的值是.3.(2014•孝感)如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为.4.(2014•浙江湖州)如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为.5.(2014年江苏南京,第11题,2分)已知反比例函数y=的图象经过点A(﹣2,3),则当x=﹣3时,y=.6.(2014•滨州)如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为.7.(2014•菏泽)如图,Rt△ABO中,∠AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:,若点A(x0,y0)的坐标x0,y0满足y0=,则点B(x,y)的坐标x,y所满足的关系式为.8.(2014•济宁)如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=的图象上,OA=1,OC=6,则正方形ADEF的边长为.三.解答题1.(2014年四川资阳)如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.(1)求一次函数和反比例函数的解析式;(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?2.(2014年云南省)将油箱注满k升油后,轿车科行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?3.(2014•舟山)实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=(k>0)刻画(如图所示).(1)根据上述数学模型计算:①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?②当x=5时,y=45,求k的值.(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.4.(2014•襄阳)如图,一次函数y1=﹣x+2的图象与反比例函数y2=的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=,点B的坐标为(m,n).(1)求反比例函数的解析式;(2)请直接写出当x<m时,y2的取值范围.5.(2014•四川自贡)如图,一次函数y=kx+b与反比例函数的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;(2)根据图象直接写出的x的取值范围;(3)求△AOB的面积.6.(2014•浙江湖州)如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=的图象上,过点A的直线y=x+b交x轴于点B.(1)求k和b的值;(2)求△OAB的面积.7.(2014•德州)如图,双曲线y=(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).(1)确定k的值;(2)若点D(3,m)在双曲线上,求直线AD的解析式;(3)计算△OAB的面积.8.(2014•菏泽)如图,在平面直角坐标系xOy中,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数y=(x>0)的图象相交于点B(2,1).①求m的值和一次函数的解析式;②结合图象直接写出:当x>0时,不等式kx+b>的解集.9.(2014年山东泰安)如图①,△OAB中,A(0,2),B(4,0),将△AOB向右平移m 个单位,得到△O′A′B′.(1)当m=4时,如图②.若反比例函数y=的图象经过点A′,一次函数y=ax+b的图象经过A′、B′两点.求反比例函数及一次函数的表达式;(2)若反比例函数y=的图象经过点A′及A′B′的中点M,求m的值.。
中考数学真题《反比例选填题》专项测试卷(附答案)
中考数学真题《反比例选填题》专项测试卷(附答案)学校:___________班级:___________姓名:___________考号:___________一.选择题(共1小题)1.(2024•丰台区二模)已知点1(A x 1)y 2(B x 2)y 在反比例函数2y x=的图象上 且120x x <<,则下列结论一定正确的是( ) A .120y y +<B .120y y +>C .120y y -<D .120y y ->二.填空题(共9小题)2.(2024•顺义区二模)已知点1(A x 1)y 2(B x 2)y 在反比例函数(0)ky k x=≠的图象上 当120x x <<时 12y y >,则k 的取值范围是 .3.(2024•大兴区二模)在平面直角坐标系xOy 中 若点1(3,)A y 和2(2,)B y 在反比例函数(0)ky k x=<的图象上,则1y 2y (填“>”“ =”或“<” ). 4.(2024•昌平区二模)在平面直角坐标系xOy 中 若点(1,)m 和(4,2)在反比例函数(0)k y k x=≠图象上,则m = .5.(2024•海淀区二模)在平面直角坐标系xOy 中 点1(1,)A y 2(2,)B y 在反比例函数(0)k y k x=≠的图象上.若12y y <,则满足条件的k 的值可以是 (写出一个即可).6.(2024•朝阳区二模)在平面直角坐标系xOy 中 若反比例函数(0)k y k x=≠的图象位于第二 四象限 且点1(,)A m y (B m - 2)(0)y m >都在该图象上,则1y 2.y (填“<” “ >”或“=” )7.(2024•石景山区二模)在平面直角坐标系xOy 中 若函数(0)ky k x=≠的图象经过点(1,6)A -和(3,)B m ,则m 的值为 .8.(2024•北京二模)在平面直角坐标系xOy 中 若点1(1,)y 2(4,)y 在反比例函数(0)ky k x=>的图象上,则1y 2y (填“>” “ =”或“<” ).9.(2024•西城区二模)如图,(2,)A m (3,2)B 两点在反比例函数(0)ky x x=>的图象上.若将横 纵坐标都是整数的点称为整点,则线段OA OB 及反比例函数图象上A B 两点之间的部分围成的区域(不含边界)中 整点的坐标为 .10.(2024•东城区二模)在平面直角坐标系xOy 中 若点(2,4)是函数11(0)y k x k =≠和22(0)k y k x=≠的图象的一个交点,则这两个函数图象的另一个交点的坐标是 . 11.(2024房山二模)在平面直角坐标系xOy 中 若反比例函数(0)ky k x=≠的图象经过点(12)A -,和(4)B m ,,则m 的值为 .参考答案与试题解析一.选择题(共1小题)1.(2024•丰台区二模)已知点1(A x 1)y 2(B x 2)y 在反比例函数2y x=的图象上 且120x x <<,则下列结论一定正确的是( ) A .120y y +< B .120y y +> C .120y y -< D .120y y ->【答案】C【考点】反比例函数图象上点的坐标特征【分析】先根据反比例函数2y x=判断此函数图象所在的象限 再根据120x x <<判断出1(A x1)y 2(B x 2)y 所在的象限即可得到答案.【解答】解:反比例函数2y x=的图象在一 三象限 而120x x <<∴点1(A x1)y 在第三象限反比例函数2y x =的图象上 2(B x 2)y 在第一象限反比例函数2y x=的图象上210y y ∴>> 120y y ∴-<故选:C .二.填空题(共9小题)2.(2024•顺义区二模)已知点1(A x 1)y 2(B x 2)y 在反比例函数(0)ky k x=≠的图象上 当120x x <<时 12y y >,则k 的取值范围是 0k > .【答案】0k >.【考点】反比例函数图象上点的坐标特征【分析】根据反比例函数图象上点的坐标特征进行解答即可. 【解答】解:当120x x <<时 12y y >∴反比例函数图象上分布在第一三象限此时0k >. 故答案为:0k >.3.(2024•大兴区二模)在平面直角坐标系xOy 中 若点1(3,)A y 和2(2,)B y 在反比例函数(0)ky k x=<的图象上,则1y > 2y (填“>”“ =”或“<” ). 【答案】>.【考点】反比例函数图象上点的坐标特征【分析】根据反比例函数图象上点的坐标特征进行解答即可.【解答】解:反比例函数(0)k y k x=<的图象分布在第二 四象限 在每个象限内 y 随x 的增大而增大32> 12y y ∴>故答案为:>.4.(2024•昌平区二模)在平面直角坐标系xOy 中 若点(1,)m 和(4,2)在反比例函数(0)k y k x=≠图象上,则m = 8 . 【答案】8.【考点】反比例函数图象上点的坐标特征【分析】根据比例函数(0)ky k x=≠中的系数k xy =得到关于m 的方程 求解即可得到答案.【解答】解:点(1,)m 和(4,2)在反比例函数(0)k y k x=≠图象上42k m ∴=⨯=解得8m = 故答案为:8.5.(2024•海淀区二模)在平面直角坐标系xOy 中 点1(1,)A y 2(2,)B y 在反比例函数(0)ky k x=≠的图象上.若12y y <,则满足条件的k 的值可以是 1-(答案不唯一) (写出一个即可). 【答案】1-(答案不唯一).【考点】反比例函数图象上点的坐标特征【分析】根据点的坐标特点得出反比例函数的图象在二 四象限 根据反比例函数的性质得出0k <.【解答】解:点1(1,)A y 2(2,)B y 在反比例函数(0)k y k x=≠的图象上 且12y y <∴点点1(1,)A y2(2,)B y 在第四象限∴反比例函数(0)ky k x=≠的图象在二 四象限 0k ∴<k ∴的值可以为1-.故答案为:1-(答案不唯一).6.(2024•朝阳区二模)在平面直角坐标系xOy 中 若反比例函数(0)ky k x=≠的图象位于第二 四象限 且点1(,)A m y (B m - 2)(0)y m >都在该图象上,则1y < 2.y (填“<” “ >”或“=” ) 【答案】<.【考点】反比例函数的图象 反比例函数的性质 反比例函数图象上点的坐标特征 【分析】根据反比例函数图象上点的坐标特征进行分析解答即可. 【解答】解:反比例函数(0)k y k x=≠的图象位于第二 四象限∴在每个象限内y 随x 的增大而增大点1(,)A m y (B m - 2)(0)y m >∴点A 在第四象限点B 在第二象限12y y ∴<故答案为:<.7.(2024•石景山区二模)在平面直角坐标系xOy 中 若函数(0)ky k x=≠的图象经过点(1,6)A -和(3,)B m ,则m 的值为 2- .【答案】2-.【考点】反比例函数图象上点的坐标特征【分析】根据反比例函数图象上点的坐标特征进行解答即可. 【解答】解:函数(0)k y k x=≠的图象经过点(1,6)A -和(3,)B m163k m ∴=-⨯=解得:2m =-. 故答案为:2-.8.(2024•北京二模)在平面直角坐标系xOy 中 若点1(1,)y 2(4,)y 在反比例函数(0)ky k x=>的图象上,则1y > 2y (填“>” “ =”或“<” ). 【答案】>.【考点】反比例函数图象上点的坐标特征【分析】先根据函数解析式中的比例系数k 确定函数图象所在的象限 再根据各象限内点的坐标特征及函数的增减性解答. 【解答】解:0k >∴反比例函数(0)ky k x=>的图象在一 三象限 410>>∴点1(1,)A y2(4,)B y 在第一象限 y 随x 的增大而减小12y y ∴>故答案为:>.9.(2024•西城区二模)如图,(2,)A m (3,2)B 两点在反比例函数(0)ky x x=>的图象上.若将横 纵坐标都是整数的点称为整点,则线段OA OB 及反比例函数图象上A B 两点之间的部分围成的区域(不含边界)中 整点的坐标为 (1,1)和(2,2) .【答案】(1,1)和(2,2).【考点】反比例函数图象上点的坐标特征【分析】利用反比例函数系数k xy =求得(2,3)A 求得直线OA 为132y x = OB 为223y x = 当1x =时 132y =223y = 当2x =时 243y = 结合图象即可求解.【解答】解:(2,)A m (3,2)B 两点在反比例函数(0)ky x x=>的图象上232k m ∴==⨯ 6k ∴= 3m =∴反比例函数为6y x=(2,3)A (2,3)A (3,2)B∴直线OA 为132y x =OB 为223y x =当1x =时 132y = 223y = 当2x =时 243y =∴线段OAOB 及反比例函数图象上A B 两点之间的部分围成的区域(不含边界)中整点有(1,1) (2,2).故答案为:(1,1)和(2,2).10.(2024•东城区二模)在平面直角坐标系xOy 中 若点(2,4)是函数11(0)y k x k =≠和22(0)k y k x=≠的图象的一个交点,则这两个函数图象的另一个交点的坐标是 (2,4)-- .【答案】(2,4)--.【考点】反比例函数与一次函数的交点问题 【分析】根据点(2,4)是函数11(0)y k x k =≠和22(0)k y k x=≠的图象的一个交点 求出两个函数的解析式 再联立方程组 解方程组求出另一交点坐标. 【解答】解:函数1y k x =经过点(2,4)124k ∴=解得12k =2y x ∴= 22(0)k y k x=≠的图象经过点(2,4) 2248k ∴=⨯=8y x∴=联立方程组28y xy x =⎧⎪⎨=⎪⎩解得24x y =⎧⎨=⎩或24x y =-⎧⎨=-⎩∴这两个函数图象的另一个交点的坐标是(2,4)--故答案为:(2,4)--.11.(2024房山二模)在平面直角坐标系xOy 中 若反比例函数(0)ky k x=≠的图象经过点(12)A -,和(4)B m ,,则m 的值为 .【答案】12-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年瓶窑一中初三数学余高自主招生考试辅导材料—反比例之填空题 一.填空题(共30小题) 1.(2013•重庆)如图,菱形OABC的顶点O是坐标原点,顶点A在x轴的正半轴上,顶点B、C均在第一象限,OA=2,∠AOC=60°.点D在边AB上,将四边形OABC沿直线0D翻折,使点B和点C分别落在这个坐标平面的点B′和C′处,且∠C′DB′=60°.若某反比例函数的图象经过点B′,则这个反比例函数的解析式为 _________ .
2.(2013•武汉)如图,已知四边形ABCD是平行四边形,BC=2AB.A,B两点的坐标分别是(﹣1,0),(0,2),C,D两点在反比例函数y=(k<0)的图象上,则k等于 _________ .
3.(2013•日照)如右图,直线AB交双曲线于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,S△OAC=12.则k的值为 _________ .
4.(2013•宁波)如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2,反比例函数y=(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为 _________ . 2
5.(2013•泸州)如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An﹣1An都在x轴上(n是
大于或等于2的正整数),则点P3的坐标是 _________ ;点Pn的坐标是 _________ (用含n的式子表示).
6.(2013•成都)若关于t的不等式组,恰有三个整数解,则关于x的一次函数的图象与反比例函数的图象的公共点的个数为 _________ .
7.(2013•北京)如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y=,在l上取一点A1,过A1
作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2= _________ ,a2013= _________ ;若要将上述操作无限次地进行下去,则a1不可能取的值是 _________ .
8.(2012•遵义)如图,平行四边形ABCD的顶点A、C在双曲线y1=﹣上,B、D在双曲线y2=上,k1=2k2
(k1>0),AB∥y轴,S▱ABCD=24,则k1= _________ . 3
9.(2012•武汉)如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 _________ .
10.(2012•温州)如图,已知动点A在函数的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 _________ .
11.(2012•苏州)如图,已知第一象限内的图象是反比例函数y=图象的一个分支,第二象限内的图象是反比例函数y=﹣图象的一个分支,在x轴的上方有一条平行于x轴的直线l与它们分别交于点A、B,过点A、B作x轴的垂线,垂足分别为C、D.若四边形ABCD的周长为8且AB<AC,则点A的坐标为 _________ . 4
12.(2012•绍兴)如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为 _________ (用含n的代数式表示)
13.(2012•宁德)如图,点M是反比例函数y=在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=A3M,△A3C3B的面积记为S3;以此类推…;则S1+S2+S3+…+S8= _________ .
14.(2012•河南)如图,点A、B在反比例函数y=(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为 _________ . 5
15.(2012•河池)如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数的图象交EF于点B,则点B的坐标为 _________ .
16.(2012•成都)如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若(m为大于l的常数).记△CEF的面积为S1,△OEF的面积为S2,则= _________ . (用含m的代数式表示)
17.(2011•武汉)如图,▱ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y=上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= _________ . 6
18.(2011•十堰)如图,平行四边形AOBC中,对角线交于点E,双曲线(k>0)经过A,E两点,若平行四边形AOBC的面积为18,则k= _________ .
19.(2011•金华)如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´. (1)当点O´与点A重合时,点P的坐标是 _________ ; (2)设P(t,0),当O´B´与双曲线有交点时,t的取值范围是 _________ .
20.(2011•荆门)如图,双曲线 (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是 _________ .
21.(2011•恩施州)如图,△AOB的顶点O在原点,点A在第一象限,点B在x轴的正半轴上,且AB=6,∠AOB=60°,反比例函数(k>0)的图象经过点A,将△AOB绕点O顺时针旋转120°,顶点B恰好落在的图象上,则k的值为 _________ . 7
22.(2010•咸宁)如图,一次函数y=ax+b的图象与x轴,y轴交于A,B两点,与反比例函数的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论: ①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④AC=BD. 其中正确的结论是 _________ .(把你认为正确结论的序号都填上).
23.(2010•南平)函数y=和y=在第一象限内的图象如图,点P是y=的图象上一动点,PC⊥x轴于点C,交y=的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=AP.其中所有正确结论的序号是 _________ .
24.(2010•南宁)如图所示,点A1,A2,A3在x轴上,且OA1=A1A2=A2A3,分别过点A1,A2,A3作y轴的平行线,与反比例函数y=(x>0)的图象分别交于点B1,B2,B3,分别过点B1,B2,B3作x轴的平行线,分别于y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为 _________ . 8
25.(2010•昆明)如图,点A(x1,y1)、B(x2,y2)都在双曲线上,且x2﹣x1=4,y1﹣y2=2;分别过点A、B向x轴、y轴作垂线段,垂足分别为C、D、E、F,AC与BF相交于G点,四边形FOCG的面积为2,五边形AEODB的面积为14,那么双曲线的解析式为 _________ .
26.(2009•贵港)已知P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(n为正整数)是反比例函数y=图象上的点,其中x1=1,x2=2,…、xn=n.记T1=x1y2,T2=x2y3、…、T2009=x2009y2010.若T1=,则T1•T2•…•T2009= _________ .
27.(2008•荆州)如图,一次函数y=x﹣2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数(k>0)的图象于Q,S△OQC=,则k的值和Q点的坐标分别为k= _________ ,Q _________ .
28.(2013•武汉模拟)矩形OABC有两边在坐标轴的正半轴上,如图所示,双曲线与边AB、BC分别交于D、E两点,OE交双曲线于G点,DG∥OA,OA=3,则CE的长为 _________ .
29.(2013•温州模拟)如图,在Rt△OAB中,∠B=Rt∠,OB=2AB.线段AB的垂直平分线交反比例函数y=(x>0)的图象于点C,D为垂足,过C作CE⊥OB于点E.当四边形CDBE为正方形时,正方形CDBE的面积为 _________ .
