漳州一中自主招生试卷 漳州一中高中自主招生考试数学试卷
2023年漳州一中高中自主招生考试数学试卷参考答案
漳州一中高中自主招生考试 数学参照答案及评分意见11. 且 12. （或 ）13.4016 14. 15. 16. 三、解答题（本大题共有7小题, 共86分）17. （8分）原式 …………………………………………6分1-=………………………………………………………………8分 18. （10分）原式 ………………………………2分x x --=4162)4()4)(4(---+=x x x 4--=x ………………………7分∴当 时, 原式 ……………………10分19. （10分）（1）（4分） ………………………………………4分 （2）①（4分）树状图为:或列表法为:（画出树状图或列出表格得4分） ……………………………………………4分 ②（2分）因此411234==的倍数p …………………………………………2分 20. （12分）解法一：设参与 处公共场所旳义务劳动, 则学校派出 名学生^…………………………………………………………………………………2分依题意得: ………………………6分 由（1）得： , 由（2）得： ∴434433≤<x ………………………………………………………………8分 又 为整数, ∴ ……………………………………………………10分∴当 时, ………………………………………………11分答: 这所学校派出55名学生, 参与4处公共场所旳义务劳动 …………12分解法二：设这所学校派出 名学生, 参与 处公共场所旳义务劳动……1分 依题意得: ……………………………6分解得: …………………………………………………………8分 为整数, ∴ ………………………………………………………10分∴当 时, ………………………………………11分答: 这所学校派出55名学生, 参与4处公共场所旳义务劳动 …………12分 21. （14分）证法一：如图, 分别延长 、 相交于点 ………………1分 设 , ∵ ,∴ ,得 ………3分∴322=-=AM BM AB …………4分∵ , ∴ , 且 ,在 中, ………………………………6分 又∵ 、 ,∴)(ASA ECN MDN ∆≅∆……………………………………………………9分 ∴ 、 , ………………………………………11分 ∴ 、 , ∴ …………13分∴MBC NMB ∠=∠…………………………………………………………14分 证法二: 设 , 同证法一 ………………6分如图, 将 绕点 顺时针旋转 得到 , 连结 , ∵ , ∴ 是平角, 即点 三点共线,………………………………………………………………………………… 7分 ∴BEC BMA ∠=∠……………………………8分1==AM CE 、BM BE = …………………9分∴BEM BME ∠=∠…………………………10分 ∵MN CE CN NE ==+=+=25123 ……11分 ∴NEM NME ∠=∠…………………………12分 ∴NEM BEM NME BME ∠+∠=∠+∠ ∴AMB BEC BMN ∠=∠=∠………………13分 又∵MBC AMB ∠=∠∴MBC BMN ∠=∠…………………………14分 22. （16分）（1）（4分）设抛物线旳解析式为89252-⎪⎭⎫ ⎝⎛-=x a y ………………………1分∵抛物线通过 , ∴ , 解得: …………3分∴8925212-⎪⎭⎫ ⎝⎛-=x y （或225212+-=x x y ） …………………………4分（2）（4分）令 得 , ∴ ……………………………………1分 令 得 , 解得 、 ………………………3分∴)0 , 1(C 、) 0, 4(D …………………………………………………………4分（3）（8分）结论: …………………………………1分理由是: ①当点重叠时, 有………………………………2分②当 , ∵直线 通过点 、 , ∴直线 旳解析式为………3分设直线 与 轴相交于点 , 令 , 得 , ∴ ,则)2,0()2,0(B E 与点-有关x 轴对称………………4分 ∴ , 连结 , 则 ,∴ , …………………5分∵在 中, 有 …………………………………………6分∴BC AC AE PE PA PB PA +=>+=+…………………………………7分 综上所得BC AC BP AP +≥+………………………………………………8分 23. （16分）（1）（6分）解法一: 当点 在⊙ 上时, 设 与⊙交于点 ,∵ , ∴ ………………………1分 ∵ ∥ , ∴ ………………2分∴PD AP =…………………………………………3分又 , …………………4分………………………………………5分∴︒︒=⨯⨯=∠⨯=∠3018031213121AOB APE …6分 解法二: 设点 在⊙ 上时, 由已知有 , ……………………1分 ∴△ △ , ……………………………………………2分 ∴ , …………………………………………3分 在 △ 中, ……5分∴︒=∠30APC ……………………………………………………6分（2）（10分）k 值不随点P 旳移动而变化.理由是:∵ 是⊙ 右半圆上旳任意一点, 且 ∥ ,∴ ……………………………1分∵ 是⊙ 旳切线, ∴ ,⌒ ⌒又∵ , ∴ ,∴ABQ ACP ∠=∠ ……………………………2分 ∴ACP ∆∽OBQ ∆ ……………………………3分 ∴QBPCOB AC =……………………………………4分 又∵ 、 ,∴ACF ∆∽ABQ ∆……………………………………………………………6分 ∴BQCFAB AC = …………………………………………………………………7分 又∵ , ∴ 即 …………………………8分∴CF PC 2= 即CF PF ＝ …………………………………………………9分 ∴ ，即 值不随点 旳移动而变化. ………………………10分。
高中自主招生考试 数 学 试 卷(2)
高中自主招生考试 数 学 试 卷 （2）（满分：150分；考试时间：120分钟）亲爱的同学：欢迎你参加本次考试！请细心审题，用心思考，耐心解答．祝你成功！答题时请注意：请将答案或解答过程写在答题卷的相应位置上，写在试卷上不得分．一、选择题（本大题共有10小题，每小题4分，共40分．每小题都有A 、B 、C 、D 四个选项，其中有且只有一个选项是正确的，请将正确答案的代号填写在答题卷中相应的表格内，答对得4分，答错、不答或答案超过一个的得零分）1．若等腰梯形的三边长分别为3，4，11，则这个等腰梯形的周长为 【 】A ．21B ．29C ．21或29D ．21或22或292．图中的矩形被分成四部分，其中三部分面积分别为2，3，4，那么， 阴影三角形的面积为 【 】（A ）5 （B ）6 （C ）7 （D ）83．如图，AB ，CD 分别是⊙O 的直径和弦，AD ，BC 相交于点E ，∠AEC=α，则△CDE 与△ABE 的面积比为 【 】（A ）cos α （B ）sin α （C ）cos2α （D ）sin 2α4．设A ，B ，C 是三角形的三个内角，满足B C B A 23,53<>，这个三角形是 【 】（A ）锐角三角形 （B ）钝角三角形 （C ）直角三角形 （D ）都有可能5（2011年黄冈）设关于x 的方程09)2(2=+++a x a ax ，有两个不相等的实数根1x 、2x ，且1x <<12x ，那么实数a 的取值范围是 【 】 A 、112-<a B 、5272<<-a C 、52>a D 、0112<<-a 6（2011年黄冈）如图，正方形ABCD 的边1=AB ，和都是以1为半径的圆弧，则无阴影部分的两部分的面积之差是 【 】A 、12-π B 、41π- C 、13-π D 、61π- 7.（2011年黄冈）已知锐角三角形的边长是2、3、x ，那么第三边x 的 取值范围是 【 】ACB DP OOA 、51<<xB 、135<<xC 、513<<xD 、155<<x8．用三种边长相等的正多边形地砖铺地，其顶点拼在一起，刚好能完全铺满地面．已知正多边形的边数为x 、y 、z ，则zy x 111++的值为【 】 （A ）1 （B ）32 （C ）21 （D ）319.（2011蚌埠市七中）如图：⊙1O 与⊙2O 外切于P ，⊙1O ，⊙2O 的半径分别为1,2.A O 1为⊙2O 的切线，AB 为⊙2O 的直径，B O 1分别交⊙1O ，⊙2O 于D C ,，则PD CD 3+的值为 【 】 DA ．37B ．325C ．3112D ．33410．如图，正方形OABC ADEF ，的顶点A D C ，，在坐标轴上，点F在AB 上，点B E ，在函数xy 4=（x ＞0）的图象上，则点E 的坐标是 【 】(Ａ)()15,15-+(B)()53,53-+ (C)()15,15+- (D) ()53,53+-二、填空题（本大题共有6小题，每小题4分，共24分．请将正确的答案直接填写在答题卷中相应的横线上） 11、设21≤≤-x ，则2212++--x x x 的最大值与最小值之差为 12、抛物线2ax y =与直线1=x ，2=x ，1=y ，2=y 围成的正方形有公共点，则实数a 的取值范围是13、有铅笔、练习本、圆珠笔三种学习用品，若购铅笔3支，练习本7本，圆珠笔1支共需15.3元；若购铅笔4支，练习本10本，圆珠笔1支共需2.4元，那么，购铅笔、练习本、圆珠笔各1件共需14、在矩形ABCD 中, A B ＝5, BC ＝12, ⊙A 的半径为2, 若以C 为圆心作一个圆, 使⊙C 与A O DCEF x yB⊙A 相切, 那么⊙C 的半径为 ．15、.三角形的三边为,,,10,,,c b a c a b c b a ≤≤=为整数，且若则该三角形是等边三角形的概率是 。
福建省自主招生试题
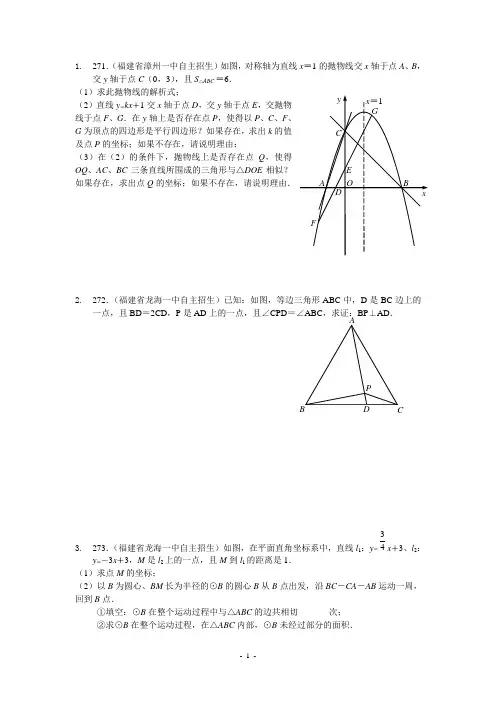
1. 271．（福建省漳州一中自主招生）如图，对称轴为直线x ＝1的抛物线交x 轴于点A 、B ，交y 轴于点C （0，3），且S △ABC＝6． （1）求此抛物线的解析式；（2）直线y ＝kx ＋1交x 轴于点D ，交y 轴于点E ，交抛物线于点F 、G ．在y 轴上是否存在点P ，使得以P 、C 、F 、G 为顶点的四边形是平行四边形？如果存在，求出k 的值及点P 的坐标；如果不存在，请说明理由；（3）在（2）的条件下，抛物线上是否存在点Q ，使得OQ 、AC 、BC 三条直线所围成的三角形与△DOE 相似？如果存在，求出点Q 的坐标；如果不存在，请说明理由．2. 272．（福建省龙海一中自主招生）已知：如图，等边三角形ABC 中，D 是BC 边上的一点，且BD ＝2CD ，P 是AD 上的一点，且∠CPD ＝∠ABC ，求证：BP ⊥AD ．3. 273．（福建省龙海一中自主招生）如图，在平面直角坐标系中，直线l 1：y ＝43x ＋3、l 2：y ＝－3x ＋3，M 是l 2上的一点，且M 到l 1的距离是1． （1）求点M 的坐标；（2）以B 为圆心、BM 长为半径的⊙B 的圆心B 从B 点出发，沿BC －CA －AB 运动一周，回到B 点．①填空：⊙B 在整个运动过程中与△ABC 的边共相切_______次； ②求⊙B 在整个运动过程，在△ABC 内部，⊙B 未经过部分的面积．AB CD P4. 274．（福建省龙海一中自主招生）如图1，在平面直角坐标系中，⊙M 是以（1，－1）为圆心、面积为5π的圆，⊙M 交x 轴于点A 、B ，交y 轴于点C ，抛物线经过A 、B 、C 三点，与⊙M 交于另一点G ． （1）求抛物线的解析式；（2）P 是抛物线上一点，直线OP 将四边形ABGC 的面积分成1 :2的两部分，求P 点的坐标；（3）如图2，E 是⊙M 上一点，将CE ︵沿直线CE 翻折，翻折后的弧恰好与AC 相切，且与y 轴交于点F ．①求F 点的坐标及CE 的长；②判断翻折后的弧与x 轴的位置关系，并说明理由．。
【2020-2021自招】福建漳州第一中学初升高自主招生数学模拟试卷【4套】【含解析】
第一套：满分150分2020-2021年福建漳州第一中学初升高自主招生数学模拟卷一．选择题（共8小题，满分48分）1．（6分）如图，△ABC中，D、E是BC边上的点，BD：DE：EC=3：2：1，M在AC边上，CM：MA=1：2，BM交AD，AE于H，G，则BH：HG：GM=（）A．3：2：1 B．5：3：1C．25：12：5 D．51：24：102.（6分）若关于x的一元二次方程（x－2）（x－3）=m有实数根x1,x2，且x1≠x2，有下列结论：①x1=2，x2=3；②1> ；m4③二次函数y=（x－x1）（x－x2）＋m的图象与x轴交点的坐标为（2，0）和（3，0）．其中，正确结论的个数是【】A.0B.1C.2D.33.（6分）已知长方形的面积为20cm2，设该长方形一边长为ycm，另一边的长为xcm，则y与x之间的函数图象大致是（）A. B. C. D.4.（6分）如图，在平面直角坐标系中，⊙O 的半径为1，则直线y x 2=-与⊙O 的位置关系是（ ）A ．相离B ．相切C ．相交D ．以上三种情况都有可能 5．（6分）若一直角三角形的斜边长为c ，内切圆半径是r ，则内切圆的面积与三角形面积之比是（ ）A ．B ．C ．D ．6．（6分）如图，Rt △ABC 中，BC=，∠ACB=90°，∠A=30°，D 1是斜边AB 的中点，过D 1作D 1E 1⊥AC 于E 1，连结BE 1交CD 1于D 2；过D 2作D 2E 2⊥AC 于E 2，连结BE 2交CD 1于D 3；过D 3作D 3E 3⊥AC 于E 3，…，如此继续，可以依次得到点E 4、E 5、…、E 2013，分别记△BCE 1、△BCE 2、△BCE 3、…、△BCE 2013的面积为S 1、S 2、S 3、…、S 2013．则S 2013的大小为（ ） A.31003 B.320136 C.310073 D.67147．（6分）抛物线y=ax 2与直线x=1，x=2，y=1，y=2围成的正方形有公共点，则实数a 的取值范围是（ ）A ．≤a ≤1B ．≤a ≤2C ．≤a ≤1D ．≤a ≤28．（6分）如图，矩形ABCD 的面积为5，它的两条对角线交于点O 1，以AB ，AO 1为两邻边作平行四边形ABC 1O 1，平行四边形ABC 1O 1的对角线交BD 于点02，同样以AB ，AO 2为两邻边作平行四边形ABC 2O 2．…，依此类推，则平行四边形ABC 2009O 2009的面积为（ ）A.n 25 B.n 22 C.n 31 D.n 23二．填空题：（每题7分，满分42分）9．（7分）方程组的解是 ．10．（7分）若对任意实数x 不等式ax ＞b 都成立，那么a ，b 的取值范围为 ．11．（7分）如图，圆锥的母线长是3，底面半径是1，A 是底面圆周上一点，从A 点出发绕侧面一周，再回到A 点的最短的路线长是 ．12．（7分）有一张矩形纸片ABCD ，AD=9，AB=12，将纸片折叠使A 、C 两点重合，那么折痕长是 ．13．（7分）设﹣1≤x ≤2，则|x ﹣2|﹣|x|+|x+2|的最大值与最小值之差为 ．14．（7分）两个反比例函数y=，y=在第一象限内的图象如图所示．点P 1，P 2，P 3、…、P 2007在反比例函数y=上，它们的横坐标分别为x 1、x 2、x 3、…、x 2007，纵坐标分别是1，3，5…共2007个连续奇数，过P 1，P 2，P 3、…、P 2007分别作y 轴的平行线，与y=的图象交点依次为Q 1（x 1′，y 1′）、Q 1（x 2′，y 2′）、…、Q 2（x 2007′，y 2007′），则|P 2007Q 2007|= ．三．解答题：（每天12分，满分60分）15.(12分).已知正实数,,x y z 满足：1xy yz zx ++≠ ,且222222(1)(1)(1)(1)(1)(1)4x y y z z x xy yz zx------++= .(1) 求111xy yz zx++的值. (2) 证明:9()()()8()x y y z z x xyz xy yz zx +++≥++.16．（12分）如图，ABC △是等腰直角三角形，CA CB =，点N 在线段AB 上（与A 、B 不重合），点M 在射线BA 上，且45NCM ∠=︒。
2007年漳州一中高中自主招生考试数学试卷参考答案
2007年漳州一中高中自主招生考试数学参考答案及评分意见11. 2-≥x 且1≠x 12. xy 3-)3(+x )3(-x （或)3)(3(3x x xy -+）13. 4016 14．23 15．2 16．40三、解答题（本大题共有7小题，共86分） 17．（8分）原式233331-+⨯-= …………………………………………6分 1-=………………………………………………………………8分18．（10分）原式xx x x x --⋅---+=42212)2)(2( ………………………………2分 x x --=4162)4()4)(4(---+=x x x 4--=x ………………………7分 ∴当42-=x 时，原式=4)42(---2-= ……………………10分19．（10分）（1）（4分）42=偶数p 21= ………………………………………4分 （2）①（4分）树状图为：或列表法为：（画出树状图或列出表格得4分） ……………………………………………4分13 4 2 4 1 2 3 4 1 1 23 4 （12） （13）（14）（21）（23）（24）（31）（32）（34）（41） （42） （ 43）②（2分）所以411234==的倍数p …………………………………………2分 20．（12分）解法一：设参加x 处公共场所的义务劳动，则学校派出)1510(+x 名学生^…………………………………………………………………………………2分依题意得：⎩⎨⎧≥--+<--+)2(10)1(14)1510()1(14)1(14)1510( x x x x ………………………6分 由（1）得：433>x ，由（2）得：434≤x ∴434433≤<x ………………………………………………………………8分 又x 为整数，∴4=x ……………………………………………………10分 ∴当4=x 时，551510=+x ………………………………………………11分答：这所学校派出55名学生，参加4处公共场所的义务劳动 …………12分解法二：设这所学校派出x 名学生，参加y 处公共场所的义务劳动……1分依题意得：⎩⎨⎧<--≤=+)2(14)1(1410)1(1510 y x x y ……………………………6分解得：434433≤<y …………………………………………………………8分 y 为整数，∴4=y ………………………………………………………10分 ∴当4=y 时，5515410=+⨯=x ………………………………………11分 答：这所学校派出55名学生，参加4处公共场所的义务劳动 …………12分21．（14分）证法一：如图，分别延长BC 、MN 相交于点E ………………1分设1=AM ，∵1010sin =∠ABM ， ∴1010=BMAM ，得10=BM ………3分 ∴322=-=AM BM AB …………4分 ∵是正方形四边形ABCD ，∴2=-=AM AD DM ，且2321===DC CN DN ， 在DMN Rt ∆中，2522=+=DN MD MN ………………………………6分 又∵∠=∠=∠Rt ECN MDN 、ENC MND ∠=∠，∴)(ASA ECN MDN ∆≅∆……………………………………………………9分∴2==MD CE 、25==MN NE ，………………………………………11分∴5=+=NE MN ME 、5=+=CE BC BE ，∴BE ME = …………13分∴MBC NMB ∠=∠…………………………………………………………14分证法二：设1=AM ，同证法一2522=+=DN MD MN ………………6分 如图，将ABM ∆绕点A 顺时针旋转︒90得到BCE ∆，连结ME ，∵∠=∠=∠Rt BCD BCE ，∴NCE ∠是平角，即点E C N 、、三点共线， ………………………………………………………………………………… 7分∴BEC BMA ∠=∠……………………………8分1==AM CE 、BM BE = …………………9分 ∴BEM BME ∠=∠…………………………10分∵MN CE CN NE ==+=+=25123 ……11分 ∴NEM NME ∠=∠…………………………12分∴NEM BEM NME BME ∠+∠=∠+∠ ∴AMB BEC BMN ∠=∠=∠………………13分又∵MBC AMB ∠=∠ ∴MBC BMN ∠=∠…………………………14分22．（16分）（1）（4分）设抛物线的解析式为89252-⎪⎭⎫ ⎝⎛-=x a y ………………………1分 ∵抛物线经过)14,8(A ，∴89258142-⎪⎭⎫ ⎝⎛-a ＝，解得：21=a …………3分 ∴8925212-⎪⎭⎫ ⎝⎛-=x y （或225212+-=x x y ） …………………………4分 （2）（4分）令0=x 得2=y ，∴)2,0(B ……………………………………1分令0=y 得0225212=+-x x ，解得11=x 、42=x ………………………3分 ∴)0 , 1(C 、) 0, 4(D …………………………………………………………4分（3）（8分）结论：BC AC PB PA +≥+ …………………………………1分理由是：①当点C P 与点重合时，有BC AC PB PA +=+ ………………………………2分 ②当时异于点点C P ，∵直线AC 经过点)14,8(A 、)0,1(C ，∴直线AC 的解析式为22-=x y ………3分设直线AC 与y 轴相交于点E ，令0=x ，得2-=y ， ∴)2,0(-E ，则)2,0()2,0(B E 与点-关于x 轴对称………………4分 ∴EC BC =，连结PE ，则PB PE =，∴AE EC AC BC AC =+=+， …………………5分 C D N E∵在APE ∆中，有AE PE PA >+ …………………………………………6分∴BC AC AE PE PA PB PA +=>+=+…………………………………7分综上所得BC AC BP AP +≥+………………………………………………8分23．（16分）（1）（6分）解法一：当点E 在⊙O 上时，设OQ 与⊙O 交于点D ，∵PC AB ⊥，∴AP AE = ………………………1分 ∵AP ∥OQ ，∴PEQ APE ∠=∠ ………………2分∴PD AP =…………………………………………3分 又BOD AOE ∠=∠，BD AE = …………………4分APB AE 31=即………………………………………5分 ∴︒︒=⨯⨯=∠⨯=∠3018031213121AOB APE …6分 解法二：设点E 在⊙O 上时，由已知有CP EC =， ……………………1分 ∴△≅EOC △PAC ，……………………………………………2分 ∴CA OC =，AP OE = …………………………………………3分在Rt △APC 中，212sin ====∠AC AC OA AC AP AC APC ……5分 ∴︒=∠30APC ……………………………………………………6分（2）（10分）k 值不随点P 的移动而变化.理由是:∵P 是⊙O 右半圆上的任意一点，且AP ∥OQ ，∴QOB PAC ∠=∠ ……………………………1分∵BM 是⊙O 的切线，∴∠=∠Rt ABQ ，又∵AB PC ⊥，∴∠=∠Rt ACP ， ∴ABQ ACP ∠=∠ ……………………………2分 ∴ACP ∆∽OBQ ∆ ……………………………3分 ∴QB PC OB AC =……………………………………4分 又∵BAQ CAF ∠=∠、∠=∠=∠Rt ABQ ACF ，∴ACF ∆∽ABQ ∆……………………………………………………………6分 ∴BQCF AB AC = …………………………………………………………………7分 又∵OB AB 2=，∴BQ CF OB AC =2即BQCF OB AC 2= …………………………8分 ∴CF PC 2= 即CF PF ＝ …………………………………………………9分 ∴==PC PF k 21，即k 值不随点P 的移动而变化. ………………………10分 ⌒ ⌒ ⌒ ⌒ ⌒ ⌒ ⌒ ⌒B A BC E F P M O．页眉内容阅读使人充实，会谈使人敏捷，写作使人精确。
福建省漳州一中2011年中考数学自主招生预录考试模拟试题(无综述
2011年漳州一中高中自主招生考试数学试卷（满分：150分；考试时间：120分钟）亲爱的同学：欢迎你参加本次考试！请细心审题，用心思考，耐心解答．祝你成功！答题时请注意：请将答案或解答过程写在答题卷的相应位置上，写在试卷上不得分．一、选择题（本大题共有10小题，每小题4分，共40分．每小题都有A 、B 、C 、D 四个选项，其中有且只有一个选项是正确的，请将正确答案的代号填写在答题卷中相应的表格内，答对得4分，答错、不答或答案超过一个的得零分）1. 下列运算正确的是…………………………………………………………（） A.2ab +3ab =5a 2b 2B.a 2⋅a 3=a 6C.a-2=1a 2(a ≠0 D.x +y =x +y 2. 如图，点A 在数轴上表示的实数为a ，则a -2等于…………………（）A –1 0 1 2 3 （第2题图）A. a -2B.a +2C.-a -2D.-a +2 3. 甲、乙两名运动员在10次的百米跑练习中，平均成绩分别为x甲＝10. 7秒，x 2乙＝10. 7秒，方差分别为S 甲=0. 054，S 2乙=0. 103，那么在这次百米跑练习中，甲、乙两名运动员成绩较为稳定的是……………………………（） A. 甲运动员 B.乙运动员 C.甲、乙两人一样稳定 D.无法确定 4. 如图，A 、B 、C 、D 是直线l 上顺次四点，M 、N 分别是AB 、CD 的中点，且MN =6cm ，BC =1cm ，则AD 的长等于……………………（）A MBC ND l（第4题图）A. 10cmB.11cmC.12cmD.13cm5. 已知等腰三角形的一个外角等于140︒，则这个三角形的三个内角的度数分别是……………………………………………………………………………（）A. 20︒、20︒、140︒ B.40︒、40︒、100︒C.70︒、70︒、40︒D. 40︒、40︒、100︒或70︒、70︒、40︒6. 如图，点A 在函数y =-6x(x <0 的图象上，过点A 作AE 垂直x 轴，垂足为E ，过点A 作AF 垂直y 轴，垂足为F ，则矩形AEOF 的面积是……（ A. 2 B.3C. 6D.不能确定（第6题图）7. 用大小和形状完全相同的小正方体木块搭成一个几何体，使得它的正视图和俯视图如图所示，则搭成这样的一个几何体至少需要小正方体木块的个数为………………（） A. 22个 B.19个 C. 16个 D.13个8. 用半径为6cm 、圆心角为120的扇形做成一个圆锥的侧面, 则这个圆锥的底面半径是……………………………………………………………………（） A. 2cm B.3cm C.4cm D.6cm 9. 若n 为整数，则能使︒n +1也为整数的n 的个数有……………………（） n -1A.1个B.2个C.3个D.4个10. 已知a 为实数，则代数式27-12a +2a 2的最小值为………………（） A. 0 B.3 C.33D.9二、填空题（本大题共有6小题，每小题4分，共24分．请将正确的答案直接填写在答题卷中相应的横线上） 11. 函数y =x +2的自变量xx -1（第13题图）12. 分解因式：-3x 3y +27xy =13. 把2007个边长为1图形，则这个图形的周长是． 14. 如图，正方形ABCD 的边长为4cm ，正方形AEFG 的边长为1cm ．如果正方形AEFG 绕点A 旋转，那么FDEABC（第14题图）C 、F 两点之间的最小距离为．15. 若规定：①{ m }表示大于m 的最小整数，例如： { 3 }=4，{-2. 4 }=-2；②[ m ]表示不大于m 的最大整数，例如： [ 5 ]=5，[-3. 6 ]=-4. 则使等式2{ x }-[ x ]=4成立的整数．．x = 16. 如图，E 、F ABCD 的边AB 、CD 上的点，AF 与DE 相交于点P ，BF 与CE 相交于点Q ，若S△APD=15cm 2，S△BQC=25cm 2，2则阴影部分的面积为 cm ．（第16题图）三、解答题（本大题共有7小题，共86分．其中第17题8分，第18、19题各10分，第20题12分，第21题14分，第22、23题各16分．请将解答过程写在答题卷的相应位置上）17. 计算：(-2 -3tan 30-18. 先化简，再求值： x +2--2.⎛⎝12⎫4-x，其中x =2-4. ⎪÷x -2⎭x -219. 将背面相同，正面分别标有数字1、2、3、4的四张卡片洗匀后，背面朝上放在桌面上. （1）从中随机抽取一张卡片，求该卡片正面上的数字是偶数的概率；（2）先从中随机抽取一张卡片（不放回），将该卡片正面上的数字作为十位上的数字；．．．再随机抽取一张，将该卡片正面上的数字作为个位上的数字，则组成的两位数恰好是4的倍数的概率是多少？请用树状图或列表法加以说明.20. 为配合我市“创卫”工作，某中学选派部分学生到若干处公共场所参加义务劳动．若每处安排10人，则还剩15人；若每处安排14人，则有一处的人数不足14人，但不少于10人．求这所学校选派学生的人数和学生所参加义务劳动的公共场所个数.21. 如图，四边形ABCD 是正方形，点N 是CD 的中点，M 是AD 边上不同于点A 、D 的点，若sin ∠ABM =22. 如图，抛物线的顶点坐标是⎪，且经过点A ( 8 , 14 .(1求该抛物线的解析式；(2设该抛物线与y 轴相交于点B ，与x 轴相交于C 、D 两点（点C 在点D 的左边），试求点B 、C 、D 的坐标；(3设点P 是x 轴上的任意一点，分别连结AC 、BC ．试判断：PA +PB 与AC +BC 的大小关系，并说明理由.，求证:∠NMB =∠MBC . 10N(第21题图⎛5⎝29⎫8⎭(第22题图23. 如图，AB 是⊙O 的直径，过点B 作⊙O 的切线BM ，点P 在右半圆上移动点P 与点A 、B 不重合），过点P 作PC ⊥AB ，垂足为C ；点Q 在射线BM 上移动（点M 在点B 的右边），且在移动过程中保持OQ ∥AP .(1若PC 、QO 的延长线相交于点E ，判断是否存在点P ，使得点E 恰好在⊙O 上？若存在，求出∠APC 的大小；若不存在，请说明理由； (2连结AQ 交PC 于点F ，设k =的结论．PF，试问：k 的值是否随点P 的移动而变化？证明你PC C BPQ M（第23题图）用心爱心专心 6。
高中自主招生考试 数 学 试 卷(1)
高中自主招生考试 数 学 试 卷 （1）（满分：150分；考试时间：120分钟）亲爱的同学：欢迎你参加本次考试！请细心审题，用心思考，耐心解答．祝你成功！答题时请注意：请将答案或解答过程写在答题卷的相应位置上，写在试卷上不得分．一、选择题（本大题共有10小题，每小题4分，共40分．每小题都有A 、B 、C 、D 四个选项，其中有且只有一个选项是正确的，请将正确答案的代号填写在答题卷中相应的表格内，答对得4分，答错、不答或答案超过一个的得零分）1.（2011年漳州一中自主招生）用半径为cm 6、圆心角为︒120的扇形做成一个圆锥的侧面, 则这个圆锥的底面半径是 【 】A.2cmB.3cmC.4cmD.6cm 2.（2011年漳州一中自主招生）若n 为整数，则能使11-+n n 也为整数的n 的个数有 【 】A.1个B.2个C.3个D.4个3.（2011年漳州一中自主招生）已知a 为实数，则代数式221227a a +-的最小值为 【 】A.0B.3C.33D.94．（2011年浙江省象山）为解决四个村庄用电问题，政府投资在已建电厂与这四个村庄之间架设输电线路.现已知这四个村庄及电厂之间的距离如图所示(距离单位：公里)，则能把电力输送到这四个村庄的输电线路的最短总长度应该是 【 】 (A)19．5 (B)20．5 (C)21．5 (D)25．55.（2011年浙江省象山）若等腰△ABC 的三边长都是方程x 2-6x+8=0的根，则△ABC 的周长是 【 】(A)10或8 (B)1O (C)12或6 (D)6或10或126．（2011年浙江省象山）A 、B 、C 、D 四人参加某一期的体育彩票兑奖活动，现已知：如果A 中奖，那么B 也中奖： 如果B 中奖，那么C 中奖或A 不中奖：如果D 不中奖，那么A 中奖，C 不中奖： 如果D 中奖，那么A 也中奖则这四个人中，中奖的人数是 【 】 (A)1 (B)2 (C)3 (D)47．（2011年浙江省象山）已知三条抛物线y 1=x 2-x+m ，y 2=x 2+2mx+4，y 3=mx 2+mx+m-1中至少有一条与x 轴相交，则实数m 的取值范围是 【 】(A)4/3<m<2 (B)m≤3/4且m≠0 (C)m≥2 (D)m≤3/4且m≠0或m≥28．（2011年浙江省象山）如图，在正ABC 中，D 为AC 上一点，E 为AB 上一点，BD 、CE 交于P ，若四边形ADPE 与△BPC 面积相等，则∠BPE 的度数为 【 】 (A)60° (B)45° (C)7 5° (D)50°3．如图，在菱形ABCD 中，∠BAD ＝80°，AB 的垂直平分线交对角 线AC 于点F ，E 为垂足，连结DF . 则∠CDF 等于 【 】A ．60°B ．65°C ．70°D ．80°10.（2011年黄冈）如图，ABC ∆中，D 、E 是BC 边上的点，1:2:3::=EC DE BD ，M 在AC 边上，2:1:=MA CM ，BM交AD 、AE 于H 、G ，则GM HG BH ::等于 【 】 A 、1:2:3 B 、1:3:5 C 、5:12:25 D 、10:24:51二、填空题（本大题共有6小题，每小题4分，共24分．请将正确的答案直接填写在答题卷中相应的横线上）11.（2011蚌埠市七中）已知m bac a c b c b a =+=+=+232323 ,且0≠++c b a ，那么直 线m mx y -=一定不通过．．．第 象限. 12.（2011年黄冈）如右图，圆锥的母线长是3，底面半径是1，A 是底面圆周上一点，从A 点出发绕侧面一周，再回到A 点的最短的路线长是 13.（2011年漳州一中自主招生）如图，E 、F 分别是A BEABCD 的边AB 、CD 上的点，AF 与DE 相交于点P ，BF 与CE 相交于点Q ，若S △APD 15=2cm ，S △BQC 25=2cm ，则阴影部分的面积为 2cm ．14.（2011年漳州一中自主招生）如图，正方形ABCD 的边长 为4cm ，正方形AEFG 的边长为1cm ．如果正方形AEFG 绕点A 旋转，那么C 、F 两点之间的最小距离 为 cm ．15.（2011年漳州一中自主招生）若规定：①{} m 表示大于m 的最小整数，例如：{}4 3 =，{}2 4.2-=-； ②[] m 表示不大于m 的最大整数，例如：[]5 5 =，[]4 6.3-=-.则使等式{}[]4 2=-x x 成立的整数．．=x ． 16（2011年黄冈）两个反比例函数x y 3=，xy 6=在第一象限内的图象，点1P 、2P 、3P 、…、2007P 在反比例函数xy 6=上，它们的横坐标分别为1x 、2x 、3x 、…、2007x ，纵坐标分别是1、3、5…共2007个连续奇数，过1P 、2P 、3P 、…、2007P 分别作y 轴的平行线，与xy 3=的图象交点依次为)','(111y x Q 、)','(222y x Q 、…、),('2007'20072007y x Q ，则=20072007Q P三、解答题（本大题共有7小题，共86分．其中第17题8分，第18、19题各10分，第20题12分，第21题14分，第22、23题各16分．请将解答过程写在答题卷的相应位置上）17、（8分）设m 是不小于1-的实数，关于x 的方程033)2(222=+-+-+m m x m x 有两个不相等的实数根1x 、2x ，（1）若21x 622=+x ，求m r 值；（2）求22212111x mx x mx -+-的最大值。
高中自主招生考试数学试题(含答案详解)
一中自主招生考试数学试题一．选择题（共6小题，满分24分，每小题4分）1．（4分）如果关于x的方程x2﹣ax+a2﹣3=0至少有一个正根，则实数a的取值围是（）A．﹣2＜a＜2B．C．D．2．（4分）假期里王老师有一个紧急通知，要用尽快通知给50个同学，假设每通知一个同学需要1分钟时间，同学接到后也可以相互通知，那么要使所有同学都接到通知最快需要的时间为（）A．8分钟B．7分钟C．6分钟D．5分钟3．（4分）如图是一个正方体的表面展开图，已知正方体的每一个面都有一个实数，且相对面上的两个数互为倒数，那么代数式的值等于（）A．B．﹣6C．D．64．（4分）（2008•）如图，把图1中的△ABC经过一定的变换得到图2中的△A′B′C′，如果图1中△ABC上点P的坐标为（a，b），那么这个点在图2中的对应点P′的坐标为（）A．（a﹣2，b﹣3）B．（a﹣3，b﹣2）C．（a+3，b+2）D．（a+2，b+3）5．（4分）如图，四边形BDCE接于以BC为直径的⊙A，已知：，则线段DE的长是（）A．B．7C．4+3D．3+46．（4分）如图，三同学把一个直角边长分别为3cm，4cm的直角三角形硬纸板，在桌面上翻滚（顺时针方向），顶点A的位置变化为A1⇒A2⇒A3，其中第二次翻滚时被桌面上一小木块挡住，使纸板一边A2C1与桌面所成的角恰好等于∠BAC，则A翻滚到A2位置时共走过的路程为（）A．8cm B．8πcm C．2cm D．4πcm二．填空题（共6小题，满分24分，每小题4分）7．（4分）若x+=3，则x2+=_________．8．（4分）如图，E、F分别是平行四边形ABCD的边AB、CD上的点，AF与DE相交于点P，BF与CE相交于点Q，若S△APD=15cm2，S△BQC=25cm2，则阴影部分的面积为_________cm2．9．（4分）如图，正方形ABCD的边长为4cm，正方形AEFG的边长为1cm．如果正方形AEFG绕点A旋转，那么C、F两点之间的最小距离为_________cm．10．（4分）对于正数x，规定f（x）=，计算f（）+f（）+f（）+…+f（）+f（）+f（1）+f（2）+f（3）+…+f（98）+f（99）+f（100）=_________．11．（4分）甲，乙，丙3人用擂台赛形式进行训练，每局2人进行单打比赛，另1人当裁判，每﹣局的输方去当下﹣局的裁判，而由原来的裁判向胜者挑战．半天训练结束时发现甲共打了12局，乙共打了21局，而丙共当裁判8局．那么，整个比赛的第10局的输方一定是_________．12．（4分）（2002•）如图所示，在正方形ABCD中，AO⊥BD，OE，FG，HI都垂直于AD，EF，GH，IJ都垂直于AO，若已知S△AIJ=1，则正方形ABCD的面积为_________．三．解答题（共6小题，满分52分）13．（6分）把几个数用大括号围起来，中间用逗号断开，如：{1，2，3}，{2，7，8，19}，我们称之为集合，其中的数称其为集合的元素．如果一个集合满足：当实数a是集合的元素时，实数8﹣a也必是这个集合的元素，这样的集合我们称为好的集合．（1）请你判断集合{1，2}，{1，4，7}是不是好的集合；（2）请你写出满足条件的两个好的集合的例子．14．（8分）（2007•）在课外活动时间，小王、小丽、小华做“互相踢踺子”游戏，踺子从一人传到另一人就记为踢一次．（1）若从小丽开始，经过两次踢踺后，踺子踢到小华处的概率是多少？（用树状图或列表法说明）（2）若经过三次踢踺后，踺子踢到小王处的可能性最小，应确定从谁开始踢，并说明理由．15．（8分）某中学为了进一步改善办学条件，决定计划拆除一部分旧校舍，建造新校舍．拆除旧校舍每平方米需80元，建造新校舍每平方米需要800元，计划在年拆除旧校舍与建造新校舍共9000平方米，在实施中为扩大绿化面积，新建校舍只完成了计划的90%而拆除旧校舍则超过了计划的10%，结果恰好完成了原计划的拆、建总面积．（1）求原计划拆、建面积各是多少平方米？（2）若绿化1平方米需要200元，那么把在实际的拆、建工程中节余的资金全部用来绿化，可绿化多少平方米？16．（10分）如图，⊙O的直径EF=cm，Rt△ABC中，∠ACB=90°，∠BAC=30°，AB=cm．E、F、A、B 四点共线．Rt△ABC以1cm/s的速度沿EF所在直线由右向左匀速运动，设运动时间为t（s），当t=0s时，点B与点F重合．（1）当t为何值时，Rt△ABC的直角边与⊙O相切？（2）当Rt△ABC的直角边与⊙O相切时，请求出重叠部分的面积（精确到0.01）．17．（10分）（2008•）（1）如图1，点O是线段AD的中点，分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD，连接AC和BD，相交于点E，连接BC．求∠AEB的大小；（2）如图2，△OAB固定不动，保持△OCD的形状和大小不变，将△OCD绕点O旋转（△OAB和△OCD不能重叠），求∠AEB的大小．18．（10分）（2008•）我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图所示，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D 的坐标为（0，﹣3），AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2．（1）请你求出“蛋圆”抛物线部分的解析式，并写出自变量的取值围；（2）你能求出经过点C的“蛋圆”切线的解析式吗？试试看；（3）开动脑筋想一想，相信你能求出经过点D的“蛋圆”切线的解析式．答案与评分标准一．C ，C ，A ，C ，D ，D甲，256，二．7，40，3，，三．解：（1）集合{1，2}不是好的集合，这是因为8﹣1=7，而7不是{1，2}中的数，所以{1，2}不是好的集合，{1，4，7}是好的集合，这是因为8﹣1=7，7是{1，4，7}中的数，8﹣4=4，4也是{1，4，7}中的数，8﹣7=1，1又是{1，4，7}中的数．所以{1，4，7}是好的集合；（2）答案不唯一．集合{4}、{3，4，5}、{2，6}、{1，2，4，6，7}、{0，8}等都是好的集合．解：（1）踺子踢到小华处的概率是．树状图如下：列表法如下：小丽小王小华小王（小丽，小王）（小王，小华）小华（小华，小丽）（小华，小王）（2）小王．树状图如下：理由：若从小王开始踢，三次踢踺后，踺子踢到小王处的概率是，踢到其它两人处的概率都是，因此，踺子踢到小王处的可能性是最小．解：（1）由题意可设拆旧舍x平方米，建新舍y平方米，则答：原计划拆建各4500平方米．（2）计划资金y1=4500×80+4500×800=3960000元实用资金y2=1.1×4500×80+0.9×4500×800=4950×80+4050×800=396000+3240000=3636000∴节余资金：3960000﹣3636000=324000∴可建绿化面积=平方米答：可绿化面积1620平方米．解：（1）∵∠BAC=30°，AB=，∴BC=又∵⊙O的直径EF=，即半径为，∠ACB=90°，∴当点B运动到圆心O时，AC边与⊙O相切．（如图1所示）（1分）此时运动距离为FO=，∴t=s．（2分）当BC边与⊙O相切时（如图2所示），设切点为G．连接OG ，则OG⊥BC．（3分）由已知，∠BOG=∠BAC=30°，OG=，∴BO=2．（4分）又FO=，∴BF=．（此步亦可利用相似求解，请参照给分）∴此时s．（5分）由上所述，当秒时，Rt△ABC的直角边与⊙O相切．（6分）（2）由图1，此时⊙O与Rt△ABC的重叠部分为扇形COF．（7分）由已知，∠COF=60°，∴．（8分）由图2，设AC与⊙O交于点M，此时⊙O与Rt△ABC的重叠部分为扇形OMGE加上△OAM ．（9分）过点M作MN⊥OG于N，则MN=GC．由（1）可知BG=1则MN=GC=．（10分）∴，∴∠MON=25°，即∠MOE=55°．（11分）∴．（12分）又∵OM=，∴点M到AB的距离h=OM•sin∠MOE≈1.419，（13分）∴S△AOM=•OA•h≈1.229cm2此时⊙O与Rt△ABC的重叠部分的面积为S扇形OMEF+S△AOM≈2.67cm2．（14分）解：（1）如图3，∵△DOC和△ABO都是等边三角形，且点O是线段AD的中点，∴OD=OC=OB=OA，∠1=∠2=60°，∴∠4=∠5．又∵∠4+∠5=∠2=60°，∴∠4=30°．同理∠6=30°．∵∠AEB=∠4+∠6，∴∠AEB=60°．（2）如图4，∵△DOC和△ABO 都是等边三角形，∴OD=OC，OB=OA，∠1=∠2=60°．又∵OD=OA，∴OD=OB，OA=OC，∴∠4=∠5，∠6=∠7．∵∠DOB=∠1+∠3，∠AOC=∠2+∠3，∴∠DOB=∠AOC．∵∠4+∠5+∠DOB=180°，∠6+∠7+∠AOC=180°，∴2∠5=2∠6，∴∠5=∠6．又∵∠AEB=∠8﹣∠5，∠8=∠2+∠6，∴∠AEB=∠2+∠6﹣∠5=∠2+∠5﹣∠5=∠2，∴∠AEB=60°．解：（1）根据题意可得：A（﹣1，0），B（3，0）；则设抛物线的解析式为y=a（x+1）（x﹣3）（a≠0），又∵点D（0，﹣3）在抛物线上，∴a（0+1）（0﹣3）=﹣3，解之得：a=1∴y=x2﹣2x﹣3（3分）自变量围：﹣1≤x≤3（4分）（2）设经过点C“蛋圆”的切线CE交x轴于点E，连接CM，在Rt△MOC中，∵OM=1，CM=2，∴∠CMO=60°，OC=在Rt△MCE中，∵MC=2，∠CMO=60°，∴ME=4∴点C、E的坐标分别为（0，），（﹣3，0）（6分）∴切线CE的解析式为（8分）（3）设过点D（0，﹣3），“蛋圆”切线的解析式为：y=kx ﹣3（k≠0）（9分）由题意可知方程组只有一组解即kx﹣3=x2﹣2x﹣3有两个相等实根，∴k=﹣2（11分）∴过点D“蛋圆”切线的解析式y=﹣2x﹣3．（12分）。
漳州一中自主招生考试数学试卷
实验班自主招生考试数学学科试卷考试时间：120分钟满分150分就读学校：姓名：考场号：座位号：一、选择题（本大题共10小题，每小题3分，共30分。
每小题只有一个正确答案）1.设21≤≤-x，则22+--xx的值是( )A. 4B.x2- C. 42+x D.42-x2.某班有54人，在一次数学考试中，得分均为整数，全班最低分为48分，最高分为96分，那么该班考试中（）A. 至少有两人得分相同B. 至多有两人得分相同C. 得分相同的情况不会出现D. 以上结论都不对3.若一直角三角形的斜边长为c，内切圆半径是r，则内切圆的面积与三角形面积之比是( )A.rcr2+πB.rcr+πC.rcr+2πD.22rcr+π4. 如图，已知矩形ABCD，AB＝5，BC＝4，E是BC边上的一个动点，AE⊥EF，EF交CD于点F．设BE=x，FC=y，则点E从点B运动到点C时，能表示y关于x的函数关系的大致图象是（）AB C D5.反比例函数)0(≠=kxky的图象与直线1=x，3=x，1=y，2=y围成的矩形有公共点，则实数k的取值范围是 ( )A.32≤≤k B．61<≤k C．61≤≤k D．42≤≤k6. 已知实数cba,,满足0=++cba且1=abc，那么cb11+的值一定是( )A . 正数B . 负数C . 非负数D . 非正数7. 如图，点CA,都在函数)0(3>=xxy的图象上，点DB,都在x轴上，且使得BCDOAB∆∆,都是等边三角形，则点C的坐标是( )第4题图A.()36,12-+ B.()12,12-+ C.()36,13-+ D.()23,12-+8.已知20152016+=x a ，20162016+=x b ，20172016+=x c ，则多项式ca bc ab c b a ---++222的值为（ ）A.0B. 1C. 2D. 3 9.如图，点A 、B 分别在反比例函数xay =（0>a , x ＞0）， xby =（0<b ， x ＞0）的图象上，点A 沿着曲线自左向右运 动且满足OA ⊥OB ，则OAB ∠的变化情况是（ ）A.逐渐变大B.逐渐变小C.不变D.先变大再变小 10.如图，在长方体ABCD - A 1B 1C 1D 1中，AB ＝20，AD ＝5.7， AA 1＝12，点E 在上底面A 1B 1C 1D 1内，且E 到边A 1D 1和A 1B 1 距离分别为4和3，一质点从顶点A 射向点E ，遇长方体的面 反射(反射服从光的反射原理)，记L 1＝AE ，经过三次反射，依 次连接反射点之间的线段，分别记为L 2，L 3，L 4，将线段L 1， L 2，L 3，L 4竖直放置在同一水平线上，则大致的图形是( )AB C D二、填空题（本大题4小题，每小题4分，共16分）11.已知b a <<0,1=+b a ,那么b 22b a + (填“>”“<”“≥”“≤”)12.若抛物线142++-=p px x y 无论p 取何值都过某一定点，则该定点坐标为 . 13.如图，在直角∆ABC 中，6,90==∠CA ACB，点P 是半 圆弧AC 的中点，连接BP ，线段BP 把图形APCB 分成两部分， 则这两部分面积之差的绝对值是 .14.在四边形ABCD 中，90,60=∠=∠=∠D B A ,4=AD ,设AB 的 长为a ，那么a 的取值范围是 .第9题图第9题图A第13题图第18题图三、简答题（本大题5小题，共54分）15.（本题满分6分） 计算：1222245cos 2)2(0-+-+-π16.（本题满分8分）掷一枚六个面编号分别为6,5,4,3,2,1的质地均匀的正方体骰子,记掷出的点数为a ，求满足方程组⎩⎨⎧=+=+2234y x y ax 的解y x ,均为正数的概率。
漳州高一自主招生考试卷
漳州高一自主招生考试卷一、语文（共100分）（一）文言文阅读（共20分）阅读以下文言文选段，回答1-4题。
（文言文选段略）1. 解释文中划线词语的含义。
（5分）2. 翻译文中划线句子。
（5分）3. 概括选段的主要内容。
（5分）4. 分析文中人物的性格特点。
（5分）（二）现代文阅读（共30分）阅读以下现代文选段，回答5-8题。
（现代文选段略）5. 概括文章的中心思想。
（5分）6. 分析文中的主要写作手法。
（5分）7. 论述文中某一观点或论据。
（10分）8. 根据文章内容，提出自己的见解。
（10分）（三）作文（共50分）请以“我眼中的漳州”为题，写一篇不少于800字的作文。
要求：内容具体，感情真挚，语言流畅。
二、数学（共100分）（一）选择题（共20分）1-10题，每题2分。
（具体题目略）（二）填空题（共20分）11-20题，每题2分。
（具体题目略）（三）解答题（共60分）21-30题，每题分值不同。
（具体题目略）三、英语（共100分）（一）阅读理解（共40分）A. 阅读理解选择题（20分）B. 阅读理解简答题（10分）C. 阅读理解填空题（10分）（二）完形填空（共20分）（三）语法填空（共10分）（四）翻译（共10分）A. 中译英（5分）B. 英译中（5分）（五）写作（共20分）请根据所给情景，写一封不少于100词的英文信件。
四、科学（共100分）（一）物理部分（共40分）1. 选择题（共10分）2. 填空题（共10分）3. 计算题（共20分）（二）化学部分（共30分）1. 选择题（共10分）2. 填空题（共10分）3. 实验题（共10分）（三）生物部分（共30分）1. 选择题（共10分）2. 填空题（共10分）3. 简答题（共10分）五、综合能力测试（共100分）（一）逻辑思维题（共20分）1-10题，每题2分。
（具体题目略）（二）数据分析题（共30分）11-20题，每题3分。
（具体题目略）（三）案例分析题（共50分）21-30题，每题5分。
福建省漳州市漳州一中区域联考2023-2024学年七年级下学期期中数学试题(解析版)
2023～2024学年第二学期期中考七年级数学科试卷考试时间：120分钟 满分：150分一、选择题（每题4分，共40分，请将答案涂在答题卡的相应位置上）1. 计算a 2·a 3 的结果是 （ ）A. a 4B. a 5C. a 6D. a 8【答案】B【解析】【分析】根据同底数幂相乘，底数不变，指数相加，计算后即可选取答案．【详解】a 2•a 3=a 2+3=a 5，故选B ．【点睛】本题考查了同底数幂的乘法的法则，熟练掌握运算是解题的关键．2. 如图，直线相交于点，若，则的度数是（ ）A. B. C. D. 【答案】C【解析】【分析】本题考查对顶角，根据对顶角相等，即可得出结果．【详解】解：由题意，得：是对顶角，，∴；故选C ．3. 对于圆的周长公式，下列说法正确的是（ ）A. C ，是变量，2是常量B. r 是变量，C 是常量C. C 是变量，r 是常量D. C ，r 是变量，是常量【答案】D【解析】【分析】常量就是在变化过程中不变的量，变量是指在变化过程中随时可以发生变化的量．【详解】解：圆的周长公式表明圆的周长与半径成正比，比值为是一个常数，变量为周长和半径AB CD 、O 130∠=︒2∠10︒20︒30︒40︒1,2∠∠130∠=︒2130∠=∠=︒2πC r =π2π2πC．故选：D ．【点睛】本题考查了常量、变量，熟记相关概念是解题关键．4. 如图，△ABC 中，∠A =60°，∠B =40°，则∠C 等于（ ）A. 100°B. 80°C. 60°D. 40°【答案】B【解析】【详解】由三角形内角和定理得，∠C =180°﹣∠A ﹣∠B =80°，故选：B ．5. 下列运算正确的是（ ）A. B. C. D.【答案】D【解析】【分析】本题主要考查了积的乘方计算，幂的乘方计算，完全平方公式和平方差公式，熟知相关计算法则是解题的关键．【详解】解：A 、，原式计算错误，不符合题意；B 、，原式计算错误，不符合题意；C 、，原式计算错误，不符合题意；D 、，原式计算正确，符合题意；故选：D ．6. 如图，某同学在体育课上跳远后留下的脚印，在图中画出了他的跳远距离，能正确解释这一现象的数学知识是（）r ()235a a =()33626a a =()222a b a b +=+()()22a b a b a b -+=-()236a a =()33928a a =()2222a b a ab b +=++()()22a b a b a b -+=-A. 两点之间，线段最短B. 垂线段最短C. 两点确定一条直线D. 经过一点有且只有一条直线与已知直线垂直【答案】B【解析】【分析】由点到直线的距离的定义及跳远比赛的规则作出判断．【详解】解：能正确解释这一现象的数学知识是垂线段最短，故选：B ．【点睛】此题考查了垂线段最短的性质的运用，解答此题的关键是熟练掌握由点到直线的距离的定义及跳远比赛的规则．7. 变量与之间的关系式是，当自变量时，因变量的值是（ ）A. B. C. 2 D. 1【答案】C【解析】【分析】本题主要考查了求函数值，直接把代入中进行求解即可．【详解】解：在中，当时，，故选：C ．8. 用直尺和圆规作一个角等于已知角的示意图如图所示，则说明的依据是（ ）A B. C. D. 【答案】A【解析】【分析】本题主要考查了全等三角形的判定，关键是掌握全等三角形的判定定理．由作法易得.y x 112y x =+2x =y 2-1-2x =112y x =+112y x =+2x =12122y =⨯+=A O B AOB '''∠=∠SSS SAS AAS ASA，，，根据可得到三角形全等．【详解】解：由作图可知，，，，．故答案为：A ．9. 如图，下列条件中，能判定的是（ ）A. B. C. D. 【答案】A【解析】【分析】根据平行线的判定条件逐一判断即可．【详解】解：由，可以判定（内错角相等，两直线平行），故A 符合题意；由，不能判定，故B 不符合题意；由，能判定（同位角相等，两直线平行），不能判定，故C 符合题意；由，可以判定（同旁内角互补，两直线平行），不能判定，故D 不符合题意；故选A ．【点睛】本题主要考查了平行线判定，熟知平行线的判定条件是解题的关键．10. 如图，为上方一点，H 、G 分别为上的点，、的角平分线交于点的角平分线与的延长线交于点，下列结论：①；②；③；④，则．其中正确的结论有（ ）A. ①②③B. ②③④C. ①③④D. ①②③④【答案】D的OD O D ''=OC O C ''=CD C D ''=SSS OD O D ''=OC O C ''=CD C D ''=∴()SSS COD C O D ''' ≌AB CD ∥23∠∠=14∠=∠15∠=∠4180ADC ∠+∠=︒23∠∠=AB CD ∥14∠=∠AB CD ∥15∠=∠AD BC ∥AB CD ∥4180ADC ∠+∠=︒AD BC ∥AB CD ∥,AB CD P ∥AB AB CD 、PHB ∠PGD ∠,E PGC ∠EH F EG FG ⊥P PHB PGD ∠+∠=∠2P E ∠=∠AHP PGC F ∠-∠=∠60F ∠=︒【解析】【分析】由角平分线的性质以及平行线的性质可求出，即可判断①；设交于点M ，交于点N ，根据平行的性质即有，再结合三角形外角的性质即可判断②；根据角平分线的性质有，再证即可得∠PGD =2∠EGD ，即可判断③；先证，根据，即有，再结合，即可判断④正确；【详解】∵平分，平分，∴，∵，∴，∴，故①正确；设交于点M ，交于点N ，如图，∵，∴，∵，∴，故②正确；∵平分，平分，∴，∵，∴，∵，∴，∵，∴，故③正确；90EGF ∠=︒PG AB GE AB PGD PMB ∠=∠2,2PHB EHB PGD EGD ∠=∠∠=∠,P PHB PGD E EHB EGD ∠+∠=∠∠+∠=∠，P F ∠=∠90E F ∠+∠=︒90P E ∠+∠=︒2P E ∠=∠GF PGC ∠EG PGD ∠1122PGF PGC PGE PGD ∠=∠∠=∠，180PGC PGD ∠+∠=︒90PGF PGE ∠+∠=︒EG FG ⊥PG AB GE AB AB CD PGD PMB ∠=∠P PHB PMB ∠+∠=∠P PHB PGD ∠+∠=∠HE PHB ∠EG PGD ∠2,2PHB EHB PGD EGD ∠=∠∠=∠AB CD ∥,ENB EGD PMB PGD ∠=∠∠=∠,P PHB PMB E EHB ENB ∠+∠=∠∠+∠=∠,P PHB PGD E EHB EGD ∠+∠=∠∠+∠=∠2,2PHB EHB PGD EGD ∠=∠∠=∠2P E ∠=∠∵，∴，∴，∵，∴，∵，∴，∴，∵，∴，∴，故④正确；故选：D ．【点睛】本题考查了平行线的性质、角平分线的性质、三角形外角的性质以及直角三角形中两个锐角互余等知识，灵活运用平行线的性质和三角形的外角的性质是解答本题的关键．二、填空题（每题4分，共24分，请将答案填在答题卡相应的横线上）11. 很多人可能都知道蓝鲸是迄今发现的地球上最大的动物，却都不了解体积最小的动物，世界上体积最小的动物要比蚂蚁小很多倍，它是被命名为H 39的原生动物，它的最长直径也不过才0.0000003米．其中数据0.0000003用科学记数法表示为______．【答案】【解析】【分析】本题主要考查科学记数法，根据科学记数法的表示方法求解即可．科学记数法的表示形式为的形式，其中，n 为整数．解题关键是正确确定a 的值以及n 的值．【详解】0.0000003用科学记数法表示为．故答案为：．12. 已知，，则______．【答案】【解析】【分析】本题主要考查同底数幂的除法．根据逆用同底数幂的除法运算法则进行计算即可得到答案．【详解】解：∵，，AB CD ∥PMA PGC ∠=∠AHP PGC AHP PMH P ∠-∠=∠-∠=∠AHP PGC F ∠-∠=∠P F ∠=∠90FGE ∠=︒90E F ∠+∠=︒90P E ∠+∠=︒2P E ∠=∠30E ∠=︒260P F E ∠=∠=∠=︒7310-⨯10n a ⨯1<10a ≤7310-⨯7310-⨯2m a =3n a =m n a -=232m a =3n a =∴，故答案为：．13. 等腰三角形的两条边长分别为3和6，则这个等腰三角形的周长是______．【答案】15【解析】【分析】分两种情况讨论，当3为底时和当3为腰时，再求和即可；本题主要考查等腰三角形的知识，熟练掌握构成三角形的定义是解题的关键．【详解】解：①当3为底时，其它两边都为6，3、6、6可以构成三角形，周长为：．②当3为腰时，其它两边为3和6，,不能构成三角形，故舍去，故答案为：15．14. 某汽车生产厂对其生产的型汽车进行油耗试验（油箱已加满），试验中汽车为匀速行驶，在行驶过程中，油箱的余油量（升）与行驶时间（小时）之间的关系如下表：（小时）0123（升）80726456则与之间的关系式为______．【答案】【解析】【分析】本题主要考查了求函数关系式，根据行驶时间每增加1小时，油箱的余油量减少8升进行求解即可．【详解】解：观察表格可知，行驶时间每增加1小时，油箱的余油量减少8升，∴，故答案为：．15. 如图，，点在直线上，点在直线上，．若，则∠1的度数为2233m n m n a a a -=¸=¸=2336615++=336+= ∴A y t t y y t ()808010y t t =-≤≤()808010y t t =-≤≤()808010y t t =-≤≤a b ∥A b C a AB BC ⊥2140∠=︒【答案】##130度【解析】【分析】本题主要考查平行线的性质，解答的关键是熟记平行线的性质：两直线平行，同旁内角互补．过点B 作，则有，由平行线的性质可得，，再由，即可求解．【详解】解：过点B 作，如图，，，，，，，，，，．故答案为：．16. 如图，已知四边形中，厘米，厘米，厘米，，点E 为线段的中点．如果点P 在线段上以3厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段上由C 点向D 点运动．当点Q 的运动速度为______厘米/秒时，能够使与以C 、P 、Q三点所构成的三角130︒BD a ∥BD b ∥2180CBD ∠+∠=︒1180ABD ∠+∠=︒90ABC ∠=︒BD a ∥2180CBD ∴∠+∠=︒2140∠=︒ 180240CBD ∴∠=︒-∠=︒AB BC ⊥ 90ABC ∴∠=︒9050ABD CBD ∴∠=︒-∠=︒a b BD b ∴∥1180ABD ∴∠+∠=︒1180130ABD ∴∠=︒-∠=︒130︒ABCD 12AB =8BC =14CD =B C ∠=∠AB BC CD BPE【答案】或【解析】【分析】分两种情况讨论，依据全等三角形的对应边相等，即可得到点Q 的运动速度．【详解】解：设点P 运动的时间为t 秒，则，，∵，∴①当，时，，此时，解得，∴，此时，点Q 的运动速度为厘米/秒；②当，时，，此时，，解得，∴点Q 的运动速度为厘米/秒；综上所述，点Q 的运动速度为3厘米/秒或厘米/秒时，能够使与以C 、P 、Q 三点所构成的三角形全等．3923BP t =83CP t =-B C ∠=∠6BE CP ==BP CQ =BPE CQP ≅ 683t =-23t =2BP CQ ==2233÷=6BE CQ ==BP CP =BPE CPQ ≅ 383t t =-43t =49632÷=92BPE故答案为：或．【点睛】本题考查了全等三角形的性质和判定的应用．解决问题的关键是掌握全等三角形的对应边相等．三、解答题（本题共9小题，共86分，解答应写出文字说明、证明过程或演算步骤）17. 计算：（1）（2）（3）（4）（简便计算）【答案】（1）2 （2） （3）（4）1【解析】【分析】本题考查负整数指数幂，零指数幂，整式的运算：（1）先进行负整数指数幂，零指数幂和乘方运算，再进行加减运算即可；（2）利用多项式乘多项式的法则，进行计算即可；（3）先利用平方差公式进行计算，再利用完全平方公式进行计算即可；（4）利用平方差公式进行简算即可．【小问1详解】解：原式；【小问2详解】原式；【小问3详解】原式；【小问4详解】原式．18. 先化简，再求值：，其中．3921020241( 3.14)(1)2π-⎛⎫+--- ⎪⎝⎭(39)(68)x x ++()()x y z x y z +-++2202420252023-⨯2187872x x ++2222x xy y z ++-2112=+-=2218245472187872x x x x x =+++=++22222()2x y z x xy y z =+-=++-()()222202420241202412024202411=-+⨯-=-+=()()()222x y x y x y xy y ⎡⎤+---+÷⎣⎦x 1,y 2==-【答案】，【解析】【分析】本题主要考查了整式的化简求值，先根据完全平方公式和平方差公式去小括号，然后合并同类项，接着根据多项式除以单项式的计算法则化简，最后代值计算即可．【详解】解：，当时，原式．19. 如图，已知，试说明：．【答案】见解析【解析】【分析】本题考查平行线的判定，邻补角求出的度数，进而得到，即可得证．【详解】证明：∵，∴，∵，∴，∴．20. 阅读并完成相应的任务：如图，小明站在堤岸凉亭A 点处，正对他的B 点（与堤岸垂直）停有一艘游艇，他想知道凉亭与这艘游艇之间的距离，于是制定了如下方案．2x y -4()()()222x y x y x y xy y⎡⎤+---+÷⎣⎦()2222222x y x xy y xy y ⎡⎤=---++÷⎣⎦()2222222x y x xy y xy y =--+-+÷()2422xy y y=-÷2x y =-x 1,y 2==-()2124=⨯--=1105275∠=︒∠=︒，a b ∥3∠13∠=∠275∠=︒31802105∠=︒-∠=︒1105∠=︒13∠=∠a b ∥AB课题测量凉亭与游艇之间的距离测量工具皮尺测量方案示意图（不完整）测量步骤①小明沿堤岸走到电线杆C旁（直线与堤岸平行）；②再往前走相同的距离，到达D点；③他到达D点后向左转90度直行，当自己，电线杆与游艇在一条直线上时停下来，此时小明位于点E处测量数据米，米，米问题解决：（1）任务一：根据测量步骤将测量方案示意图补充完整；（2）任务二：小明的解答如下，请你帮忙补充完整；米，米，，，在和中（③）（④）（）米【答案】（1）见详解；（2）①；②对顶角相等；③；④．【解析】【分析】本题考查了三角形全等的判定与性质，根据题意画出图形并进行全等三角形的证明是解题的关键．结合测量方案示意图，证明，再通过全等三角形的性质，推出的长度．【详解】（1）AC20AC=20CD=8DE=20AC=20CD=90A∠= 90D∠=AC DC∴=A D∠=∠ABCDEC()____A DAC DC⎧∠=∠⎪=⎨⎪⎩①②ABC DEC∴≌AB DE∴=AB∴=BCA ECD∠=∠ASA8ABC DEC≌△△AB（2）由题意可知，米，米，米，，，在和中（）（全等三角形对应边相等）米故答案为：①；②对顶角相等；③全等三角形对应边相等；④8．21. 完成下面推理填空：如图，点E ，F 分别在和上，与互余，于点．求证：．证明：（ ① ）② （ ③ ）（ ④ ）与互余（ ⑤ ）（ ⑥ ）【答案】垂直的定义；；同位角相等，两直线平行；两直线平行，同位角相等；同角的余角相等；内错角相等，两直线平行【解析】20AC =20CD =8DE =90A ∠= 90D ∠=AC DC ∴=A D∠=∠ABC DEC A D AC DCBCA ECD ∠=∠⎧⎪=⎨⎪∠=∠⎩（对顶角相等）ABC DEC ∴ ≌ASA AB DE ∴=8AB ∴=BCA ECD ∠=∠AB CD 1,2D ∠=∠∠C ∠AF CE ⊥G AB CD ∥AF CE ⊥ 90CGF ∴∠=︒1D ∠=∠ AF ∴∥4CGF ∴∠=∠234180∠+∠+∠=︒ 2390∴∠+∠=︒2∠ C ∠290C ∴∠+∠=︒3C ∴∠=∠AB CD ∴∥DE【分析】本题主要考查了平行线的性质与判定，垂直的定义，根据平行线的性质和判定条件，垂直的定义结合已给推理过程进行证明即可．【详解】证明：（垂直的定义）（同位角相等，两直线平行）（两直线平行，同位角相等）与互余（同角的余角相等）（内错角相等，两直线平行）故答案为：垂直的定义；；同位角相等，两直线平行；两直线平行，同位角相等；同角的余角相等；内错角相等，两直线平行．22. 如图，点B ，E ，C ，F 在一条直线上．（1）过点E 向上作射线，使得；（要求：尺规作图，不写作法，保留作图痕迹）（2）在（1）的条件下，在射线上截取，连接，若，试说明：．【答案】（1）见解析 （2）证明见解析【解析】【分析】此题考查了过一个点作已知直线的平行线，全等三角形的性质和判定，（1）利用尺规作出即可；（2）首先根据题意画出图形，然后由得到，然后证明出，即可得到．【小问1详解】AF CE ⊥ 90CGF ∴∠=︒1D ∠=∠ AF DE ∴∥4CGF ∴∠=∠234180∠+∠+∠=︒ 2390∴∠+∠=︒2∠ C ∠290C ∴∠+∠=︒3C ∴∠=∠AB CD ∴∥DE EM EM AB ∥EM ED BA =FD BE CF =A EDF ∠=∠MEC B ∠=∠BE CF =BC EF =()SAS ABC DEF ≌A EDF ∠=∠如图所示，射线即为所求；【小问2详解】如图所示，∵∴，即∵，∴∴．23. 甲、乙两人从A 地出发，骑自行车沿同一条路行驶到B 地，他们离出发地的距离s （单位：）和行驶时间t （单位：h ）之间的关系的图象如图所示，且甲停止一段时间后再次行走的速度是原来的一半，回答下列问题：（1）求乙的速度；（2）两人相遇时，离B 地的路程是多少千米？【答案】（1）乙的速度为（2）两人相遇时，离B 地的路程是10千米【解析】EM BE CF=BE EC FC EC +=+BC EF =ED BA =MEC B ∠=∠()SAS ABC DEF ≌A EDF ∠=∠km 40km/h 3【分析】本题考查了从函数图象获取信息、一元一次方程的应用，读懂函数图象，正确获取信息是解题关键．（1）根据乙在内骑行了即可得；（2）首先求出，设乙骑行了小时与甲相遇，根据相遇时，两人离出发地的距离相等建立方程，解方程求出的值，由此即可得．【小问1详解】解：乙速度为，答：乙的速度为．【小问2详解】解：甲停止前的速度为，甲停止一段时间后再次行走的速度为，则，设乙骑行了小时与甲相遇，则可列方程为，解得，则，答：两人相遇时，离B 地的路程是10千米．24. 若x 满足，求的值．解：设，则，则请仿照上面的方法求解下面问题：（1）若满足，则的值为；（2）若满足，求的值；（3）已知正方形的边长为x ，E ，F 分别是、上的点，且，长方形的面积是15，分别以、为边作正方形，求阴影部分的面积．的 1.5h 20km ()()2.520881h a =--÷=x x ()()402020.5km/h 3÷-=40km/h 3()80.516km/h ÷=()1628km/h ÷=()()2.520881h a =--÷=x ()40880.53x x =+-34x =40403202010334x -=-⨯=()()944x x --=()()2249x x -+-9,4x a x b -=-=()()944x x ab --==945a b x x +=-+-=()()()22222294252417x x a b a b ab ∴-+-=+=+-=-⨯=x ()()722x x --=()()2272x x -+-n ()()222021202334n n -+-=()240442n -ABCD AD DC 1,3AE CF ==EMFD MF DF【答案】（1）21 （2）64（3）16【解析】【分析】本题考查代数式求值，涉及完全平方公式、整体代入求值等，读懂题意，找准条件与所求代数式的练习，利用完全平方公式变形，整体代入求值即可得到答案．（1）设，，根据材料中的方法，求出和与差，利用完全平方公式代值求解即可得到答案；（2）设，，根据材料中的方法，求出和与差，利用完全平方公式代值求解即可得到答案；由，代值求解即可得到答案；（3）根据题意，得到正方形边长，数形结合得到，设，，利用材料中的方法，求出，代值求解即可得到答案．【小问1详解】解：设，，则，，；故答案：21；【小问2详解】解：，，设，，则，，，即，解得，为7x a -=2x b -=2023n a -=2021n b -=()()()()222404422404420212023n n n n ⎡⎤-=-=-+-⎣⎦()42S x =-影3x a -=1x b -=()228x -=7x a -=2x b -=()()722ab x x =--=()()725a b x x +=-+-=()()()22222272252221x x a b a b ab ∴-+-=+=+-=-⨯=()()222021202334n n -+-= ()()222023202134n n ∴-+-=2023n a -=2021n b -=()()()()2023202120212023ab n n n n =--=---()()202320212a b n n +=-+-=()()()22222202320212n n a b a b ab ∴-+-=+=+-23422ab =-2342152ab --==；，；【小问3详解】解：根据题意可知正方形的边长为，正方形的边长为，正方形的边长为不为负值，，即，，长方形的面积是15，，设，，则，，，即，负值舍去；，阴影部分的面积是．25. 如图，在中，，动点是线段上一点，连接，以为边向右作，使得，连接与交点为．（1）若，则 ， ；（2）点D 在线段上运动的过程中，试说明：是的角平分线．∴()()2021202315n n --=()()()()222404422404420212023n n n n ⎡⎤-=-=-+-⎣⎦ ∴()()22224044223421564n b a a b ab -=-=+-=+⨯=GFDH 3x -MFRN 1x - GFDH 3x -30x ∴->3x >()()()221342MFRN GFDH S S S x x x ∴=-=---=-影正方形正方形 EMFD ∴()()1315EMFD S x x =--=长方形3x a -=1x b -=()()3115ab x x =---=-()()312a b x x +=-+-=()()()()()2222231244241564x x x a b a b ab ⎡⎤∴-+-=-=-+=+-=+⨯=⎣⎦()228x -=()4216S x ∴=-=影∴16ABC AB AC =D BC AD AD ADE V ,AD AE DAE BAC α=∠=∠=CE DE DE ，，AC M 40α=︒DCA ∠=ACE ∠=BC CM DCE △（3）点在线段上运动的过程中，若是的中线时，如图所示，依照题意补全图形，并说明此时是的高．【答案】（1）； （2）见解析 （3）画图见解析，说明见解析【解析】【分析】本题主要考查了等腰三角形的性质与判定，全等三角形的性质与判定，三角形内角和定理：（1）先由等边对等角和三角形内角和定理求出，再证明，即可得到，（2）根据等边对等角和全等三角形的性质可得，是的角平分线；（3）根据三角形中线的定义和全等三角形的性质得到，根据（2）的结论结合三线合一定理即可得到是的高．【小问1详解】解：∵，∴，∵，∴，又∵，，∴，∴，故答案：；；【小问2详解】证明：∵，∴，∵，∴，∴，∴是的角平分线；【小问3详解】解：补全图形如下：为D BC AD ABC CM DCE △70︒70︒70DCA B ==︒∠∠()SAS ABD ACE ≌70ACE B ==︒∠∠ACE ACB ∠=∠CM DCE △CD CE =CM DCE △40AB AC BAC ==︒，∠180702BACDCA B ︒-===︒∠∠∠DAE BAC α∠=∠=BAD CAE ∠=∠AD AE =AB AC =()SAS ABD ACE ≌70ACE B ==︒∠∠70︒70︒AB AC =B ACB ∠=∠ABD ACE ≌△△ACE B ∠=∠ACE ACB ∠=∠CM DCE △∵是的中线，∴，∵，∴，∴，∵是的角平分线，∴是的高．AD ABC BD CD =ABD ACE ≌△△BD CE =CD CE =CM DCE △CM DCE △。
2007年漳州一中自主招生考试数学试卷
2007 年漳州一中高中自主招生考试数 学 试卷（ 分： 150 分；考 ：120 分 ）的同学：迎你参加本次考 ！ 心 ，专心思虑，耐心解答．祝你成功！答 注意：将答案或解答 程写在答 卷的相 地点上，写在 卷上不得分．一、 （本大 共有10 小 ，每小 4 分，共 40 分．每小 都有A 、B 、C 、D 四个 ，此中有且只有一个 是正确的， 将正确答案的代填写在答 卷中相 的表格内，答 得4 分，答 、不答或答案超 一个的得零分）1.以下运算正确的选项是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（）A. 2ab 3ab5a 2 b 2B. a 2 a 3 a 6C. a 21 (a 0)D. xyxya 22.如 ，点 A 在数 上表示的 数a ， a2 等于⋯⋯⋯⋯⋯⋯⋯（）．．．．．．A –1 0123（第 2 题图）A. a 2B. a2C.a 2D.a 23.甲、乙两名运 在10次的百米跑 中，均匀成 分x 甲 ＝10.7 秒， x 乙 ＝10.7 秒，方差分S 甲20.054 ， S 乙2 0.103 ，那么在 次百米跑 中，甲、乙两名运 成 定的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（ ）A. 甲运B. 乙运C.甲、乙两人一 定D.没法确立4.如 ， A 、 B 、 C 、 D 是直 l 上 次四点， M 、 N 分 是 AB 、 CD 的中点，且 MN 6 cm ，BC 1 cm ， AD 的 等于⋯⋯⋯⋯⋯⋯⋯⋯（）． ． ．．．．lAMBCND（第 4 题图）A. 10 cmB. 11cmC.12 cmD. 13 cm5. 已知等腰三角形的一个外角等于140 ，个三角形的三个内角的度数分 是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（）A. 20 、20 、140B. 40 、40 、100C. 70 、70 、40D. 40 、40 、100 或 70 、70 、406.如 ，点 A 在函数 y6(x 0) 的 象上， 点yxA 作 AE 垂直 x ，垂足 E ， 点 A 作 AF 垂直 y，垂足 F ， 矩形 AEOF 的面 是⋯⋯（ AF）A. 2B. 3EOxC. 6D. 不可以确立（第 6 题图）7.用大小和形状完整同样的小正方体木 搭成一个几何体，使得它的正 和俯 如 所示， 搭成 的一个几何体起码需要小正方体木 的个数 ⋯⋯⋯⋯⋯⋯（ ）A.22个B. 19个C. 16个D. 13个（正视图） （俯视图）（第 7 题图）8. 用 半 径 6cm 、 心 角 120 的 扇 形 做 成 一 个的 面 ,个的 底 面 半 径是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯（ ）A. 2 cmB. 3cmC. 4 cmD. 6 cm9.若 n 整数， 能使n1也 整数的 n 的个数有 ⋯⋯⋯⋯⋯⋯⋯⋯（）n 1A.1 个B.2 个C.3 个D.4 个10.已知 a 数， 代数式27 12a2a 2 的最小 ⋯⋯⋯⋯⋯⋯（）A. 0B. 3C.3 3D.9二、填空 （本大 共有6 小 ，每小4 分，共 24 分． 将正确的答案直接填写在答 卷中相的横 上）⋯x 2．11.函数 y的自 量 x 的取 范 是x 112.分解因式：3x 3 y 27 xy．GF13.把 2007 个 1的正方形排成如右 所示的形， 个 形的周 是．（第 13题图）ADE14.如 ，正方形ABCD 的 4 cm ，正方形 AEFG的 1cm ．假如正方形 AEFG 点 A 旋 ，那么BCC 、 F 两点之 的最小距离cm ．（第 14 题图）15.若 定：①m 表示大于 m 的最小整数，比如：3 4 ，2.4 2 ；② m 表示不大于 m 的最大整数，比如：55， 3.64 .使等式 2 xx4 建立的整数 x．．．16.如 ， E 、 F 分 是AB CD 的 AB 、CD 上AEB的点， AF 与 DE 订交于点 P ， BF 与 CE 订交于P点 Q ，若 S △APD 15 cm 2， S △BQC 25 cm 2 ，QDC暗影部分的面cm 2．F（第 16 题图）三、解答 （本大 共有 7 小 ，共 86 分．此中第 17 8 分，第 18、 19 各 10 分，第 20 12 分，第21 题14 分，第22、23题各16 分．请将解答过程写在答题卷的相应地点上）17.计算：( 2)03tan 30 3 2.124x18.先化简，再求值：x 2÷，此中 x2 4 .x 2x219.将反面同样，正面分别标有数字1、 2 、 3 、 4 的四张卡片洗匀后，反面向上放在桌面上.（ 1）从中随机抽取一张卡片，求该卡片正面上的数字是偶数的概率；（ 2）先从中随机抽取一张卡片（不放回），将该卡片正面上的数字作为十位上的数字；再随机抽取一张，．．．将该卡片正面上的数字作为个位上的数字，则构成的两位数恰巧是 4 的倍数的概率是多少？请用树状图或列表法加以说明.20.为配合我市“创卫”工作，某中学选派部分学生到若干处公共场所参加义务劳动．若每处安排10人，则还剩 15人；若每处安排14 人，则有一处的人数不足14人，但许多于 10人．求这所学校选派学生的人数和学生所参加义务劳动的公共场所个数.21.如图，四边形ABCD 是正方形，点 N 是 CD A M D的中点， M 是 AD 边上不一样于点A、 D的点，若 sin ABM10NMBMBC .N ，求证 :10B C(第 21题图)22.如图，抛物线的极点坐标是(1)求该抛物线的分析式；5，－ 9，且经过点 A( 8 ,14 ) . 28(2)设该抛物线与y轴订交于点B，与x轴订交于C、D两点（点C在点D的左侧），试求点 B、C、 D的坐标；y．(3)设点P是x轴上的随意一点，分别连接AC、 BC．A试判断： PA PB 与 AC BC 的大小关系，并说明原因.BO C D x(第 22题图)23.如图，AB是⊙ O 的直径，过点 B 作⊙O的切线 BM ，点 P 在右半圆上挪动（点 P 与点 A 、B 不重合），过点 P 作 PC ⊥ AB ，垂足为 C ；点Q在射线 BM上挪动（点M在点B 的右侧），且在挪动过程中保持 OQ ∥AP.(1)若PC、QO的延伸线订交于点 E ，判断能否存在点P ，使得点 E 恰幸亏⊙O上？若存在，求出APC 的大小；若不存在，请说明原因；(2)连接AQ交PC于点F，设k PF，试问： k 的值能否随点 P 的挪动而变化？PC证明你的结论．AEO．C F PB Q M（第 23 题图）。
福建省漳州第一中学2023届高三下学期期初考试数学试题(含答案解析)
福建省漳州第一中学2023届高三下学期期初考试数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知集合{{23},A x x B x y =∈-<==Z∣∣ ，则A B = （）A ．{}2,1,0,1,2--B ．{}1,2C ．[]2,e -D ．(]0,e 2．已知角α的顶点与坐标原点O 重合，始边与x 轴的非负半轴重合．若角α终边上一点P 的坐标为2π2πcos ,sin 33⎛⎫ ⎪⎝⎭，则sin tan αα=（）A ．32-B ．C ．2D ．323．下列结论中，错用基本不等式做依据的是（）A ．a ，b 均为负数，则222a b b a+≥．B 22≥．C ．4sin 4sin x x+≥．D ．()3R ,310a a a +⎛⎫∈--≤ ⎪⎝⎭．4．我国有着丰富悠久的“印章文化”，古时候的印章一般用贵重的金属或玉石制成，本是官员或私人签署文件时代表身份的信物，后因其独特的文化内涵，也被作为装饰物来使用.图1是明清时期的一个金属印章摆件，除去顶部的环以后可以看作是一个正四棱柱和一个正四棱锥组成的几何体，如图2.已知正四棱柱和正四棱锥的高相等，且底面边长均为4，若该几何体的所有顶点都在同一个球面上，则这个球的表面积是（）图1图2A ．12πB ．24πC ．36πD ．48π5．下列结论正确的是（）A ．若A ，B ，C 是一组两两相互独立的事件，则()()()()P ABC P A P B P C =B ．若A ，B 事件满足()()1P A P B +=，则A ，B 是对立事件C ．若A ，B 是互斥事件，则()1P A B = D ．“A ，B 是互斥事件”是“A ，B 是对立事件”的充分不必要条件6．已知非零向量,a b的夹角正切值为，且()()32a b a b +⊥- ，则a b= （）A ．2B ．23C ．32D ．17．已知等比数列{}n a 中，0n a >，其前n 项和为n S ，前n 项积为n T ，且248S =，460S =，则使得1n T <成立的正整数n 的最小值为（）A ．9B ．10C ．11D ．128．设1sin 11a =，ln1.1b =，1c -，则（）A ．c b a<<B ．a b c<<C ．a c b<<D ．c a b <<二、多选题9．下列结论正确的是（）A ．若随机变量X 服从两点分布，1(1)2P X ==，则1()2D X =B ．若随机变量Y 的方差()2D Y =，则(32)8D Y +=C ．若随机变量ξ服从二项分布14,2B ⎛⎫⎪⎝⎭，则1(3)4P ξ==D ．若随机变量η服从正态分布()25,N σ，(2)0.1P η<=，则(28)0.8P η<<=10．关于函数1()sin 2sin 2f x x x=+，下列说法正确的是（）A ．()f x 的最小值为2B ．π()2f x +是奇函数C ．()f x 的图象关于直线π4x =对称D ．()f x 在π(0,)4上单调递减11．设抛物线2:2(0)C y px p =>的焦点为F ，O 为坐标原点，直线:220l x y p --=与C 交于A ，B 两点，以AB 为直径的圆与y 轴交于D ，E 两点，则（）A ．||3AB p =B．||DE =C ．DFE ∠是钝角D ．DEF 的面积小于OAB 的面积12．已知函数()()11e x f x x -=-，则（）A ．曲线()y f x =在点（1，0）处的切线方程为10x y --=B ．()f x 的极小值为1e-C ．当323e 2e 2a ≤<时，()()2f x a x <-有且仅有一个整数解D ．当2213e 2ea ≤<时，()()2f x a x <-有且仅有一个整数解三、填空题13．已知3i1ia ++（i 为虚数单位，a ∈R ）为纯虚数，则=a ____________．14．如图，在正三棱柱111ABC A B C -中，13AA =，2AB =，则异面直线1A B 与1B C 所成角的余弦值为______．15．单位圆中，AB 为一条直径，,C D 为圆上两点且弦CDAC BD ⋅的取值范围是___________.16．已知函数()f x 的定义域为R ，()()()()2f x y f x y f x f y ++-=⋅对任意的,x y ∈R 恒成立，若()112f =，则20231()n f n =∑=__________四、解答题17．已知数列{}n a 的前n 项和为n S ，且满足11a =，121nn S a n+=-，(1)求数列{}n a 的通项公式；(2)若数列2,4,n n nn C a n ⎧=⎨+⎩为奇数为偶数，求数列{}n C 的前2n 项和2n T ．18．在①cos sin c A C =；②()(sin sin )()sin a b A B c C -+=-；③3cos cos b A a B c ++这三个条件中任选一个，补充在下面的问题中，并解决该问题．问题：在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且满足___________．(1)求角A 的大小；(2)若D 为线段CB 延长线上的一点，且2,CB BD AD AC ===，求ABC 的面积．19．已知三棱柱111ABC A B C -，侧面11AAC C 是边长为2的菱形，13CAA π∠=，侧面四边形11ABB A 是矩形，且平面11AA C C ⊥平面11ABB A ，点D 是棱11A B的中点．(1)在棱AC 上是否存在一点E ，使得AD ∥平面11B C E ，并说明理由；(2)当三棱锥11B A DC -11AC D 与平面1CC D 夹角的余弦值．20．2021年5月12日，2022北京冬奥会和冬残奥会吉祥物“冰墩墩”、“雪容融”亮相上海展览中心.为了庆祝吉祥物在上海的亮相，某商场举办了赢取冰墩墩、雪容融吉祥物挂件答题活动.为了提高活动的参与度，计划有13的人只能赢取冰墩墩挂件，另外23的人既能赢取冰墩墩挂件又能赢取雪容融挂件，每位顾客若只能赢取冰墩墩挂件，则记1分，若既能赢取冰墩墩挂件又能赢取雪容融挂件，则记2分，假设每位顾客能赢取冰墩墩挂件和赢取雪容融挂件相互独立，视频率为概率.(1)从顾客中随机抽取3人，记这3人的合计得分为X ，求X 的分布列和数学期望；(2)从顾客中随机抽取n 人()*N n ∈，记这n 人的合计得分恰为1n +分的概率为n P ，求1nii p=∑21．已知双曲线Γ：2222=1(0,0)a x y a b b ->>的焦距为4，且过点P ⎛ ⎝⎭(1)求双曲线Γ的方程；(2)过双曲线Γ的左焦点F 分别作斜率为12,k k 的两直线1l 与2l ，直线1l 交双曲线Γ于,A B 两点，直线2l 交双曲线Γ于,C D 两点，设,M N 分别为AB 与CD 的中点，若121k k -⋅=，试求OMN 与FMN △的面积之比.22．已知函数()e (1)x f x a a x =--．(1)讨论()f x 的单调性；(2)当a ＝1时，若函数()e (ln )t y f x x t =-+有两个零点，求实数t 的取值范围．参考答案：1．B【分析】求出集合A 中元素，注意它是由整数构成的集合；集合B 是函数y =的定义域，注意真数要大于0，最后求交集.【详解】{}{}{Z23}2,1,0,1,2,ln 1{0e}A x x B x x x x =∈-≤<=--=≤=<≤∣∣∣所以{}1,2A B = .故选：B.2．A【分析】计算得到122P ⎛⎫- ⎪⎝⎭，在根据三角函数定义计算得到答案.【详解】2π2πcos ,sin33P ⎛⎫ ⎪⎝⎭，即122P ⎛⎫- ⎪⎝⎭，则sin 2α==，tan yxα==故3sin tan 2αα=-.故选：A 3．C【分析】根据均值不等式解题必须满足三个基本条件：“一正，二定、三相等”，可知选项ABD 不符合要求，而选项C ，只需要举反例（不满足“一正”）即可判断其符合要求．【详解】对于A ，因为a ，b 均为负数，所以20,02a bb a>>，所以222a b b a +≥，当且仅当22a b b a =，即2b a =时，等号成立，所以222a b b a+≥，故A 不符合要求；对于B 10≥>22=≥=，=0x =时，等号成立，22≥，故B 不符合要求；对于C ，当sin 1x =-时，44sin 154sin 1x x +=-+=-<-，显然是因为不满足“一正”导致的错误，故C 符合要求；对于D ，因为R a +∈，所以()393133620a a a a ⎛⎫⎛⎫--=+-+≤- ⎪ ⎪⎝⎭⎝⎭，当且仅当9a a=，即3a =时，等号成立，所以()3310a a ⎛⎫--≤ ⎪⎝⎭，故D 不符合要求.故选：C ．4．C【分析】结合勾股定理求得球的半径，进而求得球的表面积.【详解】底面边长为4，底面的对角线长为设正四棱柱和正四棱锥的高为h ，外接球的半径为R ，则222222h R h R h ⎧⎛⎫⎛⎫⎪+= ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎨⎪=+⎪⎩，解得2,3h R ==，所以外接球的表面积为24π336π⨯=.故选：C 5．C【分析】根据互斥事件与对立事件的概念对各个选项一一判断即可得出答案.【详解】对于选项A ，例如，从1，2，3，4中随机选出一个数字，记事件A 为“选出的数字为1或2”，事件B 为“选出的数字为1或3”，事件C 为“选出的数字为1或4”，则事件AB ，AC ，BC ，ABC 同时发生的事件为“选出的数字为1”，因为()()()12P A P B P C ===，()()()()14P AB P AC P BC P ABC ====，所以()()()P AB P A P B =，()()()P AC P A P C =，()()()P BC P B P C =，故A ，B ，C 是一组两两独立的事件，但是()()()()P ABC P A P B P C ≠，A 不正确.对于选项B ，例如，投掷一枚质地均匀的骰子，记事件A 为“点数为1，2，3”，事件B 为“点数为2，4，6”，则()()11122P A P B +=+=，但是A ，B 不是对立事件，B 不正确.对于选项C ，因为A ，B 是互斥事件，所以A B ⋃为必然事件，则()1P A B = ，C 正确.对于选项D ，互斥事件不一定是对立事件，对立事件一定是互斥事件，所以“A ，B 是互斥事件”是“A ，B 是对立事件”的必要不充分条件，D 不正确.故选：C.6．D【分析】先求出非零向量,a b的夹角余弦值，再利用向量数量积的运算律和定义处理()()32a b a b +⊥-，即可得到答案.【详解】解析设a ，b 的夹角为θ，由tan θ=1cos 5θ=.因为()()32a b a b +⊥- ，所以()()222232253230a b a b a a b b a a b b +⋅-=+⋅-=+-= ，得22230a ab b+-= ，解得1ab =或32a b=- （舍去）.故选：D.7．D【分析】根据等比数列的通项关系，求得1,a q ，从而得n a ，于是有n T ，解不等式即可.【详解】解：因为248S =，460S =，所以12123448,60a a a a a a +=+++=，即12344812a a a a +=⎧⎨+=⎩，则()2341212a a a a q +=+=，214q ∴=，12q ∴=或12q =-，又0n a >，12q ∴=，1113482a a q a ∴+==，132a ∴=，则16113222n n n a --⎛⎫⎛⎫=⨯= ⎪⎪⎝⎭⎝⎭，()115462121111222n n n n n T a a a ---+-⎛⎫⎛⎫⎛⎫===<= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭，则()1102n n ->，得11n >，则min 12n =.选选：D.8．B【分析】根据题意，先构造函数()sin f x x x =-，比较111a <，再构造函数1()ln (1g x x x=--，通过求导，判断单调性，比较111与ln1.1b =的大小，最后构造函数()ln(1)1h x x =+-，进而确定b 与c 的大小关系，从而得出结果.【详解】令()sin f x x x =-，则()cos 10f x x '=-<，所以()f x 在(0,)+∞上单调递减，所以sin x x <，也即11sin1111<，令1()ln (1)g x x x =--，则()22111x g x x x x='-=-，当(0,1]x ∈时，()0g x '<，函数()g x 单调递减；当1x >时，()0g x '>，函数()g x 单调递增，所以()(1)0g x g ≥=，故当1x >时有1ln 1x x>-，所以111ln1.11sin 1.11111b a =>-=>=，令()ln(1)1h x x =++，则(0.1)b c h -=，因为1()1h x x '=-+当0x ≥时，1x +=≥，所以()0h x '≤，函数()h x 在[0,)+∞上单调递减，所以(0.1)(0)0h h <=，也即0b c -<，所以b c <，故a b c <<，故选：B.9．CD【分析】根据两点分布、二项分布、正态分布以及方差的性质，对每个选项进行逐一分析，即可判断和选择.【详解】对A ：若随机变量X 服从两点分布，1(1)2P X ==，则()D X =1111224⎛⎫⨯-= ⎪⎝⎭，故A 错误；对B ：若随机变量Y 的方差()2D Y =，则(32)D Y +=()918D Y =，故错误；对C ：若随机变量ξ服从二项分布14,2B ⎛⎫ ⎪⎝⎭，则(3)P ξ==31341111224C ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭，故正确；对D ：若随机变量η服从正态分布()25,N σ，(2)0.1P η<=，则(8)0.1P η>=，故(28)1(2)(8)0.8P P P ηηη<<=-<->=，故正确.故选：CD.10．BCD【分析】根据sin 2x 的范围，三角函数的奇偶性、对称性、单调性对选项进行分析，从而确定正确答案.【详解】A 选项，由于1sin 21x -≤≤，所以()f x 的值可以为负数，A 选项错误.B 选项，()()ππ11sin 2sin 2π22sin 2ππsin 22f x x x x x ⎡⎤⎛⎫⎛⎫+=++=++⎪ ⎪⎢⎥+⎡⎤⎛⎫⎝⎭⎝⎭⎣⎦+ ⎪⎢⎥⎝⎭⎣⎦1sin 2sin 2x x ⎛⎫=-+ ⎪⎝⎭，所以π2f x ⎛⎫+ ⎪⎝⎭为奇函数，B 选项正确.C 选项，ππ1sin 222πsin 22f x x x ⎡⎤⎛⎫⎛⎫-=-+⎪ ⎪⎢⎥⎡⎤⎛⎫⎝⎭⎝⎭⎣⎦- ⎪⎢⎥⎝⎭⎣⎦()()()11sin π2sin 2sin π2sin 2x x f x x x=-+=+=-，所以()f x 的图象关于直线π4x =对称，C 选项正确.D 选项，ππ0,0242x x <<<<，所以sin 2y x =在区间π0,4⎛⎫⎪⎝⎭上递增，令()sin 20,1t x =∈，()()101g t t t t=+<<，令1201t t <<<，()()()()121212121212111t t t t g t g t t t t t t t ---=+--=，其中1212120,10,0t t t t t t -<-<>，所以()()()()12120,g t g t g t g t ->>，所以()g t 在()0,1上递减，根据复合函数单调性同增异减可知1()sin 2sin 2f x x x=+在π(0,)4上单调递减，D 选项正确.故选：BCD 11．BCD【分析】联立方程，根据韦达定理得到根与系数的关系，计算4AB p =，A 错误；计算圆方程为：()222342x p y p p 骣琪-+-=琪桫，计算得到B 正确；计算0FD FE ⋅< ，得到C正确；24DEF S p =△，22OAB S p =△，D 正确；得到答案.【详解】直线:220l x y p --=过抛物线焦点,02p F ⎛⎫⎪⎝⎭，设()11A x y ，()22,B x y ，则22 220y px x y p ⎧=⎨--=⎩，22304px px -+=，280p ∆=>，122123 4x x p p x x +=⎧⎪⎨=⎪⎩，124AB x x p p =++=，A 错误；AB 中点坐标为3,2M p p ⎛⎫⎪⎝⎭，42AB p r ==，2r p =，圆方程为：()222342x p y p p 骣琪-+-=琪桫，取0x =得到2y p p =±，DE =，B 正确；不妨取0,D p p ⎛⎫ ⎪ ⎪⎝⎭，0,E p p ⎛⎫+ ⎪ ⎪⎝⎭，故21,,022222p p FD FE p p p p p ⎛⎫⎛⎫⋅=--⋅-+=-< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，,,D E F 不共线，故DFE ∠是钝角，C正确；2112224DEF p S DE OF p =⋅=⨯⨯=△，2142OAB S p p =⨯=△，DEF OAB S S <△△，D 正确；故选：BCD 12．ABD【分析】由导数的几何意义求切线方程判断A ，由导数求极值判断B ，利用导数确定函数的性质后结合函数图象判断CD ．【详解】1()e x f x x -'=，(1)1f '=，∴切线方程为1y x =-，即10x y --=，A 正确；0x <时，()0f x '<，()f x 递减，0x >时，()0f x '>，()f x 递增，所以0x =时，()f x 取得极小值1(0)ef =-，B 正确；作出1()(1)e x f x x -=-的图象，再作直线(2)y a x =-，如图，直线(2)y a x =-过定点(2,0)P ，斜率为a ，由2(1)2e (12)f a --=-≥--得223e a ≥，1(0)e (02)f a -=-<-得12e a <，∴在2213e 2ea ≤<时，不等式()(2)f x a x <-只有一个整数解0x =，D 正确；作出1()(1)e x f x x -=-的图象，再作直线(2)y a x =-，如图，直线(2)y a x =-过定点(2,0)P ，斜率为a ，图中为了说明问题对()y f x =的图象进行了放缩处理，由(3)(32)f a =-得22e a =．即22e a =时，直线(2)y a x =-过点(3,(3))f ，3x ≥时，12()e 3e x f x x a -'=≥>，()f x 图象在3x ≥时切线斜率大于a ，因此此时()(2)f x a x >-，2x ≤时，()(2)f x a x >-，()(2)f x a x <-无整数解，C 错、故选：ABD ．【点睛】方法点睛：用导数确定不等式的整数解问题，数形结合是重要的方法，一般是把不等式适当变形，转化为一个固定函数的图象在动直线的一侧，可利用导数确定函数的性质，动直线动起来后观察交点情况，从而可得解的情况．13．3-【分析】根据复数的除法运算法则，化简复数，根据复数的概念即可求解.【详解】()()()()()()3i 1i 33i 33i 3i1i 1i 1i 222a a a a a a +⋅-++--++===+++⋅-因为复数为纯虚数，所以302a +=，3a =-.故答案为：-3.14．713【分析】建立空间直角坐标系，求得相关点坐标，求出向量1A B uuu r ,1B C的坐标,利用向量的夹角公式即可求得答案.【详解】以A 为原点，在平面ABC 内过点A 作AC 的垂线为x 轴，AC 为y 轴，1AA 为z 轴，建立空间直角坐标系，在正三棱柱111ABC A B C -中，13AA =，2AB =，则11(),(),),0,0,00,0,3,0(0,2,0)A A B C B ，故13)A B =-,1(3)B C =-,设异面直线1AB 与1B C 所成角为π,(0,]2θθ∈，所以111113||7c ||os ||B C AB B C AB θ⋅==,∴异面直线1AB 与1B C 所成角的余弦值为713,故答案为：713.15．3322⎡---⎢⎣【分析】由题设()()()(1,0),(1,0),(cos ,sin ),cos 120,sin 120A B C D θθθθ︒-++，再根据数量积坐标运算计算即可.【详解】解：如图，由弦CD120COD ∠=︒，不妨设()()()(1,0),(1,0),(cos ,sin ),cos 120,sin 120A B C D θθθθ︒-++，则()()()(cos 1,sin ),cos 1201,sin 120AC BD θθθθ=+=+-︒+，所以()()(cos 1)cos 1201sin sin 120AC BD θθθθ︒︒⋅=++-++⎡⎤⎣⎦11(cos 1)cos 1sin sin 2222θθθθθθ⎛⎫⎛⎫=+---+-+ ⎪ ⎪⎝⎭⎝⎭33cos 222θθ=---()33360222θ⎡=+-∈--+⎢⎣︒.故答案为：3322⎡---⎢⎣.16．12##0.5【分析】先根据题意求出函数()f x 的周期，求出一个周期内的特殊的函数值，再得出结果即可.【详解】已知()()()()2f x y f x y f x f y ++-=⋅，令1y =，()112f =则()()()()()1121f x f x f x f f x ++-=⋅=，即()()()11f x f x f x +=--.因为()()()()()()()2111f x f x f x f x f x f x f x +=+-=---=--，即()()3f x f x +=-，所以()()()63f x f x f x +=-+=，即函数()f x 的周期为6.令1,0x y ==，()()()21210f f f =⋅，又()112f =，则()01f =，令1y =，()()()11f x f x f x +=--()()()12102f f f =-=-，同理()31f =-，()142f =-，()152f =，()61f =，()20236111()337()12n n f n f n f ===+=∑∑.故答案为：12.17．(1)21n a n =-(2)()22241253nn T n n =-++【分析】（1）利用121nn S a n+=-进行类比作差法即可求解；（2）分组求和，等比数列求和以及等差数列求和方法即可得解.【详解】（1）∵121nn S a n+=-，∴12n n S na n +=-，当2n ≥时，()()1211n n S n a n -=---，∴()1211n n n a na n a +=---，即()111n n na n a +-+=，∴()1111111n n a a n n n n n n +-==-+++，∴112321111111111232121232n n n n a a a a a a n n n n n n n n n----+-++-=-+-++-=------- ，∴21122n a a n n-=-，又当1n =时，1221S a =-，23a =，∴()212n a n n =-≥，又11a =，适合上式，则数列{}n a 的通项公式为21n a n =-；（2）由题意可得，2,23,n n n C n n ⎧=⎨+⎩为奇数为偶数则()()21321242n n n T C C C C C C -=+++++++ ()()()2214743241251423n nn n n n -++=+=-++-，∴()22241253nn T n n =-++．18．(1)条件选择见解析，π6A =【分析】（1）选择①：由正弦定理边化角得方程，求解即可.选择②：由正弦定理角化边得关于三边的方程，代入余弦定理可得.选择③：由正弦定理边化角，再由sin sin()sin cos sin cos C B C B C C B =+=+展开计算可得结果.（2）设BD x =，AB y =，ABD θ∠=，在△ABC 中，由cos ABC ∠、cos CAB 列等式①②，在ABD △中，由cos ABD ∠列等式③，由①②③解方程可得x ，y .代入三角形面积公式可得结果.【详解】（1）若选择①，∵cos sin c A C =．∴sin cos sin C A A C =，∵sin 0C ≠，∴cos sin A A =，即tan 3A =，∵(0,π)A ∈∴π6A =；若选择②，∵()(sin sin )()sin a b A B c C -+=，∴()()()a b a b c c -+=，∴222a b c -=-，∴222a b c =+，222cos 222b c A bc bc a +===-，∵(0,π)A ∈∴π6A =；若选择③，∵3cos cos b A a B c ++，∴3sin cos sin cos sin B A A B B C +=+，∴3sin cos sin cos sin()B A A B B A B +=++，∴3sin cos sin cos sin cos cos sin B A A B B A B A B +=++，∴2sin cos B A B ，又∵(0,π)B ∈．∴sin 0B ≠，∴cos 2A =，∵(0,π)A ∈，∴π6A =；（2）设BD x =，AB y =，ABD θ∠=，在ABC 中，用余弦定理可得2222cos AC BC BA BC BA ABC =+-⋅⋅∠，即2212422cos(π)x y xy θ=+-⨯-①，又∵在ABC 中，2222cos BC AC AB AC AB CAB =+-⋅⋅∠，即224122cos x y CAB =+-⨯∠.即224612x y y =-+，即226124y y x -+=②，在ABD △中，用余弦定理可得2222cos AD BD BA BD BA ABD =+-⋅⋅∠，即2232cos x y xy θ=+-③，③2⨯+①可得226318x y +=，将②式代入上式可得2,1y x ==，1sin 2ABC S AB AC A =⋅⋅= 19．(1)存在，理由见解析【分析】（1）取11B C 的中点F ，连接EF ，DF ，易得//,DF AE DF AE =，则四边形DFEA 是平行四边形，从而AD ∥EF ，再利用线面平行的判定定理证明；（2）根据四边形11ABB A 是矩形，结合平面11AA C C ⊥平面11ABB A ，得到11A B ⊥面11A ACC ，由111111B A DC A A DC D A AC V V V ---==，得到116A B =，再由160A AC ∠=︒，得到1A E AC ⊥，然后以1A 为坐标原点建立空间直角坐标系，求得平面1C DC 的一个法向量为(),,m x y z = ，易知平面11AC D的一个法向量()1,0,0n =r ，由cos ,m nm n m n⋅=⋅求解.【详解】（1）解：存在，当E 为AC 的中点时，AD ∥平面11B C E ，理由如下：如图所示：取11B C 的中点F ，连接EF ，DF ，∵DF 是111A B C △的中位线，∴111111//,22DF AC DF AC =，又111111//,22AE AC AE AC =，∴//,DF AE DF AE =，∴四边形DFEA 是平行四边形，∴AD ∥EF ，又AD ⊄面11B C E ，EF ⊂面11B C E ，∴AD ∥平面11B C E ．（2）∵四边形11ABB A 是矩形，∴111A B AA ⊥，11AB A B ∥，又∵平面11AA C C ⊥平面11ABB A ，∴11A B ⊥面11A ACC ，∵1111111111111132B A DC A A DC D A AC AA C V V V S A B A B ---===⋅⨯==△∴116A B =，∵侧面11ACC A 是菱形，160A AC ∠=︒，∴1A AC △是正三角形，∵E 是AC 的中点，∴1A E AC ⊥，以1A为坐标原点建立如图所示的空间直角坐标系，则()10,0,0A ，()10,2,0C ，()0,0,3D，C ，则()10,2,3C D =-，)11,0C C =- ，设平面1C DC 的一个法向量为(),,m x y z =，由1100m C D m C C ⎧⋅=⎪⎨⋅=⎪⎩，得2300y z y -+=⎧⎪⎨-=⎪⎩，令1x =，则y =，z =∴m ⎛= ⎝ ，又平面11AC D 的一个法向量()1,0,0n =r，∴cos ,m n = ∴平面11AC D 与平面1CC D20．(1)分布列见解析，()5E X =(2)1323123n n ++⎛⎫- ⎪⎝⎭【分析】（1）由X 的取值，计算相应的概率，得到分布列，利用公式计算数学期望；（2）n 人的合计得分恰为1n +分，有且只有1人既能赢取冰墩墩挂件又能赢取雪容融挂件，计算概率，用错位相减法求数列前n 项和.【详解】（1）X 的取值为3，4，5，6所以()3113327P X ⎛⎫=== ⎪⎝⎭，()2132124C 339P X ⎛⎫==⨯⨯= ⎪⎝⎭，()2232145C 339P X ⎛⎫==⨯⨯= ⎪⎝⎭，()3286327P X ⎛⎫=== ⎪⎝⎭.所以X 的分布列为：X3456P1272949827所以()124834565279927E X =⨯+⨯+⨯+⨯=；（2）因为这n 人的合计得分恰为1n +分，则其中有且只有1人既能赢取冰墩墩挂件又能赢取雪容融挂件，所以11212C 333n n nnn P -⎛⎫=⨯⨯=⎪⎝⎭，设122324623333n n n nS P P P =++⋅⋅⋅+=+++⋅⋅⋅+，23411246233333n n nS +=+++⋅⋅⋅+，两式相减得23111111222222223332113333333313n n n n n n n nn S +++⎛⎫- ⎪+⎝⎭=+++⋅⋅⋅+-=⨯-=--，所以1231323123n n n n S P P P P ++⎛⎫=+++⋅⋅⋅+=- ⎪⎝⎭，所以121323123n n n P P P ++⎛⎫++⋅⋅⋅+=- ⎪⎝⎭；21．(1)2213x y -=(2)3【分析】（1）由题意得24c =，再将P ⎛ ⎝⎭代入双曲线方程，结合222c a b =+可求出22,a b ，从而可求出双曲线方程，（2）设直线1l 方程为1(2)y k x =+，1122(,),(,)A x y B x y ，将直线方入双曲线方程化简后利用根与系数的关系，结合中点坐标公式可表示点M 的坐标，再利用121k k -⋅=表示出点N 的坐标，再表示出直线MN 的方程，可求得直线MN 过定点(3,0)E -，从而可求得答案.【详解】（1）由题意得24c =，得=2c ，所以224a b +=，因为点P ⎛ ⎝⎭在双曲线上，所以22413=1a b -，解得223,1a b ==，所以双曲线方程为2213x y -=，（2）(2,0)F -，设直线1l 方程为1(2)y k x =+，1122(,),(,)A x y B x y ，由122=(+2)=13y k x x y -⎧⎪⎨⎪⎩，得2222111(13)121230k x k x k ----=则22111212221112123,1313k k x x x x k k --+==--，所以2121216213x x k k +=-，所以AB 的中点211221162,1313k k M k k ⎛⎫⎪--⎝⎭，因为121k k -⋅=，所以用11k -代换1k ，得1221126,33k N k k ⎛⎫- ⎪--⎝⎭，当212211661313k k k =--，即11k =±时，直线MN 的方程为3x =-，过点(3,0)E -，当11k ≠±时，112211122112211221332663(1)133MNk k k k k k k k k k ----==-----，直线MN 的方程为2111222111226133(1)13k k k y x k k k ⎛⎫-=-- ⎪---⎝⎭，令=0y ，得221122113(1)631313k k x k k -=+=---，所以直线MN 也过定点(3,0)E -，所以12312N M OMN FMN M N y y OE OE S S FE y y FE -===- 22．(1)答案见解析(2)()1,+∞【分析】（1）分1a ≥，01a <<，0a ≤讨论求解即可；（2）由题意可知关于x 的方程()e e ln x t x t =+有两个不同的实根，进而()ln e eln x t x x x t +=+，令()()e 0x g x x x =>，要使()()ln g x g x t =+有两个不同的实根，则需ln x x t =+有两个不同的实根．令()ln h x x x t =--，利用导数法研究()ln h x x x t =--的零点即可【详解】（1）因为()()e 1x f x a a x =--，所以()()e 1x f x a a '=--．当1a ≥时，()0f x ¢>恒成立，所以()f x 在R 上单调递增；当01a <<时，令()0f x '=，得1ln a x a-=，由()0f x ¢>解得1ln a x a ->，由()0f x '<解得1ln a x a-<，所以()f x 在1,ln a a -⎛⎫-∞ ⎪⎝⎭上单调递减，在1ln ,a a -⎛⎫+∞ ⎪⎝⎭上单调递增；当0a ≤时，()0f x '<恒成立，所以()f x 在R 上单调递减．综上可知：当1a ≥时，()f x 在R 上单调递增；当01a <<时，()f x 在1,ln a a -⎛⎫-∞ ⎪⎝⎭上单调递减，在1ln ,a a -⎛⎫+∞ ⎪⎝⎭上单调递增；当0a ≤时，()f x 在R 上单调递减．（2）当1a =时，()e x f x =，则()()()e ln e e ln t x t y f x x t x t =-+=-+，所以关于x 的方程()e e ln 0x t x t -+=有两个不同的实根，即关于x 的方程()e e ln x t x t =+有两个不同的实根．因为x ＞0，所以()ln e eln x t x x x t +=+．令()()e 0x g x x x =>，则()()1e 0x g x x '=+>，所以()g x 在()0,∞+上单调递增．要使()()ln g x g x t =+有两个不同的实根，则需ln x x t =+有两个不同的实根．令()ln h x x x t =--，则11()1x h x x x-'=-=．当()0,1x ∈时，()0h x '<，()h x 单调递减，当()1,x ∈+∞时，()0h x '>，()h x 单调递增，所以()()min 11h x h t ==-．当t ＜1时，()0h x >，()h x 没有零点；当t ＝1时，()0h x ≥，当且仅当x ＝1时，等号成立，()h x 只有一个零点；当t ＞1时，()110h t =-<，()e e 0t t h --=>，()e e 2t t h t =-．令()e 2(1)t t t t ϕ=->，则()e 2e 20t t ϕ'=->->，即()t ϕ在()1,+∞上单调递增，所以()(1)e 20t ϕϕ>=->，即()e 0t h >．所以()h x 在()0,1上有一个零点，在()1,+∞上有一个零点，符合条件．综上，实数t 的取值范围是()1,+∞．【点睛】方法点睛：已知函数有零点(方程有根)求参数值(取值范围)常用的方法：（1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
漳州一中自主招生试卷 2011年漳州一中高中自主招生考
试数学试卷
2011年漳州一中高中自主招生考试数学试卷
1.下列运算正确的是…………………………………………………………( ) A.2ab,3ab 5ab
B.a2 a3 a6
2
2
1
(a 0) D.x,y x,y 2a
2.如图，点A在数轴上表示的实数为a，则a～2等于…………………( )
C.a
～2
1
A
0 –1 1 2 3 (第2题图)
A.a～2
B.a,2
C.～a～2
D.～a,2
4.如图，A、B、C、D是直线l上顺次四点，M、N分别是
AB、CD的中点，且MN 6cm，BC 1cm，则AD的长等于……………………( ) l
A M
B
C N
D (第4题图)
A.10cm
B.11cm
C.12cm
D.13cm
7.用大小和形状完全相同的小正方体木块搭成
一个几何体，使得它的正视图和俯视图如图所示，则搭成这样的一个几何体至少需要小正方体木块的个数为………………( ) A.22个 B.19个 C.16个 D.13个
(正视图)
(俯视图)
(第7题图)
2
8.用半径为6cm、圆心角为120的扇形做成一个圆锥的侧
面, 则这个圆锥的底面半径
是………………………………………………………………
……( ) A.2cm B.3cm C.4cm
D.6cm 9.若n为整数，则能使
…
n,1
也为整数的n的个数有……………………( n～1
A.1个
B.2个
C.3个
D.4个10.已知a为实数，则代数式27～12a,2a2的最小值
为………………( 13 题图) ) (第A.0 B.3 C.33 D.9
x,211.函数y 的自变量x的取值范围是(
x～1
12.分解因式:～3xy,27xy 13.把2007个边长为1的正方形
排成如右图所示的图形，则这个图形的周长
是 ( 14.如图，正方形ABCD的边长
为4cm，正方形AEFG
3
A
F
3
D
(第14题
C
的边长为1cm(如果正方形AEFG绕点A旋转，那么
C、F两点之间的最小距离为(
15.若规定:? m 表示大于m的最小整数，例如: 3 4，～2.4 ～2; 则使等式2 x ～ x 4成立的整数((x ( 16.如图，E、F分别是
BCD的边AB、CD上的点，AF与
DE相交于点P，BF与CE相交于点Q，若S
?
APD
? m 表示不大于m的最大整数，例如: 5 5，
～3.6 ～4.
15cm2，S
?BQC
25cm2，
2
则阴影部分的面积为 cm(。