圆锥曲线的常用结论
圆锥曲线常用的二级结论

圆锥曲线常用的二级结论圆锥曲线是平面上一类特殊的曲线,包括椭圆、双曲线和抛物线。
在数学中,对于圆锥曲线,有一些常用的二级结论,它们的推导和应用具有重要意义。
本文将介绍圆锥曲线常用的二级结论,包括离心率和焦点与直径的关系、切线与法线的性质、以及曲线参数方程等。
一、离心率和焦点与直径的关系对于椭圆和双曲线而言,离心率是一个重要的参数,它描述了曲线的扁平程度。
对于椭圆而言,离心率的取值范围是0到1之间,而对于双曲线而言,离心率大于1。
离心率和焦点与直径之间存在着紧密的关系。
对于任意一点P在椭圆或双曲线上,假设焦点为F,直径为D,那么有以下结论:1. 离心率与焦点到点P的距离与直径之间的关系:离心率e等于焦点到点P的距离PF与直径D的比值,即e=PF/AD,其中AD为直径D 的长度;2. 焦点到点P的两条切线的夹角等于直径与椭圆或双曲线的短轴之间的夹角;3. 过焦点F的切线与过点P的切线的交点为曲线上的另一点P',那么点P与点P'到直径D的距离之比等于焦点到点P的距离与焦点到点P'的距离之比。
二、切线与法线的性质曲线上的每一点都可以有一条切线和一条法线,它们有一些重要的性质。
1. 切线与曲线的斜率之积等于-1,即两者是互相垂直的;2. 切线的斜率等于曲线在该点的导数,法线的斜率等于切线的负倒数;3. 曲线上任意一点的切线与法线的交点即为该点在曲线上的坐标。
三、曲线的参数方程曲线的参数方程是描述曲线上每一点的坐标的函数。
对于圆锥曲线而言,它们都可以用参数方程表达。
1. 椭圆的参数方程为:x = a*cosθ,y = b*sinθ,其中a和b分别为椭圆的长轴和短轴的长度,θ为参数;2. 双曲线的参数方程为:x = a*coshθ,y = b*sinhθ,其中a和b分别为双曲线的长轴和短轴的长度,θ为参数;3. 抛物线的参数方程为:x = a*t,y = b*t^2,其中a和b分别为抛物线的参数,t为参数。
圆锥曲线常用结论

圆锥曲线一椭圆1椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).2:点00(,)P x y 和椭圆12222=+by a x (0a b >>)的关系:(1)点00(,)P x y 在椭圆外⇔2200221x y a b +>;(2)点00(,)P x y 在椭圆上⇔220220by a x +=1;(3)点00(,)P x y 在椭圆内⇔2200221x y a b+<。
3:圆锥曲线焦点位置的判断(首先化成标准方程,然后再判断)(1)椭圆:由x2,y2母的大小决定,焦点在分母大的坐标轴上。
如已知方程12122=-+-my m x 表示焦点在y 轴上的椭圆,则m 的取值范围是())23,1(1,⋃-∞-(2)双曲线:由x2,y 2项系数的正负决定,焦点在系数为正的坐标轴上;(3)抛物线:焦点在一次项的坐标轴上,一次项的符号决定开口方向。
4;设椭圆()222210x y a b a b+=>>的左焦点、右焦点分别为1F 、2F ,点P 在椭圆上,122F PF θ∠=,求证:θcos 12221+=b PF PF 且12PF F ∆的面积2tan S b θ=。
解:设1PF m =,2PF n =,则1sin 22S mn θ=,又122F F c =,由余弦定理()22222cos 2c m n mn θ=+-=()222cos m n mn mn θ+--=()()2221cos 2a mn θ-+,于是()2221cos244mn a c θ+=-=24b,所以221cos 2b mn θ=+,从而有212sin 221cos2b S θθ=⋅⋅+=2tan b θ。
5:从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上。
圆锥曲线的常用二级结论

圆锥曲线的常用二级结论圆锥曲线是由平面上一固定点(焦点)和一条固定直线(准线)构成的几何图形。
它们包括椭圆、双曲线和抛物线。
在学习圆锥曲线的过程中,常用的二级结论有以下几个:一、椭圆的性质1. 椭圆的离心率小于1:椭圆是由一个固定点(焦点)到平面上所有点到另一个固定点(焦点)的距离之和等于一个常数的所有点构成的集合。
这个常数就是椭圆的长轴长度,而短轴长度等于长轴长度乘以离心率。
因此,椭圆的离心率小于1。
2. 椭圆的两个焦点在长轴上:椭圆的两个焦点与长轴垂直,并且它们都在长轴上。
3. 椭圆是对称图形:椭圆具有对称性,即如果将它绕着中心旋转180度,它仍然保持不变。
4. 椭圆的周长公式:设椭圆长轴为2a,短轴为2b,则椭圆周长公式为C=π(a+b)。
二、双曲线的性质1. 双曲线的离心率大于1:双曲线是由一个固定点(焦点)到平面上所有点到另一个固定点(焦点)的距离之差等于一个常数的所有点构成的集合。
这个常数就是双曲线的长轴长度,而短轴长度等于长轴长度乘以离心率。
因此,双曲线的离心率大于1。
2. 双曲线有两条渐近线:双曲线有两条渐近线,它们与双曲线趋近于无限远时重合。
3. 双曲线不具有对称性:与椭圆不同,双曲线不具有对称性。
4. 双曲线的渐近线方程:设双曲线方程为x^2/a^2-y^2/b^2=1,则它的两条渐近线方程分别为y=±(b/a)x。
三、抛物线的性质1. 抛物线是对称图形:抛物线具有轴对称性,即如果将它绕着轴旋转180度,它仍然保持不变。
2. 抛物线焦点和准线相等距离:抛物线是由平面上所有点到一条直线(准线)的距离等于这些点到一个固定点(焦点)的距离的所有点构成的集合。
它的焦点和准线相等距离。
3. 抛物线方程:设抛物线方程为y=ax^2+bx+c,则它的焦点坐标为(-b/2a,1/4a),准线方程为y=-1/4a。
4. 抛物线与直线交点坐标:如果抛物线与直线y=kx+m相交,则交点坐标为(x,y)=(k^2a+bk+c-m,-ka^2-kb+m)。
圆锥曲线常用的二级结论

圆锥曲线常用的二级结论圆锥曲线是数学中重要的概念之一,它们的性质和应用广泛存在于各个领域中。
在研究圆锥曲线时,我们常常需要掌握一些基本的二级结论。
本文将介绍一些圆锥曲线常用的二级结论,帮助读者更好地理解和应用这些曲线。
第一,圆是一种特殊的圆锥曲线。
圆的定义是所有离中心点相等距离的点组成的图形。
它的二级结论包括:直径是圆的最长线段,圆的周长公式为C=2πr,其中r为半径;圆的面积公式为A=πr^2,其中r为半径。
第二,椭圆是另一种常见的圆锥曲线。
椭圆的定义是所有离两个焦点之和相等的点组成的图形。
它的二级结论包括:焦距的定义为两个焦点之间的距离,椭圆的离心率定义为焦距与长轴长度的比值,离心率小于1时为椭圆;椭圆的周长和面积的计算公式与圆不同,需要通过积分等方法求解。
第三,双曲线是圆锥曲线中的另一个重要概念。
双曲线的定义是所有离两个焦点之差相等的点组成的图形。
它的二级结论包括:焦距的定义与椭圆相同,双曲线的离心率定义为焦距与长轴长度的比值,离心率大于1时为双曲线;双曲线的周长和面积的计算公式也与圆不同,需要通过积分等方法求解。
第四,抛物线是圆锥曲线中的另一类。
抛物线的定义是所有离焦点距离等于焦距的点组成的图形。
它的二级结论包括:焦距的定义与椭圆和双曲线不同,抛物线的焦距等于焦点到准线的垂直距离;抛物线的顶点是曲线的最高点或最低点;抛物线的标准方程为y^2=4ax,其中a为焦距。
综上所述,圆锥曲线常用的二级结论包括圆、椭圆、双曲线和抛物线的定义、性质和计算公式等。
通过掌握这些结论,我们可以更好地理解和应用圆锥曲线,在数学和实际问题中更加准确地计算和分析相关情况。
希望本文能对读者有所帮助,更深入地了解圆锥曲线的奥妙。
高考必背经典结论(圆锥曲线)

椭圆与双曲线的对偶性质--(必背的经典结论)椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2. PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5. 若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y y a b +=.6. 若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y y a b +=. 7. 椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8. 椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P和A 1Q 交于点N ,则MF ⊥NF.11. AB 是椭圆22221x y a b+=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a x b K AB -=。
12. 若000(,)P x y 在椭圆22221x y a b +=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b +=+.13. 若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y y x y a b a b +=+.双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2. PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4. 以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5. 若000(,)P x y 在双曲线22221x y a b -=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y y a b -=.6. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=.7. 双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PF S b co γ∆=.8. 双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c - , 2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9. 设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10. 过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11. AB 是双曲线22221x y a b -=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
圆锥曲线常用的二级结论和椭圆与双曲线对偶结论

圆锥曲线常用的二级结论:
1.零点定理:设F1,F2为椭圆E的两个焦点,P为椭圆上一点,则PF1 + PF2 = 2a(a
为椭圆长轴的一半);对于双曲线,PF1 - PF2 = 2a,其中a为双曲线的长轴的一半。
2.切线定理:设点P(x0,y0)在曲线C上,则C在点P处的切线方程为F_x(x0,y0)
x + F_y(x0,y0)y = F(x0,y0),其中F(x,y)为曲线C的方程,F_x和F_y为它的偏导数。
3.法线定理:设点P(x0,y0)在曲线C上,则C在点P处的法线方程为F_y(x0,y0)
x - F_x(x0,y0)y = F_y(x0,y0)x0 - F_x(x0,y0)y0。
4.离心率计算公式:设椭圆E的长轴为a,短轴为b,则椭圆的离心率为e = √(a² - b²)
/ a。
5.弦长定理:对于椭圆E,设以焦点F1,F2为端点的弦所对应的直角顶点为P,则弦PF1
+ PF2的长度等于椭圆长轴的长度;对于双曲线,弦PF1 - PF2的长度等于双曲线长轴的长度。
椭圆与双曲线的对偶结论:
1.椭圆E的对称中心为它所包围的正方形的中心,长、短半轴分别为正方形的对角线之
一和另外一边。
2.椭圆的纵轴端点为它所包围正方形的中心连通它上下角的一条直线,椭圆的焦点在这
条直线上。
3.双曲线的渐近线为对应椭圆的渐近线的转置。
4.对于椭圆E的焦点F和双曲线H的焦距f,有e² = 1 + f² / b²。
把椭圆的参数a,b
换成双曲线的参数a,b,即可得到双曲线的离心率计算公式。
有关圆锥曲线的经典结论

一、椭 圆1.点P 处的切线PT 平分△ PFF 2在点P 处的外角.2.PT 平分△ PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆, 的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离2 2X y8.椭圆—务 1 ( a > b > 0)的焦半径公式:I MF j I a eX) , | MF 2 | a b F 2(G 0)M (X o , y o )).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结 AP 和AQ 分别交相应于焦点F 的椭圆准线于 M N 两点,贝y MFL NF.二、双曲线1.点P 处的切线 PT 平分△ PF1F2在点P 处的内角.2.PT 平分△ PF1F2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3.以焦点弦PQ 为直径的圆必与对应准线相交4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相除去长轴4. 以焦点半径PF 为直径的圆必与以长轴为直径的圆内切x25. 若P o (X o , y o )在椭圆—a2X 2爲 1上,则过F 0的椭圆的切线方程是 竽ba2笃 1外,则过Po 作椭圆的两条切线切点为by o y 1 P 、P 2, 则切点弦 PP2的直线方程是竽a27.椭圆务ay o yb 22*1 1. (a >b >0)的左右焦点分别为F i , F 2,点P 为椭圆上任意一点F 1PF 2,则椭圆的焦点角形的面积为2S F1 PF2bt 形.a ex o ( F i ( c,0),10.过椭圆一个焦点 F 的直线与椭圆交于两点P Q, A i 、A 为椭圆长轴上的顶点, A i P 和AQ 交于点M AP和AQ 交于点N,则2 211.AB 是椭圆笃与 a 2 b 2KK AB2MFX NF.1的不平行于对称轴的弦,M (X o ,y o )为AB 的中点,则k OM kABb 2 a12.若 F 0(x o , y o )在椭圆 2X —2 a 2込 1内,则被Po 所平分的中点弦的方程是 2 b aX o X b 2 2 X o 2a 2b 213.若 Rdo, y o )在椭圆 2 2 鶴 1内,则过Po 的弦中点的轨迹方程是 b a 2 y2X o X ~2~ay o y b 2切.(内切:P在右支;外切:P在左支)有关解析几何的经典结论5.若P 0(x 0,y 0)在双曲线6.若P o (X o , y o )在双曲线 点弦P i P 2的直线方程是 2 Xp a2 X p a X 0X a2y_ 1 b 212r 1 b 21y 0y (a > 0,b > 0)上,则过P 0的双曲线的切线方程是X 0X —2a (a >0,b >0) 外,则过Po 作双曲线的两条切线切点为 1.2 27.双曲线—2 ^2 1 ( a > 0,b > 0)的左右焦点分别为 F 1,F 2,点 a b P 为双曲线上任意一点 则双曲线的焦点角形的面积为 S F I PF 2 叽. y 0y 1P i 、P 2,则切F 1PF 22 28.双曲线—2 ^2 1 ( a > 0,b > 0) ab当M (X 0, y 0)在右支上时,当M(X 0,y 0)在左支上时, 的焦半径公式: | MF 1 | eX 0 | MF 1 | eX 0 (F i ( c,0), F 2(C ,0) a . a , | MF 21 eX 0 a , | MF 2 | eX 0 a9.设过双曲线焦点 F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结 AP 和AQ 分别交 相应于焦点F 的双曲线准线于 M N 两点,贝y MFI NF. 10.过双曲线一个焦点 F 的直线与双曲线交于两点 P 、Q, A 1、A 为双曲线实轴上的顶点,A i P 和AaQ 交于点 M AP 和AQ 交于点N,贝U MF1 NF. 11.AB 是双曲线 K OM KAB 2 X —2 a b 2X 01 ( a > 0,b > 0)的不平行于对称轴的弦, M (X 0,y 0)为 AB 的中点,则2 a y 。
圆锥曲线常用的二级结论(非常实用)
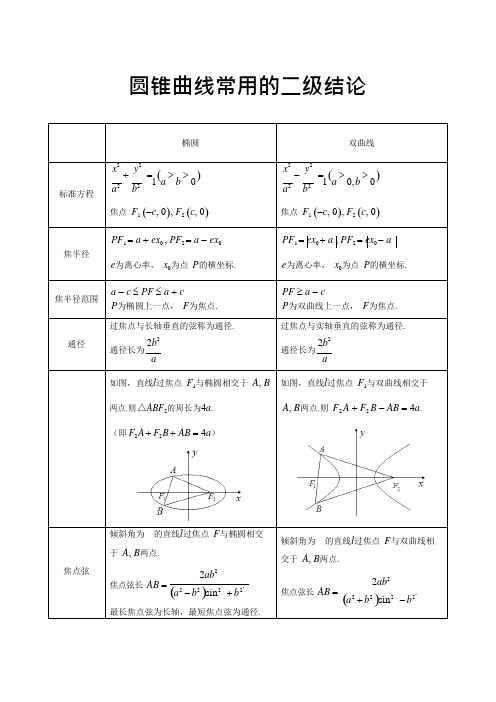
圆锥曲线常用的二级结论如图,直线l过焦点F1与椭圆相交于A, B 两点.则△ABF2的周长为4a.(即F2 A +F2 B +AB = 4a)如图,直线l过焦点F1与双曲线相交于A, B两点.则F2A +F2B -AB = 4a.倾斜角为的直线l过焦点F与椭圆相交于A, B两点.2ab2焦点弦长AB =(a2-b2)sin2+b2.最长焦点弦为长轴,最短焦点弦为通径. 倾斜角为的直线l过焦点F与双曲线相交于A, B两点.2ab2焦点弦长AB =(a2+b2)sin2-b2.. .AF与BF 数量关系直线l过焦点F与椭圆相交于A, B两点,1 1 2a则+=.AF BF b2直线l过焦点F与双曲线相交于A, B两点1 1 2a,则+=.AF BF b2已知点P是椭圆上一点,O坐标原点,则b ≤PO ≤a.已知点P是双曲线上一点,O坐标原点,则PO ≥a.焦三角形如图,P是椭圆上异于长轴端点的一点,已知∠F1PF2 =,∠PF1F2 =,∠PF2F1=,则(1)S =b2 tan;△PF1F2 2sin(2)离心率e =.sin+ sin如图,P是双曲线上异于实轴端点的一点,已知∠F1PF2 =,∠PF1F2 =,∠PF2F1=,则2b2(1)S△PF1F2=b cot2=;tan2sin(2)离心率e =.sin- sin垂径定理如图,已知直线l与椭圆相交于A, B两点,点M为AB的中点,O为原点,则b2kOMkAB=-a2如图,已知直线l与双曲线相交于A, B两点,点M为AB的中点,O为原点,则b2kOMkAB=a2(注:直线l与双曲线的渐近线相交于A, B两点,其他条件不变,结论依然成立).周角定理如图,已知点 A , B 椭圆长轴端点(短轴端点), P 是椭圆上异于 A , B 的一点,b 2则 k PA k PB = - a2.推广:如图,已知点 A , B 是椭圆上关于原点对称的两点, P 是椭圆上异于 A , B 的一点,若直线 PA , PB 的斜率存在且不为零 ,b 2k PA k PB = - a2如图,已知点 A , B 双曲线实轴端点, P 是双曲线上异于 A , B 的一点,b 2则 k PA k PB = a2.推广:如图,已知点 A , B 是双曲线上关于原点对称的两点, P 是双曲线上异于 A , B 的一点,若直线 PA , PB 的斜率存在且不为零,b 2 k PA k PB =a2直线l 过焦点 F (c , 0)与椭圆相交于 A , B ⎛ a 2 ⎫两点,点 P c , 0 ⎪,⎝ ⎭则∠APF = ∠BPF (即 k PA + k PB = 0).直线l 过焦点 F (c , 0)与双曲线相交于⎛ a 2 ⎫A ,B 两点,点 P c , 0 ⎪,⎝ ⎭则∠APF = ∠BPF (即 k PA + k PB = 0).切线方程已知点 P (x 0 , y 0 )是椭圆上一点,则椭圆x x y y 在点 P 处的切线方程为0 + 0 = 1. a 2b 2已知点 P (x 0 , y 0 )是双曲线上一点,则双 曲线在点 P 处的切线方程为x 0 x - y 0 y = 1. a 2 b2双曲线的结论1.过定点(定点在双曲线外且不在渐近线上)的直线与双曲线交点个数问题:x 2 y 2设斜率为 k 的直线l 过定点 P (0, t )(t ≠ 0),双曲线方程为 a 2 - b2 线相切时的斜率为 k 0.b= 1(a > 0, b > 0),过点 P 与双曲(1)当0 ≤ k b<时,直线l 与双曲线有两个交点,且这两交点在双曲线的两支上; a(2)当 k b =时,直线l 与双曲线只有一个交点;a(3)当 < k a< k 0 时,直线l 与双曲线有两个交点,且这两交点在双曲线的同一支上;(4)当 k(5)当 k = k 0> k 0 时,直线l 与双曲线只有一个交点;时,直线l 与双曲线没有交点.x 2 y 22.如图, F (c , 0)是双曲线 a 2 - b2 = 1(a > 0, b > 0)的焦点,过点 F 作 FH 垂直双曲线的其中一条渐近线,垂足为 H , O 为原点,则OH = a , FH = b .x 2 y 2 3.点 P 是双曲线-a2b 2= 1(a > 0, b > 0)上任意一点,则点 P 到双曲线的渐近线的距离之积为定值a 2b 2a 2 +b 2.x 2 y 2 4.点 P 是双曲线-a2b 2= 1(a > 0, b > 0)上任意一点,过点 P 作双曲线的渐近线的平行线分别与渐ab 近线相交于 M , N 两点, O 为原点,则平行四边形OMPN 的面积为定值.21 ⎪ 1 2. =p 2抛物线的结论 如图,抛物线方程为 y = 2 px (p > 0),准线 x = - p与 x 轴相交于点 P ,过焦点 F⎛ p, 0 ⎫的直线l 与 22 ⎪ ⎝ ⎭抛物线相交于 A (x 1 , y 1 ), B (x 2 , y 2 )两点, O 为原点,直线l 的倾斜角为.⎧x x = p , ⎨ 4 ⎪⎩ y 1 y 2 = - p 2 .pp 2.焦半径: AF = x 1 + 2, BF = x 2 + 2, AB = x 1 + x 2 + p .2 p3.焦点弦: AB . sin 211 2p 24. AF , BF 的数量关系:+=, AF ⋅ BF = .AF BF psin 225.三角形 AOB 的面积 S △ AOB =2 sin.6.以焦点弦 AB 为直径的圆与准线相切;以焦半径 AF 为直径的圆与 y 轴相切.7.直线 PA , PB 的斜率之和为零( k PA + k PB = 0),即∠APF = ∠BPF .8.点 A , O , N 三点共线;点 B , O , M 三点共线.9.如图,点 A , B 是抛物线 y = 2 px (p > 0), O 为原点,若∠AOB = 90o ,则直线 AB 过定点(2 p , 0).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1讲 圆锥曲线的常用结论 一.椭圆 焦点的位置 焦点在x轴上 焦点在y轴上
图形 标准方程 222210xyabab 222210yxabab
范围 axa且byb
bxb
且aya
顶点 1,0a、2,0a 10,b、20,b 10,a、20,a
1,0b、2,0b
轴长 短轴的长2b 长轴的长2a
焦点 1,0Fc、2,0Fc 10,Fc、20,Fc
焦距 222
122FFccab
对称性 关于x轴、y轴、原点对称
离心率 22101cbeeaae越小,椭圆越圆;e越大,椭圆越扁
1.(1)与椭圆22221xyab共焦点的椭圆的方程可设为222221,0xybab. (2)与椭圆22221xyab有相同的离心率的椭圆可设为2222xyab,2222,0xyba. 2.椭圆的两焦点分别为12,FF,P是椭圆上任意一点,则有以下结论成立: (1)122PFPFa; (2)1acPFac; (3)2212bPFPFa; (4)焦半径公式10||PFaex,20||PFaex(1(,0)Fc , 2(,0)Fc00(,)Mxy). 3.椭圆的方程为22221xyab(a>b>0), 左、右焦点分别为12,FF,00,Pxy是椭圆上任意一点,则有: (1)22222222000022,bayaxxbyab; (2)参数方程00cossinxayb为参数; 4.设P点是椭圆上异于长轴端点的任一点,F1、F2为其焦点记12FPF,则(1)2122||||1cosbPFPF. (2)焦点三角形的面积: 122||=tan2PFFPScyb. (3)当P点位于短轴顶点处时, 最大,此时12PFFS也最大; (4) .21cos2e (5)点M是21FPF内心,PM交21FF于点N,则caMNPM||||.
5.有关22ba的经典结论 (1).AB是椭圆22221xyab的不平行于对称轴的弦,M),(00yx为AB的中点,则22OMABbkka. (2).椭圆的方程为22221xyab(a>b>0),12,AA为椭圆的长轴顶点,P点是椭圆上异于长轴顶点的任一点,则有1222PAPAbKKa (3). 椭圆的方程为22221xyab(a>b>0),12,BB为椭圆的短轴顶点,P点是椭圆上异于短轴顶点的任一点,则有1222PBPBbKKa (4). 椭圆的方程为22221xyab(a>b>0),过原点的直线交椭圆于,AB两点,P点是椭圆上异于,AB两点的任一点,则有22PAPBbKKa 6. 若000(,)Pxy在椭圆22221xyab上,则 (1)以000(,)Pxy为切点的切线斜率为2020bxkay; (2)过0P的椭圆的切线方程是00221xxyyab. 7.若000(,)Pxy在椭圆22221xyab外 ,则过000(,)Pxy作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221xxyyab. 8.椭圆的两个顶点为1(,0)Aa,2(,0)Aa,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程
是22221xyab. 9.过椭圆上任一点00(,)Axy任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且2020BC
bxkay(常数).
10. 若P为椭圆上异于长轴端点的任一点,F1, F 2是焦点, 12PFF, 21PFF,则sinsinsincea
.
11. P为椭圆上任一点,F1,F2为二焦点,A为椭圆内一定点,则2112||||||2||aAFPAPFaAF,当且仅当2,,AFP三点共线时,等号成立. 12.O为坐标原点,P、Q为椭圆上两动点,且OPOQ.
(1)22221111||||OPOQab; (2)|OP|2+|OQ|2的最大值为22224abab;(3)OPQS的最小值是2222abab. 13. 已知A、B、是椭圆上的两点,线段AB的垂直平分线与x轴相交于点0(,0)Px, 则22220ababxaa
.
14. 离心率e=ac=21)(ab、e2=1-2)(ab 15. 过焦点且垂直于长轴的弦叫通经,其长度为ab22 16. 从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线必经过椭圆的另一个焦点. 17. 过椭圆22221(0)xyabab左焦点的焦点弦为AB,则)(221xxeaAB;过右焦点的弦)(221xxeaAB.
18. 内接矩形最大面积:2ab. 19. 若椭圆方程为22221(0)xyabab,半焦距为c,焦点12,0,,0FcFc,设
(1).过1F的直线l 的倾斜角为,交椭圆于A、B两点,则有
①2211,coscosbbAFBFacac ;②2cosabABac2222 (2).若椭圆方程为22221(0)xyabab,半焦距为c,焦点12,0,,0FcFc,设 过F2的直线l 的倾斜角为,交椭圆于A、B两点,则有:① 22,coscosbbAFBFacac22+- ;②22cosab
ABac
222
结论:椭圆过焦点弦长公式:222cos2sinabxacABabyac222222焦点在轴上焦点在轴上 20.若AB是过焦点F的弦,设,AFmBFn,则2
112a
mnb
二.双曲线 焦点的位置 焦点在x轴上 焦点在y轴上 图形
标准方程 222210,0xyabab 222210,0yxabab
范围 xa或xa,yR ya或ya
,xR
顶点 1,0a、2,0a 10,a、20,a
轴长 虚轴的长2b 实轴的长2a
焦点 1,0Fc、2,0Fc 10,Fc、20,Fc
焦距 222
122FFccab
对称性 关于x轴、y轴对称,关于原点中心对称
离心率 2211cbeeaa,e越大,双曲线的开口越阔
渐近线方程 byxa ayxb
1.(1)与22221xyab共轭的双曲线方程为22221xyab,①它们有公共的渐近线;②四个焦点都在以原点为圆心,C为半径的圆上;③2212111ee。 (2)与22221xyab有相同焦点的双曲线方程为2222221,0,0,0xyabab (3)与22221xyab有相同焦点的椭圆方程为: 2222221,0,0xyabab (4)与22221xyab有相同焦点的双曲线方程为:2222221,0,0,0xyabab (5)与22221xyab有相同离心率的双曲线方程为:①焦点在x轴上时:2222,0,1xyab ②焦点在y轴上时:2222,0yxab (6)与22221xyab有相同的渐近线方程为:2222,0,1xyab; 2.双曲线的两焦点分别为12,FF,P是双曲线上任意一点,则有以下结论成立: (1)122PFPFa; (2)12minmin,PFacPFcaP在右支上; 21minmin
,PFacPFcaP在左支上
3. 双曲线的方程为22221xyab(a>0,b>0), ,00,Pxy是双曲线上任意一点,则有: 22222222000022
,bayxaxbyab;
4.设P点是双曲线上异于长轴端点的任一点,F1、F2为其焦点记12FPF,则 (1)2122||||1cosbPFPF. (2)焦点三角形的面积 122||=cot2PFFPScyb. 5.有关22ba的经典结论 (1)AB是双曲线22221xyab的不平行于对称轴的弦,M),(00yx为AB的中点,则22OMABbkka, 即2020ABbxKay。 (2)双曲线的方程为22221xyab(a>0,b>0),12,AA为双曲线的实轴顶点,P点是双曲线上异于实轴
