理论力学思考题
理论力学(1.6)--静力学公理和物体受力分析-思考题

第一章 静力学公理和物体的受力分析1-1说明下列式子与文字的意义和区别:
(1)F1=F2 (2) F1=F2 (3) 力F1等效于力F2。
1-2试区别F R=F1+F2和F R=F1+F2两个等式代表的意义。
1-3 图中各物体的受力图是否有错误?如何改正?
(1) (2)
(3)
(4)
1-4刚体上A点受力F作用,如图所示,问能否在B点加一个力使刚体平衡?
为什么?
1-5 如图所示结构,若力F作用在B点,系统能否平衡?若力F仍作用在B点,但可以任意改变力F的方向,F在什么方向上结构能平衡?
1-6 将如下问题抽象为力学模型,充分发挥你们的想象、分析和抽象能力,试画出它们的力学简图和受力图。
(1)用两根细绳将日光灯吊挂在天花板上;
(2)水面上的一块浮冰;
(3)一本打开的书静止放于桌面上;
(4)一个人坐在一只足球上。
1-7 如图所示,力F作用于三铰拱的铰链C处的销钉上,所有物体重量不计。
(1)试分别画出左、右两拱和销钉C的受力图;
(2)若销钉C属于AC,分别画出左、右两拱的受力图;
(3)若销钉C属于BC,分别画出左、右两拱的受力图。
理论力学第三章思考题

第三章思考题3.1刚体一般是由n (n 是一个很大得数目)个质点组成。
为什么刚体的独立变量却不是3n 而是6或者更少?3.2何谓物体的重心?他和重心是不是 总是重合在一起的? 3.3试讨论图形的几何中心,质心和重心重合在一起的条件。
3.4简化中心改变时,主矢和主矩是不是也随着改变?如果要改变,会不会影响刚体的运动? 3.5已知一匀质棒,当它绕过其一端并垂直于棒的轴转动时,转动惯量为231ml ,m 为棒的质量,l 为棒长。
问此棒绕通过离棒端为l 41且与上述轴线平行的另一轴线转动时,转动惯量是不是等于224131⎪⎭⎫ ⎝⎛+l m ml ?为什么?3.6如果两条平行线中没有一条是通过质心的,那么平行轴定理式(3.5.12)能否应用?如不能,可否加以修改后再用?3.7在平面平行运动中,基点既然可以任意选择,你觉得选择那些特殊点作为基点比较好?好处在哪里?又在(3.7.1)及(3.7.4)两式中,哪些量与基点有关?哪些量与基点无关? 3.8转动瞬心在无穷远处,意味着什么?3.9刚体做平面平行运动时,能否对转动瞬心应用动量矩定理写出它的动力学方程?为什么?3.10当圆柱体以匀加速度自斜面滚下时,为什么用机械能守恒定律不能求出圆柱体和斜面之间的反作用力?此时摩擦阻力所做的功为什么不列入?是不是我们必须假定没有摩擦力?没有摩擦力,圆柱体能不能滚?3.11圆柱体沿斜面无滑动滚下时,它的线加速度与圆柱体的转动惯量有关,这是为什么?但圆柱体沿斜面既滚且滑向下运动时,它的线加速度则与转动惯量无关?这又是为什么? 3.12刚体做怎样的运动时,刚体内任一点的线速度才可以写为r ω⨯?这时r 是不是等于该质点到转动轴的垂直距离?为什么?3.13刚体绕固定点转动时,r ω⨯dtd 为什么叫转动加速度而不叫切向加速度?又()r ωω⨯⨯为什么叫向轴加速度而不叫向心加速度?3.14在欧勒动力学方程中,既然坐标轴是固定在刚体上,随着刚体一起转动,为什么我们还可以用这种坐标系来研究刚体的运动?3.15欧勒动力学方程中的第二项()21I I -y x ωω等是怎样产生的?它的物理意义又是什么?第三章思考题解答3.1 答:确定一质点在空间中得位置需要3个独立变量,只要确定了不共线三点的位置刚体的位置也就确定了,故须九个独立变量,但刚体不变形,此三点中人二点的连线长度不变,即有三个约束方程,所以确定刚体的一般运动不需3n 个独立变量,有6个独立变量就够了.若刚体作定点转动,只要定出任一点相对定点的运动刚体的运动就确定了,只需3个独立变量;确定作平面平行运动刚体的代表平面在空间中的方位需一个独立变量,确定任一点在平面上的位置需二个独立变量,共需三个独立变量;知道了定轴转动刚体绕转动轴的转角,刚体的位置也就定了,只需一个独立变量;刚体的平动可用一个点的运动代表其运动,故需三个独立变量。
理论力学(1.7)--静力学公理和物体受力分析-思考题答案

第一章 静力学公理和物体的受力分析
答 案
1-1
(1)若F1=F2表示力,则一般只说明两个力大小相等,方向相同。
(2)若F1=F2表示力,则一般只说明两个力大小相等,方向是否相同,难以判定。
(3)说明两个力大小、方向、作用效果均相同。
1-2
前者为两个矢量相加,后者为两个代数量相加。
1-3
(1)B处应为拉力,A处力的方向不对。
(2)C、B处力方向不对,A处力的指向反了。
(3)A处力的方向不对,本题不属于三力汇交问题。
(4)A、B处力的方向不对。
受力图略。
1-4
不能。
因为在B点加和力F等值反向的力会形成力偶。
1-5
不能平衡。
沿着AB的方向。
1-6略。
1-7
提示:单独画销钉受力图,力F作用在销钉上;若销钉属于AC,则力F作用在AC上。
受力图略。
哈工大第七版理论力学课后思考题答案

集美大学诚毅学院机械1093期末复习材料理论力学(思考题答案)思考题i-i猛明下列戏子与丈宇的盘义和区別.(D科二孔,(2)幵一盼⑶力靳等效于力列,*W?答】⑴力乌和町,大小相等帯柯相岡g(2)N和&大小相萄⑶耐刑耳的夫小相等, 方向si^ats同亠1-2试X别片=眄|压和血=凤+骂两个等戎代表的意义。
【岸答】町一耐十用朮示朋是任意方向上箭个为门和A的合力洽力弘的大小和方问由平行四边形抚阳鴉定;打=片一%表示忌足同方向上蘭个力几和月的合.乩含力A的大小为F L和E的大小的和I方向与Fl和F.的方向科同3【解答】均有错•正确图如答1一1图。
1—3图1 - 1C1)〜1-1(0中各物体的受力番是否错谋?如何改正?1-4 刚体上△点受力尸作用.in 18 1-2所示,问罷否在。
点加一个力懐刚体平箕。
为什么?Ul 1 -2(a)也fS P= 0【解答1 不能。
当在E 点械抑力怖时,不能同时保订丿 1,故不能平衡B2JM= o1- 5 如摆】一3所冻结均•科丿JF 作用在E 点,至统能否乎猶?若力F 仍作用在丑点,袒可住 愆改变F 的方向,F 在什么方向上结购能平衡? 上匕解答】不能, 来/在如簷范围内可以令结构平鸳,如着? 一 3圖所示.1- 6 将如下间题抽象为力学模型,充分发挥你们的想象、分析和抽躱能力*试画出它心的力 学荒圏及受力<1)用两根细绳將B 光灯吊挂在天花板上»(?)水面匕的一块浮冰*G) 本打开的韦静止于桌面上; <4) 一个人坐在一只足球上*【解答】⑴⑵图1-4<4)u1 -7若将图1-5屮力F作用于三锻拱供较陡C处的请订上,所有物体里虽不计试分别画出左、右两拱茂销匚的受力圈八刃若傭订匚碾于AC•分别画岀汗、右两拱的受力图H3)若洌订C 属于EC,分鬧画出古、右两拱的量力阳°3 1-5mA2_1输亀钱普麦/相同时,电线下垂量片趙小■电线捷易亍拉Wh 为什么?【網答】可儒得J = F B =疵;=好也越小恥越小不和尸庞儿助以电线更易于拉2-2图2 — 1所赤时三种机构,构件自童不计9翅略靡擦,, 平力F,问Aifc 的妁京力是否相同。
理论力学第一章题及解答(文末)

理论⼒学第⼀章题及解答(⽂末)第⼀章思考题1.1平均速度与瞬时速度有何不同?1.2 在极坐标系中,r v r =,θθ r v =.为什么2θ r r a r-=⽽⾮r ?为什么θθ r r a 20+=⽽⾮θθ r r +?你能说出r a 中的2θ r -和θa 中另⼀个θ r 出现的原因和它们的物理意义吗?1.3 在内禀⽅程中,n a 是怎样产⽣的?为什么在空间曲线中它总沿着主法线⽅向?当质点沿空间运动时,副法线⽅向的加速度b a 等于零,⽽作⽤⼒在副法线⽅向的分量b F ⼀般不等于零,这是不是违背了⽜顿运动定律呢?1.4 在怎样的运动中只有τa ⽽⽆n a ?在怎样的运动中⼜只有n a ⽽⽆τa ?在怎样的运动中既有n a ⽽⽆τa ?1.5dt r d 与dt dr 有⽆不同?dt v d与dtdv 有⽆不同?试就直线运动与曲线运动分别加以讨论. 1.6⼈以速度v 向篮球⽹前进,则当其投篮时应⽤什么⾓度投出?跟静⽌时投篮有何不同?1.7⾬点以匀速度v 落下,在⼀有加速度a 的⽕车中看,它⾛什么路经?1.8某⼈以⼀定的功率划船,逆流⽽上.当船经过⼀桥时,船上的渔竿不慎落⼊河中.两分钟后,此⼈才发现,⽴即返棹追赶.追到渔竿之处是在桥的下游600⽶的地⽅,问河⽔的流速是多⼤?1.9物体运动的速度是否总是和所受的外⼒的⽅向⼀致?为什么?1.10在那些条件下,物体可以作直线运动?如果初速度的⽅向和⼒的⽅向⼀致,则物体是沿⼒的⽅向还是沿初速度的⽅向运动?试⽤⼀具体实例加以说明.1.11质点仅因重⼒作⽤⽽沿光滑静⽌曲线下滑,达到任⼀点时的速度只和什么有关?为什么是这样?假如不是光滑的将如何?1.12为什么被约束在⼀光滑静⽌的曲线上运动时,约束⼒不作功?我们利⽤动能定理或能量积分,能否求出约束⼒?如不能,应当怎样去求?1.13质点的质量是1千克,它运动时的速度是k j i v 323++=,式中i 、j 、k 是沿x 、y 、z 轴上的单位⽮量。
理论力学(3.7)--空间任意力系-思考题
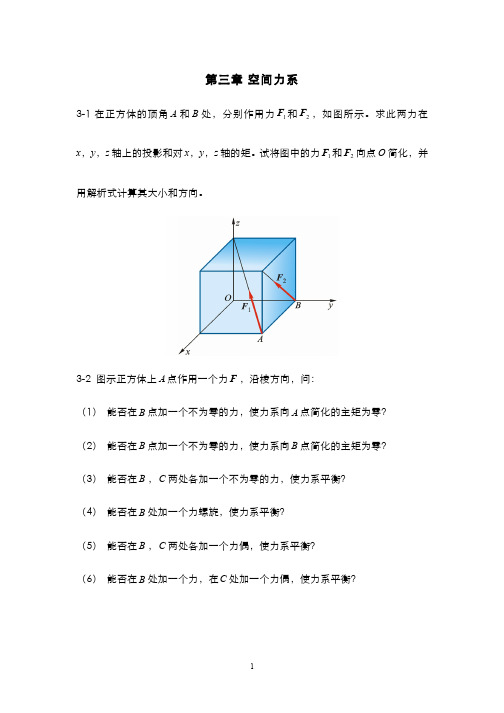
第三章 空间力系3-1 在正方体的顶角A 和B 处,分别作用力1F 和2F ,如图所示。
求此两力在x ,y ,z 轴上的投影和对x ,y ,z 轴的矩。
试将图中的力1F 和2F 向点O 简化,并用解析式计算其大小和方向。
3-2 图示正方体上A 点作用一个力F ,沿棱方向,问:(1)能否在B 点加一个不为零的力,使力系向A 点简化的主矩为零?(2)能否在B 点加一个不为零的力,使力系向B 点简化的主矩为零?(3)能否在B ,C 两处各加一个不为零的力,使力系平衡?(4)能否在B 处加一个力螺旋,使力系平衡?(5)能否在B ,C 两处各加一个力偶,使力系平衡?(6)能否在B 处加一个力,在C 处加一个力偶,使力系平衡?3-3 图示为一边长为a的正方体,已知某力系向B点简化得到一合力,向Cᄁ点简化也得一合力。
问:(1)力系向A点和'A点简化所得主矩是否相等?(2)力系向A点和'O点简化所得主矩是否相等?3-4 在上题图中,已知空间力系向'B点简化得一主矢(其大小为F)及一主矩(大小、方向均未知),又已知该力系向A点简化为一合力,合力方向指向O点试:(1)用矢量的解析表达式给出力系向'B点简化的主矩;(2)用矢量的解析表达式给出力系向C点简化的主矢和主矩。
3-5 (1)空间力系中各力的作用线平行于某一固定平面;(2)空间力系中各力的作用线分别汇交于两个固定点。
试分析这两种力系最多能有几个独立的平衡方程。
3-6 传动轴用两个止推轴承支持,每个轴承有三个未知力,共6个未知量。
而空间任意力系的平衡方程恰好有6个,是否为静定问题?3-7 空间任意力系总可以由两个力来平衡,为什么?3-8 某一空间力系对不共线的三点主矩都为零,问此力系是否一定平衡?3-9 空间任意力系向两个不同的点简化,试问下述情况是否可能?(1)主矢相等,主矩相等。
(2)主矢不相等,主矩相等。
(3)主矢相等,主矩不相等。
理论力学习题(5)
第五章 思考题5.1 虚功原理中的“虚功”二字作何解释?用虚功原理解平衡问题,有何优缺点?答:“虚功”是指作用在质点上的力(包括约束反力),在任意虚位移过程中所做的功。
因虚位移是假想的位移,所以虚功也是假想的功。
不一定是质点在任何真实运动中力实际所完成的“真实功”。
而虚功原理中的“虚功”只包括所有主动力的“虚功”,不包括约束反力的“虚功”,因为根据理想约束的条件:∑==⋅ni i i10r Rδ,即作用在一力学体系上的所有约束反力在任意虚位移中所做的虚功之和为零。
用虚功原理解平衡问题时,约束反力自动消去,这是它的优点。
但因此就不能直接用它来求约束反力,这是它的缺点。
5.2 为什么在拉格朗日方程中,αQ 不包括约束反作用力?又广义坐标及广义力的含义为何?我们根据什么关系可以由一个量的量纲定出另一个量的量纲?答:决定力学体系的位置状态的独立参数叫广义坐标。
广义坐标不一定是长度,也可以是角度、面积或体积等。
与广义坐标对应的广义力定义为:∑=∂∂⋅=ni ii q Q 1ααr F 它可以是力或力矩,也可以是其它物理量。
我们根据关系:∑==sq Q W 1αααδδ,可由广义坐标的量纲定出广义力αQ 的量纲(功的量纲已知)。
根据广义力的定义,我们可以计算与约束反力相应的广义力:∑=∂∂⋅=ni ii Rq Q 1ααr R 但理想约束条件:0)(11111=∂∂⋅=∂∂⋅=⋅∑∑∑∑∑=====ααααααδδδq q q q ni i i s ni si i ni i rR r R r R i ,由于αδq 是独立的,所以有:),2,1(01s q Q ni ii R==∂∂⋅=∑=αααr R 。
我们看到,只要满足理想的约束条件,约束反力对广义力的贡献为零。
因此,αQ 中不包含约束反力。
5.3 广义动量αp 和广义速度αq是不是只相差一个乘数m ?为什么αp 比αq更富有物理意义?答:广义动量αp 和广义速度αq的关系只能由定义式:ααqLp ∂∂=求出,他们不一定是只相差一个乘数m 。
理论力学第六章思考题
理论⼒学第六章思考题第六章思考题6.1. 相同的两匀质杆AO 和BO ⽤铰链连接于固定点O , 并可在⽔平⾯内绕O 点转动.某时刻AOB 位于同⼀直线上, ⼆杆以同样⼤⼩的⾓速度ω转动, 如思考题6.1图所⽰. 有⼈认为:“以⼆杆为系统, 此时质⼼为O 点, O 点为固定点, 故此时质⼼速度为零.”这种说法对吗?思考题6.1图6.2. 有时称c t c v m r ?为质⼼对O 点的⾓动量, 称221c t v m 为质⼼的动能. 这是否说明质⼼是⼀个质量为t m 、位置⽮量为c r 、速度为c v 的质点? 6.3. 有⼀半径为R , 质量为m 的匀质圆球被旋转抛出. 某时刻球⼼速度为v ,球旋转⾓速度为ω , 求此时圆球的动量.6.4. 将⼀半圆柱置于⼀光滑⽔平⾯上, 初始时半圆柱静⽌于如思考题6.4图所⽰位置, 求质⼼C 的运动轨迹.思考题6.4图6.5. 有⼀⽔平圆台, 可绕过其圆⼼的竖直轴z 轴转动, 轴承处有较⼩但不可忽略的摩擦⼒.有⼈站在台边上, 初始时圆台与⼈均静⽌, 如思考题6.5图所⽰.之后⼈沿台边跑⼀段时间后, ⼜停⽌跑动. 问⼈停⽌跑动后, ⼈与圆台将如何运动? 在整个过程中, 以⼈、圆台和轴为质点系, 其对z 轴总⾓动量如何变化?思考题6.5图6.6. 思考题6.5中, 把轴包括在质点系内, 这样做有何好处?6.7. 思考题6.5中, 如轴承是光滑的, 情况⼜当如何?6.8. 思考题6.5中, ⼈与盘运动状态的改变是由⼈跑动引起的. ⽽质点系的⾓动量定理指出, 质点系⾓动量的变化与内⼒⽆关. 这两者之间是否发⽣⽭盾?6.9. 试证明: 若质点系总动量为零, 则质点系对任意固定点的总⾓动量均相等.6.10. 有两个形状相同的匀质齿轮位于同⼀竖直⾯内, 可绕过各⾃中⼼的⽔平轴1O 和2O 转动, 转动惯量同为I , 如思考题6.10图所⽰. 开始时轮1绕固定轴1O 以⾓速度ω转动, 轮2静⽌. 之后可沿竖直线移动的轴2O 向下移动使⼆齿轮啮合. 已知齿轮啮合后转动⾓速度的⼤⼩均为2ω. 有⼈说: “以⼆齿轮为质点组, 所受外⼒对轮轴⼒矩均为零. 且啮合前总⾓动量为ω I , 啮合后总⾓动量仍为ωωωI I I =+?22, 可见啮合过程⾓动量守恒.”试分析该说法是否正确.思考题6.10图6.11. 质量相同的两⼩球⽤轻杆相连, 静⽌地放在光滑⽔平⾯上. 初始时给其中⼀⼩球以垂直于杆的⽔平初速度0v , 试证两球各⾃的轨道均为旋轮线.6.12. ⾃⾏车由静到动, 其动量变化靠的是地⾯对后轮向前的摩擦⼒f F , 这个摩擦⼒f F 对⾃⾏车做的功是否为⾃⾏车向前移动距离)(?=f F W ?6.13. 以⼀般的动坐标系z y x O ''''代替质⼼系, 关系式O O t O OL v m r L ''''+?= 和T v m T O t '+='221(O L ''和T 分别为质点系在z y x O ''''系中对O '点的⾓动量和动能)能否成⽴?6.14. ⼀匀质细杆可绕过端点的⽔平轴⽆摩擦地转动, 初始时杆静⽌于竖直位置, 如思考题6.14图所⽰. 之后⼀⼩球沿⽔平⽅向飞来与杆做完全弹性碰撞. 以⼩球和杆为质点系, 在碰撞过程中系统动量、⾓动量和机械能是否守恒?思考题6.14图6.15. 在光滑⽔平⾯上有⼀长为l 、质量为m 的匀质细杆, 绕过其中点的竖直轴以⾓速度0ω转动, 但其中⼼不固定, 如思考题6.15图所⽰. 现突然将杆的A 端按住, 以杆为研究对象, 有⼈认为:“⽤⼿按住A 点, 系统在A 点受外⼒作⽤, 但在按住A 点的过程中A 点⽆位移,故该外⼒不做功, 所以杆的机械能守恒.”你认为这样的看法正确吗?思考题6.15图第六章习题6.1. 椭圆规尺AB 质量为12m , 曲柄OC 质量为1m , 套管B A ,质量为2m ,l CB AC OC ===, 尺和曲柄的质⼼均位于其中点, 曲柄以匀⾓速度ω绕z 轴转动,如题6.1图所⽰. 求此机构总动量的⼤⼩和⽅向.题6.1图6.2. 质量分别为1m 和2m 的重物以跨过滑轮A 的不可伸长的轻绳相连, 并可沿直⾓三棱柱的斜⾯滑动. 三棱柱底⾯放在光滑⽔平⾯上, 如题 6.2图所⽰. 已知三棱柱质量21164m m m ==初始时各物体均静⽌, 求当重物下降⾼度为m 1.0时, 三棱柱沿⽔平⾯的位移.题6.2图 6.3. 质量为0m 的⼈⼿持质量为m 的物体, 此⼈以与地⾯成α⾓的初速度0v 向前跳出.当他跳到最⾼点时, 将物体以相对⾃⼰的速度u ⽔平向后抛出. 问由于物体的抛出, 跳的距离增加了多少?6.4. 两个质点A 和B 质量分别为A m 和B m , 初始时位于同⼀竖直线上, A 质点有⽔平初速度0v , B 质点静⽌, B 点⾼度为h , A 点在B 点的上⽅, A 和B 间距离为l . 在以下3种情况中求质点A 和B 的质⼼轨迹. (1) A 和B 两质点间没有相互作⽤;(2) 质点A 和B 以万有引⼒相互作⽤; (3) A 和B 间以轻杆相连.6.5. 质量为m 的薄板在竖直⾯内, 绕过O 点的⽔平轴按t ωθθcos 0=规律转动, 其质⼼C 离O 点的距离为a , 如题6.5图所⽰. 求在任⼀瞬时⽔平轴对板的约束⼒.题6.5图 6.6. ⽡特节速器装置如题6.6图, ⼆杆长l OB OA ==, A 和B ⼆球质量均为m . 初始时A 和B ⼆球被⼀根线连结, 装置以⾓速度0ω绕竖直轴转动, 杆的张⾓为0θ. ⾃某⼀时刻线被烧断, 求⾓速度ω与张⾓θ的关系. 设轴承光滑, 不受主动⼒矩, 杆的质量均可忽略不计. 若杆的质量不可忽略, 但各杆质量分布均匀, 结果⼜当如何?题6.6图6.7. ⼀质量为0m 、底半径为R 的匀质圆锥, 它的光滑固定对称轴沿竖直⽅向, 圆锥尖端向上, 在圆锥表⾯上有⼀沿母线的细槽.初始时, 圆锥绕其对称轴以⾓速度0ω转动, 同时有⼀质量为m 的⼩球开始⾃槽的顶端沿槽⾃由下滑. 试求⼩球滑出槽⼝时圆锥的⾓速度. 若此槽不是沿母线的直线, 试问此槽曲线应满⾜什么条件, 才能使⼩球滑出槽⼝时圆锥⾓速度与槽为沿母线的直线情况相同.6.8. 质量为1m 和2m 的⼆质点, ⽤⼀根长为l 的不可伸长的轻绳相连. 初始时1m 被握在⼿中不动, 2m 以匀速率0v 绕1m 做圆周运动. 在某瞬时将1m 放⼿, 试求以后⼆质点的运动, 并证明绳内张⼒l m m v m m F T )(212021+=. 不考虑重⼒及质点间引⼒作⽤, 并已知绳⼀直是张紧的.6.9. 传送机由两个相同的滑轮B 和C 和套在其上的传送带构成, 每个滑轮质量为1m 、半径为R , 均可视为匀质圆盘, 传送带质量为2m , 相对⽔平⾯倾⾓为α, 被传送物体质量为3m . 初始时各物体均静⽌, 在B 上施加⼀不变⼒矩M , 如题6.9图所⽰. 设滑轮轴承处光滑, 传送带与滑轮及传送带与被传送物体间均⽆滑动, 传送带在EF 间为直线. 试求当被传送物体在EF 间运动时, 传送带运⾏速率v 与运⾏距离s 间的关系.题6.9图6.10. ⼀炮弹质量为21m m +, 发射时⽔平及竖直速度分别为Ox v 和Oy v . 当炮弹达到最⾼点时, 其内部炸药爆炸产⽣能量E , 使此炮弹分为1m 和2m 两部分, 开始时两部分均沿原⽅向飞⾏, 不计空⽓阻⼒, 试求炮弹的两部分落地时相距的距离.6.11. 质量为0m 、半径为R 的光滑半球, 其底⾯放在光滑⽔平⾯上, 有⼀质量为m 的质点沿球⾯滑下. 初始时⼆物体均静⽌, 质点初位置与球⼼连线和竖直向上的直线间夹⾓为α.求质点滑到它与球⼼连线和竖直向上直线间夹⾓为θ时θ的值.6.12. 轻杆AB 长为l ,两端固定有质量分别为1m 和2m 的质点A 和B , 杆只能在竖直平⾯内运动, 某瞬时A 点速度为1v , B 速度为2v , 分别与杆夹⾓1α和2α, 如题 6.12图所⽰. (1) 试求此系统在质⼼系中相对质⼼的⾓动量; (2) 考虑重⼒作⽤, 试求此系统在以后的运动中⾓速度的变化情况.题6.12图6.13. ⼀质量为m , 长为a 2的细杆AB , 它的两端可沿⼀⽔平固定圆环⽆摩擦地滑动,圆环半径为)(a R R >. 初始时杆静⽌, 同时有⼀质量亦为m 的质点静⽌地位于杆的中点C . ⾃某⼀瞬时开始, 质点以相对杆的不变速度0v 沿杆运动, 如题6.13图所⽰. 试求当质点运动到杆的端点A 时, 杆相对⾃⼰的初始位置转过多少⾓度?题6.13图6.14. 质量分别为1m 和2m 的两⾃由质点, 它们以万有引⼒互相吸引. 开始时, 两质点均处于静⽌状态, 其间距离为a . 试求两质点相距为2a 时两质点的速度.6.15. 参见思考题6.14, 试证明若⼩球撞击在距O 点2/3杆长的A 点时, 系统沿⽔平⽅向动量守恒.6.16. 参见思考题6.15, 试求按住A 点后瞬时杆的⾓速度, 及按住A 点的过程中杆的动能损失了百分之⼏?6.17. 电风扇的转动部分对其固定转动轴的转动惯量为I , 所受空⽓阻⼒矩与⾓速度⼤⼩成正⽐,⽐例系数为k .通电时风扇以匀⾓速度0ω转动, 求断电以后经过多长时间其⾓速度的⼤⼩减为初始时的⼀半,在这段时间内风扇⼜转过了多少圈?6.18. 由薄⽚刚体构成的复摆可绕与其垂直的光滑⽔平固定轴转动, 对转动轴的回转半径为k (k 定义为m I k =,I 为刚体对转动轴的转动惯量,m 为刚体质量), 转动轴到刚体质⼼的距离为a . 已知复摆⽆初速地⾃偏离平衡位置0θ⾓处开始摆动, 求复摆在悬点处所受约束⼒的⽔平分量和垂直分量.6.19. 有⼀半径为r 的⼩圆柱, ⾃半径为R 的⼤圆柱的最⾼位置⽆滑滚下, 同时⼤圆柱也沿⽔平⾯做⽆滑滚动,试写出两圆柱间⽆滑条件的数学表达式.6.20. 质量为m , 半径为R 的匀质细圆环被限定在竖直平⾯内运动, 开始时将其放在粗糙⽔平⾯上,⽤⼿按其后侧边缘, 使圆环质⼼获得向前的初速度0v , 同时圆环有向后转动的初⾓速度0ω , 如题6.20图所⽰.设圆环与⽔平⾯间摩擦因数为µ,试求圆环的运动规律.题6.20图6.21. 长为a 2的匀质棒AB , 以光滑铰链悬于A 点, 棒可在竖直⾯内摆动. 初始时棒⾃⽔平位置⽆初速地开始运动, 当棒摆⾄垂直位置时铰链突然脱落, 试证在以后的运动中棒质⼼的运动轨迹为⼀抛物线.并求当棒的质⼼下落h 距离后, 棒⼀共转了⼏圈?6.22. ⼀匀质棒被限制在竖直平⾯内运动, 开始时把棒⼀端置于光滑⽔平地⾯上,⼀端靠在光滑的竖直墙上,且棒与地⾯夹⾓为α, 并任其从此位置开始⽆初速地滑动.试证当棒与地⾯夹⾓变为)sin 32arcsin(α时,棒与墙分离.6.23. 试研究6.22题中棒与墙分离后的运动,设棒长为a 2, 求棒落地时的⾓速度.6.24. 如题 6.24图所⽰, ⼀⾯光滑⼀⾯粗糙的平板,质量为1m .将其光滑的⼀⾯放在光滑⽔平桌⾯上, 粗糙⾯上放⼀质量为2m 的球.初始时板与球均静⽌, 若板沿其长度⽅向突然获得⼀速度0v . 问经多少时间后球开始做⽆滑滚动? 设球与板间摩擦因数为µ,板的长度⾜够长.题6.24图6.25. 如题6.25图所⽰, ⼀质量为m , 半径为a 的匀质⼩圆球, 初始时位于另⼀个半径为b 的固定⼤圆球的顶点, 并⽆初速地⽆滑滚下, 设球⼀直保持⽆滑状态, 试证当两球连⼼线与竖直向上的直线间夹⾓)1710arccos(=?时,两球将分离.题6.25图6.26. 试⽤计算机通过数值求解⽅法研究习题6.20中圆环的运动, 并描绘其运动情况.参考答案第六章思考题6.1. 不对. 质⼼不是固定点. 6.2. 质⼼是⼀个⼏何点. 严格说C t C v m r ?是位于质⼼假想质点对O 点⾓动量, 2C t )2/1(v m 是位于质⼼的假想质点的动能. 6.3. v m .6.4. 质⼼C 竖直向下运动. 6.5. 圆盘以kω沿⼈跑动⽅向转动.在⼈跑动时对z 轴总⾓动量增加, 在⼈停⽌跑动后对z 轴总⾓动量逐渐减⼩到零. (因受轴承摩擦⼒矩所致.)6.6. 由于圆盘与轴间的相互作⽤⽐较复杂, 把轴包括在质点系内, 只需分析轴受轴承的⼒和⼒矩, 较为简单.6.7. 如轴承光滑,则总⾓动量不变. ⼈停⽌跑动后,圆盘亦停⽌转动.6.8. 质点系的总⾓动量的变化与内⼒⽆关, 但内⼒可使⾓动量在质点间等量转移. 6.9. 质点系总动量为零, 则0C =v . 于是C C C tC 0L L v m r L '='+?= , 与O 点选取⽆关. 6.10. 不正确. 啮合后⼆齿轮转动⾓速度⽅向相反, 对1O 或2O 轴⾓动量都不守恒.(1N F和2N F都不沿21O O ⽅向.) 6.11. 初始时⼀球静⽌, ⼀球以0v 运动, 质⼼初速度2/0v , ⼆球在质⼼系内速率为2/0v . 由于运动中系统动量守恒, 在质⼼系中对质⼼⾓动量守恒, 故其质⼼速度和⼆⼩球在质⼼系内绕质⼼运动的速率均不变. 因此两球的轨道与在直线轨道上作⽆滑滚动的圆盘边缘上⼀点的轨道相同.6.12. 后轮所受向前的摩擦⼒不可能对⾃⾏车作正功.6.13. 不能成⽴.6.14. 由于⽔平轴施与的约束⼒不⼀定沿竖直⽅向, 故动量不守恒, 沿⽔平⽅向动量也不⼀定守恒. 对⽔平轴⾓动量守恒, 机械能守恒.6.15. 在按住A 点的过程中, A 点不可能设有位移. 如果位移⾜够⼩则外⼒必⾜够⼤, 我们可以忽略其位移⽽认为“按住A 点”, 但外⼒作负功不可忽略.第六章习题6.1. 可以分别求出AB、OC、A和B的动量,之后求和得)cos sin ()25(21j t i t lm m m p ωω+-+=. 也可先求AB 、OC 、A 和B 的公共质⼼位置⽮量c r . 由c 21)23(r m m p +=求出. 6.2. 以m 、1m 和2m 为质点组,⽔平向右Ox ⽅向动量守恒02211=++x m x m xm . 即02211=?+?+?x m x m x m ,x x x ?+'?=?11,x x x ?+'?=?22. 1m 下降0.1m 则31.01-='?x 、1.02-='?x ,可求出21077.3-?≈?x m. 6.3. 以⼈与物体为质点组,⽔平⽅向动量守恒)(cos )(000u v m v m v m m -+=+α,可求出u m M m v v ++=αcos 0. 因落地时间g v t αsin 0=,所以跳的距离增加了g m M muv t v v l )(sin )cos (00+=-=?αα.6.4. 三种情况均为B m m l m h x v m m m g y A A A A A +++-=2c 20c )(21. 6.5. 按质⼼运动轨道⽤⾃然坐标法,根据质⼼运动定理t a v mg F v m mg F v m N N ωωθθθαsin .sin ,cos 0t n t n 2-=-=-= .可求出t ma mg F t ma mg F N N ωθωθωωθθcos sin ,sin cos 2n 2220n -=+=. 6.6. 以⼆球、四杆和轴为质点组,根据绕竖直轴⾓动量守恒022022sin 2sin 2θωθωl m l m =,可求出0022)sin /(sin ωθθω=. 当杆的质量不可忽略时,结果不变.6.7. 以圆锥、⼩球为质点组,据绕竖直轴⾓动量守恒2202001030103R m R m R m ωωω+=+,可求出)103/(000m m m +=ωω. 只要槽出⼝处的切线⽅向沿母线,则结果不变.6.8. 初始时1m 和2m 的质⼼速度)/(21020c m m v m v += ,由系统动量守恒知以后质⼼速度0c v 不变,由质⼼系中绕质⼼⾓动量守恒可知1m 和2m 相对质⼼系速度不变)(),(2101221021m m v m v m m v m v +='+='. 以τ表⽰质点在质⼼系内作圆周运动的轨道切线⽅向,则ττ )()(',)()('210121022210221021m m v m m m v m v m m v m m m v m v +++=+++=. 质⼼系为惯性系. 由⽜顿定律可求出l m m v m m F T )(212021+=. 6.9. 以传送机及被传送物体为质点组,运动过程中只有⼒矩M 及物体3m 所受重⼒做功,由动能定理αsin 02121)(2121232322221gs m R s M v m v m R v R m -=-++??. 可求出213213])()sin (2[s m m m R g Rm M v ++-=α.6.10. 以1m 和2m 为质点组,爆炸过程中沿⽔平⽅向动量守恒(设1m 和2m 爆炸后速度为21,v v )c 212211)(v m m v m v m +=+,再据动能定理E v m m v m v m =+-+2c 21222211)(212121,可解出)(22112c 1m m m E m v v +±=,)(221211m m m E m v v c += ,1m 和2m 落地时间均为g v t =,故212121)(2m m m m E g vv v t L +=-?=.6.11. 以0m 和m 为质点组,沿⽔平Ox ⽅向动量守恒0)cos (0=++θθ R x m x m ,求出)/(cos 0m m mR x +-=θθ,代⼊机械能守恒⽅程)cos (cos ])sin ()cos [(2121220θαθθθθ-=+++mgR R R x m x m ,即可求出2/120])cos 1()cos (cos 2[θθαθm m m R g +--= . 6.12. 设质⼼速度为c v ,杆⾓速度为ω . 以地为S 系;质⼼系为S '系,将'c v v v +=⽤于B A .,两质点,并沿平⾏于和垂直于杆⽅向投影2211//c cos cos ααv v v == (1)11c sin αωv CA v =+⊥(2)22c sin αωv CB v =+-⊥(3)[请分析(1)式的物理意义. ]由(2)和(3)式可求出l v v /)sin sin (2211ααω+=,所以)/()sin sin ()/(2122112121221c c m m v v l m m m m l m m I L ++=+=='ααωω.根据系统在质⼼系中对质⼼⾓动量守恒,可知ω保持不变.6.13. 以杆和质点为质点组,对过环⼼的竖直轴⾓动量守恒. 设质点遇到杆后的⾓速度为ω,则])([)32(2202202222221a R mv t v a R m a R m L I L L L --+-+-=+=+=ωωω0)352(22022022=--+-=a R mv t mv a R m ωω,即,])352[(22022220t v a R a R v +--=ω因t d d θω=. 将上式积分可求出)352(tan )352(2212222a R a a R a R -?--=-ω.6.14. 以1m ,2m 为质点组,根据动量守恒2211v m v m =,机械能守恒a m Gm a m Gm v m v m 212122*********-=-+,即可求出,2121221])([m m a Gm v +=,2121212])([m m a Gm v +=.6.15. 设杆质量为m 、长为l ,撞击点到O 点距离为a . 由⾓动量Fa ml =? 231,质⼼运动定理--=N F F l m ? 2(-N F 为O 点⽀撑⼒⽔平分量). 由上述⼆式可证明:当l a 32=时,0=-N F . 0=-N F 则系统沿⽔平⽅向动量守恒.6.16. 按住A 点过程中,杆对过A 点竖直轴⾓动量守恒,可求出按住A 点后杆绕A 点转动⾓速度40ωω=,杆的动能损失43. 6.17. 由对固定轴的⾓动量定理t k I d )(d ωω-=,积分可求出0021,e ωωωω==-t l k 则2ln k I t =,把t t l k d e d 0-=ωθ积分得)e 1(0t l k k I --=ωθ,2ln k I t =代⼊则k I k I π4)rad (200ωωθ==(圈).6.18. 以固定轴为Oz 轴,Oy Ox ,轴在刚体所在平⾯内,Ox 轴⽔平向后,Oy 轴竖直向上,规定摆⾓θ正⽅向于Oz 轴正⽅向⼀致. 复摆的运动微分⽅程为x R F x m =c (1)mg F y m y R -=c (2)θθsin amg I -= (3)因θsin c a x =,θcos c a y -=,所以θθθθsin cos 2c a a x -= (4)θθθθcos sin 2c a a y += (5)由(3)式θθsin 2k ag -= ,即θθθθd sin d 2k ag -= ,积分可求出)cos (cos 2022θθθ-=k ag . 把θ及2θ代⼊(4)、(5)式,由(1)、(2)式可求出,sin )cos 2cos 3(022R θθθ--=k mg a F xmg k mg a F y +--=]1cos )cos 2cos 3[(022R θθθ.6.19. 以过⼤圆柱圆⼼2C 竖直向上半直线为定线1. 由定线1到⼤圆柱半径A C 2为?(逆时针为正),定线1到⼆圆柱连⼼线为α(顺时针为正). 以过⼩圆柱圆⼼1C 竖直向下半直线为定线2. 由定线2到⼩圆柱半径B C 1为θ(顺时针为正). 初始时A 、B点重合于⼤圆柱最⾼点,则0)(=-++r r R R θα? 或0)(=-++r r R R θα?.6.20. 沿0v ⽅向建⽴Ox 轴,Oy 轴竖直向上,?⾓正⽅向沿0ω⽅向. 第⼀阶段圆环作有滑滚动,动⼒学⽅程为 f F x m -=c (1)mg F ym N -=c (2) R F mR f -=? 2 (3)R y =c (4) N f F F µ= (5)。
理论力学与材料力学复习思考题
《理论力学与材料力学》复习思考题梁AC 重W =6kN ,在其上作用有力, 力偶矩M =4kN·m ,均布荷载的集度q =2 =30α。
求支座A 、B 的约束反力。
13.77KN BN F =,9.89KN Ax F =-(所设方向与实际方向相反), 1.27KN Ay F =如下图所示的组合梁由AC 和CD 在C 处铰接而成。
梁的A 端插入墙内,B 处为滚动支座。
已知:q =10KN/m ,M =20kN·m,λ=1m ,F =20KN 求:A 、B 处约束反力45.77KN B F =,32.89KN Ax F =, 2.32KN Ay F =-(所6KNP F =213M Fa qa +-求当起重机的伸臂和梁AB 在同一铅垂面内时,支座A 和B 的反力。
0Ax F =,53KN Ay F =,37KN NB F =答案:0Ax =,1510N Ay F =,6840N m A M =⋅ 2280N Bx =-,1785N By F =- 2280N Cx =,455N Cy F =如图变截面杆,已知:2AB BC A =A =500mm ,2CD A =200mm ,5E=210MPa ⨯,求:①做2233答案:2864.7A M KN m =⋅,954.9B M KN m =⋅,716.2C M KN m =⋅,1193.6D M KN m =⋅)剪力图:画出剪力与弯矩图:,P=20kN,b=80mm,h=120mm,答案: 画出下列各图的整体受力图。
答案: AxF AxF AyF AyF DF CF悬臂梁AC上作用有力偶矩M和力P,2⨯E=210MPa A=500mm,50.3mm1 4.78KN m T =-⋅,29.56KN m T =-⋅,3 6.37KN m T =⋅ 扭矩图 、q 、a. 求:支座A 和B 处的约束反力。
答案:1 12 23 3A M ∑=212302e B qa M F a F a -+⋅-⋅=31224e B M F F qaa =+-答案:答案:max26 maxZM FlW bhσ==FF答案:已知M=16KN ·m ,P=20KN 处支座反力。
理论力学思考的题目
第一章静力学公理和物体的受力分析1-1 说明下列式子与文字的意义和区别:(1) F1 = F2(2) F1 = F2(3) 力F1等效于力F2 。
答:(1)若F1 = F2 ,则一般只说明这两个力大小相等,方向相同。
(2)若F1 = F2 ,则一般只说明两个力大小相等,方向是否相同,难以判定。
(3)力F1等效于力F2 ,则说明两个力大小相等,方向、作用效果均相同。
1-2 试区别F R = F1 + F2和F R = F1 + F2两个等式代表的意义。
答:前者为两个矢量相加,后者为两个代数量相加。
1-3 图中各物体的受力图是否有错误?如何改正?(1)(2)(3)(4)答:(1)B处应为拉力,A处力的方向不对;(2)C、B处力方向不对,A处力的指向反了;(3)A处力的方向不对,本题不属于三力汇交问题;(4)A、B处力的方向不对。
(受力图略)1-4 刚体上A点受力F作用,如图所示,问能否在B点加一个力使刚体平衡?为什么?答:不能;因为力F的作用线不沿AB连线,若在B点加和力F等值反向的力会组成一力偶。
1-5 如图所示结构,若力F作用在B点,系统能否平衡?若力F仍作用在B点,但可以任意改变力F的方向,F在什么方向上结构能平衡?答:不能平衡;若F沿着AB的方向,则结构能平衡。
1-6 将如下问题抽象为力学模型,充分发挥你们的想象、分析和抽象能力,试画出它们的力学简图和受力图。
(1)用两根细绳将日光灯吊挂在天花板上;(2)水面上的一块浮冰;(3)一本打开的书静止放于桌面上;(4)一个人坐在一只足球上。
答:略。
(课后练习)1-7 如图所示,力F 作用于三铰拱的铰链C 处的销钉上,所有物体重量不计。
(1)试分别画出左、右两拱和销钉C 的受力图;(2)若销钉C 属于AC ,分别画出左、右两拱的受力图;(3)若销钉C 属于BC ,分别画出左、右两拱的受力图。
提示:单独画销钉受力图,力F 作用在销钉上;若销钉属于AC ,则力F 作用在AC 上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WORD格式 专业资料整理 第一章静力学公理和物体的受力分析 1-1说明下列式子与文字的意义和区别: (1)F1=F2(2)F1=F2(3)力F1等效于力F2。 答:(1)若F1=F2,则一般只说明这两个力大小相等,方向相同。 (2)若F1=F2,则一般只说明两个力大小相等,方向是否相同,难以判定。 (3)力F1等效于力F2,则说明两个力大小相等,方向、作用效果均相同。 1-2试区别FR=F1+F2和FR=F1+F2两个等式代表的意义。 答:前者为两个矢量相加,后者为两个代数量相加。 1-3图中各物体的受力图是否有错误?如何改正?
(1)(2) (3) (4) 答:(1)B处应为拉力,A处力的方向不对;(2)C、B处力方向不对,A处力的指向反了;
(3)A处力的方向不对,本题不属于三力汇交问题;(4)A、B处力的方向不对。(受力图略) 1-4刚体上A点受力F作用,如图所示,问能否在B点加一个力使刚体平衡?为什么? 答:不能;因为力F的作用线不沿AB连线,若在B点加和力F等值反向的力会组成一力偶。WORD格式 专业资料整理 1-5如图所示结构,若力F作用在B点,系统能否平衡?若力F仍作用在B点,但可以任意改变 力F的方向,F在什么方向上结构能平衡? 答:不能平衡;若F沿着AB的方向,则结构能平衡。 1-6将如下问题抽象为力学模型,充分发挥你们的想象、分析和抽象能力, 试画出它们的力学简图和受力图。 (1)用两根细绳将日光灯吊挂在天花板上; (2)水面上的一块浮冰; (3)一本打开的书静止放于桌面上; (4)一个人坐在一只足球上。 答:略。(课后练习) 1-7如图所示,力F作用于三铰拱的铰链C处的销钉上,所有物体重量不计。 (1)试分别画出左、右两拱和销钉C的受力图; (2)若销钉C属于AC,分别画出左、右两拱的受力图; (3)若销钉C属于BC,分别画出左、右两拱的受力图。 提示:单独画销钉受力图,力F作用在销钉上;若销钉属于AC, 则力F作用在AC上。(此作为课堂练习)
第二章平面力系 2-1输电线跨度l相同,电线下垂量h越小,电线越易于拉断,为什么? 答:根据电线所受力的三角形可得结论。 h F
T
由图可知:Wsin2h F 、 T
2sinl
W W 2
F T
∵h越小→α越小→sinα越小;则:FT越大→电线越易于拉断。 2-2图示三种结构,构件自重不计,忽略摩擦,θ=60o。如B处作用相同的作用力F,问铰链A 处的约束力是否相同?WORD格式 专业资料整理 答:不同(自己作出各受力图)。 2-3如图所示,力或力偶对点A的矩都相等,它们引起的支座约束力是否相等?
答:只有图(a)和图(b)中B处的约束力相同,其余都不同。 2-4从力偶理论知道,一力不能与力偶平衡。但是为什么螺旋压榨机上,力偶似乎可以用被压榨 物体的反抗力FN来平衡(如图所示)?为什么如图所示的轮子上的力偶M似乎与重物的力P相平衡? 这种说法错在哪里? 答:图(a)中力偶由螺杆上的摩擦力和法向力的水平分力形 成的力偶平衡,螺杆上的摩擦力与法向力的铅直方向的分 力与FN平衡;图(b)中重力P与O处的约束力构成力偶与 M平衡。 2-5某平面力系向A、B两点简化的主矩皆为零,此 力系最终的简化结果可能是一个力吗?可能是一个力偶 吗?可能平衡吗? 答:可能是作用线过A、B两点的一个力或平衡,不可能是一个力偶。 2-6平面汇交力系向汇交点以外一点简化,其结果可能是一个力吗?可能是一个力偶吗?可能是 一个力和一个力偶吗? 答:可能是一个力(作用线过汇交点);不可能是一个力偶;可能是一个力(作用线不过汇交点)和一 个力偶。 2-7某平面力系向平面内任意一点简化的结果都相同,此力系简化的最终结果可能是什么? 答:可能是一个力偶或平衡。 2-8某平面任意力系向A点简化得一个力FRAFRA0及一个矩为MAMA0的力偶,B为平WORD格式 专业资料整理 面内另一点,问: (1)向B点简化仅得一力偶,是否可能? (2)向B点简化仅得一力,是否可能? (3)向B点简化得FRAFRB,MAMB,是否可能? (4)向B点简化得FRAFRB,MAMB,是否可能? (5)向B点简化得 FF,MM,是否可能?
RARBAB
(6)向B点简化得FRAFRB,MAMB,是否可能? 答:(1)不可能;(2)可能;(3)可能;(4)可能(AB∥FRA的作用线时);(5)不可能;(6)不可能。 2-9图中OABC为正方形,边长为a。已知某平面任意力系向A点 简化得一主矢(大小为FRA)及一主矩(大小、方向均未知),又已知该 力系向B点简化得一合力,合力指向O点。给出该力系向C点简化的主 矢(大小、方向)及主矩(大小、转向)。
答:主矢:FRCFRA、平行于BO,主矩: 2 MaF、顺时针。 CRA
2
2-10在上题中,若某平面任意力系满足F=0、M=0,则 yB
(判断正误): A.必有MA=0;C.可能有Fx=0、MO0; B.必有M=0;D.可能有F0、M=0。 CxO
答:正确:B;不正确:A、C、D。(∵题设条件说明该力系的合力过B点且∥x轴) 2-11不计图示各构件自重,忽略摩擦。画出 刚体ABC的受力图,各铰链均需画出确切的约束 力方向,不得以两个分力代替。图中DE∥FG。 提示:左段OA部分相当一个二力构件,A处 约束力应沿OA,从右段可以判别B处约束力应平 行于DE。(受力图略)
第三章空间力系 3-1在正方体的顶角A和B处,分别作用力F1和F2,如图 所示。求此两力在x、y、z轴上的投影和对x、y、z轴的矩;试 将图中的力F1和F2向点O简化,并用解析式计算其大小和方 向。 答:设正方体的棱长为a,则由题图可知:WORD格式 专业资料整理 333 FF、FF、FF, 1x11y11z1
333
330 MFaF、MFaF、MF; x11y11z1 33 22 FF、F0、FF, 2x22y2z2
22
22 MFaF、MF0、MFaF; x22y2z22
22向O点简化的主矢:
32332 FFFiFjFFk R12112
32332
主矩: 3232 MFFaiFajFak O1212
3232
3-2图示正方体上A点作用一个力F,沿棱方向,问:
(1)能否在B点加一个不为零的力,使力系向A点简化的主矩为零? (2)能否在B点加一个不为零的力,使力系向B点简化的主矩为零? (3)能否在B、C两处各加一个不为零的力,使力系平衡? (4)能否在B处加一个力螺旋,使力系平衡? (5)能否在B、C两处各加一个力偶,使力系平衡? (6)能否在B处加一个力,在C处加一个力偶,使力系平衡? 答:(1)能;(2)不能;(3)不能;(4)不能;(5)不能;(6)能。 3-3图示为一边长为a的正方体,已知某力系向B点简化得 到一合力,向C点简化也得一合力。问: (1)力系向A点和A点简化所得主矩是否相等? (2)力系向A点和O点简化所得主矩是否相等? 答:(1)不等;(2)相等。(题设条件说明该力系的合力过BC点) 3-4在上题图中,已知空间力系向B点简化得一主矢(其大 小为F)及一主矩(大小、方向均未知),又已知该力系向A点简 化为一合力,合力方向指向O点。试:(1)用矢量的解析表达式给出力系向B点简化的主矩; (2)用矢量的解析表达式给出力系向C点简化的主矢和主矩。 答:(1)MBFajk;(2)FRCFi,MCFak。 WORD格式 专业资料整理 3-5(1)空间力系中各力的作用线平行于某一固定平面;(2)空间力系中各力的作用线分别汇交 于两个固定点。试分析这两种力系最多能有几个独立的平衡方程。 答:各为5个。 3-6传动轴用两个止推轴承支持,每个轴承有三个未知力,共6个未知量。而空间任意力系的平 衡方程恰好有6个,是否为静定问题?WORD格式
专业资料整理 答:为超静定问题。 3-7空间任意力系总可以由两个力来平衡,为什么? 答:空间任意力系简化的最终结果为合力、合力偶、力螺旋、平衡四种情况,分别考虑两个力能否与 一个力、一个力偶、力螺旋(力螺旋可以看成空间不确定的两个力、)平衡四种情况平衡。 3-8某一空间力系对不共线的三点主矩都为零,问此力系是否一定平衡? 答:一定平衡。 3-9空间任意力系向两个不同的点简化,试问下述情况是否可能? (1)主矢相等,主矩相等;(2)主矢不相等,主矩相等; (3)主矢相等,主矩不相等;(4)主矢、主矩都不相等。 答:(2)(4)可能;(1)(3)不可能。 3-10一均质等截面直杆的重心在哪里?若把它弯成半圆形,重心位置是否改变? 答:在杆正中间。改变。
第四章摩擦 4-1已知一物块重P=100N,用水平力F=500N的力压在一铅直表面上, 如图所示,其摩擦因数fs=0.3,问此时物块所受的摩擦力等于多少? 答:摩擦力为100N。 4-2如图所示,试比较用同样材料、在相同的光洁度和相同的胶带压力F作 用下,平胶带与三角胶带所能传递的最大拉力。 答:三角带传递的拉力大。 取平胶带与三角带横截面分析正压力(如右下图所示),可见三角带的正压力大于平胶带的正压力。 F ∵接触面处的正压力分别为:平胶带:FNF,三角带:F; N
2sin
∴它们所能传递的最大拉力分别为:平胶带:FT,maxfsF,
三角带: fF s
F,; Tmaxsin
而sin<1,因此,三角带传递的拉力大。 4-3为什么传动螺纹多用方牙螺纹(如丝杠)?而锁紧螺纹多用三角 螺纹(如螺钉)? 答:参考上题分析可知,在相同外力(力偶或轴向力)作用下,方牙螺纹产生的摩擦力较小,而三角 螺纹产生的摩擦力较大,这正好符合传动与锁紧的要求。 4-4如图所示,砂石与胶带间的静摩擦因数fs=0.5,试问
