理论力学习题册答案
合工大理论力学习题册答案

RY = ∑ Y = Y1 + Y2 + Y3 =− 2 3 1 × 150 − × 200 + × 300 2 10 5
= −161.6 N
合力 R 大小为:
2 2 R = RX + RY = (−437.6) 2 + (−161.6) 2 = 466.5 N
方向: 合力偶矩大小为:
α = arctg
PDF created with FinePrint pdfFactory trial version
第四章
平面任意力系
9
4 – 8 均质球重为 P,半径为 r,放在墙与杆 CB 之间,杆长为 ,其与墙的夹角为 α ,
B 端用水平绳 BA 拉住,不计杆重,求绳索的拉力,并求 α 为何值时绳的拉力为最小? [解] 以球为研究对象, A B
1 1 M A = − q1L2 − (q2 − q1 ) L 2 3 1 = − (q1 + 2q2 ) L2 6
PDF created with FinePrint pdfFactory trial version
第四章
平面任意力系
7
4–4
m。 [解]
求下列各梁和刚架的支座反力,长度单位为
∑ X = 0 : −F ∑Y = 0 : −F
AB
− FCB cos 30° − T sin 30° = 0 sin 30° − P − T cos 30° = 0
C
30 30 D P
CB
T =P
联立上述方程可解得:
FAB = 54.64 KN ; (拉) FCB = −74.64 KN ; (压)
∑m
i
= 0, RA ⋅ AB + 15 − 24 = 0 R A = RB = 1.5 KN
理论力学习题答案

2-3 梁的支承及载荷如图示,梁的自重不计。
以载荷M、P、q表示支承处的约束力。
(a) (b)(c) (d)(e) (f)(a)题2-3(a)图题2-3(a)答案图解: 对象:AB杆,受力如图示:建立参考基如图示∑==niixF1=AxF∑==niiAzFm1)(22=⋅+-⋅-⋅aqaMaFaFByaMqaFFBy2412+-=∑==niiyF1=--+qaFFFByAyaMqaFFAy2452-+=(b)、题2-3(b )图 题2-3(b )答案图解: 对象AB 杆,受力如图示,建立参考基如图示∑==n i ix F 100=Ax F∑==ni i Az F m 10)( 03212=-⋅⋅-⋅+⋅M a a q a F a F ByaMF qa F By 2243+-=∑==ni iy F 10 0321=-⋅-+F a q F F By AyaM F qa F Ay 22343-+=(C )、题2-3(C )图 题2-3(C )答案图 解:以AD 梁为研究对象,画出受力图如图所示。
建立参考基如图示0)(1=∑=i n i A F m 02342=⋅-⋅-⋅b qb b qb b F N C 得qb F N C 85= 01=∑=n i iy F 04=--+qb qb F F N C Ay 得qb F Ay 85= 01=∑=n i ix F0=Ax F(d )题2-3(d )图 题2-3(d )答案图解:以AB 梁为研究对象,画受力图如图所示。
建立参考基如图示0)(1=∑=i n i A F m 0222=-⋅⋅-⋅qb b b q b F N B 得qb F N B 23=01=∑=n i iy F 02=⋅-+b q F F Ay N B 得qb F Ay21= 01=∑=n i ix F0=Ax F(e )、题2-3(e )图 题2-3(e )答案图解:以AB 梁为研究对象,画受力图如图所示。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学课后习题解答
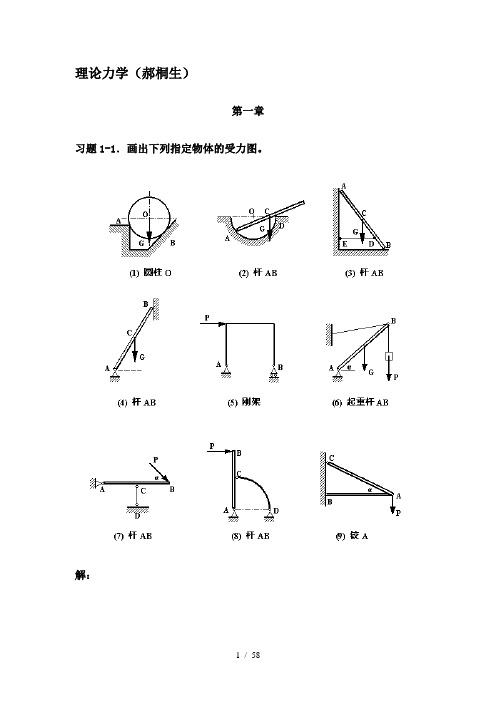
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B 的约束反力。
解:(1) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B 端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向及假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB及水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
《理论力学》课后习题解答(赫桐生高教版)
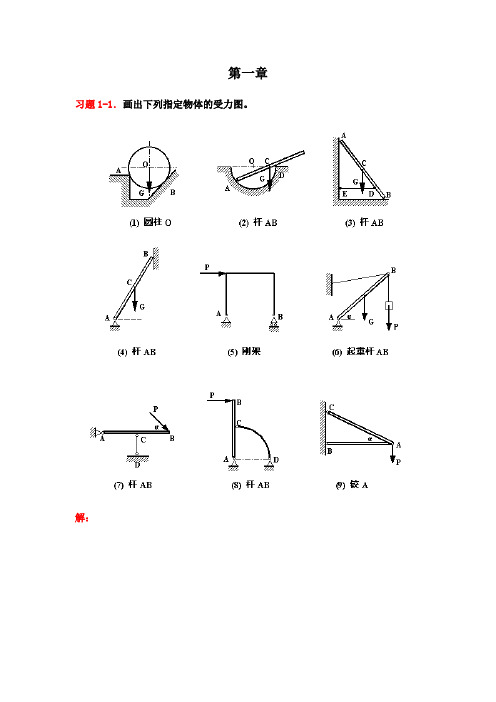
习题4-3.起重机装在三轮小车ABC上,机身重G=100kN,重力作用线在平面LMNF之内,至机身轴线MN的距离为0.5m;已知AD=DB=1m,CD=1.5m,CM=1m;求当载重P=30kN,起重机的平面LMN平行于AB时,车轮对轨迹的压力。
解:(1)研究AB杆,受力分析,画受力图:
列平衡方程:
解方程组:
反力的实际方向如图示。
校核:
结果正确。
(2)研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:
列平衡方程:
解方程组:
反力的实际方向如图示。
校核:
结果正确。
(3)研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:
解:(1)研究重物,受力分析(支承面约束用全反力R表示),画受力图:
(2)由力三角形得
(3)当T与R垂直时,T取得最小值,此时有:
习题5-2.欲转动一放在V形槽中的钢棒料,需作用一矩M=15N.m的力偶,已知棒料重400N,直径为25cm;求棒料与槽间的摩擦系数f。
解:(1)研究钢棒料,受力分析(支承面约束用全反力R表示),画受力图:
解:(1)研究ABC部分,受力分析(注意AC是二力杆),画受力图:
列平衡方程:
解方程组:
(2)研究滚轮C,受力分析(注意BC、CG是二力杆),画受力图:
由力三角形得:
(3)研究平台和联动机构,受力分析(注意CG、DH为二力杆),画受力图:
列平衡方程:
解方程得:
可见结果与d无关;
由几何关系知:
第四章
习题4-1.用图示三脚架ABCD和绞车E从矿井中吊起重30kN的30的重物,△ABC为等边三角形,三脚架的三只脚及绳索DE均与水平面成60o角,不记架重;求当重物被匀速吊起时各叫所受的力。
理论力学习题答案

第一章静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × )1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ ) 1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图所示三铰拱,受力F ,F1作用,其中F作用于铰C的销子上,则AC、BC构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
1.2.2 对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学习题及答案1-7整理

第1章静力分析习题1.是非题(对画√,错画×)1-1.凡在二力作用下的约束称为二力构件。
()1-2.在两个力作用下,使刚体处于平衡的必要条件与充分条件式这两个力等值、反向、共线。
()1-3.力的可传性只适用于一般物体。
()1-4.合力比分力大。
()1-5.凡矢量都可以用平行四边形法则合成。
()1-6.汇交的三个力是平衡力。
()1-7.约束力是与主动力有关的力。
()1-8.作用力与反作用力是平衡力。
()1-9.画受力图时,对一般的物体力的可沿作用现任以的滑动。
()1-10. 受力图中不应出现内力。
()2.填空题(把正确的答案写在横线上)1-11.均质杆在A、B两点分别于矩形光滑槽接触,并在如图所示情况下平衡。
A点的受力方向为,B点的受力方向为。
1-12.AB杆自重不计,在5个已知力作用下处于平衡,则作用于B点的四个力的合力F R的大小F R= ,方向沿。
题1-11图F3R题1-12图3. 简答题1-13.如图所示刚体A、B自重不计,在光滑斜面上接触。
其中分别作用两等值、反向、共线的力F1和F2,问A、B是否平衡?若能平衡斜面是光滑的吗?1-14.如图所示,已知A点作用力F,能否在B点加一力使AB杆平衡?若能平衡A点的力F的方向应如何?1-15.如图所示刚架AC和BC,在C 处用销钉连接,在A、B处分别用铰链支座支承构件形成一个三铰拱。
现将作用在杆BC上的力F沿着其作用线移至刚体AC上。
不计三铰刚架自重。
试问移动后对A、B、C约束反力有没有影响?为什么?1-16.在刚体上的加上任意个的平衡力系,能改变原来力系对刚体的作用吗?但对于变形体而言又是如何?1-17.为什么说二力平衡条件、加减平衡力系原理和力的可传性等只能适用于刚体?1-18.如何区分二力平衡力和作用力与反作用力?1-19.为什么受力图中不画内力?如何理解?1-20.如何判定二力体或者二力杆?(a)(c)(d) (e)(g)(h)题1-21图题1-13图题1-14图题1-15图4.受力分析题1-21.画出下列标注字母物体的受力图,未画重力的各物体其自重不计,所有接触面均为光滑接触。
《理论力学》练习册答案

《理论力学》练习册答案习题一一、填空:1、在作用于刚体的任意力系中加入或减去一个(平衡)力系,并不改变原来力系对刚体的作用。
2、周围物体对被研究物体的限制称为被研究物体的(约束)。
3、平面一般力系平衡的充分必要的解析条件是力系中的所有各力(在力系平面内任一轴上投影的代数各等于零)以及(各力对力系平面内任一点的力矩的代数和也等于零)。
4、力对物体的作用取决于(大小、方向、作用点)这三个要素。
几何条件。
6、可将作用于刚体上的力沿其作用线滑动到刚体上的另一点而不(改变)它对刚体的作用,这称为刚体上力的可传性。
习题二一、填空1、汇交力系就是所有各力的作用线都(汇交于一点)的力系。
2、平行力系就是所有各力的作用线都(平行)的力系。
3、平面汇交力系可合成为一个合力,此(合力)作用线通过(各力的汇交点)。
几何条件。
5、合力在某轴上的投影等于力系中各力在同一轴上(投影)的代数和。
6、平面汇交力系平衡的必要与充分的解析条件是(力系中各力系平面内任一轴上投影的代数各等于零)。
二、选择1.图示汇交力系的力多边形表示:A。
A 力系的合力等于零B 力系的主矢为RC 力系的合力为RD 力系的主矩不为零三、计算压路机碾子垂W =20KN ,半径R =400mm, 若用水平力P 拉碾子越过高h=80mm 的石坎,问P 应多大?若要使P 为最小,,力P 与水平线夹角应为多大?此时力P 等于多少?解:此题用几何法较简单:(拉过石坎时N A =0)1) 作出力三角形如图示:由图中几何关系: 2)P 沿水平方向: 3) 如图:当P 与N B 垂直时其值最小,此时 KNw 125320=⨯=⨯αsin KN tg w p 154320=⨯=⨯=α5354==-=ααsin ,cos R h RP min=习题三一、填空1、一般情况下,力使物体同时发生移动和转动。
而力偶使物体(单纯的发生转动)。
2、当力偶矩保持不变时,力偶可以在其作用面内(转),不改变它对(刚体)作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
( )2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
( )3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
( )4、凡是受两个力作用的刚体都是二力构件。
( )5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
( ) 二.选择题1、在下述公理、法则、原理中,只适于刚体的有( )①二力平衡公理 ②力的平行四边形法则③加减平衡力系公理 ④力的可传性原理 ⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a (球A )b (杆AB)c (杆AB 、CD 、整体)d (杆AB 、CD 、整体)e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADBCEOriginal FigureADBCEWWF AxF Ay F BFBD of the entire frame )a(杆AB、BC、整体)b(杆AB、BC、轮E、整体)c(杆AB、CD、整体)d(杆BC带铰、杆AC、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N,放在水平梁AC的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的交角为300。
忽略梁和撑杆的重量,求撑杆BC 的内力及铰支座A 的约束力。
F BC=5000N(压力);FA=5000N三、图示液压加紧机构中,D 为固定铰链,B、C、E 为活动铰链。
已知力,机构平衡时角度如图,求此时工件H 所受的压紧力。
F H=F/2sin2α五.在图示结构中,各构件的自重不计。
在构件AB上作用一矩为M 的力偶,求支座A 和C的约束力。
F A =F C =aM42六. 图示为曲柄连杆机构。
主动力F=400N 作用在活塞上。
不计构件自重,试问在曲柄上应加多大的力偶矩M 方能使机构在图示位置平衡?M=60N.m第三章平面任意力系(1)一.是非题1.平面力系的主矢量是力系的合力。
()2.某一平面力系,如其力多边形不封闭,则该力系对任意一点的主矩都不可能为零。
3.当平面一般力系向某点简化为力偶时,如果向另一点简化,则其结果是一样的。
4.首尾相接构成一封闭力多边形的平面力系是平衡力系。
()5.若一平面力系对某点之主矩为零,且主矢亦为零,则该力系为一平衡力系。
()二.选择题1、平面内一非平衡汇交力系和一非平衡力偶系,最后可能合成的情况是()①合力偶②一合力③相平衡④无法进一步合成2、将平面力系向平面内任意两点简化,所得的主矢相等,主矩也相等,且主矩不为零,则该力系简化的最后结果为()①一个力②一个力偶③平衡三. 一大小为50N的力作用在圆盘边缘的C点上,如图所示,试分别计算此力对O三点之矩。
AB四、.图示平面任意力系中F1=402N,F2=80N,F3=40N,F4=110N,M=2000N•m m。
各力作用位置如图所示,图中尺寸的单位为mm。
求:(1)力系向O 点简化的结果;(2)力系的合力。
F R =-150i(N),作用线方程y=-6mm四. 图示简支梁中,求AB 两端约束的约束反力。
五.在图示刚架中,已知q m =3Kn/m ,F=62kN ,M=10kN •m ,不计刚架自重。
求固定端A 处的约束力。
0;2;0===By Ay Ax F qL F FF AX=0,F AY=6kN,M A=12kN六.由AC 和CD 构成的组合梁通过铰链C 连接。
支承和受力如图所示。
已知均布载荷强度q=10kN/m,力偶矩M=40kN•m,不计梁重。
求支座A、B、D 的约束力和铰链C 处所受的力。
F A=-15kN;F B=40 kN;F C=5 kN;F D=15 kN七.图示一滑道连杆机构,在滑道连杆上作用水平力。
已知,滑道倾角为β,机构重量和各处摩擦均不计。
试求当机构平衡时,作用在曲柄OA 上的力偶的矩M 与角之间的关系。
ββsinαM=Frcos(-/)第三章平面任意力系(2)一.构架由杆AB,AC 和DF 铰接而成,如图所示。
在DEF 杆上作用一矩为M 的力偶。
不计各杆的重量,求AB 杆上铰链A,D 和B 所受的力。
F AX =0,F AY =-aM 2;F BX =0,F BY =-a M 2;F DX =0,F DY =aM 2 二. 图示构架中,物体重W=1200N ,由细绳跨过滑轮E 而水平系于墙上,尺寸如图。
不计杆和滑轮的重量,求支承A 和B 处的约束反力,以及杆BC 的内力F BC 。
三. 平面桁架的支座和载荷如图所示。
ABC 为等边三角形,E ,F为两腰中点,又AD =DB 。
求杆CD 的内力F CD 。
N F BC 1500-=F CD =-0.866F四、桁架受力如图所示,已知kN 101=F ,kN 2032==F F 。
试求桁架4、5、7、10各杆的内力。
第四章 空间力系一.是非题1. 物体的重心可能不在物体之内。
( )2. 力沿坐标轴分解就是力向坐标轴投影。
( )3. 当力与轴共面时,力对该轴之矩等于零。
( )4. 在空间问题中,力偶对刚体的作用完全由力偶矩矢决定。
( )5. 将一空间力系向某点简化,若所得的主矢和主矩正交,则此力系简化的最后结果为一合力。
( )二、填空题1. 空间力系有( )个独立的平衡方程,空间汇交力系有( )个独立的平衡方程,空间力偶系有( )个独立的平衡方程,空间平行力系有( )个独立的平衡方程;平面力系有( )个独立的平衡方程,平面汇交力系有( )个独立的平衡方程,平面力偶系有( )个独立的平衡方程,平面平行力系有( )个独立的平衡方程。
①1 ②2 ③3 ④4 ⑤5 ⑥62、力对点之矩是------,力对轴之矩是------,空间力偶矩矢是------。
① 代数量 ② 滑动矢量 ③ 定位矢量 ④ 自由矢量三、水平圆盘的半径为 r ,外缘C 处作用力F 。
力F 位于铅垂平面内,且与 C 处圆盘切线夹角为600,其他尺寸如图所示。
求力 F 对x ,y ,z 轴之矩。
;6.43;20;7.16;8.2110754KN F KN F KN F KN F N N N N -=-===M X=F(h-3r)/4,M y=3 F(r+h)/4,M Z=-Fr/2四、挂物架如图所示,三杆的重量不计,用球铰链连接于O 点,平面 BOC为水平面,且OB = OC ,角度如图。
若在 O 点挂一重物 G,重为1000N,求三杆所受的力。
F OA=-1414N,F OB=F OC=707N五.图示六杆支撑一水平板,在板角处受铅直力F作用。
设板和杆自重不计,求各杆的内力。
F1=F5=-F,F3=F,F2=F4=F6=0六.图示平面图形中每一方格的边长为20mm,求挖去一圆后剩余部分面积重心的位置。
yOx七、均质块尺寸如图所示,求其重心的位置。
x c =23.1mm ,y c =38.5mm ,z c =-28.1mmmm y mm x c c 53.59,73.81==第五章 摩 擦(1)一、是非题1、当一物体上有几处与周围物体接触时,这几个接触面的摩擦力同时达到临界平衡状态。
( )2、摩擦力属于未知的约束反力,它的大小和方向完全可由平衡方程决定。
( )3、物体受到支承面的全反力(摩擦力与法向反力的合力)与支承面法线间的夹角称为摩擦角。
( )二、一物块重为Q = 400N ,置于水平地面上,受到大小为80N 的拉力作用,如图所示,假设拉力T 与水平夹角为ο45=α,物块与地面的摩擦因数为2.0=s f ,试求: ① 判断物块是否发生移动,并确定此时的摩擦力大小;② 要使物块发生移动,拉力至少要多大?答案:(1)摩擦力为56.56N(2)94.3N三、如图所示,置于V 型槽中的棒料上作用一力偶,力偶的矩m N 15⋅=M 时,刚好能转动此棒料。
已知棒料重N 400=W ,直径m 25.0=D ,不计滚动摩阻。
试求棒料与V 形槽间的静摩擦因数f s 。
答案:0.223四、梯子AB 长为2a ,重为P ,其一端置于水平面上,另一端靠在铅垂墙上,如图所示。
设梯子与地和墙的静摩擦因数均为s f ,问梯子与水平线的夹角α多大时,梯子能处于平衡?答案:222m παϕπ≤≤-五、均质箱体A 的宽度b =1m ,高h =2m ,重P =200kN ,放在倾角α=200的斜面上。
箱体与斜面之间的摩擦因数f s =0.2。
今在箱体的C 点系一无重软绳,方向如图示,绳的另一端绕过滑轮D 挂一重物E 。
已知BC =a =1.8m 。
求使箱体处于平衡的重物E 的重量。
答案:kN P kN E 2.10421.40≤≤第五章摩擦(2)一、鼓轮B 重500N,放在墙角里,如图所示。
已知鼓轮与水平地板间的摩擦因数为0.25,而铅直墙壁则假定是绝对光滑的。
鼓轮上的绳索下端挂着重物。
设半径R=200mm,r=100mm,求平衡时重物A 的最大重量。
答案:500N二、如图所示,A 块重500N,轮轴B 重1000N,A 块与轮轴的轴以水平绳连接。
在轮轴外绕以细绳,此绳跨过一光滑的滑轮D,在绳的端点系一重物C。
如A块与平面间的摩擦因数为0.5,轮轴与平面间的摩擦因数为0.2,不计滚动摩阻,试求使系统平衡时物体C的重量P的最大值。
答案:208N三、如图所示,一轮半径为R ,在其铅直直径的上端B 点作用水平力F ,轮与水平面间的滚阻系数为δ。
问使轮只滚不滑时,轮与水平面的摩擦系数f s 需满足什么条件?答案:Rf s 2δ≥四、在半径为r 、重为1W 的两个滚子上放一木板,木板上放一重物,板与重物共重2W 如图,在水平力F 的作用下,木板与重物以匀速沿直线缓慢运动。
设木板与滚子之间及滚子与地面之间的滚动摩擦因数分别为δ′及δ,并且无相对滑动,试求力F 的大小。
答案:)(21'2δδ+=W rF第六章 点的运动学一.是非题1、点作曲线运动时,其加速度的大小等于速度的大小对时间的导数。
