2018届高考数学艺术生短期集训专题知识突破:考点1 集合的概念与运算
高考数学总复习 第一章 第一节集合的概念与运算课件 理

第十七页,共35页。
考点(kǎo 集合(jíhé)的基本关系及空集的妙用 diǎn)三
【例3】 设集合A={x|x2-3x-10≤0},B={x|m+1≤x≤2m -1},若B⊆A,求实数(shìshù)m的取值范围.
思路点拨:考查集合间的包含、相等关系,关键搞清A,B两 集合谁是谁的子集.若B⊆A,说明B是A的子集,即集合B中元素 都在集合A中,注意B是∅的情况;同样若A⊆B,说明A是B的子集, 此时注意B是不是∅;若A=B,说明两集合元素完全相同.
A.A=B B.B=C C.C=E D.B=E
思路点拨:要注意分辨各集合的代表元素是什么,如果性质 相同,但代表元素不同,则它们所表示的集合也是不一样的.因此 对于集合问题(wèntí),要首先确定它属于哪类集合(数集、点集或某 类图形).
第十五页,共35页。
解析:集合 A 是用列举法表示,它只含有一个元 素,即函数 y=x2+2,集合 B,C,E 中的元素都是数, 即这三个集合都是数集,集合 B 表示的是函数 y=x2 +2 的值域2,+∞,集合 C 表示的是函数 y=x2+2 的 定 义 域 R, 集 合 E 是不 等 式 x - 2≥0 的 解集 2,+∞,集合 D 的元素则是平面上的点,此集合是 函数 y=x2+2 的图象上所有点所组成的集合.故只有 B=E.故选 D.
第七页,共35页。
2.并集. (1)定义: 由所有属于集合A或集合B的元素组成的集合,称 为(chēnɡ w集éi)合__(_j_íh_é_)_A_与__集__合__(_j_íh的é)并B集,记作___A__∪__B_____(读作 “A并B”).即 A∪B={ x|x∈A,或x∈B}. (2)性质:
2018届高考数学专题1.1集合的概念及运算同步单元双基双测(B卷)文

专题1.1 集合的概念及运算(测试时间:120分钟 满分:150分)一、选择题(共12小题,每题5分,共60分)1. 集合{}{}0,2,022>==>-=x y y B x x x A x,R 是实数集,则A B C R )(等于( )A .RB .),1()0,(+∞-∞C .(]10,D .(]()∞+∞-,21, 【答案】D 【解析】考点:集合的运算 2. 若集合{0}A xx =≥,且A B B = ,则集合B 可能是( )A .{}1,2B .{1}x x ≤C .{1,0,1}-D .R【答案】A 【解析】试题分析:由A B B = 知B A ⊆,故选A 考点:集合的交集.3. 已知集合{}ln(12)A x y x ==-,{}2B x x x =≤,则()=A BC A B ( )A .(,0)-∞B .1(,1]2-C .(,0)-∞1[,1]2D .1(,0]2-【来源】2018届浙江省富阳市二中高三上学期第二次质量检测理科数学试卷(带解析) 【答案】C 【解析】试题分析:集合)21,(-∞=A ;]1,0[=B ,]1,(-∞=B A ,)21,0[=B A ,故1()=(-,0)[,1]2∞ A B C A B 考点:集合的运算;4. 集合{}2*|70,A x x x x =-<∈N ,则*6|,B y y A y ⎧⎫=∈∈⎨⎬⎩⎭N 中元素的个数为A. 1个B. 2个C. 3个D. 4个【来源】河北省武邑中学2018届高三下学期第四次模拟考试理科数学试题 【答案】D【解析】{}{}{}2**|70,|07,1,2,3,4,5,6A x x x x x x x =-<∈=<<∈=N N ,{}*6|,1,2,3,6B y y A y ⎧⎫=∈∈=⎨⎬⎩⎭N ,则B 中的元素个数为4个.本题选择D 选项.5. 已知()(){}3,3,,202y M x y N x y ax y a x ⎧-⎫===++=⎨⎬-⎩⎭且∅=⋂N M ,则=a ( )A .-6或-2B .-6C .2或-6D .2 【答案】A 【解析】考点:1.集合的运算;直线的位置关系.6. {}2|1, B y y x x A ==+∈,则集合B 的子集个数为( ) A. 5 B. 8 C. 3 D. 2【来源】【全国百强校】黑龙江省大庆实验中学2017届高三考前得分训练(一)数学(文)试题 【答案】B 【解析】解答:A ={−1,0,1,2},B ={1,2,5},子集个数为23=8个,故选B.点睛:1.用描述法表示集合,首先要弄清集合中代表元素的含义,再看元素的限制条件,明确集合类型,是数集、点集还是其他的集合.2.求集合的交、并、补时,一般先化简集合,再由交、并、补的定义求解.3.在进行集合的运算时要尽可能地借助Venn 图和数轴使抽象问题直观化.一般地,集合元素离散时用Venn 图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍. 7. 已知集合{}{}2120,3,1x M x x x N y y x =+-≤==≤,则集合{}x x M x N ∈∉且为( )A .(]0,3B .[]4,3-C .[)4,0- D .[]4,0- 【来源】【百强校】2016届安徽师大附中高三最后一卷文科数学试卷(带解析) 【答案】D 【解析】 试题分析:{}[]{}(]21204,3,3,10,3x M x x x N y y x =+-≤=-==≤= ,∴{}[]4,0x x M xN ∈∉=-且.故选D . 考点:集合运算. 8. 的一切实数x 也满足不等式,则b 的取值范围是( )【来源】【全国市级联考word 】河北省张家口市2016-2017学年高二下学期期中考试数学(文)试题 【答案】B9. 设集合{}2|230A x x x =+->,集合{}2|210,0B x x ax a =--≤>.若A B 中恰含有一个整数u ,则实数a 的取值范围是( ) A .30,4⎛⎫ ⎪⎝⎭ B .34,43⎡⎫⎪⎢⎣⎭ C .3,4⎡⎫+∞⎪⎢⎣⎭D .()1,+∞ 【答案】B 【解析】考点:1.集合的运算.2.不等式的解法.3.分类的思想. 10. 集合⎭⎬⎫⎩⎨⎧<+-=011x x xA ,{}a b x x B <-=,若“1=a ”是“A B ≠∅ ”的充分条件,则b 的取值范围是( )A .-2≤b<2B .-2<b≤2C .-3<b <-1D .-2<b <2 【答案】D 【解析】试题分析:{}11A x x =-<< ,{}B x a b x a b =-+<<+,若“1=a ”是“A B ≠∅ ”的充分条件,则1111b b -+<⎧⎨+>-⎩,解得-2<b <2。
高三数学复习课件 1.1 集合的概念与运算

因为A={1,2,3},B={2,3,4},所以A∪B={1,2,3,4},故选A. A
关闭 关闭
解析 答案
-11-
课堂练习
4.已知集合A={x|x<2},B={x|3-2x>0},则( )
A.A∩B=
������
������
<
3 2
C.A∪B=
������
������
<
3 2
B.A∩B=⌀ D.A∪B=R
-5-
知识梳理
2.集合间的基本关系 (1)子集:若对任意x∈A,都有 x∈B ,则A⊆B或B⊇A. (2)真子集:若A⊆B,但 存在x∈B,且x∉A ,则A⫋B或B⫌A. (3)相等:若A⊆B,且 B⊆A ,则A=B. (4)空集:⌀是 任何 集合的子集,是任何 非空 集合的真x<2},B={x|3-2x>0}=
������
������
<
3 2
,
∴A∪B={x|x<2},A∩B=
������
������
<
3 2
,故选 A.
A
关闭
关闭
解析 答案
-12-
课堂练习
5.(2018天津,文1)设集合A={1,2,3,4},B={-1,0,2,3},
C={x∈R|-1≤x<2},则(A∪B)∩C=( )
-8-
课堂练习
1.下列结论正确的打“√”,错误的打“×”.
(1)在集合{x2+x,0}中,实数x可取任意值. ( × ) (2){x|y=x2+1}={y|y=x2+1}={(x,y)|y=x2+1}.( × )
(3)A⊆B⇔A∩B=A⇔A∪B=B;(A∩B)⊆(A∪B).( √ )
高考数学复习考点知识专题讲解课件1---集合的概念及运算

解得 2≤m≤3.
由①②可得,符合题意的实数 m 的取值范围为(-∞,3].
答案:(-∞,3]
返回导航
新高考 大一轮复习 · 数学
引申探究 在本例(2)中,若“B⊆A”变为“B A”,其他条件不变,如何求解? 解:∵B A,∴①若 B=∅,成立,此时 m<2.
②若 B≠∅,则2mm+-11≥≥-m2+,1, 2m-1<5
1.集合与元素 (1)集合中元素的三个特征: 确定性 、 互异性、 无序性. (2)元素与集合的关系是 属于 或 不属于 ,用符号 ∈ 或 ∉ 表示. (3)集合的表示法: 列举法 、 描述法 、 图示法 .
返回导航
新高考 大一轮复习 · 数学
(4)常见数集的记法
集合 自然数集 正整数集 整数集 有理数集 实数集
范围为( )
A.(8,+∞)
B.[8,+∞)
C.(16,+∞)
D.[16,+∞)
解析:因为集合 A 中至少有 3 个元素,所以 log2k>4,所以 k>24=16,故选 C. 答案:C
返回导航
新高考 大一轮复习 · 数学
3.已知集合 A={m+2,2m2+m},若 3∈A,则 m 的值为________.
③当 B=∅时,Δ=4(a+1)2-4(a2-1)<0, 解得 a<-1. 综上所述,所求实数 a 的取值范围是(-∞,-1]∪{1}.
返回导航
新高考 大一轮复习 · 数学
由根与系数的关系,得
Δ=4a+12-4a2-1>0, -2a+1=-4, a2-1=0,
解得 a=1;
②当 B≠∅且 B A 时,B={0}或 B={-4},
并且 Δ=4(a+1)2-4(a2-1)=0, 解得 a=-1,此时 B={0}满足题意;
01集合的概念及运算

251 16, 261 32, 271 64, 281 128,
且1 4 16 64 128 211,
i1 1, i2 2, i3 5, i4 7, i5 8.
走进高考
综上知,当A⊆B时,a<-8或a≥2.
(2)当 a=0 时,显然 B ⊆A;
当 则 又当∵ 当a则则 又则又<a- 4aaa∵<0≤∵<>1a0-4a-0时 0a4a-- 时4aa≤, 时<≤1a≥>1a<, 0≤1a2,-20∴ ,,2->,若-12>2∴- 若若12212∴, B-12BB⊆ ,<-⊆⊆∴ 12a,,<∴AA1<2a∴,,<0<∴- - .a0- -如如如 <.00128<<1208≤ <--图图图 <≤aa. a≤ ≤a128a,,a<,<<≤<22<0000aa.<<0.0.
走进高考
【2】(10 湖南文 15)若规定 E={a1,a2 ,..., a10}的子集{ai1 ai2 ,..., ain }
为 E 的第 k 个子集,其中 k 2i11 2i2 1 2in 1 ,则
(1){a1, a3} 是 E 的第_____5____个子集;
(2)E 的第 211 个子集是_{__a_1_,__a_2_,__a_5_,__a_7__,_a_8_}___.
(4)常用数集的记法
数集
自然 数集
正整数集
整数 集
有理 数集
实数 集
复数 集
记法 N N(或N ) Z Q R C
最新-2018高考数学 夯实基础 集合的含义、基本关系和
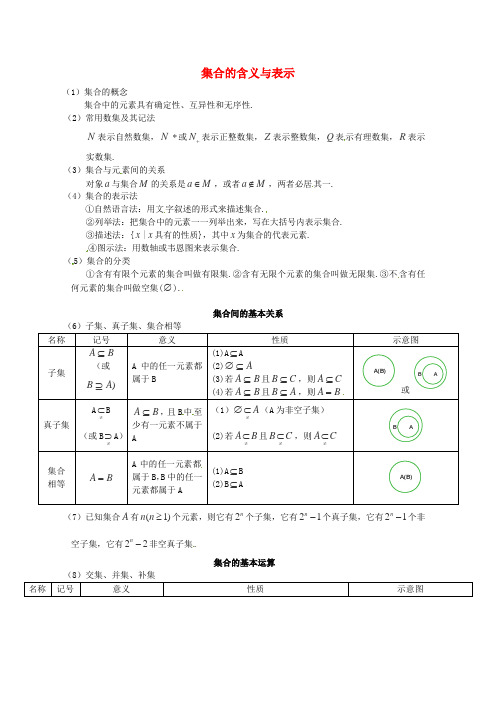
集合的含义与表示(1)集合的概念集合中的元素具有确定性、互异性和无序性. (2)常用数集及其记法N 表示自然数集,N *或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R 表示实数集.(3)集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. (4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. (5)集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).集合间的基本关系(6)子集、真子集、集合相等中至(7)已知集合A 有(1)n n ≥个元素,则它有2n个子集,它有21n-个真子集,它有21n-个非空子集,它有22n-非空真子集.集合的基本运算B B ⊇A{|x x2A【补充知识】含绝对值的不等式与一元二次不等式的解法(1)含绝对值的不等式的解法解集{|x a -<|x x a <-|0)c >b +看成一个整(0)a a >型不等式来求解(2)一元二次不等式的解法∆=0∆> 0∆= 二次函数0)y ax =一元二次方程2ax bx +22b b a-±-(其中12x x <122b x x a==-2ax bx +1x <或x >{|x }2b x a≠-2ax bx +12|x x x <<∅ )()()U U B A B =?)()()U U B A B =?。
(浙江版)2018年高考数学一轮复习(讲+练+测): 专题1.1 集合的概念及其基本运算(讲)
专题1.1 集合的概念及其基本运算【考纲解读】【知识清单】1.元素与集合(1)集合元素的特性:确定性、互异性、无序性.(2)集合与元素的关系:若a 属于集合A ,记作a A ∈;若b 不属于集合A ,记作b A ∉. (3)集合的表示方法:列举法、描述法、图示法. (4)常见数集及其符号表示对点练习:【2017浙江嘉兴一中模拟】若集合{}1,2,3A =, (){},40,,B x y x y x y A =+-∈,则集合B 中的元素个数为( )A. 9B. 6C. 4D. 32.集合间的基本关系(1)子集:对于两个集合A 与B ,如果集合A 的任何一个元素都是集合B 的元素,我们就说集合A 包含于集合B ,或集合B 包含集合A ,也说集合A 是集合B 的子集。
记为A B ⊆或B A ⊇. (2)真子集:对于两个集合A 与B ,如果A B ⊆,且集合B 中至少有一个元素不属于集合A ,则称集合A 是集合B 的真子集。
记为A B ⊂≠.(3)空集是任何集合的子集, 空集是任何非空集合的真子集.(4)若一个集合含有n 个元素,则子集个数为2n个,真子集个数为21n-. 对点练习:【2017辽宁锦州质检(一)】集合{|3,}n M x x n N ==∈,集合{|3,}N x x n n N ==∈,则集合M 与集合N 的关系( )A. M N ⊆B. N M ⊆C. M N φ⋂=D. M ⊆N 且N ⊆M 【答案】D【解析】因为1,1;6,6M N N M ∈∉∈∉ ,所以M ⊆N 且N ⊆M ,选D. 3.集合的运算(1)三种基本运算的概念及表示(2)三种运算的常见性质A A A =, A ∅=∅ , AB B A = , A A A =, A A ∅=, A B B A =.(C A)A U U C =,U C U =∅,U C U ∅=.A B A A B =⇔⊆, A B A B A =⇔⊆, ()U U U C A B C A C B =,()U U U C A B C A C B =.【2017浙江卷】已知}11|{<<-=x x P ,}20{<<=x Q ,则=Q PA .)2,1(-B .)1,0(C .)0,1(-D .)2,1(【答案】A【考点深度剖析】高考对集合知识的考查要求较低,均是以小题的形式进行考查,要求考生熟练掌握与集合有关的基础知识,集合的基本运算.纵观近5年的高考试题,主要考查集合的基本运算,其中集合以描述法呈现,元素的性质以不等式为主,偶有离散元素呈现.解决这类问题的关键在于正确理解集合中元素所具有属性的,明确集合中含有的元素,进一步进行交、并、补等运算.【重点难点突破】考点1 集合的概念【1-1】若a b R ∈,,集合,{10,,a b a b ba}={+},,求b a -的值________. 【答案】2【解析】由,{10,,a b a b ba}={+},可知0a ≠,则只能0a b +=,则有以下对应关系: 0,,1,a b b a ab +=⎧⎪⎪=⎨⎪=⎪⎩① 或0,,1,a b b a b a⎧⎪+=⎪=⎨⎪⎪=⎩ ② 由①得1,1,a b =-⎧⎨=⎩符合题意;②无解.∴2b a -=.【1-2】集合2*{|70,}A x x x x N =-<∈,则*6{|,}B y N y A y=∈∈中元素的个数为( ) A . 1个 B .2个 C .3个 D .4个 【答案】D 【解析】试题分析:2*{|70,}A x x x x N =-<∈}6,5,4,3,2,1{=,}6,3,2,1{B =,因为B B A = ,∴集合2*{|70,}A x x x x N =-<∈,则*6{|,}B y N y A y=∈∈中元素的个数为个. 【领悟技法】与集合元素有关问题的思路:(1)确定集合的元素是什么,即确定这个集合是数集还是点集. (2)看这些元素满足什么限制条件.(3)根据限制条件列式求参数的值或确定集合元素的个数,但要注意检验集合是否满足元素的互异性. 【触类旁通】【变式一】【2017河北唐山期末】已知集合{}{}22,1,0,2,3,|1,A B y y x x A =--==-∈,则A B 中元素的个数是( )A .B .C .D . 【答案】B【变式二】设P 、Q 为两个非空集合,定义集合{|}P Q a b a P b Q ∈∈+=+,.若{}{}0,2,51,2,6P Q =,=,则P Q +中元素的个数是( )A .9B .8C .7D .6 【答案】B【解析】P Q +={}1,2,3,4,6,7,8,11,故P Q +中元素的个数是8. 考点2 集合间的基本关系【2-1】【2017四川适应性测试】设集合{}1 1A =-,,集合{}1 B x ax a R ==∈,,则使得B A⊆的的所有取值构成的集合是( )A .{}0 1,B .{} 1-0 ,C .{}1 1-,D .{}1 0 1-,, 【答案】D【解析】:因为B A ⊆,所以,{1},{1}B =∅-,因此0,1,1a =-,选D.【2-2】已知集合2{|()}A x y lg x x ==-,2{|00}B x x cx c <>=-,,若A B ⊆,则实数的取值范围是( ) A .(0,1] B .1,+∞) C .(0,1) D .(1,+∞)【答案】 B【领悟技法】1.判断两集合的关系常用两种方法:一是化简集合,从表达式中寻找两集合间的关系;二是用列举法表示各集合,从元素中寻找关系.2.已知两集合间的关系求参数时,关键是将两集合间的关系转化为元素间的关系,进而转化为参数满足的关系,解决这类问题常常运用数轴、Venn 图帮助分析. 【触类旁通】【变式1】设集合10{|}P m m <<=-,24{4|0Q m mx mx <=+-对任意实数x 恒成立,且}m R ∈,则下列关系中成立的是( )A .P Q ⊂≠B .Q P ⊂≠C .P Q =D .PQ ∅=【答案】A【解析】10{|}P m m <<=-,20,:16160,m Q m m <⎧⎨∆=+<⎩或0m =. ∴10m <≤-.∴10{|}Q m m <≤=-.∴P Q ⊂≠.【变式2】已知集合,44k M x x k Z ππ⎧⎫==+∈⎨⎬⎩⎭,集合,84k N x x k Z ππ⎧⎫==-∈⎨⎬⎩⎭,则( ) A. M N =∅ B. M N ⊆ C. N M ⊆ D. MN N =【答案】B 【解析】(22),,8484k n M x x k Z x x k Z ππππ⎧+⎫⎧⎫==-∈==-∈⎨⎬⎨⎬⎩⎭⎩⎭,284k N x x ππ⎧==-⎨⎩或(21),84k k Z ππ-⎫-∈⎬⎭,所以M N ⊆. 考点3 集合的基本运算【3-1】【2017新课标1】已知集合A ={}|2x x <,B ={}|320x x ->,则A .AB =3|2x x ⎧⎫<⎨⎬⎩⎭B .A B =∅C .AB 3|2x x ⎧⎫=<⎨⎬⎩⎭D .AB=R【解析】由320x ->得32x <,所以33{|2}{|}{|}22A B x x x x x x ⋂=<⋂<=<,选A . 【3-2】【2017浙江五校联考】设全集U R =,集合{|3},{|05},A x x B x x =≥=≤<则集合()U C A B ⋂= ( )A. {|03}x x <<B. {|03}x x ≤≤C. {|03}x x <≤D. {|03}x x ≤< 【答案】D【3-3】【2017浙江台州一模】若集合,则( )A.B.C.D.【答案】C 【解析】,所以或,故选C.【领悟技法】1. 集合的运算要注意灵活运用韦恩图和数轴,一般情况下,有限集的运算用维恩图分析,无限集的运算用数轴,这实际上是数形结合的思想的具体运用。
2018高三数学(理)一轮复习课件:1-1集合的概念与运算
关闭
由题意可知,B={x|-1<x<2,x∈Z}={0,1},而A={1,2,3}, 故A∪B={0,1,2,3},故选C. C
解析
关闭
答案
知识梳理 知识梳理 双基自测
-11-
1 2 3 4 5
3.(2016河南郑州一模)设全集U={x∈N*|x≤4},集合 A={1,4},B={2,4},则∁U(A∩B)=( ) A.{1,2,3} B.{1,2,4} C.{1,3,4} D.{2,3,4}
A=B
或
知识梳理 知识梳理 双基自测
-6-
1 2 3 4 5
3.集合的运算
集合的并集 图形 符号 A∩B ∁U A A∪B {x|x∈A,且x∈B} ={x|x∈U,且x∉A} ={x|x∈A或x∈B} = 集合的交集 集合的补集
知识梳理 知识梳理 双基自测
-7-
1 2 3 4 5
4.集合的运算性质 (1)并集的性 质:A∪⌀=A;A∪A=A;A∪B=B∪A;A∪B=A⇔ B⊆A . (2)交集的性 质:A∩⌀=⌀;A∩A=A;A∩B=B∩A;A∩B=A⇔ A⊆B . (3)补集的性 质:A∩(∁UA)=⌀;A∪(∁UA)=U;∁U(∁UA)= A ;∁U(A∪B)=(∁UA)∩(∁ UB);∁U(A∩B)=(∁UA)∪(∁UB).
知识梳理 知识梳理 双基自测
-8-
1 2 3 4 5
5.集合关系的常用结论 若有限集A中有n个元素,则A的子集有 2n-1 个,真子集有 2n-1 个.
2n
个,非空子集有
知识梳理 知识梳理 双基自测
-9-
1 2 3 4 5
1.下列结论正确的打“√”,错误的打“×”. (1)在集合{x2+x,0}中,实数x可取任意值. ( ) (2){x|y=x2+1}={y|y=x2+1}={(x,y)|y=x2+1}.( ) (3)A⊆B⇔A∩B=A⇔A∪B=B;(A∩B)⊆(A∪B).( ) (4)若A∩B=A∩C,则B=C. ( ) (5)(教材习题改编P5T2(3))直线y=x+3与y=-2x+6的交点构成的集 合是{1,4}. ( )
专题01 集合的概念与运算 (解析版)
专题01 集合的概念与运算【名师预测】江苏高考对集合知识的考查比较低,以填空题的形式进行考查,主要考查集合与集合、元素与集合间的关系以及集合的交集、并集、补集的运算,同时注重对Venn图、数轴等数形结合思想的考查。
集合的基本运算有时会以集合知识为载体,往往与函数、方程、不等式等知识结合考查,体现出小题目综合化的命题趋势。
集合的学习要有弹性,要有所取舍.比如我们不必在集合间的关系上过于深究,也不必在集合的概念等内容上过于钻研。
【知识精讲】1.集合的相关概念(1)集合元素的三个特性:确定性、无序性、互异性.(2)元素与集合的两种关系:属于,记为∈;不属于,记为∉.(3)集合的三种表示方法:列举法、描述法、图示法.(4)五个特定的集合:2.集合间的基本关系3.集合的基本运算4.集合关系与运算的常用结论(1)若集合A中有n个元素,则A的子集有2n个,真子集有12n-个,非空子集有12n-个.(2)集合的传递性:A⊆B,B⊆C⇒A⊆C.(3)A⊆B⇔A∩B=A⇔A∪B=B.(考虑A是空集和不是空集两种情况)(4)C U(A∩B)=(C U A)∪(C U B),C U(A∪B)=(C U A)∩(C U B).【典例精练】考点一集合的基本概念例1. A={1,2,4},则集合B={(x,y)|x∈A,y∈A}中元素的个数为________.【解析】集合B中元素有(1,1),(1,2),(1,4),(2,1),(2,2),(2,4),(4,1),(4,2),(4,4),共9个.故答案为9.例2.若-1∈{a-1,2a+1,a2-1},则实数a的取值集合是________.【解析】若a-1=-1,解得a=0,此时集合中的元素为-1,1,-1,不符合元素的互异性;若2a+1=-1,解得a=-1,此时集合中的元素为-2,-1,0,符合题意;若a2-1=-1,解得a=0,不符合题意,综上所述,a=-1.故答案为{-1}.例3.若集合A={x∈R|ax2-3x+2=0}中只有一个元素,则a=________.【解析】若集合A中只有一个元素,则方程ax2-3x+2=0只有一个实根或有两个相等实根.①当a=0时,x=23,符合题意;②当a ≠0时,由Δ=(-3)2-8a =0,得a =98. ∴a 的值为0或98故答案为0或98.例4.已知集合A ={1,2,3},B ={1,m },若3-m ∈A ,则非零实数m 的值是________. 【解析】由题意知,若3-m =1,则m =2,符合题意;若3-m =2,则m =1,此时集合B 不符合元素的互异性,故m ≠1; 若3-m =3,则m =0,不符合题意. 故m =2. 故答案为2.【方法点睛】与集合中元素有关问题的求解策略 (1)确定集合的元素是什么,即集合是数集还是点集; (2)看这些元素满足什么限制条件;(3)根据限制条件列式求参数的值或确定集合中元素的个数,但要注意检验集合是否满足元素的互异性.在解决集合中含有字母的问题时,一定要返回代入验证,防止与集合中元素的互异性相矛盾. 考点二 集合间的基本关系例5.已知集合{}1,2,3,4,5A =,{}(,),,,B x y x A y A x y x y A =∈∈<+∈,则集合B 的子集的个数是 . 【解析】∵集合{}1,2,3,4,5A =,{}(,),,,B x y x A y A x y x y A =∈∈<+∈ ∴{}(1,2),(2,3),(1,3),(1,4)B = ∴集合B 的子集个数是4216=. 故答案为16.例6.设集合{}2,4A =,{}2,2B a =,(其中0a <),若A B =,则实数a =________. 【解析】∵集合{}2,4A =,{}2,2B a =,且A B = ∴24a = 又0a < ∴2a =- 故答案为-2.例7.已知集合{}1,2a A =,集合{}1,1,4B =-,且A B ⊆,则正实数a =________.【解析】∵集合{}1,2a A =,集合{}1,1,4B =-,且A B ⊆ ∴24a = ∴2a = 故答案为2.例8.已知集合{}15A x x =≤<,{}3B x a x a =-<≤+,若()B A B ⊆,则实数a 的取值范围为________.【解析】∵()B A B ⊆∴B A ⊆①当B =∅时,满足B A ⊆,此时3a a -≥+,即32a ≤-. ②当B ≠∅时,要使B A ⊆,则3135a a a a -<+⎧⎪-≥⎨⎪+<⎩,解得312a -<≤-由①②可知,实数a 的取值范围为(,1]-∞-. 故答案为(,1]-∞-.【方法点睛】判断集合间关系的3种方法①列举法:根据题中限定条件把集合元素表示出来,然后比较集合元素的异同,从而找出集合之间的关系;②结构法:从元素的结构特点入手,结合通分、化简、变形等技巧,从元素结构上找差异进行判断; ③数轴法:在同一个数轴上表示出两个集合,比较端点之间的大小关系,从而确定集合与集合之间的关系,运用数轴图示法时要特别注意端点是实心还是空心.注意:空集是任何集合的子集,在涉及集合关系时,必须优先考虑空集的情况,否则会造成漏解. 考点三 集合的基本运算例9.设全集{}*5,U x x x N =<∈,集合{}1,2A =,{}2,4B =,则()U C AB = .【解析】∵集合{}{}*5,1,2,3,4U x x x N =<∈=,且集合{}1,2A =,{}2,4B = ∴{}1,2,4AB =∴{}()3U C AB =故答案为{}3.例10.已知全集{}22,3,23U a a =+-,{}21,2A a =-,{}5U C A =,则实数a =________. 【解析】由题意知,2235a a +-=,解得a =-4或a =2.① 当a =-4时,|2a -1|=9,而9U ∉,所以a =-4不满足题意,舍去; ② 当a =2时,|2a -1|=3,3U ∈,满足题意. 故实数a 的值为2. 故答案为2.例11.设集合{}(,)1A x y y ax ==+,集合{}(,)B x y y x b ==+,且{}(2,5)A B =,则a b +=____.【解析】∵集合{}(,)1A x y y ax ==+,{}(,)B x y y x b ==+,且{}(2,5)A B =∴521a =+,且52b =+ ∴2a =,3b = ∴5a b += 故答案为5.例12.设A ,B 是非空集合,定义{}()()A B x x A B x A B ⊗=∈∉且.已知集合{}02A x x =<<,{}0B y y =≥,则A B ⊗=________.【解析】∵{}02A x x =<<,{}0B y y =≥ ∴{}0AB x x =≥,{}02A B x x =<<∴{}02A B x x x ⊗==≥或 故答案为{}02x x x =≥或.【方法点睛】解集合运算问题4个技巧① 看元素构成:集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的关键; ② 对集合化简:有些集合是可以化简的,先化简集合再研究其关系并进行运算,可使问题简单明 了、易于解决;③ 数形结合:常用的数形结合形式有数轴、坐标系和Venn 图;④新定义型问题:以集合为依托,对集合的定义、运算、性质加以深入的创新,但最终化为原来的集合知识和相应数学知识来解决.【名校新题】一、填空题1.(2019·江苏徐州第一次质量检测)已知集合{}0,1,2,3A =,{}|02B x x =<…,则A B =_________.【解析】取集合,A B 的公共部分即可,所以,{1,2}A B ⋂= 故答案为:{}1,22.(2019·苏北七市第二次质量检测)已知集合{}13A a =,,,{45}B =,.若A B ={4},则实数a 的值为____.【解析】∵A B ⋂= {}4,∴a=4 故答案为43.(2019·江苏金陵中学高考第四次模拟)设全集U ={}5N x x x *<∈,,集合A ={1,2},B ={2,4},则∁U (A ⋃B)=_______.【解析】集合U ={}5N x x x *<∈,={}1,2,3,4,且A ={1,2},B ={2,4},得A ⋃B ={1,2,4},所以∁U (A ⋃B)={3} 故答案为:{3}4.(2019·江苏南通四月质量检测)已知集合 ,B ,则A B _____.【解析】∵由题意可知A∩B 中的元素是2的整数倍,且在(-2,3)内, ∴A∩B ={0,2}. 故答案为:{0,2}.5.(2019·江苏徐州高考考前模拟)集合{}1,0,1A =-,{}|20B x x =-<<,则A B 中元素的个数是______.【解析】A 中仅有1B -∈,故AB 中元素的个数为1,填1 .6.(2019·江苏宿迁调研测试)已知集合[)1,4,(,)A B a ==-∞,若A B ⊆,则实数a 的取值范围是 。
2018版高考数学一轮复习 第一章 集合与常用逻辑用语 第1讲 集合的概念和运算 理
第一章 集合与常用逻辑用语第1讲 集合的概念和运算一、选择题1.已知集合A ={y|x2+y2=1}和集合B ={y|y =x2},则A∩B 等于( )A .(0,1)B .[0,1]C .(0,+∞)D .{(0,1),(1,0)}解析 ∵A ={y|x2+y2=1},∴A ={y|-1≤y≤1}.又∵B ={y|y =x2},∴B ={y|y≥0}.A∩B={y|0≤y≤1}.答案 B2. 设全集U =M ∪N ={1,2,3,4,5},M∩∁UN ={2,4},则N =( )A .{1,2,3}B .{1,3,5}C .{1,4,5}D .{2,3,4}解析 由M∩∁UN ={2,4}可得集合N 中不含有元素2,4,集合M 中含有元素2,4,故N ={1,3,5}.答案 B3.设集合U ={x |x <5,x ∈N *},M ={x |x 2-5x +6=0},则∁U M =( ).A .{1,4}B .{1,5}C .{2,3}D .{3,4} 解析 U ={1,2,3,4},M ={x |x 2-5x +6=0}={2,3},∴∁U M ={1,4}.答案 A4.若A ={2,3,4},B ={x|x =n·m,m ,n ∈A ,m≠n},则集合B 中的元素个数是( ).A .2B .3C .4D .5解析 B ={x|x =n·m,m ,n ∈A ,m≠n}={6,8,12}.答案 B5.设集合M ={1,2},N ={a2},则“a=1”是“N ⊆M”的( ).A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件解析 若N ⊆M ,则需满足a2=1或a2=2,解得a =±1或a =± 2.故“a=1”是“N ⊆M”的充分不必要条件.答案 A6.设集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x 24+3y 24=1,B ={y |y =x 2},则A ∩B =( ). A .[-2,2] B .[0,2]C .[0,+∞)D .{(-1,1),(1,1)}解析 A ={x |-2≤x ≤2},B ={y |y ≥0},∴A ∩B ={x |0≤x ≤2}=[0,2].答案 B二、填空题7.设集合A ={-1,1,3},B ={a +2,a 2+4},A ∩B ={3},则实数a =________. 解析 ∵3∈B ,又a 2+4≥4,∴a +2=3,∴a =1.答案 18.已知集合A ={0,2,a2},B ={1,a},若A ∪B ={0,1,2,4},则实数a 的值为________.解析 若a =4,则a2=16∉(A ∪B),所以a =4不符合要求,若a2=4,则a =±2,又-2∉(A ∪B),∴a =2.答案 29.给定集合A ,若对于任意a ,b ∈A ,有a +b ∈A ,且a -b ∈A ,则称集合A 为闭集合,给出如下三个结论:①集合A ={-4,-2,0,2,4}为闭集合;②集合A ={n |n =3k ,k ∈Z }为闭集合;③若集合A 1,A 2为闭集合,则A 1∪A 2为闭集合.其中正确结论的序号是________.解析 ①中,-4+(-2)=-6∉A ,所以不正确.②中设n 1,n 2∈A ,n 1=3k 1,n 2=3k 2,n 1+n 2∈A ,n 1-n 2∈A ,所以②正确.③令A 1={n |n =3k ,k ∈Z },A 2={n |n =2k ,k ∈Z },3∈A 1,2∈A 2,但是,3+2∉A 1∪A 2,则A 1∪A 2不是闭集合,所以③不正确.答案 ②10.已知集合A =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ 6x +1≥1,x ∈R ,B ={x |x 2-2x -m <0},若A ∩B ={x |-1<x <4},则实数m 的值为________.解析 由6x +1≥1,得x -5x +1≤0, ∴-1<x ≤5,∴A ={x |-1<x ≤5}.又∵B ={x |x 2-2x -m <0},A ∩B ={x |-1<x <4},∴有42-2×4-m =0,解得m =8.此时B ={x |-2<x <4},符合题意,故实数m 的值为8.答案 8三、解答题11.若集合A ={-1,3},集合B ={x |x 2+ax +b =0},且A =B ,求实数a ,b .解 ∵A =B ,∴B ={x |x 2+ax +b =0}={-1,3}.∴⎩⎪⎨⎪⎧ -a =-1+3=2,b =-=-3,∴a =-2,b =-3.12.已知集合A ={-4,2a -1,a 2},B ={a -5,1-a,9},分别求适合下列条件的a 的值.(1)9∈(A ∩B );(2){9}=A ∩B .解 (1)∵9∈(A ∩B ),∴9∈A 且9∈B ,∴2a -1=9或a 2=9,∴a =5或a =-3或a =3,经检验a =5或a =-3符合题意.∴a =5或a =-3.(2)∵{9}=A ∩B ,∴9∈A 且9∈B ,由(1)知a =5或a =-3.当a =-3时,A ={-4,-7,9},B ={-8,4,9},此时A ∩B ={9},当a =5时,A ={-4,9,25},B ={0,-4,9},此时A ∩B ={-4,9},不合题意.∴a =-3.13.设A ={x |x 2-8x +15=0},B ={x |ax -1=0}.(1)若a =15,试判定集合A 与B 的关系; (2)若B ⊆A ,求实数a 组成的集合C .解 由x 2-8x +15=0,得x =3或x =5.∴A ={3,5}.(1)当a =15时,由15x -1=0,得x =5. ∴B ={5},∴B A .(2)∵A ={3,5}且B ⊆A ,∴若B =∅,则方程ax -1=0无解,有a =0.若B ≠∅,则a ≠0,由方程ax -1=0,得x =1a, ∴1a =3或1a =5,即a =13或a =15, ∴C =⎩⎨⎧⎭⎬⎫0,13,15. 14.设集合A ={x2,2x -1,-4},B ={x -5,1-x,9},若A∩B={9},求A ∪B.解 由9∈A ,可得x2=9或2x -1=9,解得x =±3或x =5.当x =3时,A ={9,5,-4},B ={-2,-2,9},B 中元素重复,故舍去;当x =-3时,A ={9,-7,-4},B ={-8,4,9},A∩B={9}满足题意,故A ∪B ={-7,-4,-8,4,9};当x=5时,A={25,9,-4},B={0,-4,9},此时A∩B={-4,9}与A∩B={9}矛盾,故舍去.综上所述,A∪B={-8,-4,4,-7,9}.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点一 集合的概念与运算 知识梳理 1.集合与元素 (1)集合元素的三个特征:确定性、互异性、无序性. (2)元素与集合的关系是属于或不属于关系,用符号∈或∉表示. (3)集合的表示法:列举法、描述法、Venn图法. (4)常见数集的记法 集合 自然数集 正整数集 整数集 有理数集 实数集 符号 N N+(或N*) Z Q R
(5)集合的分类 若按元素的个数分类,可分为有限集、无限集、空集;若按元素的属性分类,可分为点集、数集等.特别注意空集是一个特殊而又重要的集合,如果一个集合不包含任何元素,这个集合就叫做空集,空集用符号“∅”表示,规定:空集是任何集合的子集,是任何非空集合的真子集.解题时切勿忽视空集的情形. 2.集合间的基本关系 关系 自然语言 符号语言 Venn图
子集 集合A中所有元素都在集合B中(即若x∈A,则x∈B) A⊆B (或B⊇A)
真子集 集合A是集合B的子集,且集合B中至少有一个元素不在集合A中 AB
(或BA)
集合相等 集合A,B中元素完全相同或集合A,B互为子集 A=B 子集与真子集的区别与联系:一个集合的真子集一定是其子集,而其子集不一定是其真子集. 3.全集与补集 (1)如果一个集合包含了我们所要研究的各个集合的全部元素,这样的集合就称为 全集 ,全集通常用字母 U 表示; (2) 对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,记作∁UA,即∁UA={x|x∈U,且x∉A}. 4.集合的运算 集合的并集 集合的交集 集合的补集 图形 符号 A∪B={x|x∈A,或x∈B} A∩B={x|x∈A,且x∈B} ∁UA={x|x∈U,且x∉A} 5.集合关系与运算的常用结论 (1)子集个数公式:若有限集A中有n个元素,则A的子集个数为2n个,非空子集个数为2n
-1个,真子集有2n-1个. (2) A∩B=A⇔A⊆B,A∪B=B⇔A⊆B.
(3)(∁UA)∩(∁UB)=∁U(A∪B),(∁UA)∪(∁UB)=∁U(A∩B) . 典例剖析 题型一 集合的基本概念 例1 已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是 答案 5 解析 列表
根据集合中元素的互异性知,B中元素有0,-1,-2,1,2,共5个. 变式训练 已知集合A={0,1,2},B={(x,y)|x∈A,y∈A,x-y∈A},则集合B中有________个元素. 答案 6 解析 因为x-y∈A,∴x≥y. 当x=0时,y=0; 当x=1时,y=0或y=1; 当x=2时,y=0,1,2. 故集合B={(0,0),(1,0),(1,1),(2,0),(2,1),(2,2)}, 即集合B中有6个元素. 解题要点 研究集合问题,通常从代表元素入手,考查其所代表的是数还是点,如果代表元素是数x,则是数集,如果代表元素是数对(x,y),则是点集.在列举集合的元素时可借助表格,或根据元素特征分类列举,列举时应做到不重不漏. 例2 设a,b∈R,集合{1,a+b,a}=0,ba,b,则b-a=________. 答案 2
解析 因为{1,a+b,a}=0,ba,b,且由a在分母的位置可知a≠0, 所以a+b=0,则ba=-1, 所以a=-1,b=1.所以b-a=2. 变式训练 已知集合A={m+2,2m2+m},若3∈A,则m的值为________. 答案 -32 解析 因为3∈A,所以m+2=3或2m2+m=3. 当m+2=3,即m=1时,2m2+m=3, 此时集合A中有重复元素3,所以m=1不符合题意,舍去;
当2m2+m=3时,解得m=-32或m=1(舍去),
此时当m=-32时,m+2=12≠3符合题意,
所以m=-32. 解题要点 对于含字母参数的集合,应准确进行分类讨论,列出方程或方程组求出字母参数的值.需要特别注意的是,求出字母参数值后,还要检验是否违反了集合中元素的互异性. 题型二 集合间的基本关系 例3 集合A={-1,0,1},A的子集中,含有元素0的子集共有 个 答案 4 解析 根据题意,在集合A的子集中, 含有元素0的子集有{0}、{0,1}、{0,-1}、{-1,0,1},共四个. 变式训练 设M为非空的数集,M⊆{1,2,3},且M中至少含有一个奇数元素,则这样的集合M共有 个
答案 6 解析 集合{1,2,3}的所有子集共有23=8(个),其中一个奇数元素也没有的集合有两个:∅
和{2},故满足要求的集合M共有8-2=6(个). 解题要点 解题关键是弄清符合题意的集合其元素应满足的条件.在元素较少时可以采取穷举法列出所有满足条件的集合. 例4 设,若,则a的取值范围是 . 答案 解析 根据题意作图:
由图可知,,则只要即可,即a的取值范围是. 变式训练 已知集合2{|540},,,AxxxBaAB,则a的取值范围是 . 答案 (4,)
解析 2{|540}1,4Axxx,∵,根据题意作图:
由图可知,只要即可,即a的取值范围(4,). 解题要点 对于这类用不等式表示的数集之间的包含关系时,常常借助数轴进行求解.在解题时应注意端点是否可以取到.
题型三 集合的基本运算 例5 已知集合A={1,2,3},B={2,4,5},则集合A∪B中元素的个数为________.
答案 5 解析 A∪B={1,2,3,4,5},共有5个元素.
变式训练 已知集合A={x|x2-x-2≤0},集合B为整数集,则A∩B等于________. 答案 {-1,0,1,2} 解析 A={x|x2-x-2≤0}={x|-1≤x≤2},B为整数集,A∩B={-1,0,1,2}. 解题要点 求解集合交、并首先应对各个集合进行化简,准确弄懂集合中的元素,求并集时相同的元素只算一个. 例6 已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B) =________.
答案 {x|0解析 ∵A={x|x≤0},B={x|x≥1}, ∴A∪B={x|x≤0或x≥1},
在数轴上表示如图. ∴∁U(A∪B)={x|0变式训练 已知集合A={x|x2-2x>0},B={x|-<x<},则A∪B=________. 答案 R 解析 ∵x(x-2)>0,∴x<0或x>2. ∴集合A与B可用数轴表示为:
由图象可以看出A∪B=R. 解题要点 集合的基本运算是历年高考的热点,常与不等式的解集、函数的定义域、值域相结合命题,解题时先求出各个集合,然后借助数轴求交并是基本方法.
当堂练习 1. 已知集合{1,2,3,4}U,集合={1,2}A,={2,3}B,则()UABð________. 答案 {4} 解析 因为A∪B={1,2,3},全集U={1,2,3,4},所以ðU(A∪B)={4}. 2.若集合M={-1,0,1},N={0,1,2},则M∩N等于________. 答案 {0,1} 解析 由集合M={-1,0,1},N={0,1,2},得到M∩N={0,1}. 3.已知{菱形},{正方形},{平行四边形},则之间的关系为_______ 答案 4.已知集合A={(x,y)|-1≤x≤1,0≤y<2,x、y∈Z},用列举法可以表示集合A为________. 答案 {(-1,0),(-1,1),(0,0),(0,1),(1,0),(1,1)}
解析 集合A表示不等式组-1≤x≤1,x∈Z,0≤y<2,y∈Z确定的平面区域上的格点集合,所以用列举法表示集合A为{(-1,0),(-1,1),(0,0),(0,1),(1,0),(1,1)}. 5.设集合M={0,1,2},N={x|x2-3x+2≤0},则M∩N= . 答案 {1,2} 解析 由x2-3x+2=(x-1)(x-2)≤0, 解得1≤x≤2,故N={x|1≤x≤2},∴M∩N={1,2}.
课后作业 1.已知集合A={x|2<x<4},B={x|(x-1)(x-3)<0},则A∩B等于________. 答案 (2,3) 解析 ∵A={x|2<x<4},B={x|(x-1)(x-3)<0}={x|1<x<3}, ∴A∩B={x|2<x<3}=(2,3). 2.设集合M={x|x2+2x=0,x∈R},N={x|x2-2x=0,x∈R},则M∪N=________.
答案 {-2,0,2} 解析 先确定两个集合的元素,再进行并集运算.集合M={0,-2},N={0,2}, 故M∪N={-2,0,2}. 3.已知集合M={x|-34},则M∪N等于________. 答案 {x|x<-5或x>-3} 解析 在数轴上表示集合M和N,如图所示,
则数轴上方所有“线”下面的部分就是M∪N={x|x<-5或x>-3}. 4.若集合A={x∈R|ax2+ax+1=0}中只有一个元素,则a=________. 答案 4 解析 a=0时,ax2+ax+1=0无解,此时,A=,不合题意;
a≠0时,由题意得方程ax2+ax+1=0有两个相等实根,则 Δ=a2-4a=0a≠0,解得a=4. 5.已知全集{0,1,2,3,4}U,集合{1,2,3}A,{2,4}B,则UABð()= ________. 答案 {0,2,4} 解析 ∵UAð={0,4},UABð()={0, 2,4}.
6.已知集合{1,2,3,4}A,2{|,}BxxnnA,则AB________. 答案 {1,4} 解析 ∵x=n2,n∈A,∴x=1,4,9,16. ∴B={1,4,9,16}.∴A∩B={1,4}.
7.满足条件{0,2}∪M={0,1,2}的所有集合M的个数为________. 答案 4 解析 由题可知集合M中必有1,满足条件的M可以为{1},{0,1},{2,1},{0,1,2}共4个. 8.已知集合A={1,3,m},B={1,m},A∪B=A,则m=________. 答案 0或3
