六年级组合图形试题训练(求面积)
组合图形面积练习题

组合图形面积练习题组合图形面积练习题在数学学习中,组合图形面积是一个重要的概念。
通过组合不同的几何图形,我们可以计算出复杂图形的面积。
在这篇文章中,我们将通过一些练习题来巩固和应用这个概念。
练习题1:假设有一个由一个正方形和一个半圆组成的图形。
正方形的边长为8cm,半圆的直径与正方形的边长相等。
求整个图形的面积。
解答:首先,我们需要计算半圆的面积。
半圆的半径等于直径的一半,而直径等于正方形的边长,所以半圆的半径为4cm。
半圆的面积可以通过公式A = πr²/2来计算,其中π取近似值3.14。
代入半圆的半径,我们得到半圆的面积为3.14 * 4² / 2 = 25.12cm²。
接下来,我们计算正方形的面积。
正方形的边长为8cm,所以正方形的面积可以通过边长的平方来计算,即8² = 64cm²。
最后,我们将正方形的面积和半圆的面积相加,得到整个图形的面积。
64cm² + 25.12cm² = 89.12cm²。
所以,整个图形的面积为89.12平方厘米。
练习题2:现在,我们来考虑一个稍微复杂一些的图形。
假设有一个由一个矩形和一个等边三角形组成的图形。
矩形的长为10cm,宽为6cm,而等边三角形的边长与矩形的宽相等。
求整个图形的面积。
解答:首先,我们计算矩形的面积。
矩形的长为10cm,宽为6cm,所以矩形的面积可以通过长乘以宽来计算,即10 * 6 = 60cm²。
接下来,我们计算等边三角形的面积。
等边三角形的边长与矩形的宽相等,即6cm。
等边三角形的面积可以通过公式A = (√3/4) * a²来计算,其中a为边长。
代入边长的值,我们得到等边三角形的面积为(√3/4) * 6² = 15.59cm²。
最后,我们将矩形的面积和等边三角形的面积相加,得到整个图形的面积。
60cm² + 15.59cm² = 75.59cm²。
六年级数学组合图形的面积试题答案及解析

六年级数学组合图形的面积试题答案及解析1.我们开始提到的“乡村小屋”的面积是多少?【答案】18【解析】图形内部格点数;图形边界上的格点数;根据毕克定理,则(单位面积).2.两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为,右下角的阴影部分(线状)面积为,求大正方形的面积.【答案】19【解析】块状部分与线状部分之间的部分称为D,则D与前者共14个方格,与后者共17个方格,因此每个方格的面积是大正方形的面积为.3.如图,平行四边形,,,,,平行四边形的面积是,求平行四边形与四边形的面积比.【答案】1/18【解析】连接、.根据共角定理∵在和中,与互补,∴.又,所以.同理可得,,.所以.所以.4.如图,有三个正方形的顶点、、恰好在同一条直线上,其中正方形的边长为10厘米,求阴影部分的面积.【答案】100【解析】对于这种几个正方形并排放在一起的图形,一般可以连接正方形同方向的对角线,连得的这些对角线互相都是平行的,从而可以利用面积比例模型进行面积的转化.如右图所示,连接、、,则,根据几何五大模型中的面积比例模型,可得,,所以阴影部分的面积就等于正方形的面积,即为平方厘米.5.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少?【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.6.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.7.右图中,和是两个正方形,和相交于,已知等于的三分之一,三角形的面积等于6平方厘米,求五边形的面积.【答案】49.5【解析】连接、,由于与平行,可知四边形构成一个梯形.由于面积为6平方厘米,且等于的三分之一,所以等于的,根据梯形蝴蝶定理或相似三角形性质,可知的面积为12平方厘米,的面积为6平方厘米,的面积为3平方厘米.那么正方形的面积为平方厘米,所以其边长为6厘米.又的面积为平方厘米,所以(厘米),即正方形的边长为3厘米.那么,五边形的面积为:(平方厘米).8.如图,长方形的面积是2平方厘米,,是的中点.阴影部分的面积是多少平方厘米?【答案】【解析】如下图,连接,、的面积相等,设为平方厘米;、的面积相等,设为平方厘米,那么的面积为平方厘米.,.所以有.比较②、①式,②式左边比①式左边多,②式右边比①式右边大0.5,有,即,.而阴影部分面积为平方厘米.9.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少.【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.10.如图,是梯形的一条对角线,线段与平行,与相交于点.已知三角形的面积比三角形的面积大平方米,并且.求梯形的面积.【答案】28【解析】连接.根据差不变原理可知三角形的面积比三角形大4平方米,而三角形与三角形面积相等,因此也与三角形面积相等,从而三角形的面积比三角形的大4平方米.但,所以三角形的面积是三角形的,从而三角形的面积是(平方米),梯形的面积为:(平方米).11.如图,已知,,,,线段将图形分成两部分,左边部分面积是38,右边部分面积是65,求三角形的面积.【答案】40【解析】连接,.根据题意可知,;;所以,,,,,于是:;;可得.故三角形的面积是40.12.如图,长方形的面积是36,是的三等分点,,则阴影部分的面积为多少?【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.13.如图,如果长方形的面积是平方厘米,那么四边形的面积是多少平方厘米?【答案】32.5【解析】如图,过、、、分别作长方形的各边的平行线.易知交成中间的阴影正方形的边长为厘米,面积等于平方厘米.设、、、的面积之和为,四边形的面积等于,则,解得(平方厘米).14.已知正方形的边长为10,,,则?【答案】53【解析】如图,作于,于.则四边形分为4个直角三角形和中间的一个长方形,其中的4个直角三角形分别与四边形周围的4个三角形相等,所以它们的面积和相等,而中间的小长方形的面积为,所以.15.如下图,长方形和长方形拼成了长方形,长方形的长是20,宽是12,则它内部阴影部分的面积是多少.【答案】120【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半,为.16.长方形的面积为36,、、为各边中点,为边上任意一点,问阴影部分面积是多少?【答案】13.5【解析】解法一:寻找可利用的条件,连接、,如下图:可得:、、,而即;而,.所以阴影部分的面积是:解法二:特殊点法.找的特殊点,把点与点重合,那么图形就可变成右图:这样阴影部分的面积就是的面积,根据鸟头定理,则有:.17.在长方形内部有一点,形成等腰的面积为16,等腰的面积占长方形面积的,那么阴影的面积是多少?【答案】3.5【解析】先算出长方形面积,再用其一半减去的面积(长方形面积的),再减去的面积,即可求出的面积.根据模型可知,所以,又与的面积相等,它们的面积和等于长方形面积的一半,所以的面积等于长方形面积的,所以.18.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分的面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.19.如图所示,长方形内的阴影部分的面积之和为70,,,四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和,以及三角形和的面积之和,进而求出四边形的面积.由于长方形的面积为,所以三角形的面积为,所以三角形和的面积之和为;又三角形、和四边形的面积之和为,所以四边形的面积为.另解:从整体上来看,四边形的面积三角形面积三角形面积白色部分的面积,而三角形面积三角形面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即,所以四边形的面积为.20.如图,长方形的面积是36,是的三等分点,,求阴影部分的面积.【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.。
六年级总复习组合图形面积经典习题

组合图形1、求以下组合图形阴影局部的面积。
2、①求它的周长和面积。
〔单位:厘米〕②圆的周长是18.84,求阴影局部面积。
③长方形的面积和圆的面积相等,圆④求直角三角形中阴影局部的面积。
的半径是3,求阴影局部的周长和面积。
〔单位:分米〕
⑤以下图中长方形长6,宽4,阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少32,求的长。
40,求的长。
⑦平行四边形的面积是302,⑧一个圆的半径是4,求阴影局部面积。
求阴影局部的面积。
⑨8,12,三角形和三角形的面积,各占长方形的1/3,求三角形的面积。
⑩梯形上底8,下底16,阴影⑾求阴影局部面积。
〔单位:〕局部面积642,求梯形面积。
⑿梯形面积是48平方厘米,阴影局部比空白⒀阴影局部比空白局部大62,求S阴。
局部12平方厘米,求阴影局部面积。
六年级5.4组合图形的周长与面积练习题
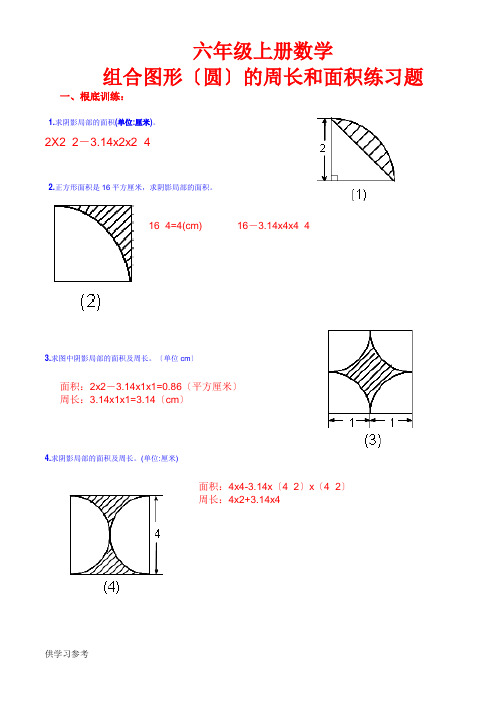
六年级上册数学组合图形〔圆〕的周长和面积练习题一、根底训练:1.求阴影局部的面积(单位:厘米)。
2X2÷2-3.14x2x2÷42.正方形面积是16平方厘米,求阴影局部的面积。
16÷4=4(cm) 16-3.14x4x4÷43.求图中阴影局部的面积及周长。
〔单位cm〕面积:2x2-3.14x1x1=0.86〔平方厘米〕周长:3.14x1x1=3.14〔cm〕4.求阴影局部的面积及周长。
(单位:厘米)面积:4x4-3.14x〔4÷2〕x〔4÷2〕周长:4x2+3.14x45.求阴影局部的面积。
7.如图〔8〕,求阴影局部的面积。
(单位:厘米)8.如图〔9〕求阴影局部的面积。
(单位:厘米)S=〔2+1〕X2=6〔平方厘米〕9. 如图〔11〕求阴影局部的面积。
(单位:厘米)〖3.14x4x4-3.14x3x3〗÷610.在如图〔12〕是正三角形中求阴影局部的面积及周长。
(单位:厘米) 面积:3.14x3x3÷2 周长:3.14x3+3x612. 如图〔13〕求阴影局部的面积。
(单位:厘米)13.如图〔14〕求阴影局部的面积。
(单位:厘米)16.如右图〔33〕,求阴影局部的面积及周长。
(单位:厘米)二、能力提升:17.如右图〔19〕正方形边长为4厘米,求阴影局部的面积及周长。
18.如图〔20〕,正方形ABCD的面积是36平方厘米,求阴影局部的面积。
19.如图〔22〕,正方形边长为8厘米,求阴影局部的面积。
20.如图〔28〕求阴影局部的面积。
(单位:厘米)21.如图〔33〕求阴影局部的面积。
完整版六年级54组合图形的周长与面积练习题

趁自己年纪,好好把握时光六年级上册数学组合图形(圆)的周长和面积练习题一、基础训练:) 1.求阴影部分的面积(单位:厘米。
43.14x2x2÷2X2÷2-平方厘米,求阴影部分的面积。
正方形面积是16 2.43.14x4x4÷16-16÷4=4(cm)cm)求图中阴影部分的面积及周长。
(单位3. 3.14x1x1=0.86(平方厘米)面积:2x2-)周长:3.14x1x1=3.14(cm)(单位:厘米4.求阴影部分的面积及周长。
(x4÷2))4÷4x4-3.14x面积:(24x2+3.14x4周长:1趁自己年纪,好好把握时光5.求阴影部分的面积。
) 厘米求阴影部分的面积。
(单位:7.如图(8),:厘米) 98.如图()求阴影部分的面积。
(单位2+1)X2=6(平方厘米)(S=) 厘米求阴影部分的面积。
如图(11)(单位:9.3.14x4x4-3.14x3x3〖〗6÷2趁自己年纪,好好把握时光10.在如图(12)是正三角形中求阴影部分的面积及周长。
(单位:厘米)面积:3.14x3x3÷2 周长:3.14x3+3x612. 如图(13)求阴影部分的面积。
(单位:厘米))厘米单位:)13.如图(14求阴影部分的面积。
() 单位右图(16.如33),求阴影部分的面积及周长。
(:厘米二、能力提升:19如17.右图()正方形边长为厘米,求阴影部分的面积及周长。
4 3 趁自己年纪,好好把握时光平方厘米,求阴影部分的面积。
ABCD的面积是3618.如图(20),正方形厘米,求阴影部分的面积。
如图(22),正方形边长为819.单位:厘米)(2820.如图()求阴影部分的面积。
4趁自己年纪,好好把握时光求阴影部分的面积。
)如图(3321. 5。
六年级总复习组合图形面积经典习题

组合图形
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。(单位:厘米) ②圆的周长是,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆 ④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。 (单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影 ⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。 AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2, ⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影 ⑾求阴影部分面积。(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白 ⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
六年级总总结复习组合图形面积经典习题

组合图形1、求以下组合图形阴影局部的面积。
2、①求它的周长和面积。
〔单位:厘米〕②圆的周长是,求阴影局部面积。
③长方形的面积和圆的面积相等,圆
的半径是3cm,求阴影局部的周长和面积。
④求直角三角形中阴影局部的面积。
〔单位:分米〕
⑤以下图中长方形长①
比阴影②面积少6cm,宽 4cm,阴影
2
3cm ,求 EC的长。
⑥图中阴影①比阴影②面积小
AB=40cm,求 BC的长。
48 平方厘米,
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影局部面积。
求阴影局部的面积。
⑨ AB=8cm, AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的 1/3 ,求三角形AEF的面积。
⑩梯形上底8cm,下底 16cm,阴影⑾求阴影局部面积。
〔单位:cm〕
局部面积64cm2,求梯形面积。
⑿梯形面积是48 平方厘米,阴影局部比空白⒀阴影局部比空白局部大6cm2,求S 阴。
局部 12 平方厘米,求阴影局部面积。
六年级数学组合图形面积经典习题
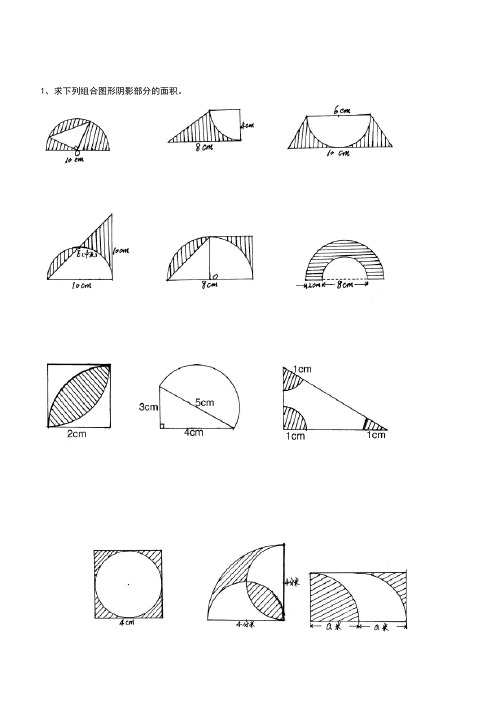
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)(单位:厘米) ②圆的周长是,求阴影部分面积。
②圆的周长是,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆③长方形的面积和圆的面积相等,已知圆 ④求直角三角形中阴影部分的面积。
④求直角三角形中阴影部分的面积。
的半径是3cm 3cm,求阴影部分的周长和面积。
,求阴影部分的周长和面积。
,求阴影部分的周长和面积。
(单位:分米)(单位:分米)⑤下图中长方形长6cm 6cm,宽,宽4cm 4cm,已知阴影,已知阴影,已知阴影 ⑥图中阴影①比阴影②面积小⑥图中阴影①比阴影②面积小48平方厘米,①比阴影②面积少3cm 2,求EC 的长。
的长。
AB=40cm AB=40cm AB=40cm,求,求BC 的长。
⑦平行四边形的面积是30cm 2, ⑧一个圆的半径是⑧一个圆的半径是4cm 4cm,求阴影部分面积。
,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm AB=8cm,,AD=12cm AD=12cm,三角形,三角形ABE 和三角形ADF 的面积,各占长方形ABCD 的1/31/3,求三角形,求三角形AEF 的面积。
⑩梯形上底8cm 8cm,下底,下底16cm 16cm,阴影,阴影,阴影 ⑾求阴影部分面积。
⑾求阴影部分面积。
(单位:(单位:cm cm cm)) 部分面积64cm264cm2,求梯形面积。
,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白平方厘米,阴影部分比空白 ⒀阴影部分比空白部分大⒀阴影部分比空白部分大6cm 2,求S 阴。
部分12平方厘米,求阴影部分面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学六年级(组合图形)试题训练
求阴影部分面积
1、求下列组合图形阴影部分的面积。
B .
BN
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求
三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
