小学六年级组合图形复习题
六年级下册数学试题-专题复习 平面图形的周长与面积03-北师大版

廉江市实验学校六年级复习专题——平面图形的周长与面积(3)一、组合图形1、求下列组合图形阴影部分的面积。
学校班级姓名密封线内不要答题考号2、求平面图形的周长和面积。
①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分积。
④求直角三角形中阴影部分的面积。
(单位:分米)⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平①比阴影②面积少3cm2,求EC的长。
方厘米,AB=40cm,求BC的长。
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平①比阴影②面积少3cm2,求EC的长。
方厘米,AB=40cm,求BC的长。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD 的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
4.如图15-3,求各图形中阴影部分的面积.(图中长度单位为厘米,л取3.14)5.如图154,求各图中阴影部分的面积.(图中长度单位为厘米,л取3.14)6.图15-5中甲区域比乙区域的面积大57平方厘米,且半圆的半径是10厘米.其中直角三角形竖直的直角边的长度是多少?(л取3.14)7.求图15-6中阴影部分的面积.(л取3.14)8.如图15-7,在3×3的方格表中,分别以A、E为圆心,3、2为半径,画出圆心角都是90°的两段圆弧.图中阴影部分的面积是多少?(л取3.14)9.如图15—8,在一块面积为36平方厘米的圆形铝板中,裁出了7个同样大小的圆铝板.问:余下的边角料的总面积是多少平方厘米?二、周长、面积计算能力拓展题1.(1)已知一个扇形的半径为2厘米,弧长为3.14,这个扇形的面积是多少?(2)已知一个半圆形的面积是56.52平方厘米,求这个半圆形的周长.(л取3.14)2.如图15-10,求各图中阴影部分的面积.(图中长度单位为厘米,л取3.14)3.如图15-11,直角三角形ABC的面积是45,分别以曰、C为圆心,3为半径画圆.已知图中阴影部分的面积是35.58.请问:角A是多少度?(л取3.14)4.图15-12是一个直径是3厘米的半圆,AB是直径.如图15-13所示,让A点不动,把整个半圆逆时针转60。
(完整版)六年级组合图形、圆形、阴影部分面积

专题:圆与求阴影部分面积求下面图形中阴影部分的面积。
姓名:小圆半径为3厘米,大圆半径为10,问:空白部分甲比乙的面积多多少厘米?(6)已知直角三角形面积是12平方厘米, 求阴影部分的面积 图中圆的半径为5厘米,求阴影部分的 面积。
AE京T(13)(10)05)(巧正方形ABCD的面积是36cm 2L厂17$(20)例21 .图中四个圆的半径都是1厘米,一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴大正方形的边长为6厘A米,小正方形的边长为4厘米。
求阴影的面积。
E B C(32)完整答案2个叶形,叶形面积为:n( ) *-4X4=8n-16所以阴影部分的面积为:n()-8n+16=41.12平方厘3阴影部分面积为:(3 n -6) X =5.13平方厘米例17解:上面的阴影部分以 AB 为轴翻转后,整个阴影部分 例18解:阴影部分的周长为三个扇形弧,拼在一起为一个半 成为梯形减去直角三角形,或两个小直角三角形面积和。
圆弧,所以圆弧周长为:2X 3.14 X 3*2=9.42厘米所以阴影部分面积为:5X 5*2+5X 10*2=37.5平方厘米例19解:右半部分上面部分逆时针,下面部分顺时针旋转到 左半部分,组成一个矩形。
所以面积为:1X 2=2平方厘米2例20 解:设小圆半径为r, =36, r=3,大圆半径为R ,R=21 :=18,将阴影部分通过转动移在一起构成半个圆环,所以面积为:n( f 3) *2=4.5 n =14.13平方厘米 2 21—(1)例23解:面积为4个圆减去8个叶形, 叶形面积为:.n' 1-1 X = 2 n -1,1 (1) — 所以阴影部分的面积为:4 n W-8(2 n -1)=8平方厘米例24分析:连接角上四个小圆的圆心构成一个正方形,各个2小圆被切去4个圆,这四个部分正好合成3个整圆,而正方形中的空白部分合成 两个小圆.解:阴影部分为大正方形面积与一个小圆面积之和.为:4X 4+n =19.1416平方厘米AC 面积,例22解法一:将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.阴影部分为一个三角形和一个半圆面积之和.L Zn( ) * 2+4 X 4=8 n +16=41.1牡方厘米 解法二:补上两个空白为一个完整的圆.所以阴影部分面积为一个圆减去一AED 、 BCD例21.解:把中间部分分成四等分,分别放在上面圆的四个 角上,补成一个正方形,边长为 2厘米, 所以面积为:2X 2=4平方厘米(22)例25分析:四个空白部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积, 4X(4+7) *2- n =22- 4 n =9.44 平方厘米例27解:因为2血2=4,所以MF =2以AC 为直径的圆面积减去三角形ABC 面积加上弓形例26解:将三角形CEB 以B 为圆心,逆时针转动90度,到 三角形ABD 位置,阴影部分成为三角形 ACB 面积减去LI 个小 圆面积,为:5 X*2-*4=12.25-3.14=9.36 平方厘米例28解法一:设AC 中点为B,阴影面积为三角形 ABD 面积加弓形BD 的面积,三角形ABD 的面积为:5 X5-2=12.5弓形面积为:[QF 吃-5 X5]吃=7.125所以阴影面积为:12.5+7.125=19.625 平方厘米解法二:右上面空白部分为小正方形面积减去 J 小圆面积,其I 2 艺 值为:5X5# n (勺 =25-4 n阴影面积为三角形 ADC 减去空白部分面积,为:10X 5-2-2525(25- J n) = ■' n =19.625 平方厘米例29.解:甲、乙两个部分同补上空白部分的三角形后合成一 个扇形BCD ,一个成为三角形 ABC ,例30.解:两部分同补上空白部分后为直角三角形 ABC ,个为半圆,设BC 长为X ,则20s40X- 2- n煜=28所以 40X-400n =56 则 X=32.8 厘米方厘米例31.解:连PD 、PC 转换为两个三角形和两个弓形,1两三角形面积为:△ APD 面积+△ QPC 面积=二(5X 10+5X 5) =37.51两弓形PC 、PD 面积为:2它们面积相等,则三角形ADF 面积等于三角形 EBF 面积,阴例33.解:用■.大圆的面积减去长方形面积再加上一个以 2为丄半径的•:圆ABE 面积,为& -例34解:两个弓形面积为: n-3 X 4*2=…n -6阴影部分为两个半圆面积减去两个弓形面积,结果为所以阴影部分的面积为:2537.5+n -25=51.75 平方厘影部分可补成4圆ABE 的面积,其面积为:n ■- 4=9 n =28.26平方厘米=4.205平方厘米n -6) =n厘米)+6=6平方(L)3(AD)an-2X 2*4+[ n詔-2] 1 1=2 n -1+( 2 n -1)=n -2=1.14平方厘米此两部分差即为:梯形ABCD 的面积为(4+6) X 4=20平方厘米从而知道例32解:三角形DCE 的面积为X 4X 10=20平方厘米组合图形专项练习姓名_____________1、求下列组合图形阴影部分的面积。
六年级数学组合图形的面积试题答案及解析

六年级数学组合图形的面积试题答案及解析1.我们开始提到的“乡村小屋”的面积是多少?【答案】18【解析】图形内部格点数;图形边界上的格点数;根据毕克定理,则(单位面积).2.两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为,右下角的阴影部分(线状)面积为,求大正方形的面积.【答案】19【解析】块状部分与线状部分之间的部分称为D,则D与前者共14个方格,与后者共17个方格,因此每个方格的面积是大正方形的面积为.3.如图,平行四边形,,,,,平行四边形的面积是,求平行四边形与四边形的面积比.【答案】1/18【解析】连接、.根据共角定理∵在和中,与互补,∴.又,所以.同理可得,,.所以.所以.4.如图,有三个正方形的顶点、、恰好在同一条直线上,其中正方形的边长为10厘米,求阴影部分的面积.【答案】100【解析】对于这种几个正方形并排放在一起的图形,一般可以连接正方形同方向的对角线,连得的这些对角线互相都是平行的,从而可以利用面积比例模型进行面积的转化.如右图所示,连接、、,则,根据几何五大模型中的面积比例模型,可得,,所以阴影部分的面积就等于正方形的面积,即为平方厘米.5.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少?【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.6.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.7.右图中,和是两个正方形,和相交于,已知等于的三分之一,三角形的面积等于6平方厘米,求五边形的面积.【答案】49.5【解析】连接、,由于与平行,可知四边形构成一个梯形.由于面积为6平方厘米,且等于的三分之一,所以等于的,根据梯形蝴蝶定理或相似三角形性质,可知的面积为12平方厘米,的面积为6平方厘米,的面积为3平方厘米.那么正方形的面积为平方厘米,所以其边长为6厘米.又的面积为平方厘米,所以(厘米),即正方形的边长为3厘米.那么,五边形的面积为:(平方厘米).8.如图,长方形的面积是2平方厘米,,是的中点.阴影部分的面积是多少平方厘米?【答案】【解析】如下图,连接,、的面积相等,设为平方厘米;、的面积相等,设为平方厘米,那么的面积为平方厘米.,.所以有.比较②、①式,②式左边比①式左边多,②式右边比①式右边大0.5,有,即,.而阴影部分面积为平方厘米.9.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少.【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.10.如图,是梯形的一条对角线,线段与平行,与相交于点.已知三角形的面积比三角形的面积大平方米,并且.求梯形的面积.【答案】28【解析】连接.根据差不变原理可知三角形的面积比三角形大4平方米,而三角形与三角形面积相等,因此也与三角形面积相等,从而三角形的面积比三角形的大4平方米.但,所以三角形的面积是三角形的,从而三角形的面积是(平方米),梯形的面积为:(平方米).11.如图,已知,,,,线段将图形分成两部分,左边部分面积是38,右边部分面积是65,求三角形的面积.【答案】40【解析】连接,.根据题意可知,;;所以,,,,,于是:;;可得.故三角形的面积是40.12.如图,长方形的面积是36,是的三等分点,,则阴影部分的面积为多少?【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.13.如图,如果长方形的面积是平方厘米,那么四边形的面积是多少平方厘米?【答案】32.5【解析】如图,过、、、分别作长方形的各边的平行线.易知交成中间的阴影正方形的边长为厘米,面积等于平方厘米.设、、、的面积之和为,四边形的面积等于,则,解得(平方厘米).14.已知正方形的边长为10,,,则?【答案】53【解析】如图,作于,于.则四边形分为4个直角三角形和中间的一个长方形,其中的4个直角三角形分别与四边形周围的4个三角形相等,所以它们的面积和相等,而中间的小长方形的面积为,所以.15.如下图,长方形和长方形拼成了长方形,长方形的长是20,宽是12,则它内部阴影部分的面积是多少.【答案】120【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半,为.16.长方形的面积为36,、、为各边中点,为边上任意一点,问阴影部分面积是多少?【答案】13.5【解析】解法一:寻找可利用的条件,连接、,如下图:可得:、、,而即;而,.所以阴影部分的面积是:解法二:特殊点法.找的特殊点,把点与点重合,那么图形就可变成右图:这样阴影部分的面积就是的面积,根据鸟头定理,则有:.17.在长方形内部有一点,形成等腰的面积为16,等腰的面积占长方形面积的,那么阴影的面积是多少?【答案】3.5【解析】先算出长方形面积,再用其一半减去的面积(长方形面积的),再减去的面积,即可求出的面积.根据模型可知,所以,又与的面积相等,它们的面积和等于长方形面积的一半,所以的面积等于长方形面积的,所以.18.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分的面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.19.如图所示,长方形内的阴影部分的面积之和为70,,,四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和,以及三角形和的面积之和,进而求出四边形的面积.由于长方形的面积为,所以三角形的面积为,所以三角形和的面积之和为;又三角形、和四边形的面积之和为,所以四边形的面积为.另解:从整体上来看,四边形的面积三角形面积三角形面积白色部分的面积,而三角形面积三角形面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即,所以四边形的面积为.20.如图,长方形的面积是36,是的三等分点,,求阴影部分的面积.【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.。
六年级下册数学总复习试题-图形的组合与观察专项练全国版(含答案)
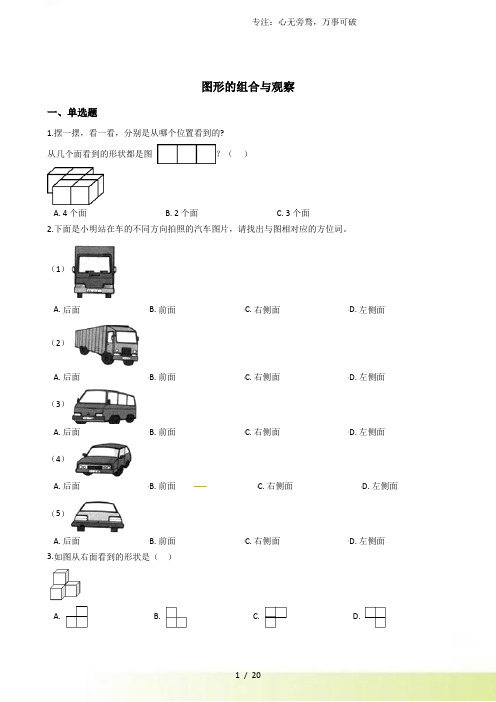
图形的组合与观察一、单选题1.摆一摆,看一看,分别是从哪个位置看到的?从几个面看到的形状都是图?()A. 4个面B. 2个面C. 3个面2.下面是小明站在车的不同方向拍照的汽车图片,请找出与图相对应的方位词。
(1)A. 后面B. 前面C. 右侧面D. 左侧面(2)A. 后面B. 前面C. 右侧面D. 左侧面(3)A. 后面B. 前面C. 右侧面D. 左侧面(4)A. 后面B. 前面C. 右侧面D. 左侧面(5)A. 后面B. 前面C. 右侧面D. 左侧面3.如图从右面看到的形状是()A. B. C. D.4.小明准备过马路时,一辆汽车从他的面前驶过,哪幅图是他第一个看到的?()A. B. C.5.王大伯晚上散步,当他走向路灯时,他的影子会越来越( )A. 小B. 长C. 短6.如果你按照下面的步骤做,当你完成第五步的时候,将纸展开,你会得到()A. B. C. D.7.看图回答.下面的图形是从上边物体的哪一面看到的?().A. 正面B. 侧面C. 上面8.小强用同样大的小正方体摆了一个长方体,从正面和上面看,看到的图形分别是:如图小强摆这个长方体一共用了()个小正方体.A. 12B. 18C. 249.从上面看到的形状不同的是()A. B. C.10.用相同的小正方体拼成一个大正方体,至少需要( )个小正方体。
A. 4B. 8C. 16D. 32二、判断题11.这四个图形中只有一个图形不能密铺….12.若干个完全相同的三角形能密铺.13.由远往近观察某一物体时,距离物体越近,看到的范围越大。
14.把两个一样的正方体拼成一个长方体后,体积和表面积都不变.(判断对错)15.正五边形是轴对称图形,它也能密铺.16.淘气看到的是。
17.从侧面看到的是圆形。
18.人越来越远离窗子时,看到的窗外的范围会越来越窄.19.从上面看小药箱,应该是。
()20.两个正方体摆成一排,从正面和上面看到的都是长方形。
三、填空题21.把一个棱长是10分米的正方体木料削成一个最大的圆柱体木料,圆柱体木料的体积是________.22.下面的三个图形分别是从哪个方向看到的?填一填。
六年级数学下册典型例题系列之第三单元:组合立体图形的表面积专项练习(原卷版)
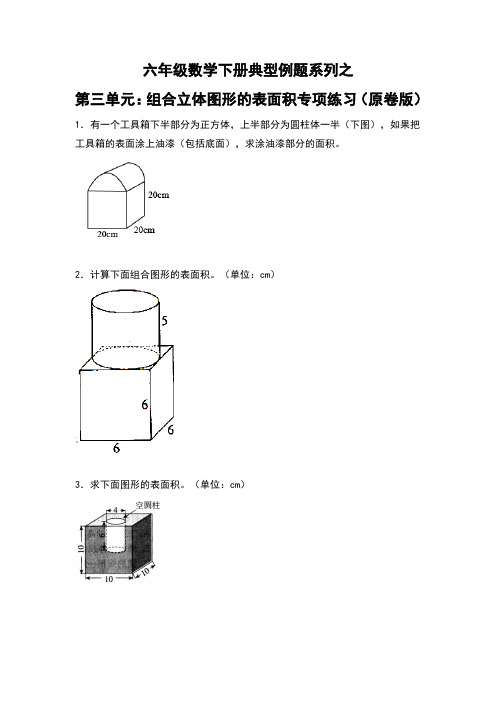
六年级数学下册典型例题系列之第三单元:组合立体图形的表面积专项练习(原卷版)1.有一个工具箱下半部分为正方体,上半部分为圆柱体一半(下图),如果把工具箱的表面涂上油漆(包括底面),求涂油漆部分的面积。
2.计算下面组合图形的表面积。
(单位:cm)3.求下面图形的表面积。
(单位:cm)4.下图是一个灯笼图片,阿姨做这个灯笼至少需要多大的彩纸?5.有三个圆柱,一个堆在一个上面,底层圆柱最大,上层最小,它们的直径分别是4分米、 3分米、2分米,高都是2分米,这样的立体图形的表面积是多少?6.如下图的“博士帽”是用黑色卡纸做成,上面是边长30厘米的正方形,下面是底面直径20厘米,高10厘米的无底无盖的圆柱。
制作20顶这样的“博士帽”,至少需要多少平方分米的黑色卡纸?7.如图所示的百宝箱,上部是一个圆柱的一半,下部是一个长50cm,宽40cm,高20cm的长方体,这个百宝箱的表面积是多少?8.下面是一个零件的示意图(单位:厘米),是由一个长方体从前往后挖掉(挖通)一个底面直径为10厘米的圆柱体得到的,求这个零件的表面积。
(π取3.14)9.把一个底面直径是8cm、高是12cm的圆柱沿底面直径劈开,得到如下图所示的图形。
请你计算出这个图形的表面积。
10.求下面图形的表面积。
11.求下图的表面积。
(单位:cm)12.计算出下面组合图形的表面积。
(单位:厘米)13.如图,将三个高都是1米,底面半径分别是1.5米、1米、0.5米的3个圆柱体组成一个物体。
求这个物体的表面积?14.计算下面图形的表面积。
半圆柱的底面直径是10cm15.在一个棱长为4米的正方体六个面的正中间各挖去一个底面半径和高是1米的圆柱体,求剩下的几何体的表面积。
六年级数学组合图形的应用——阴影部分面积
六年级数学总复习资料 〖组合图形的应用〗
班级: 姓名:
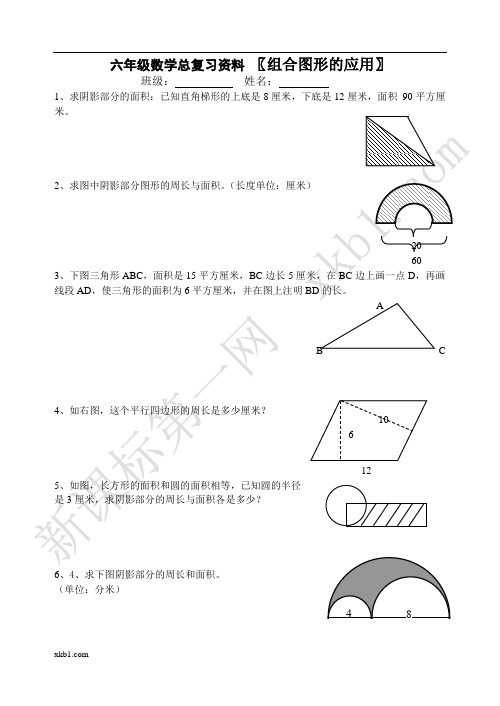
1、求阴影部分的面积:已知直角梯形的上底是8厘米,下底是12厘米,面积 90平方厘米。
2、求图中阴影部分图形的周长与面积。
3、下图三角形ABC ,面积是15平方厘米,BC 边长5线段AD ,使三角形的面积为6
C
4、如右图,这个平行四边形的周长是多少厘米?
12
5、如图,长方形的面积和圆的面积相等,已知圆的半径
是3厘米,求阴影部分的周长与面积各是多少?
6、4、求下图阴影部分的周长和面积。
(单位:分米)
7、求图中阴影部分的面积(单位:厘米)
8、求下图阴影部分面积。
(单位:厘米)
9、三角形ABC的面积是24.6平方厘米,BF是FC的2倍,E是AC的中点,连接EF,求阴影部分的面积。
10、如右图,已知甲三角形面积为3.6平方厘米,乙三角形的面积为5.4平方厘米。
线段BD的长是DC的长的多少倍?
11、下图是一个直角三角形,AD为底边BC上的高。
根据图中的已知条件,求出AD的长度。
(单位:厘米)
12
、如右图,已知直角三角形的面积是12
13、有一块长20米,宽10米的长方形地,草地面积是多少?小路的面积是多少?
面积增加了7.5平方厘米,。
六年级下册数学总复习试题-组合图形的面积专项练 (含答案)
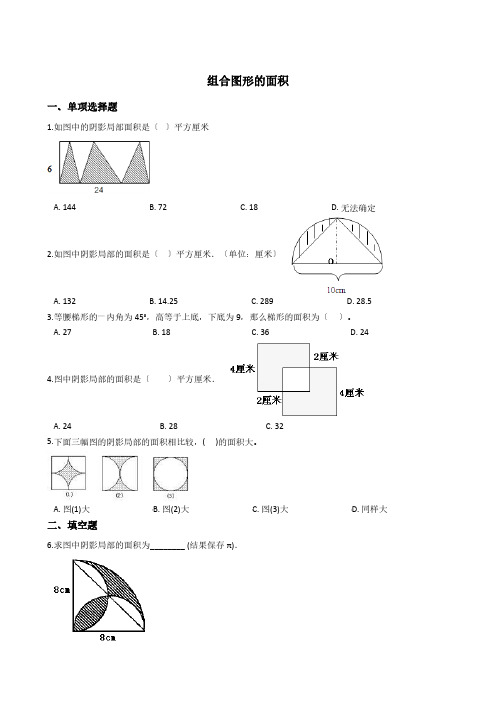
组合图形的面积一、单项选择题1.如图中的阴影局部面积是〔〕平方厘米A. 144B. 72C. 18D. 无法确定2.如图中阴影局部的面积是〔〕平方厘米.〔单位:厘米〕A. 132B. 14.25C. 289D. 28.53.等腰梯形的一内角为45°,高等于上底,下底为9,那么梯形的面积为〔〕。
A. 27B. 18C. 36D. 244.图中阴影局部的面积是〔〕平方厘米.A. 24B. 28C. 325.下面三幅图的阴影局部的面积相比较,( )的面积大。
A. 图(1)大B. 图(2)大C. 图(3)大D. 同样大二、填空题6.求图中阴影局部的面积为________ (结果保存π).7.如图中三角形的面积是10平方厘米,图中圆的面积是________平方厘米.8.看图计算〔单位:厘米〕组合图形的面积是________平方厘米9.求以下列图形的面积是________dm2。
〔单位:dm〕10.图中正方形的面积是12平方厘米,圆的面积是________平方厘米.11.计算下面图形阴影局部的面积________.(单位:厘米)12.〔2021•长沙〕如图,两个正方形的边长分别是8厘米和4厘米,那么阴影局部的面积是________平方厘米.13.先求右面图形中涂色局部的面积,再求小正方形的面积.涂色面积________平方分米,小正方形面积________平方分米.14.看图计算〔单位:厘米〕平行四边形AFEB的面积S=________平方厘米平行四边形CFED的面积S=________平方厘米15.以下列图表示的是一间房子侧面墙的形状.它的面积是________平方米.16.求下面各图阴影局部的面积〔1〕________〔2〕________17.计算下面图形的面积________.(单位:厘米)18.有一条引水渠穿过了一块麦地,这块地的总面积是引水渠占去的面积的________倍?19.把一个长12厘米,宽8厘米的长方形纸片剪下一个最大的正方形,剩下局部的面积是________平方厘米.20.求阴影局部的面积.________平方厘米21.大正方形边长为8厘米,小正方形边长为4厘米,阴影局部的面积是________平方厘米。
六年级下册数学-小升初平面图形组合专项试题-s1-人教版

-小升初平面图形组合专项试题-人教版一、解答题(题型注释)(1)(2)2.仔细数一数,填一填。
(1)右图是由个小三角形拼成的。
(2)右图有个三角形。
(3)右图共有个正方形。
3.根据游戏的需要,幼儿园阿姨用两个长8米、宽4米的长方形地垫先后拼成一个长方形游戏垫和一个正方形游戏垫(如图所示),拼成的长方形游戏垫和正方形游戏垫的周长分别是多少?4.如图,长方形中,,,三角形的面积为平方厘米,求长方形的面积.5.如图在中,,求的值.6.请你画出已学过的4种图形,使它们的面积相等,并计算出它们的面积.7.为了迎接“六•一”儿童节,学校做了一幅长方形的宣传画,长7米,宽50分米.这幅宣传画的周长和面积各是多少?8.如下图,在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
9.如下图,是一块长方形草地,长方形的长是14米,宽是12米。
中间有三条宽为2米的道路,两条是长方形,一条是平行四边形。
则草地的面积有多大?10.如图(1)(2)(3)(4)都是由9个边长为1厘米的正方形组成的3×3平方厘米的正方形,其中的阴影四边形的面积分别记为,,和,则,,ABCD:2:3BE EC=:1:2DF FC=DFG2ABCDAB CDEFGABC△12DC EA FBDB EC FA===GHIABC△的面积△的面积IHGFED CBA和中最小的与最大的和是多少平方厘米?参数答案1.(1)解:(2)解:【解析】1.根据题干的要求画图相应图形。
2.(1)4(2)3(3)5【解析】2.3.解:拼成长方形的周长是:(8+8+4)×2=20×2=40(米)答:拼成的长方形游戏垫的周长是40米.拼成后正方形的周长是:8×4=32(米)答:拼成的正方形游戏垫的周长是32米【解析】3.用两个长8米,宽4米的长方形,拼成一个大长方形,这个大长方形的长是(8+8)米,宽是4米;拼成正方形的边长是8米,然后根据长方形的周长公式:C=(a+b)×2,正方形的周长公式:C=4a,代入数据解答即可.4.72【解析】4.连接,.因为,,所以.因为,,所以平方厘米,所以平方厘米.因为,所以长方形的面积是平方厘米.5.17【解析】5.连接BG,设1份,根据燕尾定理,,得(份),(份),则(份),因此,同理连接AI、CH得,,所以如果任意一个三角形各边被分成的比是相同的,那么在同样的位置上的图形,虽然形状千变万化,但面积是相等的,这在这讲里面很多题目都是用“同理得到”的,即再重复一次解题思路,因此我们有对称法作辅助线.6.16平方厘米AE FEAB CDEFG:2:3BE EC=:1:2DF FC=3111()53210DEF ABCD ABCDS S S=⨯⨯=V长方形长方形12AED ABCDS S=V长方形11::5:1210AG GF==510AGD GDFS S==V V12AFDS=V16AFD ABCDS S=V长方形ABCD 72IHGFED CBABGCS△=::2:1AGC BGCS S AF FB==△△::2:1ABG AGCS S BD DC==△△2AGCS=△4ABGS=△7ABCS=△27AGCABCSS=△△27ABHABCSS=△△27BICABCSS=△△7222177GHIABCSS---==△△【解析】6.试题分析:此题没有具体数据,答案不唯一:把每个方格的长度看作1厘米,这里可以指定画面积为16平方厘米的正方形与长方形,则正方形的边长是4厘米,长方形的长可以是8厘米,则宽就是2厘米,梯形的上底是4厘米,下底是12厘米,高是2厘米,三角形的底是8厘米,高是4厘米,由此即可画图解:根据题干分析画图如下:答:它们的面积都是16平方厘米.7.24米,35平方米【解析】7.试题分析:根据长方形的周长=(长+宽)×2,长方形的面积=长×宽,代入数据即可解答.解:50分米=5米,(7+5)×2=24(米),7×5=35(平方米),答:这幅画的周长是24米,面积是35平方米.8.120平方厘米【解析】8.本题考查三角形面积和比的相关知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
