小学六年级组合图形复习题
六年级数学拓展题之《12平面组合图形(含答案)》

12.平面组合图形1.正方形ABCD的边长为8厘米,三角形ABC三角形CEF的面积大10平方厘米,求阴影部分的面积。
2.如图,两图中的两个圆的半径都是5厘米,两个图中阴影部分的面积相比较,()。
A.图①大B.图②大C.一样大3.如图,小圆的半径是1厘米,大圆的半径是5厘米,小圆沿着大圆外延滚动直至回到起点位置,(1)小圆扫过的面积是多少平方厘米?(2)小圆圆心经过的长度是多少厘米?(3)小圆一共转了多少圈?4.如图,正方形中阴影部分的面积是53c㎡,那么正方形的面积是多少平方厘米?5.墙角O点处的一木桩上栓着一只羊(如图),栓羊的绳子长4米,墙角两边的墙长2米。
这只羊能吃到草的面积最多是多少?6.如图,已知一个五边形的三条边的长和四个角,试求这个五边形的面积。
(单位厘米)7.如图在大正方形中,三个涂色部分图形周长的和是60厘米,大正方形的面积是多少平方厘米?8.在一个底面是长方形的洗脸盆中,有一个直径6厘米的圆形塑料片在盆地任意滑动。
这个塑料片不可能滑到的面积是多少平方厘米?9.下图中空白部分是一个正方形,求阴影部分的周长和面积。
10.求图中阴影部分的面积,其中A为边的中点。
(单位:cm)11.如图,大正方形的边长比小正方形的长2厘米,小正方形的面积比大正方形小36平方厘米。
小正方形的面积是()平方厘米。
12.如图,大、小两个正方形中阴影部分的面积比是3:1,小正方形的面积是大正方形的( )。
13.已知右图中长方形被分成四部分,三角形BCO的面积是4cm²,三角形CDO 的面积是8cm²,涂色部分的面积是()cm²。
14.如图,涂色部分的面积是10平方厘米,空白部分的面积是多少平方厘米。
15.正方形的面积是12平方厘米,求阴影部分的面积。
参考答案1.222.B3. 24π、12π、54.1005.6π6.187.1448.7.749.21.42、10.2610.9π11.6412.1 913.2014.52.815.3π详细讲解,请参阅“小学六年级数学思维提升培优拓展题讲解之《12平面组合图形》”。
六年级秋季班-第17讲:圆的组合图形的相关练习-教师版

第十三讲 圆的组合图形练习1、三角形的面积 =2⨯底高. 2、等腰直角三角形的面积 =24=直角边的平方斜边的平方. 3、长方形的面积 =⨯长宽. 4、正方形的面积 = 边长的平方 = 2对角线的平方.5、菱形的面积 =2对角线之积.6、梯形的面积 =()2⨯上底+下底高.7、圆的面积 =π⨯半径的平方. 8、扇形的面积 =360π⨯⨯︒圆心角半径的平方.【例1】 如图,以半圆的半径8厘米为直径在半圆内作一个圆,求图中阴影部分的面积.(π取3.14)【难度】★【答案】50.24平方厘米.【解析】2222118432161650.2422S R r πππππππ=-=⨯⨯-⨯=-==平方厘米.【总结】阴影部分的面积等于大半圆的面积减去中间圆的面积.【例2】 如图,正方形的边长是6厘米,则阴影部分的周长是______厘米,面积是______平方厘米.(π取3.14)【难度】★知识精讲习题精炼【答案】61.68;7.74.【解析】3644224422C r ππ=⨯+⨯⨯⨯=+⨯⨯⨯241261.68π=+=厘米; 223664364()3697.742S r πππ=⨯-⨯=-⨯⨯=-=平方厘米.【总结】阴影部分的周长等于正方形的周长加上四个等圆的周长,阴影部分的面积等于正方 形的面积减掉四个等圆的面积.【例3】 如图,正方形的边长为6分米,求阴影部分的面积.(π取3.14) 【难度】★【答案】7.74平方分米.【解析】24566623697.74360S ππ⨯⨯=⨯-⨯=-=平方分米.【总结】阴影部分的面积等于正方形的面积减掉两个扇形的面积.【例4】 如图,求阴影部分的面积.(π取3.14) 【难度】★ 【答案】6.【解析】326S =⨯=阴影.【总结】通过割补法将阴影部分的扇形移到空白部分的扇处,从而阴影部分的面积就是长方 形的面积.【例5】 如图,长方形的宽是8厘米,求阴影部分的面积.(π取3.14) 【难度】★★【答案】50.24平方厘米.【解析】21908168168882360S π⎛⎫⨯⨯=⨯-⨯⨯-⨯- ⎪⎝⎭()6464161650.24ππ=--==平方厘米.【总结】此题中阴影部分的面积等于长方形的面积减去三角形的面积再减去弯角处的空白部 分的面积.【例6】 图中,三个同心圆的半径分别为2、6、10,则图中阴影部分占大圆面积的______%. 【难度】★★22AB【答案】3333%100S S ==阴影总. 【解析】222111106225833444S ππππππ⎛⎫=⨯+⨯-⨯=+= ⎪⎝⎭阴影,210100S ππ=⨯=总,33100S S =阴影总. 【总结】考查阴影部分图形的面积所占的百分比,注意通过割补,将阴影部分的面积移到一 起.【例7】 如图,圆O 的直径为8厘米,则阴影部分的面积是多少平方厘米?(π取3.14) 【难度】★★ 【答案】18.24.和一个半圆的面积的和.故222111482(484)422S πππ=⨯+⨯⨯-⨯⨯⨯+⨯⨯16162(168)163218.24ππππ=+-⨯+=-=平方厘米.【总结】考查阴影部分图形的面积的求法,注意用规则图形的面积去表示阴影部分的面积.【例8】 如图,正方形的边长为2厘米,以圆弧为分界线的A 、B 两部分的面积的差是______平方厘米.(π取3.14)【难度】★★ 【答案】2.28.【解析】由题可得:112222124A B S S +=⨯⨯-⨯⨯=平方厘米;而214522 3.1422 1.570.432360A S =⨯⨯-⨯⨯=-=平方厘米;所以10.430.57B S =-=平方厘米,故0.570.430.14B A S S -=-=平方厘米. 【总结】本题中一方面要区分A 与B 两部分的面积,另一方面要认真观察,进行分析.【例9】 如图,其中四个圆的直径均为4厘米,那么阴影部分的面积为______平方厘米.(π取3.14)G 【难度】★★ 【答案】16.【解析】222(442)16S ππ=⨯+⨯-⨯=平方厘米.【总结】本题中阴影部分的面积等于一个正方形的面积减掉一个圆的面积,解题时要认真分 析.【例10】 如图,扇形AFB 恰为一个圆的14,BCDE 是正方形,边长为3,AFBG 也是正方形,边长为4,求图中阴影部分的面积.(π取3.14)【难度】★★【答案】10.56.【解析】2114744424S π=⨯⨯-⨯-⨯()141644210.56ππ=--=-=()【总结】阴影部分面积等于三角形面积减去左下角空白部分的面积.【例11】 如图,ABC ∆是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径.已知:AB = BC = 10,求阴影部分的面积.(π取3.14)【难度】★★ 【答案】32.125.【解析】连接BD .因为1105252ABD S ∆=⨯⨯=,21125555424BD S ππ=⨯⨯-⨯⨯=弓所以25252532.12542S π=+-=阴影. 【总结】本题中连接BD 是关键点,这样就可以将阴影部分进行分割,从而进行求解.【例12】 如图,ABC ∆是等腰直角三角形,腰AB 长为4厘米,求阴影部分的面积.(π取3.14) 【难度】★★ 【答案】4平方厘米.【解析】连接BD ,则上面阴影的弓形的面积等于空白弓形的面积,则阴影部分的面积就是直角三角形ABD 的面积,故14242S =⨯⨯=阴影.【总结】本题主要考查通过割补法求阴影部分面积.AABABC DO【例13】 如图,一个大正方形各边都被四等分,分成十六个小正方形,图A 是一个圆,图B 是由三个半圆围成的图形,那么图A 与图B 的周长的大小关系是______,图A 与图B 的面积的大小关系是______.【难度】★★【答案】2B A C C =;A B S S =.【解析】设正方形边长为4,则2A C π=,A S π=,224B C πππ=+=,2122B S πππ=⨯⨯-=, 故2B AC C =;A B S S =.【总结】本题中图A 就是一个圆,图B 是由三个半圆构成的,因此主要考查圆的周长和面 积的运用.【例14】 如图,有半径为5厘米、4厘米、3厘米的三个圆,A 分)的面积与阴影部分的面积相比,哪个大?大多少?【难度】★★ 【答案】相等.【解析】大圆的面积为:2525ππ⨯=;两个内圆的面积分别是:239ππ⨯=;2416ππ⨯=;A 部分的面积为:916ππ+-白色区域面积=25π-白色区域面积; 阴影部分面积为:25π-白色区域面积;所以,两部分面积相等.【总结】半径为5的大圆的面积,减掉半径为3和半径为4的两个小圆的面积的和,再加上 一个A 部分的面积,即为阴影部分面积.【例15】 如图,梯形ABCD 的面积是25平方厘米,求圆环的面积.(π取3.14) 【难度】★★【答案】157平方厘米.【解析】圆环的面积等于大圆面积减小圆面积,即22()OB OC π-;同时,已知梯形的面积又等于两个三角形的面积的差,即:2222111()25222OBA OCD S S S OB OC OB OC ∆∆=-=-=-=梯形,所以圆环的面积为:50157π=平方厘米.【总结】本题综合型较强,亮点在于把圆环面积与三角形面积和梯形的面积结合起来.【例16】 如图是由正方形和半圆形组成的图形,其中P 点为半圆周的中点,Q 点为正方形一边的中点,那么阴影部分的面积是多少平方厘米?(π取3.14)【难度】★★【答案】51.75平方厘米. 【解析】连接PB .ABP BPQ ABCD S S S S S =+--△△阴影正方形半圆21111010 3.145101555222=⨯+⨯⨯-⨯⨯-⨯⨯51.75=平方厘米.【总结】本题主要考查如何将不规则的图形转化成规则图形的组合,从而求出面积.【例17】 如图,直角梯形的面积是54平方厘米,求阴影部分的面积.(π取3.14) 【难度】★★★【答案】11.61平方厘米.【解析】由题意,得圆的半径6r =厘米,所以21355 3.14611.61360S S S =-=-⨯⨯=阴影梯形扇形平方厘米.【总结】本题主要要理解梯形的下底是2个半径长,从而求出阴影部分的面积.【例18】 如图,直径AB 为3厘米的半圆以点A 为圆心逆时针旋转60°,使AB 到达AC的位置,求图中阴影部分的面积.(π取3.14)【难度】★★★【答案】4.71平方厘米.【解析】2603.1434.71360ABC S S ==⨯⨯=阴影扇形平方厘米.【总结】本题主要考查利用割补法将阴影部分转化成一个扇形,从而求出面积.B10【例19】 如图,90AOB ∠=︒,C 为AB 的中点,已知阴影甲的面积为16平方厘米,求阴影乙的面积.(π取3.14)【难度】★★★【答案】16平方厘米.【解析】由图可知:S S S +=甲空半圆,S S S +=乙空扇形,故16S S ==乙甲平方厘米.【总结】本题中要认真观察两个阴影部分之间的关系,进行和差运算之后求出面积.【作业1】 如图,正方形的边长为4厘米,阴影部分的面积是______平方厘米. 【难度】★【答案】5.72平方厘米.【解析】221122(222)4242442S πππππ=⨯-⨯⨯⨯-⨯⨯=-+=+空,故44(24)122 5.72S S S ππ=-=⨯-+=-=正阴影空白平方厘米. 【总结】考查阴影部分的面积的求法.【作业2】 如图,阴影部分的面积是100平方厘米,求圆环的面积. 【难度】★★【答案】100π平方厘米.【解析】设大圆半径为R ,小圆半径为r ,则2222()S S S R r R r πππ=-=-=-圆环小圆大圆,课后作业甲乙COS 空EA BCDFG H又22100S S S R r =-=-=阴影小正方形大正方形, 所以100S π=圆环平方厘米.【总结】本题中要注意正方形的边长就是相应的圆的半径.【作业3】 边长为1的正方形中,分别以边长为直径作3个半圆.求围成的阴影部分的面积. 【难度】★★【答案】12.【解析】方法一:一个半圆面积加上一个正方形面积一半减去两个四分之一 扇形的面积的和,即22111111111()1()()222228282S ππππ⎡⎤=⨯⨯+⨯-⨯⨯=+-=⎢⎥⎣⎦阴影;方法二:下面的半圆拆为两个四分一直扇形拼在上面空白部分,正好与上方阴影部分组 成一个长方形,这个长方形的面积就等于正方形面积的一半. 【总结】本题主要考查利用割补法求阴影部分的面积.【作业4】 如图,长方形的长为5厘米,宽为4厘米,则阴影部分的周长为______厘米,面积是______平方厘米.【难度】★★【答案】16.13;12.185.【解析】9059049(54)(54)216.131801802C πππ⨯⨯⨯⨯=++-+-=+=阴影厘米,2290590441(54)2012.1853603604S πππ⨯⨯⨯⨯=-⨯-=-=扇形平方厘米.【总结】阴影部分的周长是两段弧的长加上两条线段的长,阴影部分的面积等于大扇形的面 积减去长方形的面积再加上小扇形的面积.【作业5】 已知等腰直角三角形ABC ,D 为斜边中点,AC = BC = 2分米,弧DF 、弧DH 分别是以B 、C 为圆心画的弧,求阴影部分的面积.【难度】★★ 【答案】1平方分米.【解析】通过割补法可知,阴影部分的面积的等于正方形的面积,故21(2)12CEDG S S ==⨯=阴影正方形平方分米.E【总结】考查利用割补法求阴影部分的面积.【作业6】 如图,圆的半径都是3厘米,则阴影部分的面积为______平方厘米. 【难度】★★ 【答案】3.87.【解析】三个扇形的圆心角的度数的和为180度,故而将三个扇形面积拼在一起,也就等于去求一个半径为3厘米的圆的面积.三角形面积:166182⨯⨯=,三个扇形的面积:2180393602ππ⨯⨯=,故阴影部分面积为:918 3.872π-=平方厘米.【总结】等腰直角三角形面积减去三个扇形面积既得阴影的部分面积.【作业7】 如图,小正方形的边长4厘米,大正方形边长6厘米,DBE ∆的面积为3.2平方厘米,求阴影部分的面积.【难度】★★★ 【答案】1.38平方厘米.【解析】由图可知: 3.224 1.6BD =⨯÷=厘米,所以 3.6AB =厘米, 所以23.66303.1462360ABC S S S ⨯=-=-⨯⨯△阴影扇形10.89.42 1.38=-=平方厘米.【总结】阴影部分的面积等于三角形ABC 的面积减去小扇形的面积.0.6775=平方米.。
六年级数学组合图形的面积试题答案及解析

六年级数学组合图形的面积试题答案及解析1.我们开始提到的“乡村小屋”的面积是多少?【答案】18【解析】图形内部格点数;图形边界上的格点数;根据毕克定理,则(单位面积).2.两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为,右下角的阴影部分(线状)面积为,求大正方形的面积.【答案】19【解析】块状部分与线状部分之间的部分称为D,则D与前者共14个方格,与后者共17个方格,因此每个方格的面积是大正方形的面积为.3.如图,平行四边形,,,,,平行四边形的面积是,求平行四边形与四边形的面积比.【答案】1/18【解析】连接、.根据共角定理∵在和中,与互补,∴.又,所以.同理可得,,.所以.所以.4.如图,有三个正方形的顶点、、恰好在同一条直线上,其中正方形的边长为10厘米,求阴影部分的面积.【答案】100【解析】对于这种几个正方形并排放在一起的图形,一般可以连接正方形同方向的对角线,连得的这些对角线互相都是平行的,从而可以利用面积比例模型进行面积的转化.如右图所示,连接、、,则,根据几何五大模型中的面积比例模型,可得,,所以阴影部分的面积就等于正方形的面积,即为平方厘米.5.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少?【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.6.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.7.右图中,和是两个正方形,和相交于,已知等于的三分之一,三角形的面积等于6平方厘米,求五边形的面积.【答案】49.5【解析】连接、,由于与平行,可知四边形构成一个梯形.由于面积为6平方厘米,且等于的三分之一,所以等于的,根据梯形蝴蝶定理或相似三角形性质,可知的面积为12平方厘米,的面积为6平方厘米,的面积为3平方厘米.那么正方形的面积为平方厘米,所以其边长为6厘米.又的面积为平方厘米,所以(厘米),即正方形的边长为3厘米.那么,五边形的面积为:(平方厘米).8.如图,长方形的面积是2平方厘米,,是的中点.阴影部分的面积是多少平方厘米?【答案】【解析】如下图,连接,、的面积相等,设为平方厘米;、的面积相等,设为平方厘米,那么的面积为平方厘米.,.所以有.比较②、①式,②式左边比①式左边多,②式右边比①式右边大0.5,有,即,.而阴影部分面积为平方厘米.9.如图,与均为正方形,三角形的面积为6平方厘米,图中阴影部分的面积为多少.【答案】6【解析】如图,连接,比较与,由于,,即与的底与高分别相等,所以与的面积相等,那么阴影部分面积与的面积相等,为6平方厘米.10.如图,是梯形的一条对角线,线段与平行,与相交于点.已知三角形的面积比三角形的面积大平方米,并且.求梯形的面积.【答案】28【解析】连接.根据差不变原理可知三角形的面积比三角形大4平方米,而三角形与三角形面积相等,因此也与三角形面积相等,从而三角形的面积比三角形的大4平方米.但,所以三角形的面积是三角形的,从而三角形的面积是(平方米),梯形的面积为:(平方米).11.如图,已知,,,,线段将图形分成两部分,左边部分面积是38,右边部分面积是65,求三角形的面积.【答案】40【解析】连接,.根据题意可知,;;所以,,,,,于是:;;可得.故三角形的面积是40.12.如图,长方形的面积是36,是的三等分点,,则阴影部分的面积为多少?【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.13.如图,如果长方形的面积是平方厘米,那么四边形的面积是多少平方厘米?【答案】32.5【解析】如图,过、、、分别作长方形的各边的平行线.易知交成中间的阴影正方形的边长为厘米,面积等于平方厘米.设、、、的面积之和为,四边形的面积等于,则,解得(平方厘米).14.已知正方形的边长为10,,,则?【答案】53【解析】如图,作于,于.则四边形分为4个直角三角形和中间的一个长方形,其中的4个直角三角形分别与四边形周围的4个三角形相等,所以它们的面积和相等,而中间的小长方形的面积为,所以.15.如下图,长方形和长方形拼成了长方形,长方形的长是20,宽是12,则它内部阴影部分的面积是多少.【答案】120【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半,为.16.长方形的面积为36,、、为各边中点,为边上任意一点,问阴影部分面积是多少?【答案】13.5【解析】解法一:寻找可利用的条件,连接、,如下图:可得:、、,而即;而,.所以阴影部分的面积是:解法二:特殊点法.找的特殊点,把点与点重合,那么图形就可变成右图:这样阴影部分的面积就是的面积,根据鸟头定理,则有:.17.在长方形内部有一点,形成等腰的面积为16,等腰的面积占长方形面积的,那么阴影的面积是多少?【答案】3.5【解析】先算出长方形面积,再用其一半减去的面积(长方形面积的),再减去的面积,即可求出的面积.根据模型可知,所以,又与的面积相等,它们的面积和等于长方形面积的一半,所以的面积等于长方形面积的,所以.18.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分的面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.19.如图所示,长方形内的阴影部分的面积之和为70,,,四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和,以及三角形和的面积之和,进而求出四边形的面积.由于长方形的面积为,所以三角形的面积为,所以三角形和的面积之和为;又三角形、和四边形的面积之和为,所以四边形的面积为.另解:从整体上来看,四边形的面积三角形面积三角形面积白色部分的面积,而三角形面积三角形面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即,所以四边形的面积为.20.如图,长方形的面积是36,是的三等分点,,求阴影部分的面积.【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.。
六年级数学下册典型例题系列之第三单元:组合立体图形的表面积专项练习(原卷版)
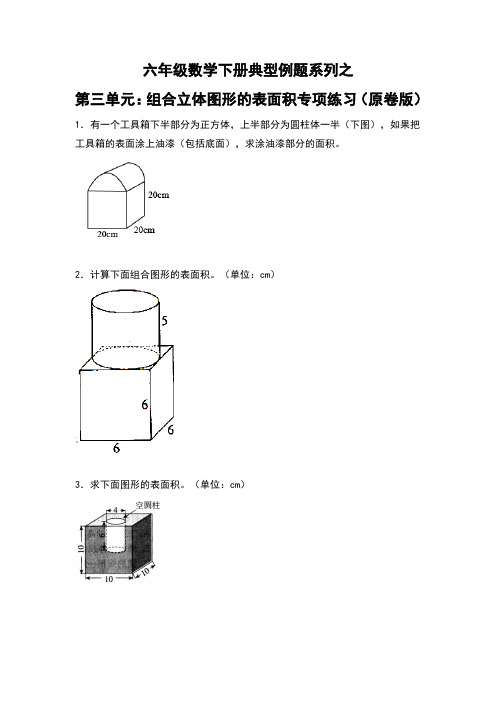
六年级数学下册典型例题系列之第三单元:组合立体图形的表面积专项练习(原卷版)1.有一个工具箱下半部分为正方体,上半部分为圆柱体一半(下图),如果把工具箱的表面涂上油漆(包括底面),求涂油漆部分的面积。
2.计算下面组合图形的表面积。
(单位:cm)3.求下面图形的表面积。
(单位:cm)4.下图是一个灯笼图片,阿姨做这个灯笼至少需要多大的彩纸?5.有三个圆柱,一个堆在一个上面,底层圆柱最大,上层最小,它们的直径分别是4分米、 3分米、2分米,高都是2分米,这样的立体图形的表面积是多少?6.如下图的“博士帽”是用黑色卡纸做成,上面是边长30厘米的正方形,下面是底面直径20厘米,高10厘米的无底无盖的圆柱。
制作20顶这样的“博士帽”,至少需要多少平方分米的黑色卡纸?7.如图所示的百宝箱,上部是一个圆柱的一半,下部是一个长50cm,宽40cm,高20cm的长方体,这个百宝箱的表面积是多少?8.下面是一个零件的示意图(单位:厘米),是由一个长方体从前往后挖掉(挖通)一个底面直径为10厘米的圆柱体得到的,求这个零件的表面积。
(π取3.14)9.把一个底面直径是8cm、高是12cm的圆柱沿底面直径劈开,得到如下图所示的图形。
请你计算出这个图形的表面积。
10.求下面图形的表面积。
11.求下图的表面积。
(单位:cm)12.计算出下面组合图形的表面积。
(单位:厘米)13.如图,将三个高都是1米,底面半径分别是1.5米、1米、0.5米的3个圆柱体组成一个物体。
求这个物体的表面积?14.计算下面图形的表面积。
半圆柱的底面直径是10cm15.在一个棱长为4米的正方体六个面的正中间各挖去一个底面半径和高是1米的圆柱体,求剩下的几何体的表面积。
小学六年级组合图形试题训练(求面积)

小学六年级(组合图形)试题训练
求阴影部分面积
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
六年级下册数学-小升初平面图形组合专项试题-s1-人教版

-小升初平面图形组合专项试题-人教版一、解答题(题型注释)(1)(2)2.仔细数一数,填一填。
(1)右图是由个小三角形拼成的。
(2)右图有个三角形。
(3)右图共有个正方形。
3.根据游戏的需要,幼儿园阿姨用两个长8米、宽4米的长方形地垫先后拼成一个长方形游戏垫和一个正方形游戏垫(如图所示),拼成的长方形游戏垫和正方形游戏垫的周长分别是多少?4.如图,长方形中,,,三角形的面积为平方厘米,求长方形的面积.5.如图在中,,求的值.6.请你画出已学过的4种图形,使它们的面积相等,并计算出它们的面积.7.为了迎接“六•一”儿童节,学校做了一幅长方形的宣传画,长7米,宽50分米.这幅宣传画的周长和面积各是多少?8.如下图,在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
9.如下图,是一块长方形草地,长方形的长是14米,宽是12米。
中间有三条宽为2米的道路,两条是长方形,一条是平行四边形。
则草地的面积有多大?10.如图(1)(2)(3)(4)都是由9个边长为1厘米的正方形组成的3×3平方厘米的正方形,其中的阴影四边形的面积分别记为,,和,则,,ABCD:2:3BE EC=:1:2DF FC=DFG2ABCDAB CDEFGABC△12DC EA FBDB EC FA===GHIABC△的面积△的面积IHGFED CBA和中最小的与最大的和是多少平方厘米?参数答案1.(1)解:(2)解:【解析】1.根据题干的要求画图相应图形。
2.(1)4(2)3(3)5【解析】2.3.解:拼成长方形的周长是:(8+8+4)×2=20×2=40(米)答:拼成的长方形游戏垫的周长是40米.拼成后正方形的周长是:8×4=32(米)答:拼成的正方形游戏垫的周长是32米【解析】3.用两个长8米,宽4米的长方形,拼成一个大长方形,这个大长方形的长是(8+8)米,宽是4米;拼成正方形的边长是8米,然后根据长方形的周长公式:C=(a+b)×2,正方形的周长公式:C=4a,代入数据解答即可.4.72【解析】4.连接,.因为,,所以.因为,,所以平方厘米,所以平方厘米.因为,所以长方形的面积是平方厘米.5.17【解析】5.连接BG,设1份,根据燕尾定理,,得(份),(份),则(份),因此,同理连接AI、CH得,,所以如果任意一个三角形各边被分成的比是相同的,那么在同样的位置上的图形,虽然形状千变万化,但面积是相等的,这在这讲里面很多题目都是用“同理得到”的,即再重复一次解题思路,因此我们有对称法作辅助线.6.16平方厘米AE FEAB CDEFG:2:3BE EC=:1:2DF FC=3111()53210DEF ABCD ABCDS S S=⨯⨯=V长方形长方形12AED ABCDS S=V长方形11::5:1210AG GF==510AGD GDFS S==V V12AFDS=V16AFD ABCDS S=V长方形ABCD 72IHGFED CBABGCS△=::2:1AGC BGCS S AF FB==△△::2:1ABG AGCS S BD DC==△△2AGCS=△4ABGS=△7ABCS=△27AGCABCSS=△△27ABHABCSS=△△27BICABCSS=△△7222177GHIABCSS---==△△【解析】6.试题分析:此题没有具体数据,答案不唯一:把每个方格的长度看作1厘米,这里可以指定画面积为16平方厘米的正方形与长方形,则正方形的边长是4厘米,长方形的长可以是8厘米,则宽就是2厘米,梯形的上底是4厘米,下底是12厘米,高是2厘米,三角形的底是8厘米,高是4厘米,由此即可画图解:根据题干分析画图如下:答:它们的面积都是16平方厘米.7.24米,35平方米【解析】7.试题分析:根据长方形的周长=(长+宽)×2,长方形的面积=长×宽,代入数据即可解答.解:50分米=5米,(7+5)×2=24(米),7×5=35(平方米),答:这幅画的周长是24米,面积是35平方米.8.120平方厘米【解析】8.本题考查三角形面积和比的相关知识。
小学数学六年级奥数《圆和组合图形(2)》练习题(含答案)
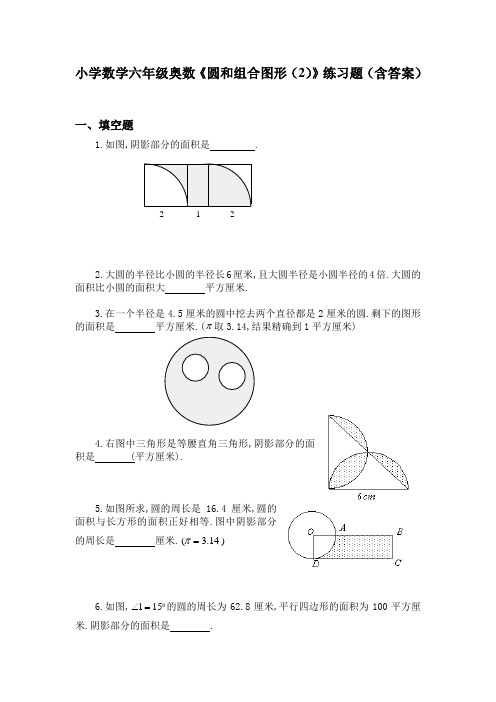
小学数学六年级奥数《圆和组合图形(2)》练习题(含答案)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 . 2 1 27.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解答题E D C B A GF O D C A B 2 甲 乙11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率22) 取12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++= 5.204.1645=⨯=(厘米). 6. 6548(平方厘米). 如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为 ⌒61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米). 8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ, 解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r ,则①的面积为: 72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯, ②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1) 又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求,它的面积为: )420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ 07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).D。
小学六年级数学小升初珍藏版复习资料第19讲 组合图形的认识、表面积与体积(解析)

2022-2023学年小升初数学精讲精练专题汇编讲义第19讲 组合图形的认识、表面积与体积小学阶段所学的立体图形主要有长方体、正方体、圆柱体和圆锥体,这四种立体图形的表面积和体积的计算是小升初数学的热点内容,特别是涉及到立体图形的切拼时,立体图形的表面积和体积发生了变化,牢固掌握这些立体图形的特征和有关的计算方法及切拼时表面积和体积的变化规律是解题的关键,本讲将在前面两讲学习的基础上进一步总结整理立体图形切拼时表面积和体积的变化规律。
知识点一:立体图形的表面积和体积计算常用公式: 立体图形 表面积体积 长方体S=2)(bh ah ab ++a :长 b:宽 h :高 S :表面积 V abh = V Sh = 正方体S=26a a :棱长 S :表面积 3V a = V Sh = 圆柱222π2πS rh r =+=+圆柱侧面积个底面积 2πV r h =圆柱圆锥 22ππ360n S l r =+=+圆锥侧面积底面积 注:l 是母线,即从顶点到底面圆上的线段长 21π3V r h =圆锥体 知识点二:解决立体图形的表面积和体积问题时的注意事项(1)要充分利用正方体六个面的面积都相等,每个面都是正方形的特点.(2)把一个立体图形切成两部分,新增加的表面积等于切面面积的两倍;反之,把两个立体图形拼合到一起,减少的表面积等于重合部分面积的两倍。
(3)若把几个长方体拼成一个表面积最大的长方体,应把它们最小的面拼合起来;若把几个长方体拼成一个表面积最小的长方体,应把它们最大的面拼合起来。
2.解答立体图形的体积问题时,要注意以下几点:(1)物体沉入水中,水面上升部分的体积等于物体的体积;把物体从水中取出,水面下降部分的体积等干物体的体积,这是物体全部浸没在水中的情况。
如果物h r hr 知识精讲体不全部浸在水中,那么排开水的体积就等于浸在水中的那部分物体的体积. (2)把一种形状的物体变为另一种形状的物体后,形状变了,但它的体积保持不变.(3)求一些不规则物体体积时,可以通过变形的方法求体积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm ,下底16cm ,阴影 ⑾求阴影部分面积。
(单位:cm ) 部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白 ⒀阴影部分比空白部分大6cm 2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
