大学物理 第十六讲 毕萨定律
合集下载
《大学物理》第八章 毕萨定律S

”
. 例Id载ly任流意2长一r直解点导:P根线的取据,磁任毕其其感意—电在应电萨流P强流点定强度元产理度BI生d为l的I?,磁试场d计为B 算方:导向线为旁Idl r
ol
ro
P
dB
各电流元产生的
o Idlsin 4dB 方r向2 垂直纸面向里。
I
1
B dB
B
ab
dr
其中B adbr、0cd与B板 d面r 等 距B离 d。0r
bc
cd
da
B
c
Bab Bcd 2Bab
而 o Ii o j ab
B
1 2
o
j
. . . . 与P点到平板的距离无关。
dl
dl
aB
b
B
1 2
o
j
与P点到平板的距离无关。
)
0m 2x3
r
B
xP
2)
在圆心处(x=0):
B
0 I
2R
(磁偶极子的场)
如考虑一段“圆弧形”载流线在圆心的磁场贡
献:
B 0I 2R 2
圆弧对圆心 所张的角
例 一直螺线管轴线上的磁场 B ?
已知:导线通有电流I,单位长度
B
2
oI R2
(
x2
R2
)
3 2
I
若令L 积分B回 d路r LL的L 绕B向dl 相反:0 若积分回L 路不包围电流I : B
I
dr
0
L
B
r
I
L
L
几点注意事项:
3毕萨定律

Idl
R I
r
dB
θ
x
o
解:将圆环分 割为无限多个 电流元; 电流元; 建立坐标系, 建立坐标系,电流元在轴线上产生的 磁感应强度 dB 为:
毕奥-萨伐尔定律 §3.毕奥 萨伐尔定律 / 二、应用毕萨定律解题方法 毕奥
P
x
µ 0Idl sin α dB = 2 4πr π α=
Idl
r
dBy dB
2
l
θ2
dB ⊗ P
B = ∫ dB
=∫
θ2 θ1
µ0 I sin θdθ 4πa
Idl θ r l o
x
µ0 I = (cosθ1 − cosθ 2 ) 4πa
θ1
a
毕奥-萨伐尔定律 §3.毕奥 萨伐尔定律 / 二、应用毕萨定律解题方法 毕奥
µ0 I B= (cos θ1 − cos θ 2 ) 4πa
Idl
θ
r
P
-1
毕奥-萨伐尔定律 §3.毕奥 萨伐k= 4π
Idl
θ
r
P
真空中的磁导率 µ 0 = 4π k
= 4π × 10 T ⋅ m ⋅ A µ 0 Idl sin θ dB = 2 4π r
−7 -1
由矢量乘积法则: 由矢量乘积法则:
| A × B | | A|| B |sin θ =
毕奥-萨伐尔定律 §3.毕奥 萨伐尔定律 / 二、应用毕萨定律解题方法 毕奥
µ0 IR 2πR B= dl 3 ∫0 4πr
Idl
R
r
µ0 IR = 2πR 3 4πr 2 µ0 IR
=
=
dBy dB
I
θ
x
10-3-毕-萨定律
0 nI
x
0 nI cos 2 cos 1 B 2
1 0 nI 2
B O
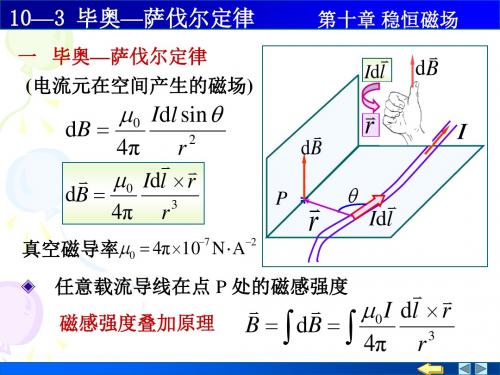
10—3 毕奥—萨伐尔定律
第十章 稳恒磁场
例4 半径 为 R 的带电薄圆盘的电荷面密度 为 , 并以角速度 绕通过盘心垂直于盘面的轴转 动 ,求圆盘中心的磁感强度.
R o r
解法一
圆电流的磁场
( 1) I (2 ) R o ( 3) I R
第十章 稳恒磁场
R B x 0 I 0 o B0 2R
I
( 4)
0 I BA 4π d
d *A
R1
R2
B0
0 I
4R
( 5) I
*o
B0
o
0 I
8R
B0
0 I
4 R2
0 I
4 R1
0 I
4π R1
10—3 毕奥—萨伐尔定律
j
S
dB
Idl j Sdl nSdlqv 0 nSdlqv r
4π r
3
dl
运动电荷的磁场
适用条件
q
+
Hale Waihona Puke rv c v +B
dN nS dl d B 0 qv r B 3 d N 4π r
q
r
v
B
10—3 毕奥—萨伐尔定律
dB
0 Id l
2
B
0 IR 2π R B dl 3 0 4π r 2 0 IR
( 2 x R )2
2 2 3
10—3 毕奥—萨伐尔定律 第十章 稳恒磁场 2 0 IR 0 pm B I R *B 3 2 2 3/ 2 2 2 o x x ( 2 x R )2 2 ( x R ) 讨 论
x
0 nI cos 2 cos 1 B 2
1 0 nI 2
B O
10—3 毕奥—萨伐尔定律
第十章 稳恒磁场
例4 半径 为 R 的带电薄圆盘的电荷面密度 为 , 并以角速度 绕通过盘心垂直于盘面的轴转 动 ,求圆盘中心的磁感强度.
R o r
解法一
圆电流的磁场
( 1) I (2 ) R o ( 3) I R
第十章 稳恒磁场
R B x 0 I 0 o B0 2R
I
( 4)
0 I BA 4π d
d *A
R1
R2
B0
0 I
4R
( 5) I
*o
B0
o
0 I
8R
B0
0 I
4 R2
0 I
4 R1
0 I
4π R1
10—3 毕奥—萨伐尔定律
j
S
dB
Idl j Sdl nSdlqv 0 nSdlqv r
4π r
3
dl
运动电荷的磁场
适用条件
q
+
Hale Waihona Puke rv c v +B
dN nS dl d B 0 qv r B 3 d N 4π r
q
r
v
B
10—3 毕奥—萨伐尔定律
dB
0 Id l
2
B
0 IR 2π R B dl 3 0 4π r 2 0 IR
( 2 x R )2
2 2 3
10—3 毕奥—萨伐尔定律 第十章 稳恒磁场 2 0 IR 0 pm B I R *B 3 2 2 3/ 2 2 2 o x x ( 2 x R )2 2 ( x R ) 讨 论
磁场强度毕奥萨伐尔定律及运动电荷产生的磁场大学物理电子教案

R sin r
B
讨论:
2 x R
2
0 IR
2 2 3/ 2
R
I
x = 0;
B
xP x
o
1.载流圆环环心处
Bo 有:
0 I
2R
R B
o
I
2.圆弧电流中心处
0 I 0 I 有: Bo 2 R 2 4R
R
B
O
14
例4:一根无限长导线通有电流I,中部弯成圆弧形, 如图所示。求圆心o点的磁感应强度B。
4
二、磁场
磁铁和运动电荷(电流)会在周围空间激发场 ---磁场。 磁场的基本性质:对运动电荷(电流)有力的作用。 磁场是一种物质, 其物质性体现在: 1)磁场对磁铁、对电流、对运动电荷均有作用力; 2)载流导体在磁场中移动时,磁场的作用力对它作功。 3)变化的磁场在空间传播,表明磁场具有动量。 恒定磁场—在空间的分布不随时间变化的磁场。 注意:无论电荷是运动还是静止,它们之间都存在库仑 相互作用,但只有运动着的电荷才存在着磁相互作用。
0 I B cos 1 cos 2 4a
讨论: 1.无限长载流直导线的磁场:
l 2
Idl
l o
r
I 0 1 0, 2 ; B 2a
1
dB P x
a
I
2.半无限长载流直导线的磁场:
1 , 2 ; B
例2:一宽为 a 无限长载流平面,通 有电流 I , 求距平面左侧为 b 与电流 共面的 P 点磁感应强度 B 的大小。 解:以 P 点为坐标原点,向右为坐 标正向; 分割电流元为无限多宽为 dx P 的无限长载流直导线; B
第16章磁力

-
--
-
vd
UH
+
P 型半导体 2)测量磁场 霍耳电压
N 型半导体
IB U H RH d
第十六章
磁力
第三节 磁场对载流 导线的作用
第十六章
磁力
一、安培力公式
一个载流子受的磁场力:
f qv B
Id l
B
在dl中有nSdl个载流子,其 受力总和为:
l B Idl B dF nSdlq v B nSvqd
B
en
M,N F1
俯视图
O,P
B
en
MN l2 NO l1
M BIS sin
线圈有N匝时
M F1l1 sin BIl2l1 sin
M ISen B m B M NISen B
第十六章
磁力
1)en方向与 B 相同
第十六章 例2
磁力
有一回旋加 速器,他 的交变 电压的 频率 6 为 1210 Hz ,半圆形电极的半径为0.532m . 问 加速 氘核所需的磁感应强度为多大?氘核所能达到的最大 动能为多大?其最大速率有多大?(已知氘核的质量 27 19 为 3.3 10 kg ,电荷为 1.6 10 C ). 解 由粒子的回旋频率公式,可得
第十六章
磁力
磁聚焦 螺距与 V 无关只与 V// 成正比。一束发散角 不大的带电粒子束,当 V// 大致相同时,螺距同。经一个周 3
期它们将重新会聚在另一点,这种发散粒子束会聚到一点的 现象与透镜将光束聚焦现象十分相似,因此叫磁聚焦
应用电子显微镜,电子光学 等 .
磁场及毕萨定律

B r B I
磁场呈轴对称分布
例题2 :
dB
0
Idl sin
4 r 2
求均匀载流圆环轴线上的磁感应强度分布。
定义:刚性平面截流线圈的磁矩
r pm
r IS
解:建立轴极坐标系ox
电流元在P点激发的磁场
大小
dB
μ
0
4
Idl r2
方向
由
r Idl
r r
决定
分析对称性、写出投影式
B dB 0
BP
r r
dB
r dB
dBP
Px
x
I
r B
讨论
B
0 IR2
2(R2 x2 )32
①将圆电流在轴线上的磁感应强度用磁矩表示
B
μ 0
IR2
2(R2
x
2
3
)
2
μ 0
I
R2
2 (R2
x2
3
)2
μ 0
IS
2 (R2
x2
3
)2
μ 0
n
IN
S
等效环形电流
电荷的运动是一切磁现象的根源。
所有磁现象可归结为
生 产
A的 磁场
运动电荷 A
+
作用于
B的 磁场
作用于
运动电荷 B
产生
15.1 磁场 磁感应强度
一、磁场
1、磁场对进入场中的运动电荷或载流导体有磁力作用。
2、载流导体在磁场中移动时,磁力将对载流导体作功。
这表明磁场具有能量。
二、磁感应强度
引言:
•静止电荷——静电场 •运动电荷——电场、磁场 •稳恒电流产生的磁场不随时间变化——稳恒磁场
11-4毕萨定律(新)
右手螺旋前进法则
I
r
dB
二. 运动电荷的磁场
dB = 4 π
=4 π
μ
o
I dl sina r
2 2
S +
dl
+
μ
o
n qv S dl sina r
<
I
v
+
r r ) dB μ qv sin( v 、 B= = r π dN 4
μ qv dN sin( v 、 r =
π 4
o 2 o
I = n qvS
o 2 2 o 2 2
μ
dB
a
μ I cosβ dβ = πa
o
4
电流元的dB已经有了,接 下去对整体载流导线产生 磁感应强度量值的积分。
μ I cosβ dβ dB = π a
o
4
电流元的dB已经有了,接 下去对整体载流导线产生 磁感应强度量值的积分。
dl
I dl
B = dB = β
o
β2
讨论:
当螺线管为无限长时:
B =μ o n I
作为经验公式记住!
β1
π
、
β2
0
归纳总结
利用毕奥 萨伐尔 (Biot-savart) 解题思路: 定律求磁感应强度的分布
1.将载流导线无限分割成电流元Idl ,任一电流 元在空间某点处产生磁感应强度用dB 表示。 2.由磁场的叠加原理求得整根载流导线所产生的 磁感应强度B = dB
比例系数
dB ∝ I dl sin a r
2 o 2
a 表示电流元和
矢径之间的夹角 ∨
可写为
真空磁导率
μ I dl sin a dB = r π 4
毕萨定律
叠加原理
=?
叠加原理
B
E dE
dB
三、毕奥-萨伐尔定律 大小: dB
4
0 Idl sin
r
2
0 4 10 N A
7
2
真空中的 磁导率
方向:右手螺旋法则 毕-萨定律:
dB
0 Id l r
4 r3
r
3
I
P
叠加原理
2013/9/3
r
I
B
0 Idl 0 I B dB 2 4 R 2R
m
S I
定义
m ISn
2
磁矩
n
0 I R 0 m B 2 2R 2R R 2R3
2013/9/3
0 I
B
DUT 常葆荣
0m
2 R
3
10
例题
求:圆电流轴线上的磁感应强度。 方向: 右手定则
B
dB 4
0 Id l r
DUT 常葆荣
Id l
r
6
B
例如:
r
P
dB
Id l
r
dB
r
I d l
dB
dB 0 Id l r
2013/9/3
DUT 常葆荣
7
例题 求:长度为L,载流为I的载流直导线的磁场分布。
dB B dB 方向 L 0 I d l r 0 I d l sin dB 3 dB 4 r 4 r2
dB
2013/9/3
DUT 常葆荣
11
《大学物理》第八章毕萨定律S
0
B 0 B B
x
都适用。
例半径为R的无限长圆柱载流直导线,电流I沿轴线 方向流动,并且载面上电流是均匀分布。计算任 意点P的B=? I 解:先分析P点的B方向 由电流对称分布可知: B oP . 取过P点半径为 r =op 的圆周L, P L上各点B大小相等,方向沿切线 r >R时 由安培环路定理得: L d B ds dB dB B dr Bdr cos 0o B 2 r I 0 . 又 B O B d r I 0 2 r P ds 与毕萨 定理结 果一致
L
若r<R 同理:
r
R
例求通电螺绕环的磁场分布。已知环管轴线的半径 为R,环上均匀密绕N匝线圈,设通有电流I。 解: 由于电流对称分布,与环共轴 的圆周上,各点B大小相等, R R1 方向沿圆周切线方向。 取以o为中心,半径为r的圆周为L R2 当R1< r <R2 I B dr Bdr cos 0o B 2 r 0 NI × × × B ×× ×× × 而 I NI × 2 r 0 i 0 × ×
4)载流回路的磁场 电流元 在空间P点产生的磁场: 0 Idl er Idl I dB
二. 磁场的高斯定理
4 r o Idl r B dB 3 4 r
2
(磁通连续原理)
定理的内容:穿过任一闭合曲面(高斯面)的总磁通量总为0
S
B
o q v r B 4 r 3
例8.4
对低速运动的 带电粒子成立!
8.3 安培环路定理
一、安培环路定理 静电场理论中,有“静电场的环路定理”L : 对于稳恒磁场,相应的“稳恒磁场的环路定理”应如何 ? B dr ?
B 0 B B
x
都适用。
例半径为R的无限长圆柱载流直导线,电流I沿轴线 方向流动,并且载面上电流是均匀分布。计算任 意点P的B=? I 解:先分析P点的B方向 由电流对称分布可知: B oP . 取过P点半径为 r =op 的圆周L, P L上各点B大小相等,方向沿切线 r >R时 由安培环路定理得: L d B ds dB dB B dr Bdr cos 0o B 2 r I 0 . 又 B O B d r I 0 2 r P ds 与毕萨 定理结 果一致
L
若r<R 同理:
r
R
例求通电螺绕环的磁场分布。已知环管轴线的半径 为R,环上均匀密绕N匝线圈,设通有电流I。 解: 由于电流对称分布,与环共轴 的圆周上,各点B大小相等, R R1 方向沿圆周切线方向。 取以o为中心,半径为r的圆周为L R2 当R1< r <R2 I B dr Bdr cos 0o B 2 r 0 NI × × × B ×× ×× × 而 I NI × 2 r 0 i 0 × ×
4)载流回路的磁场 电流元 在空间P点产生的磁场: 0 Idl er Idl I dB
二. 磁场的高斯定理
4 r o Idl r B dB 3 4 r
2
(磁通连续原理)
定理的内容:穿过任一闭合曲面(高斯面)的总磁通量总为0
S
B
o q v r B 4 r 3
例8.4
对低速运动的 带电粒子成立!
8.3 安培环路定理
一、安培环路定理 静电场理论中,有“静电场的环路定理”L : 对于稳恒磁场,相应的“稳恒磁场的环路定理”应如何 ? B dr ?
大学物理(上册) 7.3 毕奥-萨伐尔定律
3
(5)
B
0 IR 2
( 2 x 2 R 2)2
3
i
(6)
讨论: 1.若线圈有 N 匝:
( 2 x R )2 I 和 B 成右螺旋关系; 2. x 0 B 的方向不变;
2 2
B
N 0 IR2
3
3. x 0 4. x R
B
0 I
2R
2 3
B
0 IR
0 Idl sin ; 方向:右手法则; 大小: dB 4π r2
2.有限载流导线在空间产生的磁场
任意形状电流在空间产生的磁场:等于各电流元在 空间产生磁场的矢量和,磁感应强度用积分表示:
B dB
L
0 I dl r
4π r
3
(2)
a.上式即为任意形状的电流产生磁场的分布规律;
1 8 7 6 5
0 Idl
4π R 2
+
R
2
Idl
+4
+3
2、 4、 6 、 8 点 : 0 Idl 0 dB sin 45 4π R 2
1. 载流直导线的磁场
z
B
2
设真空中有长L的载流直导线如 dz 图所示,电流为I,场点 P 到 r z 导线的垂距为 r0 ,且 P 与导线 I r0 两端点的连线与电流的夹角分 o 别为1、2 ,试应用毕-萨定律 x 1 A 计算 P 点的磁感应强度。
7.3 毕奥——萨伐尔定律 7.3.1 毕—萨定律 1.电流元在真空产生的磁场 对应的磁感应强度: 0 Idl r dB (1) 4π r3
7 2 4 π 10 N A 真空磁导率 :0
(5)
B
0 IR 2
( 2 x 2 R 2)2
3
i
(6)
讨论: 1.若线圈有 N 匝:
( 2 x R )2 I 和 B 成右螺旋关系; 2. x 0 B 的方向不变;
2 2
B
N 0 IR2
3
3. x 0 4. x R
B
0 I
2R
2 3
B
0 IR
0 Idl sin ; 方向:右手法则; 大小: dB 4π r2
2.有限载流导线在空间产生的磁场
任意形状电流在空间产生的磁场:等于各电流元在 空间产生磁场的矢量和,磁感应强度用积分表示:
B dB
L
0 I dl r
4π r
3
(2)
a.上式即为任意形状的电流产生磁场的分布规律;
1 8 7 6 5
0 Idl
4π R 2
+
R
2
Idl
+4
+3
2、 4、 6 、 8 点 : 0 Idl 0 dB sin 45 4π R 2
1. 载流直导线的磁场
z
B
2
设真空中有长L的载流直导线如 dz 图所示,电流为I,场点 P 到 r z 导线的垂距为 r0 ,且 P 与导线 I r0 两端点的连线与电流的夹角分 o 别为1、2 ,试应用毕-萨定律 x 1 A 计算 P 点的磁感应强度。
7.3 毕奥——萨伐尔定律 7.3.1 毕—萨定律 1.电流元在真空产生的磁场 对应的磁感应强度: 0 Idl r dB (1) 4π r3
7 2 4 π 10 N A 真空磁导率 :0
