最新中考数学夺分培优复习 (第1讲)实数及其运算
中考数学知识点专题分类复习:第1讲实数及其运算

中考数学知识点专题分类复习:第1讲实数及其运算 【知识巩固】 1.实数的分类:
注意:在理解无理数时,要注意“无限不循环”,归纳起来有四类: (1)开方开不尽的数,如,等; (2)有特定意义的数,如圆周率π,或化简后含有π的数,如等; (3)有特定结构的数,如0.1010010001…等; (4)某些三角函数,如sin60o等 2.倒数 如果a与b互为倒数,则有ab=1,反之亦成立。倒数等于本身的数是1和-1。零没有倒数。 3.绝对值 一个数的绝对值就是表示这个数的点与原点的距离,|a|≥0。零的绝对值是它本身,也可看成它的相反数,若|a|=a,则a≥0;若|a|=-a,则a≤0。 4.相反数 实数与它的相反数时一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零).从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果a与b互为相反数,则有a+b=0,a=-b,反之亦成立。 5.平方根 如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方根)。一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根。正数a的平方根记做“”。 正数a的正的平方根叫做a的算术平方根,记作“”。 正数和零的算术平方根都只有一个,零的算术平方根是零。 六、立方根 如果一个数的立方等于a,那么这个数就叫做a的立方根(或a的三次方根)。一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。 注意:,这说明三次根号内的负号可以移到根号外面。 6.实数大小的比较 (1)数轴 规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。 解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵活运用。 (2)实数大小比较的几种常用方法 ①数轴比较:在数轴上表示的两个数,右边的数总比左边的数大。 ②求差比较:设a、b是实数, ③求商比较法:设a、b是两正实数, ④绝对值比较法:设a、b是两负实数,则。 ⑤平方法:设a、b是两负实数,则。 7.科学记数法和近似数 (1)有效数字 一个近似数四舍五入到哪一位,就说它精确到哪一位,这时,从左边第一个不是零的数字起到右边精确的数位止的所有数字,都叫做这个数的有效数字。 (2)科学记数法 把一个数写做的形式,其中,n是整数,这种记数法叫做科学记数法。 8.实数的运算 (1)加法交换律 (2)加法结合律 (3)乘法交换律 (4)乘法结合律 (5)乘法对加法的分配律 (6)实数的运算顺序:先算乘方,再算乘除,最后算加减,如果有括号,就先算括号里面的。 【典例解析】 典例一、实数的分类 【例题】 下列各数中,不是负数的是( ) A.﹣2 B.3 C.﹣ D.﹣0.10 【考点】正数和负数. 【分析】利用负数的定义判断即可得到结果. 【解答】解:A、﹣2是负数,故本选项不符合题意; B、3是正数,不是负数,故本选项符合题意; C、﹣是负数,故本选项不符合题意; D、﹣0.10是负数,故本选项不符合题意; 故选:B. 【点评】此题考查了正数与负数,分清正数与负数是解本题的关键. 【变式训练】 如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )
中考数学第1讲实数及其运算PPT课件
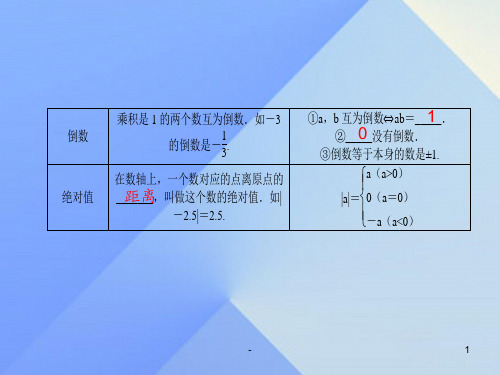
1≤|a|<10,n 是整数),这种记数法叫做科学记数法;一个近似数,_四___舍__五___入到哪
一位,就说这个数精确到哪一位.如:3.14549 精确到 0.01 为___3__.1__5__,精确到
0.001 为___3_._1_4__5_.
4.零指数幂,负整数指数幂
任何一个不等于零的数的零次幂都等于 1,即__a_0_=__1__(_a_≠_0;)任何不等于零的
-
9
1.(2016·金华)如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其
中不合格的是( B)
A.Φ45.02 B.Φ44.9 C.Φ44.98 D.Φ45.01
2.(2016·河南)-13的相反数是( B)
A.-13
1 B.3
C.-3
D.3
-
10
3.(2015·河南)下列各数中最大的数是( A)
A.5 B. 3 C.π D.-8
4.(2016·盐城)下列实数中,是无理数的为( D)
A.-4 B.0.101 001
1 C.3 D. 2
5.(2016·河南)某种细胞的直径是 0.000 000 95 米,将 0.000 000 95 米用科学记数法表示
为( A)
A.9.5×10-7 B.9.5×10-8
(5)平方比较法:∵由 a>b>0,可得 a> b,∴可以把 a与 b的大小问题转化成比较 a 和 b 的大小问题。
-
8
4.三个非负数 初中阶段所涉及的三个非负数:|a|,a2, a(a≥0).若几个非负数的和为 0,则这几个 非负数都同时为 0.如:若|a|+b2+ c=0,则 a=b=c=0.
示为( B)
A.7.6×10-9 B.7.6×10-8 C.7.6×109 D.7.6×108
中考数学全程复习方略第一讲实数课件

)
B
A.|m|<1 C.mn>0
B.1-m>1 D.m+1>0
2.(2019·黄石中考)下列四个数:-3,-0.5, 2,5 中,
3
绝对值最大的数是 (
)
A
A.-3
B.-0.5
C.
2
3
D. 5
3.(2019·广州三模)已知:|x|=3,|y|=2,且x>y,则x-y
的值为 A.5
世纪金榜导学号(
(2)有特定意义的数,如圆周7,率3 2π,或化简后含有π的数,
如 +8等. 3
(3)具有特定结构的数,如0.101 001 000 1…等. (4)某些三角函数,如sin 60°等.
【题组过关】
1.(2019·自贡中考)实数m,n在数轴上对应点的位置如
图所示,则下列判断正确的是 世纪金榜导学号(
2 -1=1+
3
3.
3 -1)+6×
3 -1=13
+1+ 3
【明·技法】 实数运算的一般步骤 (1)利用绝对值、负整数指数幂的运算、零次幂的运算、 二次根式化简特殊角三角函数值的运算、乘方等运算 法则,将算式中的每项运算化为最简.
(2)根据原式中的运算符号进行实数的加减运算(注:若 最简根式不能合并,可直接连同前面的符号照搬到下一 步). (3)写出最简结果.
【题组过关】
1.计算: | 1 | 1 的结果是 ( 24
A.1
B.
C.0
1
2
) C D.-1
2.(2019·云南模拟)若x,y为实数,且|x+3|+Leabharlann y 3 =0,则 (x
中考数学总复习《实数》

中考数学总复习《实数》实数是中考数学中的重要基础知识,对于后续的数学学习和解题起着关键作用。
在中考复习阶段,对实数进行系统、全面的梳理和巩固是十分必要的。
一、实数的概念实数包括有理数和无理数。
有理数是能够表示为两个整数之比的数,包括整数、有限小数和无限循环小数。
例如,5、-3、025、0333(3 循环)等都是有理数。
无理数则是无限不循环小数,不能表示为两个整数之比。
常见的无理数有圆周率π、根号 2(√2)、根号 3(√3)等。
二、实数的分类1、按定义分类实数可以分为有理数和无理数。
有理数又可分为整数和分数,整数包括正整数、零和负整数;分数包括正分数和负分数。
2、按性质分类实数可以分为正实数、零和负实数。
正实数包括正有理数和正无理数;负实数包括负有理数和负无理数。
三、实数的运算1、加法和减法同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
减法法则:减去一个数,等于加上这个数的相反数。
2、乘法和除法两数相乘,同号得正,异号得负,并把绝对值相乘。
除法法则:除以一个数等于乘以这个数的倒数。
3、乘方和开方求 n 个相同因数乘积的运算叫做乘方。
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。
如果一个数的平方等于 a,那么这个数叫做 a 的平方根;如果一个数的立方等于 a,那么这个数叫做 a 的立方根。
四、实数的性质1、实数的相反数实数 a 的相反数是 a,0 的相反数是 0。
2、实数的绝对值正数的绝对值是它本身,负数的绝对值是它的相反数,0 的绝对值是 0。
3、实数的大小比较正数大于 0,0 大于负数,正数大于负数;两个负数比较大小,绝对值大的反而小。
五、科学记数法把一个数表示成a×10ⁿ的形式(其中1≤|a|<10,n 为整数),这种记数方法叫做科学记数法。
当原数绝对值大于 1 时,n 是正数;当原数绝对值小于 1 时,n 是负数。
中考数学复习专题一、实数及其运算

第一章 实数及其运算(宋体三号字加粗,居中) 【知识要点】(宋体小四号字加粗) 1、实数的分类:(宋体五号字)
数)无理数(无限不循环小负分数正分数分数负整数零正整数整数有理数实数
注意:可以化成分数的数都为有理数,有限小数和无限循环小数都可以化成分数。
2、数轴三要素:原点、单位长度、正方向。 3、相反数、绝对值:实数a的相反数是a; 正数的绝对值是它本身,0的绝对值是0,负数的绝对值是它的相反数,
即:)0()0(0)0(aaaaaa 4、平方根:若2(0)xaa,则x叫做a的平方根。 正数有两个互为相反数的平方根;0的平方根是0;负数没有平方根。 正数a的正的平方根叫做a的算术平方根。 5、立方根:若3xa,则x叫做a的立方根。 每个实数都有且只有一个立方根。 6、实数的大小比较:两个正数比较,绝对值大的数较大; 两个负数比较,绝对值大的数反而小; 正数>0>负数。 注意:①数轴上右边的点对应的实数大于数轴上左边的点对应的实数。 ②能用有理数估计一个无理数的大致范围。 7、二次根式:形如)0(aa的式子叫二次根式。 8、实数的运算 加法:同号两数相加,绝对值相加,符号不变; 异号两数相加,较大绝对值的减去较小绝对值,符号同绝对值大的数的符号; (简记为:同号相加,符号不变;异号相减,符号从大) 一个实数加0,就等于这个数。 减法:减去一个数等于加上这个数的相反数。 乘法:同号得正/异号得负,并把绝对值相乘;0乘任何数等于0。 除法:除以一个数等于乘上这个数的倒数(0不能作除数)。 乘方:annaaaa个 ;
)0(1aaapp )0(10aa 开平方:22(0)()(0)(0)aaaaaaaaa 运算顺序:首先乘方开方,再乘除,最后加减;同级运算,先左后右。 9、特殊三角函数值:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实数及其运算
(一):【知识梳理】
1.实数的有关概念
(1)有理数: 和 统称为有理数。
(2)有理数分类
①按定义分: ②按符号分:
有理数()()0()()()();有理数()()()0()()()
(3)相反数:只有 不同的两个数互为相反数。若a、b互为相反数,
则 。
(4)数轴:规定了 、 和 的直线叫做数轴。
(5)倒数:乘积 的两个数互为倒数。若a(a≠0)的倒数为1a.
则 。
(6)绝对值:
(7)无理数: 小数叫做无理数。
(8)实数: 和 统称为实数。
(9)实数和 的点一一对应。
2.实数的分类:实数
3.科学记数法、近似数和有效数字
(1)科学记数法:把一个数记成±a³10n的形式(其中1≤a<10,n是整数)
(2)近似数是指根据精确度取其接近准确数的值。取近似数的原则是“四舍五入”。
(3)有效数字:从左边第一个不是0的数字起,到精确到的数位止,所有的数字,都
叫做这个数字的有效数字。
4. 有理数加、减、乘、除、幂及其混合运算的运算法则
(1)有理数加法法则:
()()()()()()()()()()()()
零
①同号两数相加,取________的符号,并把__________
②绝对值不相等的异号两数相加,取___________的符号,并用 ____________。互为相反数
的两个数相加得____。
③一个数同0相加,__________________。
(2)有理数减法法则:减去一个数,等于加上____________。
(3)有理数乘法法则:
①两数相乘,同号_____,异号_____,并把_________。任何数同0相乘,都得________。
②几个不等于0的数相乘,积的符号由___________决定。当____________,积为负,当
___________,积为正。
③几个数相乘,有一个因数为0,积就为__________.
(4)有理数除法法则:
①除以一个数,等于_______________________.__________不能作除数。
②两数相除,同号_____,异号_____,并把_________。 0除以任何一个___________的数,
都得0
(5)幂的运算法则:正数的任何次幂都是__________; 负数的_________是负数,负
数的_________是正数
(6)有理数混合运算法则:
先算________,再算__________,最后算___________。如果有括号,就________。
5.实数的运算顺序:在同一个算式里,先 、 ,然后 ,最后 .有
括号时,先算 里面,再算括号外。同级运算从左到右,按顺序进行。
6.运算律
(1)加法交换律:_____________。 (2)加法结合律:____________。
(3)乘法交换律:_____________。 (4)乘法结合律:____________。
(5)乘法分配律:_________________________。
7.实数的大小比较
(1)差值比较法:
ab>0a>b,ab=0ab,ab<0a< b
(2)商值比较法:
若ab、为两正数,则ab>1a>b;1;aabbab<1a<b
(3)绝对值比较法:
若ab、为两负数,则a>ba<bababa;;<ba>b
(4)两数平方法:如155137与
8.三个重要的非负数:
(二):【经典例题】
1.下列各数中:-1,0,169,2,1.1010016.0,,12,45cos,-60cos,
7
22
,2,722.
有理数集合{ „}; 正数集合{ „};
整数集合{ „}; 自然数集合{ „};
分数集合{ „}; 无理数集合{ „};
绝对值最小的数的集合{ „};
2. 已知(x-2)2+|y-4|+6z=0,求xyz的值..
3.已知a与 b互为相反数,c、d互为倒数,m的绝对值是2求32122()2()mmabcdm
的值
4. a、b在数轴上的位置如图所示,且a>b,化简aabba
5.计算
(1) 32÷(-3)2+|- 16 |³(- 6)+49;
(2) 2(32-23)-(32+23)
三:【课后训练】
一、选择题
1.(2014²安徽)(-2)³3的结果是( )
A.-5 B.1 C.-6 D.6
2.(2014²呼和浩特)下列实数是无理数的是( )
A.-1 B.0 C.π D.13
3.(2014²武汉)在实数-2,0,2,3中,最小的实数是( )
A.-2 B.0 C.2 D.3
4.(2014²滨州)估计5在( )
A.0~1之间 B.1~2之间
C.2~3之间 D.3~4之间
5.(2013²菏泽)如图,数轴上的A,B,C三点所表示的数分别是a,b,c,其中AB=
BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在( )
A.点A的左边
B.点A与点B之间
C.点B与点C之间
D.点B与点C之间或点C的右边
6.(2013²淮安)如图,数轴上A,B两点表示的数分别为2和5.1,则A,B两点之间
表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
二、填空题
7.(2014²珠海)比较大小:-2__ __-3.
8.(2014²玉林)3的倒数是__ __.
9.(2013²鄂州)若|p+3|=0,则p=__ __.
0
b
a
10.(2014²湘潭)如图,按此规律,第6行最后一个数字是__ _,第_ __行最后
一个数是2014.
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
„
11.计算:21-1=1,22-1=3,23-1=7,24-1=15,25-1=31,„.归纳各计算结
果中的个位数字规律,猜测266-1的个位数字是__ __.
12.(2013²咸宁)在数轴上,点A(表示整数a)在原点的左侧,点B(表示整数b)在原点
的右侧.若|a-b|=2013,且AO=2BO,则a+b的值为__ __.
三、解答题
13.(2014²扬州)计算:(3.14-π)0+(-12)-2-2sin30°.
14.(2014²温州)计算:12+2³(-5)+(-3)2+20140.
15.某公路规定汽车行驶速度不得超过70千米/时,当发生交通事故时,交通警察通常
根据刹车后车轮滑过的距离估计车辆行驶的速度,所用的经验公式是v=16df,其中v表
示车速(单位:千米/时),d表示刹车后车轮滑过的距离(单位:米),f表示摩擦因数.经测
量d=20 米,f=1.2,请你帮助判断一下,肇事汽车当时的速度是否超出了规定的速度.
16.(2014²滨州)计算下列各式的值:
92+19;992+199;9992+1999;99992+19999.
观察所得结果,总结存在的规律,应用得到的规律求99„922014个9+199„9,2014个9) )的值.
17.(2013²台州)任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[3]=
1,现对72进行如下操作:
72――→第1次[72]=8――→第2次[8]=2――→第3次[2]=1,这样对72只需进行3次操作后变为1,
类似地.
(1)对81只需进行几次操作后变为1?
(2)只需进行3次操作后变为1的所有正整数中,最大的是多少?
