小升初数学专项题-第七讲 一笔画与七桥问题-通用版
数学七桥问题解答如下

数学七桥问题解答如下城中的居民经常沿河过桥散步。
城中有位青年很聪明,爱思考,有一天,这位青年给大家提出了这样一个问题:能否一次走遍7座桥,而每座桥只许通过一次,最后仍回到起始地点。
这就是举世闻名的七桥问题,当时的人们始终没有能找到答案。
大数学家欧拉从朋友那里听到这个问题,很快便证明了这样的走法不存在。
欧拉是这样解决问题的:把图中被河隔开的陆地看成A、B、C、D4个点,7座桥表示成7条连接这4个点的线,思考过程如下图:伟大的数学家欧拉,睿智地把这样一个实际问题抽象成了一个由点线组成的简单的几何图形,把要解决的问题转化成图(二)的一笔画问题了。
这样一个抽象化的过程是欧拉解决这个问题时最精彩的思考,也是最值得我们学习的地方。
因为图(二)不能一笔画成,所以人们不能一次走遍7座桥。
1736年,欧拉把这题的结果发表在圣彼得堡科学院学报上,欧拉对“七桥问题”的研究是图论研究的开始,可以说,正是这个问题的研究使其成为“图论”的鼻祖。
那么欧拉是如何判断图(二)不可以一笔画成呢?为了便于大家看懂,结合这个例子,我用自己的语言来说明一下一笔画问题的解题思路:这个图形中共有4个点7条线,每个点都是若干条路线的公共端点。
如果一个点是偶数条线的公共端点,我们称这个点为双数点(或偶点);如果一个点是奇数条线的公共端点,我们称这个点为单数点(或奇点)。
图(二)中A点是5条线的公共端点,B、C、D点都是3条线的公共端点,因此图(二)有4个奇点。
一般,我们把起笔的点称为起点,停笔的点称为终点,其它的点称为路过点。
显然一笔画图形中所有路过点如果有进去的线就必须有出来的线,从而每个点连接的线数必须有偶数个才能完成一笔画,如果路过点中出现奇点,必然就会出现没有走过的路线或重复路线。
因此在一笔画图形中,只有起点和终点可以是奇点(起点可以只出不进,终点可以最后进这个点就不出了),也就是说最多只能有两个奇点,以一个奇点为起点,另一个奇点为终点。
七桥问题Seven Bridges Problem

七桥问题Seven Bridges Problem著名古典数学问题之一。
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图)。
问是否可能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到起点?欧勒于1736年研究并解决了此问题,他把问题归结为如下右图的“一笔画”问题,证明上述走法是不可能的。
有关图论研究的热点问题。
18世纪初普鲁士的柯尼斯堡,普雷格尔河流经此镇,奈发夫岛位于河中,共有7座桥横跨河上,把全镇连接起来。
当地居民热衷于一个难题:是否存在一条路线,可不重复地走遍七座桥。
这就是柯尼斯堡七桥问题。
L.欧拉用点表示岛和陆地,两点之间的连线表示连接它们的桥,将河流、小岛和桥简化为一个网络,把七桥问题化成判断连通网络能否一笔画的问题。
他不仅解决了此问题,且给出了连通网络可一笔画的充要条件是它们是连通的,且奇顶点(通过此点弧的条数是奇数)的个数为0或2。
当Euler在1736年访问Konigsberg, Prussia(now Kaliningrad Russia)时,他发现当地的市民正从事一项非常有趣的消遣活动。
Konigsberg城中有一条名叫Pregel的河流横经其中,这项有趣的消遣活动是在星期六作一次走过所有七座桥的散步,每座桥只能经过一次而且起点与终点必须是同一地点。
Euler把每一块陆地考虑成一个点,连接两块陆地的桥以线表示。
后来推论出此种走法是不可能的。
他的论点是这样的,除了起点以外,每一次当一个人由一座桥进入一块陆地(或点)时,他(或她)同时也由另一座桥离开此点。
所以每行经一点时,计算两座桥(或线),从起点离开的线与最后回到始点的线亦计算两座桥,因此每一个陆地与其他陆地连接的桥数必为偶数。
七桥所成之图形中,没有一点含有偶数条数,因此上述的任务无法完成.欧拉的这个考虑非常重要,也非常巧妙,它正表明了数学家处理实际问题的独特之处——把一个实际问题抽象成合适的“数学模型”。
一笔画问题与图论
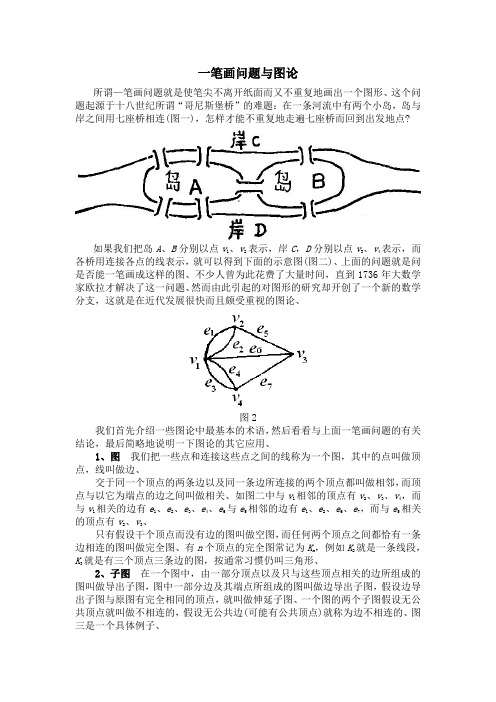
一笔画问题与图论所谓—笔画问题就是使笔尖不离开纸面而又不重复地画出一个图形、这个问题起源于十八世纪所谓“哥尼斯堡桥”的难题:在一条河流中有两个小岛,岛与岸之间用七座桥相连(图一),怎样才能不重复地走遍七座桥而回到出发地点?如果我们把岛A、B分别以点v l、v2表示,岸C,D分别以点v3、v4表示,而各桥用连接各点的线表示,就可以得到下面的示意图(图二)、上面的问题就是问是否能一笔画成这样的图、不少人曾为此花费了大量时间,直到1736年大数学家欧拉才解决了这一问题、然而由此引起的对图形的研究却开创了一个新的数学分支,这就是在近代发展很快而且颇受重视的图论、图2我们首先介绍一些图论中最基本的术语,然后看看与上面一笔画问题的有关结论,最后简略地说明一下图论的其它应用、1、图我们把一些点和连接这些点之间的线称为一个图,其中的点叫做顶点,线叫做边、交于同一个顶点的两条边以及同一条边所连接的两个顶点都叫做相邻,而顶点与以它为端点的边之间叫做相关、如图二中与v l相邻的顶点有v2、v3、v4,而与v l相关的边有e l、e2、e3、e4、e6与e5相邻的边有e l、e2、e6、e7,而与e5相关的顶点有v2、v3、只有假设干个顶点而没有边的图叫做空图,而任何两个顶点之间都恰有一条边相连的图叫做完全图、有n个顶点的完全图常记为K n,例如K2就是一条线段,K就是有三个顶点三条边的图,按通常习惯仍叫三角形、32、子图在一个图中,由一部分顶点以及只与这些顶点相关的边所组成的图叫做导出子图,图中一部分边及其端点所组成的图叫做边导出子图,假设边导出子图与原图有完全相同的顶点,就叫做伸延子图、一个图的两个子图假设无公共顶点就叫做不相连的,假设无公共边(可能有公共顶点)就称为边不相连的、图三是一个具体例子、子图是一个相对的概念,假设H是G的子图,那么G可称为H的上图、通过子图来研究较复杂的图是图论中一个基本方法、3、顶点的度在一个图中与任一顶点v有关的边的数目,叫做这个顶点的度,记作d(v),如图三中的G,d(v l)=2,d(v2)=5,d(v3)=4,d(v4)=2,d(v5)=3、这样一来,我们就看到在计算各个顶点的度时,实际上就是计算了边的数目,但每一条边在它的两个顶点处各计算一次,从而我们可以得到:定理一任一个图中各顶点的度数之总和等于其边数的二倍、由此事实,我们知道图中顶点度数之和为偶数,从而奇数度顶点的个数必为偶数、4、连通性在一个图中,我们从任一顶点v0出发,经过与之相关的一条边el到达另一个顶点v l,再经过与v l相关的一条边e2到达v2,……,如此继续下去,便得到一个顶点和边交替出现的序列v0e l v l e2v2……e k v k、当其中所经过的边彼此皆不相同时,我们就叫做一条迹,这时其中诸顶点有可能相同,假设连顶点也都彼此不同,这种迹就叫做路,起点与终点闭合的路又叫做圈、这些都是一些特殊的边导出子图,如图三中的G,假设取v l av2cv3dv2f v5gv3就是—条迹,而v l av2f v5gv3就是—条路,假设取v l av2f v5gv3bv l就得到一个圈、一条迹可以删去一段而成为路、图3一个图中的任意两点都存在一条连接这两点的路,那么称这个图是连通的、对于一个不连通的图,我们可以把它分成假设干个连通的分支、有了这些概念以后,我们就来看看上面的一笔画问题、为了表达方便起见,我们把包含图中所有的边的迹叫做欧拉迹,首尾闭合的欧拉迹叫做欧拉途、如果一个图含有一个欧拉途就说明从任一顶点山发,可以经过每一条边恰好一次并且回到出发点,换言之,它可以一笔画成、这种含有欧拉途的图就叫做欧拉图、不难证明下面两个定理:定理二 一个连通图是欧拉图的充分必要条件是它不含奇数度顶点、定理三 一个连通图含有欧拉迹的充分必要条件是最多有两个奇数度顶点、 由这两个定理可知,一个图可以一笔画成的充分必要条件是,或者不含奇数度顶,或者恰含有两个奇数度顶点、即使复杂的图,也不消一分钟就可以看出它是否能够一笔画成、在我们上面提到的七桥问题中,相应的图的四个顶点皆是奇数度的,所以无法—笔画成,即使不要求回到原出发点,也无法—笔画成、 一笔画问题只是图论中一个很小的侧面、事实上,我们在画出—个图的时候,可以赋予图中的顶点和边以各种不同的含义,从而也就可以用来研究五花八门的问题、下面举几个简单的例子、例— 在世界各国中,必能找到这样两个国家,它们与同样数目的国家有外交关系、我们用顶点表示国家,两国间有外交关系的就用边相连,这样一来就只须证明在任意—个这种图中必有两个顶点有相同的度数,事实上,设诸顶点以v l ,v 2,……v n 表示,假设各顶点的度数皆不相同,那么它们分别是0,1,2,…,(n -1)这n 个数、但这是不可能的,因为既然有0度的顶点就不可能再有n -1度的顶点,故必有两个顶点具有相同的度数、可见与之相应的两国与同样数目的国家有外交关系、例二 平面上有n 个点,其任意两点之间的距离不小于1,试证至多存在3n 对点,其距离恰是l 、以v l ,v 2,…,v n 表示平面上这n 个点,我们规定某两点v i 与v j 的距离恰是1时才用边相连,在如此所得到的图中,边的数日就是距离恰是1的顶点的对数、与任一顶点v 相邻的顶点必在以v 为圆心,1为半径的圆周上,但题设这些点之间的距离又不小于1,所以至多只能有六个顶点与v 相邻,换言之,对于任意1≤i ≤n 皆d 〔v i 〕≤6,于是,1()6ni i d v n =≤∑由定理一,左边就是图中边数的二倍,所以边数≤3n ,即至多有3n 对点距离恰是1、例三 在随意凑集的六个人中,一定能找列三个人,他们或者彼此认识,或者彼此不认识、这是一个Ramsey 问题,曾经是著名的难解问题之一,现在用图论方法很齐易解决、我们用六个点表示六个人,两个人认识就将扪应的两点用线连起来、于是这个问题就转化成下述形式:在任何一个六个顶点的图中,必有三个顶点存在,它们或者连成—个三角形,或者彼此不相邻、设v 是某一顶点,那么其余五个顶点中与v 相邻的顶点数和与v 不相邻的顶点数中必有一个是超过3的、不妨设u 1,u 2,u 3,是与v 相邻的,假设u l ,u 2,u 3中有某两点是相邻的,那么它们与v 将构成——个三角形,假设u 1,u 2,u 3中任意两点都不相邻,那么它们就是题中所要求的三点、下面我们再来看看图论中所研究的其它—些问题、邮路:利用欧拉途的概念可以解决所谓邮递路线问题、我们知道,邮递员总想从邮局出发以最短的路程走遍每一条街道,最后回到邮局,如果这位邮递员所负责的街道可以画成一个欧拉图,那么只须求出其欧拉途就一定是最理想的邮路了、而对于欧拉图要求出其中的欧拉途是不成问题的、但当街道画出一个非欧拉图时,情形就比较复杂了、这时须引入“重量”的概念而转化成求欧拉途的问题、当合理地规定图中的每一条边的重量以后,我们就得到一个所谓“赋重图”、这里的重量可以表示路程的长短,也可以表示运费的多少,也可以表示造价的高低,如此等等,于是有许多实际问题便可转化成求赋重图中的最轻通路问题、图论中已经建立了一些有效的方法、可靠性:要建立一个交通或通讯系统,就要设法使假设干个点之间皆有通路相连,并且还力求使总的造价是比较少的、这一类问题在图论中已通过对一种特殊的子图——“树”的研究得以解决、另一方面,如果在—种交通或通讯系统中任意两点之间都只有一条路相通,那么这种系统是很不可靠的,一旦有一处发生故障,就可能仗整个系统陷于瘫痪,于是图论中又进一步研究了连通的可靠性问题,这主要是将连通程度数量化、货郎担问题:我们把包含图中每一个顶点的路叫做哈密顿路,假设是闭的就叫做哈密顿圈,相应的图就叫做哈密顿图、与欧拉途不同的是哈密顿圈只要求走遍每一个顶点,并不要走遍每条边,著名的货郎担问题与此有关、这个问题是:寻找一条最短路线,使一个货郎不走回头路而走遍几个村镇,这是一个看起来简单却尚未得到解决的问题,没有一个有效方法可以用来判断一个图是否为哈密顿图、印刷电路:当我们设计一种印刷电路时,必须要求有关的电路图是一个平面图,由于我们在画出一个图的时候,其边的长短以及准确位置是无关紧要的,只是关心某条边是连接哪两个顶点而已、所以—个图是否为一个平面图并不是一眼就能看出来的、某些图乍看起来不是平面的,但可以重新画出使成平面图、这在图论中叫做平面嵌入,并且已经找到一些有效方法可以判断任意给出的图是否为平面图,以及如果是平面图怎样进行平面嵌入、四色问题:我们可以把图的顶点或边涂以各种颜色,并研究任意一个图最少要几种颜色)才能合理地进行上色(即使得相邻的顶点或边颜色不同)、著名的四色问题与此有关,四色问题是一种猜想:任一平面图只须四种颜色即可将顶点染色,使每每两相邻顶点皆有不同颜色、这与地图的染色是密切相关的、在图论中图论是一门比较新的学科,它当然可以尽量采取近代数学的概念及方法,诸如集合、映射、矩阵等等来处理其内容,还可以建立图与图之间的一些运算关系、用它可以解决的问题无法估量、图论的内容是丰富的,方法是新颖的,上面罗列的仅是其【一】二而已、。
哥尼斯堡七桥问题讲解

欧拉
问题抽象
岸,岛 点
桥线
实际问题
一笔画问题
“一笔画”是一个 有趣的数学问题,那么 什么样的图形可以一笔 画成呢?有没有什么规 律可循呢?
问题内容
“一笔画”是指笔不离开纸,而且每条 线都只画一次不准重复而画成的图形。
有奇数条边相连的点叫奇点,如:
有偶数条边相连的点叫偶点,如: Nhomakorabea欧拉一笔画的三条结论
当一个图形只有偶点时可以一笔画; 当图形只有2个奇点的时候,也可以一笔画,但
是只能以这两个奇点作为起点和终点; 当图形的奇点数大于2个的时候就不能一笔画了。
读读欧拉,他是我们大家的老师。 ——拉普拉斯
1736年,著名数学家欧拉证明了这个问题的不可能性。
岸,岛 点
桥线
点号 A B C D
边数 3 5 3 3
哥尼斯堡七桥(一笔画)问题
7(2)班:张宸志
故事发生在18世纪的哥尼斯堡城,流经那里的一条 河中有两个小岛,还有七座桥把这两个小岛与河岸联 系起来。
那里风景优美,游人众多,在这美丽的地方, 人们议论着一个有趣的问题:一个游人怎样才能 不重复的一次性走完这七座桥呢?
1736年,29岁的著名数学 家欧拉向圣彼得堡科学院递交 了《哥尼斯堡的七座桥》的论 文,证明了这个问题的不可能 性。在解答问题的同时,开创 了数学的一个分支—图论和几 何拓扑,也由此展开了数学史 上的新历程。
奇点 奇点 奇点 奇点
所以,根据定理
三可知:此图形无法 一笔画。
数学七年级上 主题六 七桥问题与一笔画

主题六七桥问题与一笔画探究问题哥尼斯堡是一座美丽的城市,布勒格尔河从这里流过,这条河有两条支流在城中交汇,汇合处有两座小岛,人们在这里建起了一座公园,公园中七座桥把河两岸和小岛连接起来.当时,那里的居民们热衷于一个有趣的数学游戏:一个游人怎样才能一次走完七座桥,每座桥只能经过一次,最后又回到出发点呢?许多人包括许多数学家都无法找到问题的答案,后来,这个问题被著名的数学家欧拉解决,同时,产生了一门新兴的学科:图论.我们提出这个主题就是要重温七桥问题的解决过程和解决方法.哥尼斯堡七桥问题本来是一个闲人的游戏,但是数学家欧兰通过用数学的方法对这个问题进行研究、解决,为数学开创了一门学科——图论,因此,对这个问题的讨论有利于向学生示范一个现实问题是怎么样成为数学问题的,有利于学生理解数学方法是如何作用于现实生活的.另外,学生刚刚学习了《图形的初步认识》一章,对于几何图形的现实意义有了一些认识,而图论中的图于几何图形的涵义有着本质的区别,所以通过本主题的学习,能够丰富学生对图形的涵义和作用的认识,有利于学生抽象能力的发展,对于引导学生增强数学应用意识,提高学习数学的兴趣具有重要的意义.① 学生已初步具有将实际问题抽象为数学问题的能力;② 学生能够借助归纳的方法能通过对一些特殊的情形进行分析进而得出一些一般性的结论.探究目标了解哥尼斯堡七桥问题,理解“一笔画”的原理,能够利用一笔画的规律判别一个图形能否进行一笔画,并能运用一笔画的原理解决实际问题.通过对“七桥问题与一笔画”的探究,培养将具体问题抽象为数学问题的能力.使学生认识到生活中的许多问题,可以用数学方法解决,但首先要通过抽象化和理想化建立数学模型.通过“七桥问题与一笔画”的探究,锻炼学生克服困难的意志及勇于发表见解的习惯,增强交流合作意识.同时,扩大知识视野,提高数学学习的兴趣.建议子主题探究七桥问题与一笔画的本质学生并不会感到有多少问题,但一笔画原理的应用范围比较广泛,而且,难度差异也比较大,因此,本探究主题的侧重点将放在一笔画的应用方面,考虑到应用的范围和难度,本主题分为如下三个子主题:子主题1:哥尼斯堡人的困惑(案例)1课时子主题2:无路可走了吗1课时子主题3:生活中的一笔画1课时其中第1、2个子主题为必修内容,另一个子主题为选学内容.媒体资源工具和方法本探究活动需要用到的工具包括:有关地图、设计图纸、一些画图工具.一笔画游戏◇ 本主题探究方法:实验操作法和小组学习法,以小组为单位进行合作学习,同时,由学生通过实际操作和画图实验进行探究.◇ 拓展资源、资料:连通点:笔沿着某条边进去后,沿另一条边出去的点.连通图:笔不离纸,连续画出来的图形.一笔画:指下笔后笔尖不离开纸且每条线都只画一次没有重复.。
一笔画和最短路线问题

(Leonhard Euler 公元1707-1783年) 欧拉
欧拉出生在牧师家庭,自幼受到父亲的教育。13岁时入读 巴塞尔大学,15岁大学毕业,16岁获得硕士学位。欧拉是18世 纪数学界最杰出的人物之一,他不但为数学界作出贡献,更把 数学推至几乎整个物理的领域。此外,他是数学史上最多产的 数学家,圣彼得堡科学院为了整理他的著作,足足忙碌了四十 七年。 欧拉著作的惊人多产并不是偶然的,他可以在任何不良的环 境中工作,他常常抱着孩子在膝上完成论文,也不顾孩子在旁 边喧哗.他那顽强的毅力和孜孜不倦的治学精神,使他在双目 失明以后, 也没有停止对数学的研究,在失明后的17年间, 他还口述了几本书和400篇左右的论文.19世纪伟大数学家高 斯(Gauss,1777-1855年)曾说:"研究欧拉的著作永远是了 解数学的最好方法."
“内部”与“外部”
“内部”与“外部”是拓扑 学中很重要的一组概念
以下有趣的故事,将增加你 对这两个概念的理解:
传说古波斯穆罕默德的继承人 哈里发,有一位才貌双全的女儿。 姑娘的智慧和美貌,使许多聪明英 俊的小伙子为之倾倒,致使求婚者 的车马络绎不绝。哈里发决定从中 挑选一位才智超群的青年为婿。于 是便出了一道题目,声明说:谁能 解出这道题,便将女儿嫁给谁!
小 结: 把几何体适当展开成平面图 形,再利用“两点之间线段最 短”,或点到直线“垂线段最短” 等性质来解决问题。
四、长方体中的最值问题
例4、如图,一只蚂蚁从实心长方体的顶点A出发, 沿长方体的表面爬到对角顶点C1处(三条棱长如图 所示),问怎样走路线最短?最短路线长为多少?
D1 A1 D A 4 C1 1 B1 C 2 B
.
解决“最短”问题的总思路:
化曲为平,化折为直
小学数学《一笔画》练习题(含答案)精选全文
可编辑修改精选全文完整版小学数学《一笔画》练习题(含答案)什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.所谓一笔画,就是从图形上的某点出发,笔不离开纸,而且每条线都只画一次不准重复.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点.判断图形能否一笔画的规律:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点.以另一个奇点作为终点;(4)奇点个数超过两个的图形,一定不能一笔画.(一) 一笔画以及多笔画【例1】 观察下面的图形,说明哪些图可以一笔画完,哪些不能,为什么?对于可以一笔画的图形,指明画法.(f)(e)(d)JIH G F ED C BAJ K IHGFED CB A分析:(a )图:可以一笔画,因为只有两个奇点A 、B ;画法为A →头部→翅膀→尾部→翅膀→嘴. (b )图:不能一笔画,因为此图不是连通图.(c )图:不能一笔画,因图中有四个奇点:A 、B 、C 、D.(d )图:可以一笔画,因为只有两个奇点;画法为:A →C →D →A →B →E →F →G →H →I →J →K →B. (e )图:可以一笔画,因为没有奇点;画法可以是:A →B →C →D →E →F →G →H →I →J →B →D →F →H →J →A.(f )图:不能一笔画出,因为图中有八个奇点.[注意]在上面能够一笔画出的图中,画法并不是惟一的.事实上,对于有两个奇点的图来说,任一个奇点都可以作为起点,以另一个奇点作为终点;对于没有奇点的图来说,任一个偶点都可以作为起点,最后仍以这点作为终点.[巩固]判断下列图a、图b、图c能否一笔画.E分析:图a是一个连通的图形,图中只有点A和点F两个奇点,所以它能一笔画,其中一种画法如下:A —M—N—A—F—B—C—B—K—C—D—E—D—L—E—F.‘图b是一个不连通的图形,所以不能一笔画.图c是连通图,图中所有点都是偶点,所以能一笔画.其中一种画法如下:A—B—C—D—E—F—D—A—F —C—A.【例2】右图是某地区所有街道的平面图.甲、乙二人同时分别从A、B出发,以相同的速度走遍所有的街道,最后到达 C.如果允许两人在遵守规则的条件下可以选择最短路径的话,问两人谁能最先到达C?分析:本题要求二人都必须走遍所有的街道最后到达C,而且两人的速度相同.因此,谁走的路程少,谁便可以先到达C.容易知道,在题目的要求下,每个人所走路程都至少是所有街道路程的总和.仔细观察上图,可以发现图中有两个奇点:A和C.这就是说,此图可以以A、C两点分别作为起点和终点而一笔画成.也就是说,甲可以从A出发,不重复地走遍所有的街道,最后到达C;而从B出发的乙则不行.因此,甲所走的路程正好等于所有街道路程的总和,而乙所走的路程则必定大于这个总和,这样甲先到达C.[巩固]在六面体的顶点B和E处各有一只蚂蚁(见右图),它们比赛看谁能爬过所有的棱线,最终到达终点D.已知它们的爬速相同,哪只蚂蚁能获胜?分析:许多同学看不出这是一笔画问题,但利用一笔画的知识,能非常巧妙地解答这道题.这道题只要求爬过所有的棱,没要求不能重复.可是两只蚂蚁爬速相同,如果一只不重复地爬遍所有的棱,而另一只必须重复爬某些棱,那么前一只蚂蚁爬的路程短,自然先到达D点,因而获胜.问题变为从B到D与从E到D哪个是一笔画问题.图中只有E,D两个奇点,所以从E到D可以一笔画出,而从B到D却不能,因此E点的蚂蚁获胜.[数学小游戏] 用一笔画成四条线段把所有的点连起来,怎样画?分析:通过试画,似乎不可以画,但通过仔细观察,对照一笔画的规律,便可发现,若添上两个辅助点,就可画成.如右图:FE DCB ADCBA我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.公式如下: 奇点数÷2=笔画数,即2n ÷2=n.【例3】 判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.IH G FED CBA 图aH G I KLJ F EDCBA 图b DC HG EFBA图c分析:图a :原图有四个奇点,所以不能一笔画,在B,D 两点之间加一条线后,图中只有两个奇点,故可以一笔画出,如图d 所示.画法:H →A →B →C →D →E →F →I →D →B →I →H →G →F .图b :原图有四个奇点,所以不能用一笔画.去掉K ,L 两点之间的连线,图中只有两个奇点,故 可以一笔画出,如图e 所示.画法:B →C →D →E →F →→J →H →G →I →A →B →K →I →L →E .图c :原图有四个奇点,所以不能用一笔画.在B ,C 两点之间加一条线后,图中只有两个奇点, 故可以一笔画出,如图f 所示.画法:A →E →D →H →A →B →F →C →G →B →C →D注意:a 、b 、c 三个图都是连通的图形,但由于每个图的奇点个数均超过两个,所以都不能一笔画.图dA BCD EFG H IH GI KLJ F EDCB A 图eDC HG EFBA图f[前铺]观察下面的图,看各至少用几笔画成?分析:(1)图中有8个奇点,因此需用4笔画成. (2)图中有12个奇点,需6笔画成. (3)图是无奇点的连通图,可一笔画成.DC BA(2)(1)FEC DB A分析:图(1)中有6个奇点,因此可添上两条(或3条)边后可改为一笔画;又因为这个图中,把这6个奇点任意分为3对后,最多只有两对奇点间有边相连,因此,可去掉两条边后改为一笔画,举例如图(3)~(6).图(2)中有4个奇点,因此,可添上2条(或1条)边后改为一笔画;又因为把奇点按A 与B ,C 与D (或A 与D ,B 与C )分为两对后,每对间均有边相连,因此,可去掉两条(或1条)边后改为一笔画.举例如图(7)~(8).说明:图(6)运用了两种方法,去掉边BC ,添上边AD 与EF.(二)一笔画的实际应用【例5】 18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛A 和一座半岛D ,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来(如图a).如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?:这个有趣的问题引起了著名数学家欧拉的注意,他证明了七桥问题中提到的走法根本不存在. 下面,我们考虑如下两个问题:(1)如果再架一座桥,游人能否走遍所有这八座桥?若能,这座桥应架在何处?若不能,请说明理由. (2)架设几座桥可以使游人走遍所有的桥回到出发地?而得到一个由四个点和七条线组成的图形(如图b).在图b 中,点A ,B ,C ,D 四个点均为奇点,显然不能一笔画出这个图形.若将其中的两个奇点改成偶点,即在某两个奇点之间连一条线,这样奇点个数由四个变为两个,此时,图形可以一笔画出.如我们可以选择奇点B ,D ,在B ,D 之间连一条线(架一座桥),如图c .在图c 中只有点A 和C 两个奇点,那么我们可以以A 为起点,C 为终点将图形一笔画出.其中一种画法为:A →C →A →B →A →D →B →D →C所以,如果在河岸B 与小岛D 之间架一座桥,游人就可以不重复地走遍所有的桥.(2)在(1)的基础上,再在另外两个奇点A 与C 之间连一条线(即架一座桥),使这两个奇点也变成偶点,如图d .那么A ,B ,C ,D 四个点均为偶点,所以图d 可以一笔画出,并且可以以任意点为起点,最后 仍回到这个点.其中一种画法为:A →C →A →C →D →A →B →D →B →A这表明:在河岸B 与小岛D 之间架一座桥后,再在小岛A 与河岸C 之间架一座桥,共架设两座桥,就可以使游人不重复地走遍所有的桥并回到出发地.[巩固]如图所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河岸.问:一个散步者能否一次不重复地走遍这七座桥?分析:用点表示小岛与河岸,用连接两点的线表示连接相应两地的桥,如图,有2个奇点,所以该图可以一笔画,即可以一次不重复地走遍这七座桥.例如右下图的走法.EDCBA【例6】 有一个邮局,负责21个村庄的投递工作,右图中的点表示村庄,线段表示道路.邮递员从邮局出发,怎样才能不重复地经过每一个村庄,最后回到邮局?分析:图中有两个奇点,所以该图可以一笔画,但因为邮局所在点为奇点,所以要一笔画就不可能回到邮局.又图中A,B,C,D,E,F,G,H,I,J十点均有4条线段与之相连,如果我们将上图一笔画的话,就要经过以上十点各两次,这也不满足题目的要求,所以要将这些点相连的线段去掉一些,使得与这些点相连的线段均只有两条,并且将两个奇点也变成只有两条线段与之相连,这样得到的图形即可一笔画,又只经过每个点一次,并且可以回到邮局,一种可行路线如下:邮局I JHGF E D C B A 邮局邮局【例7】 右图是某博物馆的平面图,相邻两个展厅之间有一扇门相通,每一个展厅都有一门通往馆外.问参观者能否不重复地一次穿过每一扇门?若能,请找出一条可行路径;若不能,请说明理由.如果允许关闭某一扇门,问参观者能否不重复地穿过每一扇开着的门?分析:我们把展厅A,B,C,D,E 及馆外F 看成某个图中的点,把两个展厅之间的门看作是连接表示这两个展厅的点的线.根据题中条件知,馆外F 与A ,B ,C ,D ,E 各展厅相通,这样将点F 与点A ,B ,C ,D ,E 用线连接;展厅A 与展厅B ,C ,D 相通,将点A 与点B ,C ,D 用线连接;展厅B 除与A 相通外,它还与D ,E 展厅相通,将B 与D ,E 连接;除此之外,展厅C ,D 相通,展厅D ,E 相通,将点C ,D 连接,再将点D ,E 连接(如图a).于是本题要解决的问题就变成了能否将图a 一笔画的问题.可以看出:图a 中共有六个点,其中有四个奇点,它们分别为C ,D ,E ,F ,由一笔画的规律可知,图a 不能一笔画.也就是说,参观者不能够不重复地一次穿过每一扇门.如果允许关闭某一扇门,这相当于在图a 中去掉一条线,那么参观者就有可能不重复地一次穿过每一扇门.我们知道,在图a 中有四个奇点C ,D ,E ,F 为了把图a 改成一笔画图形,我们设法减少奇点个数,使奇点数变为两个.为此,我们可以去掉一条连接两个奇点的线,如去掉E 与F 间的连线,相应的图a 就变成了图b .在图b 中,除了原来的C 和D 是奇点外,其余点全部是偶点,故图b 可以一笔画.其中一种画法为:C →F →D →E →B →F →A →B →D →A →C →D .上面的分析表明,如果关闭连接E 、F 两展厅之间的门,参观者就可以不重复地一次穿过每一扇开着的门. 本题与七桥问题类似,只是将行人过桥换成了参观者穿过每一扇门.我们将这个问题转化为一笔画问题来研究.[前铺]右图是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由.如果能,应从哪开始走? FFF F E C D BA EB A分析:我们将每个展室看成一个点,室外看成点E ,将每扇门看成一条线段,两个展室间有门相通表示两个点间有线段相连,于是得到下图.能否不重复地穿过每扇门的问题,变为下图是否一笔画问题.EDC BA图中只有A ,D 两个奇点,是一笔画,所以答案是肯定的,应该从A 或D 展室开始走. 【例8】 已知长方体木块的长是80厘米,宽40厘米,高80厘米(如右图),并且要求蜘蛛在爬行过程中只能前进,不能后退,同一条棱不能爬两次.请问这只蜘蛛最多要爬行多少厘米?分析:图中八个顶点均为奇点,所以不能一笔画,要使其能一笔画,至少要去掉三条棱,使上图只有两个奇点,就可以满足一笔画的条件.长方体的棱长总和一定,(80+80+40)×4=800(厘米),因此去掉的三条棱越短,蜘蛛爬过的距离就越远.所以我们去掉三条棱长为40厘米的棱,于是可知,蜘蛛爬行的最远距离为: 800-40×3=680(厘米).蜘蛛的爬行路径为:G →F →C →D →G →H →A →B →E →H(如右图).[注意]这是一个立体图形,它有八个顶点,我们把长方体的棱看作顶点与顶点之间的连线,蜘蛛只能前进不能后退,并且每一条棱不能爬两次,这实质上是一个一笔画问题.【例9】 右图是某小区的街道分布图,街道长度如图所示(单位:公里),图中各点表示不同楼的代号.一辆垃圾清扫车从垃圾站(垃圾站位于C 楼与D 楼之间的P 处)出发要清扫完所有街道后仍回到垃圾站,问怎样走路线最短,最短路线是多少公里?分析:为了少走冤枉路和节省时间,题目中要求最短路线,根据一笔画原理,我们知道一笔画路线就是最短路线.本题要求清扫车从P点出发,仍回到P 点.通过观察上图可知,图中有六个奇点,根据一笔画规律可知,清扫车想清扫完所有街道而又不走重复的路是不可能的.要使清扫车从P 点出发,最后仍回到P 点,就必须把图中所有的奇点都变成偶点,即在两奇点之间添加一条线.在实际问题中,就是清扫车在哪些街道上重复走的问题,由于每条街道的长度不同,因此需要我们考虑清扫车重复走哪条街道才使总路线最短.为使六个奇点都变成偶点,我们可以有下图中的四种方法表示清扫车所走的重复路线,其中填虚线的地方表示的是重复路线.重复的路程分别为:图a :2×2+3=7;图b :3+4×2=11;图C :3×3=9; 图d :3+6×2=15.显然,重复走的路线最短,总路程就最短.从上述计算中就可找到最短路线图,即下面四个图中的图a .408080H G F ED C BA804080H GFED CBA图b 图a图d图c在图a 中,所有点均为偶点,是一笔画图形.清扫车可按如下路径走:P →D →G →D →E →F →G →H →L →H →C →B →L →M →A →B →C →P ,全程为:(1+2+4+2)×2+3×5+2×2+3=40(公里).【例10】 邮递员李文投送邮件的街道以及街道的长度如右图所示(单位:千米),每天小李要从邮局出发,走遍所有街道后回到邮局.请你帮他设计一条最短路线,并计算出这条路线有多少千米?分析:本题仍可以用一笔画图形的方法来解决.在图a 中共有六个奇点E ,F ,G ,H ,I ,J ,把这些奇点配对,每对之间用虚线连接(如图a),其中要用到D 点,这样图中就没有奇点了,从而可以不重复地走遍所有的街道.由于邮递员李文要重复走一些路段,因此重复走的路越短越好,即添上去的重复线段的总长度越短越好.在图a 中H 与E 之间有重叠,这样势必会增加李文所走路程的长度,应作调整.经调整后,将重叠部分去掉便得图b .在图b 的圈形闭路IHGJI 中,I ,J ,G ,H 各点没有连线时是奇点,连线后变成偶点,增加长度为50×2=100千米.而如果连IJ 和HG ,增加的长度仅为10×2=20,由此可知图b 需继续作调整,改成图c ,这种连接方法是最好的,它使李文行走的路线最短.根据以上分析,为了保证添上去的线段之和最短,应遵循下面的两条原则:(1)连线不能有重叠的线段;(2)在每一个圈形闭路上,连线长度之和不能超过 这个闭路总圈长的一半.经过分析可以知道,图c 的连接方法能使邮递员李文行走路线最短,而且能保证李文从邮局出发又回到邮局.这时他的行走路线为:邮局→A →I →J →I →H →G →H →E →D →F →D →G →J →B →C →D →E →邮局 他行走的全程为: (50+15)×4+20×4+10×6+20×2=440(千米).图a图b图c[小结]本题中采用的方法叫做“奇偶点图上作业法”,用这种方法来确定最短路线比较简便实用.此方法可以用下面的口诀来描述:画出路线图,确定奇偶点;奇点对对连,连线不重叠;闭路添连线.不得过半圈.[巩固]右图是某地区街道的平面图,图上的数字表示那条街道的长度.清晨,洒水车从A 出发,要洒遍所有的街道,最后再回到A.问:如何设计洒水路线最合理? 分析:这又是一个最短路线的问题.通过分析可以知道:在洒水路线中,K 是中间点,因此必须成为偶点,这样洒水车必须重复走KC 这条边(如下左图).至此,奇点的个数并未减少,仍是6个.容易得出,洒水车必须重复走的路线有:GF 、IJ 、BC.即洒水路线如下右图.全程45+3+6=54(里).1. (例1)判断下列各图能否一笔画.图aG I H F ECD BA图bF ED CBA分析:图a 中九个点全是偶点,因此可以一笔画,其中一种画法为:A →F →B →G →C →H →D →E →H →l →→F →G →l →E →A .图b 中A ,B ,C ,D 四个点均为奇点,故不可以一笔画.图c 中,只有A,C 为奇点,故可一笔画.其中一种画法为:A →D →E →C →H →N →G →M →F →A →B →C .2. (例3)下列各图至少要用几笔画完?分析:(1)4笔;(2)4笔;(3)2笔;(4)1笔;(5)1笔;(6)1笔.3.(例6)右图是某展览厅的平面图,它由五个展室组成,任两展室之间都有门相通,整个展览厅还有一个进口和一个出口,问游人能否一次不重复地穿过所有的门,并且从入口进,从出口出?分析:把每个展室看作一个结点,整个展厅的外部也看作一个点,两室之间有门相通,可以看作两点之间有边相连.这样,展厅的平面图就转化成了我们数学中的图,一个实际问题也就转化为这个图(如下图)能否一笔画成的问题了,即能否从A出发,一笔画完此图,最后再回到A.上图(b)中,所有的结点都是偶点,因此,一定可以以A作为起点和终点而一笔画完此图.也即游人可以从入口进,一次不重复地穿过所有的门,最后从出口出来.下面仅给出一种参观路线:A→E→B→C→E→F→C→D→F→A.4.(例7)一辆清洁车清扫街道,每段街道长1公里,清洁车由A出发,走遍所有的街道再回到A.怎样走路程最短,全程多少公里?分析:清洁车走的路径为: ABCNPBCDEFMNEFGHOLMHOIJKPLJKA. 即:清洁车必须至少重复走4段1公里的街道,如下图.最短路线全程为28公里.5.(例10)一个邮递员的投递范围如右图,图上的数字表示各段街道的长度.请你设计一条最短的投递路线,并求出全程是多少?分析:邮递员的投递路线如下图,即:路线为:ABCDEDOBOMNLKLGLNEFGHIMOJIJA.最短路线的全程为39+9=48.。
一笔画问题
一笔画问题画一个图案,如果用笔既不重复也不遗漏,纸不离笔,一笔画成,那么就称这个图案是一笔画图案.现在我们来研究的问题是:(1)怎样的图案才能一笔画成?(2)如果一个图案能一笔画成,那么该从哪里起笔到哪里收笔?需提醒大家的是,这些问题与图案中的“奇点”的个数有关.何谓奇点呢?我们知道,任何图案都是由线条(直线或曲线)连成的.在图案中,由三条或三条以上的方向各不相同的线连接在一起的点叫做图案点,通过图案点的线是奇数条就称奇点(当然,通过图案点的线是偶数条就称偶点,现在只需回答前面的问题而与偶点无关).例如,在下面各图案中的奇点个数见统计表(请读者对照图案辨认奇点).统计表:接着就请读者朋友拿起你的笔来逐个试画以上各图案,看能否一笔画成,将结论填在统计表内.并注意体会能一笔画的图案应该怎样画.最后,请根据上表归纳出前面两个问题的答案.【规律】(1)奇点数为0或2的图案可以一笔画成.奇点数多于2的图案不能一笔画成.(2)画奇数为0的图案时,可以选择任意点起笔都能一笔画成;画奇数为2的图案时,必须选择其中的一个奇点起笔,而到另一个奇点收笔才能一笔画成.【练习】1.下面各图案,能一笔画出来吗?试一试.2.容易看出,下面的两个图案都不能一笔画成,请在每个图案上各补画一条线就能使新图案一笔画成了.会吗?3.这是大数学家欧拉曾经研究过的一个著名数学问题----七桥问题.东普士的多尼斯堡城中有一条横贯城区的河流,河上有两个岛,两岸和两岛之间共架有七座桥、如下图所示:问人们能不重复地走遍这七座桥吗?4.回龙州公园的游览点与路线示意图如下.如果要使游人游完所有的游览点而不重复行走的路线,请问入口处和出口处应该设在什么位置?如果一个图形可以用笔在纸上连续不断而且不重复地一笔画成,那么这个图形就叫一笔画。
显然,在下面的图形中,(1)(2)不能一笔画成,故不是一笔画,(3)(4)可以一笔画成,是一笔画。
同学们可能会问:为什么有的图形能一笔画成,有的图形却不能一笔画成呢?一笔画图形有哪些特点?关于这个问题有一个著名的数学故事——哥尼斯堡七桥问题。
哥尼斯堡七桥问题
现在已发展成为研究连续性现象的数学分支。
拓扑学应用实例
前面所提的哥尼斯堡七桥问题、四色问题? 左手套能否在空间掉转位置后变成右手套? 一条车胎能否从里朝外的把他翻转过来? 一只有把的茶杯与救生圈更相似,还是与花瓶更相
互相衔接的两两不同的一串“弧”称为“路”。路中弧的端 点称为路的“顶点”。如果起点与终点相同称为“闭路”。 如果闭路的顶点又不相同,称为“圈”。如下所示:
路
闭路
圈
网络与一笔画问题
于是我们可以给出一笔画的理论叙述。
“一笔画”问题相当于给定一个网络。问: “有没有可能把所有的弧排成一条路”。
如果一个网络的全部弧可以排成一条路,那 么我们称这个网络为一个一笔画。
纸圈,然后只允许用一种颜色,在纸圈上的一面涂抹,最后 把整个纸圈全部抹成一种颜色,不留下任何空白。 这个纸圈应该怎样粘? 如果是纸条的首尾相粘做成的纸圈有两个面,势必要涂完一 个面再重新涂另一个面,不符合涂抹的要求。 能不能做成只有一个面、一条封闭曲线做边界的纸圈?
莫比乌斯带的发现
对于这样一个看来十分简单的问题,数百年间,曾有许多科 学家进行了认真研究,结果都没有成功。后来,德国的数学 家莫比乌斯对此发生了浓厚兴趣,他长时间专心思索、试验, 也毫无结果。
当地的市民正从事一项非常有趣的消遣活动。这项有趣的消 遣活动是在星期六作一次走过所有七座桥的散步,每座桥只 能经过一次而多人对此很感兴趣,纷纷进行试验,但在相 当长的时间里,始终未能解决。
而利用普通数学知识,每座桥均走一次,那这七座桥所有的 走法一共有5040种,而这么多情况,要一一试验,这将会是 很大的工作量。
哥尼斯堡七桥问题与一笔画 ppt课件
●G F ● D●
பைடு நூலகம்
C●
●
●A
B
PPT课件
19
课堂练习
3、 甲乙两个邮递员去送信,两人同时出发以 同样的速度走遍所有的街道,甲从A点出发, 乙从B点出发,最后都回到邮局(C点)。如果 要选择最短的线路,谁先回到邮局?
PPT课件
20
PPT课件
21
课堂小结
1、 在探究七桥问题中,我们运用了哪些 数学思想和方法去研究问题?谈谈你活动 后的感受。
11
问题分析
问题的答案如何呢?让我们先来了解三个新概念。
①有奇数条边相连的点叫奇点。如:
●
●
●
②有偶数条边相连的点叫偶点。如:
●
●
●
③一笔画指:1、下笔后笔尖不能离开纸。 2、每条线PPT都课件只能画一次而不能重复。12
活动探究 下列图形中。请找出每个图的奇点个数,偶点个数。试一试哪 些可以一笔画出,请填表,从中你能发现什么规律?
这在人类智慧所未及的领域,是很常见的事!
PPT课件
7
拿起栓有15个圆环的绳子,任选一个桥的支柱作为起点,沿桥依次套圈,看看
是否可以让除起点之外的13个桥柱上都有一个圈。(起点的柱子上有两个圈)。
结论是,不可能实现完成该任务。
PPT课件
8
欧拉
欧拉(L.Euler,1707.4.151783.9.18)著名的数学家。生于 瑞士的巴塞尔,卒于彼得堡。大 部分时间在俄国和德国度过。他 早年在数学天才贝努里赏识下开 始学习数学, 17岁获得硕士学位, 毕业后研究数学,是数学史上最高 产的作家。在世发表论文700多篇, 去世后还留下100多篇待发表。其 论著几乎涉及所有数学分支。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七讲 一笔画与七桥问题
【知识梳理】
1.一笔画是指能够一笔画成的图形。
2.把和一条、三条、五条等奇数条线相连的点叫做奇点,把和两条、四条、六条
等偶数条线相连的点叫做偶点,这样图形中要么是奇点,要么是偶点。
3.有2个奇点或0个奇点(全部是偶点)连通图能够一笔画成,否则不能一笔画
成。
4.七桥问题可以转化成一笔画问题解决。
【典例精讲1】一笔画就是笔不离纸,笔画不重复,一笔画出一个图形.你能用
一笔画出下列图形吗?
思路分析:能够一笔画成的图形,首先必须要相连,结果不相连就一定不能一笔
画成,能否一笔画成,关键在于判别奇点、偶点的个数:只有偶点,可以一笔画,
并且可以以任意一点作为起点;只有两个奇点,可以一笔画,但必须以这两个奇
点分别作为起点和终点;奇点超过两个,则不能一笔画。
解答:观察图形可知(1)第一个图形全是偶点,所以能一笔画出;
(2)第二个图形是2个奇点,剩下的都是偶点,所以能一笔画出。
小结:解决这类问题首先要看是不是连通图,其次看奇点或偶点的个数,由偶点
组成的,或只有两个奇点的连通图才能一笔画成。
【举一反三】1、下面这些图形,哪个能一笔画?哪个不能一笔画?
2. “九点连线”是一道著名的数学题,你能用一笔画4条连续的直线段,把图
中所有的9个点都连起来吗?请你在下图画出来。
【典例精讲2】在一个城市中有七座桥和四个区域:能不能一次走遍所有的七座
桥,而每座桥只准经过一次?
思路分析:用“1、2、3、4、5、6、7”表示七座桥,它们连接着A、B、C、D
四个区域(如图所示),这样一来,七座桥的问题,就转变为一个一笔画问题,
即能不能一笔从头到尾不重复地画出这个图形.
解答:图中有4个奇点和一个偶点,奇点个数不是2个,
所以不能一笔完成。
小结:解决这类问题要学会转化,即把七桥问题转化成一笔画问题。
【举一反三】3、如图是某层楼房间的平面图,每个房间都有门道通往过道,每
相邻两个房间之间各有一扇门道.你能不能不重复地走一次穿过每扇门?如果不
能,关闭哪扇门后,就能走一次不重复地穿过所
有的门。
4、送信
下面是一个住宅区的示意图.邮递员小王从邮局出发,要送信到四个住宅楼.为
了节省时间,小王选择了一条最短的路线,走这条路线既能把每个楼的信送到,
又不走重复的路,你能找到这条最短路线吗?把这条
路线画出来。
答案及解析:
1.【解析】图(1)有4个偶点,可以一笔画出;图(2)有4个奇点,大于2,
不能一笔画出;图(3)不是连通的,不能一笔画出;图(4)有10个偶点,也
能一笔画出。
【答案】:图(1)可以一笔画出,可以从图中任意一点开始画该图,画到同一点
结束;经过尝试后,可以发现图(2)不能一笔画出;图(3)不是连通的,显然
也不能一笔画出;图(4)也可以一笔画出,且从任何一点出发都可以.
再看图(1)、(4),其中每一点都是偶点,都可以一笔画,且可以从任意一点画
起.而图(2)有4个奇点,2个偶点,不能一笔画成.
2.【解析】:本题单独考虑奇点的个数和偶点的个数是不能解决问题的,它不同
于一般的一笔画,考虑到直线段如果不超出一些点,是不能画4条线段的,所以
可以从右上角的点开始,沿对角线画,再向上画,再向右下画,
最后向左画即可。
【答案】: 可以把图中所有的9个点都连起来,如下图:
3.【解析】(1)“能不能不重复地走一次穿过每扇门”,首先观察偶数点和奇数点
的个数.因为C、D、E都是奇数点(3个门相通),超过了两个奇数点,所以不
能一笔画出.也就不能不重复地走一次穿过每扇门。
(2)要想“走一次不重复地穿过所有的门”,就得从C、D、E房间的门入手,
因为C、D、E都是奇数点。
【答案】::(1)不能不重复地走一次穿过每扇门。
(2)当关闭C和D之间的门;或关闭D和E之间的门;或关闭E通向过道的
门时,可一次通过.(用A、B、C、D、E五个点表示五个房间,F点表示过道,
用线把两个点连起来,于是走的路线就简化成一笔画问题。)
4.【解析】利用一笔画定理,画出从邮局出发,经过四个住宅楼的路线,且尽量
使行走的路线不重复,且尽量走短边,即可找出最短路线。
【答案】:如图就是最短路程:
