5月2018届九年级第三次模拟大联考(湖北卷)数学卷(参考答案)
2018年5月2018届高三第三次全国大联考(新课标Ⅲ卷)理数卷

理科数学试题 第1页(共6页) 理科数学试题 第2页(共6页)绝密★启用前|2018年第三次全国大联考【新课标Ⅲ卷】理科数学(考试时间:120分钟 试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集U =R ,集合}043|{2≤--=x x x A ,{|||0}B x x =>,则以下结论成立的是 A .A B =RB .=B A ]4,0(C .()U AB A =ðD .}0{=B A2.已知复数z 满足14i 1z z -=-+,其中i 为虚数单位,则在复平面内,复数z 对应的点在A .第一象限B .第二象限C .第三象限D .第四象限3.已知椭圆C :22221(0)x ya b a b+=>>的左、右焦点分别为1F ,2F ,过点1F 作长轴的垂线与椭圆C 的一个交点为P ,若43tan 12=∠F PF ,则椭圆C 的离心率为 A .21B .31C .41D .514.若执行如图所示的程序框图,则输出的结果为A .122018-B .222018-C .122019-D .222019-5.已知甲、乙、丙、丁四人在某次高考模拟考试后交流各自的数学考试情况,甲说:“我分数肯定最低”;乙说:“我肯定不是最低分的那个人”;丙说:“我不会最低,但也不可能得最高分”;丁说:“那只有我是最高分了”.考试公布结果后,发现四人的分数各不相同,且仅有一人没有说对,则四人中得最高分的是A .甲B .乙C .丙D .丁6.《九章算术》卷五《商功》中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何?问题中“刍甍”指的是底面为矩形的屋脊状的几何体,如图1,该几何体可由图2中的八边形ABCDEFGH 沿BG ,CF 向上折起,使得AH 与DE 重合而成,设网格纸上每个小正方形的边长为1,则此“刍甍”中EF 与平面BCFG 所成角的正弦值为A .515 B .552 C .510D .557.已知曲线e xy =,直线1=x 及)0(1<+=k kx y 围成的封闭图形的面积大于e ,则实数k 的取值范围为理科数学试题 第3页(共6页) 理科数学试题 第4页(共6页)A .)0,4(-B .)0,4[-C .)4,(--∞D .]4,(--∞8.若不等式组⎪⎩⎪⎨⎧≥+≤--≥+-102201y x y x y x 表示的平面区域为Ω,则区域Ω的内切圆半径为A .532-B .352-C .252-D .522-9.已知函数)sin()(ϕω+=x A x f (0,0A ω>>)的部分图象与坐标轴交于点Q P M ,,,如图,其中)0,21(-Q ,32PQ OP =-,且PMQ ∠为钝角,则A 的取值范围为A .)36,0(B .),36(+∞ C .)2,0(D .)2,36( 10.关于函数xx x f ln 21)(2-=有如下说法,其中正确的是A .函数()f x 的定义域为),0(+∞B .1x =是函数()f x 的零点C .函数()f x 在定义域内为减函数D .函数()f x 在定义域内不存在极值点11.某校高三(1)班周二的课表安排如下,其中上午有四节课,下午有三节课,现需要对课表进行重新调整,将其中的历史改成数学,其他科目既不增加也不减少,且调整后两节数学课不连续(如数学安排在第4,第5节也符合要求),语文课不能安排在第1节,则不同的安排方法种数为A .48C .612D .82812.已知双曲线)0,0(12222>>=-b a by a x 的离心率为2,1F ,2F 分别是双曲线的左、右焦点,点)0,(a M -,),0(b N ,点P 为线段MN 上的动点,若12PF PF ⋅取得最小值和最大值时,12PF F △的面积分别为1S ,2S ,则=21S S A .21B .31 C .41 D .51 第Ⅱ卷二、填空题(本题共4小题,每小题5分,共20分)13.若向量(1,2)=a ,(1,)λ=-b ,|2|+=a b ,则=λ . 14.如图是一个几何体的三视图,则该几何体的外接球的表面积为 .15.在ABC △中,4A π∠=,P 为BC 边上一点,且2=AP ,若PAB PAC ∠=∠2,则PC PB 11+的最大值为 . 16.若关于x 的不等式12e e 2e 2x x m x +-+>+(其中e 为自然对数的底数,0,x m >∈Z )恒成立,则m 的最大值为 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)已知数列}{n a满足11=a ,131+=+n n n a a a (n *∈N ).(1)求数列}{n a 的通项公式;(2)令nn n a b 2=,n S 为数列}{n b 的前n 项和,若0)23(11≥-⋅-+n n S n λ有解,求实数λ的取值范围.18.(本小题满分12分)如图,几何体PDBAC 中,⊥PA 平面ABC ,ABC △为正三角形,BDC △为等腰直角三角形,理科数学试题 第5页(共6页) 理科数学试题 第6页(共6页)BDC ∠为直角,平面⊥BDC 平面ABC ,2==AC PA ,M 为PB 的中点.(1)求证://DM 平面ABC ; (2)求二面角C DM B --的余弦值.19.(本小题满分12分)如图是某市2017年12个月高层住宅网签情况的统计图:(1)求该市2017年高层住宅月成交均价的平均数;(2)利用(1)中计算的平均数,若当月成交均价高于月成交均价的平均数时,则视为价格上升,反之为下降;若当月成交套数高于月成交套数的平均数时,则视为成交量上升,反之为下降.若从全年中任选两个月,记所选两个月价格上升且成交量下降的个数为ξ,求随机变量ξ的分布列和期望(月成交套数的平均数约为3537套);(3)在(2)的条件下,补充完整下列的22⨯列联表,并分析该市在2017年12个月中高层住宅月成交套数与月成交均价的升降是否有关?附:))()()(()(22d b c a d c b a bc ad n K ++++-=,其中d c b a n +++=.20.(本小题满分12分)在抛物线C :2ax y =(0>a )上取两点),(11n m A ,),(22n m B ,且412=-m m ,过点B A ,分别作抛物线C 的切线,两切线交于点)3,1(-P . (1)求抛物线C 的方程;(2)设直线l 交抛物线C 于N M ,两点,记直线OM ,ON (其中O 为坐标原点)的斜率分别为,OM ON k k ,且2-=⋅ON OM k k ,若OMN △的面积为32,求直线l 的方程.21.(本小题满分12分)已知函数21()(1)e 2x f x ax x =--()a ∈R . (1)讨论函数)(x f 的单调性;(2)若对任意实数]1,0[,,321∈x x x ,都有)()()(321x f x f x f ≥+,求实数a 的取值范围. 请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.(本小题满分10分)选修4-4:坐标系与参数方程已知曲线1C 的参数方程为sin x y ϕϕ⎧=⎪⎨=⎪⎩(ϕ为参数),以直角坐标系xOy 的原点O 为极点,x 轴的正半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为32=ρ. (1)将曲线1C 的参数方程化为极坐标方程;(2)射线4θπ=(0≥ρ)与曲线1C ,2C 分别交于P ,Q 两点,曲线1C 与极轴的交点为A ,求PAQ △的面积.23.(本小题满分10分)选修4-5:不等式选讲已知函数x x x f 2|23|)(-+=.(1)若3)(<x f ,求满足条件的实数x 的值所组成的集合A ; (2)若A ∈μλ,,求证:1||||||2-+>μλλμ.。
2018年秋九上第三次月考数学试卷
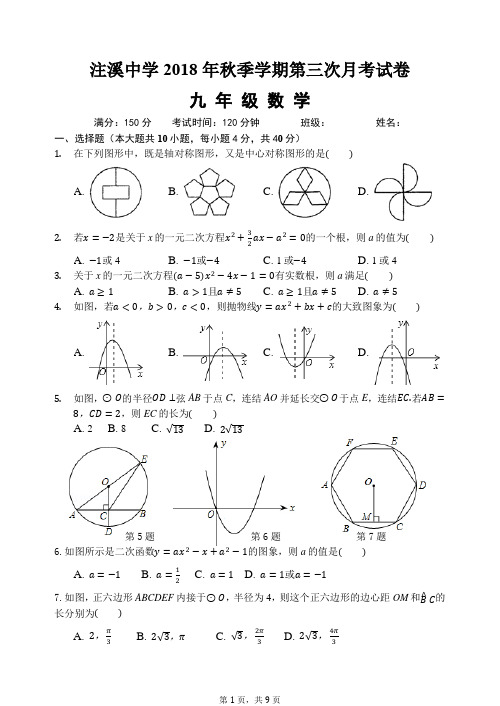
注溪中学2018年秋季学期第三次月考试卷九年级数学满分:150分考试时间:120分钟班级:姓名:一、选择题(本大题共10小题,每小题4分,共40分)1.在下列图形中,既是轴对称图形,又是中心对称图形的是A. B. C. D.2.若是关于x的一元二次方程的一个根,则a的值为A. 或4B. 或C. 1或D. 1或43.关于x的一元二次方程有实数根,则a满足A. B. 且 C. 且 D.4.如图,若,,,则抛物线的大致图象为A. B. C. D.5.如图,的半径弦AB于点C,连结AO并延长交于点E,连结若,,则EC的长为A. 2B. 8C.D.第5题第6题第7题6.如图所示是二次函数的图象,则a的值是A. B. C. D. 或7.如图,正六边形ABCDEF内接于,半径为4,则这个正六边形的边心距OM和的长分别为A. ,B. ,C. ,D. ,8.如图,某小区规划在一个长,宽的矩形场地ABCD上修建三条同样宽的通道图中阴影部分,使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是若设通道的宽度为,则根据题意所列的方程是A. B.C. D.9.如图,的半径为,是的内接等边三角形,点D、E在圆上,四边形BCDE为矩形,这个矩形的面积是A. 2B.C.D.10.如图,是抛物线图象的一部分已知抛物线的对称轴为,与x轴的一个交点是,有下列结论:;;;抛物线与x轴的另一个交点是,;点,,,都在抛物线上,则有.其中正确的是A. B. C. D.二、填空题(本大题共6小题,每小题4分,共24分)11.已知,是方程的两个实数根,则.12.如图,在中,已知, ,,以C圆心,为径的圆A于点D,则BD的长为______ .13.如图,已知圆锥的高为,高所在直线与母线的夹角为,圆锥的侧面积为______ .14.如图,二次函数的图象经过点,,,,那么一元二次方程的根是______ .15.如图,的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与相切于点Q,则PQ的最小值为______ .第13题第14题第15题16.如图,在中,,,,将绕顶点C按顺时针方向旋转至的位置,则线段AB扫过区域图中的阴影部分的面积为______ .三、解答题(本大题共8小题,共86分)17.(10分)用适当的方法解下列方程:;.18.(10分)已知二次函数的图象如图所示,它与x轴的一个交点坐标为,,与y轴的交点坐标为,.求出,的值,并写出此二次函数的解析式;根据图象,写出函数值y为正数时,自变量x的取值范围.19.(12分)如图,的顶点都在方格线的交点格点上.将绕C点按逆时针方向旋转得到,请在图中画出.将向上平移1个单位,再向右平移5个单位得到,请在图中画出.若将绕原点O旋转,的对应点的坐标是______ .20.(8分)已知关于x的一元二次方程.若方程有实数根,求实数m的取值范围;若方程两实数根分别为,,且满足,求实数m的值.21.(10分)如图,等腰中,, ,点D在AC上,将绕点B沿顺时针方向旋转后,得到.求的度数;若,,求DE的长.22.(12分)如图,的边AB为的直径,BC与交于点,为BC的中点,过点D作于E.求证:DE是的切线;若,,求CE的长.23.(12分)施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系如图所示.直接写出点M及抛物线顶点P的坐标;求出这条抛物线的函数解析式;施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A、D点在抛物线上,B、C点在地面OM上为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?请你帮施工队计算一下.24.(12分)如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,,抛物线经过点,,交正x轴于点,是OC上的动点不与C重合连接EB,过B点作交y轴与F求,的值及D点的坐标;求点E在OC上运动时,四边形OEBF的面积有怎样的规律性?并证明你的结论;连接,,设,与的面积之差为S,问:当m为何值时S最小,并求出这个最小值.【答案】1. A2. C3. C4. B5. D6. C7. D8. B9. B10. C11. 312.13.14.15. ,16.17. 解:,,解得:,;故,,则,.18. 解:将点,,,代入中,得,解得..令,解方程,得,,抛物线开口向下,当时,.19. ,20. 解:由题意有,整理得,解得,实数m的取值范围是;由两根关系,得,,,,,解得或.21. 解:为等腰直角三角形,.由旋转的性质可知.., ,.,,.由旋转的性质可知:..22. 证明:连接OD为BC的中点,O为AB的中点,;,,是圆O的切线.解:连接AD是直径,;为BC的中点,是BC的垂直平分线,;, ,∽ ,,而,,.23. 解:,,,顶点坐标,设又图象经过,这条抛物线的函数解析式为,即;设,,四边形ABCD是矩形,,根据抛物线的轴对称性,可得:,,即,令.当,最大值为15、AD、DC的长度之和最大值为15米.24. 解:把点,、,代入抛物线得解得,;;令解得,点坐标为,.点E在OC上运动时,四边形OEBF的面积不变;四边形OABC是正方形,又≌四边形OEBF的面积始终等于正方形OABC的面积.如图,可以看出梯形两个三角形的面积差最小为0,即,解得,是OC上的动点,当时S最小为0.。
2018届九年级数学上学期联考试题

湖北省××市东片八校2018 届九年级数学上学期联考试题考生姓名:考号:学校:注意事项:1. 本试卷分为试题卷和答题卷两部分。
考试时间为120 分钟,满分120 分。
2.考生在答题前请阅读答题卷中的”注意事项”,而后按要求答题。
3.全部答案均须做在答题卷相应地区,做在其余地区无效。
一、选择题(本大题共10 小题,共 30 分)1. 一元二次方程 x2=9 的解是()A. x 1=3, x2=-3B. x=3C. x=-3D. x 1=3,x2=02. 以下图案是部分汽车的标记,此中是中心对称的是()A. 雪佛莱B. 雪铁龙C. 梅赛德斯 ?奔驰D. 枭龙3. 用配方法解方程 x2+2x-1=0 时,配方结果正确的选项是()A. ( x+2)2=2B. ( x+1)2=2C. ( x+2)2=3D. ( x+1)2=34. 以下事件是必定事件的是()A.有两边及一角对应相等的两三角形全等B.若 a2=b2则有 a=b2C.方程 x -x+1=0 有两个不等实根D.圆的切线垂直于过切点的半径5. 如右图, AB是⊙ O的直径, CD是⊙ O的弦,∠ ACD=30°,则∠ BAD为()A. 30 °B. 50 °C. 60°D. 70 °6. 将抛物线 y=-3x 2平移,获得抛物线y=-3 (x-1 )2-2 ,以下平移方式中,正确的选项是()A. 先向左平移 1 个单位,再向上平移 2 个单位B. 先向左平移 1 个单位,再向下平移 2 个单位C.先向右平移 1 个单位,再向上平移 2 个单位D.先向右平移 1 个单位,再向下平移 2 个单位7. 若点 A( -5 ,y1),B( 1,y2),C( 2,y3)在反比率函数 y= a21(a 为常数)x的图象上,则y1, y2, y3的大小关系是()A. y < y < yB. y1 < y < y C. y <y < y D. y < y <y31 2 3 3 2 2 3 1 2 18. 已知二次函数y=-3 (x-h )2+5,当 x> -2 时, y 随 x 的增大而减小,则有()A. h ≥ - 2B. h ≤ -2C. h > -2D. h < -29.如图, AB,CD是⊙ O的直径,⊙ O的半径为 R, AB⊥ CD,以 B 为圆心,以 BC为半径作弧 CED,则弧 CED与弧 CAD围成的新月形ACED的面积为()平方单位.A. (π -1 )R2B. R 2C. (π+1) R2D. πR210.如图,在菱形 ABCD中, AB=3,∠ BAD=120°,点 E 从点 B 出发,沿 BC和 CD边挪动,作 EF⊥直线 AB 于点 F,设点 E 挪动的行程为x,△ DEF的面积为 y,则 y 对于 x 的函数图象为()A B C二、填空题(本大题共 6 小题,共 18.0 分)11. 2 2将二次函数 y=x -2x+3 写成 y=a( x-h ) +k 的形式为 ______.12. 如图,点 C 为线段 AB 上一点,将线段CB绕点 C 旋转,获得线段CD,若 DA⊥ AB, AD=1,BD= 17,则 BC的长为 ______ .13.已知方程 x2 -2x-5=0 的两个根是 m和 n,则 2m+4n-n2的值为 ______ .14.如图,管中搁置着三根相同的绳索 AA1、 BB1、 CC1.小明在左边选两个打一个结,小红在右边选两个打一个结,则这三根绳索能连结成一根长绳的概率为 ______ .15.半径为 2 的⊙ O中有两条弦 AB、 AC, AB=2, AC=2,则∠ BAC= ______ .16. 如右图,△ OAC和△ BAD都是等腰直角三角形,∠ACO=∠ ADB=90°,反比率函数y= 6在第一象限x的图象经过点B,则△ OAC与△ BAD的面积之差S△OAC- S△BAD为.三、解答题(本大题共9 小题, 8+7+7+8+8+8+8+9+9=72 分)17.解方程:(1)( x+3)2=2x+5(2)3x2-1=6x(用配方法)18.求不等式组的整数解19. 先化简再求值( x 2 12)÷x4,期中 x 知足 x 2- 2x=0 x 2 x2 2x20. 如图,已知反比率函数y=与一次函数y=x+b 的图形在第一象限订交于点A( 1,﹣ k+4).( 1)试确立这两函数的表达式;(2)求出这两个函数图象的另一个交点 B 的坐标,并求△AOB的面积;( 3)依据图象直接写出反比率函数值大于一次函数值的x 的取值范围.21.已知:如图,△ ABC内接于⊙ O, AF 是⊙ O的弦, AF⊥ BC,垂足为 D,点 E为弧 BF 上一点,且 BE=CF,(1)求证: AE是⊙ O的直径;(2)若∠ ABC=∠ EAC, AE=8,求 AC的长.22. A 、 B、 C三把外观相同的电子钥匙对应翻开a、b、 c 三把电子锁.(1)随意拿出一把钥匙,恰巧能够翻开 a 锁的概率是;(2)求随机拿出A、B、 C 三把钥匙,一次性对应翻开a、b、 c 三把电子锁的概率.23. 某大学生利用业余时间参加了一家网店经营,销售一种成本为30 元 / 件的文化衫,依据过去的销售经验,他整理出这类文化衫的售价y1(元 / 件),销量y2(件)与第x( 1≤x< 90)天的函数图象如下图(销售收益=(售价 - 成本)×销量)(1)求 y1与 y2的函数表达式;(2)求每日的销售收益 w 与 x 的函数关系表达式;(3)销售这类文化衫的第多少天,每日销售收益最大,最大收益是多少?24.如图 1,在 Rt △ ABC中,∠ A=90°, AB=AC,点 D,E 分别在边 AB,AC上, AD=AE,连结 DC,点M,P, N 分别为 DE, DC, BC的中点.(1)察看猜想图 1 中,线段 PM与 PN的数目关系是 ______ ,地点关系是 ______ ;(2)研究证明把△ ADE绕点 A 逆时针方向旋转到图 2 的地点,连结MN,BD, CE,判断△ PMN的形状,并说明原因;(3)拓展延长把△ ADE绕点 A 在平面内自由旋转,若AD=4, AB=10,请直接写出△PMN面积的最大值。
5月2018届九年级第三次模拟大联考(广东卷)数学卷(考试版)
数学试题 第1页(共6页) 数学试题 第2页(共6页)绝密★启用前|学科网试题命制中心2018届九年级第三次模拟大联考【广东卷】数 学(考试时间:100分钟 试卷满分:120分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
5.考试范围:中考全部内容。
第Ⅰ卷一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.以下4个有理数中,最小的是 A .-2B .1C .0D .-12.过度包装既浪费资源又污染环境.据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨,把数3120000用科学记数法表示为 A .3.12×105B .3.12×106C .31.2×105D .0.312×1073.如图,一个由相同小正方体堆积而成的几何体,该几何体的主视图是A .B .C .D .4.下列计算正确的是 A .a •a 2=a 3 B .(a 3)2=a 5C .a +a 2=a 3D .a 6÷a 2=a 35.如图,AB ∥CD ,直线l 交AB 于点E ,交CD 于点F ,若∠2=70°,则∠1等于A .70° B.100° C .110° D .80°6.已知x =1是方程x 2+bx -2=0的一个根,则方程的另一个根是 A .1B .2C .-2D .-17.点P (5,-3)关于原点对称的点的坐标是 A .(3,-5) B .(-5,-3)C .(-5,3)D .(-3,5)8.某班5名同学在一次“1分钟仰卧起坐”测试中,成绩为(单位:次):38,44,42,38,39.这组数据的众数是 A .40.2B .40C .39D .389.如图,在矩形ABCD 中,点E 在AB 边上,将长方形ABCD 沿直线DE 折叠,点A 恰好落在BC 边上的点F 处.若AE =5,BF =3,则CF 的长为A .9B .10C .12D .1510.如图,△ABC 是等腰直角三角形,∠A =90°,BC =4,点P 是△ABC 边上一动点,沿B →A →C 的路径移动,过点P 作PD ⊥BC 于点D ,设BD =x ,△BDP 的面积为y ,则下列能大致反映y 与x 函数关系的图象是。
2018~2019-1长郡教育集团九年级第三次月考数学试卷--答案

4
马思特考试研究院
教育是良心事业, 教育是千秋伟业, 我们用心办教育。
5
19.
20.
21.
教育是良心事业, 教育是千秋伟考试研究院
22. 23.
教育是良心事业, 教育是千秋伟业, 我们用心办教育。
2
马思特考试研究院
24.
25.
教育是良心事业, 教育是千秋伟业, 我们用心办教育。
3
马思特考试研究院
26.
教育是良心事业, 教育是千秋伟业, 我们用心办教育。
马思特考试研究院
2018~2019-1 长郡教育集团初三第三次月考
数学试卷 参考答案
一、选择题(在下列各题的四个选项中,只有一项是符合题意的。本题共 12 个小题,每小题 3 分,共 36 分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B A B A D C C B A A A C
二、填空题(本大题共 6 个小题,每小题 3 分,共 18 分) 13.x≥1 14.21 15.2 16.m≥﹣3 17.18
18. 5 1 2
三、解答题(本题共 8 个小题,第 19、20 题每小题 6 分,第 21、22 题每小题 8 分,第 23、24 题每小题 9 分,第 25、26 题每小题 10 分,共 66 分。解答应写出必要的文字说明、证明过程或演算步骤)
2018学年第一学期九年级第三次阶段测试试卷

2018学年第一学期九年级数学第三次阶段测试试卷2018.12(时间:100分钟,满分:150分)一.选择题(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.在Rt △ABC 中,︒=∠90C ,2=AC ,1=BC ,那么B sin 的值是(▲)(A )2;(B )21;(C )55;(D )552.2.如果将抛物线122-=x y 向左平移1个单位,那么得到的新抛物线的表达式为(▲)(A )22x y =;(B )1)1(22-+=x y ;(C )1)1(22-+=x y ;(D )1)1(22--=x y .3.如图1,△ABC 是正方形网格中的格点三角形(顶点在格点上),点D 、E 、F 、G 都是格点,下列三角形中与△ABC 相似的是(▲)(A )以点A 、B 、D 为顶点的三角形;(B )以点A 、B 、E 为顶点的三角形;(C )以点A 、B 、F 为顶点的三角形;(D )以点A 、B 、G 为顶点的三角形.4.如图2,在△ABC 中,点G 是△ABC 的重心,过点G 作DE//BC 分别交边AB 、AC 于点D 、E ,联结DC ,那么DBC DCE S S △△:=(▲)(A )5:4;(B )4:3;(C )3:2;(D )2:1.5.已知非零向量a 、b 和c ,下列条件中,不一定能判定b a //的是(▲)(A )-=;(B )21=,2=;(C )=+2,-=-;(D )||||=,||2||=.6.如图3,在△ABC 中,点D 是边AB 的中点,点E 在边AC 上,且满足AC =4EC ,联结DE 并延长,交边BC 的延长线于点F ,那么CB FC :的值为(▲)(A )21;(B )32;(C )43;(D )53.(图1)(图2)(图3)二.填空题(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置】7.已知25=y x ,那么y x x 2-=▲.8.已知二次函数1)2(2+-=x a y 的图像开口向下,那么a 的取值范围是▲.9.计算:CA BC AB ++=▲.10.已知线段AB 的长为2cm ,点P 在线段AB 上,如果AB PB AP ⋅=2,那么线段AP 的长是▲cm .11.如果抛物线m x m x y +-+=)4(2的顶点在y 轴上,那么m =▲.12.如果点A (-1,1y )和点B (0,2y )在二次函数322++-=x x y 的图像上,那么1y ▲2y .(用“>”、“<”或“=”填空)13.在Rt △ABC 中,∠ABC =90°,135sin =A ,如果AB =12,那么AC =▲.14.如图4,在平行四边形ABCD 中,点E 在边BC 上,射线AE 交边DC 的延长线于点F ,AB =4,BC =3EC ,那么DF 的长是▲.15.如图5,某同学站在距离教学楼BE 底部10米的A 处,用测角仪测得教学楼顶端E 的仰角是α,已知测角仪AC 的高为1.5米,那么这栋教学楼BE 的高度为▲米.(结果用含有α的式子表示)16.如图6,在Rt △ABC 中,∠ABC =90°,AC BD ⊥垂足为点D ,如果AD =3,DC =2,那么CBD ∠cos =▲.17.如图7,在△ABC 中,已知DE //FG //BC ,如果FBCG DFGE ADE S S S 四边形四边形△==,那么BF AD :的值是▲.18.如图8,在Rt △ABC 中,∠ACB =90°,BC =4cm ,以点B 为圆心,以BC 为半径画弧交边AB 于点D ,联结CD ,将△BCD 沿CD 翻折,记点B 的对应点为点E ,联结BE 交边AC 于点F ,如果2:1:=FB EF ,那么AC =▲cm .(图8)(图4)(图5)(图6)(图7)三.解答题(本大题共7题,满分78分)19.(本题满分10分)计算:︒-︒+︒-︒60sin 245cot 30cos 2160tan 2.20.(本题第(1)小题5分,第(2)小题5分,满分10分)如图9,在梯形ABCD 中,AD //BC ,BC =2AD ,对角线AC 、BD 相交于点O ,设a AD =,b AB =.(1)试用向量a 、b 表示向量OB ;(2)作出向量AO 分别在向量a 、b 方向上的分向量.21.(本题第(1)小题4分,第(2)小题6分,满分10分)如图10,二次函数)0(2≠++=a c b a c bx ax y 为常数,且、、的图像与x 轴交于点A 、B 两点,与y 轴交于点C ,已知点A 、B 在y 轴的左侧,且︒=∠30CAO ,︒=∠60CBO ,点C 的坐标为)3,0(.(1)直接写出点A 、B 的坐标;(2)求这个二次函数的解析式.22.(本题第(1)小题4分,第(2)小题6分,满分10分)如图11,某河堤的横断面为梯形ABCD ,AD //BC ,河堤顶宽AD 为6米,河堤的高为8米,迎水坡CD 的坡角为30°,背水坡AB 的长为10米.(1)求背水坡AB 的坡比i ;(2)现为了加固河堤,河堤顶宽需要加宽4米,背水坡的坡角变为了40°,求此时河堤横断面下底FC 的长度.(结果保留一位小数,64.040sin ≈︒,77.040cos ≈︒,84.040tan ≈︒,19.140cot ≈︒,41.12≈,73.13≈)(图9)(图10)(图11)23.(本题第(1)小题6分,第(2)小题6分,满分12分)已知:如图12,在△ABC 中,点D 、E 分别在边AB 、AC 上,BE 、CD 交于点G ,且AB AD AC AE ⋅=⋅.(1)求证:∠ABE =∠ACD ;(2)如果BE 平分∠ABC ,求证:DE =CE .24.(本题第(1)小题4分,第(2)小题4分,第(3)小题4分,满分12分)如图13,在平面直角坐标系xOy 中,抛物线)0(2≠++=a c b a c bx ax y 为常数,且、、与x 轴交于点A (-1,0)和点B ,与y 轴交于点C (0,3),已知该抛物线的对称轴是直线1=x .(1)求抛物线的表达式及顶点D 的坐标;(2)联结AC 、BC ,求∠ACB 的正切值;(3)已知点P 是抛物线上的一点,联结AP ,当∠PAB =∠ACB 时,求点P 的坐标.25.(本题第(1)小题4分,第(2)小题的5分,第(3)小题5分,满分14分)如图14,在△ABC 中,︒=∠90ABC ,8=AB ,6=BC ,点D 在边AC 上,AC DE ⊥,交边AB 于点E ,点F 在边BC 上,且A EDF ∠=∠,联结EF .(1)当4=AD 时,求BE 的长;(2)设AD 为x ,DF 为y ,求y 关于x 的函数解析式,并写出定义域;(3)当△DEF 为直角三角形时,求AD的长.(图12)(图13)(图14)(备用图)。
【九年级数学试题】2018年三门初三中考数学第三次适应性试题(带答案)
2018年三门初三中考数学第三次适应性试题(带答案)
考生须知
1.全卷满分150分,考试时间13 (c)(D)
2.我县新建的体育中心建筑面积约为55115平方米,55115用科学记数法表示且保留三个有效数字正确的是()
(A)551×103 (B)55115×104 (c)551×104 (D)55×104 3.下列四个角中,哪个角最可能与47°角互余()
4.某班六名同学在一次知识抢答赛中答对的题数分别是7,5,7,9,8,6,这组数据的中位数是()
(A)6 (B)7 (c)8 (D)9
5.下列运算正确的是()
(A)a2+a3=a5 (B)(c)(a3)2=a9 (D)
6.如图,△ AB绕点逆时针旋转80°得到△cD,若∠A=110°,∠D=40°,则∠α的度数是()
(A)60° (B)50° (c)40° (D)30°
7.如图是某几何体的三视图及相关数据,则该几何体的侧面积是()
(A)(B)(c)(D)
8.如图,D、E分别是等边△ABc两边的中点,连结BE、DE,下列结论
①△ADE是等边三角形;②△B Ec是直角三角形;③△BDE是等腰三角形;④Bc=2DE.其中正确的个数有()
(A)4个(B)3个(c)2个(D)1个
9.甲、乙两人在一条长为600的笔直马路上进行跑步,速度分别为4/s和6/s,
起跑前乙在起点,甲在乙前面50处,若两人同时起跑,则从起跑出发到其中一人先到达终点的过程中,两人之间的距离()与时间。
5月2018届九年级第三次模拟大联考(四川卷)数学卷(考试版)
数学试题 第1页(共6页) 数学试题 第2页(共6页)………○………………○………____________姓绝密★启用前|学科网考试研究中心命制2018届九年级第三次模拟大联考【四川卷】数 学(考试时间:120分钟 试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
5.考试范围:中考全部内容。
A 卷一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.在实数0,-π-4中,最小的数是 A .0BC .-4D .-π2.如图是一个由7个同样的立方体叠成的几何体,则这一几何体的三视图中,既是轴对称图形又是中心对称图形的是A .俯视图B .主视图C .俯视图和左视图D .主视图和俯视图3.对于一个城市来说,地铁开通意味着生活方式的改变.正在建设的成都地铁3号线双流境内全长约15.3千米,将极大地缩短双流和主城区成都的距离.日后,双流市民乘坐地铁,仅需25分钟就可直达市中心.用科学记数法表示15.3千米为 A .15.3×103米B .15.3×104米C .1.53×103米D .1.53×104米4.下列各式正确的是A .a 5+3a 5=4a 5B .(-ab )2=-a 2b 2C 2=-D .m 4•m 2=m 85.若点A (m ,2018)与点B (2019,n )关于y 轴对称,则m +n 的值是 A .-1B .1C .2D .-26.如图,把一块含有45°角的直角三角板的两个顶点分别放在直尺的一组对边上.如果125∠=︒,那么2∠的度数是A .30︒B .25︒C .20︒D .15︒7.如图,直线y =x +b 与直线y =kx +6交于点P (1,3),则关于x 的不等式x +b >kx +6的解集是A .1x <B .1x >C .3x >D .3x <8.某数学兴趣小组6名成员通过一次数学竞赛进行组内评比,他们的成绩分别是89,92,91,93,96,91,则关于这组数据说法正确的是 A .中位数是92.5B .平均数是92C .众数是96D .方差是59.如图,在△ABC 中,AB =AC ,∠BAC =70°,∠BAC 的平分线与AB 的垂直平分线交于点O ,点E 、F 分别在BC 、AC 上,点C 沿EF 折叠后与点O 重合,则∠BEO 的度数是A .20°B .35°C .40°D .55°10.已知⊙O 为△ABC 的外接圆,圆心O 在AB 上,∠BAC 的平分线AD 交⊙O 于D ,交BC 于E ,⊙O的半径为5,AC =6,连接OD 交BC 于F ,则EF 的长是A .2B .4C .1D .3。
4月2018届九年级第二次模拟大联考(湖北卷)数学卷(参考答案)
原创精品资源学科网独家享有版权,侵权必究!
2
即 A 品牌台灯 55 盏、B 品 牌台灯 45 盏.(8 分)
∴
1 2
2a b ab
,解得
a b
1 1
,
∴一次函数的解析式为:y=-x-1.(3 分)
(2)设直线 y=-x-1 与 y 轴交于点 C,
令 x=0 代入 y=-x-1,可得 y=-1,(4 分)
2 52
[来源:学*科*网 Z*X*X*K]
易得:△AFB≌△AMC,∴∠AMC=120°,
又△AFM 为等边三角形,[来源:学+科+网]
∴∠AMB=∠BMC=60°,
∵∠BFC=90°,
∴∠MFC=90°,∠NFC=30°,(6 分)
∴△FMN 为等边三角形,且 FN=NC,
∴NC=FN=FM=AF,
即 A 品牌台灯 40 盏、B 品牌台灯 60 盏;(6 分)
②当 m=10 时,w=3000,
故当 A 品牌台灯数量在 40 至 55 间,利润均为 3000;(7 分)
③当 8<m<10 时,即 10-m>0,w 随 a 的增大而增大,
故当 a=55 时,所获总利润 w 最大,
数学 第 2 页(共 7 页)
∴PD=8,AP=10,设半径为 r.
∵OC∥AD,∴ OC OP ,即 r 10 r , AD AP 6 10
解得 r= 15 .(8 分) 4
∵AB 是直径,∴∠AEB=∠D=90°,
∴BE∥PD,
∴AE=AB•sin∠ABE=AB•sin∠P= 15
3
×
=
9
.(10
内江市高中2018 届第三次模拟考试题数学答案
2018年九年级诊断性考试数学参考答案一、选择题(本大题共10个小题,每小题3分,共30分)1.B2.C3.C4.D5.B6.C7.A8.B9.C10.B二、填空题(本大题共6个小题,每小题3分,共18分)11.x >312.(x +3)2﹣713.714.π15.y =-12x +12(0<x <24)16.85三、解答题(共9个小题,满分72分)解答应写出必要的文字说明,证明过程或验算步骤17.解:原式=211221+++-2+5………………………4分=2+5………………………6分18.证明:∵△ABC 和△ECD 都是等腰直角三角形,∴AC=BC ,CD=CE ,∵∠ACD=∠DCE=90°,∴∠ACE+∠ACD=∠BCD+∠ACD ,∴∠ACE=∠BCD ,……………………………3分在△ACE 和△BCD 中,,∴△ACE ≌△BCD (SAS ),∴BD=AE.……………………………6分19.解:(1)200……………1分补全扇形统计图……………2分补全条形统计图……………3分(2)分别用A 1、A 2、A 3表示3名喜欢50米运动的学生,B 表示1名喜欢跳绳的学生,画树状图如下……………6分共有12种情况.选出的2人来自喜欢50米运动的学生的情况有6种所以选出的2人来自喜欢50米运动的学生的概率为21126=.……8分20.解(1)由方程有两个实数根,可得△=[—(k ﹣1)]2﹣4×1×41k 2=-2k +1≥0解得,k ≤;……………………3分(2)∵x 1,x 2是原方程的两根,∴x 1+x 2=k -1,x 1x 2=41k 2.……………………4分∵x 1x 2﹣x 12-x 22=45∴3x 1x 2﹣(x 1+x 2)2=45,3×41k 2﹣(k ﹣1)2=-413整理得k 2-8k -9=0,解得k 1=9,k 2=-1……………………7分∵k ≤,k =-1……………………8分21.解:(1)∵点A (4,2)在反比例函数的图象上,∴把(4,2)代入反比例函数ky=x,得k =8。
