第6章_数据结构习题题目及答案_树和二叉树_参考答案
数据结构-6 树和二叉树

第六章树和二叉树一.选择题1. 以下说法错误的是。
A.树形结构的特点是一个结点可以有多个直接前趋B.线性结构中的一个结点至多只有一个直接后继C.树形结构可以表达(组织)更复杂的数据D.树(及一切树形结构)是一种"分支层次"结构2. 如图6-2所示的4 棵二叉树中,不是完全二叉树。
图6-2 4 棵二叉树3. 在线索化二叉树中,t 所指结点没有左子树的充要条件是。
A. t->left == NULLB. t->ltag==1C. t->ltag==1 且t->left==NULL D .以上都不对4. 以下说法错误的是。
A.二叉树可以是空集B.二叉树的任一结点最多有两棵子树C.二叉树不是一种树D.二叉树中任一结点的两棵子树有次序之分5. 以下说法错误的是。
A.完全二叉树上结点之间的父子关系可由它们编号之间的关系来表达B.在三叉链表上,二叉树的求双亲运算很容易实现C.在二叉链表上,求根,求左、右孩子等很容易实现D.在二叉链表上,求双亲运算的时间性能很好6. 如图6-3所示的4 棵二叉树,是平衡二叉树。
图6-3 4 棵二叉树7. 如图6-4所示二叉树的中序遍历序列是。
A. abcdgefB. dfebagcC. dbaefcgD. defbagc图6-4 1 棵二叉树8. 已知某二叉树的后序遍历序列是dabec,中序遍历序列是debac,它的前序遍历序列是。
A. acbedB. decabC. deabcD. cedba9. 如果T2 是由有序树T 转换而来的二叉树,那么T 中结点的前序就是T2 中结点的。
A. 前序B.中序C. 后序D. 层次序10. 某二叉树的前序遍历结点访问顺序是abdgcefh,中序遍历的结点访问顺序是dgbaechf,则其后序遍历的结点访问顺序是。
A. bdgcefhaB. gdbecfhaC. bdgaechfD. gdbehfca11. 将含有83个结点的完全二叉树从根结点开始编号,根为1号,后面按从上到下、从左到右的顺序对结点编号,那么编号为41的双亲结点编号为。
第6-10章--树和二叉树--答案

(11)在AOE网络中一定只有一条关键路径;
(12)关键活动不按期完成就会影响整个工程的完成时间;
(13)任何一个关键活动提前完成,那么整个工程将会提前完成;
(14)所有的关键活动都提前完成,那么整个工程将会提前完成;
(15)任何一个关键活动延迟,那么整个工程将会延迟。
}
}//LayerOrder
第七章图
一、基础知识题
1.画出1个顶点、2个顶点、3个顶点、4个顶点和5个顶点的无向完全图。并证明在n个顶点的无向完全图中,边的条数为n(n-1)/2。
[解答]
[证明]
在有n个顶点的无向完全图中,每一个顶点都有一条边与其他某一顶点相连,所以每一个顶点有n-1条边与其他n-1个顶点相连,总计n个顶点有n(n-1)条边。但在无向图中,顶点i到顶点j与顶点j到顶点i是同一条边,所以总共有n(n-1)/2条边。
[解答]
(1)√(2)×(3)√(4)√(5)√
(6)√(7)×(8)√(9)×(10)√
(11)×(12)√(13)×(14)√(15)√
9.填空题
(1)在一个无向图中,所有顶点的度数之和等于所有边数的倍。
(2)在一个具有n个顶点的无向完全图中,包含有条边,在一个具有n个顶点的有向完全图中,包含在条边。
4.试分别画出具有3个结点的树和3个结点的二叉树的所有不同形态。
[解答]
具有3个结点的树具有3个结点的二叉树
5.如果一棵树有n1个度为1的结点,有n2个度为2的结点,…,nm个度为m的结点,试问有多少个度为0的结点?试推导之。
[解答]
总结点数n=n0+n1+n2+…+nm
数据结构习题 第6章 树

数据结构习题第6章树(1)2007-06-03 14:33:26| 分类:数据结构习题 | 标签:数据结构练习题|字号订阅第6章树6.1选择题1.一棵具有 n个结点的完全二叉树的树高度(深度)是()A)?log2n?+1 B)log2n +1 C)? log2n ? D)log2n-1【答案】A2.有关二叉树下列说法正确的是()A)二叉树的度为2 B)一棵二叉树的度可以小于2C)二叉树中至少有一个结点的度为2 D)二叉树中任何一个结点的度都为2【答案】B3.二叉树的第I层上最多含有结点数为()A)2I B)2I-1-1 C)2I-1 D)2I-1【答案】C4.具有10个叶结点的二叉树中有()个度为2的结点A)8 B)9 C)10 D)11【答案】B5.在下述结论中,正确的是()①只有一个结点的二叉树的度为0;②二叉树的度为2;③二叉树的左右子树可任意交换;④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A)①②③ B)②③④ C)②④ D)①④【答案】D6.由3 个结点可以构造出多少种不同的二叉树?()A)2 B)3 C)4 D)5【答案】D7.引入二叉线索树的目的是()A)加快查找结点的前驱或后继的速度B)为了能在二叉树中方便的进行插入与删除C)为了能方便的找到双亲D)使二叉树的遍历结果惟一【答案】A8.有n个叶子的哈夫曼树的结点总数为()A)不确定 B)2n C)2n+1 D)2n-1【答案】D9.一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足()A)所有的结点均无左孩子 B)所有的结点均无右孩子C)只有一个叶子结点 D)是任意一棵二叉树【答案】C【解析】先序序列是“根左右”,后序序列是“左右根”,若要这两个序列相反,只有单支树,单支树的特点是只有一个叶子结点或高度等于其结点数,故选C。
10.一棵完全二叉树上有1001个结点,其中叶子结点的个数是()A)250 B)500 C)505 D)以上答案都不对【答案】D【解析】若每个结点均已经编号,则最大的编号为1001,其父亲结点的编号为500,那么从501到1001均为叶子结点。
数据结构课后习题答案第六章

第六章树和二叉树(下载后用阅读版式视图或web版式可以看清)习题一、选择题1.有一“遗传”关系:设x是y的父亲,则x可以把它的属性遗传给y。
表示该遗传关系最适合的数据结构为( )。
A.向量B.树C图 D.二叉树2.树最合适用来表示( )。
A.有序数据元素 B元素之间具有分支层次关系的数据C无序数据元素 D.元素之间无联系的数据3.树B的层号表示为la,2b,3d,3e,2c,对应于下面选择的( )。
A. la (2b (3d,3e),2c)B. a(b(D,e),c)C. a(b(d,e),c)D. a(b,d(e),c)4.高度为h的完全二叉树至少有( )个结点,至多有( )个结点。
A. 2h_lB.h C.2h-1 D. 2h5.在一棵完全二叉树中,若编号为f的结点存在右孩子,则右子结点的编号为( )。
A. 2iB. 2i-lC. 2i+lD. 2i+26.一棵二叉树的广义表表示为a(b(c),d(e(,g(h)),f)),则该二叉树的高度为( )。
A.3B.4C.5D.67.深度为5的二叉树至多有( )个结点。
A. 31B. 32C. 16D. 108.假定在一棵二叉树中,双分支结点数为15,单分支结点数为30个,则叶子结点数为( )个。
A. 15B. 16C. 17D. 479.题图6-1中,( )是完全二叉树,( )是满二叉树。
1 / 1710.在题图6-2所示的二叉树中:(1)A结点是A.叶结点 B根结点但不是分支结点C根结点也是分支结点 D.分支结点但不是根结点(2)J结点是A.叶结点 B.根结点但不是分支结点C根结点也是分支结点 D.分支结点但不是根结点(3)F结点的兄弟结点是A.EB.D C.空 D.I(4)F结点的双亲结点是A.AB.BC.CD.D(5)树的深度为A.1B.2C.3D.4(6)B结点的深度为A.1B.2C.3D.4(7)A结点所在的层是A.1B.2C.3D.411.在一棵具有35个结点的完全二叉树中,该树的深度为( )。
第六章树和二叉树习题_数据结构汇总

习题六树和二叉树一、单项选择题1.以下说法错误的是 ( )A.树形结构的特点是一个结点可以有多个直接前趋B.线性结构中的一个结点至多只有一个直接后继C.树形结构可以表达(组织)更复杂的数据D.树(及一切树形结构)是一种"分支层次"结构E.任何只含一个结点的集合是一棵树2.下列说法中正确的是 ( )A.任何一棵二叉树中至少有一个结点的度为2B.任何一棵二叉树中每个结点的度都为2C.任何一棵二叉树中的度肯定等于2D.任何一棵二叉树中的度可以小于23.讨论树、森林和二叉树的关系,目的是为了()A.借助二叉树上的运算方法去实现对树的一些运算B.将树、森林按二叉树的存储方式进行存储C.将树、森林转换成二叉树D.体现一种技巧,没有什么实际意义4.树最适合用来表示 ( )A.有序数据元素 B.无序数据元素C.元素之间具有分支层次关系的数据 D.元素之间无联系的数据5.若一棵二叉树具有10个度为2的结点,5个度为1的结点,则度为0的结点个数是()A.9 B.11 C.15 D.不确定6.设森林F中有三棵树,第一,第二,第三棵树的结点个数分别为M1,M2和M3。
与森林F 对应的二叉树根结点的右子树上的结点个数是()。
A.M1 B.M1+M2 C.M3 D.M2+M37.一棵完全二叉树上有1001个结点,其中叶子结点的个数是()A. 250 B. 500 C.254 D.505 E.以上答案都不对8. 设给定权值总数有n 个,其哈夫曼树的结点总数为( )A.不确定 B.2n C.2n+1 D.2n-19.二叉树的第I层上最多含有结点数为()A.2I B. 2I-1-1 C. 2I-1 D.2I -110.一棵二叉树高度为h,所有结点的度或为0,或为2,则这棵二叉树最少有( )结点A.2h B.2h-1 C.2h+1 D.h+111. 利用二叉链表存储树,则根结点的右指针是()。
A.指向最左孩子 B.指向最右孩子 C.空 D.非空14.在二叉树结点的先序序列,中序序列和后序序列中,所有叶子结点的先后顺序()A.都不相同 B.完全相同C.先序和中序相同,而与后序不同 D.中序和后序相同,而与先序不同15.在完全二叉树中,若一个结点是叶结点,则它没()。
数据结构习题第六章树和二叉树

第六章 树和二叉树一、选择题1.已知一算术表达式的中缀形式为 A+B*C-D/E ,后缀形式为ABC*+DE/-,其前缀形式为( )A .-A+B*C/DE B. -A+B*CD/E C .-+*ABC/DE D.-+A*BC/DE【北京航空航天大学 1999 一、3 (2分)】2.算术表达式a+b*(c+d/e )转为后缀表达式后为( )【中山大学 1999 一、5】A .ab+cde/*B .abcde/+*+C .abcde/*++D 3. 设有一表示算术表达式的二叉树(见下图),它所表示的算术表达式是( ) 【南京理工大学1999 一、20(2分)】 A. A*B+C/(D*E)+(F-G) B. (A*B+C)/(D*E)+(F-G) C. (A*B+C)/(D*E+(F-G )) D. A*B+C/D*E+F-G 4. 设树T 的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T 中的叶子数为( )A .5B .6C .7D .8【南京理工大学 2000 一、8 (1.5分)】5. 在下述结论中,正确的是( )【南京理工大学 1999 一、4 (1分)】①只有一个结点的二叉树的度为0; ②二叉树的度为2; ③二叉树的左右子树可任意交换;④深度为K 的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A .①②③B .②③④C .②④D .①④6. 设森林F 对应的二叉树为B ,它有m 个结点,B 的根为p,p 的右子树结点个数为n,森林F 中第一棵树的结点个数是( )A .m-nB .m-n-1C .n+1D .条件不足,无法确定 【南京理工大学2000一、17(1.5分)】7. 树是结点的有限集合,它( (1))根结点,记为T 。
其余结点分成为m (m>0)个((2))的集合T1,T2, …,Tm ,每个集合又都是树,此时结点T 称为Ti 的父结点,Ti 称为T的子结点(1≤i ≤m )。
数据结构与算法第六章课后答案第六章 树和二叉树
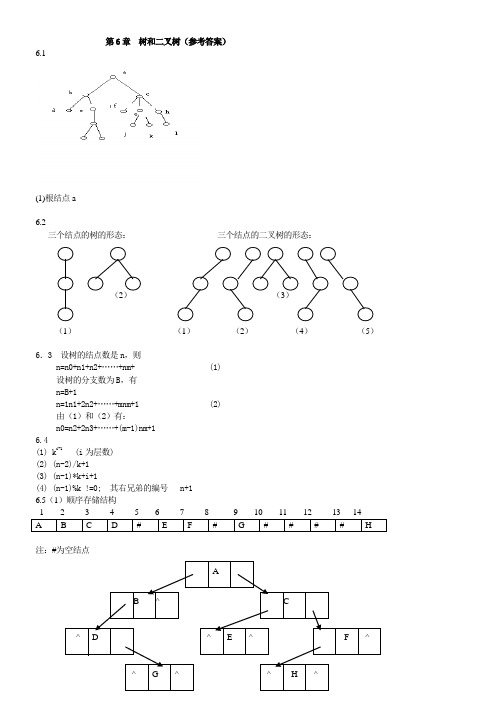
第6章 树和二叉树(参考答案)6.1(1)根结点a6.2三个结点的树的形态: 三个结点的二叉树的形态:(1) (1) (2) (4) (5)6.3 设树的结点数是n ,则n=n0+n1+n2+……+nm+ (1)设树的分支数为B ,有n=B+1n=1n1+2n2+……+mnm+1 (2)由(1)和(2)有:n0=n2+2n3+……+(m-1)nm+16.4(1) k i-1 (i 为层数)(2) (n-2)/k+1(3) (n-1)*k+i+1(4) (n-1)%k !=0; 其右兄弟的编号 n+16.5(1)顺序存储结构注:#为空结点6.6(1) 前序 ABDGCEFH(2) 中序 DGBAECHF(3) 后序 GDBEHFCA6.7(1) 空二叉树或任何结点均无左子树的非空二叉树(2) 空二叉树或任何结点均无右子树的非空二叉树(3) 空二叉树或只有根结点的二叉树6.8int height(bitree bt)// bt是以二叉链表为存储结构的二叉树,本算法求二叉树bt的高度{ int bl,br; // 局部变量,分别表示二叉树左、右子树的高度if (bt==null) return(0);else { bl=height(bt->lchild);br=height(bt->rchild);return(bl>br? bl+1: br+1); // 左右子树高度的大者加1(根) }}// 算法结束6.9void preorder(cbt[],int n,int i);// cbt是以完全二叉树形式存储的n个结点的二叉树,i是数// 组下标,初始调用时为1。
本算法以非递归形式前序遍历该二叉树{ int i=1,s[],top=0; // s是栈,栈中元素是二叉树结点在cbt中的序号 // top是栈顶指针,栈空时top=0if (n<=0) { printf(“输入错误”);exit(0);}while (i<=n ||top>0){ while(i<=n){visit(cbt[i]); // 访问根结点if (2*i+1<=n) s[++top]=2*i+1; //若右子树非空,其编号进栈i=2*i;// 先序访问左子树}if (top>0) i=s[top--]; // 退栈,先序访问右子树} // END OF while (i<=n ||top>0)}// 算法结束//以下是非完全二叉树顺序存储时的递归遍历算法,“虚结点”用‘*’表示void preorder(bt[],int n,int i);// bt是以完全二叉树形式存储的一维数组,n是数组元素个数。
数据结构树和二叉树习题(有答案)

E F D GAB/+ +* - C* 第六章树和二叉树一、选择题1.已知一算术表达式的中缀形式为 A+B*C-D/E ,后缀形式为ABC*+DE/-,其前缀形式为( )A .-A+B*C/DE B. -A+B*CD/E C .-+*ABC/DED. -+A*BC/DE【北京航空航天大学 1999 一、3 (2分)】2.算术表达式a+b*(c+d/e )转为后缀表达式后为()【中山大学 1999 一、5】A .ab+cde/*B .abcde/+*+C .abcde/*++ D.abcde*/++3. 设有一表示算术表达式的二叉树(见下图),它所表示的算术表达式是()【南京理工大学1999 一、20(2分)】A. A*B+C/(D*E)+(F-G)B. (A*B+C)/(D*E)+(F-G)C. (A*B+C)/(D*E+(F-G ))D. A*B+C/D*E+F-G4. 设树T 的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T 中的叶子数为()A .5 B.6 C.7D .8【南京理工大学 2000 一、8 (1.5分)】5. 在下述结论中,正确的是()【南京理工大学 1999 一、4 (1分)】①只有一个结点的二叉树的度为0; ②二叉树的度为2;③二叉树的左右子树可任意交换;④深度为K 的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A .①②③ B .②③④ C.②④D .①④6. 设森林F 对应的二叉树为B ,它有m 个结点,B 的根为p,p 的右子树结点个数为n,森林F中第一棵树的结点个数是()A .m-nB .m-n-1C .n+1D .条件不足,无法确定【南京理工大学2000 一、17(1.5分)】7. 树是结点的有限集合,它((1))根结点,记为T 。
其余结点分成为m (m>0)个((2))的集合T1,T2,…,Tm ,每个集合又都是树,此时结点T 称为Ti 的父结点,Ti 称为T 的子结点(1≤i ≤m )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
. 1 / 32 一、基础知识题 6.1设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1,求树T中的叶子数。 【解答】 设度为m的树中度为0,1,2,…,m的结点数分别为n0, n1, n2,…, nm,结点总数为n,分枝数为B,则下面二式成立 n= n0+n1+n2+…+nm (1) n=B+1= n1+2n2 +…+mnm+1 (2)
由(1)和(2)得叶子结点数n0=1+ 即: n0=1+(1-1)*4+(2-1)*2+(3-1)*1+(4-1)*1=8 6.2一棵完全二叉树上有1001个结点,求叶子结点的个数。 【解答】因为在任意二叉树中度为2 的结点数n2和叶子结点数n0有如下关系:n2=n0-1,所以设二叉树的结点数为n, 度为1的结点数为n1,则 n= n0+ n1+ n2 n=2n0+n1-1 1002=2n0+n1 由于在完全二叉树中,度为1的结点数n1至多为1,叶子数n0是整数。本题中度为1的结点数n1只能是0,故叶子结点的个数n0为501. 注:解本题时要使用以上公式,不要先判断完全二叉树高10,前9层是满二叉树,第10层都是叶子,……。虽然解法也对,但步骤多且复杂,极易出错。
6.3 一棵124个叶结点的完全二叉树,最多有多少个结点。 【解答】由公式n=2n0+n1-1,当n1为1时,结点数达到最多248个。
6.4.一棵完全二叉树有500个结点,请问该完全二叉树有多少个叶子结点?有多少个度为1的结点?有多少个度为2的结点?如果完全二叉树有501个结点,结果如何?请写出推导过程。 . 2 / 32 【解答】由公式n=2n0+n1-1,带入具体数得,500=2n0+n1-1,叶子数是整数,度为1的结点数只能为1,故叶子数为250,度为2的结点数是249。 若完全二叉树有501个结点,则叶子数251,度为2的结点数是250,度为1的结点数为0。
6.5 某二叉树有20个叶子结点,有30个结点仅有一个孩子,则该二叉树的总结点数是多少。 【解答】由公式n=2n0+n1-1,得该二叉树的总结点数是69。
6.6 求一棵具有1025个结点的二叉树的高h。 【解答】该二叉树最高为1025(只有一个叶子结点),最低高为11。因为210-1<1025<211-1,故1025个结点的二叉树最低高为11。
6.7 一棵二叉树高度为h,所有结点的度或为0,或为2,则这棵二叉树最少有多少结点。 【解答】第一层只一个根结点,其余各层都两个结点,这棵二叉树最少结点数是2h-1。
6.8将有关二叉树的概念推广到三叉树,则一棵有244个结点的完全三叉树的高度是多少。 【解答】设含n个结点的完全三叉树的高度为h,则有
<2n<
本题n=244, 故h=6。 6.9 对二叉树的结点从1开始进行连续编号,要求每个结点的编号大于其左、右3 / 32
孩子的编号,同一结点的左、右孩子中,其左孩子的编号小于其右孩子的编号,是采用何种次序的遍历实现编号的。 【解答】后序遍历二叉树,因为后序遍历顺序为左子树-右子树-根结点。
6.10 高度为h(h>0)的满二叉树对应的森林由多少棵树构成。 【解答】因为在二叉树转换为森林时,二叉树的根结点,根结点的右子女,右子女的右子女,……,都是树的根,所以,高度为h(h>0)的满二叉树对应的森林由h棵树构成。
6.11 某二叉树结点的中序序列为BDAECF,后序序列为DBEFCA,则该二叉树对应的森林包括几棵树? 【解答】3棵树。(本题不需画出完整的二叉树,更不需要画出森林,只需画出二叉树的右子树就可求解。如上题所述,二叉树的根结点,根结点的右子女,右子女的右子女,……,在二叉树转为森林时,都是树的根。)
6.12 对任意一棵树,设它有n个结点,这n个结点的度数之和为多少? 【解答】n-1。度数其实就是分支个数。根结点无分支所指,其余结点有且只有一个分支所指。
6.13 一棵左子树为空的二叉树在先序线索化后,其中空的链域的个数是多少? 【解答】对二叉树线索化时,只有空链域才可加线索。一棵左子树为空的二叉树在先序线索化时,根结点的左链为空,应加上指向前驱的线索,但根结点无前驱,故该链域为空。同样分析知道最后遍历的结点的右链域为空。故一棵左子树为空的二叉树在先序线索化后,其中空的链域的个数是2个。
6.14 一棵左、右子树均不空的二叉树在先序线索化后,其中空的链域的个数是多少? 【解答】1个。 4 / 32
6.15 设B是由森林F变换得的二叉树。若F中有n个非终端结点,则B中右指针域为空的结点有几个? 【解答】n+1。森林中任何一个非终端结点在转换成二叉树时,其第一个子女结点成为该非终端结点的左子女,其余子女结点成为刚生成的左子女结点的右子女,右子女结点的右子女,……,最右子女结点的右链域为空。照此分析,n个非终端结点在转换后,其子女结点中共有n个空链域。另外,森林中各棵树的根结点可以看做互为兄弟,转换成二叉树后也产生1个空链域。因此,本题的答案是n+1。
6.16 试分别找出满足以下条件的所有二叉树: (1) 二叉树的前序序列与中序序列相同; (2) 二叉树的中序序列与后序序列相同; (3) 二叉树的前序序列与后序序列相同; (4) 二叉树的前序序列与层次序列相同; (5) 二叉树的前序、中序与后序序列均相同。 【解答】前序遍历二叉树的顺序是“根—左子树—右子树”,中序遍历的顺序是“左子树—根—右子树”,后序遍历顺序是:“左子树—右子树―根",根据以上原则,本题解答如下: 若前序序列与中序序列相同,则或为空树,或为任一结点至多只有右子树的二叉树。 若中序序列与后序序列相同,则或为空树,或为任一结点至多只有左子树的二叉树。 若前序序列与后序序列相同,则或为空树,或为只有根结点的二叉树。 若二叉树的前序、中序与后序序列均相同,则或为空树,或为只有根结点的二叉树。
6.17 已知一棵二叉树的前序遍历的结果是ABECDFGHIJ,中序遍历的结果是EBCDAFHIGJ,试画出这棵二叉树,对二叉树进行中序线索化,并将该二叉树转换为森林。 . 5 / 32 【解答】
6.18 已知一棵二叉树的后序遍历序列为EICBGAHDF,同时知道该二叉树的中序遍历序列为CEIFGBADH,试画出该二叉树。 .
6 / 32 6.19设二叉树中每个结点均用一个字母表示,若一个结点的左子树或右子树为空,用#表示,现前序遍历二叉树,访问的结点序列为ABD##C#E##F##,写出中序和后序遍历二叉树时结点的访问序列。 【解答】中序遍历二叉树时结点的访问序列:#D#B#C#E#A#F# 后序遍历二叉树时结点的访问序列。##D###ECB##FA
6.20有n个结点的k叉树(k≥2)用k叉链表表示时,有多少个空指针? 【解答】k叉树(k≥2)用k叉链表表示时,每个结点有k个指针,除根结点没有指针指向外,其余每个结点都有一个指针指向,故空指针的个数为: nk-(n-1)=n(k-1)+1
6.21 一棵高度为h的满k叉树有如下性质:根结点所在层次为0;第h层上的结点都是叶子结点;其余各层上每个结点都有k棵非空子树,如果按层次自顶向下,同一层自左向右,顺序从1开始对全部结点进行编号,试问: (1)各层的结点个数是多少? (2)编号为i的结点的双亲结点(若存在)的编号是多少? (3)编号为i的结点的第m个孩子结点(若存在)的编号是多少? (4)编号为i的结点有右兄弟的条件是什么?其右兄弟结点的编号是多少? 【解答】 (1)kl(l为层数,按题意,根结点为0层) 7 / 32
(2)因为该树每层上均有kl个结点,从根开始编号为1,则结点i的从右向左数第2个孩子的结点编号为ki。设n 为结点i的子女,则关系式(i-1)k+2<=n<=ik+1成立,因i是整数,故结点i的双亲的编号为ë(i-2)/kû+1。 (3) 结点i(i>1)的前一结点编号为i-1(其最右边子女编号是(i-1)*k+1),故结点 i的第 m个孩子的编号是(i-1)*k+1+m。 (4) 根据以上分析,结点i有右兄弟的条件是,它不是双亲的从右数的第一子女,即 (i-1)%k!=0,其右兄弟编号是i+1。
6.22.证明任一结点个数为n(n>0) 的二叉树的高度至少为ë(logn)û+1。 【解答】最低高度二叉树的特点是,除最下层结点个数不满外,其余各层的结点数都应达到各层的最大值。设n个结点的二叉树的最低高度是h,则n应满足2h-1≦n≦2h-1关系式。解此不等式,并考虑h是整数,则有h=ëlognû+1,即任一结点个数为n 的二叉树的高度至少为ë(logn)û+1。
6.23 已知A[1..N]是一棵顺序存储的完全二叉树,如何求出A[i]和A[j]的最近的共同祖先? 【解答】根据顺序存储的完全二叉树的性质,编号为i的结点的双亲的编号是ëi/2û,故A[i]和A[j]的最近公共祖先可如下求出: while(i/2!=j/2) if(i>j) i=i/2; else j=j/2; 退出while后,若i/2=0,则最近公共祖先为根结点,否则最近公共祖先是i/2。
6.24已知一棵满二叉树的结点个数为20到40之间的素数,此二叉树的叶子结点有多少个? 【解答】结点个数在20到40的满二叉树且结点数是素数的数是31,其叶子数是16。
6.25求含有n个结点、采用顺序存储结构的完全二叉树中的序号最小的叶子结
