正交八面体应力空间的强度理论综述_黄辉
岩石破坏准则

2.1岩石破坏强度准则岩石的破坏主要与外荷载的作用方式、温度及湿度有关。
一般在低温、低围压及高应变率的条件下,岩石表现为脆性破坏,而在高温、高围压、低应变率作用下,岩石则表现为塑性或者塑性流动。
对于较完整的岩石来说,其破坏形式可以分为:1)脆性破坏;3)延性破坏。
图2-1给出了不同应力状态下岩石破裂前应变值、破坏形态示意图和典型的应力-应变曲线示意图。
图2-1岩石破坏形态示意图从图2-1中可以看出岩石破裂种类繁多、岩石破坏过程中的应力、变形、裂纹产生和扩展极为复杂,很难用一种模型进行描述,很多学者针对不同岩石破坏特征提出多种不同岩石的强度破坏准则。
本节主要对已有的岩石强度破坏准则进行总结,找出它们各自的优缺点。
2.1.1最大正应力强度理论最大正应力强度理论也称朗肯理论,该理论是1857年提出的。
它假定挡土墙背垂直、光滑,其后土体表面水平并无限延伸,这时土体内的任意水平面和墙的背面均为主平面(在这两个平面上的剪应力为零),作用在该平面上的法向应力即为主应力。
朗肯根据墙后主体处于极限平衡状态,应用极限平衡条件,推导出了主动土压力和被动土压力计算公式。
考察挡土墙后主体表面下深度z 处的微小单元体的应力状态变化过程。
当挡土墙在土压力的作用下向远离土体的方向位移时,作用在微分土体上的竖向应力sz 保持不变,而水平向应力sx 逐渐减小,直至达到土体处于极限平衡状态。
土体处于极限平衡状态时的最大主应力为s1=gz ,而最小主应力s3即为主动土压力强度pa 。
根据,当主体中某点处于极限平衡状态时,大主应力1σ和小主应力3σ之间应满足以下关系式:粘性土:213...2tan tan 454522c ϕϕσσ⎛⎫⎛⎫︒︒=-++ ⎪ ⎪⎝⎭⎝⎭(1)无粘性土231.tan 452ϕσσ⎛⎫︒=- ⎪⎝⎭(2)该理论认为材料破坏取决于绝对值最大的正应力。
因此,作用于岩石的三个正应力中,只要有一个主应力达到岩石的单轴抗压强度或岩石的单轴抗拉强度,岩石便被破坏。
高等土力学-土的本构关系--清华大学

sij偏应力张量,其物理意义代表作用于 该点的纯剪应力分量
偏应力张量
第二章 土的本构关系
2.2 应力和应变 – 应力
仁者乐山 智者乐水
J1 Skk 0
1 1 J 2 sijsij (1 2 )2 (2 3 )2 (3 1 )2 2 6
1 J 3 S ijS jk S ki 3 1 ( 21 2 3 )( 2 2 1 3 )( 2 3 1 2 ) 27
第 14,18,19,33题
第二章 土的本构关系
2.1 概述
仁者乐山 智者乐水
土的本构关系 Constitutive relationship 土的本构定律 Constitutive law 土的本构方程 Constitutive equation 土的数学模型 Mathematical model
本构关系与土力学分析方法
第二章 土的本构关系
2.1 概述
仁者乐山 智者乐水
传统土力学:线弹性、刚塑性或理想塑性 研究初期:20世纪60年代,高重建筑物及 深厚基础问题;计算机技术发展 迅速发展时期:80年代达到高潮,“土力 学园地中最绚烂的花朵” 目前:土的结构性、非饱和土、循环加载、 动力本构模型等
《高等土力学》之二
土的本构关系
张 丙 印
清华大学水利水电工程系 岩 土 工 程 研 究 所
第二章 土的本构关系
2.1 概述 2.2 应力和应变 2.3 土的应力变形特性
2.4 土的弹性模型
2.5 土的弹塑性模型的一般原理 2.6 剑桥模型(Cam—Clay) 2.7 其它典型弹塑性模型 2.8 土的结构性及土的损伤模型
应力分析(Stress Analysis)

推导原理: 静力平衡条件: 静力矩平衡条件:
X 0, Y 0, Z 0
M
x
0, M y 0, M z 0
2 1 f ( x ) 1 f ( x) 泰勒级数展开: f ( x dx) f ( x) ...... 2 1! x 2! x
2 2 P 总应力 8 8 8 八面体上的正应力与塑性变形无关,剪应力与塑性变形有 关。
八面体应力的求解思路:
ij (i, j x, y, z) 1, 2 , 3 8 , 8
I1, I 2
因为
2 2 8 ( I1 3I 2 ) 3
ij ij m
' ij
(i,j=x,y,z)
为柯氏符号。
1 其中 m ( x y z ) 即平均应力, 3
即
' x xy xz x xy xz 1 0 0 . . ' 0 1 0 y yz y yz m ' . . . . z z 0 0 1
' ' ' ' ' ' I1' x y z 1 2 3 0
' ' ' ' ' ' I2 1 2 2 3 3 1' (体现变形体形状改变的程度)
' ' ' ' I3 1 2 3 const
§1.4 应力平衡微分方程
直角坐标下的应力平衡微分方程* ij 0 i
讨论:1. 等效的实质? 是(弹性)应变能等效(相当于)。 2. 什么与什么等效? 复杂应力状态(二维和三维)与简单应力状态(一维)等效 3. 如何等效? 等效公式(注意:等效应力是标量,没有作用面)。 4. 等效的意义? 屈服的判别、变形能的计算、简化问题的分析等。
第五章 应力状态与强度理论

x y
(1) (2)
移项,等式两边平方后相加,消去参数2α 得,
x y x y 2 0 xy 2 2 2
应力圆:以 、 为变量的圆周方程
在σ — τ 平面内,
2
45°
2
解:
1.取单元体
圆轴扭转时,在横截面的边缘处切应力最大
y 40MPa,
y
min
x y
2
x y 2 2 ( ) xy 48.3MPa 2
2 xy
60 60 40
xy
1 68.3MP a, 2 0, 3 48.3MP a
主平面的方位: 2 0 tg
xy 2 xy B1 D1 CB1 1 x y x y 2
(4)最大切应力和最小切应力等于应力圆的半径,所在平面与主平面得 夹角为 45 ,即
max min
x y 1 2 2 2 xy 2
2.应力状态:是指研究受力构件内通过一点的各不同方位截面上的应力情况 应力状态分析:是指研究受力构件内通过一点的各不同方位截面上的应力变化规律,
确定该点处的最大正应力和最大切应力及其所在截面的方位,找出危险截面上的危险 点,并确定该点处的应力及其方向,然后建立复杂应力状态下的强度条件。
3.单元体:
60 40 sin( 60 ) 30 cos( 60 ) 58.3MPa 2
2
(2)主应力、主平面
x 60MPa,
xy 30MPa,
30。
max
第八章强度理论

σ1
O1N O3O1 代入 = O2F O3O2
[σt ] σ3 ≤ [σt ] 强度条件 σ1 − [σc ]
三、 各种强度理论的适用范围及其应用
1.适用范围 1.适用范围 (1)脆性材料:当最小主应力大于等于0时,选用第一强度 脆性材料:当最小主应力大于等于0 理论; 当最小主应力小于0而最大主应力大于0 使用莫尔理论; 理论; 当最小主应力小于0而最大主应力大于0时,使用莫尔理论; 当最大主应力小于等于0 当最大主应力小于等于0时,选用第三或第四强度理论。 选用第三或第四强度理论。 (2)塑性材料:当最小主应力大于等于0时,选用第一 塑性材料:当最小主应力大于等于0 强度理论;其他应力状态时,选用第三或第四强度理论; 强度理论;其他应力状态时,选用第三或第四强度理论; (3)简单变形时:一律用与其相对应的强度准则。 简单变形时:一律用与其相对应的强度准则。 (4)破坏形式还与温度、变形速度有关。 破坏形式还与温度、变形速度有关。
基本观点
构件受外力作用而发生破坏时, 构件受外力作用而发生破坏时,不论破坏的表面现象如何复 杂,其破坏形式总不外乎几种类型,而同一类型的破坏则可能是某 其破坏形式总不外乎几种类型, 一个共同因素所引起的. 一个共同因素所引起的.
二、材料破坏的两种类型(常温、静载荷) 材料破坏的两种类型(常温、静载荷)
§8-3 莫尔强度理论
一、引言
莫尔认为: 莫尔认为:最大切应力是使 物体破坏的主要因素, 物体破坏的主要因素,但滑移面 上的摩擦力也不可忽略(莫尔 上的摩擦力也不可忽略( 摩擦定律).综合最大切应力及 摩擦定律) 最大正应力的因素, 最大正应力的因素,莫尔得出了 他自己的强度理论. 他自己的强度理论.
1. 塑性屈服 材料出现显著的塑性变形而丧失其正常的工作能力.
高等土力学作业
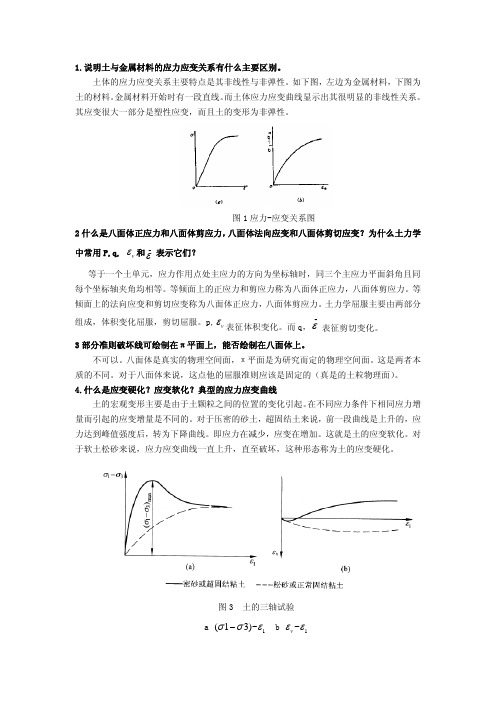
1.说明土与金属材料的应力应变关系有什么主要区别。
土体的应力应变关系主要特点是其非线性与非弹性。
如下图,左边为金属材料,下图为土的材料。
金属材料开始时有一段直线。
而土体应力应变曲线显示出其很明显的非线性关系。
其应变很大一部分是塑性应变,而且土的变形为非弹性。
图1应力-应变关系图2什么是八面体正应力和八面体剪应力,八面体法向应变和八面体剪切应变?为什么土力学中常用P,q, v ε和_ε表示它们?等于一个土单元,应力作用点处主应力的方向为坐标轴时,同三个主应力平面斜角且同每个坐标轴夹角均相等。
等倾面上的正应力和剪应力称为八面体正应力,八面体剪应力。
等倾面上的法向应变和剪切应变称为八面体正应力,八面体剪应力。
土力学屈服主要由两部分组成,体积变化屈服,剪切屈服。
p,v ε表征体积变化。
而q,_ε表征剪切变化。
3部分准则破坏线可绘制在π平面上,能否绘制在八面体上。
不可以。
八面体是真实的物理空间面,π平面是为研究而定的物理空间面。
这是两者本质的不同。
对于八面体来说,这点他的屈服准则应该是固定的(真是的土粒物理面)。
4.什么是应变硬化?应变软化?典型的应力应变曲线土的宏观变形主要是由于土颗粒之间的位置的变化引起。
在不同应力条件下相同应力增量而引起的应变增量是不同的。
对于压密的砂土,超固结土来说,前一段曲线是上升的,应力达到峰值强度后,转为下降曲线。
即应力在减少,应变在增加。
这就是土的应变软化。
对于软土松砂来说,应力应变曲线一直上升,直至破坏,这种形态称为土的应变硬化。
图3 土的三轴试验a 1(13)~σσε−b 1~v εε5.土的压硬性?土的剪胀性?解释它们的微观机理。
随着压缩过程的进行,土的压缩模量和刚度逐步提高的现象称为土的压硬性。
由剪应力引起的体积变化称为土的剪胀性。
土的压硬性,表现在微观领域,是土颗粒与颗粒间的间距更近,土颗粒与土颗粒的粘结更加有效。
而土的剪胀性表现在微观领域,为土颗粒之间位置产生了变化。
第2章 土的本构关系
2 1 3
• 应力洛德角
tg
2 2 1 3 3 ( 1 3 )
• 三轴压缩试验( >=3 ): = -30º • 三轴伸长试验( =>3 ): = 30º
传统土力 学分析方法
稳定问题 (边坡稳定性)
• 土体处于极限平衡状态 • 滑动块体间力的平衡 • 刚体+理想塑性计算安全系数
现代土力 学分析方法
应力变形的 综合分析
计算机数值模拟计算 • 土体的本构模型 • 数值计算方法:有限元等 • 应力变形稳定的综合分析
模型试验:如离心机模型试验
本构关系与土力学分析方法
偏应力张量
m球张量分量,其物理意义代表作用于该点的平均 正应力或静水压力分量,其值为m=I1/3
球应力张量与偏应力张量
第二章 土的本构关系
2.2 应力和应变 – 应力
仁者乐山 智者乐水
12 13 s11 s12 s13 11 m 1 sij ij ijkk s s s 21 22 m 23 21 22 23 3 32 33 m s31 s32 s33 31
• 剪应力q:平面上到Q距离PQ
• 洛德角:平面上的角度
三个独立的应力参数p、q和可以确 定应力点P在应力空间的位置
常用的三个应力不变量
第二章 土的本构关系
2.2 应力和应变 – 应力
仁者乐山 智者乐水
三轴应力状态: 3
• 平均主应力 • 广义剪应力
1 1 p (1 2 3 ) (1 23 ) 3 3
第二章 土的本构关系
03 混凝土的基本力学性能-001
2、混凝土的本构关系、强度理论
● 应力张量、Haigh-Westergaad坐标系 4) 八面体应力 主应力空间中,主应力轴等倾的八个面围成一个正八面体 作用在等倾面上的应力成为八面体应力
σ oct = τ oct = 1 I (σ 1 + σ 2 + σ 3 ) = 1 = σ m 3 3 1 3
6)断裂力学本构关系——断裂强度因子、J积分绕过裂纹尖端 7)损伤力学本构关系——考虑材料裂化、刚度降低 σ = ( I − D ) : C0 : ε
2、混凝土的本构关系、强度理论
Saenz 模型
σ = E 0ε E0 ε ε − 1+ 2 E ε + s 0 ε 0
σ 11 σ 12 σ 13 σ x τ xy τ xz = τ σ ij = σ σ σ σ τ 22 23 y yz yz 21 σ 31 σ 32 σ 33 τ zx τ zy σ z
ቤተ መጻሕፍቲ ባይዱ
2) 应力不变量
(σ
ij
− σδ ij ) n j = 0
表层下30mm电镜图
1、混凝土力学性能的微观机制
裂纹形成及过程区
• 混凝土力学性能的离散性
• 混凝土力学性能的离散性
•
混凝土单轴力学性能—循环加卸载
单轴应力-应变曲线是循环加载破坏的包 络曲线 加载应力低于50%fc,一般认为不会出 现疲劳破坏
If we unload in the stress range under 50 percent of fc ', the unloading curve exhibits slight nonlinearity. If reloading takes place, a small characteristic hysteresis loop is formed. However, for unloading from stress at above 50 percent of fc ', the unloading-reloading curves exhibit strong nonlinearity, and a significant degradation of stiffness can also be observed.
塑性力学 第二章 应力状态与应变状态
c 平均应力为 m 3 因此,在与 平面平行的平面上的各点 表示了这样一些点的应力状态,即它们具有 相同的弹性体积变形。
26
§2-6 应变张量及其分解 一、应变与位移的关系 1 1、小变形情况 ij ui , j u j ,i 2 2、大变形(有限变形)情况 设变形前的初始时刻t=0,物体内A点的坐 标为ai a1 , a2 , a3 ,经过变形后,在t时刻它移 到 A 。相对于同一坐标系的坐标为 xi x1, x2 , x3 变形前后的位置一一对应,可由 xi 的单值连续 函数表示 xi xi a j , t 。同样也可以表示为 a i 的 单值连续函数 ai ai x j , t 。
1 MP1 max ( 1 3 ) 2 MP2 MP 1P 2P 1
1 1 ( 1 3 ) 1 2 2 2 1 3 2 2
1925年Lode提出参数
20
MP2 2 2 1 3 2s2 s1 s3 MP 1 3 s1 s3 1
22
(1)应力空间中过原点并与坐标轴成等角的 直线L L直线的方程为 1 2 3 。该直线上 的点代表物体上承受静水应力的点。L直线上 的点所对应的应力状态将不产生塑性变形。 (2)应力空间中过原点而与L直线垂直的平 面—— 平面 平面的方程为 1 2 3 0 。该平面 上的所有点平均应力为零,只有应力偏张量, 因此这个平面也叫偏量平面。位于该平面上 的点对应于不引起体积变形的应力状态。
17
§2-5 三向应力圆 Lode应力参数 Haigh-Westergaard应力空间
一、三向应力圆
高等土力学02土的本构关系
3 oct
主应力空间与平面
第二章 土的本构关系
2.2 应力和应变 – 应力
仁者乐山 智者乐水
1 R
A
RQ:和之间 与2垂直
: PQ和RQ之间的夹角, 以PQ起逆时针为正
tg 2 2 1 3 3 ( 1 3 ) 3 2b 1 3
x2 x2
x1
x1 x 3
x3
i k , jl 与为新和原坐标系轴夹角的余弦
其中,a11=cos ,a12=cos , a13=cos
主应力:1,2,3在三个剪应力为零方向上的正应力
应力张量的坐标转换与主应力
第二章 土的本构关系
2.2 应力和应变 – 应力
• 剪应力q:平面上到Q距离PQ
• 洛德角:平面上的角度
三个独立的应力参数P、q和可以确 定应力点P在应力空间的位置
常用的三个应力不变量
第二章 土的本构关系
2.2 应力和应变 – 应力
仁者乐山 智者乐水
三轴应力状态: 3
• 平均主应力 • 广义剪应力
1 1 p (1 2 3 ) (1 23 ) 3 3
第二章 土的本构关系
2.2 应力和应变 – 应力
仁者乐山 智者乐水
6个独立变量用 矩阵表示,常用 于数值计算
x y z = xy yz zx
应力分量与应力张量
第二章 土的本构关系
2.2 应力和应变 – 应力
球应力张量与偏应力张量
第二章 土的本构关系
2.2 应力和应变 – 应力
仁者乐山 智者乐水
z
C 等倾面
3 2
z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
论,同样与双剪应力和双剪应变相关。
由此可见双剪概念内涵的丰富性。基于正交八
面体应力空间建立强度理论是一种新的思想,与基于
等倾八面体应力空间的歪形能强度理论有着类似的
思路,但假设的材料破坏面不同,即在一定的应力作
用下的连续变形,当发生最大剪切破坏时的临界单元
体状态是不同的。俞茂宏根据这种临界单元体每一
第四强度理论:该强度理论广泛应用于具有相同 拉伸屈服应力和压缩屈服应力的金属材料。通常也 称为歪形能强度理论(Huber,1904,Henchky,1925, Mises 准则,1913),或等倾八面体剪应力屈服准则 (Ros-Eichinger,1949,Nadai,1931),有时也称为 J2 理论(应力偏量张量的第二不变量),剪应变能理论, 等效应力准则(有效应力或等效应力 e)。Novozhilov (1952)、俞茂宏(1962)和 Pau(l 1968)等分别从统计 平均剪应力 m、均方根剪应力 123 和平方主应力差等 都推导出了相同的结果,沈珠江(1995)则称其为三剪 强度理论,或者称八面体强度理论(J.Wastiels 曾讨论 了混凝土在等倾八面体上的强度模型,1982),P. S. Liu 等(1999,2000,2003)则建立了金属的八面体分析模 型[4]。
与非线性)问题,其理论基础就是 Hooke 定律和广义
Hooke 定律。而对于塑性问题,则主要有全量理论和
增量理论,但都与广义 Hooke 定律密切相关。其中
全量理论是研究材料的应力和全量应变之间的关系,
也称
(1943)-Hencky(1924)理论。在材料
力学和弹性力学中的广义 Hooke 定律,则是弹性范
8=
1+ 2+ 3
3=
(4a)
8=
1 3
(1
2)2+( 2
3)2+( 3
)2
1
(4b)
通过变换,等倾八面体应力与双剪应力的关系
为:
33
+ + 13 12
23 =1 =1( < )
= 3 = 3 8
(5a)
8=
2 3
+ 2
13
+ 2
12
= 2
23
2 3
33
2 (5b)
=1 =1( < )
同样,应力张量的不变量与双剪应力有如下关系
(1. 武汉工业学院 土木工程系,湖北 武汉 430023;2.中国石化集团 河南石油工程研究院,河南 南阳 473132)
摘 要:正交八面体和等倾八面体是广义八面体理论体系中的两个重要的特征单元体,由此产
生的正交八面体理论、以及弹塑性理论中的等倾八面体理论,都是广义八面体理论体系中的重
要组成部分;正交八面体理论则是基于 Mohr-Coulom 理论、弹塑性理论和双剪理论所提出的。
以及 20 世纪的双剪统一强度理论(俞茂宏, 1961~至今,统一强度理论,俞茂宏统一强度理论,广 义双剪强度理论):俞茂宏(1961)定义了双剪应力概 念和双剪单元体(以正交八面体为基础,即以三组 45° 最大剪切破坏面所围成的单元体),并由此建立了一 种全新的强度理论体系。
2 正交八面体强度理论[2]
33
1= 1+ 2+ 3=3 = + 13 + 12 = 23 =1 =1( < )
= + + = + + 2
12
23
31
1 23
2 13
3
33
= =1 =1( < )
( +1)( +1)
(6)
12
(7)
2=
1 6
(
1
2)2 +( 2 3)2 +( 3
=
2( 3
+ 2
13
+ 2
12
223)=
2 3
33 2
收稿日期:2007-05-14 基金项目:湖北省高等学校中青年创新团队基金资助项目(T200604)。 作者简介:黄辉(1980- ),男,河南省信阳市人,研究生。
98
武汉工业学院学报
2007 年
主的情况下才可能发生,因此修正为最大拉应力理 论,而且适于脆性材料以拉应力为主的情况。
第二强度理论(最大应变理论,最大伸长线应力 理论):Mariotte(1620~1684)曾对这一理论作了首次 论述。主要以出现塑性屈服或发生显著的塑性变形 作为破坏标志,适于脆性材料以压应力为主的情况。 由于该理论不如第一强度理论在应用上的方便,因此 在工程实践中很少应用,但在某些工业部门,如炮筒 设计中则应用较为广泛。
=1 =1( < )
)2
1
(8)
3 = 1 2 3 = 217( + 13 12)( + 21 23)( + 31 ) 32
=
1 27
3
(
= 1, = 1( )
+ ) ( + 1)
(9)
注:当 +1 > 3时,取 2值;当 +1 > 3时,取
2值。
在研究材料的强度同时,若同时考虑材料的变形
问题,也就是本构关系,则对于弹性或超弹性(含线性
(2b) (2c)
/ = 12( ± ) ,=1,2,3( )(3)
注:等式左边斜线左右项分别与等式右边“+”、“-”号相一 致,即分别表示正应力和主切应力表达式。
正交八面单元体上的双剪应力(双剪主切应力与 双剪正应力)和普通单元体上的主应力具有良好的相 关性[5],通过对应力 Lode 参数和应变 Lode 参数的变 换,可解释应力与应变 Lode 参数的物理意义。假定 双剪应力可以作为独立的变量,那么可对双剪应力进 行一系列的变换,由此可发现双剪应力蕴含有中间主 应力和静水应力效应(同样,应变也具有类似的结 果);而通过双剪应力状态参数的变化,可对应力状态 进行划分,并可以是反映中间主应力 效应的参数。根 据弹性理论,有:
是相似的。而在理想弹塑性材料的 Hencky可以表示为双剪
应力和双剪应变函数。
而增量理论(流动理论)中的理想刚塑性材料的
Le′vy(1870)-Mises 理论,同样可以反映双剪应力和
双剪应变。而在 Le′vy-Mises 理论基础上发展起来
的理想弹塑性材料的 Prandt(l 1925)-Reuss(1930)理
由于正交八面体的对称性和任意一个面与其中一个直角坐标轴相平行的特点,以及与应力和应
变 Lode 参数、静水应力与中间主应力、体积应变与中间主应变密切相关等特点,因此具有丰富
内涵;并据此可建立多轴特征强度参数方程和任意加载方式下的多轴极限强度模型等新的理论
模型,以及根据应力—应变关系可将一些空间问题转换为平面问题等。
的,继 1985 年建立了双剪强度理论[7],1991 年建立的
统一强度理论[8],此后经 40 余年之精力,系统地建立
了双剪理论体系[9],并得到了国内外众多知名学者的
高度评价和广泛应用。
在双剪统一强度理论之前,各种屈服准则和破坏
准则都是单一准则,它们无论是力学模型或数学表达
式都是分散的,相互之间没有定量的联系。双剪理论
第 26 卷第 4 期 420期07 年 12 月
武汉工业学院学报 Journal of Wuhan Polytechnic University
文章编号:1009-4881(2007)04-0097-05
Vol. 26No. 4
Dec. 290707
正交八面体应力空间的强度理论综述
黄 辉 1,杨正浩 2,段文付 1,刘建军 1
的特征过渡单元体,并且连续八面体可由正交八面体 进行表征;同时也得到了多轴特征强度参数的相互关 系方程和任意加载方式下的多轴极限强度等许多模 型 [2]。由于正交八面体的对称性及任意一个面与其 中一个直角坐标轴相平行的特点,由此将得到许多新 的发现,如应力和应变 Lode 参数、静水应力与中间 主应力、体积应变与中间主应变密切相关等。因此, 正交八面体理论具有丰富的内涵和外延,值得深入研 究。
围内的应力和全量应变之间的关系,弹塑性变形的全
量理论可作为广义 Hooke 定律在弹性范围中的推广,
两者在表达形式上也是十分相似的。其中
理论是全量理论中最简单的一种理论,其小弹塑性理
论则是双剪应力和双剪应变的函数,而广义 Hooke 定
律则是
理论的一个特例,或者说全量理论
是较弹性理论更为一般性的理论,两者在表达式上也
关键词:强度理论;广义八面体理论;双剪强度理论;正交八面体;等倾八面体
中图分类号:O 346;TU 318
文献标识码:A
0 引言
材料强度是保证各种工程结构安全使用的一个 最为重要的基本条件,而强度理论则是研究材料在复 杂应力状态下屈服或破坏(疲劳、蠕变等)的规律,并 为相关工程结构设计提供强度设计的计算准则。而 一个合理又恰当的理论模型,则可提高工程的质量和 耐久性,节约材料等,并由此带来巨大的经济效益和 社会效益 [1]。因此寻找一个合理而又恰当的强度理 论模型,一直是众多学者和工程技术人员的共同目 标。20 世纪出现了建立在正交八面体基础之上的双 剪统一强度理论,它包含了以前的屈服准则、破坏模 型,其他一些光滑准则或实验准则可作为其特例或线 性逼近;它从理论上将各种线性强度理论统一了起 来;但也并非能做到真正的统一,同时也存在一些漏 洞与不足[2]。杨健辉(2007)根据 Mohr-Coulom 理论、 弹塑性理论和双剪理论提出并建立了广义八面体理 论体系,也建立了正交八面体理论,其中,等倾八面体 和正交八面体是连续八面体理论体系中的两个重要
第三强度理论(最大切应力强度理论,Tresca 屈 服准则,1864):它采用了三个主应力中的两个,但忽 略了中间主应力。由于第三强度理论是 Mohr-Coulomb(以下简称 M-C 理论或屈服准则)理论的特例, 因此也可统称为单剪强度理论。
