托勒密定理的证明过程
托勒密定理
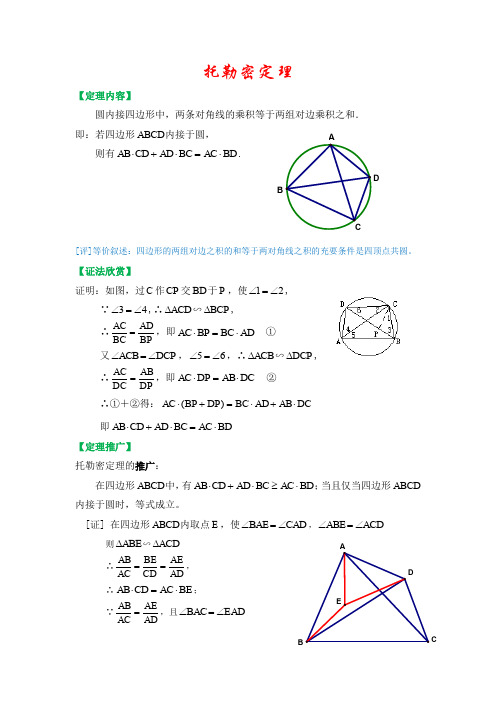
托勒密定理【定理内容】圆内接四边形中,两条对角线的乘积等于两组对边乘积之和. 即:若四边形ABCD 内接于圆,则有BD AC BC AD CD AB ⋅=⋅+⋅.[评]等价叙述:四边形的两组对边之积的和等于两对角线之积的充要条件是四顶点共圆。
【证法欣赏】证明:如图,过C 作CP 交BD 于P ,使21∠=∠,∵43∠=∠,∴ACD ∆∽BCP ∆, ∴BPAD BC AC =,即AD BC BP AC ⋅=⋅ ① 又DCP ACB ∠=∠,65∠=∠,∴ACB ∆∽DCP ∆, ∴DP AB DC AC =,即DC AB DP AC ⋅=⋅ ② ∴①+②得:DC AB AD BC DP BP AC ⋅+⋅=+⋅)(即BD AC BC AD CD AB ⋅=⋅+⋅【定理推广】托勒密定理的推广:在四边形ABCD 中,有BD AC BC AD CD AB ⋅≥⋅+⋅;当且仅当四边形ABCD 内接于圆时,等式成立。
[证] 在四边形ABCD 内取点E ,使CAD BAE ∠=∠,ACD ABE ∠=∠则ABE ∆∽ACD ∆ ∴ADAE CD BE AC AB ==, ∴BE AC CD AB ⋅=⋅; ∵ADAE AC AB =,且EAD BAC ∠=∠D BB C∴ABC ∆∽AED ∆ ∴ADED AC BC =,即ED AC BC AD ⋅=⋅; ∴)(ED BE AC BC AD CD AB +⋅=⋅+⋅∴BD AC BC AD CD AB ⋅≥⋅+⋅当且仅当E 在BD 上时“=”成立,即四点共圆时成立;、、、当且仅当D C B A【定理推广】托勒密定理的推论:等腰梯形一条对角线的平方等于一腰的平方加上两底之积. 即:若四边形ABCD 是等腰梯形,且BC AD //,则BC AD AB AC ⋅+=22.分析:因为等腰梯形必内接于圆,符合托勒密定理的条件,其对角线相等,两腰相等,结论显然成立。
【定理应用】【例1】 如图,P 是正ABC ∆外接圆的劣弧BC 上任一点(不与B 、C 重合),求证:PC PB PA +=.证明:由托勒密定理得: AB PC AC PB BC PA ⋅+⋅=⋅∵CA BC AB ==∴PC PB PA +=. [注]此例证法甚多,如“截长”、“补短”等,详情参看《初中数学一题多解欣赏》.【定理应用】【例2】 证明“勾股定理”:已知:在ABC Rt ∆中,︒=∠90B ,求证:222BC AB AC +=。
广义托勒密定理证明过程

广义托勒密定理证明过程嘿,朋友们!今天咱来聊聊广义托勒密定理的证明过程,这可有意思啦!你看啊,广义托勒密定理就像是一个神秘的宝藏,等着我们去挖掘它的奥秘。
那什么是广义托勒密定理呢?简单来说,就是在一个四边形中,两条对角线的乘积小于等于两组对边乘积之和。
这就好像是在说,一个团队里,大家齐心协力产生的力量不会小于各自为政的力量总和。
那怎么证明它呢?咱就一步一步来。
就好比爬山,一步一个脚印,总能爬到山顶。
我们先假设这个四边形的四条边分别为 a、b、c、d,对角线为e 和 f。
然后呢,我们可以通过一些巧妙的几何变换和等式推导来逐步接近真理。
比如说,我们可以把这个四边形分成两个三角形,然后利用三角形的一些性质来找到线索。
这就跟破案似的,一点点蛛丝马迹都不能放过!通过对这些三角形的研究,我们能发现一些隐藏的关系,就像在黑暗中突然找到了一盏明灯。
然后呢,我们再把这些关系组合起来,就像拼图一样,慢慢地,广义托勒密定理的真相就会浮现出来。
这过程是不是很神奇?就好像变魔术一样,一点点地揭示出神奇的结果。
你说这广义托勒密定理难不难?其实啊,只要有耐心,一点都不难。
就像骑自行车,刚开始可能会摇摇晃晃,但练着练着就熟练了。
我们在证明的过程中,会遇到各种各样的小问题,但别怕,一个一个解决掉它们,最后就能成功啦!想象一下,如果没有广义托勒密定理,我们的几何世界会变得多么无趣啊!它就像是几何大厦的一块重要基石,没有它,整个大厦都会摇摇欲坠呢!所以啊,我们可得好好珍惜这个定理,好好研究它的证明过程。
反正我觉得吧,广义托勒密定理的证明过程就像是一场奇妙的冒险,充满了挑战和惊喜。
朋友们,你们也快来加入这场冒险吧,一起感受几何的魅力!这就是广义托勒密定理的证明过程,是不是很有趣呢?让我们一起在几何的海洋中畅游吧!。
平面几何的几个重要定理--托勒密定理2
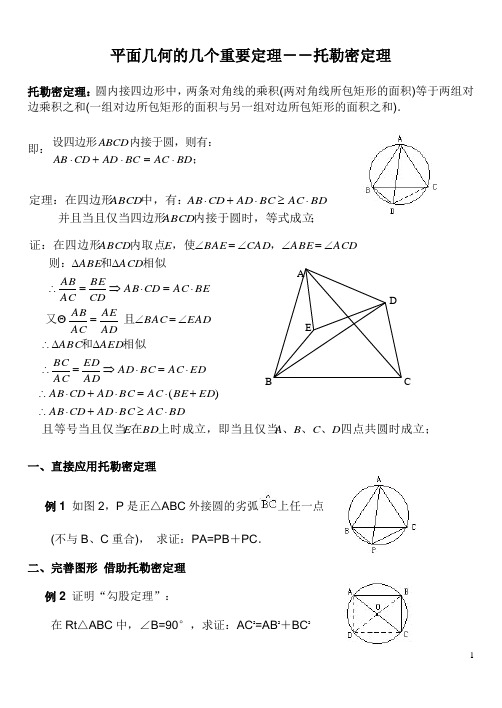
1平面几何的几个重要定理--托勒密定理托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和). 即:;内接于圆,则有:设四边形BD AC BC AD CD AB ABCD ⋅=⋅+⋅;内接于圆时,等式成立并且当且仅当四边形中,有:定理:在四边形ABCD BDAC BC AD CD AB ABCD ⋅≥⋅+⋅一、直接应用托勒密定理例1 如图2,P 是正△ABC 外接圆的劣弧上任一点(不与B 、C 重合), 求证:PA=PB +PC .二、完善图形 借助托勒密定理例2 证明“勾股定理”:在Rt △ABC 中,∠B=90°,求证:AC 2=AB 2+BC 2四点共圆时成立;、、、上时成立,即当且仅当在且等号当且仅当相似和且又相似和则:,,使内取点证:在四边形D C B A BD E BDAC BC AD CD AB ED BE AC BC AD CD AB EDAC BC AD AD EDAC BC AED ABC EAD BAC AD AE AC AB BEAC CD AB CD BEAC AB ACD ABE ACDABE CAD BAE E ABCD ⋅≥⋅+⋅∴+⋅=⋅+⋅∴⋅=⋅⇒=∴∆∆∴∠=∠=⋅=⋅⇒=∴∆∆∠=∠∠=∠)(2 例3 如图,在△ABC 中,∠A 的平分 线交外接∠圆于D ,连结BD ,求证:AD ·BC=BD(AB +AC).三、构造图形 借助托勒密定理例4 若a 、b 、x 、y 是实数,且a 2+b 2=1,x 2+y 2=1.求证:ax +by ≤1.四、巧变原式 妙构图形,借助托勒密定理例5 已知a 、b 、c 是△ABC 的三边,且a 2=b(b +c),求证:∠A=2∠B .五、巧变形 妙引线 借肋托勒密定理例6 在△ABC 中,已知∠A ∶∠B ∶∠C=1∶2∶4,练习:1.已知△ABC 中,∠B=2∠C 。
初中托勒密定理

初中托勒密定理初中托勒密定理托勒密定理是初中数学中的一个重要定理,它是由古希腊数学家托勒密发现的,因此得名。
该定理是关于四边形的一个定理,它表明,如果一个四边形的两条对角线相交于一点,那么这个四边形的两组对边乘积之和相等。
具体来说,设四边形ABCD的对角线AC和BD相交于点O,那么有以下公式:AB × CD + BC × AD = AC × BD其中,AB、BC、CD、AD分别表示四边形ABCD的四条边的长度,AC和BD分别表示四边形ABCD的两条对角线的长度。
托勒密定理的证明可以通过几何方法和代数方法来完成。
其中,几何方法是通过构造一些辅助线来证明该定理的,而代数方法则是通过将四边形的顶点坐标表示成复数来证明该定理的。
托勒密定理在初中数学中的应用非常广泛,它可以用来解决各种几何问题,例如求解四边形的面积、判断四边形是否为正方形等。
此外,托勒密定理还可以用来证明勾股定理和正弦定理等其他重要定理。
总之,托勒密定理是初中数学中的一个重要定理,它不仅具有理论意义,而且在实际应用中也有着广泛的应用。
因此,学生们应该认真学习和掌握该定理,以便在以后的学习和工作中能够灵活运用。
排版格式:初中托勒密定理托勒密定理是初中数学中的一个重要定理,它是由古希腊数学家托勒密发现的,因此得名。
该定理是关于四边形的一个定理,它表明,如果一个四边形的两条对角线相交于一点,那么这个四边形的两组对边乘积之和相等。
具体来说,设四边形ABCD的对角线AC和BD相交于点O,那么有以下公式:AB × CD + BC × AD = AC × BD其中,AB、BC、CD、AD分别表示四边形ABCD的四条边的长度,AC和BD分别表示四边形ABCD的两条对角线的长度。
托勒密定理的证明可以通过几何方法和代数方法来完成。
其中,几何方法是通过构造一些辅助线来证明该定理的,而代数方法则是通过将四边形的顶点坐标表示成复数来证明该定理的。
圆的托勒密定理怎么证明

圆的托勒密定理怎么证明托勒密定理,这名字听上去是不是有点儿高深莫测,仿佛只要你一听就得戴上眼镜,严肃地看着黑板。
但它可没那么复杂,反倒有点儿像是那种老朋友,咱们慢慢聊聊,看看它的背后故事。
想象一下,一个圆,里面有四个点,像是朋友们围坐在一起,聊着天,特别热闹。
这个时候,托勒密定理就闪亮登场,告诉我们,只要这四个点在同一个圆上,它们之间的连线关系就特别有意思。
你瞧啊,托勒密定理说的是,两个对角线的乘积等于另外两个对角线的乘积。
哎,听起来好像在说数学魔法,实际上就像是说,如果你有了这些朋友,这些连线就像是你们的感情纽带,越紧密,越有趣。
想象一下,把四个点连起来,就形成了两个三角形。
这个时候,两个三角形就好比是你和朋友们在玩游戏,玩得不可开交。
四个点的坐标,像极了你们生活中的四个重要时刻,连接起来,便是回忆的画面。
来,咱们用一个小故事来帮大家理解。
假设你们四个好朋友,分别叫A、B、C、D。
一天,你们一起去公园散步,A跟C走在一边,B跟D走在另一边。
突然间,A和C决定要赛跑,B和D则在旁边加油。
这个时候,A和C的距离和B和D的距离,就像是托勒密定理里的对角线一样,你们的友情也在这场比赛中得到了验证。
四个人的相互关系,仿佛在圆的边缘上,划出了一道优美的弧线,大家心里都明白,这就是友情的力量。
再说到证明的过程,可能会有人说:“哎,数学就是个难题,听着就头疼。
”证明托勒密定理并不是一件可怕的事,反倒像是在解开一个谜团。
可以试着把四个点连成一张网,然后找出那些能组成三角形的角度。
你会发现,角度之间的关系和弦长之间的比例,就像你们在一起时的默契,越是密切,结果越是惊人。
说到这里,不妨聊聊生活中的例子。
想象你跟朋友一起聚餐,四个人围坐一桌,桌子就像是那个圆。
每个人的盘子、碗碟就像是四个点,边吃边聊,开心得不得了。
这时候,你们的对话就像是对角线,不同的意见交织在一起,形成了一种和谐的气氛。
虽然每个人都有自己的看法,但只要互相理解,最后就能达成共识,这不就和托勒密定理的精神不谋而合吗?好了,聊了这么多,大家有没有觉得托勒密定理其实挺有趣的?在生活中,处处都有这样的“定理”。
托勒密定理的多种证明及其应用例谈

托勒密定理的多种证明及其应用例谈
作者:陶布
来源:《学校教育研究》2016年第03期
托勒密定理是初等几何的一个经典命题,它以具有十分广泛的应用而著称,托勒密定理描述的是圆内接四边形的性质,利用它可以解决与圆有关的几何命题,也可以通过构造圆解决代数问题,本文主要通过对托勒密定理的研究,从不同的角度给出了七种证法,并着重研究了托勒密定理的应用,以凸显托勒密定理在解决有关几何命题的作用。
一、托勒密定理及其证明
托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边乘积之和。
1.预备知识
引理一(西姆松定理):三角形外接圆上任意一点在三边所在直线上的射影点共线。
引理二(西姆松定理的逆定理):若一个点在三角形三边所在直线上的射影点共线,则该点在此
三角形的外接圆上。
模型27 托勒密定理(原卷版)-2023年中考数学重难点解题大招复习讲义-几何模型篇

模型介绍1.托勒密定理:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和.翻译:在四边形ABCD 中,若A 、B 、C 、D 四点共圆,则AC BD AB CD AD BC ⋅=⋅+⋅.证明:在线段BD 上取点E ,使得∠BAE =∠CAD ,易证△AEB ∽△ADC ,∴AB BE AC CD=,即AC BE AB CD ⋅=⋅,当∠BAE =∠CAD 时,可得:∠BAC =∠EAD ,易证△ABC ∽△AED ,∴AD DE AC CB=,即AC DE AD BC ⋅=⋅,∴AC BE AC DE AB CD AD BC ⋅+⋅=⋅+⋅,∴AC BD AB CD AD BC ⋅=⋅+⋅.2.(托勒密不等式):对于任意凸四边形ABCD ,有AC BD AB CD AD BC ⋅≤⋅+⋅证明:如图1,在平面中取点E 使得∠BAE =∠CAD ,∠ABE =∠ACD ,易证△ABE ∽△ACD ,∴AB BE AC CD=,即AC BE AB CD ⋅=⋅①,连接DE ,如图2,∵AB AE AC AD =,∴AB AC AE AD=,又∠BAC =∠BAE +∠CAE =∠DAC +∠CAE =∠DAE ,∴△ABC ∽△AED ,∴AD DE AC BC=,即AC DE AD BC ⋅=⋅②,将①+②得:AC BE AC DE AB CD AD BC ⋅+⋅=⋅+⋅,∴()AC BD AC BE DE AB CD AD BC⋅≤⋅+=⋅+⋅即AC BD AB CD AD BC ⋅≤⋅+⋅,当且仅当A 、B 、C 、D 共圆时取到等号.3.托勒密定理在中考题中的应用(1)当△ABC 是等边三角形时,如图1,当点D 在弧AC 上时,根据托勒密定理有:DB AC AD BC AB CD ⋅=⋅+⋅,又等边△ABC 有AB =AC =BC ,故有结论:DB DA DC =+.证明:在BD 上取点E 使得DE =DA ,易证△AEB ∽△ADC ,△AED ∽△ABC ,利用对应边成比例,可得:DB DA DC =+.如图2,当点D 在弧BC 上时,结论:DA =DB +DC .【小结】虽然看似不同,但根据等边的旋转对称性,图1和图2并无区别.(2)当△ABC是等腰直角三角形,如图3,当点D在弧BC上时,根据托勒密定理:AD BC AB CD AC BD⋅=⋅+⋅,又::1:1:2=+.AB AC BC=,代入可得结论:2AD BD CD如图4,当点D在弧AC上时,根据托勒密定理:AD BC AB CD AC BD⋅=⋅+⋅,又::1:1:2=+.BD AD CDAB AC BC=,代入可得结论:2(3)当△ABC是一般三角形时,若记BC:AC:AB=a:b:c,⋅=⋅+⋅根据托勒密定理可得:a AD b BD c CD例题精讲【例1】.如图,正五边形ABCDE内接于⊙O,AB=2,则对角线BD的长为.变式训练【变式1-1】.先阅读理解:托勒密(Ptolemy古希腊天文学家)定理指出:圆内接凸四边形两组对边乘积的和等于两条对角线的乘积.即:如果四边形ABCD内接于⊙O,则有AB•CD+AD•BC=AC•BD.再请完成:(1)如图1,四边形ABCD内接于⊙O,BC是⊙O的直径,如果AB=AC=,CD=1,求AD的长.(2)在(1)的条件下,如图2,设对边BA、CD的延长线的交点为P,求PA、PD的长.【变式1-2】.如图1,已知⊙O内接四边形ABCD,求证:AC•BD=AB•CD+AD•BC.证明:如图1,在BD上取一点P,连接CP,使∠PCB=∠DCA,即使∠1=∠2.∵在⊙O中,∠3与∠4所对的弧都是,∴∠3=∠4.∴△ACD∽△BCP.∴=.∴AC•BP=AD•BC.①又∵∠2=∠1,∴∠2+∠7=∠1+∠7.即∠ACB=∠DCP.∵在⊙O中,∠5与∠6所对的弧都是,∴∠5=∠6.∴△ACB∽△DCP.…(1)任务一:请你将“托勒密定理”的证明过程补充完整;(2)任务二:如图2,已知Rt△ABC内接于⊙O,∠ACB=90°,AC=6,BC=8,CD 平分∠ACB交⊙O于点D,求CD的长.【例2】.托勒密定理:圆的内接四边形两对对边乘积的和等于两条对角线的乘积.已知:如图1,四边形ABCD内接于⊙O.求证:AB⋅DC+AD⋅BC=AC⋅BD.证明:如图2,作∠BAE=∠CAD,交BD于点E,……∴△ABE∽△ACD,∴AB•DC=AC•BE,……∴△ABC∽△AED,∴AD•BC=AC•ED,∴AB•DC+AD•BC=AC•BE+AC•ED=AC(BE+ED)=AC•BD.(1)请帮这位同学写出已知和求证,并完成证明过程;(2)如图3,已知正五边形ABCDE内接于⊙O,AB=1,求对角线BD的长.变式训练【变式2-1】.已知:如图1,四边形ABCD内接于⊙O.求证:AB•CD+BC•AD=AC•BD下面是该结论的证明过程:证明:如图2,作∠BAE=∠CAD,交BD于点E.∵=,∠ABE=∠ACD,∴△ABE∽△ACD,∴,∴AB•CD=AC•BE;∵=,∴∠ACB=∠ADE(依据1),∵∠BAE=∠CAD,∴∠BAC=∠EAD,∴△ABC∽△AED(依据2),∴,∴AD•BC=AC•ED;∴AB•CD+AD•BC=AC•(BE+ED),即AB•CD+BC•AD=AC•BD.(1)上述证明过程中的“依据1”是指;“依据2”是指.(2)当圆内接四边形ABCD是矩形时,托勒密定理就是我们熟知的定理.(3)如图3,四边形ABCD内接于⊙O,AB=3,AD=5,∠BAD=60°,点C是的中点,求AC的长.【变式2-2】.圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.即:如图1,若四边形ABCD内接于⊙O,则有________.任务:(1)材料中划横线部分应填写的内容为.(2)已知,如图2,四边形ABCD内接于⊙O,BD平分∠ABC,∠COD=120°,求证:BD=AB+BC.1.如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,对角线交于点O,连接AO,如果AB=4,AO=4,那么AC的长等于()A.12B.16C.4D.82.如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD 的中点,则AC的长是.3.如图,在等腰△ABC中,AB=AC=4,BC=6,点D在底边BC上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为.4.如图,P是正方形ABCD内一点,CP=CD,AP⊥BP,则的值为.5.如图,正方形ABCD的边长是6,对角线的交点为O,点E在边CD上且CE=2,CF⊥BE,连接OF,则:(1)∠OFB°;(2)OF=.6.如图,在Rt△ABC中,∠BAC=90°,D为BC的中点,过点D作DE⊥DF,交BA的延长线于点E,交AC的延长线于点F.若CF=,AC=4,AB=2.则AE=.7.设△ABC是正三角形,点P在△ABC外,且与点A在直线BC异侧,∠BPC=120°,求证:PA=PB+PC.8.⊙O半径为2,AB,DE为两条直线.作DC⊥AB于C,且C为AO中点,P为圆上一个动点.求2PC+PE的最小值.9.如图,点P为等边△ABC外接圆,劣弧为BC上的一点.(1)求∠BPC的度数;(2)求证:PA=PB+PC.10.如图,⊙O的直径AB的长为10,弦BD的长为6,点C为上的一点,过点B的切线EF,连接AD,CD,CB;(1)求证:∠CDB=∠CBF;(2)若点D为的中点,求CD的长.11.阅读下列材料,并完成相应的任务.托勒密定理:托勒密(Ptolemy)(公元90年~公元168年),希腊著名的天文学家,他的要著作《天文学大成》被后人称为“伟大的数学书”,托勒密有时把它叫作《数学文集》,托勒密从书中摘出并加以完善,得到了著名的托勒密(Ptolemy)定理.托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边乘积之和.已知:如图1,四边形ABCD内接于⊙O,求证:AB•CD+BC•AD=AC•BD下面是该结论的证明过程:证明:如图2,作∠BAE=∠CAD,交BD于点E.∵∴∠ABE=∠ACD∴△ABE∽△ACD∴∴AB•CD=AC•BE∵∴∠ACB=∠ADE(依据1)∵∠BAE=∠CAD∴∠BAE+∠EAC=∠CAD+∠EAC即∠BAC=∠EAD∴△ABC∽△AED(依据2)∴AD•BC=AC•ED∴AB•CD+AD•BC=AC•(BE+ED)∴AB•CD+AD•BC=AC•BD任务:(1)上述证明过程中的“依据1”、“依据2”分别是指什么?(2)当圆内接四边形ABCD是矩形时,托勒密定理就是我们非常熟知的一个定理:.(请写出)(3)如图3,四边形ABCD内接于⊙O,AB=3,AD=5,∠BAD=60°,点C为的中点,求AC的长.12.在学习了《圆》和《相似》的知识后,小明自学了一个著名定理“托勒密定理:圆内接四边形对角线的乘积等于两组对边乘积之和.”(1)下面是小明对托勒密定理的证明和应用过程,请补充完整.已知:四边形ABCD内接于⊙O.求证:AC•BD=AB•CD+AD•BC.证明:作∠CDE=∠BDA,交AC于点E,∵⊙O中,∠1=∠2,∴△ABD∽△ECD().∴.∴AB•CD=BD•EC①,.又∵∠BDA+∠3=∠CDE+∠3,即∠ADE=∠BDC,∴△DAE∽△DBC().∴.∴AD•BC=BD•AE②.,∴AB•CD+AD•BC=AC•BD.(2)利用托勒密定理解决问题:是否存在一个圆内接四边形,它的两条对角线长为5和,一组对边长为1和3,另一组对边的和为4.若存在,求出未知的两边;若不存在,说明理由.13.阅读下列相关材料,并完成相应的任务.布拉美古塔定理婆罗摩笈多是古印度著名的数学家、天文学家,他编著了《婆罗摩修正体系》,他曾经提出了“婆罗摩笈多定理”,也称“布拉美古塔定理”.定理的内容是:若圆内接四边形的对角线互相垂直,则垂直于一边且过对角线交点的直线平分对边.某数学兴趣小组的同学写出了这个定理的已知和求证.已知:如图,在圆内接四边形ABCD中,对角线AC⊥BD,垂足为P,过点P作AB的垂线分别交AB,DC于点H,M.求证:M是CD的中点任务:(1)请你完成这个定理的证明过程.(2)该数学兴趣小组的同学在该定理的基础上写出了另外一个命题:若圆内接四边形的对角线互相垂直,则一边中点与对角线交点的连线垂直于对边请判断此命题是命题.(填“真”或“假”)(3)若PD=2,HP=,BP=3,求MH的长.14.已知△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,连接DB,DC.(1)如图①,当∠BAC=120°时,请直接写出线段AB,AC,AD之间满足的等量关系式:;(2)如图②,当∠BAC=90°时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;(3)如图③,若BC=5,BD=4,求的值.15.问题探究:(1)已知:如图①,△ABC中请你用尺规在BC边上找一点D,使得点A到点BC的距离最短.(2)托勒密(Ptolemy)定理指出,圆的内接四边形两对对边乘积的和等于两条对角线的乘积.如图②,P是正△ABC外接圆的劣弧BC上任一点(不与B、C重合),请你根据托勒密(Ptolemy)定理证明:PA=PB+PC.问题解决:(3)如图③,某学校有一块两直角边长分别为30m、60m的直角三角形的草坪,现准备在草坪内放置一对石凳及垃圾箱在点P处,使P到A、B、C三点的距离之和最小,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离(结果保留根号);若不存在,请说明理由.16.(1)方法选择如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD =AD+CD.小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…小军认为可用补短法证明:延长CD至点N,使得DN=AD…请你选择一种方法证明.(2)类比探究【探究1】如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,并证明你的结论.【探究2】如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD之间的等量关系式是.(3)拓展猜想如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是.17.数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB =∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.18.问题背景:如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE=CD,从而得出结论:AC+BC=CD.简单应用:(1)在图①中,若AC=,BC=2,则CD=.(2)如图③,AB是⊙O的直径,点C、D在⊙上,=,若AB=13,BC=12,求CD的长.拓展规律:(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD 的长(用含m,n的代数式表示)(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE=AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是或.。
欧拉定理 直线上的托勒密定理

欧拉定理欧拉定理是数学领域的一项重要定理,它在数论和代数领域具有广泛的应用。
这一定理由瑞士数学家欧拉在18世纪提出,是数学史上的重要里程碑之一。
欧拉定理提出了一种关于数论中幂运算的模运算的特殊情况的性质。
它的表述非常简洁,但却蕴含了深刻的数学内涵,对当今数学研究和应用都有着重要的影响。
欧拉定理的表述欧拉定理的表述如下:如果a和n是两个正整数,且它们互质(即它们的最大公约数为1),那么a与n的欧拉函数值φ(n)对n取模所得的结果,等于a的φ(n)次幂对n取模所得的结果。
即公式表达为:a^φ(n) ≡ 1 (mod n)视具体应用情况,这个公式的表述还可以有多种等价的形式。
当n为素数时,欧拉函数值φ(n)即为n-1,此时欧拉定理表述为:a^(n-1) ≡ 1 (mod n)欧拉定理推论欧拉定理的一个重要推论是费马小定理。
费马小定理是欧拉定理的一个特殊情况,即当n为素数时的情况。
费马小定理表述为:若p为素数,a为任一整数,且a与p互质,则a^(p-1) ≡ 1 (mod p)。
从费马小定理可以看出,欧拉定理是费马小定理的一种推广,它适用于更广泛的情况,包括了n为合数的情况。
欧拉定理的应用欧拉定理在密码学、数据传输等领域有重要应用。
在RSA公钥密码系统中,欧拉定理为RSA加密算法的安全性提供了数学基础。
另外,在数据传输的校验过程中,欧拉定理也可以用来检验数据的完整性和准确性。
欧拉定理的证明欧拉定理的证明源于欧拉对模运算和数论的深刻理解。
欧拉定理的证明虽然并不复杂,但需要涉及到一定的数论知识和初等数学的知识。
在证明过程中,需要运用到欧拉函数、模运算、同余关系等概念和定理。
对于初学者来说,欧拉定理的证明可能有一定的难度,但掌握了相关的数论知识之后,欧拉定理的证明也显得非常自然和简洁。
直线上的托勒密定理托勒密定理是古希腊数学中的一项重要定理,它研究了直角三角形中的几何关系,对三角学的发展有着重要的影响。
托勒密定理由古希腊数学家托勒密提出,其内容涉及到了平面几何和三角函数的性质,是古代几何学中的一项重要成果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
托勒密定理的证明过程
托勒密定理是一个关于四边形的定理,它可以描述四边形的四个顶点构成一个凸四边形的必要与充分条件。
设四边形的四个顶点分别为ABCD,边长分别为a,b,c,d,对角线交叉点为O。
则托勒密定理可以表示为:
AC² = BD² + AB² + CD² - 2 * AB * CD * cos(∠BAD)
要证明托勒密定理,我们可以利用向量和向量的内积的性质来推导。
首先,利用向量的加法和减法,将ABCD四边形分割成两个
三角形ABO和CDO:
1. AB = AO - BO
2. CD = CO - DO
接下来,我们可以利用向量的内积公式展开AB和CD的平方:
3. AB² = (AO - BO) · (AO - BO) = AO² + BO² - 2 * AO · BO *
cos(∠BAO)
4. CD² = (CO - DO) · (CO - DO) = CO² + DO² - 2 * CO · DO *
cos(∠CDO)
将上面的公式3和4代入托勒密定理的等式中,得到:
AC² = BD² + (AO² + BO² - 2 * AO · BO * cos(∠BAO)) + (CO² +
DO² - 2 * CO · DO * cos(∠CDO)) - 2 * AB * CD * cos(∠BAD)
接下来,我们可以利用向量的内积的性质展开其中的一些乘积项和∠BAO 和∠CDO 的关系:
5. AO · BO = AB² / 2
6. CO · DO = CD² / 2
7. cos(∠CDO) = -cos(∠BAO)
将公式5、6和7代入上述等式中,得到:
AC² = BD² + (AO² + BO² - AB²) + (CO² + DO² - CD²) + 2 * AB * CD * cos(∠BAO)
再次利用向量的内积和向量的长度平方之间的关系,可以得到:
8. AO² + BO² = AB²
9. CO² + DO² = CD²
将公式8和9代入上述等式中,得到:
AC² = BD² + 2 * AB * CD * cos(∠BAO)
最后,我们知道∠BAO 和∠BAD 是同一角度,即∠BAO =
∠BAD ,所以可以进一步得到:
AC² = BD² + 2 * AB * CD * cos(∠BAD)
这就是托勒密定理的证明过程。
