电磁场与电磁波课后习题及答案
电磁场与电磁波课后习题答案(杨儒贵编着)(第二版)全套

2-2 已知真空中有三个点电荷,其电量及位置分别为:)0,1,0( ,4 )1,0,1( ,1 )1,0,0( ,1332211P C q P C q P C q === 试求位于)0,1,0(-P 点的电场强度。
解 令321,,r r r 分别为三个电电荷的位置321,,P P P 到P 点的距离,则21=r ,32=r ,23=r 。
利用点电荷的场强公式r e E 204rq πε=,其中r e 为点电荷q 指向场点P 的单位矢量。
那么,1q 在P 点的场强大小为021011814πεπε==r q E ,方向为()z yr e ee +-=211。
2q 在P 点的场强大小为0220221214πεπε==r q E ,方向为()z y xr e e ee ++-=312。
3q 在P 点的场强大小为023033414πεπε==r q E ,方向为y r e e -=3则P 点的合成电场强度为⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+++-=++=z e e e E E E E y x 312128141312128131211 0321πε2-4 已知真空中两个点电荷的电量均为6102-⨯C ,相距为2cm , 如习题图2-4所示。
试求:①P 点的电位;②将电量为6102-⨯C 的点电荷由无限远处缓慢地移至P 点时,外力必须作的功。
解 根据叠加原理,P 点的合成电位为()V 105.24260⨯=⨯=rq πεϕ因此,将电量为C 1026-⨯的点电荷由无限远处缓慢地移到P 点,外力必须做的功为()J 5==q W ϕ2-6 已知分布在半径为a 的半圆周上的电荷线密度πφφρρ≤≤=0 ,sin 0l ,试求圆心处的电场强度。
解 建立直角坐标,令线电荷位于xy 平面,且以y 轴为对称,如习题图2-6所示。
那么,点电荷l l d ρ在圆心处产生的电场强度具有两个分量E x 和E y 。
由于电荷分布以y 轴为对称,因此,仅需考虑电场强度的y E 分量,即习题图2-4习题图2-6φπερsin 4d d d 20a lE E l y ==考虑到φρρφsin ,d d 0==l a l ,代入上式求得合成电场强度为y y aa e e E 0002008d sin 4ερφφπερπ==⎰2-12 若带电球的内外区域中的电场强度为⎪⎪⎩⎪⎪⎨⎧<>=a r aqr a r r q, ,2r e E 试求球内外各点的电位。
电磁场与电磁波(杨儒贵_版)课后思考题答案

电磁场与波课后思考题1-1 什么是标量与矢量?举例说明.仅具有大小特征的量称为标量.如:长度,面积,体积,温度,气压,密度,质量,能量及电位移等.不仅具有大小而且具有方向特征的量称为矢量.如:力,位移,速度,加速度,电场强度及磁场强度.1-2 矢量加减运算及矢量与标量的乘法运算的几何意义是什么?矢量加减运算表示空间位移.矢量与标量的乘法运算表示矢量的伸缩.1-3矢量的标积与矢积的代数定义及几何意义是什么? 矢量的标积: ,A 矢量的模与矢量B 在矢量A 方向上的投影大小的乘积.矢积: 矢积的方向与矢量A,B 都垂直,且 由矢量A 旋转到B,并与矢积构成右 旋关系,大小为1-4 什么是单位矢量?写出单位矢量在直角坐标中的表达式. 模为1的矢量称为单位矢量.1-5 梯度与方向导数的关系是什么?试述梯度的几何意义,写出梯度在直角坐标中的表示式.标量场在某点梯度的大小等于该点的最大方向导数, 方向为该点具有最大方向导数的方向.梯度方向垂直于等值面,指向标量场数值增大的方向在直角坐标中的表示式: 1-6 什么是矢量场的通量?通量值为正,负或零时分别代表什么意义?矢量A 沿某一有向曲面S 的面积分称为矢量A 通过该有向曲面S 的通量,以标量表示,即 通量为零时表示该闭合面中没有矢量穿过. 通量为正时表示闭合面中有源;通量为负时表示闭合面中有洞.1-7 给出散度的定义及其在直角坐标中的表示式. 散度:当闭合面S 向某点无限收缩时,矢量A 通过该闭合面S 的通量 与该闭合面包围的体积之比的极限称为矢量场A 在该点的散度。
直角坐标形式: 1-8 试述散度的物理概念,散度值为正,负或零时分别表示什么意义?物理概念:通过包围单位体积闭合面的通量。
散度为正时表示辐散,为负时表示辐合,为零时表示无能量流过.1-9 试述散度定理及其物理概念.散度定理:建立了区域 V 中的场和包围区域V 的闭合面S 上的场之间的关系θcos B A BA B A B A B A z z y y x x =++=⋅z y x z y x z y x B B B A A A e e e B A =⨯θsin B A e z θsin B A a e zy x e e e γβαcos cos cos ++=z y x e ze y e x ∂∂+∂∂+∂∂=∇⎰⋅=S S A Ψ d VS V Δd lim div 0Δ⎰⋅=→S A A zA y A x A A div z y x ∂∂+∂∂+∂∂= A ⋅∇=物理概念: 散度定理建立了区域 V 中的场和包围区域 V 的闭合面 S 上的场之间的关系。
电磁场与电磁波课后习题及答案六章习题解答

第六章时变电磁场有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场之中,如题图所示。
滑片的位置由确定,轨道终端接有电阻,试求电流i.解穿过导体回路abcda的磁通为故感应电流为一根半径为a的长圆柱形介质棒放入均匀磁场中与z轴平行。
设棒以角速度绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解介质棒内距轴线距离为r处的感应电场为故介质棒内的极化强度为极化电荷体密度为极化电荷面密度为则介质体积内和表面上同单位长度的极化电荷分别为平行双线传输线与一矩形回路共面,如题图所示。
设、、,求回路中的感应电动势。
解由题给定的电流方向可知,双线中的电流产生的磁感应强度的方向,在回路中都是垂直于纸面向内的。
故回路中的感应电动势为式中故则有一个环形线圈,导线的长度为l,分别通过以直流电源供应电压U0和时变电源供应电压U(t)。
讨论这两种情况下导线内的电场强度E。
解设导线材料的电导率为,横截面积为S,则导线的电阻为而环形线圈的电感为L,故电压方程为当U=U0时,电流i也为直流,。
故此时导线内的切向电场为当U=U(t)时,,故即求解此微分方程就可得到。
一圆柱形电容器,内导体半径为a,外导体内半径为b,长为l。
设外加电压为,试计算电容器极板间的总位移电流,证明它等于电容器的传导电流。
解当外加电压的频率不是很高时,圆柱形电容器两极板间的电场分布与外加直流电压时的电场分布可视为相同(准静态电场),即故电容器两极板间的位移电流密度为则式中,是长为l的圆柱形电容器的电容。
流过电容器的传导电流为可见由麦克斯韦方程组出发,导出点电荷的电场强度公式和泊松方程。
解点电荷q产生的电场满足麦克斯韦方程和由得据散度定理,上式即为利用球对称性,得故得点电荷的电场表示式由于,可取,则得即得泊松方程试将麦克斯方程的微分形式写成八个标量方程:(1)在直角坐标中;(2)在圆柱坐标中;(3)在球坐标中。
解(1)在直角坐标中(2)在圆柱坐标中(3)在球坐标系中已知在空气中,求和。
电磁场与电磁波课后习题及答案四章习题解答

如题图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为,求槽内的电位函数。
解根据题意,电位满足的边界条件为①②③根据条件①和②,电位的通解应取为题图由条件③,有两边同乘以,并从0到对积分,得到故得到槽内的电位分布两平行无限大导体平面,距离为,其间有一极薄的导体片由到。
上板和薄片保持电位,下板保持零电位,求板间电位的解。
设在薄片平面上,从到,电位线性变化,。
题图解应用叠加原理,设板间的电位为其中,为不存在薄片的平行无限大导体平面间(电压为)的电位,即;是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为:①②③根据条件①和②,可设的通解为由条件③有两边同乘以,并从0到对积分,得到故得到求在上题的解中,除开一项外,其他所有项对电场总储能的贡献。
并按定出边缘电容。
解在导体板()上,相应于的电荷面密度则导体板上(沿方向单位长)相应的总电荷相应的电场储能为其边缘电容为如题图所示的导体槽,底面保持电位,其余两面电位为零,求槽内的电位的解。
解根据题意,电位满足的边界条件为①题图②③根据条件①和②,电位的通解应取为由条件③,有两边同乘以,并从0到对积分,得到故得到槽内的电位分布为一长、宽、高分别为、、的长方体表面保持零电位,体积内填充密度为的电荷。
求体积内的电位。
解在体积内,电位满足泊松方程(1)长方体表面上,电位满足边界条件。
由此设电位的通解为代入泊松方程(1),可得由此可得或(2)由式(2),可得故如题图所示的一对无限大接地平行导体板,板间有一与轴平行的线电荷,其位置为。
求板间的电位函数。
解由于在处有一与轴平行的线电荷,以为界将场空间分割为和两个区域,则这两个区域中的电位和都满足拉普拉斯方程。
而在的分界面上,可利用函数将线电荷表示成电荷面密度。
电位的边界条件为题图①②③由条件①和②,可设电位函数的通解为由条件③,有(1)(2)由式(1),可得(3)将式(2)两边同乘以,并从到对积分,有(4)由式(3)和(4)解得故如题图所示的矩形导体槽的电位为零,槽中有一与槽平行的线电荷。
电磁场与电磁波 课后答案(冯恩信 著)

第一章 矢量场 1.1 z y x C z y x B z y x A ˆˆˆ3;ˆ2ˆˆ;ˆˆ3ˆ2+-=-+=-+= 求:(a) A ; (b) b ; (c) A B ⋅ ; (d) B C ⨯ ; (e) () A B C ⨯⨯ (f) () A B C ⨯⋅ 解:(a) 14132222222=++=++=z y x A A A A ; (b) )ˆ2ˆˆ(61ˆz y x BB b -+== ( c) 7=⋅B A ; (d) z y xC B ˆ4ˆ7ˆ---=⨯ (e) z y x C B A ˆ4ˆ2ˆ2)(-+=⨯⨯ (f) 19)(-=⋅⨯C B A 1.2 A z =++2 ρπϕ; B z =-+- ρϕ32 求:(a) A ; (b) b ; (c) A B ⋅ ; (d) B A ⨯ ; (e) B A + 解:(a) 25π+=A ;(b) )ˆ2ˆ3ˆ(141ˆz b -+-=ϕρ;(c) 43-=⋅πB A (d) z A B ˆ)6(ˆ3ˆ)23(+--+=⨯πϕρπ (e) z B A ˆˆ)3(ˆ-++=+ϕπρ 1.3 A r =+-22 πθπϕ; B r =- πθ 求:(a) A ; (b) b ; (c) A B ⋅ ; (d) B A ⨯ ; (e) A B + 解:(a) 254π+=A ; (b) )ˆˆ(11ˆ2θππ-+=r b ; (c) 22π-=⋅B A ;(d) ϕπθππˆ3ˆ2ˆ22++=⨯r A B ; (e) ϕπˆ2ˆ3-=+r B A 1.4 A x y z =+- 2; B x y z =+-α 3 当 A B ⊥时,求α。
解:当 A B ⊥时, A B ⋅=0, 由此得 5-=α 1.5 将直角坐标系中的矢量场 F x y z x F x y z y 12(,,) ,(,,) ==分别用圆柱和圆球坐标系中的坐标分量表示。
电磁场与电磁波典型习题及答案(恒定磁场)
E
=
ez
π
a12γ 1
+π
I (a22
−
a12 )γ 2
J1
=
γ1E
=
ez
5 ×10 7 12π
A/m2
,
J2
=
γ2E
=
ez
5 ×10 7 3π
A/m2
(2) 当 r < a1 时,有 2π rB = π r 2 µ0 J1 ⇒ B = 0.833r
当 a1
<
r
<
a2
时,有
2π rB
=
µ0[π a12 J1
解:(1) 由安培环路定律,可得
H
= eφ
I 2π r
所以得到
B1
= µ0H
= eφ
µ0I 2π r
B2
= µH
= eφ
µI 2π r
(2) 磁介质的磁化强度为
则磁化电流体密度为
M
=
1 µ0
B2
−
H
= eφ
(µ − µ0 )I 2πµ0 r
JM
=∇× M
= eZ
1 r
d dr
(rM
φ
)
=
eZ
(µ − µ0 )I 2πµ0
习题四
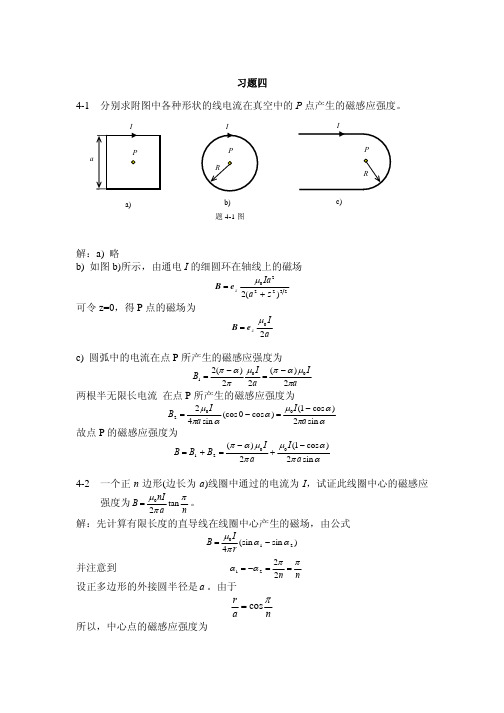
4-1 分别求附图中各种形状的线电流在真空中的 P 点产生的磁感应强度。
I
I
I
P
P
P
a
R R
a)
b)
c)
题 4-1 图
解:a) 略
b) 如图 b)所示,由通电 I 的细圆环在轴线上的磁场
B = ez
µ0 Ia 2 2(a 2 + z 2 )3 2
电磁场与电磁波课后练习及答案(谢处方第四版)

一章习题解答1.1给定三个矢量、和如下:求:(1);(2);(3);(4);(5)在上的分量;(6);(7)和;(8)和。
解(1) (2)(3)-11 (4)由,得 (5)在上的分量(6) (7)由于所以(8)A B C 23x y z =+-A e e e 4y z =-+B e e 52x z =-C e e A a -A B A B AB θA B ⨯A C ()⨯A B C ()⨯A B C ()⨯⨯A B C ()⨯⨯A B C 23A x y z +-===+-e e e A a e e e A -=A B (23)(4)x y z y z +---+=e e e e e 64x y z +-=e e e =A B (23)x y z +-e e e (4)y z -+=e ecos AB θ===A B A B 1cos AB θ-=(135.5= A B B A =A cos AB θ==A B B ⨯=A C 123502xy z-=-e e e 41310x y z ---e e e ⨯=B C 041502x yz-=-e e e 8520x y z ++e e e ⨯=A B 123041xyz-=-e e e 1014x y z ---e e e ()⨯=A B C(23)x y z +-e e e (8520)42x y z ++=-e e e ()⨯=A B C (1014)x y z ---e e e (52)42x z -=-e e ()⨯⨯=A B C 1014502x y z---=-e e e 2405x y z -+e e e1.2三角形的三个顶点为、和。
(1)判断是否为一直角三角形; (2)求三角形的面积。
解(1)三个顶点、和的位置矢量分别为,,则,,由此可见故为一直角三角形。
(2)三角形的面积 1.3求点到点的距离矢量及的方向。
解,, 则 且与、、轴的夹角分别为1.4给定两矢量和,求它们之间的夹角和在上的分量。
电磁场与电磁波第二版课后练习题含答案

电磁场与电磁波第二版课后练习题含答案一、选择题1. 一物体悬挂静止于匀强磁场所在平面内的位置,则这个磁场方向?A. 垂直于所在平面B. 并行于所在平面C. 倾斜于所在平面D. 无法确定答案:B2. 在运动着的带电粒子所在区域内,由于其存在着磁场,因此在该粒子所处位置引入一个另外的磁场,引入后,运动着的电荷将会加速么?A. 会加速B. 不会加速C. 无法确定答案:B3. 一台电视有线播出系统, 将信号源之中所传输的压缩图像和声音还原出来,要利用的是下列过程中哪一个?A. 光速传输B. 超声波传输C. 磁场作用D. 空气振动答案:C4. 一根充足长的长直电导体内有恒定电流I通过,则令曼培尔定律最适宜描述下列哪一项观察?A. 两个直平面电流之间的相互作用B. 当一个直平面电流遇到一个平行于它的磁场时, 会发生什么C. 当两个平行电流直线之间的相互作用D. 当电磁波穿过磁场时会发生什么答案:C5. 电磁波的一个特点是什么?A. 电磁波是一种无质量的相互作用的粒子B. 电磁波的速度跟频率成反比C. 不同波长的电磁波拥有的能量不同D. 电磁波不会穿透物质答案:C二、填空题1. 一个悬挂静止的电子放在一个以5000 G磁场中,它会受到的磁力是____________N. 假设电子的电荷是 -1.6×10^-19 C.答案:-8.0×10^-142. 在一个无磁场的区域内,放置一个全等的圆形和正方形输电线, 则这两个输电线产生的射界是_____________.答案:相同的3. 一个点电荷1.0×10^-6 C均匀带电一个闪电球,当位于该点电荷5.0 cm处时, 该牛顿计的弦向上斜,该牛顿计的尺度读数是4.0N. 该电荷所处场强的大小约为_____________弧度.答案:1.1×10^4三、简答题1. 解释什么是麦克斯韦方程式?麦克斯韦方程式是一组描述经典电磁场的4个偏微分方程式,包括关于电场的高斯定律、关于磁场的高斯定律、安培环路定理和法拉第电磁感应定律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁场与电磁波课后习题及答案14exeyez1,R23r3r22exey4ez8,R31r1r36exeyez3,由于R12R23411)21430,R 23R31214)61384,R31R12613)41136,故PP 2不是一直角三角形。
2)三角形的面积可以用矢量积求得:S12R12R23的模长,即S122411)214214613)411411613)21461332begin{n}1)三个顶点P、$P_2$(4,1,-3)和$P_3$(0,1,-2)的位置矢量分别为$r_1=e_y-e_z$,$r_2=e_x+4e_y-e_z$,$r_3=e_x+6e_y+2e_z$,则$R_{12}=r_2-r_1=4e_x+e_y+e_z$,$R_{23}=r_3-r_2=2e_x+e_y+4e_z$,$R_{31}=r_1-r_3=-6e_x+e_y-e_z$,由于$R_{12}\cdotR_{23}=(4+1+1)(2+1+4)=30$,$R_{23}\cdotR_{31}=(2+1+4)(6+1+3)=84$,$R_{31}\cdot R_{12}=(-6+1-3)(4+1+1)=-36$,故$\triangle PP_2P_3$不是一直角三角形。
2)三角形的面积可以用矢量积求得:$S=\frac{1}{2}|R_{12}\times R_{23}|$的模长,即$S=\frac{1}{2}\sqrt{(4+1+1)(2+1+4)(2+1+4)-(-6+1-3)(4+1+1)(4+1+1)-(-6+1-3)(2+1+4)(6+1+3)}=\frac{3\sqrt{2}}{2}$。
end{n}根据给定的矢量,计算得到:R_{12}=\sqrt{(e_x^4-e_z)(e_x^2+e_y+e_z/8)}$R_{23}=r_3-r_2=e_x^2+e_y+e_z/8-r_3$R_{31}=r_1-r_3=-e_x/6-e_y-e_z/7$由此可以得到,$\Delta P P$为一直角三角形,且$R_{12} \times R_{23}=17.13$。
要求点$P'(-3,1,4)$到点$P(2,-2,3)$的距离矢量$R$及其方向。
首先计算出两个点的矢量:r_{P'}=-e_x/3+e_y+e_z/4$r_P=e_x^2-e_y^2+e_z/3$然后计算得到$R=r_P-r_{P'}=e_x^5-e_y^3-e_z$,并且$R$与$x$、$y$、$z$轴的夹角分别为$\phi_x=32.31^\circ$,$\phi_y=120.47^\circ$,$\phi_z=99.73^\circ$。
给定两个矢量$A=e_x^2+e_y^3-e_z^4$和$B=e_x^4-e_y^5+e_z^6$,求它们之间的夹角和$A$在$B$上的分量。
首先计算它们的夹角:cos \theta = \frac{A \cdot B}{|A||B|}=\frac{29 \cdot77}{\sqrt{14^2+22^2+10^2} \cdot \sqrt{6^2+4^2+1^2}}$theta=131^\circ$然后计算$A$在$B$上的分量:A_B=\frac{A \cdot B}{|B|}=-3.532$给定两个矢量$A=e_x^2+e_y^3-e_z^4$和$B=-e_x^6-e_y^4+e_z$,求$A \times B$在$C=e_x-e_y+e_z$上的分量。
首先计算$A \times B$:A \times B=-e_x^{13}+e_y^{22}+e_z^{10}$然后计算$A \times B$在$C$上的分量:A \times B)_C=\frac{(A \times B) \cdot C}{|C|}=-14.43$最后,证明如果$AB=AC$且$A \times B=A \times C$,则$B=C$。
根据题意,可以得到$A \cdot (B-C)=0$,即$A$与$B-C$垂直。
同时,根据向量叉乘的性质,$A \times (B-C)=0$,即$A$、$B-C$和$A \times B$共面。
由于$A \neq 0$,所以$B-C$必须在$A$所在的平面上,即$B-C$与$A$平行。
因此,$B-C$与$A \times B$垂直,即$B-C$与$A$垂直。
由于$AB=AC$,所以$B-C$与$A$共线,因此$B=C$。
1.7 如果已知一个未知矢量与一个已知矢量的标量积和矢量积,可以确定该未知矢量。
设A为已知矢量,p=AX,P=A×X,已知p和P,求X。
解由P=A×X,有A×P=A×(A×X)=(AX)A-(AA)X=pA-(AA)X,故得X=(pA-A×P)/(AA)。
1.8 在圆柱坐标中,一点的位置由(4,θ,3)定出,求该点在直角坐标系和球坐标系中的坐标。
解:在直角坐标系中,x=4cosθ,y=4sinθ,z=3,故该点的直角坐标为(4cosθ,4sinθ,3)。
在球坐标系中,r=sqrt(4^2+3^2)=5,θ=tan^-1(4/3)=53.1°,φ=2π/3=120°,故该点的球坐标为(5,53.1°,120°)。
1.9 用球坐标表示的场E=er。
求在直角坐标系中点(-3,4,-5)处的E和Ex。
解:在直角坐标系中点(-3,4,-5)处,r^2=(-3)^2+4^2+(-5)^2=50,故E=er=2/√50(-3er+4er-5er)=-3er+4er-5er=-4er。
Ex=Ecosθ=-4cosφsinθ=-4cos(2π/3)sin(tan^-1(4/3))=-3/√50.1.10 球坐标中两个点(r1,θ1,φ1)和(r2,θ2,φ2)定出两个位置矢量R1和R2.证明R1和R2间夹角的余弦为cosγ=cosθ1cosθ2+sinθ1sinθ2cos(φ1-φ2)。
解:由R1=er1r1sinθ1cosφ1+er1r1sinθ1sinφ1+er1r1cosθ1,R2=er2r2sinθ2cosφ2+er2r2sinθ2sinφ2+er2r2cosθ2,得到cosγ=R1·R2/R1R2=sinθ1sinθ2(cosφ1cosφ2+sinφ1sinφ2)+cosθ1co sθ2=cosθ1cosθ2+sinθ1sinθ2cos(φ1-φ2)。
1.求解球面积分计算矢量r对球面S的积分,其中球心在原点,半径为5.解:首先,根据球面积分的公式,有iint_S \mathbf{r}\cdot d\mathbf{S} = \int_0^{2\pi}\int_0^\pi \mathbf{r}\cdot \mathbf{e}_r r^2\sin\theta d\theta d\phi$$其中,$\mathbf{e}_r$为球坐标系中的单位向量,$\theta$为极角,$\phi$为方位角。
代入题目中的数据,有iint_S \mathbf{r}\cdot d\mathbf{S} = \int_0^{2\pi}\int_0^\pi (5\mathbf{e}_r)\cdot \mathbf{e}_r (5)^2\sin\theta d\theta d\phi = 75\pi$$因此,矢量r对球面S的积分为$75\pi$。
2.验证散度定理在由$r=5$、$z=0$和$z=4$围成的圆柱形区域,对矢量$\mathbf{A}=e_r(r^2+e_z^2)$验证散度定理。
解:首先,根据圆柱坐标系中的散度公式,有nabla\cdot\mathbf{A} = \frac{1}{r}\frac{\partial}{\partial r}(rA_r) + \frac{1}{r}\frac{\partial}{\partial \phi}(A_\phi) +\frac{\partial}{\partial z}(A_z)$$代入题目中的数据,有nabla\cdot\mathbf{A} = \frac{1}{r}\frac{\partial}{\partial r}(r(r^2+e_z^2)) + \frac{1}{r}\frac{\partial}{\partial \phi}(0) + \frac{\partial}{\partial z}(e_z(r^2+e_z^2)) = 3r+2$$接下来,计算$\mathbf{A}$对圆柱体积的积分,有iiint_V \nabla\cdot\mathbf{A}\ dV =\int_0^{2\pi}\int_0^5\int_0^4 (3r+2)r\ dr\ dz\ d\phi = 1200\pi$$最后,计算$\mathbf{A}$对圆柱体侧面的积分,有iint_S \mathbf{A}\cdot d\mathbf{S} = \int_0^{2\pi}\int_0^4 \mathbf{A}\cdot \mathbf{e}_z r\ dr\ d\phi = \int_0^{2\pi}\int_0^4 e_z(r^2+e_z^2)r\ dr\ d\phi = 0$$因此,散度定理得到验证。
3.计算散度和验证散度定理1)求矢量$\mathbf{A}=e_x(x^2+e_y^2)/(x^2y^2+e_z)$的散度;2)求$\nabla\cdot\mathbf{A}$对中心在原点的一个单位立方体的积分;3)求$\mathbf{A}$对此立方体表面的积分,验证散度定理。
解:首先,根据直角坐标系中的散度公式,有nabla\cdot\mathbf{A} = \frac{\partial}{\partialx}\left(\frac{x^2+e_y^2}{x^2y^2+e_z}\right) +\frac{\partial}{\partial y}\left(\frac{e_x^2y^2}{x^2y^2+e_z}\right) + \frac{\partial}{\partialz}\left(\frac{e_x(x^2+e_y^2)}{(x^2y^2+e_z)^2}\right)$$对各项分别求偏导,有frac{\partial}{\partialx}\left(\frac{x^2+e_y^2}{x^2y^2+e_z}\right) =\frac{(2x)(x^2y^2+e_z)-(x^2+e_y^2)(2xy^2)}{(x^2y^2+e_z)^2}$$frac{\partial}{\partialy}\left(\frac{e_x^2y^2}{x^2y^2+e_z}\right) =\frac{(e_x^2)(x^2y^2+e_z)-(e_y^2)(2xy^2)}{(x^2y^2+e_z)^2}$$frac{\partial}{\partialz}\left(\frac{e_x(x^2+e_y^2)}{(x^2y^2+e_z)^2}\right) =\frac{(e_x)(x^2+e_y^2)(-2e_z)}{(x^2y^2+e_z)^2}$$将上述结果代入散度公式,有nabla\cdot\mathbf{A} = \frac{(2x)(x^2y^2+e_z)-(x^2+e_y^2)(2xy^2)}{(x^2y^2+e_z)^2} +\frac{(e_x^2)(x^2y^2+e_z)-(e_y^2)(2xy^2)}{(x^2y^2+e_z)^2} + \frac{(e_x)(x^2+e_y^2)(-2e_z)}{(x^2y^2+e_z)^2}$$接下来,计算$\nabla\cdot\mathbf{A}$对中心在原点的一个单位立方体的积分,有iiint_V \nabla\cdot\mathbf{A}\ dV = \int_{-1/2}^{1/2}\int_{-1/2}^{1/2}\int_{-1/2}^{1/2} \nabla\cdot\mathbf{A}\ dx\ dy\ dz = \frac{5}{6}$$最后,计算$\mathbf{A}$对此立方体表面的积分,有iint_S \mathbf{A}\cdot d\mathbf{S} = \iint_{S_1}\mathbf{A}\cdot \mathbf{e}_x\ dS + \iint_{S_2} \mathbf{A}\cdot (-\mathbf{e}_x)\ dS + \iint_{S_3} \mathbf{A}\cdot \mathbf{e}_y\ dS + \iint_{S_4} \mathbf{A}\cdot (-\mathbf{e}_y)\ dS +\iint_{S_5} \mathbf{A}\cdot \mathbf{e}_z\ dS + \iint_{S_6}\mathbf{A}\cdot (-\mathbf{e}_z)\ dS$$其中,$S_1$、$S_2$、$S_3$、$S_4$、$S_5$、$S_6$分别为立方体的六个面。
