云南2020届高三下学期高考适应性月考卷(七)理科数学(含答案)
【精准解析】江西省赣州市2020届高三5月适应性考试数学(理)试题

- 1 - 赣州市2020年高三年级适应性考试 理科数学 一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知z是复数,且21zii(其中i为虚数单位),则z在复平面内对应的点的坐标为( ) A. 3,1 B. 3,1 C. 1,3 D. 1,3 【答案】A 【解析】 【分析】 由复数的综合运算求出z后可得其对应点的坐标. 【详解】由题意2(1)223ziiiii,对应点坐标为(3,1). 故选:A. 【点睛】本题考查复数的综合运算,考查复数的几何意义,属于基础题.
2.已知集合|lg0Pxx,1|12xQx,则( ) A. |1RQxx B. PQ C. PQR D. |1PQxx
【答案】B 【解析】 【分析】 解对数不等式和指数不等式得集合,PQ,再根据集合的运算得正确选项. 【详解】由题意{|1}Pxx,{|0}Qxx,所以|0RQxx,PQ. 故选:B. 【点睛】本题考查集合的运算,考查指数函数、对数函数的性质,掌握指数函数、对数函数的单调性是解题关键. 3.从某班50名同学中选出5人参加户外活动,利用随机数表法抽取样本时,先将50名同学 - 1 -
按01,02,……,50进行编号,然后从随机数表的第1行第5列和第6列数字开始从左往右依次选取两个数字,则选出的第5个个体的编号为( )(注:表为随机数表的第1行与第2行)
A. 24 B. 36 C. 46 D. 47 【答案】A 【解析】 【分析】 按要求两个数字为一个号,不大于50且前面未出现的数依次写出即可得. 【详解】由随机数表.抽样编号依次为43,36,47,36前面出现过去掉,46,24,第5个是24. 故选:A. 【点睛】本题考查随机数表法,属于简单题. 4.已知函数fx在R上单调递减,且当0,2x时,有24fxxx,则关于x的不等式30fx的解集为( ) A. ,1 B. 1,3 C. 1, D. 3, 【答案】C 【解析】 【分析】 由已知解析式求出函数值为-3的自变量x的值,然后由单调性解出不等式. 【详解】令243xx,则1x或3x(舍去),∴(1)3f, 不等式()30fx可化为()3fx,即()(1)fxf,又()fx是R上的减函数,∴1x. 故选:C. 【点睛】本题考查函数的单调性,掌握单调性的定义是解题关键. 5.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的侧面积为( ) - 1 -
复杂的三视图问题-玩转压轴题,(原卷版)

一.方法综述三视图几乎是每年的必考内容,一般以选择题、填空题的形式出现,一是考查相关的识图,由直观图判断三视图或由三视图想象直观图,二是以三视图为载体,考查面积、体积的计算等,均属低中档题.还原几何体的基本要素是“长对齐,高平直,宽相等”.要切实弄清常见几何体(圆柱、圆锥、圆台、棱柱、棱锥、棱台、球)的三视图的特征,熟练掌握三视图的投影方向及正视图原理,才能迅速破解三视图问题,由三视图画出其直观图.对于简单几何体的组合体的三视图,首先要确定正视、侧视、俯视的方向,其次要注意组合体由哪些几何体组成,弄清它们的组成方式,特别应注意它们的交线的位置.解题时一定耐心加细心,观察准确线与线的位置关系,区分好实线和虚线的不同. 根据几何体的三视图确定直观图的方法: (1)三视图为三个三角形,对应三棱锥;(2)三视图为两个三角形,一个四边形,对应四棱锥; (3)三视图为两个三角形,一个带圆心的圆,对应圆锥; (4)三视图为一个三角形,两个四边形,对应三棱锥; (5)三视图为两个四边形,一个圆,对应圆柱.对于几何体的三视图是多边形的,可构造长方体(正方体),在长方体(正方体)中去截得几何体.二.解题策略类型一 构造正方体(长方体)求解【例1】某几何体的三视图如图所示,关于该几何体有下述四个结论:①体积可能是56;②体积可能是23;③AB 和CD 在直观图中所对应的棱所成的角为3;④在该几何体的面中,互相平行的面可能有四对;其中所有正确结论的编号是( )A .①③B .②④C .①②③D .①②③④【来源】河南省开封市2021届高三三模文科数学试题专题4.1 复杂的三视图问题【答案】D【举一反三】1.(2020·江西高三)某几何体的三视图如图所示,其中网格纸上小正方形的边长为1,则该几何体的体积为()A.9B.92C.6D.32、某三棱锥的三视图如图所示,则该三棱锥的体积为()A.16B.13C.12D.13.若一个几何体的三视图如图所示,则该几何体的体积为()A .4B .8C .12D .14类型二 旋转体与多面体组合体的三视图【例2】(2020·内蒙古高三)如图所示,是某几何体的正视图(主视图),侧视图(左视图)和俯视图,其中俯视图为等腰直角三角形,则该几何体体积为( )A .620π+B .916π+C .918π+D .2063π+【举一反三】一个四棱柱被截去一个半圆柱后剩余部分的三视图如图,则截去部分与剩余几何体的体积比为( )A .18ππ- B .318ππ-C .12ππ-D .312ππ-类型三 与三视图相关的外接与内切问题【例3】(2020·辽宁鞍山一中高三月考)已知四棱锥P ABCD -的三视图如图所示,则四棱锥P ABCD -外接球的表面积是( )A.20πB.1015πC.25πD.22π【举一反三】1.(2020·四川成都七中高考模拟)某多面体的三视图如图所示,则该几何体的体积与其外接球的体积之比为()A.618πB.69πC.63πD.13π2.如图,网格纸上小正方形的边长为2,粗实线及粗虚线画出的是某几何体的三视图,则该几何体的外接球的表面积为A .30B .41C .30D .64【来源】甘肃省兰州市第一中学2020届高三冲刺模拟考试(一)数学(文)试题 3.(2020·山西高三)某棱锥的三视图如图所示,则该棱锥的外接球的表面积为( )A .11πB .12πC .13πD .14π类型四 与三视图相关的最值问题【例4】(2020·武邑宏达学校高考模拟(理))已知在直三棱柱111ABC A B C -中,120BAC ∠=︒,12AB AC AA ===,若棱1AA 在正视图的投影面α内,且AB 与投影面α所成角为(3060)θθ︒≤≤︒.设正视图的面积为m ,侧视图的面积为n ,当θ变化时,mn 的最大值是__________.【举一反三】1.某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a+b 的最大值为 (A )22 (B )23 (C )4 (D )252、某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy 的最大值为( )A.32 732.B C.64 764.D3.(2020·西安市长安区第五中学高三(理))如图是一个几何体的三视图,在该几何体的各个面中,面积最小的面的面积为()A.8 B.4C.42D.43三.强化训练1.(2020·福建高三)中国古代数学名著《九章算术》中记载了公元前344年商鞅监制的一种标准量器——商鞅铜方升,某商鞅铜方升模型的三视图,如图所示(单位:寸),若 取3,则该模型的体积(单位:立方寸)为()A.11.9 B.12.6 C.13.8 D.16.22.(2020·北京人大附中高三)已知某多面体的三视图如图所示,则在该多面体的距离最大的两个面中,两个顶点距离的最大值为()A.2 B5C6D.23.(2020·北京市十一学校高三)某四棱锥的三视图如图所示,网格纸上小正方形的边长为1,则该四棱锥的体积为A.43B.4C.423D.424.(2020·湖南雅礼中学高三月考(理))一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积为()A.168 B.98 C.108 D.885.(2020·重庆一中高三月考(理))如图的虚线网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图.在该几何体的直观图中,直线AB与CD所成角的余弦值为()A.15B.25C5D256.(2020·江西高三)半正多面体(semiregular solid) 亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形为面的半正多面体.如图所示,图中网格是边长为1的正方形,粗线部分是某二十四等边体的三视图,则该几何体的体积为()A.83B.4C.163D.2037.(2020·江西高三期末(理))如图,网格纸上小正方形的边长为1,粗实线画出的是一个三棱锥的三视图,则该三棱锥的外接球的表面积是()A.B.C.D.8.(2020合肥市高三)我国古代《九章算术》将上、下两面为平行矩形的六面体称为刍童.右图是一个刍童的三视图,其中正视图及侧视图均为等腰梯形,两底的长分别为2和4,高为2,则该刍童的表面积为A. B.40 C. D.9.一个几何体的三视图如图所示,则这个几何体的体积为A. B. C. D.10.榫卯(sǔnmǎo)是两个木构件上所采用的一种凹凸结合的连接方式.凸出部分叫榫,凹进去的部分叫卯,榫和卯咬合,起到连接作用.代表建筑有北京的紫禁城、天坛祈年殿,山西悬空寺等,如图是一种榫卯构件中榫的三视图,则该榫的表面积和体积为()A. B. C. D.11.如图是某几何体的三视图,其中网格纸上小正方形的边长为1,则该几何体的表面积为()A .3682+B .3282+C .3242+D .3642+【来源】云南师范大学附属中学2021届高三高考适应性月考卷(六)理科数学试题12.(2020·安徽高三月考)一副三角板由一块有一个内角为60︒的直角三角形和一块等腰直角三角形组成,如图所示,1AB =,60A ∠=︒,90B F ∠=∠=︒,BC DE =.现将两块三角板拼接在一起,使得二面角F BC A --为直二面角,则三棱锥F ABC -的外接球表面积为( )A .4πB .3πC .2πD .π13.已知正方体1111ABCD A B C D -(如图1),点P 在侧面11CDD C 内(包括边界).若三棱锥1B ABP -的俯视图为等腰直角三角形(如图2),则此三棱锥的左视图不可能是( )A.B.C.D.【来源】北京市海淀区2021届高三二模数学试题14.如图,网格纸上小正方形的边长为1,粗线是某几何体的三视图,则该几何体的各个面中最大面积为()A.6 B22C.32D13【来源】贵州省普通高等学校招生2021届高三适应性测试(3月)数学(文)试题15.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球表面积()A.3πB.23πC.43πD.12π【来源】四川省泸州市泸县第五中学2021届高三高考数学(文)一诊试题16.已知某几何体的三视图如图所示,则该几何体的体积为()A.12B.32C.1D.3317.某几何体的三视图如图所示(单位:cm),则该几何体内切球的表面积(单位:2cm)是()A .9π16B .9π4C .1π4D .9π2【来源】安徽省江淮十校2021届高三下学期4月第三次质量检测理科数学试题18.某三棱锥的三视图如图所示,已知网格纸上小正方形的边长为1,该三棱锥所有表面中,最大的面积为( )A .2B .22C .23D .42【来源】安徽省五校联盟2021届高三下学期第二次联考理科数学试题19.如图,正四棱锥P ABCD -的高为12,62AB =,E ,F 分别为PA ,PC 的中点,过点B ,E ,F 的截面交PD 于点M ,截面EBFM 将四棱锥分成上下两个部分,规定BD 为主视图方向,则几何体CDAB FME -的俯视图为( )A.B.C.D.【来源】江西省南昌市2021届高三二模数学(理)试题20.三棱柱被一平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为()A.203B.6 C.52D162【来源】景德镇市2021届高三第三次质检数学(理)试题21.某几何体的三视图如图所示,则该几何体的体积为()A .246π-B .86π-C .246π+D .86π+【来源】河南省六市2021届高三第二次联考(二模)数学(文科)试题22.某几何体的三视图如图所示,则该几何体的体积为( )A .2B .4C .163D .22323.正三棱锥(底面为正三角形,顶点在底面的射影为底面中心的棱锥)的三视图如图所示,俯视图是正三角形,O是其中心,则正视图(等腰三角形)的腰长等于()A.5B.2 C.3D.224.某几何体的三规图如图所示. 则其外接球的表面积为()A.803πB.1369πC.5449πD.483π【来源】百师联盟2020-2021学年高三下学期开年摸底联考考理科数学试卷(全国Ⅰ卷)25.已知一个三棱锥的三视图如图所示,则该三棱锥的外接球的体积为()A.32πB.823πC.833πD.8π26.(2020·湖北高三期末(理))中国的计量单位可以追溯到4000多年前的氏族社会末期,公元前221年,秦王统一中国后,颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”(无盖,不计量厚度)的三视图(其正视图和侧视图为等腰梯形),则此“斗”的体积为(单位:立方厘米)27.(2020·陕西高三(理))某几何体的三视图如图所示,若该几何体的体积为103,则棱长为a的正方体的外接球的表面积为28.(2020·深圳市高级中学高三(理))某几何体的三视图如图所示,主视图是直角三角形,侧视图是等腰三角形,俯视图是边长为3的等边三角形,若该几何体的外接球的体积为36 ,则该几何体的体积为__________.29.(2020·福建高三期末(理))农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.30.某三棱锥的正视图和俯视图如图所示,已知该三棱锥的各顶点都在球O的球面上,过该三棱锥最短的棱的中点作球O的截面,截面面积最小为______.【来源】内蒙古锡林郭勒盟全盟2021届高三第二次模拟考试数学(理科)试题31.一个直三棱柱的三视图如图所示,则该直三棱柱的体积为_______,它的外接球的表面积为________.。
广西南宁市2020届高三第二次适应性测试数学(理科)试题(解析版)
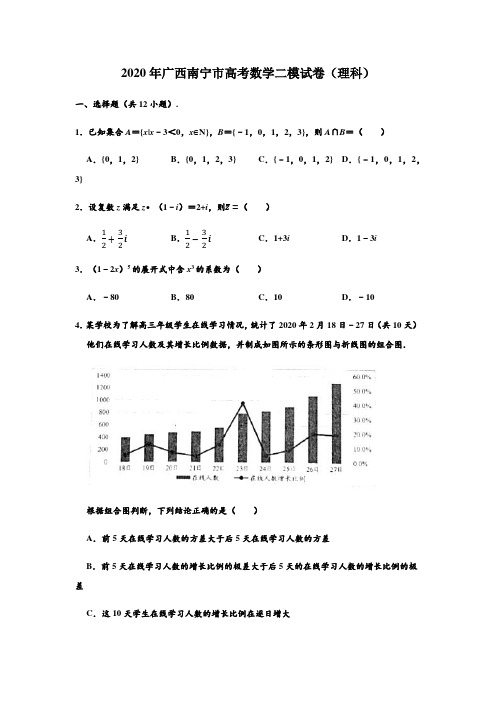
2020年广西南宁市高考数学二模试卷(理科)一、选择题(共12小题).1.已知集合A={x|x﹣3<0,x∈N},B={﹣1,0,1,2,3},则A∩B=()A.{0,1,2}B.{0,1,2,3}C.{﹣1,0,1,2}D.{﹣1,0,1,2,3}2.设复数z满足z•(1﹣i)=2+i,则z=()A.12+32i B.12−32i C.1+3i D.1﹣3i3.(1﹣2x)5的展开式中含x3的系数为()A.﹣80B.80C.10D.﹣104.某学校为了解高三年级学生在线学习情况,统计了2020年2月18日﹣27日(共10天)他们在线学习人数及其增长比例数据,并制成如图所示的条形图与折线图的组合图.根据组合图判断,下列结论正确的是()A.前5天在线学习人数的方差大于后5天在线学习人数的方差B.前5天在线学习人数的增长比例的极差大于后5天的在线学习人数的增长比例的极差C.这10天学生在线学习人数的增长比例在逐日增大D .这10天学生在线学习人数在逐日增加5.已知各项不为0的等差数列{a n }的前n 项和为S n ,若a 5=2a 2,则S 6a 2=( )A .4B .162C .9D .126.若函数y =a |x |(a >0,且a ≠1)的值域为{y |0<y ≤1},则函数y =log a |x |的图象是( )A .B .C .D .7.椭圆C :x 2a 2+y 2=1(a >1)的左、右焦点为F 1,F 2,过F 1的直线l 交C 于A ,B 两点,且△ABF 2的周长为8,则a 为( ) A .√2B .2C .2√2D .48.某同学在课外阅读中国古代数学名著《孙子算经》时,为解决“物不知数”问题,设计了如图所示的程序框图.执行此程序框图,则输出的a 的值为( )A .13B .18C .23D .289.如图,在正方体ABCD﹣A1B1C1D1中,M,N分别为AC,A1B的中点,则下列说法错误的是()A.MN∥平面ADD1A1B.MN⊥ABC.直线MN与平面ABCD所成角为45°D.异面直线MN与DD1所成角为60°10.已知双曲线E:x2a−y2b=1(a>0,b>0)的右焦点为F,以OF(O为原点)为直径的圆与双曲线E的两条渐近线分别交于点M,N(M,N异于点O).若∠MFN=120°,则双曲线E的离心率为()A.4B.2C.43D.2√3311.已知函数f(x)=sin(ωx+φ)(ω≠0)的图象经过点(π24,0),一条对称轴方程为x=π6.则函数f(x)的周期可以是()A.3π4B.π2C.π4D.π1212.已知函数f(x)={lnx,x>0kx+1,x≤0,则当k>0时,函数y=f[f(x)]﹣1的零点个数为()A.4B.3C.2D.1二、填空题:本题共4小题,每小题5分,共20分.13.已知向量a →=(√3,1),向量b →=(−1,−√3),则a →与b →的夹角大小为 . 14.某部门从已参与报名的甲、乙、丙、丁四人中选派1人去参加志愿者服务,结果出来前,甲、乙、丙、丁四人对选派人选做了如下预测: 甲说:丙或丁被选上;乙说:甲和丁均未被选上; 丙说:丁被选上;丁说:丙被选上.若这四人中有且只有2人说的话正确,则被选派参加志愿者服务的是 . 15.已知数列{a n }中,a 1=2,且对于任意正整数m ,n 都有a m +n =a m a n ,则数列{a n }的通项公式是 .16.如图,正方形ABCD 中,E ,F 分别是BC ,CD 的中点,沿AE ,EF ,AF 把这个正方形折成一个四面体,使B ,C ,D 三点重合,重合后的点记为G .若四面体A ﹣EFG 外接球的表面积为π4,则正方形ABCD 的边长为 .三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生依据要求作答.(一)必考题:共60分.17.如图,在平面四边形ABCD 中,∠B =120°,AB =2.∠BAC 的平分线与BC 交于点E ,且AE =√6. (1)求∠BEA 及AC ;(2)若∠ADC =60°,求四边形ABCD 周长的最大值.18.红铃虫(Pectinophoragossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①y=e bx+a,②y=cx2+d分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.根据收集到的数据,计算得到如表值:x z t∑8i=1(x i−x)2∑8i=1(t i−t)2∑8i=1(z i−z)(x i−x)∑8i=1(y i−y)(t i−t)25 2.8964616842268848.4870308表中z i=lny i;z=18∑8i=1z i;t i=x i2;t=18∑8i=1t i;(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.(参考数据:e5.18≈178,e5.46≈235,e5.52≈250,e5.83≈340)附:对于一组数据(ω1,v1),(ω2,v2),…,(ωn,v n),其回归直线v=α+βω的斜率和截距的最小二乘估计分别为β=∑ n i=1(ωi −ω)(v i −v)∑ ni=1(ωi −ω)2,α=v −βω.19.如图,在四棱锥S ﹣ABCD 中,四边形ABCD 是等腰梯形,AD ∥BC ,AD =DC ,∠ADC =120°,三角形SAB 是等边三角形,平面SAB ⊥平面ABCD ,E ,F 分别为AB ,AD 的中点.(1)求证:平面SCD ⊥平面SEF ;(2)若AB =2,求直线SF 与平面SCD 所成角的正弦值.20.已知函数f (x )=e x ﹣a •x ,其中e 是自然对数的底数. (1)若a =e ,证明:f (x )≥0;(2)若x ∈[0,+∞)时,都有f (x )≥f (﹣x ),求实数a 的取值范围.21.已知抛物线C :x 2=2y ,过点A (1,1)且互相垂直的两条动直线l 1,l 2与抛物线C 分别交于P ,Q 和M ,N .(1)求四边形MPNQ 面积的取值范围;(2)记线段PQ 和MN 的中点分别为E ,F ,求证:直线EF 恒过定点.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,已知曲线C 1:{x =−2+t 1cosθ1y =t 1sinθ1(t 1为参数),曲线C 2:{x =2+t 2cosθ2y =t 2sinθ2(t 2为参数),且tan θ1tan θ2=﹣1,点P 为曲线C 1与C 2的公共点. (1)求动点P 的轨迹方程;(2)在以原点O 为极点,x 轴的非负半轴为极轴的极坐标系中,直线l 的极坐标方程为2ρcosθ﹣ρsinθ+10=0,求动点P到直线l的距离的取值范围.[选修4-5:不等式选讲]23.已知a,b,c都为正实数,且a+b+c=3.证明:(1)√2a+1+√2b+1+√2c+1≤3√3;(2)(1a−13)(1b−13)(1c−13)≥827.参考答案一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x﹣3<0,x∈N},B={﹣1,0,1,2,3},则A∩B=()A.{0,1,2}B.{0,1,2,3}C.{﹣1,0,1,2}D.{﹣1,0,1,2,3}【分析】求出集合A,由此能求出A∩B.解:由集合A={x|x﹣3<0,x∈N}={0,1,2},所以A∩B={0,1,2}.故选:A.【点评】本小题主要考查一元一次不等式的自然数解和集合的交集运算等基础知识,考查交集定义等基础知识,考查运算求解能力,是基础题.2.设复数z满足z•(1﹣i)=2+i,则z=()A.12+32i B.12−32i C.1+3i D.1﹣3i【分析】把已知等式变形,再由复数代数形式的乘除运算化简得答案.解:∵z=2+i1−i=(2+i)⋅(1+i)2=12+32i,∴z=12−32i.故选:B.【点评】本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.(1﹣2x)5的展开式中含x3的系数为()A.﹣80B.80C.10D.﹣10【分析】根据二项式展开式的通项公式,令x的指数为3,求出展开式中x3的系数.解:(1﹣2x)5展开式的通项公式为T r+1=C5r•(﹣2x)r,令r=3,得(1﹣2x)5展开式中x3的系数为C53•(﹣2)3=﹣80.故选:A.【点评】本题考查了二项式展开式通项公式的应用问题,是基础题.4.某学校为了解高三年级学生在线学习情况,统计了2020年2月18日﹣27日(共10天)他们在线学习人数及其增长比例数据,并制成如图所示的条形图与折线图的组合图.根据组合图判断,下列结论正确的是()A.前5天在线学习人数的方差大于后5天在线学习人数的方差B.前5天在线学习人数的增长比例的极差大于后5天的在线学习人数的增长比例的极差C.这10天学生在线学习人数的增长比例在逐日增大D.这10天学生在线学习人数在逐日增加【分析】根据图象逐一进行分析即可解:对于A,由柱状图可得前5天学习人数的变化幅度明显比后5天的小,故方差也小,故A错误对于B:前5天的增长比例极差约为15%﹣5%=10%,后5天增长比例极差约为40%﹣20%=20%,故B错误;对于C:由折线图很明显,23﹣24的增长比例在下降,故C错误;对于D:由柱状图,可得学习人数在逐日增加,故D正确,故选:D.【点评】本小题考查统计图表等基础知识,考查统计思想以及学生数据处理等能力和应用意识.5.已知各项不为0的等差数列{a n}的前n项和为S n,若a5=2a2,则S6a2=()A.4B.162C.9D.12【分析】利用等差数列通项公式和前n项和公式即可得出.解:由题S6a2=S6a2=3(a1+a6)a2=3(a2+a5)a2=3(a2+2a2)a2=9.故选:C.【点评】本小题主要考查等差数列通项公式和前n项和公式等基础知识,考查运算求解等数学能力,属于基础题.6.若函数y=a|x|(a>0,且a≠1)的值域为{y|0<y≤1},则函数y=log a|x|的图象是()A.B.C .D .【分析】根据指数函数的图象和性质求出0<a <1,利用对数函数的图象和性质进行判断即可.解:∵|x |≥0,∴若函数y =a |x |(a >0,且a ≠1)的值域为{y |0<y ≤1}, ∴0<a <1,当x >0时,数y =log a |x |=log a x ,为减函数,当x <0时,数y =log a |x |=log a (﹣x ),为增函数,且函数是偶函数,关于y 轴对称, 故选:A .【点评】本题主要考查函数图象的识别和判断,根据指数函数的图象和性质求出a 的取值范围是解决本题的关键.7.椭圆C :x 2a +y 2=1(a >1)的左、右焦点为F 1,F 2,过F 1的直线l 交C 于A ,B 两点,且△ABF 2的周长为8,则a 为( ) A .√2B .2C .2√2D .4【分析】由椭圆的定义可得:|AF 1|+|AF 2|=2a ,|BF 1|+|BF 2|=2a ,即可得出答案. 解:由椭圆C :x 2a 2+y 2=1(a >1)的焦点在x 轴上,则椭圆的定义可得:|AF 1|+|AF 2|=|BF 1|+|BF 2|=2a .∴△ABF 2的周长=|AB |+|AF 2|+|BF 2|=|AF 1|+|BF 1|+|AF 2|+|BF 2|=8=4a .解得a =2. 故选:B .【点评】本题考查椭圆的定义、方程和性质,主要考查椭圆的定义的运用,考查运算能力,属于基础题.8.某同学在课外阅读中国古代数学名著《孙子算经》时,为解决“物不知数”问题,设计了如图所示的程序框图.执行此程序框图,则输出的a 的值为( )A .13B .18C .23D .28【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量a 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案. 解:模拟程序的运行,可得 n =1,得a =8, 不满足a−221∈Z ,n =2,得a =13,不满足a−221∈Z ,n =3,得a =18,不满足a−221∈Z ,n =4,得a =23,此时,满足a−221∈Z ,退出循环,输出a 的值为23.故选:C .【点评】本小题主要考查程序框图的应用等基础知识,考查阅读理解能力、运算求解能力、数据处理能力以及应用意识,属于基础题.9.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,M ,N 分别为AC ,A 1B 的中点,则下列说法错误的是( )A.MN∥平面ADD1A1B.MN⊥ABC.直线MN与平面ABCD所成角为45°D.异面直线MN与DD1所成角为60°【分析】连结BD,A1D,可得MN∥A1D,得到MN∥平面ADD1A1,判定A正确;证明AB⊥平面ADD1A1,得AB⊥A1D,结合MN∥A1D,得MN⊥AB,判断B正确;求出直线MN与平面ABCD所成角判断C正确;求出异面直线MN与DD1所成角判断D错误.解:如图,连结BD,A1D,由M,N分别为AC,A1B的中点,知MN∥A1D,而MN⊄平面ADD1A1,A1D⊂平面ADD1A1,∴MN∥平面ADD1A1,故A正确;在正方体ABCD﹣A1B1C1D1中,AB⊥平面ADD1A1,则AB⊥A1D,∵MN∥A1D,∴MN⊥AB,故B正确;直线MN与平面ABCD所成角等于A1D与平面ABCD所成角等于45°,故C正确;而∠A1DD1为异面直线MN与DD1所成角,应为45°,故D错误.故选:D.【点评】本题主要考查直线与平面平行、垂直的判定与性质、直线与平面所成角、异面直线所成角等基础知识;考查空间想象能力、论证推理能力,是中档题.10.已知双曲线E:x2a−y2b=1(a>0,b>0)的右焦点为F,以OF(O为原点)为直径的圆与双曲线E的两条渐近线分别交于点M,N(M,N异于点O).若∠MFN=120°,则双曲线E的离心率为()A.4B.2C.43D.2√33【分析】画出图形,结合圆的对称性,求出∠MOF=30°.然后求解双曲线的离心率即可.解:因为OF为直径,点M在圆上,所以OM⊥MF.又∠MFN=120°,由圆的对称性,有∠MFO=60°,所以∠MOF=30°.由渐近线斜率tan∠MOF=ba=√33,所以离心率为e=√1+(ba)2=2√33.故选:D.【点评】本小题主要考查双曲线及其性质等基础知识;考查运算求解、推理论证能力;考查数形结合等数学思想.11.已知函数f(x)=sin(ωx+φ)(ω≠0)的图象经过点(π24,0),一条对称轴方程为x=π6.则函数f(x)的周期可以是()A.3π4B.π2C.π4D.π12【分析】直接根据对称中心和对称轴之间的距离即可求解结论.解:由π6−π24=2k+14T,则T=π4k+2,k∈Z,当k=0时,T=π2.故选:B.【点评】本小题主要考查三角函数的图象和性质、正弦型函数f(x)=sin(ωx+φ)图象和性质等基本知识;考查推理论证等数学能力,化归与转化等数学思想.12.已知函数f(x)={lnx,x>0kx+1,x≤0,则当k>0时,函数y=f[f(x)]﹣1的零点个数为()A.4B.3C.2D.1【分析】先作出函数的图象,然后结合图象即可求解函数的零点个数.解:在平面直角坐标系中作出函数y=f(x)(k>0)的图象如图所示.令f[f(x)]﹣1=0,得f[f(x)]=1,则f(x)=0或f(x)=t(t>1).当f(x)=0时,显然存在2个零点x1=−1k,x2=1;当f(x)=t(t>1)时,存在1个零点x3.故函数y=f[f(x)]﹣1的零点个数为3.故选:B .【点评】本小题主要考查分段函数的图象,函数的零点等基础知识;考查逻辑推理能力,分类讨论思想,数形结合思想,方程思想, 二、填空题:本题共4小题,每小题5分,共20分.13.已知向量a →=(√3,1),向量b →=(−1,−√3),则a →与b →的夹角大小为 150° .【分析】根据向量a →,b →的坐标即可得出a →⋅b →,|a →|和|b →|的值,从而可得出cos <a →,b →>=−√32,从而可得出a →,b →夹角的大小.解:∵cos <a →,b →>=a →⋅b→|a →||b →|=−√3−√32×2=−√32,且0≤<a →,b →>≤π, ∴a →与b →的夹角为150°. 故答案为:150°.【点评】本小题主要考查平面向量的数量积,两个向量的夹角等基础知识,考查运算求解能力,属于基础题.14.某部门从已参与报名的甲、乙、丙、丁四人中选派1人去参加志愿者服务,结果出来前,甲、乙、丙、丁四人对选派人选做了如下预测: 甲说:丙或丁被选上;乙说:甲和丁均未被选上; 丙说:丁被选上;丁说:丙被选上.若这四人中有且只有2人说的话正确,则被选派参加志愿者服务的是 丁 . 【分析】逐个假设甲,乙,丙,丁被选上,检验是否符合题意即可. 解:若甲被选上,甲、乙、丙、丁错误,不满足条件; 若乙被选上,甲、丙、丁错误,乙正确,不满足条件; 若丙被选上,甲、乙、丁正确,丙错误,不满足条件; 若丁被选上,甲、丙正确,乙、丁错误,满足条件, 所以被选派参加志愿者服务的是丁, 故答案为:丁.【点评】本题主要考查了逻辑推理等基础知识,考查学生逻辑推理能力等能力,是基础题.15.已知数列{a n }中,a 1=2,且对于任意正整数m ,n 都有a m +n =a m a n ,则数列{a n }的通项公式是 a n =2n .【分析】利用数列的递推关系式,通过m =1,推出数列是等比数列,然后求解通项公式即可.解:数列{a n }中,a 1=2,且对于任意正整数m ,n 都有a m +n =a m a n ,令m =1,得a n +1=2a n ,则{a n }是首项和公比均为2的等比数列,则a n =2n . 故答案为:a n =2n .【点评】本小题主要考查数列以及前n 项和等基本知识,考查化归与转化等数学思想以及推理论证、运算求解等数学能力.16.如图,正方形ABCD 中,E ,F 分别是BC ,CD 的中点,沿AE ,EF ,AF 把这个正方形折成一个四面体,使B ,C ,D 三点重合,重合后的点记为G .若四面体A ﹣EFG 外接球的表面积为π4,则正方形ABCD 的边长为 2 .【分析】画出折叠后的四面体图形,利用等积法求出四面体内切球半径,再求内接球的表面积.解:依题意,折叠后的四面体如图1, 设正方形边长为a ,内切球半径为r , 则AG =a ,EG =FG =a2; 记四面体内切球球心为O ,如图2,则V A ﹣EFG =V O ﹣EFG +V O ﹣AEF +V O ﹣AEG +V O ﹣AFG ,即V A−EFG =13(S △EFG +S △AEF +S △ABG +S △AFG )⋅r ,即13×12×a 2×a 2×a =13×a 2×r ,所以a =8r ;又4πr 2=π4,即r =14,所以a =2. 故答案为:2.【点评】本题主要考查了直线与平面垂直的判定、球体表面积公式、几何体切割等基础知识,也考查了空间想象能力与运算求解能力.三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生依据要求作答.(一)必考题:共60分.17.如图,在平面四边形ABCD中,∠B=120°,AB=2.∠BAC的平分线与BC交于点E,且AE=√6.(1)求∠BEA及AC;(2)若∠ADC=60°,求四边形ABCD周长的最大值.【分析】(1)在△ABE中,由正弦定理可求sin∠AEB的值,又∠AEB<∠B,可求∠AEB=45°,利用三角形的内角和定理可求∠BAE的值,进而可求∠ACB的值,可得BC=AB=2,在△ABC中,根据余弦定理即可解得AC的值.(2)令AD=m,CD=n,在△ACD中,根据余弦定理,基本不等式可求m+n≤4√3,即可求解四边形ABCD周长的最大值.解:(1)在△ABE中,由正弦定理得:sin∠AEB=ABsinBAE=6=√22.又∠AEB<∠B,则∠AEB=45°,于是∠BAE=180°﹣120°﹣45°=15°,所以∠BAC=30°,∠ACB=180°﹣120°﹣30°=30°.所以BC=AB=2.在△ABC中,根据余弦定理得AC2=22+22﹣2×2×2×cos120°=12,所以AC=2√3.(2)令AD=m,CD=n,在△ACD中,根据余弦定理得(2√3)2=m2+n2−2mncos60°=(m+n)2−3mn,即有(m+n)2=12+3mn≤12+3×(m+n2)2,即(m+n)24≤12,所以m+n≤4√3,当且仅当m=n=2√3时,“=”成立.所以,四边形ABCD周长的最大值为4+4√3.【点评】本小题主要考查正弦定理、余弦定理等基本知识,考查化归与转化等数学思想以及推理论证、运算求解等数学能力,属于中档题.18.红铃虫(Pectinophoragossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①y=e bx+a,②y=cx2+d分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.根据收集到的数据,计算得到如表值:x z t∑8i=1(x i−x)2∑8i=1(t i−t)2∑8i=1(z i−z)(x i−x)∑8i=1(y i−y)(t i−t) 25 2.8964616842268848.4870308表中z i=lny i;z=18∑8i=1z i;t i=x i2;t=18∑8i=1t i;(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.(参考数据:e5.18≈178,e5.46≈235,e5.52≈250,e5.83≈340)附:对于一组数据(ω1,v1),(ω2,v2),…,(ωn,v n),其回归直线v=α+βω的斜率和截距的最小二乘估计分别为β=∑n i=1(ωi−ω)(v i−v)∑n i=1(ωi−ω)2,α=v−βω.【分析】(1)由模型①残差点比较均匀地落在水平的带状区域中,且带状区域的宽度比模型②带状宽度窄,说明模型①的拟合精度更高,回归方程的预报精度相应就会越高;(2)令z=lny,z与温度x可以用线性回归方程来拟合,则z=a+b x,由已知数据求得b与a的值,可得产卵数y关于温度x的回归方程,取x=34求得y值得结论.解:(1)应该选择模型①.由于模型①残差点比较均匀地落在水平的带状区域中,且带状区域的宽度比模型②带状宽度窄,所以模型①的拟合精度更高,回归方程的预报精度相应就会越高,故选模型①比较合适.(2)令z=lny,z与温度x可以用线性回归方程来拟合,则z=a+b x,b=∑8i=1(z i−z)(x i−x)∑8i=1(x i−x)2=48.48168≈0.289,∴a=z−b x=2.89−0.289×25≈−4.34,则z关于x的线性回归方程为z=0.29x−4.34.于是有lny=0.29x﹣4.34,∴产卵数y关于温度x的回归方程为y=e0.29x−4.34.当x=34时,y=e0.29×34﹣4.34=e5.52≈250(个).∴在气温在34℃时,一个红铃虫的产卵数的预报值为250个.【点评】本题主要考查回归方程、统计案例等基本知识,考查统计基本思想以及抽象概括、数据处理等能力和应用意识,是中档题.19.如图,在四棱锥S﹣ABCD中,四边形ABCD是等腰梯形,AD∥BC,AD=DC,∠ADC =120°,三角形SAB是等边三角形,平面SAB⊥平面ABCD,E,F分别为AB,AD 的中点.(1)求证:平面SCD⊥平面SEF;(2)若AB=2,求直线SF与平面SCD所成角的正弦值.【分析】(1)由已知结合平面与平面垂直的性质可得SE⊥平面ABCD,进一步得到SE ⊥CD.连接BD,得BD∥EF.再证明BD⊥CD,结合BD∥EF,得CD⊥EF.再由直线与平面垂直的判定可得CD⊥平面SEF.进一步得到平面SCD⊥平面SEF;(2)过E作EN∥CD,则ES,EF,EN两两垂直,以E为坐标原点建立空间直角坐标系.求出平面SCD的法向量与SF→的坐标,由两向量所成角的余弦值可得直线SF与平面SCD所成角的正弦值.【解答】(1)证明:∵平面SAB ⊥平面ABCD ,平面SAB ∩平面ABCD =AB , SE ⊂平面SAB ,SE ⊥AB ,∴SE ⊥平面ABCD . 又∵CD ⊂平面ABCD ,∴SE ⊥CD .连接BD ,∵E ,F 分别为AB ,AD 的中点,∴BD ∥EF . ∵AD =DC =AB ,∴∠ABD =∠ADB .又∵∠BAD =∠ADC =120°,∴∠ADB =30°, ∴∠BDC =90°,得BD ⊥CD . 又∵BD ∥EF ,∴CD ⊥EF . 又SE ∩EF =E ,∴CD ⊥平面SEF .又∵CD ⊂平面SCD ,∴平面SCD ⊥平面SEF ;(2)解:过E 作EN ∥CD ,则ES ,EF ,EN 两两垂直, 故可如图建立空间直角坐标系.在△BDC 中,求得BD =2√3,CD =2,BC =4. 则E (0,0,0),F(0,√3,0),S(0,0,√3),C(52,3√32,0),D(12,3√32,0).故SD →=(12,3√32,−√3),SC →=(52,3√32,−√3),SF →=(0,√3,−√3).设平面SCD 的法向量为n →=(x ,y ,z),由{n →⋅SD →=12x +3√32y −√3z =0n →⋅SC →=52x +3√32y −√3z =0,可取n →=(0,2,3). 则|cos〈n →,SF →〉|=|n →⋅SF→n →|⋅|SF →||=√3√6⋅√13=√2626.故SF 与平面SCD 所成角的正弦值为√2626.【点评】本题主要考查平面与平面垂直的判定、平面与平面垂直的性质、直线与平面所成角、空间向量处理立体几何问题等基础知识;考查空间想象能力、运算求解能力、推理论证能力和创新意识,考查化归与转化等数学思想,是中档题. 20.已知函数f (x )=e x ﹣a •x ,其中e 是自然对数的底数. (1)若a =e ,证明:f (x )≥0;(2)若x ∈[0,+∞)时,都有f (x )≥f (﹣x ),求实数a 的取值范围.【分析】(1)若a =e ,则f (x )=e x ﹣e •x ,所以f ′(x )=e x ﹣e ,再利用导函数f '(x )的正负性与函数f (x )的单调性之间的联系即可得f (x )的单调性,从而确定f (x )min =f (1),而f (1)=0,进而得证;(2)构造函数g (x )=f (x )﹣f (﹣x )=e x ﹣e ﹣x ﹣2ax ,则原问题转化为g (x )≥0在[0,+∞)上恒成立,然后求导g '(x ),令h (x )=g ′(x ),再求导h '(x ),从而可确定g ′(x )在[0,+∞)上单调递增,由于g ′(0)=2﹣2a ,于是分a ≤1和a >1两种情形,讨论函数g (x )的单调性,以便求证g (x )min 与0的关系. 解:(1)若a =e ,则f (x )=e x ﹣e •x ,所以f ′(x )=e x ﹣e , 当x =1时,f ′(x )=0;当x ∈(﹣∞,1)时,f ′(x )<0,f (x )单调递减; 当x ∈(1,+∞)时,f ′(x )>0,f (x )单调递增; 所以f (x )在x =1时取得极小值,也是最小值.所以f (x )≥f (1)=0.(2)令g (x )=f (x )﹣f (﹣x )=e x ﹣e ﹣x ﹣2ax ,则原问题转化为g (x )≥0在[0,+∞)上恒成立.由g ′(x )=e x +e ﹣x ﹣2a ,令h (x )=g ′(x ),则h′(x)=e 2x −1ex ≥0在[0,+∞)上恒成立,所以g ′(x )在[0,+∞)上单调递增, 又g ′(0)=2﹣2a ,①当a ≤1时,g ′(x )≥g ′(0)≥0,所以g (x )在[0,+∞)上单调递增, 所以g (x )≥g (0)=0,即f (x )≥f (﹣x ),满足题意.②当a >1时,因为g ′(x )在[0,+∞)上单调递增,所以g ′(x )min =g ′(0)=2﹣2a <0,所以存在t ∈(0,+∞),使得当x ∈(0,t )时,g ′(x )<0,g (x )在(0,t )上单调递减,此时g (x )<g (0)=0,这与g (x )≥0在[0,+∞)上恒成立矛盾. 综上所述,a ≤1,故实数a 的取值范围是(﹣∞,1].【点评】本题主要考查利用导数研究函数的单调性和最值,不等式的恒成立问题等,考查学生分类讨论和转化与化归的思想,以及运算求解能力,属于中档题.21.已知抛物线C :x 2=2y ,过点A (1,1)且互相垂直的两条动直线l 1,l 2与抛物线C 分别交于P ,Q 和M ,N .(1)求四边形MPNQ 面积的取值范围;(2)记线段PQ 和MN 的中点分别为E ,F ,求证:直线EF 恒过定点.【分析】(1)两直线l 1,l 2的斜率一定存在,且不等于0.设l 1:y =k (x ﹣1)+1(k ≠0),P (x 1,y 1),Q (x 2,y 2),则l 2:y =−1k (x −1)+1(k ≠0).联立直线与抛物线方程,利用韦达定理,弦长公式转化求解四边形MPNQ 面积的表达式,利用换元法结合二次函数的求解最小值即可.(2)由(1)求出PQ 中点E 的坐标为(k ,k 2+1),同理点F 的坐标为(−1k ,1k2+1).求出直线EF 的斜率,得到直线EF 的方程,即可求解直线EF 恒过的定点. 解:(1)由题意可知两直线l 1,l 2的斜率一定存在,且不等于0.设l 1:y =k (x ﹣1)+1(k ≠0),P (x 1,y 1),Q (x 2,y 2),则l 2:y =−1k (x −1)+1(k ≠0).因为联立直线l 1与抛物线的方程,有{y =k(x −1)+1#/DEL/#x 2=2y #/DEL/#⇒x 2−2kx +2k −2=0,其中△=4k 2+8>0,由韦达定理,有{x 1+x 2=2kx 1x 2=2k −2.由上可得|PQ|=√1+k 2|x 1−x 2|=√(1+k 2)(8+4k 2),同理|MN|=√(1+1k2)(8+4k2),则四边形MPNQ 面积S =12|PQ||MN|=12√(2+k 2+1k2)(80+32k 2+32k2).令k 2+1k2=t ≥2.则S =12√(2+t)(80+32t)=√8t 2+36t +40.所以,当且仅当t =2,即k =±1时,S 取得最小值12,且当t →+∞时,S →+∞. 故四边形MPNQ 面积的范围是[12,+∞). (2)由(1)有x 1+x 2=2k ,y 1+y 2=2k 2+2,所以PQ 中点E 的坐标为(k ,k 2+1),同理点F 的坐标为(−1k ,1k2+1).于是,直线EF 的斜率为k EF =k 2+1−(1k2+1)k+1k=k 2−1k 2k+1k=k −1k ,则直线EF 的方程为:y −(k 2+1)=(k −1k )(x −k)⇒y =(k −1k )x +2,所以直线EF 恒过定点(0,2).【点评】本小题主要考查抛物线及其性质、直线与抛物线的位置关系等基础知识;考查运算求解、推理论证能力和创新意识;考查化归与转化、数形结合等数学思想. 一、选择题22.在直角坐标系xOy 中,已知曲线C 1:{x =−2+t 1cosθ1y =t 1sinθ1(t 1为参数),曲线C 2:{x =2+t 2cosθ2y =t 2sinθ2(t 2为参数),且tan θ1tan θ2=﹣1,点P 为曲线C 1与C 2的公共点. (1)求动点P 的轨迹方程;(2)在以原点O 为极点,x 轴的非负半轴为极轴的极坐标系中,直线l 的极坐标方程为2ρcos θ﹣ρsin θ+10=0,求动点P 到直线l 的距离的取值范围.【分析】(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换,进一步利用三角函数关系式的变换和余弦型函数性质的应用求出结果. (2)利用点到直线的距离公式的应用求出结果. 解:(1)设点P 的坐标为(x ,y ). 因为点P 为曲线C 1与C 2的公共点, 所以点P 同时满足曲线C 1与C 2的方程. 曲线C 1消去参数可得tanθ1=yx+2, 曲线C 2消去参数可得tanθ2=y x−2. 由tan θ1tan θ2=﹣1,所以yx+2⋅yx−2=−1.所以点P 的轨迹方程为x 2+y 2=4(x ≠±2).(2)由已知,直线l 的极坐标方程2ρcos θ﹣ρsin θ+10=0,根据x=ρcosθ,y=ρsinθ可化为直角坐标方程:2x﹣y+10=0.因为P的轨迹为圆x2+y2=4(去掉两点(±2,0)),圆心O到直线l的距离为d=5=2√5,所以点P到直线l的距离的取值范围为[2√5−2,2√5+2].【点评】本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,点到直线距离公式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.[选修4-5:不等式选讲]23.已知a,b,c都为正实数,且a+b+c=3.证明:(1)√2a+1+√2b+1+√2c+1≤3√3;(2)(1a−13)(1b−13)(1c−13)≥827.【分析】(1)由三个数的完全平方公式,结合均值不等式和不等式的性质,即可得证;(2)将1=a+b+c3代入原不等式的左边,化简整理,再由基本不等式和不等式的性质,即可得证.【解答】证明:(1)(√2a+1+√2b+1+√2c+1)2=2(a+b+c)+3+ 2√(2a+1)(2b+1)+2√(2b+1)(2c+1)+2√(2c+1)(2a+1)≤2(a+b+c)+3+(2a+1+2b+1)+(2b+1+2c+1)+(2c+1+2a+1)=6(a+b+c)+9=27(当且仅当a=b=c=1取“=”).所以√2a+1+√2b+1+√2c+1≤3√3;(2)由a,b,c都为正实数,且a+b+c=3,可得(1a−13)(1b−13)(1c−13)=(a+b+c3a−1 3)(a+b+c3b−13)(a+b+c3c−13)=b+c3a ⋅a+c3b⋅a+b3c≥127⋅2√bca⋅2√acb⋅2√abc=827(当且仅当a=b=c=1取“=”).则(1a−13)(1b−13)(1c−13)≥827.【点评】本题主要考查基本不等式、不等式的证明方法、含绝对值的不等式等基本知识,考查化归与转化等数学思想和推理论证等数学能力,是一道中档题.。
巴蜀中学2020届高考适应性月考(四)文科数学-含答案

则 2019 年的占比预计为11.42% . 20.(本小题满分 12 分)
………………………………(12 分)
解:(1)由题可知 e c a
3, 2
△PF1F2
的面积最大为
1 2
2c
b
bc
3.
由 a2 b2 c2 ,可得 a2 4,b2 1 ,椭圆的方程 E:x42 y2 1 .……………………(5 分)
(3)]
lg
34 33
lg 3 ,故选
D.
文科数学参考答案·第 1 页(共 5 页)
12.根据直线可知 F ( 3,0) ,所以 c
3
,又
P(0,1)
及
FP
2PA
,得
A
3 2
,3 2
,代入椭
圆方程有
3 4a2
9 4b2
1 ,将 b2
a2
3 代入,解得 a2
63 2
3
或 a2
6
3 2
3 c2 3(舍
去),则 e2 2 3 4 2 3 ( 3 1)2 ,故选 D. 63 3
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
题号 答案
13
y
3 3x
14
15
16
55
y 2x π 1
文科数学参考答案·第 2 页(共 5 页)
则 PE 平面ABCD .
又 PE 平面ADP ,所以平面 PAD 平面 ABCD .
………………………………(6 分)
2020届高三化学适应性考试试题A卷含解析

②BiCl3极易水解生成不溶性 BiOCl沉淀
请回答下列问题:
(1)为了提高溶浸工序中原料的浸出率,可以采取的措施有___(填标号)。
a。加入足量的蒸馏水 b。搅拌 c。粉碎矿石 d.降低温度
(2)溶浸时通常加入FeCl3溶液和浓盐酸,加入的浓盐酸需过量的目的是___,滤渣A的主要成分为___(填化学式)。
【详解】(1)可通过重结晶的方式提高原料苯甲酸的纯度;
(2)仪器A为球形冷凝管,在制备过程中乙醇易挥发,因此通过球形冷凝管冷凝回流乙醇和水;该反应中乙醇作为反应物,因此可通过水浴加热,避免乙醇大量挥发;
(3)仪器B中吸水剂为无水硫酸铜的乙醇饱和溶液,吸收水分后生成五水硫酸铜,吸水剂由白色变为蓝色;
(4)由上述分析可知,操作I为蒸馏;操作II为分液,除烧杯外,还需要的玻璃仪器为分液漏斗;
C.光纤的主要成分为二氧化硅,硅是良好的半导体材料,是制造计算机的芯片材料,故C错误;
D.浓度为95%的酒精可使细胞壁上形成一层膜,阻止酒精的渗入,则75%的酒精消毒效果好,故D错误;
答案为A。
2。 已知NA是阿伏加德罗常数的值,下列说法中正确的是
A。7.8gNa2O2晶体中离子总数为0。4NA
B。200g质量分数为17%H2O2溶液中极性键数目为2NA
A。 工业上通过电解熔融的WX来制得W
B. W、X对应的简单离子半径顺序为:W>X
C. 该漂白剂中各元素均满足8电子稳定结构
D。 Y的最高价氧化物对应水化物为弱酸
【答案】D
【解析】
【分析】
从图中可以看出,Y显4价,说明最外层电子数为4,X显2价,最外层电子数为6,W显+2价,说明它是第ⅡA族的金属元素,所以Z为氢(H);由“W、X对应的简单离子核外电子排布相同",可确定W为镁(Mg),X为氧(O),从而得出Y为碳(C).
云南师范大学附属中学2021届高三高考适应性月考卷(六)语文试题 Word版含答案

Evaluation Only. Created with Aspose.Words. Copyright 2003-2016 Aspose Pty Ltd.秘密★启用前云南师范大学附属中学2021届高三高考适应性月考卷(六)语文试卷注意事项:1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效。
3.考试结束后,请将本试卷和答题卡一并交回。
满分150分,考试用时150分钟。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
提到一座城市,人们往往会想到具有代表性的文化地标:600岁的紫禁城见证着北京城的过往,拓荒牛雕塑标记着深圳的开拓进取,珠海大剧院“日月贝”讲述着“珠生于贝,贝生于海”的城市记忆,古典园林里生长着苏州的温婉……这些城市文化地标或深植于历史文化,或投射着时代风貌,以鲜明独特的符号形象,成为一个城市的精神和文化象征,与人们产生紧密的情感连接、文化认同。
作为一种人文景观,文化地标首先应当与地理环境“不违和”。
人文景观与自然环境浑然天成、融为一体,才能给人以美的享受。
无论是中华文化天人合一、道法自然的审美意境,还是如今兴起的保护生态、亲近自然的绿色发展理念,都强调人文景观与自然环境和谐共生。
丽江古城依山傍水、以水为脉,整座古城获评世界文化遗产;国家体育场“鸟巢”充分采用自然采光和通风,勾勒出现代北京的美丽风景。
反之,若缺乏对自然的敬畏,滥造钢筋水泥地标,即便再大的“手笔”,也与审美旨趣和群众期待相差甚远。
《管子》言:“因天材,就地利,故城郭不必中规矩,道路不必中准绳。
”因地制宜,因势利导,与自然环境和谐共存,相得益彰,这是文化地标的基本要求。
作为一种符号化呈现,文化地标也应该追求形神兼备。
2023届四川省泸县高2020级高考数学(理工类)适应性考试2【含答案】
估计该体育院校学生观看雪上项目和冰上项目的时间长度的第75百分位数分别是和,则21s 22s A .,B .,C .,D .12x x >2212s s >12x x >2212s s <12x x <2212s s >1x <4.中国的5G 技术领先世界,5G 技术的数学原理之一便是著名的香农公式:为坐标原点),若过点作互相垂直的两O1,3,4 3⎫⎬⎭三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第试题考生都必须作答.第22(一)必考题:共60分。
(1)求证:平面平面BDG ⊥ABC (2)若,求平面2AB BC CP ===19.(12分)公司采用招考的方式引进入才,规定考生必须在测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每个测试点的测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点、、测试合格的概率分别为,A B C 23,,小王在上述三个测试点测试合格的概率都是.231223()问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大?请说明理由;1()假设小李选择测试点、进行测试,小王选择测试点、进行测试,记为两人在各测试点测试2A B A C X 合格的测试点个数之和,求随机变量的分布列及数学期望.X EX 20.(12分)已知椭圆的上、下顶点分别为,左顶点为,是面积为()2222:10x y C a b a b +=>>,A B D ABD △的正三角形.3(1)求椭圆的方程;C (2)过椭圆外一点的直线交椭圆于两点,已知点与点关于轴对称,点与点关C (),0M m C ,P Q P P 'x Q Q '于轴对称,直线与交于点,若是钝角,求的取值范围.x PQ 'P Q 'K AKB ∠m 21.(12分)已知函数,.若函数在定义域内有两个不同的极值点()2ln 12a f x x x x x =--+a ∈R ()f x .12x x ,(1)求实数a 的取值范围;(2)当时,证明:.02m <≤12m x x a +>(二)选考题:共10分.请考生在第22、23题中任选一题作答。
专题5.5 三角恒等变换(解析版)
专题5.5 三角恒等变换1.两角和与差的正弦、余弦、正切公式(1)()C αβ-:cos()αβ-=cos cos sin sin αβαβ+ (2)()C αβ+:cos()cos cos sin sin αβαβαβ+=- (3)()S αβ+:sin()αβ+=sin cos cos sin αβαβ+ (4)()S αβ-:sin()αβ-=sin cos cos sin αβαβ-(5)()T αβ+:tan()αβ+=tan tan π(,,π,)1tan tan 2k k αβαβαβαβ++≠+∈-Z(6)()T αβ-:tan()αβ-=tan tan π(,,π,)1tan tan 2k k αβαβαβαβ--≠+∈+Z 2.二倍角公式(1)2S α:sin2α=2sin cos αα(2)2C α:cos2α=2222cos sin 12sin 2cos 1αααα-=-=- (3)2T α:tan 2α=22tan πππ(π,)1tan 224k k k αααα≠+≠+∈-Z 且3.公式的常用变形(1)tan tan tan()(1tan tan )αβαβαβ±=±;tan tan tan tan tan tan 11tan()tan()αβαβαβαβαβ+-=-=-+-(2)降幂公式:21cos 2sin 2αα-=;21cos 2cos 2αα+=;1sin cos sin 22ααα=(3)升幂公式:21cos 22cos αα+=;21cos 22sin αα-=;21sin 2(sin cos )ααα+=+;21sin 2(sin cos )ααα-=-(4)辅助角公式:sin cos a x b x +)x ϕ=+, 其中cos ϕϕ==tan baϕ=.4.半角公式:(1)sin2α=(2)cos 2α=,(3)tan2α=sin 1cos 1cos sin αααα-==+.5.公式的常见变形(和差化积、积化和差公式) (1)积化和差公式:1cos cos [cos()cos()]2αβαβαβ=++-; 1sin sin [cos()cos()]2αβαβαβ=-+--;1sin cos [sin()sin()]2αβαβαβ=++-;1cos sin [sin()sin()]2αβαβαβ=+--.(2)和差化积公式:sin sin 2sincos22αβαβαβ+-+=;sin sin 2cossin22αβαβαβ+--=; cos cos 2coscos22αβαβαβ+-+=; cos cos 2sinsin22αβαβαβ+--=-.5.三角函数式的化简(1)化简原则:①一看角之间的差别与联系,把角进行合理的拆分,正确使用公式;②二看函数名称之间的差异,确定使用的公式,常见的有“切化弦”;③三看结构特征,找到变形的方向,常见的有“遇到分式要通分”,“遇到根式一般要升幂”等.(2)化简要求:①使三角函数式的项数最少、次数最低、角与函数名称的种类最少;②式子中的分母尽量不含根号.(3)化简方法:①切化弦,②异名化同名,③异角化同角,④降幂或升幂. 6.三角函数式的求值(1)给角求值:给角求值中一般所给出的角都是非特殊角,从表面上来看是很难的,但仔细观察会发现非特殊角与特殊角之间总有一定的关系.解题时,要利用观察得到的关系,结合公式将非特殊角的三角函数转化为特殊角的三角函数,从而得解. (2)给值求值:已知三角函数值,求其他三角函数式的值的一般思路: ①先化简所求式子.②观察已知条件与所求式子之间的联系(从三角函数名及角入手). ③将已知条件代入所求式子,化简求值.(3)给值求角:通过求角的某种三角函数值来求角,在选取函数时,有以下原则: ①已知正切函数值,则选正切函数.②已知正、余弦函数值,则选正弦或余弦函数.若角的范围是π(0,)2,则选正、余弦皆可;若角的范围是(0,π),则选余弦较好;若角的范围为ππ(,)22-,则选正弦较好. (4)常见的角的变换:①已知角表示未知角,例如:()()ααββββα=+-=--,()()()()2,2ααβαββαβαβ=++-=+--,(2)αβαβα+=++,(2)αβαβα-=-+,22αβαβα+-=+,22αβαββ+-=-.②互余与互补关系,例如:π3π()()π44αα++-=,πππ()()362αα++-=. ③非特殊角转化为特殊角,例如:15°=45°−30°,75°=45°+30°.一、单选题1.已知sin 2cos 0αα-=,则tan 4πα⎛-⎫⎪⎝⎭=A .-4B .4C .1-3D .13【试题来源】云南省昆明市第八中学2020-2021学年高一特色班下学期第一次月考 【答案】C【分析】已知sin 2cos 0αα-=,可得tan 2α=,根据两角差的正切公式计算即可得出结果. 【解析】已知sin 2cos 0αα-=,则tan 2α=,∴ tantan 1tan 1214tan ===41tan 1231tan tan 4παπααπαα---⎛⎫-=- ⎪++⎝⎭+.故选C .2.422cos sin 1212ππ=A .1B .12 C .14D .12-【试题来源】广西桂林市第十八中学2021-2022学年高二上学期期中考试 【答案】C【分析】本题利用二倍角公式和特殊角三角函数值,即可得到答案. 【解析】222214cossin (2cossin)(sin )1212121462πππππ===.故选C . 3.已知1sin 63πα⎛⎫-= ⎪⎝⎭,则cos 23πα⎛⎫-= ⎪⎝⎭A .79-B .23-C .23D .79【试题来源】四川省绵阳东辰国际学校2020-2021学年高三下学期三诊 【答案】D【分析】利用倍角公式2cos 212sin 36ππαα⎛⎫⎛⎫-=-- ⎪ ⎪⎝⎭⎝⎭,将条件代入计算即可.【解析】217cos 212sin 123699ππαα⎛⎫⎛⎫-=--=-⨯= ⎪ ⎪⎝⎭⎝⎭,故选D .4.已知tan 2α=,则22cos 2sin cos sin 2αααα--的值为A .13-B .13C .73-D .73【试题来源】山东省菏泽市一中系列学校2021-2022学年高三上学期期中考试数学(A ) 【答案】D【分析】利用倍角公式及同角的商的关系将式子转化为用tan α表示,然后带值计算即可.【解析】222222cos 2sin cos 2sin 12tan 1247cos sin 2cos 2sin cos 12tan 1223ααααααααααα----⨯====----⨯.故选D . 5.22sin 36sin 54sin15cos15++=A B .1C .97100D .54【试题来源】四川省遂宁市2021-2022学年高三上学期零诊考试 【答案】D【分析】根据诱导公式、同角三角函数的基本关系,以及降幂公式即可求得答案. 【解析】原式=22115cos 54sin 54sin 301244++=+=.故选D .6.关于函数sin (sin cos )y x x x =+描述正确的是 A.最小正周期是2π B C .一条对称轴是4x π=D .一个对称中心是1,82π⎛⎫⎪⎝⎭【试题来源】北京市第三十五中学2022届高三上学期期中考试 【答案】D【分析】利用三角恒等变换化简y 得解析式,再利用正弦型函数的图象和性质得出结论. 【解析】由题意得sin (sin cos )y x x x =+21sin sin 22x x =+1cos 21sin 222x x -=+1)42x π=-+, 选项A :函数的最小正周期为min 222T πππω===,故A 错误;选项B :由于sin(241)1x π≤-≤-12,故B 错误;选项C :函数的对称轴满足242x k πππ-=+,328k x ππ=+, 当4x π=时,14k Z =-∉,故C 错误;选项D :令8x π=,代入函数的11())828422f πππ=⨯-+=, 故1,82π⎛⎫⎪⎝⎭为函数的一个对称中心,故D 正确;故选D7.已知函数2()sin cos f x x x x =,则下列说法正确的是 A .()f x 的最小正周期为2π B .()f x 的最大值为2 C .()f x 在5,36ππ⎛⎫⎪⎝⎭上单调递增 D .()f x 的图象关于直线6x π=-对称【试题来源】重庆市江津中学校2021-2022学年高二上学期开学考试 【答案】D【分析】化简函数的解析式()1sin(2)62f x x π=-+,结合三角函数的图象与性质,逐项判定,即可求解.【解析】由题意,函数21cos 2()sin cos 22x f x x x x x -==1112cos 2sin(2)2262x x x π=-+=-+, 由函数()f x 的最小正周期,可得22T ππ==,所以A 错误; 由函数()f x 的最大值为()max 13122f x =+=,所以B 错误; 因为5,36x ππ⎛⎫∈ ⎪⎝⎭,可得32,622x πππ⎛⎫-∈ ⎪⎝⎭, 所以函数()f x 在5,36ππ⎛⎫⎪⎝⎭上单调递减,所以C 错误;由()1sin(2)62f x x π=-+,令2,62x k k Z πππ-=+∈,解得,32k x k Z ππ=+∈, 当1k =-时,可得6x π=-,所以()f x 的图象关于直线6x π=-对称,所以D 正确.故选D .8.已知角α的终边经过点(-,则sin 22πα⎛⎫-= ⎪⎝⎭A .B .19-C .19D 【试题来源】四川省攀枝花市2021-2022学年高三第一次统一考试 【答案】B【分析】由角终边上的点可得sin α=,根据诱导公式、二倍角余弦公式有2sin 212sin 2παα⎛⎫-=- ⎪⎝⎭,即可求值.【解析】由题设,sin α=,21sin 2cos 212sin 29πααα⎛⎫-==-=- ⎪⎝⎭.故选B9.已知角α的终边经过点(-,则cos2=αA .B .19-C .19D 【试题来源】四川省攀枝花市2021-2022学年高三第一次统一考试 【答案】B【分析】根据三角函数的定义求出cos α,再利用二倍角公式计算可得;【解析】因为角α的终边经过点(-,所以2222cos 325α,所以2221cos 22cos 12139αα⎛⎫=-=⨯--=- ⎪⎝⎭,故选B10.已知函数()cos sin f x x x =+,则()f x 的最大值为A .2B .1 CD .2【试题来源】陕西省咸阳市泾阳县2021-2022学年高三上学期期中 【答案】C【分析】利用辅助角公式化简后求最值.【解析】因为()cos sin 4f x x x x π⎛⎫=+=+ ⎪⎝⎭,定义域为R ,所以()f x C 11.cos80cos50sin80sin50︒︒+︒︒=A .BC .12-D .12【试题来源】陕西省咸阳市泾阳县2021-2022学年高三上学期期中 【答案】B【分析】根据两角差的余弦公式计算即可.【解析】cos80cos50sin 80sin 50cos(8050)cos30︒︒+︒︒=︒-︒=︒=,故选B 12.若tan α,tan β是方程2670x x -+=的两个根,则()tan αβ+= A .-1 B .1 C .-2D .2【试题来源】福建省长乐第七中学2022届高三上学期期中考试 【答案】A【分析】结合一元二次方程根与系数的关系、两角和的正切公式计算即可. 【解析】由于tan α,tan β是方程2670x x -+=的两个根, 所以tan tan 6,tan tan 7αβαβ+=⋅=,所以()tan tan 6tan 11tan tan 6αβαβαβ++===--⋅-.故选A13.在平面直角坐标系中,点P 在射线()403y x x =>上,点Q 在过原点且倾斜角为θ(θ为锐角)的直线上.若4POQ π∠=,则sin 2θ的值为A .2425- B .2425C .725-D .725【试题来源】江苏省南通市海门中学、泗阳中学2021-2022学年高三上学期第二次诊断测试 【答案】D 【分析】设射线()403y x x =>的倾斜角为1θ,从而可得14πθθ=-,且14tan 3θ=,再利用两角差的正切公式以及二倍角正弦公式即可求解. 【解析】设射线()403y x x =>的倾斜角为1θ,且142ππθ<<,14tan 3θ=, 由题意可得14πθθ=-,所以111tan 11tan tan 41tan 7θπθθθ-⎛⎫=-== ⎪+⎝⎭, 2222sin cos 2tan 7sin 22sin cos sin cos tan 125θθθθθθθθθ====++.故选D14.已知1sin()sin()25ππαα-+-=,且(0,)απ∈,则tan()4πα+=A .17-B .17C .7D .17-【试题来源】广东省江门市新会陈瑞祺中学2022届高三上学期10月月考 【答案】A【分析】由题意化简得1sin cos 5αα+=,平方求得242sin cos 25αα=-,进而求得7sin cos 5αα-=,联立方程组,求得sin ,cos αα,得到4tan 3α=-,结合两角和的正切公式,即可求解.【解析】由1sin()sin()25ππαα-+-=,可得1sin cos 5αα+=,两边平方得112sin cos 25αα+=,可得242sin cos 025αα=-<, 因为(0,)απ∈,所以sin 0,cos 0αα><,所以sin cos 0αα->,所以22449(sin cos )1()2525αα-=--=,所以7sin cos 5αα-=, 联立方程组,可得43sin ,cos 55αα==-,所以sin tan s 43co ααα==-,所以41tan tan134tan()4471tan tan 143παπαπα-++===--+-.故选A . 15.已知()1cos 3αβ-=,3cos 4β=,0,2παβ⎛⎫-∈ ⎪⎝⎭,0,2πβ⎛⎫∈ ⎪⎝⎭,则.A .0,2πα⎛⎫∈ ⎪⎝⎭B .,2παπ⎛⎫∈ ⎪⎝⎭C .()0,απ∈D .0,2πα⎡⎫∈⎪⎢⎣⎭【答案】B【分析】由已知得()0,απ∈,再利用同角之间的关系及两角差的余弦公式计算cos 0α<,即可得解. 【解析】()1cos 3αβ-=,0,2παβ⎛⎫-∈ ⎪⎝⎭,()sin αβ∴-=3cos 4β=,0,2πβ⎛⎫∈ ⎪⎝⎭,sin β∴=,()0,απ∴∈, 又cos cos()cos()cos sin()sin ααββαββαββ=-+=---13034=⨯=,,2παπ⎛⎫∴∈ ⎪⎝⎭,故选B16.若tan 24πα⎛⎫+=- ⎪⎝⎭,则cos2=αA .35B .45-C .45D .35【试题来源】河北省石家庄市藁城新冀明中学2021届高三上学期10月月考 【答案】B【分析】根据两角和的正切公式展开得到tan α,同时根据两角和的余弦公式展开并进行齐次化,将弦转化为切,最后计算即可.【解析】由tan tantan 14tan 241tan 1tan tan 4παπααπαα++⎛⎫+===- ⎪-⎝⎭-⋅,得到tan 3α=, 又22222222cos sin 1tan cos 2cos sin cos sin 1tan ααααααααα--=-==++,所以22221tan 134cos 21tan 135ααα--===-++,故选B17.将函数()sin cos f x x x =+的图象向左平移4π个单位,得函数()y g x =的图象,则34g π⎛⎫= ⎪⎝⎭A .12 B .1C .D .1-【试题来源】陕西省西安市八所重点中学2021-2022学年高三上学期联考 (一) 【答案】D【分析】先对()f x 变形,然后通过三角函数图象变换规律求出()g x 的解析式,从而可求出34g π⎛⎫ ⎪⎝⎭的值.【解析】()sin cos 4f x x x x π⎛⎫=+=+⎪⎝⎭,则将()f x 的图象向左平移4π个单位后得,()442g x x x x πππ⎛⎫⎛⎫=++=+= ⎪ ⎪⎝⎭⎝⎭,所以33144g ππ⎛⎛⎫===-⎪ ⎝⎭⎝⎭,故选D18.若sin 4πα⎛⎫+= ⎪⎝⎭sin2α=A .B .89-CD .89【试题来源】黑龙江省哈尔滨市第三中学2021-2022学年高三上学期第三次验收考试 【答案】B【分析】根据整体换元法结合二倍角公式即可求出.【解析】设4παθ+=,则4παθ=-,sin θ=218cos 22sin 1214189sin 2sin 2πθθθα⎛⎫-=-=-=-=- ⎪⎝⎭=⨯.故选B .19.已知()()212sin 02f x x παα⎛⎫=-+<< ⎪⎝⎭在0,6π⎛⎫ ⎪⎝⎭内有零点,且在,66ππ⎛⎫- ⎪⎝⎭上单调递减,则α的取值范围是 A .,124ππ⎛⎫⎪⎝⎭B .,126ππ⎛⎤ ⎥⎝⎦C .,64ππ⎡⎫⎪⎢⎣⎭D .,63ππ⎡⎫⎪⎢⎣⎭【试题来源】云南省昆明市第一中学2022届高三上学期第四期联考 【答案】C【分析】利用余弦二倍角公式可得()()cos 22f x x α=+,再由正弦函数的中心对称点以及单调性即可求解.【解析】()()()212sin cos 22f x x x αα=-+=+,由()0f x =得22π+()2x k k Z πα+=∈,解得()π+24k x k Z πα=-∈, 因为()f x 在π06⎛⎫⎪⎝⎭,内有零点,所以ππ046α⎛⎫-∈ ⎪⎝⎭,,解得ππ124α⎛⎫∈ ⎪⎝⎭,,又2222,k x k k Z παππ≤+≤+∈,解得,2k x k k Z ππαπα-≤≤+-∈由()f x 在ππ66⎛⎫- ⎪⎝⎭,上单调递减,所以266ππαπα⎧-≥⎪⎪⎨⎪-≤-⎪⎩,解得63ππα≤≤,即ππ63α⎡⎤∈⎢⎥⎣⎦,, 所以ππ64α⎡⎫∈⎪⎢⎣⎭,,故选C .20.已知1tan 3α=,则sin2α=A .45B .35C .310D .110【试题来源】江苏省南京市金陵中学2021-2022学年高三上学期12月月考 【答案】B【分析】根据正切值求得正弦、余弦值,从而求得二倍角的正弦值. 【解析】由1tan 3α=知,sin α=cos α=或sin α=,cos α=则3sin 22sin cos 25ααα===,故选B 21.函数22()sin 2sin cos 3cos f x x x x x =++在区间0,2π⎛⎫⎪⎝⎭上的一个对称中心是(,)m n ,则m n +的值为A .8π B .38π C .28π+D .328π+ 【试题来源】河南省部分重点高中2021-2022学年高三上学期12月适应性检测【答案】D【分析】根据三角恒等变换化简函数解析式,再根据图象性质求参数值. 【解析】由题得1cos 21cos 2()sin 23sin 2cos 2222x xf x x x x -+=++⋅=++224x π⎛⎫=++ ⎪⎝⎭,令24x k ππ+=,则28k x ππ=-,当1k =时,38m π=,2n =,故m n +的值为328π+.故选D . 22.已知3sin 45πα⎛⎫+= ⎪⎝⎭,且344ππα<<,则cos α=A .10-B .10C .D 【试题来源】黑龙江省哈尔滨市呼兰区第一中学校2021-2022学年高三上学期第二次校内检测 【答案】A【解析】3,4424ππππααπ<<∴<+<,4cos 45πα⎛⎫∴+=- ⎪⎝⎭, sin 44444cos cos cos cos sin 4ππππππ⎛⎫⎛⎫⎛⎫α+-=α++α+ ⎪ ⎪ ⎪⎝⎭⎝⎝⎭∴⎭α=4355=-=A 23.函数()()44cos tan 1f x x x =+在()0,π上的一个递增区间为A .0,2π⎛⎫ ⎪⎝⎭B .0,4π⎛⎫ ⎪⎝⎭C .3,44ππ⎛⎫ ⎪⎝⎭D .3,4ππ⎛⎫⎪⎝⎭【试题来源】河南省重点中学2021-2022学年高三上学期模拟调研(一) 【答案】D【分析】化简函数解析式为()31cos 444f x x =+,然后利用余弦型函数的单调性可求得结果. 【解析】()()444422cos tan 1sin cos 12sin cos f x x x x x x x =+=+=-=211cos 4311sin 21cos 42444x x x --=-=+,令242k x k πππ-<<,k Z ∈,得11242k x k πππ-<<,取1k =得递增区间,42ππ⎛⎫ ⎪⎝⎭,取2k =,得递增区间3,4ππ⎛⎫⎪⎝⎭,故选D .24.将函数()2ππ2cos 36f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭的图象向右平移()0ϕϕ>个单位长度,得到函数()g x 的图象关于π6x =对称,则ϕ的最小值为 A .π6B .π4C .π3D .5π6【试题来源】“超级全能生”2022届高三全国卷地区11月联考试题(甲卷) 【答案】A【分析】先利用余弦的二倍角公式和辅助角公式化简()f x ,再由图象的平移可得()g x 的图象,由()g x 的图象的对称轴列方程结合0ϕ>即可求得ϕ的最小值.【解析】()2πππ1π2cos 21cos 236323f x x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++=++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦π1π1ππ12cos 2sin 23232362x x x ⎛⎫⎛⎫⎛⎫=++++=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ππ11sin 2cos 23622x x ⎛⎫=+++=+ ⎪⎝⎭,所以()()()11cos 2cos 2222x x g x ϕϕ=-+=-+,因为函数()g x 的图象关于π6x =对称,所以()π22πZ 6k k ϕ⨯-=∈, 所以()ππZ 62k k ϕ=-∈,因为0ϕ>,所以0k =时,π6ϕ=最小,故选A . 25.已知角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边上有一点37tan ,46M ππ⎛⎫ ⎪⎝⎭,则1cos 2sin 22αα++的值为 A .12-或710B .710C .2110D .12-【试题来源】山东省青岛市4区市2021-2022学年高三上学期期中考试 【答案】B【分析】根据特殊角的三角函数值可得点(1,3)M --,再根据三角函数的定义和三角恒等变换,即可得到答案;【解析】(1,3)M --,∴sin α=cos α=,∴214cos 22cos 121105αα=-=⋅-=-,3sin 22sin cos 25ααα⎛⎛=⋅=⋅⋅= ⎝⎝, 411cos 2375sin 222510αα-+∴+=+=,故选B 26.将函数()cos2sin 222x x x f x ωωω⎛⎫=- ⎪⎝⎭,(0)>ω的图象向左平移3ωπ个单位,得到函数()y g x =的图象,若()y g x =在0,4⎡⎤⎢⎥⎣⎦π上为增函数,则ω的最大值为A .1B .2C .3D .4【试题来源】2022年高考数学一轮复习小题多维练(新高考版) 【答案】B【分析】先把函数化为()sin y A x B ωϕ=++的形式,利用图象变换规律,得到g (x )的解析式,再利用正弦函数的单调性,得出结论. 【解析】()cos 2sin 222x x x f x ωωω⎛⎫=- ⎪⎝⎭22cossin222xxxωωω=-sin x x ωω=2sin 3x πω⎛⎫=- ⎪⎝⎭,向左平移3ωπ个单位,得到函数()2sin y g x x ω==的图象,由()y g x =在0,4⎡⎤⎢⎥⎣⎦π上为增函数,则42ππω≤,所以2ω≤,故ω的最大值为2.故选B27.已知1sin 24α=-,则2πsin 4α⎛⎫+= ⎪⎝⎭A .18B .38CD .58【试题来源】山东省潍坊市2021-2022学年高三上学期期中 【答案】B【分析】利用二倍角降幂公式和诱导公式可求得2sin 4πα⎛⎫+ ⎪⎝⎭的值.【解析】由二倍角的降幂公式可得211cos 211sin 2324sin 42228παπαα⎛⎫-+-⎪+⎛⎫⎝⎭+==== ⎪⎝⎭.故选B .28.若α,β均为锐角,sin α=3sin()5αβ+=,则cos β=A BCD . 【试题来源】吉林省东北师范大学附属中学2021-2022学年高三上学期第二次摸底考试 【答案】B【分析】根据角度范围得到cos α=,()4cos 5αβ+=-,再根据和差公式展开得到答案.【解析】α,β均为锐角,sin α=cos α==,sin sin()ααβ>+,故αβ+为钝角,()4cos 5αβ+==-.()()()cos cos cos cos sin sin βαβααβααβα=+-=+++4355==B29.已知函数()()2πsin πsin 2f x x x x ⎛⎫=++ ⎪⎝⎭,则下列正确的是A .()f x 最小正周期为2πB .π,06⎛⎫⎪⎝⎭是()f x 的一个对称中心C .将()f x 图象向右平移π2个单位长度后得到()g x 的图象,此时()5πsin 26g x x ⎛⎫=-- ⎪⎝⎭D .ππ,63⎡⎤-⎢⎥⎣⎦是()f x 的一个减区间【试题来源】“四省八校”2021-2022学年高三上学期期中质量检测考试 【答案】B【分析】应用三角恒等变换可得()sin 23πx f x ⎛⎫=-- ⎪⎝⎭,结合正弦函数的性质判断各选项的正误.【解析】())21sin cos 2cos 1sin 22sin 22π3x x x x x x f x ⎛⎫=-⋅-=-=-- ⎪⎝⎭, 所以最小正周期22T ππ==,A 错误;π06f ⎛⎫= ⎪⎝⎭,则π,06⎛⎫⎪⎝⎭是()f x 的一个对称中心,B 正确;()π4()sin(2)sin(2)233g x f x x x ππ=-=--=-,C 错误;令π222232k x k ππππ--+≤≤可得1212k x k π5ππ-≤≤π+,()f x 在5[,]1212k k ππππ-+上递减,显然ππ,63⎡⎤-⎢⎥⎣⎦不是子区间,故D 错误.故选B30.已知点P 在圆O :2214x y +=上,从1,02A ⎛⎫⎪⎝⎭出发,沿圆周逆时针方向运动了弧长x (0πx <<)到达B 点,且1tan 2x =,又B 点在角π4β+终边上,则cos 2β=A .2425-B .45-C .45D .2425【试题来源】“四省八校”2021-2022学年高三上学期期中质量检测考试 【答案】D 【分析】易知212xAOB x ∠==,由1tan 2x =,进而得到4tan 3π4β⎛⎫+= ⎪⎝⎭,解得1tan 7β=求解.【解析】因为212xAOB x∠==,22tan 4tan tan 21tan 3x AOB x x ∴∠===-,4tan 43πβ⎛⎫∴+= ⎪⎝⎭,1tan 7β∴=,222222cos sin 1tan 24cos 2cos sin 1tan 25βββββββ--===++.故选D 31.若53,42ππα⎛⎫∈ ⎪⎝⎭A .cos sin αα-B .cos sin αα--C .cos sin αα+D .cos sin αα-+【试题来源】山东省临沂市2021-2022学年高三上学期期中 【答案】D【分析】再结合α的范围确定cos α和sin α的符号即可求解.【解析】由二倍角公式可知,221cos 2cos αα+=,21cos 22sin αα-=,|cos ||sin |αα-,因为53,42ππα⎛⎫∈ ⎪⎝⎭,所以cos 0α<,sin 0α<,cos sin αα-+.故选D . 32.已知函数()()211sin sin 0222xf x x ωωω=+->在区间()π,2π内没有零点,则ω的取值范围是A .1150,,848⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦⋃B .1170,,868⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦⋃C .1150,,8612⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦⋃D .1150,,12612⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦⋃【试题来源】天津市南开中学2021-2022学年高三上学期第二次月考 【答案】A【分析】先将()f x 解析式化为同名函数,再根据()f x 在区间()π,2π内没有零点则22Tππ-≤;假设()f x 在区间()π,2π内有零点,解出ω的表达式;从而推导()f x 在区间()π,2π内没有零点时ω的取值范围.【解析】()()211sin sin 0222x f x x ωωω=+->,()()111111cos sin sin cos 222224f x x x x x x πωωωωω⎛⎫∴=-+-=-=- ⎪⎝⎭, ()f x 在区间()π,2π内没有零点,22Tππ∴-≤即2T π≥, 2=2T ππω≥,且0>ω,01ω∴<≤,当()f x 在区间()π,2π内有零点时,则,4x k k z πωπ-=∈,即4,k x k z ππω+=∈,42,k x k z ππππω+∴<=<∈,11,824k k k z ω∴+<<+∈,又01ω<≤,1184ω∴<<或518ω<≤,()f x 在区间()π,2π内没有零点,ω∴的取值范围是1150,,848⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦⋃.故选A33.一列波沿x轴正方向传播,其波函数的表达式为()()111111()cos 0,0,0,02f x A x A x ωϕωπϕ=+>>>>≤≤,511,1212是函数f (x )相邻的两个零点;另一列波沿x 轴负方向传播,其波函数的表达式为()sin 2(02)3g x x x ππ⎛⎫=+≤≤ ⎪⎝⎭;在某一时刻,两列波的图象如图所示;函数()()()h x g x f x =+表示两列波叠加之后的波函数(叠加后的波函数为原来两个波函数的和),则下列说法正确的有①12ωπ=;②13x =是函数()g x 的一个零点;③函数h (x )的最小正周期是12;④函数h(x )的振幅为1;⑤函数h (xA .①②④B .①②⑤C .②③④D .③④⑤【试题来源】云南省师范大学附属中学2022届高三高考适应性月考卷(五) 【答案】B【分析】根据()f x 相邻的两个零点求得T ,进而求得1ω,从而判断①的正确性.由13g ⎛⎫⎪⎝⎭来判断②的正确性.结合三角恒等变换化简()h x ,由此求得()h x 的最小正周期、振幅,从而判断③④⑤的正确性. 【解析】因为5111212,是函数()f x 的两个相邻的零点,设()f x 的最小正周期为T , 所以1151212122T =-=,则1T =,所以12π2πT ω==,故①正确; 12ππsin 0333g ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,所以②正确; 由图知,11A =,512是函数()f x 单调增区间上的一个零点, 所以153π2π2π()122k k ϕ+=+∈Z ,由于1π0ϕ>>,所以12π3ϕ=,则2π()cos 2π3f x x ⎛⎫=+ ⎪⎝⎭,2π()()()cos 2π3h x g x f x x ⎛⎫=+=++ ⎪⎝⎭πsin 2π2π2π3x x x ⎛⎫+=⎪⎝⎭π2π4x ⎛⎫+ ⎪⎝⎭,故函数()h x 的最小正周期是1,函数()h x 的振幅为A = 所以③④错误,⑤正确.故选B 34.已知1sin 3α=,sin3α=A .2027B .2227C .2327D .2527【试题来源】中学生标准学术能力诊断性测试2021-2022学年高三上学期11月测试 【答案】C【分析】首先利用两角和的正弦公式和二倍角公式求得2sin 3sin cos 22sin cos ααααα=+,然后结合已知条件求cos2α和2cos α,进而得到答案. 【解析】由两角和的正弦公式和二倍角公式可知,2sin 3sin(2)sin cos 2sin 2cos sin cos 22sin cos ααααααααααα=+=+=+,因为1sin 3α=,所以2cos21279sin αα=-=,228cos 1sin 9αα=-=,从而171823sin 32393927α=⨯+⨯⨯=.故选C .35.哥特式建筑是1140年左右产生于法国的欧洲建筑风格,它的特点是尖塔高耸、尖形拱门、大窗户及绘有故事的花窗玻璃,如图所示的几何图形,在哥特式建筑的尖形拱门与大窗户中较为常见,它是由线段AB 和两个圆弧弧AB ,弧BC 围成,其中一个圆弧的圆心为A ,另一个圆弧的圆心为B ,圆O 与线段AB 及两个圆弧均相切,则tan ∠AOB 的值是A .247-B .724-C .43-D .34-【试题来源】江苏省扬州大学附属中学2021-2022学年高二上学期期中 【答案】A【分析】根据题意,结合勾股定理,以及正切的二倍角公式,即可求解. 【解析】如图所示,过点O 作⊥OD AB ,交AB 于点D ,设AB a ,圆O 的半径为r ,由题意知OD r =,OA a r =-,2a AD =,因为222OA OD AD =+,得()2222a a r r ⎛⎫-=+ ⎪⎝⎭,解得38a r =, 因此42tan 3aAD AOD OA r ∠===, 故2422tan 243tan tan 2161tan 719AOD AOB AOD AOD ⨯∠∠=∠===--∠-.故选A . 36.若tan 2tan10α=,则()()cos 80sin 10αα-=- A .1 B .2 C .3D .4【试题来源】湖南师范大学附属中学2021-2022学年高三上学期11月第三次月考 【答案】C【分析】利用诱导公式、两角和公式可得()()cos 80sin 10αα-=-sin cos10cos sin10sin cos10cos sin10αααα+-,再利用弦化切即得.【解析】因为tan 2tan10α=,所以()()()()cos 80cos 1090sin 10sin 10αααα-+-=--()()sin 10sin 10αα+=-sin cos10cos sin10sin cos10cos sin10αααα+=-tan tan10tan tan10αα+=-3tan103.tan10==故选C .37.设α为锐角,若cos ()6a π+=-35,则sin 26α⎛⎫- ⎪⎝⎭π的值为A .-725B .1625C .-15D .725【试题来源】海南省华侨中学2022届高三11月第三次月考 【答案】D【分析】由二倍角公式可得cos 23πα⎛⎫+ ⎪⎝⎭,再由诱导公式即可得解.【解析】因为3cos 65πα⎛⎫+=- ⎪⎝⎭,所以27cos 22cos 13625ππαα⎛⎫⎛⎫+=+-=- ⎪ ⎪⎝⎭⎝⎭,所以7sin 2sin 2cos 2632325ππππααα⎛⎫⎛⎫⎛⎫-=+-=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选D .38.函数π()cos(3π))2f x x x =--的单调增区间为A .52,2,66k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦B .22,2,33k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦C .22,2,33ππk πk πk Z ⎡⎤-++∈⎢⎥⎣⎦,D .52,2,66k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦【试题来源】山西大学附属中学2022届高三上学期11月期中 【答案】C【分析】利用三角恒等变换得到π()2sin 6f x x ⎛⎫=- ⎪⎝⎭,再计算单调区间得到答案.【解析】()ππ()cos 3πcos π2sin 26f x x x x x ⎛⎫⎛⎫=--=-=- ⎪ ⎪⎝⎭⎝⎭,取πππ2π2π262k x k -+≤-≤+,k Z ∈,解得π2π2π2π33k x k -+≤≤+,k Z ∈.故选C .39.已知α,β为锐角,且1tan 7α=,()cos αβ+=cos2β= A .35B .25C .45D 【试题来源】宁夏中卫市第一中学2022届高三上学期第三次月考 【答案】C【分析】首先根据同角三角函数的基本关系求出sin α,()sin αβ+再利用两角差的余弦公式求出cos β,最后利用二倍角公式解得.【解析】依题意,α为锐角,tan 17α=,sin α∴=,又α,β为锐角,得0αβπ<+<,()cos αβ+=()sin αβ∴+=;()()()cos cos cos cos sin sin βαβααβααβα⎡⎤∴=+-=+++⎣⎦,得cos β===因此,294cos22cos 121105ββ=-=⨯-=,故选C . 40.函数的()π2sin cos 6x x x f ⎛⎫=-+ ⎪⎝⎭所有零点为A .π,Z 2k x k =∈ B .ππ,Z 2x k k =+∈C .π,Z x k k =∈D .2π,Z x k k =∈【试题来源】华大新高考联盟(全国版)2021-2022学年高三上学期11月教学质量测评 【答案】C【分析】根据两角和的正弦公式化简()f x ,再令()0f x =即可求解. 【解析】由题可知()π2sin cos 6x x x f ⎛⎫=-+ ⎪⎝⎭2sin cos cos sin c πos π66x x x ⎛⎫=-+ ⎪⎝⎭cos cos x x x x =-+=,令()0f x x ==,可得π,Z x k k =∈,所以()f x 零点为π,Z x k k =∈,故选C . 二、多选题1.下列式子正确的是 A.sin15cos15+︒︒=B.cos 75︒=C.2tan 151︒+︒= D .tan12tan33tan12tan331︒+︒+︒︒=【试题来源】山东省济南市实验中学2021-2022学年高三上学期10月月考 【答案】ACD【分析】对于A ,利用两角差的正弦余弦公式求出sin15,cos15︒︒的值即可,对于B ,利用两角和的余弦公式求解,对于C ,求出tan15︒的值代入化简即可,对于D ,利用两角和的正切公式求解【解析】对于A,因为sin15sin(4530)sin45cos30cos45sin30︒=︒-︒=︒︒-︒︒=cos15cos(4530)cos45cos30sin45sin30︒=︒-︒=︒︒+︒︒=,所以sin15cos15+︒︒=A 正确, 对于B,因为cos75cos(4530)cos45cos30sin45sin30︒=︒+︒=︒︒-︒︒=,所以B 错误,对于C,因为11tan 30tan15tan(4530)21tan 30-︒︒=︒-︒===+︒,所以((22tan 15221︒+︒=+=,所以C 正确,对于D ,因为()tan 33tan12tan 45tan 331211tan 33tan12︒+︒︒=︒+︒==-︒︒,所以tan33tan121tan33tan12︒+︒=-︒︒,所以tan12tan33tan12tan331︒+︒+︒︒=,所以D 正确,故选ACD2.已知sin 3cos 3cos sin αααα+=-5,下列计算结果正确的是A .1tan 2α=B .tan α=2C .213cos sin225αα+=D .26sin cos25αα-=【试题来源】广东省湛江市第二十一中学2022届高三上学期9月第2次月考 【答案】BC【分析】将条件变形为用tan α表示的形式,进而可求出tan α,则可判断选项AB ,再将选项CD 变形,用tan α表示,代入tan α的值即可判断. 【解析】由sin 3cos 53cos sin αααα+=-得tan 353tan αα+=-,解得tan 2α=,故A 错误,B 正确; 222221cos sin cos 1tan 123cos sin22sin cos tan 1415ααααααααα++++====+++,故C 正确;22222222sin cos 2tan 17sin cos2s ta in cos 15n αααααααα---===++,故D 错误.故选BC .3.达芬奇是意大利著名的画家、数学家、物理学家和机械工程师.悬链线问题(固定项链的两端,使其在重力的作用下自然下垂,那么项链所形成的曲线是什么?)起源于他的画作《抱银貂的女人》(如图所示),他苦苦思索,去世时仍没找到问题的答案.随着后人深入的研究,得出了悬链线的函数解析式为()e e 2ax axf x a-+=,其中a 为悬链线系数.当1a =时,()e e 2x x f x -+=称为双曲余弦函数,记为e e ch 2x x x -+=.类似的双曲正弦函数e e sh 2x xx --=,若直线x t =与ch x 和sh x 的图象分别交于点A ,B ,则下列结论中正确的是A .()sh sh ch ch sh x y x y y x +=⋅+⋅B .()ch ch ch sh sh x y x y x y +=⋅-⋅C .线段AB 的长度随着t 的增大而变短D .ch sh y x ⋅是偶函数 【答案】AC【分析】根据函数的新定义,结合两角和与差的正弦、余弦函数的公式,逐项运算,即可求解.【解析】由()sh 2x y x ye e x y ++-+=,可得sh ch ch sh 22222x x y y x x y y x y x ye e e e e e e e e e x y x y ----+---++--⋅+⋅=⋅+⋅=, 所以A 正确;由()ch 2x y x ye e x y +--++=,可得()ch ch sh sh ch 22222x x y y x x y y x y y xe e e e e e e e e e x y x y x y ------++--+⋅-⋅=⋅-⋅=≠+,所以B 错误;由线段AB 的长度为ch sh 22t t t tt e e e e t t e ---+--=-=,且随着t 的增大,t e -越来越小,所以C 正确;因为()ch ch 2x x e e x x -+-==,()sh h 2x xe e x s x ---==-,所以chx 是偶函数,shx 是奇函数,所以ch sh x x ⋅是奇函数,所以D 错误.故选AC . 4.已知函数f (x )=2 cos 2x -cos (2x -θ)(0)2πθ<<的图象经过点3(0,)2,则A .点(,1)12π是函数f (x )的图象的一个对称中心B .函数f (x )的最大值为2C .函数f (x )的最小正周期是2πD .直线x =3π是y =f (x )图象的一条对称轴 【试题来源】海南省华侨中学2022届高三11月第三次月考 【答案】ABD【分析】根据题意求出函数 ()f x 的解析式 , 再结合函数的定义与性质判断选项中的命题是否正确.【解析】因为函数 2()2cos cos(2),02f x x x θπθ=--<<,()f x 的图象经过点3(0,)2, 所以32cos(2θ=--),解得1cos 2θ=,因为02πθ<<,所以3πθ=,21()2cos cos(2)1cos 2cos 22221cos(2)1323f x x x x x x cos x x ππ=--=+-=+=++因为y cosx =图象的对称中心是点(,0)()2k k Z ππ+∈,所以令2,3210x k k Z y πππ⎧+=+∈⎪⎨⎪-=⎩得,1221k x k Z y ππ⎧=+∈⎪⎨⎪=⎩当0k = 时,12x π=所以点(,1)12π是函数()f x 图象的一个对称中心,所以A 正确;因为1cos(2)13x π-+,所以()f x 的最大值为2,所以B 正确;因为函数 ()f x 的最小正周期22T ππ==,所以C 错误; 因为y cosx = 图象的对称轴方程是,,x k k Z π=∈ 所以令2,3x k k Z ππ+=∈,得,26k x k Z ππ=-∈, 当1k =时,3x π=,所以直线3x π=是函数()f x 图象的一条对称轴,所以D 正确.故选ABD5A B .22cos sin 1212ππ-C .cos15 sin 45 sin15cos45︒︒-︒︒D .2tan151tan 15︒-︒【试题来源】湖南省长沙市雅礼教育集团2021-2022学年高二上学期期中联考 【答案】AB【分析】结合二倍角公式和正弦的差角公式依次讨论各选项即可得答案.【解析】选项A sin 60==︒=选项B :22cos sin cos12126πππ-==选项C :()1cos15sin 45sin15cos 45sin 4515sin 302︒︒-︒︒=︒-︒=︒=;选项D :22tan1512tan1511tan 301tan 1521tan 1522︒︒=⨯=︒==-︒-︒AB .6.已知函数()2sin 2x x f x =+ A .()f x 的最小正周期为π B .()f x 在,03π⎡⎤-⎢⎥⎣⎦上单调递增C .曲线()f x 关于,03π⎛⎫⎪⎝⎭对称D .曲线()f x 关于6x π=对称【试题来源】福建省宁德市部分达标中学2022届高三上学期期中联合考试 【答案】ABC【分析】化简得到()π2sin 23f x x ⎛⎫=+ ⎪⎝⎭,计算函数周期得到A 正确,将BCD 选项带入函数判断函数单调性和对称性得到答案.【解析】())2sin 2sin 21cos2sin 2x x x x f x x x =++=π2sin 23x ⎛⎫=+ ⎪⎝⎭.()f x 的最小正周期为2ππ2T ==,A 正确;,03x π⎡⎤∈-⎢⎥⎣⎦,π2,333x ππ⎡⎤+∈-⎢⎥⎣⎦,函数单调递增,B 正确;π2ππ2sin 0333f ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,()f x 关于,03π⎛⎫⎪⎝⎭对称,C 正确; πππ2sin 2633f ⎛⎫⎛⎫=+=≠ ⎪ ⎪⎝⎭⎝⎭,D 错误.故选ABC . 7.关于函数()sin cos ()f x x x x =+∈R ,则下列说法中正确的是 A.()f x B .()f x 的最小正周期为π C .()f x 的图象关于直线4x π=对称D .()f x 在2,23ππ⎛⎫ ⎪⎝⎭上单调递增【试题来源】山东省济宁市嘉祥县第一中学2021-2022学年高三上学期期中考试 【答案】ACD【分析】计算()π()2f x f x +=得到π2是()f x 的一个周期,B 错误,0,2x π⎡⎤∈⎢⎥⎣⎦时,()4f x x π⎛⎫=+ ⎪⎝⎭,计算最值得到A 正确,()π()2f x f x -=得到C 正确,计算单调性得到D 正确,得到答案.【解析】因为()πππ()sin cos cos sin 222f x x x x x f x ⎛⎫⎛⎫+=+++=+= ⎪ ⎪⎝⎭⎝⎭所以π2是()f x 的一个周期,故B 错误;当π0,2x ⎡⎤∈⎢⎥⎣⎦时,()πsin cos 4f x x x x ⎫⎛=+=+ ⎪⎝⎭,所以当π4x =时,()max f x A 正确;因为()πππ()sin cos cos sin 222f x x x x x f x ⎛⎫⎛⎫-=-+-=+= ⎪ ⎪⎝⎭⎝⎭所以()f x 的图象关于直线π4x =对称,故C 正确;当2,23x ππ⎛⎫∈ ⎪⎝⎭时,()sin cos 4f x x x x π⎛⎫=-=- ⎪⎝⎭,因为5,4412x πππ⎛⎫-∈ ⎪⎝⎭,所以()f x 在2,23ππ⎛⎫ ⎪⎝⎭上单调递增,故D 正确.故选ACD . 8.下列函数的周期为π的是 A .sin y x =B .sin y x =C .2sin 23cos y x x =+D .tan cot y x x =-【试题来源】山东省临沂市重点高中2021-2022学年高三上学期第一次月考 【答案】BC【分析】根据三角函数的周期公式依次计算每个选项的周期得到答案. 【解析】sin y x =,2πT =,A 不满足;sin y x =的图象如图所示:根据图象知周期为π,B 满足;21cos 233sin 23cos sin 23sin 2cos 2222x y x x x x x +=+=+=++()322x ϕ=++,其中3tan 2ϕ=,2ππ2T ==,C 满足;22sin cos sin cos cos 22tan cot 1cos sin sin cos tan 2sin 22x x x x x y x x x x x x x --=-=-===-,π2T =, D 不满足.故选BC .9.已知tan 4α=,1tan 4β=-,则A .tan()tan 1αβ-=B .α为锐角C .3tan()45πβ+=D .tan 2tan 2αβ=【试题来源】河北省保定市部分学校2022届高三上学期期中 【答案】ACD【分析】由诱导公式可判断A ,由正切函数的定义可判断B ,由正切函数的两角和公式可判断C ,由二倍角公式可判断D .【解析】对于A ,因为tan 4α=,1tan 4β=-,所以tan()tan tan tan 1αβαβ-=-=,故A正确;对于B ,因为tan 40α=>,所以α为第一象限角或第三象限角,故B 错误;对于C ,因为1tan 4β=-,所以1tan 3tan()41tan 5πβββ++==-,故C 正确; 对于D ,因为tan 4α=,1tan 4β=-,所以222122tan 24884tan 2,tan 21tan 141515114ααβα⎛⎫⨯- ⎪⨯⎝⎭===-==---⎛⎫-- ⎪⎝⎭, 故D 正确.故选ACD10.对于函数()sin f x x x =,给出下列选项其中正确的是 A .()f x 的图象关于点π,06⎛⎫⎪⎝⎭对称B .()f x 的最小正周期为πC .()f x 在区间5ππ,66⎛⎫-⎪⎝⎭上单调递增 D .π0,2x ⎡⎤∈⎢⎥⎣⎦时,()f x 的值域为[1,2]【试题来源】浙江省绍兴市诸暨中学2021-2022学年高一(实验班)上学期期中 【答案】CD【分析】由辅助角公式化简()f x ,利用正弦函数的对称中心可判断A ;由正弦函数的周期公式可判断B ;利用正弦函数的单调性可判断C ;利用正弦函数的性质可判断D ,进而可得正确选项.【解析】()πsin 2sin 3f x x x x ⎛⎫=+=+ ⎪⎝⎭,对于A :令()πππZ 63k k +=∈,可得1Z 2k =∉,故选项A 不正确; 对于B :()f x 的最小正周期为2π=2π1,故选项B 不正确; 对于C :若5ππ66x -<<,则πππ232x -<+<, 所以()f x 在区间5ππ,66⎛⎫-⎪⎝⎭上单调递增,故选项C 正确; 对于D :当π0,2x ⎡⎤∈⎢⎥⎣⎦时,ππ5π336x ≤+≤,所以1πsin 123x ⎛⎫≤+≤ ⎪⎝⎭,所以π0,2x ⎡⎤∈⎢⎥⎣⎦时,()f x 的值域为[1,2],故选项D 正确;故选CD .三、填空题 1.若2sin 3α=,则cos2=α____________. 【试题来源】河南省焦作市温县第一高级中学2021-2022学年高三上学期11月月考【答案】19【分析】利用余弦的二倍角公式即可求解﹒【解析】2221cos 212sin 1239αα⎛⎫=-=-⨯= ⎪⎝⎭,故答案为192.已知角θ的终边过点P (1,2),则tan 4πθ⎛⎫+= ⎪⎝⎭____________.【试题来源】沪教版(2020) 必修第二册 堂堂清 阶段测试二 【答案】3-【分析】先利用任意角的三角函数的定义求出tan θ的值,再利用两角和的正切公式求解即可【解析】因为角θ的终边过点P (1,2),所以tan 2θ=,所以tan tan214tan 34121tan tan 4πθπθπθ++⎛⎫+===- ⎪-⎝⎭-,故答案为3- 3.已知α____________.【答案】tan α-【分析】利用余弦的二倍角公式及同角之间的关系,即可得解.tan α==, 因为α为钝角,则tan 0α<,所以原式tan α=-,故答案为tan α-. 4.已知1tan 3α=,则5tan 4πα⎛⎫+=⎪⎝⎭____________. 【试题来源】天津市部分区2021-2022学年高三上学期期中 【答案】2【分析】利用诱导公式和两角和的正切公式可求得结果.【解析】1151tan 3tan tan tan 214441tan 13πππααπααα++⎛⎫⎛⎫⎛⎫+=++=+=== ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭-.故答案为2. 5.已知tan 3πθ⎛⎫+= ⎪⎝⎭tan 2θ=____________.【试题来源】2022年全国著名重点中学领航高考冲刺试卷(七)【分析】由两角和的正切公式可得tan θ=,再利用二倍角公式即求.【解析】由题意得tan 3πθ⎛⎫+== ⎪⎝⎭7tan θ=tan θ=,则2222tan 7tan 21tan 1θθθ===--⎝⎭6.若4cos 65πα⎛⎫+= ⎪⎝⎭,则sin 26πα⎛⎫-= ⎪⎝⎭____________.【试题来源】广东省八校2022届高三上学期第二次联考 【答案】725-【分析】依题意sin 2sin 2662πππαα⎡⎤⎛⎫⎛⎫-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦利用诱导公式及二倍角公式计算可得;【解析】因为4cos 65πα⎛⎫+= ⎪⎝⎭,所以sin 2sin 2662πππαα⎡⎤⎛⎫⎛⎫-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦2247cos 22cos 12166525ππαα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=-+=-+-=-⨯-=-⎢⎥ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎢⎥⎣⎦.故答案为725-.7.已知sin 0,2πθθ⎛⎫=∈ ⎪⎝⎭,则tan 24πθ⎛⎫-= ⎪⎝⎭____________.【试题来源】四川省宜宾市普通高中2022届高三上学期第一次诊断测试 【答案】7【分析】根据已知条件求出cos θ,再求出tan θ和tan2θ,用正切的差角公式将tan 24πθ⎛⎫- ⎪⎝⎭展开,代入数值计算即可﹒【解析】sin sin 0cos tan 22cos πθθθθθθ⎛⎫∈⇒ ⎪⎝⎭,==, 所以22tan 44tan 21tan 143θθθ---===,所以41tan2tantan2134tan 27441tan21tan2tan 143πθπθθπθθ----⎛⎫- ⎪⎝⎭-====++﹒故答案为7﹒ 8.若()4cos 5πα-=,α为第三象限角,则sin 4πα⎛⎫+= ⎪⎝⎭____________.【试题来源】海南热带海洋学院附属中学2021届高三10月份月考。
[名师原创解析]2020届四川省巴蜀中学高考适应性月考卷(二)理科数学试题
3
2
A.3
B.4
C.5
D.6
第九套 - 1
全国名校
合卷:河北邯郸焦子奇
【考点】三角函数的性质
【命题意图】本题考查了三角函数的性质,分类讨论的数学思想,考查了学生的逻辑思维能
力和运算能力。
答案:D.
解析:(浙江衢州汪强)
当 ω > 0 时, 5π ≤ ω ⋅ π + π < 13π ,即 2 ≤ ω < 6 ,所以 ω = 2,3,4,5 ;
全国名校
合卷:河北邯郸焦子奇
❿ 巴蜀中学 2020 届高考适应性月考卷(二)
理数
10.(巴蜀中学 2020 届高考适应性月考卷(二)理数)已知 AB ⋅ AC = 0, BC = 4, P 是三角
形 ABC 平面内任意一点,且满足| PA |= 1, PB ⋅ PC 的最小值是( ).
x
第九套 - 4
全国名校
合卷:河北邯郸焦子奇
f (x) 的导函数,若关于 x 的方程 f '(x) − f (x) = 0 有两个不等的根,则实数a 的取值范围是 x +1
________________.
【考点】导数与零点问题
【命题意图】此题对学生能力要求较高,是拉开学生得分档次的题目.本题考查了学生利,
第九套 - 2
全国名校
合卷:河北邯郸焦子奇
y′ = x ,所以 2k =
p
p
解法 3:极限法 2
l1,l2 重合时,直线 AM 即抛物线在点 A 处的切线,直线 BN 即抛物线在点 B 处的切线,
联立直线l1 与抛物线C 消去 y 得 xA + xB = 2pk ,由阿基米德三角形知 xA + xB = 2xE ,
重庆市巴蜀中学2020届高三高考适应性月考卷( 六)文科数学含解析
x
6b 5
,A(
x1,y1
),B(
x2,y2
).
直线与椭圆方程联立
my
x
6b 5
,
消去
x2 4 y2 4b2,
x 得 (m2
4) y2
12 5
bmy
64b2 25
0,
所以
y1 y1
y2
y2
12bm 5(m2 4)
,
64b2 25(m2
4)
,
4b
所以 S△AQB
1 2
2b
6 5
所以 m 0时,(S△AQB )max
16b2 25
4 25
b2
1 4
,
故椭圆的标准方程为 x2 4 y2 1 .
……………………………………………(12 分)
21.(本小题满分 12 分)
(1)解:
f
(x)
1 2x
2ax
b
,由题有
f f
(1) a b 1 2,
(1)
1 2
2a
b
0
10.如图 2,取 △ABC,△A1B1C1 的外接圆的圆心分别为 M,N ,连接 MN ,
取 MN 的中点 O ,则 O 是三棱柱 ABC A1B1C1 的外接球的球心,设
△ABC 的外接圆的半径为 r ,三棱柱 ABC A1B1C1 的外接球的半径为
R
,由正弦定理得,∵
AB sin C
2 sin
…………………………………………(12 分)
22.(本小题满分 10 分)【选修 4−4:坐标系与参数方程】 解:(1)点 P 的直角坐标为 (0,2), 圆 M 的标准方程为 (x 2)2 y2 4.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
·1·
2020届云南高三下学期高考适应性月考卷
(理科)数学(七)
一、选择题(本大题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合
题目要求的)
1.体育节到来,多数同学都会参加至少一个运动项目.设集合U={甲班全体同学},集合A= {参加
跳高的甲班同学},集合B= {参加跳远的甲班同学},则()UABð)表示的是
A.既参加跳高又参加跳远的甲班同学 B.既不参加跳高也不参加跳远的甲班同学
C.参加跳高或跳远的甲班同学 D.不同时参加跳高和跳远的甲班同学
2.已知复数13,zi则28z
.13Ai .13Bi .13Ci .13Di
3.已知平面向量,,abrr命题“||2||abrr”是“|2||2|ababrrr”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.某工厂为了对40个零件进行抽样调查,将其编号为00, 01, 38, 39.现要从中选出5个,利用下面
的随机数表,从第一行第3列开始,由左至右依次读取,则选出来的第5个零件编号是
A.36 B.16 C.11 D.14
5.朱世杰是元代著名的数学家,有“中世纪世界最伟大的数学家”之称.其著作《四元玉鉴》是一部
成就辉煌的数学名著,受到数学史研究者的高度评价.《四元玉鉴》下卷“杂范类会”中第一问为: "今有
沈香立圆球一只,径十寸,今从顶截周八寸四分,问厚几何?"大意为现有一个直径为10的球,从上面截
一小部分,截面圆周长为8.4,问被截取部分几何体的高为多少.已知朱世杰是以圆周率为3来计算,则
《四元玉鉴》中此题答案为(注:24.823.04)
A.0.2 B.0.4 C.0.6 D.0.8
6.函数25()xxxfxee的图象大致为
·2·
7.已知抛物线22(0)ypxp的准线与椭圆22194xy相交的弦长为23,则p=
A.1 B.2 C.3 D.4
8.在正四面体A-BCD中, E. F分别为AB, CD的中点,则下列命题不正确的是
A. EF⊥AB B. EF⊥CD
C.EF与AC所成角为4 D.EF与BD所成角为3
9. 已知数列{}na满足∀1*1233,3.nnnaaannLN则na的前n项和ns
133.2nA 31.2n
B
2
.2Cnn
2.4Dnn
10. 如图1,已知在算法中“\”和“mod”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑
洞”( 即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入
x=325,则输出的i=
A.3 B.4 C.5 D.6
·3·
11. 已知函数2()sin,fxxxx若0,23(log3),(log0.2),afbfc=3(0.2),f则
A. a>b>c B. b>a>c C. c>b>a D. c>a>b
12.双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位通
过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲
线,两者相交便可确定船位我们来看一种简单的“特殊”状况:如图2所示,已知三个发射台分别为A, B.
C且刚好三点共线,已知AB=34海里,AC=20海里.现以AB的中点为原点, AB所在直线为x轴建系.
现根据船P接收到C点与A点发出的电磁波的时间差计算出距离差,得知船P在双曲线
22
(27)13664xy
的左支上,若船P上接到A台发射的电磁波比B台电磁波早185.2μs(已知电磁波
在空气中的传播速度约为0.3km/μs.1海里=1.852km),则点P的坐标(单位:海里)为
·4·
A.903211(,)77 B.135322(,)77
32
.(17,)3C
D. (45,162)
二、填空题(本大题共4小题,每小题5分,共20分)
13. 曲线2(1)lnyxx在(1, 0)处的切线方程为_____
14. 已知x, y满足315,212,,xyxyxyNN,则z=3x+2y的最大值为____
15.作家马伯庸小说《长安十二时辰》中,靖安司通过长安城内的望楼传递信息.同名改编电视剧中,
望楼传递信息的方式有一种如下:如图3所示,在九宫格中,每个小方格可以在白色和紫色(此处以阴影
代表紫色)之间变换,从而一共可以有512种不同的颜色组合,即代表512种不同的信息.现要求每一-
行,每一列上至多有一个紫色小方格(如图所示即满足要求).则一共可以传递___种信息. (用数字作答)
16.已知ω>14,函数()sin()4fxx在区间(π, 2π)上单调.
1
(,1].4①
②f(x)在区间(π, 2π)上单调递减;
③f(x)在区间(0, π)上有零点;④f(x) 在区间(0, π)上的最大值一定为1.
以上四个结论,其中正确结论的编号是____
三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)
·5·
17. (本小题满分12分)
华为手机作为全球手机销量第二位,一直深受消费者喜欢。据调查数据显示,2019年度华为手
机(含荣耀)在中国市场占有率接近40%!小明为了考查购买新手机时选择华为是否与年龄有一-定
关系,于是随机调查100个2019年购买新手机的人,得到如下不完整的列表。定义30岁以下为“年
轻用户”,30岁以上为“非年轻用户”。
购买华为 购买其他 总
计
年轻用
户
28
非年轻
用户
24
6
0
总计
附:22().()()()()nadbcKabcdacbd
(1)将列表填充完整,并判断是否有90%的把握认为购买手机时选择华为与年龄有关?
(2) 若采用分层抽样的方法从购买华为手机用户中抽出9个人,再随机抽3人,其中年轻用户的
人数为X,求X的分布列和期望.
18. (本小题满分12分)
在△ABC中,2,3BACD是BC上一点,AD⊥AC且AD=1.
(1)若3,AB求BC;
(2)求21.ABAC
·6·
19. (本小题满分12分)
如图4,已知在四棱锥P-ABCD中,底面ABCD为等腰梯形,BC//AD, AD=1, BC=3,
5,ABCD
点P在底面的投影O恰好为AC与BD的交点,32.2PO
(1)证明: AC⊥PB;
(2) 若E为PB的中点,求二面角B-EC-D的余弦值.
20. ( 本小题满分12分)
已知函数3211()1.32fxxxax
(1) 讨论函数的单调性;
(2)若a≤1,证明:当x∈[0, +∞)时, f(x)≤sinx-cosx.
21. (本小题满分12分)
已知椭圆22221(0)xyabab的长轴长为4,且经过点2(2,).2P
(1)求椭圆的方程;
(2)直线l的斜率为1,2且与椭圆相交于A, B两点(异于点P),过P作∠APB的角平分线交椭圆于另
一点Q.
·7·
(i)证明:直线PQ与坐标轴平行;
(ii) 当AP⊥BP时,求四边形APBQ的面积.
请考生在第22、23两题中任选一题作答,并用2B铅笔在答题卡上把所选题目的题号涂黑.注意
所做题目的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做
的第一题计分.
22. (本小题满分10分) [ 选修4-4:坐标系与参数方程]
已知直线l的参数方程为1,xtyt(t为参数),以坐标原点为极点, x轴的正半轴为极轴建立极坐标
系,曲线C的极坐标方程为ρ=4cosθ.
(1)写出直线l的普通方程和曲线C的直角坐标方程;
(2) 已知点P(0, -1),直线l与曲线C相交于点A, B,求|PA|+|PB|.
23. (本小题满分10分) [选修4-5:不等式选讲)
已知正实数a, b, c满足3331.abc
证明: (1)2222)()abcabc
222
(2)1.abbcca
·8·
·9·
·10·
·11·
·12·
·13·
·14·
·15·
·16·
·17·
