系统辨识大作业
系统辨识实验报告
i=1:800; figure(1) plot(i,Theta(1,:),i,Theta(2,:),i,Theta(3,:),i,Theta(4,:),i,Theta(5,:),i,T title('待估参数过渡过程') figure(2) plot(i,Pstore(1,:),i,Pstore(2,:),i,Pstore(3,:),i,Pstore(4,:),i,Pstore(5,: title('估计方差变化过程')
最小二乘法建模:
二、三次实验 本次实验要完成的内容: 1.参照index2,设计对象,从workspace空间获取数据,取二阶,三阶 对象实现最小二乘法的一次完成算法和最小二乘法的递推算法(LS and RLS); 2.对设计好的对象,在时间为200-300之间,设计一个阶跃扰动,用最 小二乘法和带遗忘因子的最小二乘法实现,对这两种算法的特点进行说 明; 实验内容结果与程序代码: 利用LS和RLS得到的二阶,三阶参数 算法 阶次 A1 A2 A3 B0 B1 B2 B3 LS 二阶 -0.78420.1373 -0.00360.5668 0.3157 RLS 二阶 -0.78240.1373 -0.00360.5668 0.3157 LS 三阶 -0.4381-0.12280.0407 -0.00780.5652 0.5106 0.1160
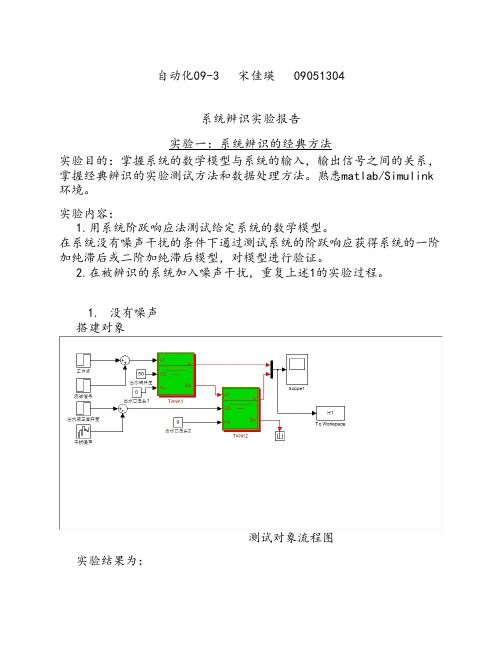
测试对象流程图 实验结果为:
2、加入噪声干扰 搭建对象
实验结果:
加入噪声干扰之后水箱输出不平稳,有波动。
实验二:相关分析法 搭建对象:
处理程序: for i=1:15 m(i,:)=UY(32-i:46-i,1);
end y=UY(31:45,2); gg=ones(15)+eye(15); g=1/(25*16*2)*gg*m*y; plot(g); hold on; stem(g); 实验结果: 相关分析法
系统辨识作业

1、利用cftool拟合曲线得Coefficients (with 95% confidence bounds):a = 0.4601 (0.3711, 0.5492)b = -5.1 (-6.108, -4.092)c = 13.42 (11, 15.83)2、最小二乘法:最小二乘的思想就是寻找一个θ 的估计值θ ,使得各次测量的Z i (i = 1,⋯ m)与由估计θ 确定的量测估计Z i = H iθ 之差的平方和最小,由于此方法兼顾了所有方程的近似程度,使整体误差达到最小,因而对抑制误差是有利的。
但是最小二乘一般方法的估计精度不够高,这是由于对各个测量数据同等对待,而各次测量数据一般不会在相同的条件下获得,造成测量数据的置信度不变较大,当新数据源源而来时,将出现以下问题:1.数据增加,要求计算机的存储空间增加2、每增加一组数据,即作一次求逆,导致计算量增加,难以用于在线辨识。
只有当模型的噪声项是独立的随机变量时,普通最小二乘法才能得到真实参数的无偏估计值,否则所得到的估计值是有偏的。
因此,最小二乘法有很多改进算法,虽然没有一个是完美的,但是能够适应不同的情况、条件,对应选择不同的算法,其各自的性能及优缺点如下:广义最小二乘法的优点是计算精度高,估计的效果比较好,是无偏估计,但广义最小二乘法缺点是计算量大,其收敛是比较缓慢的,为了得到准确的参数估值,往往需要进行多次迭代计算,另外,对于循环的循环性没有给出证明,并非总是收敛于最优估值上。
由于一般情况下,系统信噪比比较低,准则函数为非单值函数(即存在多个局部极小值),如果初值给的不合理,用GLS方法得到的将是局部极小值,若想得到总体最优解,初值应接近该最优值。
递推算法实现了实时控制,减少了计算量和存储量,但未解决最小二乘法的递推算法有偏估计问题。
矩形窗(限定记忆)RLS 方法需要保留一定的数据存储量,此存储量大小取决于矩形窗宽度,因而在应用范围上有一定程度的限制。
系统辨识研究生期末结课作业-中北大学-余红英老师

BP神经网络(一)定义误差反向传播的BP算法简称BP算法,其基本思想是梯度下降法。
它采用梯度搜索技术,以期使网络的实际输出值与期望输出值的误差均方值为最小。
(二)BP网络特点1)是一种多层网络,包括输入层、隐含层和输出层;2)层与层之间采用全互连方式,同一层神经元之间不连接;3)权值通过δ学习算法进行调节;4)神经元激发函数为S函数;5)学习算法由正向传播和反向传播组成;6)层与层的连接是单向的,信息的传播是双向的。
(三)BP主要应用回归预测(可以进行拟合,数据处理分析,事物预测,控制等)、分类识别(进行类型划分,模式识别等),但无论那种网络,什么方法,解决问题的精确度都无法打到100%的,但并不影响其使用,因为现实中很多复杂的问题,精确的解释是毫无意义的,有意义的解析必定会损失精度。
(四)BP网络各种算法的应用范围1)Traingd:批梯度下降训练函数,沿网络性能参数的负梯度方向调整网络的权值和阈值;2)Traingdm:动量批梯度下降函数,也是一种批处理的前馈神经网络训练方法,不但具有更快的收敛速度,而且引入了一个动量项,有效避免了局部最小问题在网络训练中出现;3)Trainrp:有弹回的BP算法,用于消除梯度模值对网络训练带来的影响,提高训练的速度(主要通过delt_inc和delt_dec来实现权值的改变);4)Trainlm:Levenberg-Marquardt算法,对于中等规模的BP神经网络有最快的收敛速度,是系统默认的算法.由于其避免了直接计算赫赛矩阵,从而减少了训练中的计算量,但需要较大内存量.;5)traincgb:Plwell-Beale算法:通过判断前后梯度的正交性来决定权值和阈值的调整方向是否回到负梯度方向上来;6)trainscg:比例共轭梯度算法:将模值信赖域算法与共轭梯度算法结合起来,减少用于调整方向时搜索网络的时间。
一般来说,traingd和traingdm是普通训练函数,而traingda,traingdx,traingd,trainrp,traincgf,traincgb,trainsc g,trainbgf等等都是快速训练函数.总体感觉就是训练时间的差别比较大,还带有精度的差异。
安大系统辨识作业

2012系统辨识实验姓名:周自飞学号:P4*******年级专业:09自动化线性系统参数估计的最小二乘法一、实验目的:1、掌握线性离散系统的数学模型;2、掌握线性离散系统在无噪声时的单位脉冲响应;3、掌握线性系统参数估计的最小二乘法。
二、实验原理:1、基本最小二乘算法2、递推最小二乘算法3、渐消记忆递推最小二乘算法4、辅助变量递推最小二乘算法5、增广递推最小二乘算法三、实验内容:设带有噪声的离散系统模型为:()()()()()()k213.0-13.0-+.028.11-412+ukkukyk--yξky=现给定系统的一列长度为50的输入序列:u(k)= 1,0.3,-0.5,0.9,-0.5,-0.3,-0.2,0.4,0.8,-0.6,-0.1,0,0.1,0.5,-0.6,-0.2,0.3,0.9,0.5,0.2,-0.6,-0.3,-0.1,0.7,0,0.3,-0.6,0.3,0.1,0.5,-0.7,-0.4,-0.9,-0.6,-0.2,-0.4,-0.2,0.1,-0.1,0.1,0.9,0.5,0.3,0.7,0.4,-0.2,-0.7,-0.2,0.1,01. 构造离散系统模型函数,给出无噪声时系统在单位脉冲输入下的响应序列;%zhouzifei.mb=[0.3 -0.213];a=[1 -1.28 0.41];impz(b,a,30);title(‘系统单位脉冲响应’);axis([-1 30 -0.2 0.5]);2. 给出系统在给定输入u(k)和噪声()kξ下的输出信号y(k);%zifei2.m3. 利用已有输入信号u(k)和在第2步中得出的输出信号y(k),使用下列方法辨识系统的参数:(1) 基本最小二乘算法%LS.m参数:a1 =-1.2803a2 =0.4138b0 = 0.2867b1 = -0.2104(2) 递推最小二乘算法%RLS.m参数:a1 =-1.2800 a2 =0.4100 b0 = 0.3000 b1 = -0.2130(3) 渐消记忆递推最小二乘算法%FMRLS参数:a1 =-1.2800 a2 =0.4100 b0 = 0.3000 b1 = -0.2130(4) 辅助变量递推最小二乘算法%IVLS.m参数:a1 =-1.2800 a2 =0.4100b0 = 0.3000 b1 = -0.2130(5) 增广递推最小二乘算法(可选做,有加分)%ARLS.m参数:a1 =-1.2800 a2 =0.4100 b0 = 0.3000 b1 = -0.2130四、实验结果:最小二乘法思想是使各次观测值和计算值之间差值的平方乘以度量其精确度的数值后的和为最小。
系统辨识与自适应控制论文作业

1.采用M 语言或Simulink 环境编写递推最小二乘算法,辨识模型参数)2()1()2()1()(2121-+-=-+-+k u b k u b k y a k y a k y ,其中5.11-=a ,7.02=a ,0.11=b ,5.02=b 。
写出设计程序(M 语言加注释,Simulink 环境写出设计思路)。
解: 给定一个系统模型:)2()1()2()1()(2121-+-=-+-+k u b k u b k y a k y a k y其中: 5.11-=a ,7.02=a ,0.11=b ,5.02=b设计M 语言程序如下:m = 3;N=100;uk=rand(1,N); %生成0~1的一行N 列的随机矩阵for i=1:Nuk(i)=uk(i)*(-1)^(i-1);endyk=zeros(1,N); %生成一行N 列的零矩阵for k=3:Nyk(k)=1.5*yk(k-1)-0.7*yk(k-2)+uk(k-1)+0.5*uk(k-2);endtheta=[0;0;0;0];pn=10^6*eye(4);for t=3:N %该for 循环为递推最小二乘法的程序ps=([yk(t-1);yk(t-2);uk(t-1);uk(t-2)]);pn=pn-pn*ps*ps'*pn*(inv(1+ps'*pn*ps));theta=theta+pn*ps*(yk(t)-ps'*theta);thet=theta';a1=thet(1);a2=thet(2);b1=thet(3);b2=thet(4);enda1t(t)=a1;a2t(t)=a2;b1t(t)=b1;b2t(t)=b2;t=1:N; %显示曲线plot(t,-a1t(t),t,-a2t(t),t,b1t(t),t,b2t(t));text(20,-1.4,'a1'); %在曲线旁边显示字符text(20,0.65,'a2');text(20,0.94,'b1');text(20,0.45,'b2');仿真结果为:图1 参数变化曲线图通过曲线可以看出,大约在第10步递推过程时,参数趋于稳定,5003.11-=a ,7006.02=a ,9987.01=b ,4997.02=b 。
系统辨识与自适应控制作业

一、系统辨识部分1、SISO 系统作为仿真对象)()2(5.0)1()2(7.0)1(5.1)(k e k U k U k Z k Z k Z +-+-=-+--二阶的离散的,其中{e(k)}为服从N(0,1)分布的白噪声序列;输入信号)(k U 采用四阶逆重复m 序列,其中幅值为1,数据信噪比β=14.3% 选择的辨识模型为:)()2(5.0)1()2()1()(2121k k U b k U b k Z a k Z a k Z ε+-+-=-+--用最小二乘估计的一次性完成算法和LS 递推算法分别估计参数,选取数据长度480=l ,选取的初始值⎩⎨⎧==⨯226010p 001.0Q I (遗忘因子μ=0.995)。
解:最小二乘估计的一次性完成算法程序代码:clear clc%-----产生M 序列输入信号--------------------- l=480;y1=1;y2=1;y3=1;y4=0; for i=1:l;x1=xor(y3,y4);x2=y1;x3=y2;x4=y3;y(i)=y4; if y(i)>0.143,u(i)=-1; else u(i)=1; endy1=x1;y2=x2;y3=x3;y4=x4; endfigure(1);stem(u) grid ontitle('输入信号')%-----产生白噪声信号------- A=19;x0=12;M=500; for k=1:l x=A*x0;x1=mod(x,M); v(k)=x1/512; x0=x1; endfigure(2);stem(v) title('白噪声信号')z=zeros(479,1);z(2)=0;z(1)=0;w=0.995;l=477;for k=3:479;z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2)+v(k);zstar(k)=z(k)*w^(l-k+2);endH=zeros(477,4);for k=1:477H(k,1)=-z(k+1)*w^(l-k);H(k,2)=-z(k)*w^(l-k);H(k,3)=-u(k+1)*w^(l-k);H(k,4)=-u(k)*w^(l-k);endestimate=inv(H'*H)*H'*(zstar(3:479))'辨识结果:estimate =-1.53760.6938-0.9780-0.4565最小二乘估计的递推算法的程序元代码:clearclc%-----产生M序列输入信号---------------------l=480;y1=1;y2=1;y3=1;y4=0;for i=1:l;x1=xor(y3,y4);x2=y1;x3=y2;x4=y3;y(i)=y4;if y(i)>0.143,u(i)=-1;else u(i)=1;endy1=x1;y2=x2;y3=x3;y4=x4;endfigure(1);stem(u)grid ontitle('输入信号')%-----产生白噪声信号-------A=19;x0=12;M=500;for k=1:lx1=mod(x,M);v(k)=x1/512;x0=x1;endfigure(2);stem(v)title('白噪声信号')z=zeros(479,1);z(2)=0;z(1)=0;for k=3:479;z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2)+v(k); endP=10^6*eye(4,4);e=zeros(4,478);e(:,1)=[P(1,1),P(2,2),P(3,3),P(4,4)];c=zeros(4,478);c(:,1)=[0.001 0.001 0.001 0.001]';K=[10;10;10;10];w=0.995;for k=3:479;h=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';K=P*h*inv(h'*P*h+w);c(:,k-1)=c(:,k-2)+K*(z(k)-h'*c(:,k-2));P=(eye(4)-K*h')*P/w;e(:,k-1)=[P(1,1),P(2,2),P(3,3),P(4,4)];enda1=c(1,:);a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:);ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(3);i=1:478;plot(i,a1,'r',i,a2,'y:',i,b1,'g',i,b2,':')title('最小二乘递推算法辨识曲线')axis([0,500,-2,2])figure(4);i=1:478;plot(i,ea1,'r',i,ea2,':',i,eb1,'g',i,eb2,':')title('最小二乘递推算法辨识误差曲线')axis([0,500,0,10])-2-1.5-1-0.500.511.52最小二乘递推算法辨识曲线012345678910二、自适应控制部分1、设有二阶系统,1)(122++=s a s a s D ,1)(=s N 。
系统辨识作业_梯度法最小二乘法
系统辨识一、最小二乘算法仿真对象为:)()2(5.0)1()2(7.0)1(5.1)(k v k k u k k z k z +-+-=-+-+,)(k v 为服从N(0,1)分布的白噪声,输入信号采用4阶M 序列。
辨识模型为:)()2()1()2()1()(2121k v k z b k z b k z a k z a k z +-+-+----=,观测数据长度取400=L ,加权矩阵取I =Λ。
则matlab 程序如下:% M array constructionNp=15;r=4;X1=1;X2=1;X3=1;X4=1;m_length = r*Np;a=1;for i=1:1:m_lengthY4=X4;Y3=X3;Y2=X2;Y1=X1;X4=Y3;X3=Y2;X2=Y1;X1=xor(Y3,Y4);if Y4==0M(i)=-a;elseM(i)=a;endendfigure;i=1:1:m_length;plot(i,M);% 白噪声noise = zeros(1,m_length);for i=1:1:m_lengthtemp = noise + 0.5*rands(1,m_length);noise = temp;endnoise = noise/12;%noise = temp;% parameter of systemn=2;d=1;a1=-1;a2=0.5;b1=1;b2=0.5;S_U0=0.2;S_Y0=0.2;% generate u,yu0=ones(1,m_length)*S_U0;U = M + u0 + noise;figure;i=1:1:m_length;plot(i,U);%formulationy(1)=0;y(2)=0;y(3)=0;Y(1)=S_Y0+y(1)+noise(1);Y(2)=S_Y0+y(2)+noise(2);Y(3)=S_Y0+y(3) +noise(3); for k=4:m_lengthy(k) = b1*U(k-1-d)+b2*U(k-2-d)-a1*y(k-1)-a2*y(k-2);Y(k)=S_Y0+y(k)+noise(k);endfigure;i=1:1:m_length;plot(i,Y);%辨识% premitive valuec=2;P = (c^3)*eye(3*n+d);sita(:,3) = [0,0,0,0,0,0,0]';alf = 0.995;% M%compute U0,Y0sum_U = 0;sum_Y = 0;for k=1:1:m_lengthsum_U = sum_U + U(k);sum_Y = sum_Y + Y(k);endt_U0 = sum_U/m_length;t_Y0 = sum_Y/m_length;for k=1:1:m_lengtht_u(k) = U(k) - t_U0;t_y(k) = Y(k) - t_Y0;endfigure;i=1:1:m_length;plot(i,t_u);figure;i=1:1:m_length;plot(i,t_y);v(1)=0;v(2)=0;v(3)=0;for k=4:1:m_lengthfai = [-t_y(k-1),-t_y(k-2),t_u(k-1-d),t_u(k-2-d),v(k-1),v(k-2),v(k-3)]';v(k) = t_y(k) - fai'*sita(:,k-1);W = P*fai;dan = 1/(alf + fai'*W);sita(:,k) = sita(:,k-1) + dan*W*v(k);P = ( P - dan * W*W')/alf;end仿真结果如下图所示:则各个参数的估计值为:⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛∧∧∧∧5048.00062.17003.04961.1121bbaa二、梯度校正辨识方法仿真对象为)()2(5.0)1()2(7.0)1(5.1)(kvkkukkzkz+-+-=-+--,其中)(kv为服从N(0,1)分布的白噪声,取初值0)0(=∧θ,1=α,1.0=c。
系统辨识例题
系统辨识例题注:红色标出的不太确定;本答案仅供参考。
一、选择题1、下面哪个数学模型属于非参数型(D )A 、微分方程B 、状态方程C 、传递函数D 、脉冲响应函数2、频谱覆盖宽、能量均匀分布是下面哪种信号的特点(D )A 、脉冲信号B 、斜坡信号C 、阶跃信号D 、白噪声信号3、下面哪些辨识方法属于系统辨识的经典方法(ACD )A 、阶跃响应法B 、最小二乘法C 、相关分析法D 、频率响应法二、填空题1. SISO 系统的结构辨识可归结为确定(阶次)和(时滞)2. 通过图解和(计算)方法,可以由阶跃响应求出系统的传递函数3. 多变量线性系统辨识的步骤是()4. (渐消记忆)的最小二乘递归算法和(限定记忆)的最小二乘递推算法都成为实时辨识算法5. 遗传算法中变异概率选取的原则是(变异概率一般取得比较小,在0.001~0.01之间,变异概率越大,搜索到全局最优的可能性越大,但收敛速度越慢)6. 模型中含有色噪声时可采用(增广最小二乘)和(广义最小二乘)辨识方法7. 最小二乘法是(极大似然法)和(预报误差法)的特殊情况三、判断题1. 机理建模这种建模方法也称为“白箱问题”。
(√)2. 频率响应模型属于参数模型。
(×)非参数3. 白噪声和M 序列是两个完全相同的概念。
(×)不完全相同4. 渐消记忆法适合有记忆系统。
(×)5. 增长记忆估计算法给予新、老数据相同的信度。
(√)6. 最小二乘法考虑参数估计过程中所处理的各类数据的概率统计特性。
(×)基本不考虑7. 系统辨识不需要知道系统的阶次。
(×)需要8. 自变量是可控变量时,对变量间关系的分析称为回归分析。
(√)9. Newton-Raphson 方法就是随机梯度法。
(×)10. 模型验证属于系统辨识的基本内容。
(√)四、简答题1. 举例说明数学模型的定义及用途。
数学模型:以数学结构的形式反映过程的行为特性(代数方程、微分方程、差分方程、状态方程等参数模型)。
系统辨识第三章作业
第三章作业
1:修改课本p61的程序,并画出相应的图形;
2:修改课本p63的程序,并画出相应的图形(V 的取值范围为
54-200);
前面两题所说的修改程序,指的是用LU 分解或Gauss 消元法求解方程组。
3:表1中是在不同温度下测量同一热敏电阻的阻值,根据测量值确定该电阻的数学模型,并求出当温度在C ︒70时的电阻值。
要求用递推最小二乘求解:
(a )设观测模型为
z a bt v =++
其中v 表示白噪声。
利用头两个数据给出(即20=L )
⎪⎩
⎪⎨⎧===-0L T L L T L L z H P θH H P P 000)0()0(ˆ)()()0(1
0 (b )写出最小二乘的递推公式; (c )利用Matlab 计算
⎥⎦
⎤⎢⎣⎡=)()()(ˆk a k b k θ
表1 热敏电阻的测量值
并画出相应的图形。
第三章补充习题
4:叙述并推导递推最小二乘递推公式(pp64-66)。
系统辨识与建模作业
五参数估计原理首先要写出系统的最小二乘表达式。
为此,把体积V 与压力P 之间的关系PV αβ=改为对数关系,即,log log log P V αβ=-+,此式与式()()()T z k h k e k =+θ,对比可得:()log z k P =,()[log ,1]T h k =-V ,[log ]Tαβ=θ,。
程序流程图程序清单V=[54.3,61.8,72.4,88.7,118.6,194.0]',P=[61.2,49.5,37.6,28.4,19.2,10.1]' %赋初值并显示V、P%logP=-alpha*logV+logbeita=[-logV,1][alpha,log(beita)]'=HL*sita %注释P、V之间的关系for i=1:6; Z(i)=log(P(i)); %循环变量的取值为从1到6,系统的采样输出赋值End %循环结束ZL=Z' % ZL赋值HL=[-log(V(1)),1;-log(V(2)),1;-log(V(3)),1;-log(V(4)),1;-log(V(5)),1;-log(V(6)),1] %HL赋值;%Calculating Parametersc1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c4=c2*c3 %计算被辨识参数的值%Separation of Parametersalpha=c4(1) %α为c4的第一个元素beita=exp(c4(2)) %β为以自然数为底的c4的第二个元素的指数程序运行结果:V = [54.3000, 61.8000, 72.4000, 88.7000, 118.6000, 194.0000]τP = [61.2000, 49.5000, 37.6000, 28.4000, 19.2000, 10.1000]τZL = [4.1141, 3.9020, 3.6270, 3.3464, 2.9549, 2.3125]τHL =-3.9945 1.0000-4.1239 1.0000-4.2822 1.0000-4.4853 1.0000-4.7758 1.0000-5.2679 1.0000c4 =1.4042 9.6786 alpha = 1.4042 beita = 1.5972e+004辨识结果仿真结果表明,用最小二乘一次完成算法可以迅速辨识出系统参数,即 1.4042α=, 1.5972004e β=+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系统辨识大作业——递推增广最小二乘法 题目一: 已知一系统为两输入单输出系统,观测数据受有色噪声污染,噪信比为N/S=0.1。
系统经2000次采样,存放于文件T3T.TXT中。系统输入u1为7级M序列,u2为u1的63步移位序列。模型类可选为:A(q-1)y(k)=B1(q)u1(k)+ B2(q)u2(k)+w(k)/C(q-1)。要求编制程序,辨识出该模型的结构及参数。(注:可以将模型变形,以适合算法) 作业文档要求: 描述问题; 选择辨识方法并简单说明所选方法中的结构辨识原理和参数估计原理; 程序流程图及程序清单; 说明程序中用到的一些技术,如数据标准化、UD分解、稳定性判断等; 结构搜索路线及各结构下的参数、残差; 给出最终结果:A(q-1)= B1(q)= B2(q)= C(q-1)= 并给出选择此最终结果的理由; 用你的辨识结果来预报系统输出误差e(k)=y(k)-y(k),并画出e(101)-e(400)的曲线图。 1.问题描述 已知一系统为两输入单输出系统,观测数据受有色噪声污染,噪信比为N/S=0.1。系统经2000次采样,存放于文件T3T.TXT中。系统输入u1为7级M序列,u2为u1的63步移位序列。模型类可选为:A(q-1)y(k)=B(q-1)u1(k)+ C(q-1)u2(k)+ D(q-1)w(k)A(q-1)y(k)=B1(q)u1(k)+ B2(q)u2(k)+w(k)/C(q-1)转化为问题描述的模型>。 2. 辨识原理和参数估计原理 2.1递推增广最小二乘法的辨识原理 递推增广最小二乘法(简称RELS方法)是用于控制系统参数估计和结构辩识的一种方法,它基于岱( 最小二乘) 方法,使被控对象数学模型在误差信号平方和最小的意义上由实验数据拟合,同时把有色噪声看成是由白噪声合成的, 从而解决了最小二乘法算法的有偏性和非一致性问题。 其中nc=0;nd任意时是广义递推最小二乘法就是递推增广最小二乘法。 2.3 结构辨识 在系统辨识中,系统的阶次是一个十分重要的参数,但在实际的情况中往往无法提前获知系统的阶数。这就需要在参数辨识之前先通过结构辨识,来确定阶数。一般来说经典的结构辨识方法主要有以下3种:F检验定阶法,AIC准则法,FPE准则法。 (1)F检验定阶法
假设系统的阶次为n(1,2,3...n),计算出模型输出和观测输出的残差平方和函数J
ˆˆ()()
T
Jzzzz (18)
其中z为观测输出,ˆz为模型输出。 一般来说J会随着模型阶次的增加而减少。实际进行系统辨识时,输入输出的信号采样的个数大大超过待辨识的参数个数,在这种情况下,随着模型阶次的增加J值先是显著下降,当模型的阶次大于真实系统的阶次时,J的显著下降现象就中止。利用这个原理可以判定模型应有的阶次。 (2)AIC准则法 赤池信息量准则,即Akaike information criterion、简称AIC,是衡量统计模型拟合优良性的一种标准,是由日本统计学家赤池弘次创立和发展的。赤池信息量准则建立在熵的概念基础上,可以权衡所估计模型的复杂度和此模型拟合数据的优良性。 在一般的情况下,AIC可以表示为: 22lnAICkL (19) 其中:k是参数的数量,L是似然函数。 假设条件是模型的误差服从独立正态分布。设n为观察数,RSS为剩余平方和,那么
AIC变为:2ln(/)AICkRSSn增加自由参数的数目提高了拟合的优良性,AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个。赤池信息准则的方法是寻找可以最好地解释数据但包含最少自由参数的模型。 (3)FPE准则法
对AR模型的一种定阶法.设tx是平稳AR(p)序列,12,,...Txxx是样本,ˆk是样本自协
方差函数,ˆj (j=1,2,…,n)是拟合AR(n)参数的最小二乘估计. 101ˆˆ()(1)(1)()niiinnFPEnTT
(20)
为最终预报误差.使FPE(n)达到最小的n称为AR(p)模型阶数p的估计.此方法是赤池弘次于1969年提出的所谓改进的残差方差图方法.最终预报误差准则名称的来源是对AR(p)序列观测值拟合k阶AR模型,使得一步预报均方误差达到最小,只有k取真阶p才能达到.所以定阶依据这种准则是合乎实际目的的。
3 程序流程图 3.1 结构辨识结果 在参数辨识之前首先进行结构辨识,使用F检验法。取最后200个数据计算残差平方和函数值。具体数值如表1所示 表1 F 检验法 n J t(n-1,n) 2 6.6398 3 0.8680 645.0053 4 0.2363 256.6365 5 0.2345 0.7292
系统模型为111112()()()()()()()()AqzkBqukCqukDqvk。模型阶次每增加
1,待辨识参数数目就增加4。查询F分布表可知(4,)2.3719F。观察表1中t的值,当阶次为4时,2.3719t,当阶次为5时,2.3719t。根据F检验法的思想,在模型阶次为5时,残差平方函数值显著下降的现象中止,所以实际系统的阶次为5。
3.2 程序流程图及程序清单 模型完成定阶以后,就开始参数的辨识。由于系统的阶次为5,所以模型的递推表达式可以写成
5554121110()()()()()iiiiiiiizkazkibukicukidvki
(21)
仿真程序的流程图如图1所示。 图1 递推输出误差辨识算法的程序流程图 递推增广最小二乘法的辨识程序如下: %递推增广最小二乘法 clear L = 2000; n = 5; size = 5+4*(n-1);
清零 产生有色噪声信号 画出有色噪声序列图 加载T3t.txt文件并分别赋给z,u1,u2 给辨识参数θ和P赋初值 按照式(17)的第二式计算K(k) 按照式(17)的第一式计算θ(k) 按照式(17)的第三式计算P(k) 计算被辨识参数的相对变化量
参数是否满足要求? 分离参数 画出被辨识参数θ的各次递推估计式图形 画出被辨识参数θ的相对误差的图形 停机
N Y v = sqrt(0.1)*randn(2000,1); M = load('T3t.txt'); z(:,1) = M(1:L,1); u1(:,1) = M(:,2); u2(:,1) = M(:,3); %递推增广最小二乘法 c0=0.0001*ones(size,1);%直接给出被辨识参数的初始值,即一个充分小的实向量 p0=1000000*eye(size,size);%直接给出初始状态P0,即一个充分大的实数单位矩阵 E=0.00005;%取相对误差E c=[c0,zeros(size,L-1)];%被辨识参数矩阵的初始值及大小 e=zeros(size,L);%相对误差的初始值及大小 zm = zeros(L,1); ek = zeros(L,1); for k=6:L; %开始求K
h1=[-z(k-1,1),-z(k-2,1),-z(k-3,1),-z(k-4,1),-z(k-5,1),u1(k-1,1),u1(k-2,1),u1(k-3,1),u1(k-4,1),u1(k-5,1),u2(k-1,1),u2(k-2,1),u2(k-3,1),u2(k-4,1),u2(k-5,1),v(k),v(k-1),v(k-2),v(k-3),v(k-4),v(k-5)]';%为求K(k)作准备 x=h1'*p0*h1+1; x1=inv(x); k1=p0*h1*x1; %K d1=z(k)-h1'*c0; c1=c0+k1*d1;%辨识参数c e1=c1-c0; e2=e1./c0; %求参数的相对变化 e(:,k)=e2; c0=c1;%给下一次用 c(:,k)=c1;%把辨识参数c 列向量加入辨识参数矩阵 p1=p0-k1*k1'*[h1'*p0*h1+1]; %p1=p0-k1*h1'*p0; p0=p1;%给下次用 end%循环结束 for k =6:L h2=[-zm(k-1,1),-zm(k-2,1),-zm(k-3,1),-zm(k-4,1),-zm(k-5,1),u1(k-1,1),u1(k-2,1),u1(k-3,1),u1(k-4,1),u1(k-5,1),u2(k-1,1),u2(k-2,1),u2(k-3,1),u2(k-4,1),u2(k-5,1),v(k),v(k-1),v(k-2),v(k-3),v(k-4), v(k-5)]'; zm(k) = h2'*c(:,L); ek(k,1) = z(k,1) - zm(k); end J = ek'*ek; J,c(:,L)%显示被辨识参数及参数收敛情况 figure(1); k =1:L; plot(k,z,'r',k,zm,'b'); xlabel('k');ylabel('幅值');title('观测输出与模型输出'); figure(2); k=101:400;
