2019年全国初中数学联赛(初二组)初赛试卷参考答案及评分标准
2016年全国初中数学联合竞赛(初二年级组)试题参考答案

word 格式-可编辑-感谢下载支持2016 年全国初中数学联合竞赛(初二年级)试题参考答案第一试一、选择题:(本题满分 42 分,每小题 7 分)1.用[ x ] 表示不超过 x 的最大整数,把 x -[ x ] 称为 x 的小数部分.已知 t = a 是 t 的小数部分,2-3b 是 -t 的小数部分,则 1 - 1 =( A)2b a13A..B..C.1.D. 3 .222.三种图书的单价分别为 10 元、15 元和 20 元,某学校计划恰好用 500 元购买上述图书 30 本,那么不同的购书方案共有( C ) AA .9 种.B .10 种.C .11 种.D .12 种.EDF Q3.如图,P 为△ ABC 内一点,∠ BAC =70°,∠ BPC =120°,BD 是∠ ABP 的P平分线, CE 是∠ ACP 的平分线, BD 与 CE 交于 F ,则∠ BFC = ( C )A. 85°. B .90°. C .95°. D .100°.BCS20164.记 S n = 1 + 1 +1 + 1 + 1 + 1 + + 1+ 1 + 1,则= ( D)2 22 22 ( n +1) 21 2 2 3 n 2016A. 2016 .B. 2017 .C. 2017 .D. 2018 .2017 2016 2018 20175.点 D 、 E 、 F 分别在△ ABC 的三边 BC 、 AB 、 AC 上,且 AD 、 BF 、 CE 相交于一点 M ,若 AB + AC = 5 ,则 AM = ( B )BE CF MD A. 7 . B. 3 . C. 5 . D. 2 .22 6.设 a , b , c , d 都是正整数,且 a 5 = b 2 , c3 = d4 , a - c = 319 ,则 b - c = ( B ) a 2dA. 15.B. 17.C.18.D. 20.二、填空题:(本题满分 28 分,每小题 7 分)1.如图,已知四边形 ABCD 的对角互补,且 ∠BAC = ∠DAC , AB =15 , AD =12 .过顶点 C 作CE ⊥ AB 于 E ,则 AE = ____9___.BE2.已知整数 a , b , c 满足不等式 a 2 + 2b 2 + c 2 + 211 < ab + 28b + 20c ,则 a + b - c =____2___. 3.若质数 p , q 满足: 3q - p - 4 = 0 , p + q <111.则 pq 的最大值为1007 .4.将 5 个 1、5 个 2、5 个 3、5 个 4、5 个 5 共 25 个数填入一个 5 行 5 列的表格内(每格填入一个数), 使得同一列中任何两数之差的绝对值不超过 2.考虑每列中各数之和,设这 5 个和的最小值为 M ,则 M 的最大值为10.第二试一、(本题满分 20 分)如图,ABCD 为平行四边形,E 为 BC 的中点,DF ⊥ AE AD于 F , H 为 DF 的中点,证明: CH ⊥ DF .H 证明 分别延长 AE 和 DC ,交于点 P .F因为 AB // CP ,所以 ∠ABE = ∠PCE ,又因为 CE = BE , ∠AEB = ∠PEC , BEC所以△ ABE ≌△ PCE ,所以 PC = AB .又 AB = CD ,所以 PC = CD ,故 C 为 PD 的中点.又 H 为 DF 的中点,所以 CH // PF .又已知 DF ⊥ AE ,所以 CH ⊥ DF .P二、(本题满分 25 分)设互不相等的非零实数 a , b , c 满足 a + 2 2 2 ,求 ( a + 2 2= b + = c + ) +b c a b2 2 2 2的值. (b + ) + ( c + ) c a 解 由 a + 2 = b + 2 = c + 2 可得 bc ( a -b ) = 2(b - c ) ,ab (c - a ) = 2( a -b ) ,ac (b - c ) = 2(c - a ) ,b c a三式相乘得 ( abc ) 2 ( a -b )(b - c )(c - a ) = 8( a -b )(b - c )(c - a ) ,而 a , b , c 互不相等,所以 ( abc ) 2 = 8 .设 a + 2 = b + 2 = c + 2 = k ,则 kb = ab + 2 , kc = bc + 2 , ka = ac + 2 ,于是可得 k (b - c ) =bc ab ( a -c ) , k (c - a ) = c (b - a ) , k ( a -b ) = a (c -b ) , 三式相乘得 k 3 ( a -b )(b - c )(c - a ) = abc ( a - c )(b - a )(c -b ) ,而 a , b , c 互不相等,所以 k 3 = -abc .于是可得 k 6 = ( -abc ) 2 = 8 ,所以 k 2 = 2 .因此 ( a + 2 2 2 2 2 2 2) + (b + ) + ( c + ) = 3k = 6 .b c a三、(本题满分 25 分)已知 a , b 为正整数,求 M = 3a 2 - ab 2 - 2b - 4 能取到的最小正整数值.解 因为 a , b 为正整数,要使得 M = 3a 2 - ab 2 - 2b - 4 的值为正整数,显然有 a ≥ 2 .当 a = 2 时, b 只能为 1,此时 M = 4 ,故 M = 3a 2 - ab 2 - 2b - 4 能取到的最小正整数值不超过 4. 当 a = 3时, b 只能为 1 或 2.若 b =1,则 M = 18;若 b =2,则 M = 7.当 a = 4 时, b 只能为 1 或 2 或 3.若 b =1,则 M = 38;若 b =2,则 M = 24;若 b =3,则 M = 2.下面考虑: M = 3a 2 - ab 2 - 2b - 4 的值能否为 1?若 M =1 ,即 3a 2 - ab 2 - 2b - 4 =1,即 3a 2 - ab 2 = 2b + 5 ①,注意到 2b + 5 为奇数,所以 a是奇数, b 是偶数,此时, 3a 2 - ab 2 被 4 除所得余数为 3, 2b + 5 被 4 除所得余数为 1,故①式不可能成立,即 M ≠1.因此,M=3a2-ab2-2b-4能取到的最小正整数值为 2.。
2019年初中学业质量检查(二)数学答案

2019年初中学业质量检查(二)数学试题参考答案及评分标准说明:(一)考生的正确解法与“参考答案”不同时,可参照“参考答案及评分标准”的精神进行评分.(二)如解答的某一步出现错误,这一错误没有改变后续部分的考查目的,可酌情给分,但原则上不超过后面应得的分数的二分之一;如属严重的概念性错误,就不给分.(三)以下解答各行右端所注分数表示正确做完该步应得的累计分数.一、选择题(每小题4分,共40分)1.A 2.B 3.C 4.D 5.D 6.C 7.A 8.D 9.B 10.C二、填空题(每小题4分,共24分)11.7105.6⨯12.)2)(2(3-+m m m 13.31=x ,12-=x 14.5115.(0,34)16.6或23.三、解答题(共86分)17.(本小题8分)解:原式=)13(41232-⨯+-⨯……………………………………………………………………………6分=43413-+-=535-.………………………………………………………………………………………8分18.(本小题8分)解:方程两边都乘以)1)(1(-+x x ,得1)12()1(2-=--+x x x x …………………………………………………………………………2分11222-=+-+x x x x …………………………………………………………………………4分112--=-x x 2-=-x 2=x ………………………………………………………………………………6分检验:当2=x 时,013)1)(1(≠⨯=-+x x ……………………………………………………………7分所以,2=x 是原方程的解.………………………………………………………………………………8分19.(本小题8分)证法一:∵四边形ABCD 为平行四边形,∴AD BC =,BC AD //,…………………………………………………………………………2分∴ADB ∠=CBD ∠.…………………………………………………………………………………3分∵AE BD ⊥,CF BD ⊥,∴90AED CFB ︒∠=∠=,………………………4分∴ADE ∆≌CBF ∆(A.A.S),……………………5分∴CF AE =.………………………………………6分由AE BD ⊥,CF BD ⊥可得︒=∠=∠90CFE AEF ,∴CF AE //,∴四边形AECF 为平行四边形.……………………8分证法二:连接AC 交BD 于点O ,…………………………………………………………………1分∵四边形ABCD 为平行四边形,∴OC OA =,…………………………………………………………………………………………3分∵AE BD ⊥,CF BD ⊥,∴︒=∠=∠90CFE AEF ,……………………………………………………………………………4分∴CF AE //,∵COF AOE ∠=∠,…………………………………………………………………………………5分∴AOE ∆≌COF ∆(A.A.S),………………………………………………………………………6分∴CF AE =.…………………………………………………………………………………………7分∴四边形AECF 为平行四边形.……………………………………………………………………8分证法三:连接AC 交BD 于点O ,……………………………………………………………………1分∵四边形ABCD 为平行四边形,∴OC OA =,…………………………………………………………………………………………3分∵AE BD ⊥,CF BD ⊥,∴︒=∠=∠90CFE AEF ,……………………………………………………………………………4分∵COF AOE ∠=∠,…………………………………………………………………………………5分∴AOE ∆≌COF ∆(A.A.S),………………………………………………………………………6分∴OF OE =.…………………………………………………………………………………………7分∴四边形AECF 为平行四边形.……………………………………………………………………8分注:其他证法参照以上标准给分.20.(本小题8分)解:(1)平均数6.64123120876253413=⨯+++++++⨯+⨯+⨯=x (万元);该组数据中出现次数最多的是4,所以众数为:4万元;将这些数据按从小到大的顺序排列:3,4,4,4,5,5,6,7,8,20,处于中间位置的两个数字均为5,所以中位数为:5万元;………………………………………3分(2)用中位数5万元作为今年每个销售员统一销售额标准比较合理.………………………………4分理由如下:因为平均数为6.6万元受极值20的影响较大,若把它定为标准,大多数人不能完成任务,会挫伤员工的积极性,而众数4万元,绝大多数员工不必努力就能超额完成,不利于提高销售额,若将5万元作为标准,多数人能完成任务,并且经过努力能够超额完成任务,有利于提高销售人员的积极性.…………………………………………………………………………………………8分21.(本小题8分)解:(1)如图所示,⊙O 为所求作的圆;………………3分(2)由作图可知,OC OB =,∴OCB OBC ∠=∠.∵在ABC ∆,︒=∠90ACB ,3:4:=BC AC ,∴可设a AC 4=,a BC 3=,则aAB 5=又∵25:12:=AB CD ,∴a AB CD 4.22512==.……………………………4分∵︒=∠90D ,∴a a a CD BC BD 8.1)4.2()3(2222=-=-=,∴348.14.2==a a BD CD .∵3:4:=BC AC ,∴BCAC BD CD =.∵︒=∠=∠90D ACB ,∴ABC Rt ∆∽CBD Rt ∆,………………………………………………………………………6分∴CBD OBC ∠=∠,∴CBD OCB ∠=∠.∵︒=∠+∠90CBD BCD ,∴︒=∠+∠90OCB BCD ,即OC CD ⊥,∵OC 为⊙O 的半径,∴CD 是⊙O 的切线.…………………………………………………………………………8分22.(本小题10分)解:(1)每辆甲型汽车和乙型汽车的售价分别是x 万元、y 万元.由题意,得⎩⎨⎧-=+=+8818438822y x y x ,………………………………………………………………………………3分解得:⎩⎨⎧==1826y x 经检验,⎩⎨⎧==1826y x 符合题意.答:每辆甲型汽车的售价为26万元,每辆乙型汽车的售价为18万元;………………………5分(2)设购买甲型汽车m 辆,则购买乙型汽车)6(m -辆,依题意,得140)6(1826130≤-+≤m m ,解得4432≤≤m .…………………………………………………8分∵m 是正整数,∴m =3或m =4.∴共有两种方案:方案一:购买3辆甲型汽车和3辆乙型汽车;方案二:购买4辆甲型汽车和2辆乙型汽车.………………………………………………………10分23.(本小题10分)(1)证明:当012=-m ,即21=m 时,原方程为012=+-x ,此方程为一元一次方程,其根为21=x ;当012≠-m ,即21≠m 时,=⨯--+-=∆1)12(4)]12([2m m 04)12(2>+-m ∴当21≠m 时,原方程必有两个不相等的实数根,综上所述,不论m 为何值,方程必有实数根;…………………………………………………………4分(2)解:当m 为整数时,关于x 的方程01)12()12(2=++--x m x m 没有有理根.理由如下:①当012=-m 时,21=m (不合题意舍去);………………………………………………………5分②当012≠-m 且m 为整数时,假设关于x 的方程01)12()12(2=++--x m x m 有有理根,则要4)12(2+-=∆m 为完全平方数,设2n =∆(n 为整数),即224)12(n m =+-(n 为整数),所以有4)]12()][12([=---+m n m n ,∵(21)n m +-与(21)n m --的奇偶性相同,并且m 、n 都是整数,∴(21)2(21)2n m n m +-=⎧⎨--=⎩或(21)2(21)2n m n m +-=-⎧⎨--=-⎩,……………………………………………………8分解得12m =(不合题意舍去).综上所述,当m 为整数时,关于x 的方程01)12()12(2=++--x m x m 没有有理根.……10分24.(本小题13分)解:(1)令0=y ,得022=+-mx mx ,解得01=x ,22=x ,∴1=a ,…………………………………………………1分∴P (1,3).把P (1,3)代入mx mx y 22+-=,得32=+-m m ,解得:3=m ,∴此抛物线的解析式为x x y 32321+-=.……………3分(2)又∵点A 坐标为(b ,b 3),点B 坐标为(1+b ,33+b ),∴直线AB 的解析式为x y 32=.观察图象可知,当10<<x 时,21y y >,∴不等式x mx mx 322>+-的解集为10<<x ;…………………5分∵点P 在线段AB 上,∴11b b ≤≤+.∴b 的取值范围为10≤≤b ;……………………………………………………………………………7分(3)∵点A 坐标为(b ,b 3),点D 坐标为(c ,b 3),且1≥c ∴x AD //轴.把点D 坐标为(c ,b 3)代入x x y 32321+-=,得b c c 33232=+-,解得22c c b -=.由勾股定理,得3)1()333()1(22222+--=-++-+=c c b b c b BD .………………………………………8分令41)21(22--=-=c c c u ,2BD v =,得3)1(2+-=u v .∵10≤≤b ∴1202≤-≤c c ,解得20≤≤c .又∵1≥c ∴21≤≤c ,232121≤-≤c ,∴49)21(412≤-≤c ,∴241)21(02≤--≤c ,即20≤≤u .…………………11分∵二次函数3)1(2+-=u v 开口向上,对称轴为直线1=u ,图象如图所示,∴当1=u 时,v 最小,3min =v ,此时,3=BD ;当0=u 或2时,v 最大,43)12(2max =+-=v ,此时,2=BD .∴线段BD 长度的取值范围为23≤≤BD .…………………………………………………………13分25.(本小题13分)解:(1)∵在ABC Rt ∆中,︒=∠90ACB ,BC AC 2=,BC BM =,∴2==AC MC ,121===AC BM BC ,∴︒=∠=∠45CMA CAM .设ABC ∆的外接圆的圆心为O ,连接BN ,则四边形BCAN 为⊙O 的内接四边形,法一:∴︒=∠=∠90ACB MNB ,∵︒=∠45CMA ,∴︒=∠-︒=∠4590CMA MBN∴点B 到直线MA 的距离为222==BM BN .………………………………………………………4分法二:∴︒=∠=∠45MAC MBN ∵︒=∠90ACB ,∴AB 是⊙O 的直径,∴︒=∠90ANB ,∴︒=∠90MNB ,∴BMN ∆是等腰直角三角形,∴点B 到直线MA 的距离为222==BM BN .…………………4分(2)过M 作MC MQ ⊥轴交CF 的延长线于点Q .∵AB CF ⊥,∴︒=∠+∠=∠+∠90BCF ACF CAB ACF ,∴BCF CAB ∠=∠,………………………………………………5分∴CAB BCF ∠=∠tan tan ,∴12MQ BC MC AC ==,∴.21=MC MQ ∴21=AC MQ (也可以用A.A.S 证CMQ Rt ∆≌ACB Rt ∆得到AC MC CB MQ 2121===)……6分由MC MQ ⊥可得︒=∠+∠180ACM QMC ,∴AC MQ //,则有ACD Q ∠=∠,DAC DMQ ∠=∠,∴DMQ ∆∽DAC ∆,∴21==AC MQ AD MD ,………………………………………………………………………………………7分设a AC MC ==,则有a AC MA 22==,即an 2=∴a MA MD 3231==.∵a MC BC BM 2121===∴a BM MN 422==,∴a MN MD DN 122=-=即a m 122=∴12=mn ,即n 与m 的函数表达式为m n 12=.……………………………………………………8分(3)PB PF PC 554=+,理由如下:…………………………………………………………………9分延长PF 到'P ,使得PC F P =',连接B P ',BF ,则''PP P F PF PC PF =+=+.∵B ,C ,P ,F 四点共圆,∴PCB FB P ∠=∠'.又∵⊙O 的直径CF AB ⊥,∴⌒BC =⌒BF,∴PBC ∆≌BF P '∆,∴B P PB '=.……………………………………………………………………………………………11分由⌒BC =⌒BF可得,BAC BPP ∠=∠',而a a a AC BC AB 25)21(2222=+=+=,∴552cos 'cos ==∠=∠AB AC BAC BPP .过B 作'PP BR ⊥于点R ,可得552'21'cos ===∠PB PP PB PR BPP ,∴PB PP 554'=,即PB PF PC 554=+.…………………………………………………………13分。
2019年学科素养竞赛初二年数学答案

2019年学科素养竞赛初二年数学参考答案11.解:移项得43423x x -=--+ 原方程可变形为:32035640x x +-= 解得:10x =,252x =,3710x =检验:把10x =,252x =,3710x =代入原方程,分母都不等于0∴原方程的解为:10x =,252x =,3710x =都是原方程的解.12.解:设甲施工队单独完成此项工程需要x 天,根据题意可知:1012145x x+= 解得25x =,经检验,25x =是原方程的解当25x =时,4205x =13. 解:过A 做BC 垂线交BC 于N ,交BD 于M .因为AB=AC ,∠BAC=90°. 所以∠BAM=∠DAM=∠C=45° 又因为AE ⊥BD 所以∠1=∠2,所以Rt △ABM 与Rt △CAF 中 ∠BAM =∠C ,AB=AC ,∠1=∠2 所以Rt △ABM ≌ Rt △CAF (ASA ) 所以AM=CF,所以△ADM 与△CDF 中, AD=CD, ∠DAM=∠C, AM=CF 所以△ADM ≌△CDF (SAS ) 所以∠ADB =∠CDF .B14.解:(1)证明:延长AM 到点N ,使MN =MA ,连接BN , ∵AM 是△ABC 中BC 边上的中线, ∴CM =BM , 在△MBN 和△MCA 中AM MN AMC NMB CM BM =⎧⎪∠=∠⎨⎪=⎩∴△MBN ≌△MCA (SAS ), ∴∠BNM =∠CAM ,NB =AC , ∴BN ∥AC ,NB =AG , ∴∠NBA +∠BAC =180°,∵∠GAE +∠BAC =360°﹣90°﹣90°=180°, ∴∠NBA =∠GAE , 在△NBA 和△GAE 中NB GA NBA GAE BA AE =⎧⎪∠=∠⎨⎪=⎩∴△NBA ≌△GAE (SAS ), ∴AN =EG , ∴AM =12EG ; (2)证明:由(1)△NBA ≌△GAE 得∠BAN =∠AEG , ∵∠HAE +∠BAN =180°﹣90°=90°, ∴∠HAE +∠AEH =90°, ∴∠AHE =90°, 即AH ⊥EG ;(3)证明:连接CE 、BG , 易证△ACE ≌△ABG ∴CE ⊥BG ,∴EG 2+BC 2=CG 2+BE 2, ∴EG 2+BC 2=2(AB 2+AC 2), 由(1)可知AM =12EG , ∵BM =12BC , ∴AB 2+AC 2=2(12EG )2+12BC •BC , ∴EG 2+BC 2=2(AB 2+AC 2).FF。
安海片区2019年春季期中联合考试初二年数学科 试卷答案

安海片区2019年春季期中联合教学质量监测初二数学试题参考答案及评分标准说明:(一)考生的正确解法与“参考答案”不同时,可参照“参考答案及评分标准”的精神进行评分.(二)如解答的某一步出现错误,这一错误没有改变后续部分的考查目的,可酌情给分,但原则上不超过后面应得的分数的二分之一;如属严重的概念性错误,就不给分. (三)以下解答各行右端所注分数表示正确做完该步应得的累计分数. 一、选择题(每小题4分,共40分)1.D 2.A 3.D 4.C 5.B 6.A 7.C 8.A 9.C 10.B 二、填空题(每小题4分,共24分)11、31-≠x ; 12、5-103.4⨯; 13、(-3,-2); 14、-2; 15、213y y y <<; 16、()1313,。
三、解答题17. 解:原式=1+3-4 ………6分=0 ……………8分18.解:原式=()()4222222-+⨯⎪⎭⎫ ⎝⎛----+x x x x x x …3分 =()()42224-+⨯-x x x =2+x ……………6分 当22-=x 时,原式=222+- 2= ………8分19.解:()()131118-+=+-+x x x x341822++=-+x x x ………4分1=x …………6分检验:当1=x 时,012=-x∴1=x 是原方程增根 ………8分 20.解 四边形ABCD 是平行四边形 ∴AO=CO ,CD//AB ,AD=BC=6∴EAO FCO ∠=∠ .............2分在OEA OFC ∆∆与中⎪⎩⎪⎨⎧∠=∠=∠=∠EOA COF AOCO EAOFCO ∴)(ASA OEA OFC ∆≅∆ .............4分 ∴EA FC EO FO ===,4 ..............5分∴827====+=+OF EF AB BE FC BE AE ,..............7分∴四边形BCFE 的周长为:21786=++=++AB EF BC . .............8分21、解:解:(1)由题意B (﹣2,23),.....1分把B (﹣2,23)代入xky =中,得到k=﹣3,.............................3分∴反比例函数的解析式为xy 3-=;.........4分 (2)结论:P 在第二象限,Q 在第四象限,......5分 理由:∵k=﹣3<0,∴在每个象限内y 随x 的增大而增大,.............6分 ∵P (x 1,y 1)、Q (x 2,y 2)是该反比例函数图象上的两点,且x 1<x 2时,y 1>y 2, ∴P 、Q 在不同的象限,∴P 在第二象限,Q 在第四象限..............8分22、解:(1)设原计划每天生产的零件x 个,依题意有 ..............1分3030024002400++=x x ..............3分 解得x=2400,经检验,x=2400是原方程的根,且符合题意. ..............4分 ∴规定的天数为24000÷2400=10(天).答:原计划每天生产的零件2400个,规定的天数是10天;.............5分 (2)设原计划安排的工人人数为y 人,依题意有[5×20×(1+20%)×y2400+2400]×(10﹣2)=24000, ..............8分 解得y=480,经检验,y=480是原方程的根,且符合题意.答:原计划安排的工人人数为480人. ..............10分23、解:(1)反比例函数xy 2019=是闭区间[1,2019]上的“闭函数”...............1分 理由如下: 反比例函数xy 2019=在第一象限,y 随x 的增大而减小,..............2分 当x=1时,y=2019;当x=2019时,y=1, ............................3分 所以,当1≤x ≤2019时,有1≤y ≤2019,符合闭函数的定义, 故反比例函数xy 2019=是闭区间[1,2019]上的“闭函数”; ..............4分 (2)分两种情况:k >0或k <0.①当k >0时,一次函数y=kx+b (k ≠0)的图象是y 随x 的增大而增大,故根据“闭函数”的定义知,⎩⎨⎧=+=+n b kn m b km 解得:⎩⎨⎧==01b k . ∴此函数的解析式是y=x ; ..............7分②当k <0时,一次函数y=kx+b (k ≠0)的图象是y 随x 的增大而减小,故根据“闭函数”的定义知,⎩⎨⎧=+=+m b kn n b km ,解得:⎩⎨⎧+=-=nm b k 1. ∴此函数的解析式是y=﹣x+m+n ; ..............10分24、解:(1)乙的速度v 2=120÷3=40,故答案为:40; ..............2分 (2)v 1=1.5v 2=1.5×40=60, 60÷60=1(分钟),a=1, ..............4分d 1=; .............6分(3)d 2=40t ,当0≤t <1时,d 2+d 1>10, 即﹣60t+60+40t >10,解得0≤t <2.5, .............8分 ∵0≤t <1,∴当0≤t <1时,两遥控车的信号不会产生相互干扰; .............9分 当1≤t ≤3时,d 2﹣d 1>10, 即40t ﹣(60t ﹣60)>10, 解得1≤t <2.5 ∴当1≤时,两遥控车的信号不会产生相互干扰 ............11分综上所述:当0≤t <2.5时,两遥控车的信号不会产生相互干扰. .............12分 25、解:解:(1)依题意得:a=2,b=4,∴A (2,0),B (0,4), 设直线AB 的解析式是y=kx+b ,代入得:⎩⎨⎧=+=b bk 420解得:k=-2,b=4,∴函数解析式为:y=-2x+4, .............2分 (2)如图2,分三种情况:①如图(1)当︒=∠90CBA ,且BC=BA 时,过C 作CN ⊥Y 轴于N , 易知△BCN ≌△ABO (AAS ), ∴CN=OB=4,BN=OA=2, ∴ON=2+4=6,∴C 的坐标为(4,6 ),代入y=mx 得:m=23, .............4分 ②如图(2)当︒=∠90CAB ,且AC=BA 时,过C 作CN ⊥X 轴于N ,△BOA ≌△ANC (AAS ),同理求出C 的坐标为(6,2),∴m=31, .............6分③如图(3)当︒=∠90ACB ,且AC=BC 时,过C 作CN ⊥X 轴于N ,CH ⊥Y 轴于H ,则△BHC ≌△ACN ,∴C N=CH , 设C (x ,x )代入y=mx 得:x=mx ,∴m=1, .............8分 答:m 的值是23或31或1. (3)解:如图3,结论2是正确的且定值为2, .............9分设NM 与x 轴的交点为H ,分别过M 、H 作x 轴的垂线垂足为G ,HD 交MP 于D 点,由y=2k x-2k与x 轴交于H 点, ∴H (1,0), 由y=2k x-2k与y=kx-2k 交于M 点, ∴M (3,K ),而A (2,0), ∴A 为HG 的中点, ∴△AMG ≌△ADH (ASA ),∴AD=AM .............11分 又因为N点的横坐标为-1,且在y=2k x-2k上, ∴可得N 的纵坐标为-K ,同理P 的纵坐标为-2K , ∴ND 平行于x 轴且N 、D 的横坐标分别为-1、1 ∴N 与D 关于y 轴对称,∴PN=PD , .............13分 ∴AM PN -PM =2==-AMMDAM PD PM ..............14分。
2019.6八年级数学试题参考答案6.13
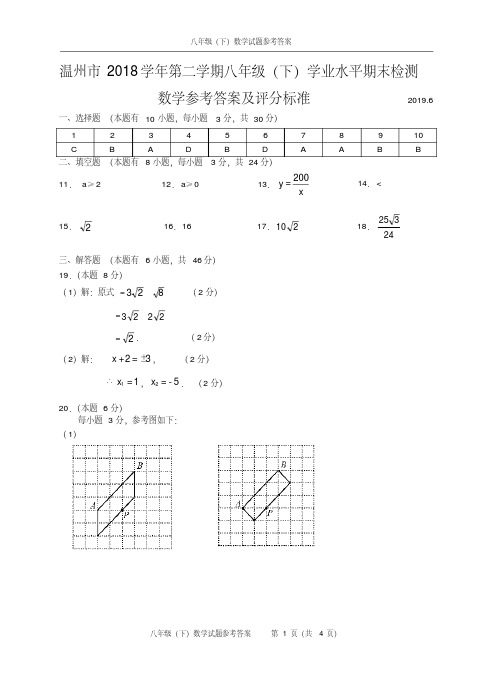
(第 22 题)
八年级(下)数学试题参考答案
第 2 页(共 4 页)
八年级(下)数学试题参考答案
23.(本题 8 分)
解:( 1)由题意,得
单位: m
100a 80a a2 (7 a)2 ,( 2 分)
A
B
化简,得 a 2 3.6a ,
C
∵a 0,
D
∴ a 3.6 .
答: 步道的宽为 3.6 m. ( 2 分)
49
八年级(下)数学试题参考答案
第 4 页(共 4 页)
∴ OA =5 .
( 1 分)
∵OD 平分∠ AOC,
∴∠ AOD =∠ DOC .
∵AD ∥ BC,
∴∠ ADO =∠ DOC ,
∴∠ ADO =∠ AOD ,
∴DA =OA=5, ( 2 分)
∴ OC=2 .
∵∠ OCD= 90°,
∴OD = OC 2 +CD 2 = 2 5 ,
∴△ AOD 的周长是 10 + 2 5 .(2 分)
八年级(下)数学试题参考答案
温州市 2018 学年第二学期八年级(下)学业水平期末检测
数学参考答案及评分标准
一、选择题 (本题有 10 小题,每小题 3 分,共 30 分)
1
2
3
4
5
6
7
C
B
A
D
B
D
A
二、填空题 (本题有 8 小题,每小题 3 分,共 24 分)
11. a≥ 2
12. a≥ 0
13. y = 200 x
2019.6
8
9
10
A
B
B
14. <
“大梦杯”福建省初中数学竞赛试题参考答案

2019年“大梦杯”福建省初中数学竞赛试题参考答案考试时间2019年3月17日9∶00-11∶00满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若一次函数2y x =+与反比例函数4y x=的图像交于11()A x y ,,22()B x y ,两点,则1212x x y y +的值为()A .8B .6C .6-D .8-【答案】D【解答】由24y x y x =+⎧⎪⎨=⎪⎩,得2240x x +-=……………①。
依题意,1x ,2x 是方程①的两根,于是122x x +=-,124x x =-。
∴121212121212441616484x x y y x x x x x x x x +=+⋅=+=-+=--。
2.如图,ABC △为圆O 的内接三角形,D 为BC 中点,E 为OA 中点,40ABC ∠=︒,80BCA ∠=︒,则OED ∠的大小为()A .15︒B .18︒C .20︒D .22︒【答案】C【解答】如图,连结OC 。
由40ABC ∠=︒,80BCA ∠=︒,得60BAC ∠=︒。
∵D 为BC 中点,∴OD BC ⊥,1602DOC BOC BAC ∠=∠=∠=︒。
∴30OCD ∠=︒,12OD OC =。
又E 为OA 中点,∴12OE OA OD ==。
结合40ABC ∠=︒,知24060140EOD AOC COD ∠=∠+∠=⨯︒+︒=︒,(第2题图)(第2题答题图)11(180)(180140)2022OED EOD ∠=︒-∠=︒-︒=︒。
3.已知二次函数2()2f x x ax b =++,若()(1)f a f b =+,其中1a b ≠+,则(1)(2)f f +的值为()A .8B .10C .12D .14【答案】A【解答】由已知条件及二次函数图像的对称性,知124a b a++=-。
2019年全国高中数学联合竞赛加试试题参考答案及评分标准(B卷)
2019年全国高中数学联合竞赛加试 试题参考答案及评分标准(B 卷)说明:1. 评阅试卷时,请严格按照本评分标准的评分档次给分.2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,10分为一个档次,不要增加其他中间档次。
一、(本题满分40分)如图,锐角三角形ABC 的外心为O ,K 是边BC 上一点(不是边BC 的中点),D 是线段AK 延长线上一点,直线BD 与AC 交于点N ,直线CD 与AB 交于点M .求证:若OK ⊥MN ,则A ,B ,D ,C 四点共圆.证明:用反证法.若A ,B ,D ,C 不四点共圆,设三角形ABC 的外接圆与AD 交于点E ,连接BE 并延长交直线AN 于点Q ,连接CE 并延长交直线AM 于点P ,连接PQ .因为2PK =P 的幂(关于⊙O )+K 的幂(关于⊙O ) ()()2222PO rKOr=-+-,同理 ()()22222QK QO r KO r =-+-, 所以 2222P O P K Q O Q K -=-,故 OK ⊥PQ . (10分)由题设,OK ⊥MN ,所以PQ ∥MN ,于是AQ APQN PM=. ① 由梅内劳斯(Menelaus )定理,得1NB DE AQBD EA QN⋅⋅=, ② 1MC DE APCD EA PM⋅⋅=. ③ 由①,②,③可得NB MCBD CD=, (30分) 所以ND MDBD DC=,故△DMN ∽ △DCB ,于是DMN DCB ∠=∠,所以BC ∥MN ,故OK ⊥BC ,即K 为BC 的中点,矛盾!从而,,,A B D C 四点共圆. (40分)注1:“2PK =P 的幂(关于⊙O )+K 的幂(关于⊙O )”的证明:延长PK 至点F ,使得PK KF AK KE ⋅=⋅, ④则P ,E ,F ,A 四点共圆,故PFE PAE BCE ∠=∠=∠,从而E ,C ,F ,K 四点共圆,于是PK PF PE PC ⋅=⋅, ⑤⑤-④,得 2PK PE PC AK KE =⋅-⋅=P 的幂(关于⊙O )+K 的幂(关于⊙O ).注2:若点E 在线段AD 的延长线上,完全类似.二、(本题满分40分)设m 和n 是大于1的整数,求证:11111112(1)().1m m n mmmk k jj m m k j i n n C n C i m -+===⎧⎫+++=+-⎨⎬+⎩⎭∑∑∑ 证明:11101)m m j jm j q C q +++=+=∑由(得到1110(1),mm m j jm j q qC q +++=+-=∑ 1,2,,q n =分别将代入上式得:11021,mm jm j C ++=-=∑1110322,mm m j jm j C +++=-=∑1110(1)(1),mm m j jm j nn C n +++=--=-∑ F E QP O NM K DCBA1110(1).mm m j jm j n nC n +++=+-=∑ n 将上面个等式两边分别相加得到:111(1)1(),mnm jjm j i n Ci++==+-=∑∑ (20分)11111(1)(1)1(1),m nnmj j mm j i i n n n Ci m i -+===++-=+++∑∑∑()11111112(1)().1m m nm mmk k j j m m k j i n n C n C i m -+===⎧⎫+++=+-⎨⎬+⎩⎭∑∑∑ (40分) 三、(本题满分50分)设,,x y z 为非负实数, 求证:22232222223()()()()()32xy yz zx x y z x xy y y yz z z zx x ++++≤-+-+-+≤.证明:首先证明左边不等式.因为 2222211[()3()]()44x xy y x y x y x y -+=++-≥+, 同理,有2221()4y yz z y z -+≥+, 2221()4z zx x z x -+≥+;(10分) 于是22222221()()()[()()()]64x xy y y yz z z zx x x y y z z x -+-+-+≥+++21[()()]64x y z xy yz zx xyz =++++-; (20分)由算术-几何平均不等式, 得 1()()9xyz x y z xy yz zx ≤++++,所以222222221()()()()()81x xy y y yz z z zx x x y z xy yz zx -+-+-+≥++++ 22221(222)()81x y z xy yz zx xy yz zx =+++++++3()3xy yz zx ++≥.左边不等式获证, 其中等号当且仅当x y z ==时成立. (30分)下面证明右边不等式.根据欲证不等式关于,,x y z 对称, 不妨设x y z ≥≥, 于是 22222()()z z x x y y zz x y-+-+≤, 所以222222222()()()()x x y y y y z z z z x x xx y y x y -+-+-+≤-+. (40分)运用算术-几何平均不等式, 得222222222()()()2x xy y xy x xy y x y x xy y xy xy xy -++-+=-+⋅⋅≤⋅22222()()22x xy y xy x y -+++≤⋅2222233()()22x y x y z +++=≤. 右边不等式获证, 其中等号当且仅当,,x y z 中有一个为0,且另外两个相等时成立. (50分)四、(本题满分50分)设k 是给定的正整数,12r k =+.记(1)()()f r f r r r ==⎡⎤⎢⎥,()()l f r = (1)(()),2l f f r l -≥.证明:存在正整数m ,使得()()m f r 为一个整数.这里,x ⎡⎤⎢⎥表示不小于实数x 的最小整数,例如:112⎡⎤=⎢⎥⎢⎥,11=⎡⎤⎢⎥. 证明:记2()v n 表示正整数n 所含的2的幂次.则当2()1m v k =+时,()()m f r 为整数.下面我们对2()v k v =用数学归纳法.当0v =时,k 为奇数,1k +为偶数,此时()111()1222f r k k k k ⎛⎫⎡⎤⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎢⎥⎝⎭为整数. (10分)假设命题对1(1)v v -≥成立.对于1v ≥,设k 的二进制表示具有形式1212222v v v v v k αα++++=+⋅+⋅+,这里,0i α=或者1,1,2,i v v =++. (20分)于是 ()111()1222f r k k k k ⎛⎫⎡⎤⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎢⎥⎝⎭2122kk k =+++ 11211212(1)2()222v v v vv v v ααα-++++=+++⋅++⋅+++12k '=+, ① (40分)这里1121122(1)2()22v v v v v v v k ααα-++++'=++⋅++⋅+++.显然k '中所含的2的幂次为1v -.故由归纳假设知,12r k ''=+经过f 的v 次迭代得到整数,由①知,(1)()v fr +是一个整数,这就完成了归纳证明. (50分)。
2019年全国初中数学联赛(初三组)初赛试卷及答案
第2题图DACB第4题图DACB2019年全国初中数学联赛(初三组)初赛试卷(3月7日下午4:00—6:00)班级:: 姓名: 成绩:考生注意:1、本试卷共五道大题,全卷满分140分;2、用圆珠笔、签字笔或钢笔作答;3、解题书写不要超出装订线;4、不能使用计算器。
一、选择题(本题满分42分,每小题7分)本题共有6个小题,每题均给出了代号为A 、B 、C 、D 的四个答案,其中有且只有一个是正确的。
将你选择的答案的代号填在题后的括号内。
每小题选对得7分;不选、错选或选出的代号字母超过一个(不论是否写在括号内),一律得0分。
1、某件商品的标价为13200元,若以8折降价出售,仍可获利10%(相对于进货价),则该商品的进货价是( )A 、9504元B 、9600元C 、9900元D 、10000元 2、如图,在凸四边形ABCD 中,BD BC AB ==,︒=∠80ABC ,则ADC ∠等于( )A 、︒80B 、︒100C 、︒140D 、︒1603、如果方程()()0422=+--m x x x 的三根可以作为一个三角形的三边之长,那么,实数m 的取值范围是( )A 、04m <≤B 、3≥mC 、4≥mD 、34m <≤4、如图,梯形ABCD 中,CD AB //,︒=∠60BAD ,︒=∠30ABC ,6=AB 且CD AD =,那么BD 的长度是( )A 、7B 、4C 、72D 、245、如果20140a -<<,那么|2014||2014|||+-+++-a x x a x 的最小值是( ) A 、2019B 、2014+aC 、4028D 、4028+a6、方程()y x y xy x +=++322的整数解有( ) A 、3组B 、4组C 、5组D 、6组二、填空题(本大题满分28分,每小题7分)1、如图,扇形AOB 的圆心角︒=∠90AOB ,半径为5,正方形CDEF 内接于该扇形,则正方形CDEF 的边长为 .2、已知四个自然数两两的和依次从小到大的次序是:23,28,33,39,x ,y ,则____=+y x .3、已知6=-y x ,922=-+-y xy xy x ,则22y xy xy x ---的值是 .4、有质地均匀的正方体形的红白骰子各一粒,每个骰子的六个面分别写有1、2、3、4、5、6的自然数,随机掷红、白两粒骰子各一次,红色骰子掷出向上面的点数比白色骰子掷出向上面的点数小的概率是 .三、(本大题满分20分)已知0422=-+a a ,2=-b a ,求ba 211++的值。
2019.1八年级数学试题参考答案
温州市2018学年第一学期八年级(上)学业水平期末检测数学参考答案及评分标准 2019.1一、选择题(本题有10小题,每小题3分,共30分)1 2 3 4 5 6 7 8 910 BBDACDCBDB二、填空题(本题有8小题,每小题3分,共24分) 11.12. (2,-3) 13. 1802y x =- 14. 20a b +>15. 11 16. 2( 17. 6 18. 17 三、解答题(本题有6小题,共46分) 19.(本题6分)()32414x x x ①②+≥+⎧⎪⎨+<⎪⎩解:由①得,1x ≥-,由②得,3x < ,∴不等式的解集为13x -≤<. (4分)∴(2分)20.(本题5分)证明:∵EF ∥BC ,∴∠ACB =∠DFE .∵AB ∥DE ,∴∠A =∠D . 又∵AB =DE ,∴△ABC ≌△DEF ,(3分)∴AC =DF ,∴AF =CD .(2分)21.(本题6分)每小题3分,参考图如下: (1)A(第20题)(2)22.(本题8分)(1)证明:∵CD ⊥AB ,∴∠AEC+∠DCE=90°. ∵∠ACB=90°,∴∠ACE+∠BCE=90°. ∵CE 平分∠DCB ,∴∠BCE =∠DCE ,∴∠AEC =∠ACE . (4分)(2)解:∵∠AEC =2∠B =∠BCE +∠B ,∴∠BCE=∠B ,∴∠ACE =∠AEC=2∠BCE ,BE =CE . ∵∠ACB=90°,∴2603ACE ACB ∠=∠=︒,∴△ACE 是等边三角形, ∴BE =CE =AE =2AD =4,∴AB =8. (4分)23.(本题10分)(1)由题意,得12201200x y +=,∴3605y x =-+. (4分)(2)①由题意,得3605y x =-+.∵x y ≥,(第22题)∴3605x x ≥-+,∴1372x ≥.(2分)∵x 是5的倍数,∴当x 的最小值为40时. (2分) 答:至少购进A 种笔记本40本.②30.(2分)24.(本题11分)(1)由翻折得,∠ABO =∠ABC .∵AC ∥x 轴,∴∠ABO =∠CAB , ∴∠ABC =∠CAB . ∴AC =BC .(3分)(2)①∵8y kx =+,∴A (0,8), ∴OA =8. ∵∠P =90°,∴PC,∴OB =PB =PC +BC =10+6=16,∴B (16,0).将点B 代入8+=kx y ,得21-=k ,∴821+=x y -. (3分)②若BC =CD =10,则AD =AC+CD =20. (1分) 若BC =BD (如图).过点B 作BE ⊥AD 于点E . ∵AC ∥x 轴, ∴BE =O A =8,∴6CE ==,∴AD =AC +2CE =22. (2分) (3)56. (2分) (第24题)。
2019全国初中数学联赛(初三组)初赛试卷-数学
2019全国初中数学联赛(初三组)初赛试卷-数学注意事项:认真阅读理解,结合历年的真题,总结经验,查找不足!重在审题,多思考,多理解!〔3月8日下午4:00—6:00〕班级::姓名:成绩:考生注意:1、本试卷共五道大题,全卷总分值140分;2、用圆珠笔、签字笔或钢笔作答;3、解题书写不要超出装订线;4、不能使用计算器。
【一】选择题〔此题总分值42分,每题7分〕此题共有6个小题,每题均给出了代号为A 、B 、C 、D 的四个答案,其中有且只有一个是正确的。
将你选择的答案的代号填在题后的括号内。
每题选对得7分;不选、错选或选出的代号字母超过一个〔不论是否写在括号内〕,一律得0分。
1、01 x -,那么2x -,x ,x1的大小关系是〔〕A 、xx x 12-B 、xx x21-C 、x x x 12- D 、21x x x- 2、如图,正方形ABCD ,点P 是对角线AC 上一点,连接BP , 过P 作BP PQ ⊥,PQ交CD 于Q ,假设2==CQ AP ,那么正方形ABCD 的面积为〔〕A 、246+B 、16C 、2812+D 、323、假设实数a ,b 满足0222=+-+b a b ,那么a 的取值范围是〔〕A 、1-≤aB 、1-≥aC 、1≤aD 、1≥aQPACBD4、如图,在四边形ABCD 中,︒=∠135B ,︒=∠120C ,6=AB ,33-=BC ,6=CD ,那么AD 边的长为〔〕A 、36B 、34C 、24D 、335、方程7311=+y x 的正整数解〔x ,y 〕的组数是〔〕A 、0B 、1C 、3D 、56、实数x ,y ,z 满足1=+++++y x z x z y z y x ,那么yx z x z y z y x +++++222的值是〔〕 A 、1-B 、0C 、1D 、2【二】填空题〔本大题总分值28分,每题7分〕1、x 是正整数,○x 表示x 的正约数个数,那么③×④÷⑥等于、 2、草原上的一片青草,到处长得一样密一样快,70头牛在24天内可以吃完这片青草,30头牛在60天内可以吃完这片青草,那么20头牛吃完这片青草需要的天数是、3、如图,在平行四边形ABCD 中,M 、N 分别是BC 、DC 的中点,4=AM ,3=AN ,且︒=∠60MAN ,那么AB 的长是、4、小明将1,2,3,…,n 这n 个数输入电脑求其平均值,当他认为输完时,电脑上只显示输入〔1-n 〕个数,且平均值为30.75,假设这〔1-n 〕个数输入无误,那么漏输入的一个数是、【三】〔本大题总分值20分〕解方程02|12|2=---x x 【四】〔本大题总分值25分〕如图,圆内接四边形ABCD 中,CD CB =. 求证:AD AB CB CA ⋅=-22 【五】〔本大题总分值25分〕二次函数c bx ax y ++=2和一次函数bx y -=,其中a 、b 、c 满足c b a ,0=++c b a 、()R c b a ∈,,、〔1〕求证:两函数的图象有两个不同的交点A 、B ;〔2〕过〔1〕中的两点A 、B 分别作x 轴的垂线,垂足为1A 、1B 、求线段11B A 的长的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学试卷
2019年全国初中数学联赛(初二组)初赛试卷
参考答案及评分标准
一、选择题(本大题满分42分,每小题7分)
1、A 2、B 3、B 4、C 5、D 6、A
二、填空题(本大题满分28分,每小题7分)
1、13 2、101 3、10 4、5.22
三、(本大题满分20分)
解原式2421222aaaaaaa (5分)
4224222a
aaaaa
21aa
(10分)
1212121
(5分)
四、(本大题满分25分)
解:∵822OCOBCB
∴B点坐标(8,6) (5分)
又∵A(10,0)
∴AB的中点坐标为(9,3)
∴OD的表达式为:xy31 (10分)
∵A(10,0),C(0,6)
∴AC的表达式为:653xy (15分)
由65331xyxy,解得: 715745yx (20分)
故点D的坐标为(745,715) (25分)
五、(本大题满分25分)
证明:连结AC,取AC的中点K,连结EK,FK (5分)
∵EDAE,KCAK
∴DCEK//,DCEK21 (10分)
y
Q x O
P A C B
D
数学试卷
同理ABFK//,ABFK21 (15分)
∴EKDCABFK2121
∴EFKFEK (20分)
∵DCEK//
∴FEKCMF
∵ABFK//
∴EFKBNF
∴CMFBNF (25分)
K
F N E M A C
B
D
