二次函数平移旋转轴对称变换
二次函数的对称性

二次函数的对称性二次函数是轴对称图形,有这样一个结论:当横坐标为x 1, x 2 其对应的纵坐标y 相等,那么对称轴122x x x +=其可以变形为:x 1 = x 2 =例、已知二次函数y=ax 2+bx+c 的图象过点A (1,2),B (3,2),C (5,7)三点,则该二次函数的对称轴为__________变形:已知二次函数y=ax 2+bx+c 的图象的对称轴为直线x=3,点A (1,2)与点B 关于对称轴对称,则点B 的坐标为____________变形:已知二次函数y=ax 2+bx+c 的图象的对称轴为直线x=3,点A (3,2)与点B 关于对称轴对称,则点B 的坐标为____________练习、已知二次函数y=ax 2+bx+c 的图象过点A (-1,2),B (3,2),C (5,7)三点,则该二次函数的对称轴为__________练习、已知二次函数y=ax 2+bx+c 的图象过点A (-1,2),B (3,2),C (5,7)三点,则点C 关于二次函数的对称轴的对称点D 的坐标为__________练习、已知二次函数y=ax 2+bx+c 的图象过点A (-3,3),B (-5,3),C (1,6)三点,则点C 关于二次函数的对称轴的对称点D 的坐标为__________练习、已知二次函数y=ax 2+bx+c 的图象的对称轴为直线x=3,点A (1,2)与点B 关于对称轴则二次函数y=ax 2+bx+c 的的对称轴为____________,在x=2时,y=___________.在y=-5时,x=____________增减性在对称中的应用已知二次函数y=ax2+bx+c(a>0)的图象过点A(-1,2),B(3,2).若点M(-2,y1),N(-1,y2),K(0,y3)也在二次函数y=ax2+bx+c的图象上,则y1、y2、y3的大小关系为__________已知二次函数y=ax2+bx+c(a>0)的图象过点A(-1,2),B(3,2).若点M(2,y1),N(4,y2),K(3,y3)也在二次函数y=ax2+bx+c的图象上,则y1、y2、y3的大小关系为__________已知二次函数y=ax2+bx+c(a<0)的图象过点A(-1,2),B(3,2).若点M(-2,y1),N(-1,y2),K(0,y3)也在二次函数y=ax2+bx+c的图象上,则y1、y2、y3的大小关系为__________已知二次函数y=ax2+bx+c(a<0)的图象过点A(-1,2),B(3,2).若点M(2,y1),N(4,y2),K(3,y3)也在二次函数y=ax2+bx+c的图象上,则y1、y2、y3的大小关系为__________例2、已知二次函数y=ax2+bx+c的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,练习1、已知点(-2,y1),(-1,y2),(3,y3)都在函数y=x2的图象上,则y1,y2,y3的大小关2、已知抛物线y=ax2+bx+c(a<0)过A(-3,0)、O(1,0)、B(-5,y1)、C(5,y2)四点,则巩固作业:则二次函数y=ax2+bx+c的的对称轴为____________,顶点坐标为___________在x= 4时,y=___________.在y= -8时,x=____________2、已知二次函数y=ax2+bx+c的图象过点A(1,2),B(3,2),C(5,-2).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数y=ax2+bx+c的图象上,则y1,y2,y3的大小关系是______________________3、已知点(-2,y1),(-1,y2),(5,y3)都在函数y=(x-1)2的图象上,则y1,y2,y3的大小关系是________________________4、已知抛物线y=ax2+bx+c(a>0)过A(-3,0)、O(1,0)、B(-5,y1)、C(5,y2)四点,则(2)二次函数图象的对称变换:①两抛物线关于x 轴对称,此时顶点关于 x 轴对称,a 的符号相反;②两抛物线关于y 轴对称,此时顶点关于y 轴对称,a 的符号不变;(3)二次函数图象的旋转:开口反向(或旋转180°),此时顶点坐标不变,只是a的符号相反.抛物线y=-(x+1)2 +2关于x轴对称的直线的解析式为:________________________抛物线y=-(x+1)2 +2关于y轴对称的直线的解析式为:________________________抛物线y=-(x+1)2 +2关于原点对称的直线的解析式为:________________________抛物线y=-(x+1)2 +2饶顶点旋转180°后的直线的解析式为:________________________练习、抛物线y=-(x+1)2 -2关于x轴对称的直线的解析式为:________________________抛物线y=(x-1)2 +2关于y轴对称的直线的解析式为:________________________抛物线y=-2(x-1)2 +2关于原点对称的直线的解析式为:________________________抛物线y=-(x+1)2 -2饶顶点旋转180°后的直线的解析式为:________________________1、在下列二次函数中,其图象的对称轴为直线x= - 2的是()A.y=(x+2)2B.y=2x2-2C.y=-2x2-2D.y=2(x-2)22、二次函数y=x2-2x+3的图象的顶点坐标为_ ( )___________3、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x= -1,下列结论:①abc<0;①2a+b=0;①a-b+c>0;①4a-2b+c<0.其中正确的是()A.①①B.只有①C.①①D.①①4、如图,在平面直角坐标系xOy中,二次函数图象的顶点坐标为(4,-3),该图象与x轴相交于点A、其中点A的横坐标为1. 求该二次函数的表达式;5、次函数y=ax2+bx+c的图象经过点(-1,0),(3,0)和(0,2),求其函数关系式,并写出其顶点坐标。
初中二次函数知识点详解助记口诀

初中二次函数知识点详解助记口诀一、基本概念:一元二次函数二种加前缀,顶点和对称轴要学记。
开口向下时,a是正的;开口向上时,a是负的。
对称轴x=-b/2a,顶点就是“反b”。
二次项系数a说明开口,a>0是开口向上的;轴对称的顶点在x轴上。
二、一元二次函数图像特点:若a>0,开口向上往后走;若a<0,开口向下导孔。
三、顶点坐标和轴对称:对称轴的坐标是x=-b/2a,顶点的坐标是(-b/2a,f(-b/2a))。
四、二次函数的平移变换:y=a(x-h)²+k,顶点平移是y坐标;a决定开口的方向;正数代表开口向上,负向下;k是y坐标增量的意思;b/c的平移还出问题。
五、二次函数的图像倒置:要记住它的奇偶图像变化特性:当a>0,图像是奇,左偏有右;当a<0,图像是偶,左右相等。
六、二次函数图像变宽窄:a>0,宽窄形状调:大弯小长,穿插中值两点;a<0,宽窄形状变:小弯大长,在其中间旋。
七、一次、二次函数交点:解方程可以求“两”交点;重联中使用可以减。
八、满二次平方差分:若f(x)=2((x-1)²)+15,f(x)-f(1)=2(x-1)²+15-2=2(x-1)²+13同理:f(x)= (x-1)²+sin(x),则f(x)-f(1)= (x-1)²+sin(x) - 0 ² + sin(0) = (x-1)²+sin(x)-sin(0)九、关于系数a1>a2,a1 red, a2 yellow,y=a1*f(x) 宽;a1 green, a2 purple,y=a2*g(x) 窄。
a1=a2,颜色滑稽,开口相同,图形相似。
十、二次函数的判别式:b²-4ac=”b”的平方差大的等于大,开口向下;大的小于零,开口向上;等于零的状况两个相同。
十一、二次函数零点以及范围:可以根据判别式来判断。
专题二次函数与几何变换

2、在平面直角坐标系中,先将抛物线y=x2+x-2
关于x轴作轴对称变换,再将所得的抛物线关于y
轴作轴对称变换,那么经两次变换后所得的新抛
物线的解析式为( )
A.y=-x2-x+2
B.y=-x2+x-2
(三)、抛物线的旋转
情况一:关于原点成中心对称(即绕原点旋转1800)
例题:若抛物线C:y=ax2+bx+c与抛物线 y=2x2-4x+3关于原点成中心对称,则抛物 线C的解析式为___________。
情况二:关于顶点成中心对称(即绕顶点旋转00)
若抛物线C:y=ax2+bx+c绕顶点旋转180后得 到抛物线y=2x2-4x+3,则抛物线C的解析式 为___________。
C.y=-x2+x+2 D.y=x2+x+2
3、将抛物线l:y=2x2-4x+3沿直线y=-1翻折 得到抛物线l′,则抛物线l′的解析式为 __________
4、已知二次函数y=x2+4x+3的顶点为A,与y 轴交于点B,作它关于以P(1,0)为中心的中 心对称的图象顶点为C,交y轴于点D,则四边 形ABCD面积为
(二)、抛物线的轴对称
情况一:关于x轴对称:
例题:若抛物线C:y=ax2+bx+c与抛物线y=2x24x+3关于x轴对称,则抛物线C的解析式为 ___________。
情况二:关于y轴对称:
例题:若抛物线C:y=ax2+bx+c与抛物线 y1=x2-4x+1关于y轴对称,则抛物线C的解析式 为___________。
二次函数的图象和性质
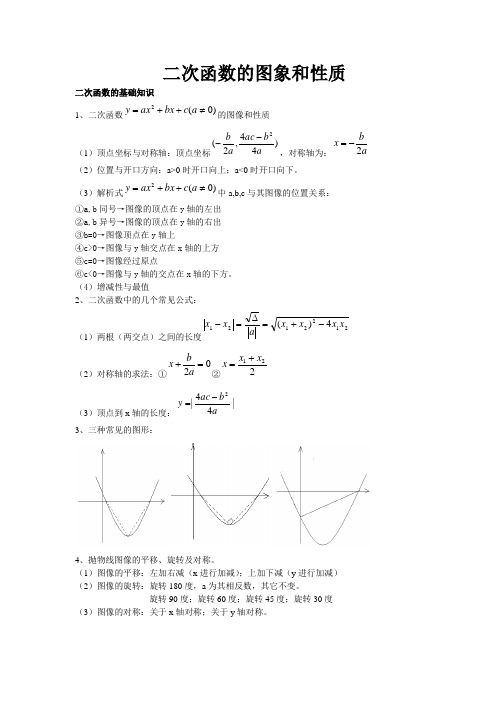
二次函数的图象和性质二次函数的基础知识1、二次函数)0(2≠++=acbxaxy的图像和性质(1)顶点坐标与对称轴:顶点坐标)44,2(2abacab--,对称轴为:abx2-=(2)位置与开口方向:a>0时开口向上;a<0时开口向下。
(3)解析式)0(2≠++=acbxaxy中a,b,c与其图像的位置关系:①a,b同号→图像的顶点在y轴的左出②a,b异号→图像的顶点在y轴的右出③b=0→图像顶点在y轴上④c>0→图像与y轴交点在x轴的上方⑤c=0→图像经过原点⑥c<0→图像与y轴的交点在x轴的下方。
(4)增减性与最值2、二次函数中的几个常见公式:(1)两根(两交点)之间的长度21221214)(xxxxaxx-+=∆=-(2)对称轴的求法:①2=+abx②221xxx+=(3)顶点到x轴的长度:|44|2abacy-=3、三种常见的图形:4、抛物线图像的平移、旋转及对称。
(1)图像的平移:左加右减(x进行加减);上加下减(y进行加减)(2)图像的旋转:旋转180度,a为其相反数,其它不变。
旋转90度;旋转60度;旋转45度;旋转30度(3)图像的对称:关于x轴对称;关于y轴对称。
例1:已知抛物线22121x x y -+=(或322--=x x y )(1)把它配方成k h x a y ++=2)(的形式; (2)写出抛物线的开口方向,顶点M 的坐标,对称轴方程; (3)求函数的最大值和最小值,并求出相应的自变量的值 (4)当12≤≤-x ,求函数y 的最值 (5)当1<x<4时,求函数y 的取值范围(6)求出与 y 轴交点N 的坐标与x 轴的交点P,Q 的坐标(点P 在点Q 的左边) (7)作出函数的大致图像(8)当x 取何值时,函数y 随x 的增大而增大,函数y 随x 的增大而减小 (9)图像过点A(-2,y 1),B(0,y 2),C(6,y 3),D(4,y 4),比较y 1,y 2,y 3,,y 4的大小 (10)观察图像,当x 为何值时,y>0,y=0,y<0 (11)当x 为何值是,y<2, (12)求ΔPQM 的面积 (13)求四边形PQMN 的面积例2:已知抛物线2222-++-=k k kx x y ,根据下列条件,求K 的值。
第8讲 二次函数的解析式和图象变换(学生版)

知识导航经典例题1在平面直角坐标系中,抛物线2已知二次函数的图象以3已知抛物线4在平面直角坐标系中,二次函数5若二次函数知识导航经典例题1如果将抛物线2如果将某一抛物线向右平移3将抛物线4已知抛物线知识导航经典例题1将二次函数2抛物线3将二次函数4先作二次函数1在平面直角坐标系中,抛物线2如图,已知抛物线帝通过数来统治宇宙。
这是毕达哥拉斯学派和其他教派的主要区别。
他们很重视数学,企图用数来解释一切。
宣称数是宇宙万物的本原,研究数学的目的并不在于使用而是为了探索自然的奥秘。
他们从五个苹果、五个手指等事物中抽象出了五这个数。
这在今天看来很平常的事,但在当时的哲学和实用数学界,这算是一个巨大的进步。
但是,他们同时任意地把非物质的、抽象的数夸大为宇宙的本原,认为'万物皆数','数是万物的本质',是'存在由之构成的原则',而整个宇宙是数及其关系的和谐的体系。
毕达哥拉斯将数神秘化,说数是众神之母,是普遍的始原,是自然界中对立性和否定性的原则。
毕达哥拉斯本人以发现勾股定理(西方称毕达哥拉斯定理)著称于世。
这定理早已为巴比伦人所知,不过最早的证明大概可归功于毕达哥拉斯。
他是用演绎法证明了直角三角形斜边平方等于两直角边平方之和,即毕达哥拉斯定理(勾股定理)。
任何一个学过代数或几何的人,都会听到毕达哥拉斯定理。
这一著名的定理,在许多数学分支、建筑以及测量等方面,有着广泛的应用.【毕达哥拉斯定理】毕达哥拉斯对数论作了许多研究,将自然数区分为奇数、偶数、素数、完全数、平方数、三角数和五角数等。
在几何学方面,毕达哥拉斯学派证明了'三角形内角之和等于两个直角'的论断;研究了黄金分割;发现了正五角形和相似多边形的作法;还证明了正多面体只有五种:正四面体、正六面体、正八面体、正十二面体和正二十面体。
【黄金分割】然而,最让毕达哥拉斯学派出名的却是他们中的一个'叛逆者'--希帕索斯,正是他发现了第一个无理数根号2的存在,从而在当时的数学界掀起了一场巨大风暴。
二次函数平移问题

二次函数的平移问题我们从两个方面进行了一些探讨,概括出二次函数平移后其解析式的变化规律.一.当解析式为一般式y=ax2+bx+c (a≠0)时1.向上或向下平移时,二次函数解析式的变化规律.将抛物线向上平移n个单位长度后,得到的新抛物线的解析式为y=ax2+bx+c+n 将抛物线向下平移n个单位长度后,得到的新抛物线的解析式为y=ax2+bx+c-n 两式比较:可得抛物线向上平移n个单位,常数项上加n,即解析式由y=ax2+bx+c 变为y=ax2+bx+c+n;同理可推出抛物线向下平移n个单位, 常数项上减去n,即解析式由y=ax2+bx+c 变为y=ax2+bx+c-n2.向左或向右平移时,解析式的变化规律.将抛物线向左平移m个单位长度后,得到的新抛物线的解析式为y= a(x+m)2+b(x+m)+c将抛物线向右平移m个单位长度后,得到的新抛物线的解析式为y= a(x-m)2+b(x-m)+c两式比较,可得出抛物线向左平移m个单位,自变量上减去m,即解析式由y=ax2+bx+c 变为y=a(x+m)2+b(x+m)+c;同理可推出抛物线向右平移m个单位,自变量上加上m,即解析式由y=ax2+bx+c 变为y=a(x-m)2+b(x-m)+c3.将抛物线向左平移m个单位长度后, 再将抛物线向上平移n个单位长度后,得到的新抛物线的解析式为y= a(x+m)2+b(x+m)+c+n将抛物线向左平移m个单位长度后, 再将抛物线向下平移n个单位长度后,得到的新抛物线的解析式为y= a(x+m)2+b(x+m)+c-n将抛物线向右平移m个单位长度后, 再将抛物线向上平移n个单位长度后,得到的新抛物线的解析式为y= a(x-m)2+b(x-m)+c+n将抛物线向右平移m个单位长度后, 再将抛物线向下平移n个单位长度后,得到的新抛物线的解析式为y= a(x-m)2+b(x-m)+c-n二.当解析式为顶点式y=a(x-h)2+k(a≠0)时1.向上或向下平移时,解析式的变化规律.将抛物线向上平移n个单位长度后,得到的新抛物线的解析式为y=a(x-h)2+k+n 将抛物线向下平移n个单位长度后,得到的新抛物线的解析式为y=a(x-h)2+k-n 将抛物线向上平移n个单位,有点的平移规律可知,顶点坐标由(h,k)变为(h,k+n)所以抛物线的解析式由y=a(x-h)2+k变为y=a(x-h)2+k+n 将抛物线向下平移n个单位,有点的平移规律可知,顶点坐标由(h,k)变为(h,k-n)所以抛物线的解析式由y=a(x-h)2+k变为y=a(x-h)2+k-n 比较两个解析式可得出向上平移n个单位,括号外加n,同理可推出向下平移n 个单位括号外减去n.即抛物线解析式由y=a(x-h)2+k变为y=a(x+m-h)2+k-n2.向右或向左平移时,解析式的变化规律.将抛物线向左平移m个单位长度后,得到的新抛物线的解析式为y=a(x-h+m)2+k 将抛物线向右平移m个单位长度后,得到的新抛物线的解析式为y=a(x-h-m)2+k 将抛物线向左平移m个单位,由点的平移规律可知,顶点坐标由(h,k)变为(h-m,k),所以抛物线解析式由y=a(x-h)2+k 变为 y=a[x-(h-m)]2+k=a (x-h+m)2+k将抛物线向右平移m 个单位,由点的平移规律可知,顶点坐标由(h,k)变为(h+m,k),所以抛物线解析式由y=a(x-h)2+k 变为 y=a[x-(h+m)]2+k=a (x-h-m)2+k两解析式比较可得出图像向左平移m 个单位,括号内加上m ,即抛物线解析式由y=a(x-h)2+k 变为y=a (x-h+m)2+k ;同理可推出向右平移m 个单位括号内减去m ,即抛物线解析式由y=a(x-h)2+k 变为y=a (x-h-m)2+k综上所述,当解析式为顶点式时,解析式的变化规律为上加下减括号外,左加右减括号内;解析式为一般式时,解析式的变化规律为左加右减自变量,上加下减常数项3.将抛物线向左平移m 个单位长度后, 再将抛物线向上平移n 个单位长度后,得到的新抛物线的解析式为y=a (x-h+m)2+k+n将抛物线向左平移m 个单位长度后, 再将抛物线向下平移n 个单位长度后,得到的新抛物线的解析式为y=a (x-h+m)2+k-n将抛物线向右平移m 个单位长度后, 再将抛物线向上平移n 个单位长度后,得到的新抛物线的解析式为y=a (x-h-m)2+k+n将抛物线向右平移m 个单位长度后, 再将抛物线向下平移n 个单位长度后,得到的新抛物线的解析式为y=a (x-h-m)2+k-n二次函数的平移练习题1.把抛物线y=-x 2向左平移一个单位,然后向上平移3个单位,则平移后抛物线的表达式为( )A. y=-(x-1)2+3B. y=-(x+1)2+3C. y=-(x-1)2-3D. y=-(x+1)2-32.抛物线y=x 2+bx+c 图像向右平移2个单位再向下平移3个单位,所得图像的解析式为y=x 2-2x-3,则b 、c 的值为( ) A . b=2,c=2 B. b=2,c=0 C . b= -2,c=-1 D. b= -3,c=23.将函数y=x 2+x 的图像向右平移a (a >0)个单位,得到函数y=x 2-3x+2的图像,则a 的值为( )A. 1B. 2C. 3D. 44.已知二次函数y=x 2-bx+1(-1≤b ≤1),当b 从-1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动,下列关于抛物线的移动方向的描述中,正确的是( )A. 先往左上方移动,再往右下方移动B.先往左下方移动,再往左上方移动B.先往右上方移动,再往右下方移动 D.先往右下方移动,再往右上方移动5.已知抛物线C :y=x 2+3x-10,将抛物线C 平移得到抛物线C ′.若两条抛物线C 、C ′关于直线x=1对称,则下列平移方法正确的是( )A. 将抛物线C 向右平移2.5个单位 B.将抛物线C 向右平移3个单位 C.将抛物线C 向右平移5个单位 D.将抛物线C 向右平移6个单位6.把二次函数y=-41x 2-x+3用配方法化成y=a(x-h)2+k 的形式 A. y=-41(x-2)2+2 B. y=41(x-2)2+4 C. y=-41(x+2)2+4 D. y= (21x-21)2+3 7.在平面直角坐标系中,将二次函数y=2x 2的图象向上平移2个单位,所得图象的解析式为A .y=2x 2-2B .y=2x 2+2C .y=2(x-2)2D .y=2(x+2)28.将抛物线y=2x 2向下平移1个单位,得到的抛物线是( )A .y=2(x+1)2B .y=2(x-1)2C .y=2x 2+1D .y=2x 2-19.将函数y=x 2+x 的图象向右平移a(a >0)个单位,得到函数y=x 2-x+2的图象,则a 的值为( )A .1B .2C .3D .410.把抛物线y=-2x 2向右平移2个单位,然后向上平移5个单位,则平移后抛物线的解析式为( )A. y=-2(x-2)2+5B. y=-2(x+2)2+5C. y=-2(x-2)2-5D. y=-2(x+2)2-511.在平面直角坐标系中,先将抛物线y=x 2+x-2关于x 轴作轴对称变换,再将所得的抛物线关于y 轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为( )A .y=-x 2-x+2B .y=-x 2+x-2 C. y=-x 2+x+2 D .y=x 2+x+212.在平面直角坐标系中,将抛物线y=x 2+2x+3绕着它与y 轴的交点旋转1800,所得抛物线的解析式是( )A .y=-(x+1)2+2B .y=-(x-1)2+4C .y=-(x-1)2+2D .y=-(x+1)2+413.要得到二次函数y=-x 2+2x-2的图象,需将y=-x 2的图象( ).A .向左平移2个单位,再向下平移2个单位B .向右平移2个单位,再向上平移2个单位C .向左平移1个单位,再向上平移1个单位D .向右平移1个单位,再向下平移1个单位14.若二次函数y=(x-m)2-1,当x ≤l 时,y 随x 的增大而减小,则m 的取值范围是( )A .m =1B .m >1C .m ≥1D .m ≤115.如图,点A ,B 的坐标分别为(1,4)和(4,4),抛物线y=a (x-m )2+n 的顶点在线段AB 上运动,与x 轴交于C 、D 两点(C 在D 的左侧),点C 的横坐标最小值为-3,则点D 的横坐标最大值为( )A .13B .7C .5D .816.抛物线y=ax 2向左平移5个单位,再向下移动2个单位得到抛物线17.二次函数y=-2(x+3)2-1由y=-2(x-1)2+1向_____平移______个单位,再向_____平移______个单位得到18.抛物线y=3(x+2)2-3可由抛物线y=3(x+2)2+2向 平移 个单位得到19.将抛物线y=53(x-3)2+5向右平移3个单位,再向上平移2个单位,得到的抛物线是 20.把抛物线y=-(x-1)2-2是由抛物线y=-(x+2)2-3向 平移 个单位,再向_____平移_____个单位得到21.把抛物线y =ax 2+bx+c 的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y =x 2-3x+5,则a+b+c=__________22.抛物线y =x 2-5x+4的图像向右平移三个单位,在向下平移三个单位的解析式23.已知二次函数的图像过点(0,3),图像向左平移2个单位后的对称轴是y 轴,向下平移1个单位后与x 轴只有一个交点,则此二次函数的解析式为24.已知a+b+c=0,a ≠0,把抛物线y=ax 2+bx+c 向下平移1个单位,再向左平移5个单位所得到的新抛物线的顶点是(-2,0),求原抛物线的解析式25.已知二次函数y =-x 2-4x-5.①指出这个二次函数图象的开口方向、对称轴和顶点坐标;②把这个二次函数的图象上、下平移,使其顶点恰好落在正比例函数y =-x 的图象上,求此时二次函数的解析式;③把这个二次函数的图象左、右平移,使其顶点恰好落在正比例函数y =-x 的图象上,求此时二次函数的解析式。
《二次函数的对称性与变换》
《二次函数的对称性与变换》《二次函数的对称性与变换》是一个关于研究二次函数形式,其中包括其对称性和变换性的课题。
人们常常会注意到,二次函数在图形上展示出来具有一定的对称性,这个对称性对于理解二次函数、构造变换和后续的数学研究有重要的意义。
首先,我们探讨一下二次函数的基本特点,它是指一元二次运算式f(x)=ax^2+bx+c(a≠0),用此式子来表示在直角坐标系中的一个曲线,当a>0时,这一曲线在x轴两侧向上凹陷,即函数图形具有拱形,即形如一个弓或蝴蝶结;a<0时,图形具有凸起,即形似一个盔甲或自环。
然后,我们再研究二次函数的对称性,它指的是曲线以某一垂直于x轴的线段或平行于x轴的线段作为中心的对称性。
二次函数的对称性主要有两种,一种是y轴对称,即以y轴作为对称轴的对称,如果以一个曲线围绕y轴的旋转180°不变的称为y轴对称;另外一种是原点对称,即以原点O(0,0)作为对称轴的对称,如果以一个形状围绕原点旋转180°不变的称为原点对称。
最后,我们来讨论二次函数的变换,其中包括平移、旋转、放大、缩小、上下颠倒、左右颠倒,同一种变换可重复多次。
平移指在原曲线上上下左右移动,旋转指以某一点为原点,曲线以该点为中心旋转,放大指曲线的变形过程中曲线的总长不变,但它的所有部分的长度均增大;上下颠倒指曲线的上半部分变成下半部分,下半部分变成上半部分;左右颠倒指曲线的左半部分变成右半部分,右半部分变成左半部分。
综上所述,《二次函数的对称性与变换》是一个关于研究二次函数形式,其中包括其对称性以及变换的课题。
从基本特点上来讲,当a>0时,函数图形具有拱形,即形如一个弓或蝴蝶结;而当a<0时,图形具有凸起,即形似一个盔甲或自环。
此外,二次函数的对称性主要有两种,一种是y轴对称,一种是原点对称。
最后,二次函数的变换包括平移、旋转、放大、缩小、上下颠倒、左右颠倒等,同一种变换可重复多次。
二次函数知识点归纳总结
二次函数知识点归纳总结二次函数是高中数学中的一个重要内容,也是数学建模和解几何问题的重要工具。
下面是关于二次函数的知识点的归纳总结。
一、基本概念1. 二次函数的定义:二次函数是形如f(x) = ax^2 + bx + c (a ≠ 0) 的函数,其中 a、b、c 是常数。
2.二次函数的图象:二次函数的图象是一个抛物线,开口方向取决于a的正负性,顶点坐标为(-b/2a,f(-b/2a))。
3.对称轴:二次函数的对称轴是与图象关于x轴对称的直线,其方程为x=-b/2a。
4. 零点:二次函数的零点是函数图象与 x 轴的交点,可以通过求解二次方程 ax^2 + bx + c =0 来得到。
5.最值:二次函数的最值取决于a的正负性,当a>0时,函数取最小值;当a<0时,函数取最大值。
二、二次函数的变形与性质1.平移变换:二次函数可以通过平移变换来改变其图象的位置。
平移变换的一般形式是f(x)→f(x-h)+k,其中h和k是任意实数。
2.缩放变换:二次函数可以通过缩放变换来改变其图象的形状。
缩放变换的一般形式是f(x)→af(x),其中a是非零实数。
3.纵坐标平移:二次函数可以通过纵坐标平移来改变其图象的位置。
纵坐标平移的一般形式是f(x)→f(x)+k,其中k是任意实数。
4.二次函数的奇偶性:如果a是偶数,则二次函数是偶函数;如果a是奇数,则二次函数是奇函数。
5.顶点坐标的性质:顶点坐标(-b/2a,f(-b/2a))是二次函数的最值点,当a>0时是最小值,当a<0时是最大值。
三、二次函数的方程与不等式1. 二次方程的解:二次方程 ax^2 + bx + c =0 的解可以通过求根公式 x = (-b ± √(b^2 - 4ac))/(2a) 来得到。
2. 解的判别式:二次方程 ax^2 + bx + c =0 的解的判别式是 D =b^2 - 4ac,根据判别式的值可以判断方程有几个实数解。
二次函数中的顶点轴对称与像变换
二次函数中的顶点轴对称与像变换二次函数是高中数学常见的一种函数形式,它的图像通常呈现出一条平滑的弧线。
在学习二次函数时,我们会关注到其中的顶点轴对称性质以及通过变换对图像进行调整的像变换。
本文将详细介绍二次函数中的顶点轴对称性质以及像变换的概念和实际应用。
一、顶点轴对称性质顶点轴对称是指二次函数图像关于某一垂直直线对称。
而这条垂直直线就是二次函数的对称轴。
对称轴可以通过函数表达式中的 x 部分来确定。
1. 一般式二次函数一般来说,一般式的二次函数表达式为:f(x) = ax^2 + bx + c。
其中a、b、c 是常数,且a ≠ 0。
当a ≠ 0 时,二次函数的图像是一个抛物线。
对于一般式的二次函数,其对称轴可以通过以下公式求得:x = -b / (2a)2. 顶点式二次函数另一种常见的二次函数表达式为顶点式:f(x) = a(x - h)^2 + k。
其中a、h、k 是常数,a ≠ 0。
a 决定了二次函数的开口方向,h、k 则决定了图像的平移。
顶点式的二次函数表达式已经将顶点的坐标(h, k)直接体现出来。
顶点是二次函数的图像中的一个重要点,它也是二次函数的对称轴上的一个点。
二、像变换通过对二次函数的变换,我们可以对其图像进行平移、伸缩、翻转等操作,从而改变原始函数的形状和位置。
1. 平移对于一般式的二次函数 f(x) = ax^2 + bx + c,平移的变换形式为:f(x) = a(x - h)^2 + k。
其中 (h, k) 表示平移的横向和纵向距离。
平移后的二次函数图像在坐标平面上的位置相对于原来的位置发生了变化,但形状不发生改变。
2. 伸缩伸缩是指通过改变二次函数图像的开口程度,将图像的形状进行改变。
伸缩的变换形式为:f(x) = a * b(x - h)^2 + k。
其中 a 和 b 是常数,a 代表纵向方向上的伸缩因子,b 代表横向方向上的伸缩因子。
当 |a| > 1 时,图像在纵向上被拉长;当 |a| < 1 时,图像在纵向上被压缩。
中考点拨:用顶点式解决二次函数图像平移问题
中考点拨:用顶点式解决二次函数图像平移问题二次函数是初中数学中最精彩的内容之一,也是历年中考的热点和难点。
其中,关于函数解析式的确定是非常重要的题型。
从近几年中考趋势来看强化了对图形变换的要求,那么二次函数和图形变化的结合,将是同学们在学习中不可忽视的内容。
图形变换包含平移、轴对称、旋转、位似四种变换,那么二次函数的图像在其图形变化(平移、轴对称、旋转)的过程中,如何完成解析式的确定呢?解决此类问题的方法很多,关键在于解决问题的着眼点。
飞杨老师认为最好的方法是用顶点式的方法。
因此解题时,先将二次函数解析式化为顶点式,确定其顶点坐标,再根据具体图形变换的特点,确定变化后新的顶点坐标及a值。
1、平移:二次函数图像经过平移变换不会改变图形的形状和开口方向,因此a值不变。
顶点位置将会随着整个图像的平移而变化,因此只要按照点的移动规律,求出新的顶点坐标即可确定其解析式。
例1.将二次函数y=x²-2x-3的图像向上平移2个单位,再向右平移1个单位,得到的新的图像解析式为_____分析:将y=x²-2x-3化为顶点式y=(x-1)2-4,a值为1,顶点坐标为(1,-4),将其图像向上平移2个单位,再向右平移1个单位,那么顶点也会相应移动,其坐标为(2,-2),由于平移不改变二次函数的图像的形状和开口方向,因此a值不变,故平移后的解析式为y=(x-2)²-2。
2、轴对称:此图形变换包括x轴对称和关于y轴对称两种方式。
二次函数图像关于x轴对称的图像,其形状不变,但开口方向相反,因此a值为原来的相反数。
顶点位置改变,只要根据关于x轴对称的点的坐标特征求出新的顶点坐标,即可确定其解析式。
二次函数图像关于y轴对称的图像,其形状和开口方向都不变,因此a值不变。
但是顶点位置会改变,只要根据关于y轴对称的点的坐标特征求出新的顶点坐标,即可确定其解析式。
例2.求抛物线y=x²-2x-3关于x轴以及y轴对称的抛物线的解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数专题训练(平移、旋转、轴对称变换)
一、二次函数图象的平移、旋转(只研究中心对称)、轴对称变换
1、抛物线的平移变换:一般都是在顶点式的情况下进行的。
抛物线的上下平移:________________________
y=a(x-h)2+ky=a(x-h)2+k±m
抛物线的左右平移:________________________
y=a(x-h)2+ky=a(x-h±m)2+k
练习:(1)函数图象沿y轴向下平移2个单位,再沿x轴向
右平移3个单位,得到函数__________________的图象。
(2)抛物线225yxx向左平移3个单位,再向下平移6个单位,所得抛物
线的解析式是。
2、抛物线的旋转变换(只研究中心对称):一般都是在顶点式的情况下进行的。
(1)将抛物线绕其顶点旋转180(即两条抛物线关于其顶点成中心对称)
2yaxhk关于顶点对称后,得到的解析式是
2
yaxhk
。
(2)将抛物线绕原点旋转180(即两条抛物线关于原点成中心对称)
2yaxhk关于原点对称后,得到的解析式是
2
yaxhk
。
练习:(1)抛物线2246yxx绕其顶点旋转180后,所得抛物线的解析式
是
(2)将抛物线y=x2+1绕原点O旋转180°,则旋转后抛物线的解析式为()
A.y=-x2B.y=-x2+1 C.y=x2-1 D.y=-x2-1
3、抛物线的轴对称变换:
关于x轴对称
2yaxbxc关于x轴对称后,得到的解析式是2
yaxbxc
;
2
yaxhk
关于x轴对称后,得到的解析式是2yaxhk;
关于y轴对称
2yaxbxc关于y轴对称后,得到的解析式是2
yaxbxc
;
2yaxhk关于y轴对称后,得到的解析式是
2
yaxhk
;
练习:已知抛物线C1:2(2)3yx
(1)抛物线C2与抛物线C1关于y轴对称,则抛物线C2的解析式为
(2)抛物线C3与抛物线C1关于x轴对称,则抛物线C3的解析式为
总结:根据平移、旋转、轴对称的性质,显然无论作何种变换,抛物线的形状
一定不会发生变化,因此a永远不变。
二、二次函数的系数与图象的关系。
热身练习:1、抛物线y=ax2+bx+c的开口方向与有关。
2、抛物线y=ax2+bx+c的对称轴是.
3、抛物线y=ax2+bx+c与y轴的交点坐标是,与x轴的交点坐标是。
由二次函数2yaxbxc(0a)的图象位置判定系数,,abc及判别式
2
4bac
和相关代数式符号的方法可以归纳成下表:
与抛物线的关系 判别方法
a a决定抛物线的开口方向和大小;a相等,抛物线的形状相同. 开口向上0a
开口向下0a
b b和a共同决定抛物线对称
轴的位置:左同右异
对称轴在y轴左侧,ab同号
对称轴在y轴右侧,ab异号
对称轴为y轴0b
c 决定抛物线与y轴的交点位
置
交点位于y轴正半轴0c
交点位于y轴负半轴0c
交点是原点0c
决定抛物线与x轴的交点个数 抛物线与x轴有两个交点
0
抛物线与x轴有一个交点
0
抛物线与x轴没有交点0
a+b+c 由x=1时抛物线上的点的位置确定
a-b+c 由x=-1时抛物线上的点的位置确定
2a与b 由抛物线的对称轴直线x=-确定
4a+2b+c 由x=2时抛物线上的点的位置确定
4a-2b+c 由x=-2时抛物线上的点的位置确定
练习:1、函数y=x2+mx-2(m<0)的图象是()
2、抛物线y=ax2+bx+c(a≠0)的图象如图2所示,那么()
A.a<0,b>0,c>0B.a<0,b<0,c>0
C.a<0,b>0,c<0D.a<0,b<0,c<0
第2题图第3题图第4题图第5题图第6题图
3、已知二次函数y=ax2+bx+c的图象如图3所示,则()
A.a>0,c>0,b2-4ac<0B.a>0,c<0,b2-4ac>0
C.a<0,c>0,b2-4ac<0D.a<0,c<0,b2-4ac>0
4、已知二次函数y=ax2+bx+c的图象如图4所示,则()
A.b>0,c>0,=0B.b<0,c>0,=0
C.b<0,c<0,=0D.b>0,c>0,>0
5、二次函数y=mx2+2mx-(3-m)的图象如图5所示,那么m的取值范围是()
A.m>0B.m>3C.m<0 D.0<m<3
6、y=ax2+bx+c(a≠0)的图象如图6所示,那么下面六个代数式:abc,b2-4ac,
a-b+c,a+b+c,2a-b,9a-4b中,值小于0的有()
A.1个B.2个C.3个 D.4个
7、抛物线图象如图7所示,根据图象可知,抛物线的解析式可能..是()
A、y=x2-x-2B、y=121212xC、y=121212xxD、y=22xx
8、如图8是二次函数y=ax2+bx+c的图象的一部分;图象过点A(-3,0),对
称轴为x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a
<b.其中正确的是________________.(填序号)
第7题图第8题图第9题图
9、如图9,看图填空:
(1)a+b+c_______0;(2)a-b+c_______0;(3)2a-b_______0;
(4)2a+b_______0;(5)4a+2b+c_______0;(6)a+2b+c_______0.
三、抛物线的对称性
思考:1、抛物线若与x轴有两个交点(x1,0)、(x2,0),则两交点关于__________
对称,对称轴可以表示为____________________。
2、一般地,若抛物线上有两点关于对称轴对称,则它们的纵坐标__________;
反之,若抛物线上有两点的纵坐标相等,则它们关于__________对称.由此可得,
若抛物线上有两点(x1,y)(x2,y)关于对称轴对称,则该抛物线的对称轴可
以表示为____________________。
练习:1、已知二次函数y=ax2+bx+c(a≠0),其中a、b、c满足a+b+
c
=0和9a-3b+c=0,则该二次函数图象的对称轴是( )
A.直线x=-2 B.直线x=-1 C.直线x=2 D.直线
x
=1
2、已知点A(2,5),B(4,5)是抛物线y=4x2+bx+c上的两点,则这条抛
物线的对称轴为_____________________.
3、已知抛物线的对称轴为直线x=2,与x轴的一个交点为),0,23(则它与x轴
的另一个交点坐标为__________.
4、抛物线y=ax2+bx+c经过(0,0),(12,0)两点,其顶点的纵坐标是3,求这
个抛物线的解析式.
四、二次函数与其他函数、方程、不等式的关系。
1、二次函数与其他函数。
练习:(1)在同一坐标系内,函数y=kx2和y=kx-2(k≠0)的图象大致如图()
(2)函数xabybaxy221,(ab<0)的图象在下列四个示意图中,可能正确的
是()
(3)已知函数y=a(x+2)和y=a(x2+1),那么它们在同一坐标系内图象的示意
图是()
(4)二次函数2yaxbxc的图象如图所示,则一次函数24ybxbac与反
比例函数abcyx在同一坐标系内的图象大致为()
(5)抛物线y=x2+1与双曲线y=的交点A的横坐标是1,则关于x的不等式+x2+1<0
的解集是()
A.x>1B.x
2、二次函数与方程、不等式(组)
(1)如图1,抛物线y=x2+1与双曲线y=的交点A的横坐标是1,则关于x的不
等式+x2+1<0的解集是()
A.x>1B.x
第1题图第2题图第3题图
(2)如图2,是二次函数y=ax2+bx+c图象的一部分,其对称轴为直线x=1,若
其与x轴一交点为A(3,0),则由图象可知,不等式ax2+bx+c<0的解集是.
(3)利用抛物线图象求解一元二次方程及二次不等式
x
y
A
y x O y x O B. C. y
x
O
A. y x O D.
1
O
y
x
y
A
①方程ax2+bx+c=0的根为___________;②方程ax2+bx+c=-3的根为
__________;
③方程ax2+bx+c=-4的根为__________;④不等式ax2+bx+c>0的解集为
________;
⑤不等式ax2+bx+c<0的解集为________;
⑥不等式组-4<ax2+bx+c<0的解集为________.
