一元二次不等式及其解法
简单的一元二次不等式及其解法

一元二次不等式及其解法
第1课时 简单的一元二次不等式及其解法
学习目标
1.理解一元二次方程、一元二次不等式与二次函数的关系.
2.掌握图象法解一元二次不等式.
3.能从实际问题中抽象出一元二次不等式并解决.
内容索引
问题导学
题型探究
达标检测
问题导学
知识点一
思考
一元二次不等式的概念
我们知道,方程x2=1的一个解是x=1,解集是{1,-1},解集中
称为 一元二次 不等式.
(2)能使不等式成立的未知数x的一个值称为不等式的一个解. (3)不等式所有解的 集合 称为解集.
知识点二
“三个二次”的关系
一元二次不等式与相应的一元二次方程、二次函数的联系,如下表.
Δ=b2-4ac
Δ>0
Δ=0
Δ<0
y=ax2+bx+c (a>0)的图象
ax2+bx+Leabharlann =0√ 1 D.xx<-2或x>1
解析 ∵2x2-x-1=(2x+1)(x-1),
1 ∴由 2x -x-1>0,得(2x+1)(x-1)>0,解得 x>1 或 x<-2,
2
1 ∴不等式的解集为xx<-2或x>1 .
1
2
3
4
解析
答案
2.若不等式ax2+8ax+21<0的解集是{x|-7<x<-1},那么a的值是 A.1 B.2 C.3 √ D.4
由于x>0,从而得x甲>30 km/h,x乙>40 km/h.
经比较知乙车超过限速,应负主要责任.
解答
类型二 “三个二次”间对应关系的应用
高中 一元二次不等式及其解法 知识点+例题 全面

辅导讲义――一元二次不等式及其解法教学内容1.一元二次不等式:只含有一个未知数,并且未知数最高次数是2的不等式. 2.二次函数、一元二次方程、一元二次不等式的关系判别式Δ=b 2-4acΔ>0Δ=0Δ<0二次函数y =ax 2+bx +c (a >0)的图象一元二次方程ax 2+bx +c =0 (a >0)的根 有两相异实根x 1,x 2(x 1<x 2) 有两相等实根 x 1=x 2=-b2a没有实数根ax 2+bx +c >0 (a >0)的解集 {x |x <x 1或x >x 2}{x |x ≠x 1}{x |x ∈R }ax 2+bx +c <0 (a >0)的解集{x |x 1< x <x 2}∅ ∅[例1] 若不等式052>++c x ax 的解集是}2131{<<x x ,则a+c 的值为________.-7[巩固1] 已知不等式02<+-b x ax 的解集是}21{<<-x x ,则a ,b 的值为___________.a=1,b=-2[巩固2] 若关于x 的不等式0622<+-t x tx 的解集是),1(),(+∞-∞ a ,则a 的值为______.-3[例2] 若1)(2+-=ax x x f 有负值,则实数a 的取值范围是____________.),2()2,(+∞--∞[巩固1] 已知二次函数c bx ax x f ++=2)(的图象与直线25=y 有公共点,且不等式02>++c bx ax 的解是知识模块1三个“二次” 精典例题透析3121<<-x ,求a ,b ,c 的取值范围.[巩固2] 已知关于x 的不等式)(0222R a a ax x ∈≤++-的解集为M . (1)当M 为空集时,求实数a 的取值范围. (2)如果]4,1[⊆M ,求实数a 的取值范围.[例3] 关于x 的方程02=++c bx x 的两根分别为21-=x 和212-=x ,则关于x 的不等式02<+-c bx x 的解集是______________.)2,21([巩固1] 方程05)2(2=-+-+m x m x 的两根都大于2,则m 的取值范围是____________.]4,5(--[巩固] 若关于x 的不等式4502≤++≤ax x 恰好只有一个解,则实数.______=a 2±[例5] 若不等式02<--b ax x 的解集为}32{<<x x ,则.______=+b a 1-[巩固1] 若关于x 的不等式0322<+-a x x 的解集是)1,(m ,则实数.______=m 21[巩固2] 关于x 的不等式0)2)(1(>--x mx ,若此不等式的解集为}21{<<x mx,则m 的取值范围是__________. )0,(-∞[例6] 已知实数R a ∈,解关于x 的不等式.02)2(2<++-a x a x[巩固] 已知关于x 的不等式0232>+-x ax 的解集是}1{b x x x ><或, (1)求a ,b 的值;(2)解关于x 的不等式).(0)(2R c bc x b ac ax ∈<++-[例7] 若不等式02<--b ax x 的解集是)3,2(, (1)求a ,b 的值;(2)求不等式012>--ax bx 的解集.[巩固] 已知不等式0)32()(<-++b a x b a 的解为43->x ,解不等式.0)2()1(2)2(2>-+--+-a x b a x b a题型一:一元二次不等式的解法 [例] 求下列不等式的解集:(1)-x 2+8x -3>0; (2)ax 2-(a +1)x +1<0.解 (1)因为Δ=82-4×(-1)×(-3)=52>0,所以方程-x 2+8x -3=0有两个不相等的实根x 1=4-13,x 2=4+13. 又二次函数y =-x 2+8x -3的图象开口向下, 所以原不等式的解集为{x |4-13<x <4+13}. (2)若a =0,原不等式等价于-x +1<0,解得x >1. 若a <0,原不等式等价于(x -1a )(x -1)>0,解得x <1a 或x >1.若a >0,原不等式等价于(x -1a)(x -1)<0.①当a =1时,1a =1,(x -1a )(x -1)<0无解;②当a >1时,1a <1,解(x -1a )(x -1)<0得1a <x <1;③当0<a <1时,1a >1,解(x -1a )(x -1)<0得1<x <1a.综上所述:当a <0时,解集为{x |x <1a或x >1};当a =0时,解集为{x |x >1};当0<a <1时,解集为{x |1<x <1a };当a =1时,解集为∅;当a >1时,解集为{x |1a <x <1}.[巩固](1)若不等式ax 2+bx +2>0的解为-12<x <13,则不等式2x 2+bx +a <0的解集是________.(2)不等式x -12x +1≤0的解集是________.知识模块3经典题型11.已知函数f (x )=(ax -1)(x +b ),如果不等式f (x )>0的解集是(-1,3),则不等式f (-2x )<0的解集是_______________.答案 (-∞,-32)∪(12,+∞) 解析 f (x )=0的两个解是x 1=-1,x 2=3且a <0,由f (-2x )<0得-2x >3或-2x <-1,∴x <-32或x >12. 12.(2013·重庆)关于x 的不等式x 2-2ax -8a 2<0(a >0)的解集为(x 1,x 2),且x 2-x 1=15,则a=_______.答案 52解析 由x 2-2ax -8a 2<0,得(x +2a )(x -4a )<0,因a >0,所以不等式的解集为(-2a,4a ),即x 2=4a ,x 1=-2a ,由x 2-x 1=15,得4a -(-2a )=15,解得a =52. 13.设0≤α≤π,不等式8x 2-(8sin α)x +cos 2α≥0对x ∈R 恒成立,则α的取值范围为______________.答案 [0,π6]∪[5π6,π] 解析 由题意,要使8x 2-(8sin α)x +cos 2α≥0对x ∈R 恒成立,需Δ=64sin 2α-32cos 2α≤0,化简得cos 2α≥12. 又0≤α≤π,∴0≤2α≤π3或5π3≤2α≤2π, 解得0≤α≤π6或5π6≤α≤π. 14.已知a ∈Z ,关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则所有符合条件的a 的值之和是________.答案 21解析 设f (x )=x 2-6x +a ,其是开口向上,对称轴是x =3的抛物线,图象如图所示.关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则⎩⎪⎨⎪⎧ f (2)≤0,f (1)>0,即⎩⎪⎨⎪⎧f (2)=4-12+a ≤0,f (1)=1-6+a >0, 解得5<a ≤8.又a ∈Z ,所以a =6,7,8,则所有符合条件的a 的值之和是6+7+8=21.15.求使不等式x 2+(a -6)x +9-3a >0,|a |≤1恒成立的x 的取值范围.解 将原不等式整理为形式上是关于a 的不等式(x -3)a +x 2-6x +9>0.令f (a )=(x -3)a +x 2-6x +9.因为f (a )>0在|a |≤1时恒成立,所以。
一元二次不等式及其解法(含参数)

含参数的一元二次不等式的解法解含参数的一元二次不等式,通常情况下,均需分类讨论,那么如何讨论呢?对含参一元二次不等式常用的分类方法有三种:一、按2x 项的系数a 的符号分类,即0,0,0<=>a a a ;例1 解不等式:()0122>+++x a ax分析:本题二次项系数含有参数,()044222>+=-+=∆a a a ,故只需对二次项 系数进行分类讨论。
二、按判别式∆的符号分类,即0,0,0<∆=∆>∆;例2 解不等式042>++ax x分析 本题中由于2x 的系数大于0,故只需考虑∆与根的情况。
例3解不等式()()R m x x m ∈≥+-+014122三、按方程02=++c bx ax 的根21,x x 的大小来分类,即212121,,x x x x x x <=<; 例4解不等式)0( 01)1(2≠<++-a x a a x 分析:此不等式可以分解为:()0)1(<--a x a x ,故对应的方程必有两解。
本题 只需讨论两根的大小即可。
考向二 含参数的一元二次不等式的解法【例2】►求不等式12x 2-ax >a 2(a ∈R )的解集.解含参数的一元二次不等式的一般步骤:(1)二次项若含有参数应讨论是等于0,小于0,还是大于0,然后将不等式转化为二次项系数为正的形式.(2)判断方程的根的个数,讨论判别式Δ与0的关系.(3)确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集形式.【训练2】 解关于x 的不等式(1-ax )2<1.考向三 不等式恒成立问题【例3】►已知不等式ax 2+4x +a >1-2x 2对一切实数x 恒成立,求实数a 的取值范围.[审题视点] 化为标准形式ax 2+bx +c >0后分a =0与a ≠0讨论.当a ≠0时,不等式ax 2+bx +c >0的解是全体实数(或恒成立)的条件是当a =0时,b =0,c >0;当a ≠0时,⎩⎨⎧ a >0,Δ<0;不等式ax 2+bx +c <0的解是全体实数(或恒成立)的条件是当a =0时,b =0,c <0;当a ≠0时,⎩⎨⎧a <0,Δ<0. 【训练3】 已知f (x )=x 2-2ax +2(a ∈R ),当x ∈[-1,+∞)时,f (x )≥a 恒成立,求a 的取值范围.规范解答12——怎样求解含参数不等式的恒成立问题【解决方案】解决这类问题的关键是将恒成立问题进行等价转化,使之转化为函数的最值问题.【试一试】设函数f(x)=ax3-3x+1,若对于任意x∈[-1,1],都有f(x)≥0成立,求实数a的值.。
一元二次不等式及其解法
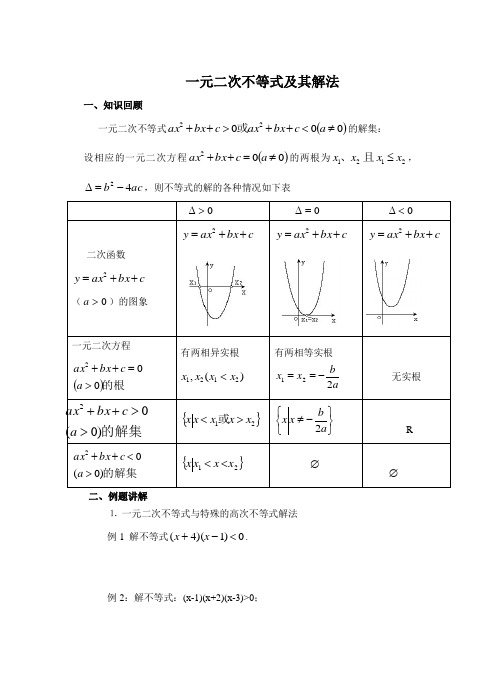
一元二次不等式及其解法一、知识回顾一元二次不等式()00022≠<++>++a c bx ax c bx ax 或的解集: 设相应的一元二次方程()002≠=++a c bx ax 的两根为2121x x x x ≤且、,ac b 42-=∆,则不等式的解的各种情况如下表0>∆0=∆0<∆二次函数c bx ax y ++=2(0>a )的图象c bx ax y ++=2c bx ax y ++=2c bx ax y ++=2一元二次方程()的根002>=++a c bx ax有两相异实根)(,2121x x x x < 有两相等实根ab x x 221-==无实根 的解集)0(02>>++a c bx ax{}21x x x x x ><或⎭⎬⎫⎩⎨⎧-≠a b x x 2R 的解集)0(02><++a c bx ax{}21x x x x <<∅∅二、例题讲解⒈ 一元二次不等式与特殊的高次不等式解法 例1 解不等式0)1)(4(<-+x x .例2:解不等式:(x-1)(x+2)(x-3)>0;例3 解不等式:(x-2)2(x-3)3(x+1)<0.2.分式不等式的解法 例4 解不等式:073<+-x x .例5 解不等式:0322322≤--+-x x x x .例6. 解关于x 的不等式:(x-x 2+12)(x+a)<0. 三、练习【1】设关于x 的不等式x >ax+23的解集为{x 4<x<m},求实数a 和m 的值。
【2】已知关于x 的不等式ax 2+bx+c<0的解集是{x x<-2或x>21-},求ax 2-bx+c>0的解集。
【3】若对x ∈R 恒有n x x x x >++++122322,(n ∈N *),试求n 的值。
一元二次不等式及其解法

一元二次不等式及其解法

∵ 32 4 2 2 7 0
∴方程 2x 2 3x 2 0 无实数根 ∴原不等式的解集为 R.
习题 1: 解下列不等式: (1) x 2 5x 6 0 ;
(2) x 2 7x 6 ;
x 2 6x 10 0
(3) 2 xx 3 0 ;
;
当 a 1 ,即 a 1或0 a 1 时,原不等式的解集为 x a x 1 .
原不等式可化为 x 22 0 或 x 22 0 ,所以原不等式的解集为 x x 2或 x x 2;
当 0 ,即 4 a 4 时 方程 x 2 ax 4 0 无实数根,所以原不等式的解集为 R.
例 7. 解不等式 m2 1x 2 4x 1≥0 m R.
第1页
(2)一元二次不等式 ax 2 bx c 0 (≤0)的解集就是二次函数 y ax 2 bx c 0a 0
的图象位于 x 轴下方(包括 x 轴)的部分所对应的自变量的取值范围.
表(1)一元二次方程、二次函数以及一元二次不等式的关系:
判别式 b 2 4ac
解:∵ m 2 ≥0 ∴m2 1 0
42 4m2 1 12 4m2
当 0 ,即
一元二次不等式及其解法
一元二次不等式及其解法【知识归纳】1.一元二次不等式的解法(1)将不等式的右边化为零,左边化为二次项系数大于零的不等式ax 2+bx +c >0 (a >0)或ax 2+bx +c <0 (a >0).(2)求出相应的一元二次方程的根.(3)利用二次函数的图像与x 轴的交点确定一元二次不等式的解集. 2.一元二次不等式与相应的二次函数及一元二次方程的关系如下表:判别式Δ=b 2-4acΔ>0 Δ=0 Δ<0 二次函数y =ax 2+bx +c(a >0)的图像一元二次方程ax 2+bx +c =0 (a >0)的根 有两相异实根x 1,x 2(x 1<x 2) 有两相等实根x 1=x 2=-b 2a没有实数根 ax 2+bx +c >0(a >0)的解集{x |x <x 1或x >x 2} {x |x ≠x 1} {x |x ∈R } ax 2+bx +c <0(a >0)的解集{x |x 1< x <x 2} ∅ ∅【难点提升】1.一元二次不等式的解集及解集的确定 一元二次不等式ax 2+bx +c <0 (a ≠0)的解集的确定受a 的符号、b 2-4ac 的符号的影响,且与相应的二次函数、一元二次方程有密切联系,可结合相应的函数y =ax 2+bx +c (a≠0)的图像,数形结合求得不等式的解集.若一元二次不等式经过不等式的同解变形后,化为ax 2+bx +c >0(或<0)(其中a >0)的形式,其对应的方程ax 2+bx +c =0有两个不等实根x 1,x 2(x 1<x 2) (此时Δ=b 2-4ac >0),则可根据“大于取两边,小于夹中间”求解集.2.解含参数的一元二次不等式,可先考虑因式分解,再对根的大小进行分类讨论;若不能因式分解,则可对判别式进行分类讨论,分类要不重不漏.【学前强化】1.不等式x 2<1的解集为________.2.函数y =x 2+x -12的定义域是____________.3.已知不等式x 2-2x +k 2-1>0对一切实数x 恒成立,则实数k 的取值范围为_____________.4.不等式x -12x +1≤0的解集为 ( ) A.⎝⎛⎦⎤-12,1 B.⎣⎡⎦⎤-12,1 C.⎝⎛⎭⎫-∞,-12∪[1,+∞) D.⎝⎛⎦⎤-∞,-12∪[1,+∞)5.若不等式ax 2+bx -2<0的解集为{x |-2<x <14},则ab 等于( ) A .-28 B .-26 C .28 D .266.设函数f (x )=⎩⎪⎨⎪⎧x 2-4x +6,x ≥0,x +6, x <0, 则不等式f (x )>f (1)的解集是________.7.已知f (x )=ax 2-x -c >0的解集为(-3,2),则a =________,c =________.8.当x ∈(1,2)时,不等式x 2+mx +4<0恒成立,则m 的取值范围为________________.题型一 一元二次不等式的解法【例1】解下列不等式:思维启迪: 解一元二次不等式的一般步骤:(1)对不等式变形,使一端为0且二次项系数大于0,即ax 2+bx +c >0(a >0),ax 2+bx +c <0(a >0);(2)计算相应的判别式;(3)当Δ≥0时,求出相应的一元二次方程的根;(4)根据对应二次函数的图象,写出不等式的解集.(1)-x 2+2x -23>0; (2)9x 2-6x +1≥0. (3)x 2+2x -3≤0;(4)x -x 2+6<0; (5)4x 2+4x +1<0; (6)x 2-6x +9≤0;【变式】 解下列不等式:(1)2x 2+4x +3<0; (2)-3x 2-2x +8≤0; (3)8x -1≥16x 2.题型二 含参数的一元二次不等式的解法【例2】已知不等式ax 2-3x +6>4的解集为{x |x <1或x >b },求a ,b 的值;思维启迪:先化简不等式为标准形式,再依据解集确定a 的符号,然后利用根与系数的关系列出a ,b 的方程组,求a ,b 的值.【变式】解关于x的不等式ax2-(a+1)x+1<0.题型三一元二次不等式恒成立问题【例3】已知f(x)=x2-2ax+2 (a∈R),当x∈[-1,+∞)时,f(x)≥a恒成立,求a的取值范围.思维启迪注意等价转化思想运用,二次不等式在区间上恒成立的问题可转化为二次函数区间最值问题.【变式1】已知不等式ax 2+4x +a >1-2x 2对一切实数x 恒成立,求实数a 的取值范围.思维启迪:化为标准形式ax 2+bx +c >0后分a =0与a ≠0讨论.当a ≠0时,有⎩⎪⎨⎪⎧a >0,Δ=b 2-4ac <0.【变式2】当x ∈(1,2)时,不等式x 2+mx +4<0恒成立,求m 的取值范围。
3.2一元二次不等式及其解法
想一想,当x取何值时,y 的值大 于零?(或小于零?) y O m x y n O x
复习
当x m时y 0 当x m时y 0
当 x n时 y 0 当 x n时 y 0
考察:对一次函数y=2x-7,当x为何值 时,y=0;当x为何值时,y<0;当x为何值 时,y>0?
-2 O
3
x
结论:
解一元二次不等式
ax2+bx+c>0
(a>0,△=0 )的步骤: ① 将二次不等式化成一般式;
② 求出方程ax2+bx+c=0的两根; ③ 画出y=ax2+bx+c的图象;
④ 根据图象写出不等式的解集.
求解一元 二次不等式 ax2+bx+c>0 (a>0)的程序框 图:
△≥0
x
结合函数图 象进行思考
Hale Waihona Puke -2 O3x思考:对二次函数 y=x2-x-6,当x为何值 时,y=0?当x为何值时,y<0?当x为何值时, y>0 ?
y
当 x=-2 或 x=3 时, y=0 即 x2x6=0 当2<x<3 时, y<0 即 x2x6<0 当 x<2 或 x>3 时, y>0 即 x2x6>0
b 2a
x< x1或x> x2
举例
例1 解不等式x2-6x-7>0 y
解:方程x2-6x-7=0的解是
x1 1, x 2 7
作函数图象的草图 所以,不等式的解集是
-1 o
7 x
{x | x<-1 或 x > 7 }
一元二次不等式及其解法
2021年新高考数学总复习第七章《不等式》一元二次不等式及其解法一元二次不等式的解集判别式Δ=b2-4ac Δ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象方程ax2+bx+c=0 (a>0)的根有两相异实根x1,x2(x1<x2)有两相等实根x1=x2=-b2a没有实数根ax2+bx+c>0(a>0)的解集{x|x<x1或x>x2}⎩⎨⎧⎭⎬⎫x⎪⎪x≠-b2a{x|x∈R} ax2+bx+c<0(a>0)的解集{x|x1< x<x2} ∅∅概念方法微思考1.一元二次不等式ax2+bx+c>0(a>0)的解集与其对应的函数y=ax2+bx+c的图象有什么关系?提示ax2+bx+c>0(a>0)的解集就是其对应函数y=ax2+bx+c的图象在x轴上方的部分所对应的x的取值范围.2.一元二次不等式ax2+bx+c>0(<0)恒成立的条件是什么?提示显然a≠0.ax2+bx+c>0恒成立的条件是⎩⎪⎨⎪⎧a>0,Δ<0;ax2+bx+c<0恒成立的条件是⎩⎪⎨⎪⎧a<0,Δ<0.题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若不等式ax 2+bx +c <0的解集为(x 1,x 2),则必有a >0.( √ )(2)若不等式ax 2+bx +c >0的解集是(-∞,x 1)∪(x 2,+∞),则方程ax 2+bx +c =0的两个根是x 1和x 2.( √ )(3)若方程ax 2+bx +c =0(a ≠0)没有实数根,则不等式ax 2+bx +c >0的解集为R .( × ) (4)不等式ax 2+bx +c ≤0在R 上恒成立的条件是a <0且Δ=b 2-4ac ≤0.( × )(5)若二次函数y =ax 2+bx +c 的图象开口向下,则不等式ax 2+bx +c <0的解集一定不是空集.( √ )题组二 教材改编2.已知集合A ={x |x 2-x -6>0},则∁R A 等于( )A .{x |-2<x <3}B .{x |-2≤x ≤3}C .{x |x <-2}∪{x |x >3}D .{x |x ≤-2}∪{x |x ≥3}答案 B解析 ∵x 2-x -6>0,∴(x +2)(x -3)>0,∴x >3或x <-2,即A ={x |x >3或x <-2}.在数轴上表示出集合A ,如图所示.由图可得∁R A ={x |-2≤x ≤3}.故选B.3. y =log 2(3x 2-2x -2)的定义域是________________.答案 ⎝ ⎛⎭⎪⎫-∞,1-73∪⎝ ⎛⎭⎪⎫1+73,+∞ 解析 由题意,得3x 2-2x -2>0,令3x 2-2x -2=0,得x 1=1-73,x 2=1+73, ∴3x 2-2x -2>0的解集为⎝ ⎛⎭⎪⎫-∞,1-73∪⎝ ⎛⎭⎪⎫1+73,+∞. 题组三 易错自纠4.不等式-x 2-3x +4>0的解集为________.(用区间表示)答案 (-4,1)。
一元二次不等式及其解法
3.2 一元二次不等式及其解法第1课时一元二次不等式及其解法1.掌握一元二次不等式的解法.(重点)2.能根据“三个二次”之间的关系解决简单问题.(难点)[基础·初探]教材整理1一元二次不等式的概念阅读教材P76第一行~P76倒数第四行,完成下列问题.1.一元二次不等式的概念只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.2.一元二次不等式的一般形式(1)ax2+bx+c>0(a≠0).(2)ax2+bx+c≥0(a≠0).(3)ax2+bx+c<0(a≠0).(4)ax2+bx+c≤0(a≠0).3.一元二次不等式的解与解集使一元二次不等式成立的未知数的值,叫做这个一元二次不等式的解,其解的集合,称为这个一元二次不等式的解集.判断(正确的打“√”,错误的打“×”)(1)mx2-5x<0是一元二次不等式.()(2)若a>0,则一元二次不等式ax2+1>0无解.()(3)x2-x >0为一元二次不等式.()【解析】(1)×.当m=0时,是一元一次不等式;当m≠0时,它是一元二次不等式.(2)×.因为a>0,所以不等式ax2+1>0恒成立,即原不等式的解集为R.(3)×.因为一元二次不等式是整式不等式,而不等式中含有x,故该说法错误.【答案】(1)×(2)×(3)×教材整理2一元二次不等式、二次函数、二次方程间的关系阅读教材P76倒数第三行~P78例2,完成下列问题.三个“二次”的关系:设f(x)=ax2+bx+c(a>0),方程ax2+bx+c=0的判别式Δ=b2-4ac判别式Δ>0Δ=0Δ<0解不等式f(x)>0或f(x)<0的步骤求方程f(x)=0的解有两个不等的实数解x1,x2有两个相等的实数解x1=x2没有实数解画函数y=f(x)的示意图得等的集不式解f(x)>0{x|x<x1_或x>x2}⎩⎨⎧x⎪⎪⎪⎭⎬⎫x≠-b2a R f(x)<0{x|x1<x<x2} ∅∅1.不等式x2≤1的解集为________.【解析】令x2-1=0,其两根分别为-1,1,故x2≤1的解集为{x|-1≤x≤1}.【答案】{x|-1≤x≤1}2.不等式2x≤x2+1的解集为________.【解析】2x≤x2+1⇔x2-2x+1≥0⇔(x-1)2≥0,∴x∈R.【答案】R3.设集合M={x|x2-x<0},N={x|x2<4},则M与N的关系为________.【解析】因为M={x|x2-x<0}={x|0<x<1},N={x|x2<4}={x|-2<x<2},所以M N.【答案】M N4.二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:x -3-2-10123 4 y 60-4-6-6-40 6 则不等式ax2+bx+c>0的解集是________.【解析】可根据图表求得两个零点为x1=-2,x2=3,结合二次函数的图象(略)求解.【答案】{x|x<-2或x>3}[小组合作型]解一元二次不等式求下列一元二次不等式的解集.(1)x2-5x>6;(2)4x2-4x+1≤0;(3)-x2+7x>6.【精彩点拨】【自主解答】 (1)由x 2-5x >6,得 x 2-5x -6>0.∵x 2-5x -6=0的两根是x =-1或6, ∴原不等式的解集为 {x |x <-1或x >6}.(2)4x 2-4x +1≤0,即(2x -1)2≤0, 方程(2x -1)2=0的根为x =12, ∴4x 2-4x +1≤0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =12. (3)由-x 2+7x >6,得x 2-7x +6<0, 而x 2-7x +6=0的两个根是x =1或6, ∴不等式x 2-7x +6<0的解集为 {x |1<x <6}.解不含参数的一元二次不等式的一般步骤(1)化标准.通过对不等式的变形,使不等式右侧为0,使二次项系数为正. (2)判别式.对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.(3)求实根.求出相应的一元二次方程的根或根据判别式说明方程有无实根. (4)画草图.根据一元二次方程根的情况画出对应的二次函数的草图. (5)写解集.根据图象写出不等式的解集.[再练一题]1.解下列不等式:(1)2x2-x+6>0;(2)(5-x)(x+1)≥0.【解】(1)∵方程2x2-x+6=0的判别式Δ=(-1)2-4×2×6<0,∴函数y=2x2-x+6的图象开口向上,与x轴无交点,∴原不等式的解集为R.(2)原不等式可化为(x-5)(x+1)≤0,∴原不等式的解集为{x|-1≤x≤5}.解含参数的一元二次不等式解关于x的不等式x2-ax-2a2<0(a∈R).【精彩点拨】【自主解答】原不等式转化为(x-2a)(x+a)<0.对应的一元二次方程的根为x1=2a,x2=-a.(1)当a>0时,x1>x2,不等式的解集为{x|-a<x<2a};(2)当a=0时,原不等式化为x2<0,无解;(3)当a<0时,x1<x2,不等式的解集为{x|2a<x<-a}.综上所述,原不等式的解集为: a >0时,{x |-a <x <2a }; a =0时,x ∈∅; a <0时,{x |2a <x <-a }.解含参数的一元二次不等式的一般步骤注:对参数分类讨论的每一种情况是相互独立的一元二次不等式的解集,不能合并.[再练一题]2.解关于x 的不等式:ax 2-2≥2x -ax (a <0). 【解】 原不等式移项得ax 2+(a -2)x -2≥0, 化简为(x +1)(ax -2)≥0. ∵a <0,∴(x +1)⎝ ⎛⎭⎪⎫x -2a ≤0.当-2<a <0时,2a ≤x ≤-1; 当a =-2时,x =-1; 当a <-2时,-1≤x ≤2a . 综上所述, 当-2<a <0时,解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2a ≤x ≤-1;当a =-2时,解集为{x |x =-1}; 当a <-2时,解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-1≤x ≤2a. [探究共研型]一元二次不等式、二次方程、二次函数的关系探究1 利用函数y =x 2-2x -3的图象说明当y >0、y <0、y =0时x 的取值集合分别是什么?这说明二次函数与二次方程、二次不等式有何关系?【提示】 y =x 2-2x -3的图象如图所示.函数y =x 2-2x -3的值满足y >0时自变量x 组成的集合,亦即二次函数y =x 2-2x -3的图象在x 轴上方时点的横坐标x 的集合{x |x <-1或x >3};同理,满足y <0时x 的取值集合为{x |-1<x <3},满足y =0时x 的取值集合,亦即y =x 2-2x -3图象与x 轴交点横坐标组成的集合{-1,3}.这说明:方程ax 2+bx +c =0(a ≠0)和不等式ax 2+bx +c >0(a >0)或ax 2+bx +c <0(a >0)是函数y =ax 2+bx +c (a ≠0)的一种特殊情况,它们之间是一种包含关系,也就是当y =0时,函数y =ax 2+bx +c (a ≠0)就转化为方程,当y >0或y <0时,就转化为一元二次不等式.探究2 方程x 2-2x -3=0与不等式x 2-2x -3>0的解集分别是什么?观察结果你发现什么问题?这又说明什么?【提示】 方程x 2-2x -3=0的解集为{-1,3}.不等式x 2-2x -3>0的解集为{x |x <-1或x >3},观察发现不等式x 2-2x -3>0解集的端点值恰好是方程x 2-2x -3=0的根.这说明:一元二次不等式ax 2+bx +c >0(a >0)和ax 2+bx +c <0(a >0)的解集分别为{x |x <x 1或x >x 2},{x |x 1<x <x 2}(x 1<x 2),则⎩⎪⎨⎪⎧x 1+x 2=-ba,x 1x 2=ca ,即不等式的解集的端点值是相应方程的根.若不等式ax 2+bx +c ≥0的解集是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-13≤x ≤2,求不等式cx 2+bx +a <0的解集.【精彩点拨】 一元二次不等式解集的两个端点值是一元二次方程的两个根.【自主解答】 法一:由ax 2+bx +c ≥0的解集是⎩⎨⎧ x ⎪⎪⎪⎭⎬⎫-13≤x ≤2,知a <0, 又⎝ ⎛⎭⎪⎫-13×2=c a <0,则c >0.又-13,2为方程ax 2+bx +c =0的两个根, ∴-b a =53, ∴b a =-53. 又c a =-23,∴b =-53a ,c =-23a ,∴不等式变为⎝ ⎛⎭⎪⎫-23a x 2+⎝ ⎛⎭⎪⎫-53a x +a <0,即2ax 2+5ax -3a >0. 又∵a <0,∴2x 2+5x -3<0,所求不等式的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫-3<x <12.法二:由已知得a <0 且⎝ ⎛⎭⎪⎫-13+2=-b a ,⎝ ⎛⎭⎪⎫-13×2=c a ,知c >0, 设方程cx 2+bx +a =0的两根分别为x 1,x 2, 则x 1+x 2=-b c ,x 1·x 2=ac , 其中a c =1⎝ ⎛⎭⎪⎫-13×2,-b c =-bac a =⎝ ⎛⎭⎪⎫-13+2⎝ ⎛⎭⎪⎫-13×2=1⎝ ⎛⎭⎪⎫-13+12,∴x 1=-3,x 2=12.∴不等式cx 2+bx +a <0(c >0)的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫-3<x <12.已知以a ,b ,c 为参数的不等式(如ax 2+bx +c >0)的解集,求解其他不等式的解集时,一般遵循:(1)根据解集来判断二次项系数的符号;(2)根据根与系数的关系把b ,c 用a 表示出来并代入所要解的不等式; (3)约去 a, 将不等式化为具体的一元二次不等式求解. [再练一题]3.已知不等式ax 2+bx +c >0的解集为{x |2<x <3},求不等式cx 2-bx +a >0的解集.【解】 由题意知⎩⎪⎨⎪⎧2+3=-b a ,2×3=ca,a <0,即⎩⎪⎨⎪⎧b =-5a ,c =6a ,a <0,代入不等式cx 2-bx +a >0, 得6ax 2+5ax +a >0(a <0), 即6x 2+5x +1<0, 解得-12<x <-13, 所以所求不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-12<x <-13.1.不等式6x 2+x -2≤0的解集为( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-23≤x ≤12 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≤-23或x ≥12 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≥12 D.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≤-23 【解析】 因为6x 2+x -2≤0⇔(2x -1)·(3x +2)≤0,所以原不等式的解集为11 ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ -23≤x ≤12. 【答案】 A2.设集合S ={x |x >-2},T ={x |x 2+3x -4≤0},则(∁R S )∪T =( )A .(-2,1]B .(-∞,-4]C .(-∞,1]D .[1,+∞)【解析】 T ={x |-4≤x ≤1},根据补集定义,∁R S ={x |x ≤-2},所以(∁R S )∪T ={x |x ≤1},选C.【答案】 C3.二次函数y =x 2-4x +3在y <0时x 的取值范围是________.【解析】 由y <0,得x 2-4x +3<0,∴1<x <3.【答案】 (1,3)4.若不等式ax 2+bx +2>0的解集为{x |-1<x <2},则实数a =________,实数b =________.【解析】 由题意可知-1,2是方程ax 2+bx +2=0的两个根.由根与系数的关系得⎩⎪⎨⎪⎧ -1+2=-b a ,-1×2=2a ,解得a =-1,b =1.【答案】 -1 15.解下列不等式:(1)x (7-x )≥12;(2)x 2>2(x -1).【解】 (1)原不等式可化为x 2-7x +12≤0,因为方程x 2-7x +12=0的两根为x 1=3,x 2=4,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教 • 创设情景——以趣激情 学 过 设问1 收入、单价、数量之间有什么关系? 程 分 设问2 如果按每间客房租金500元出租,收入 为60 000元,未达到要求,所以要提高房租增 析 加收入,如果每间房的租金提高了x个50元,
则客房少租出8x个.那么,一天的客房租金收 入为多少元?
设问3 找出问题中表示不等关系的已知条件 并列出不等式。
云南省财经学校
张 燕
一元二次不等式的图像解法
一、教材分析 二、教学法分析 三、教学过程分析 四、教学计划预评估
教 • 教学内容 材 分 《一元二次不等式与二次函数的关系》选 析
自中等职业教育国家规划教材《数学》第一册
(基础版)(语文出版社) 第2章《不等式》第3 节 《一元二次不等式及其解法》。
教 • 地位和作用 材 地位体现 分 作用体现 析
基础性 工具性
一元二次不等式是一元一次不等式(组) 的延续和深化,是求解分式不等式、含绝对 值不等式、无理不等式的基础;是集合知识 的巩固和运用。它与二次函数、一元二次方 程密切相关,与函数的定义域、值域、三角 函数等内容紧密联系,许多问题的解决都借 助一元二次不等式的解法。
分析:如果按每间客房租金500元出租,收入 为60 000元,未达到要求,所以要提高房租 增加收入
租金提高了 x个50元 一天租金 总收入
每间房的租金 500+50x
租出客房数量 120-8x
(500+50x)(120-8x)
总收入不低于62 400元。
教 • 启发引导——获得新知 学 以前学过一元一次方程、一元一次不等式和 过 一次函数的关系,知道可以利用一次函数的图象 程 求解一元一次不等式.那么,一元二次不等式与 一元二次方程、二次函数有怎样的关系? 分 析
y0
的点.
设问7: 观察图像上纵坐标 y
0 、y 0 、y 0
的那些点所对应的横坐标
x
的取值范围?
• 合作探究——形成结论
教 学 过 程 分 析
例2: 解下列不等式: 2 (1)2 x 2 3x 2 0 ;(2) 3x 6 x 2 ;
2 9 x 6x 1 0 (3)
例1: 已知二次函数 y x 2 x 6 问:
y0 x 取哪些值时, y0 (2)当 x 取哪些值时,
(1)当 (3)当
; ; .
x 取哪些值时,y 0
教 • 启发引导——获得新知 学 设问4: 根据二次函数的图像和性质,你能求出抛 2 过 y x x 6 与 x 轴的交点吗?其交 物线 程 点将 x 轴分成几段? 分 设问5:怎样画这个二次函数的草图? 析 设问6:观察抛物线找出纵坐标 y 0 、 y 0 、
y
(3)观察抛物线找出纵坐标 y 0 ,y 0 , y 0 的点?
y0 y 0 y0
纵坐标 y 0 的点是抛物线 与 x轴的交点;
3
-2
o
x
纵坐标 y 0 的点是抛物线在 x 轴上方的部分; 纵坐标 y 0 的点是抛物线在 轴下方的部分;
x
2 例1:根据二次函数的 y x x 6 图像,看图回答问题:
x
2
3
x
二次函数图象与
x 轴的交点。
例1:根据二次函数的 y x 2 x 6 图像,看图回答问题:
y
(2)其交点将
x 轴分成几段?
2
3
x
——三段, 分别为:x 2,2 x 3, x 3.
例1:根据二次函数的 y x 2 x 6 图像,看图回答问题:
教 • 知识巩固——课堂练习 学 课堂练习:解下列不等式 过 程 (1)( x 2)(x 4) 0 ; (2) x( x 3) 0 分 (3)4 x 2 4 x 1 0 ; (4) x 2 4 0 析
; .
教 • 联系实际——应用数学 学 例3 宾馆有120个高档客房,每天每套租金为500元时,客 房入住率为100%,如果提高租金,预计每提高50元就有8套客 过 房空出来,试问每套客房的租金定在什么范围内能保证宾馆 程 房租总收入不低于62 400元? 分 解:如果按每间客房租金500元出租,收入为60 000元, 析 未达到要求,所以要提高房租增加收入。 设每间房的租金提高了x个50元,即租金为
2
3 x
“三个二次”的关系
(1)一元二次方程的解对应于二次函 数图像与 x 轴的交点。 (2)一元二次不等式的解对应于使二 次函数图像位于 x 轴上方(或下方) 的自变量 x 的范围。
教 • 启发引导——获得新知 学 设问4: 根据二次函数的图像和性质,你能求出抛 2 过 y x x 6 与 x 轴的交点吗?其交 物线 程 点将 x 轴分成几段? 分 设问5:怎样画这个二次函数的草图? 析 设问6:观察抛物线找出纵坐标 y 0 、 y 0 、
(500+50x)元,此时,客房少租出8x个,即租出 客房(120-8x)套.一天的客房租金收入为 (500+50x)(120-8x)元,根据题意,得
(500+50x)(120-8x) ≥62400, 整理,得 x2-5x+6≤0
不等式的解集为 2≤x≤3 相应的租金为 600≤500+50x≤650 所以,当客房的租金在600—500之间,房租 总收入不低于62 400元
y0
的点.
设问7: 观察图像上纵坐标 y
0 、y
的取值范围?
例1:根据二次函数 y x 2 x 6 的图像,看图回答问题:
y
(1)抛物线与 轴有几个交点? 交点坐标是什么?
——两个, 其坐标为: 2,0 , 3,0 。 结论:一元二次方程的解对应于
法,灵活地运用旧知识去探究新问题, 在潜移默化中领会学习方法。
教 创设情景——以趣激情 学 启发引导——获得新知 过 合作探究——形成结论 程 知识巩固——课堂练习 分 析 联系实际——应用数学
感悟收获——小结归纳
巩固深化——布置作业
教 • 创设情景——以趣激情 学 过 程 分 析
二 次 函 数
0
y
y0
x1
0
0
y
y0
0
y
y0
y ax2 bx c 的图像 (a 0)
y0
x2
若a<0呢?
ax bx c 0 的解 ( a 0)
2
x
0
b 2a
x
0
x
一元二次方程
b 2a ( x1 x2 ) x1 , x2
x1 x 2
教 知识目标: 掌握一元二次不等式的图像解法,正确理解 材 一元二次方程、一元二次不等式和二次函数三者的关系。 分 能力目标:培养学生运用数形结合、转化、分类讨论等 析 数学思想方法解决问题的能力,同时提高运算和作图能力。 ﹡ 通过对教学过程中等与不等、特殊与一般、 教 德育目标: 个性与共性等对立统一关系的认识,让学生体会辨证唯 学 物主义思想。 目 标 情感目标:通过一元二次不等式的简单应用,使学生
教 • 感悟收获——小结归纳 学 过 (1)你学会了哪些知识? 程 分 (2)你最深刻的体验是什么? 析
(3)你获得了哪些学习数学的思想和方法?
教 • 巩固深化——布置作业 学 过 (必做题) 程 分 P46:第1题、第2题中(4)、(6)小题。 析
(选做题) 补充:m为何值时,二次方程x²+2(m-1)x+3m²-11=0
有两个不相等的实数根?
教 课堂意外预案 学 计 (1)注意处理易错题型:学生在做课本练习2(1) 划 ( x 2)(x 4) 0 一类的不等式的时候,由于受方程 预 评 ( x 2)(x 4) 0 可转化为 x 2 0或 x 4 0 求解的 x20 估 影响,有可能会出现将不等式转化为不等式组
b 2a
无 实 根
一元二次不等式
ax bx c 0
2
的解集
(a 0)
x x x 或x x
2 1
大于取两边
小于取中间
b x x 2 a
R
ax2 bx c 0 的解集 ( a 0)
一元二次不等式
x x
1
x x2
教 • 学情分析 学 • 教法分析 法 分 (1)教学手段 采用现代多媒体课件教学,形象生动地 析
展示“三个二次”的关系,有利于突出教学 重点、突破难点。
(2)教学方法 引探式教学 讨论式教学
讲议结合教学 变式教学
教 • 学情分析 学 • 教法分析 法 • 学法分析 分 通过观察、探究、类比、归纳等方 析
y
y 0、 (4)观察图象上纵坐标 y 0、 y 0 的那些点所对应的横坐标 的取值 范围?
x
2
3 x
——当 x 2 或 x 3 时, 对应图 像位于 x 轴上,此时 y 0 ; 当 x 2 或 x 3 时, 对应图 像位于 x 轴上方,此时 y 0 ; 当 2 x 3时,对应图像位 于 x 轴下方,此时 y 0 ;
x 4 0 来求解的错误做法,教师要关注学生,及时发现问题并
给予纠正,指出上面的转化不是等价转化。 (2)注意调控教学时间
教 学 • 课堂意外预案 计 • 教学效果预测 划 预 评 估
2 x 2x 3 0 . ;(4)
解一元二次不等式的一般步骤: 求根——画图——找解
(1)把二次项系数化成正数,并解对应二次 方程的根; (2)画出二次函数的简图; (3)根据对应的二次函数的图像以及不等号的 方向,写出不等式的解集.
“三个二次”关系:
