3.1.1 叠加定理
叠加定理及应用

uS +
- R2 R1 + R2
iS
= i1 + i1
i = i1 i
' 1
S =0
=
1 R1 + R2
- R2
uS
+
i = i1 u
" 1
S =0
=
R1 + R2
iS
电压u2的叠加
u2 =
R2 R1 + R2
' 2 " 2
uS +
R1 R2 R1 + R2
iS
= u +u
u = u2 i
' 2
2 u
'
==
3 1+ 1
u
"
==
2 + 0 .5
u S 2 = 0.2u S 2
(1) uS1 = 5V, uS 2 = 10V (2) uS1 = 10V, uS2 = 5V (3) uS1 = 20 cos( t )V, uS 2 = 15 sin( 2 t ) V
求解上式可得到电阻R1的电流i1和电阻R2上电压u2
- R2 1 = + = i1' + i1" i1 uS iS R1 + R2 R1 + R2
其中:
i = i1 i
' 1 " 1
S =0
=
1 R1 + R2 - R2
uS iS
i = i1 u
S =0
=
R1 + R2
电流i1的叠加
i1 =
1 R1 + R2
实验一 叠加定理

实验一叠加定理1.1.1实验目的1.用实验方法验证叠加定理,加深对该定理的理解。
2.加深对电路的电流、电压参考方向的理解。
1.1.2 实验原理叠加定理指出:在有几个独立电源共同作用下的线性电路中,通过每一个元件的电流或其两端的电压,可以看成是由每一个独立电源单独作用时在该元件上所产生的电流或电压的代数和。
在实验中当一个电源单独作用时,其他的电源必须置为零(电压源短路,电流源开路);在求电流或电压的代数和时,当电源单独作用时电流或电压的参考方向与共同作用时的参考方向一致时,符号取正,否则取负。
叠加定理反映了线性电路的叠加性,另外线性电路还具有齐次性,即当激励信号(如电源作用)增加或减小K倍时,电路的响应(即在电路其他各元件上所产生的电流和电压值)也将增加或减小K倍。
叠加性和齐次性都只适用于求解线性电路中的电流、电压。
对于非线性电路,叠加性和齐次性都不适用。
在本实验中,用直流稳压电源来近似模拟电压源,由其产生的误差可忽略不计,这是因为直流稳压电源的等效内阻很小。
1.1.3实验预习要求1.复习教材中叠加定理与计算方法,预习3.1.3中直流电压表、电流表、万用表和稳压电源的主要技术特性并掌握正确的使用方法。
2.按表1.1.1的要求,用支路电流法计算出图1.1.1电路中支路电流和各电阻元件两端的电压,注意参考方向,并把计算结果填入表1.1.1中。
3.利用EDA软件对图1.1.1电路进行仿真分析。
软件详细介绍见教材和附录1。
电流表插座图1.1.1叠加定理的实验电路1.1.4实验设备与器件1.双路可调直流稳压电源2.数字万用表3.电阻器若干4.叠加定理实验电路板1.1.5 实验内容与步骤1.实验电路如图1.1.1所示,按实验电路图连接线路并调节电源参数值。
2.在电路图中接入电压表或电流表,当E1、E2共同作用时测量各支路电流及各电阻元件两端的电压,数据记入表1.1.1中。
3.当E1单独作用时,BC两点不接电源,直接用短路线相连。
电路的叠加定理

电路的叠加定理电路的叠加定理电路的叠加定理是电路分析中最基本的定理之一,它可以简化复杂电路的分析,提高分析效率。
本文将从定义、原理、应用等方面对电路的叠加定理进行全面详细的介绍。
一、定义电路的叠加定理是指在一个线性电路中,若有多个独立源作用于不同支路上,则该电路中任意一个支路上的电压或电流等于各个独立源单独作用于该支路上时所产生的对应值之和。
二、原理1. 叠加原理假设一个线性电路中有n个独立源作用于不同支路上,则该线性电路中任意一个支路上的结果可以表示为:U=U1+U2+...+Un其中,U为该支路上所求结果,Ui为第i个独立源单独作用于该支路时所产生的结果。
2. 可叠加条件要使用叠加定理求解问题,必须满足以下两个条件:(1)各个源之间是相互独立的;(2)被求解量只与某一源有关。
三、应用1. 求解某一支路上的电压或电流使用叠加定理求解某一支路上的电压或电流时,先将其他源全部置零,只保留所要分析的源,计算该支路上的电压或电流,然后再将其他源逐一加入计算,最终得到该支路上的总电压或电流。
2. 求解某一元件上的功率使用叠加定理求解某一元件上的功率时,先将其他源全部置零,只保留所要分析的源,计算该元件上的功率,然后再将其他源逐一加入计算,最终得到该元件上的总功率。
3. 求解等效电路使用叠加定理可以简化复杂电路的分析。
通过逐一考虑各个独立源对被求解量产生的影响,可以得到等效电路。
这样就可以用更简单、更易于分析和设计的等效电路来代替原来较为复杂、难以分析和设计的原始电路。
四、注意事项1. 线性条件叠加定理只适用于线性电路。
如果线性条件不成立,则不能使用叠加定理进行求解。
2. 独立条件在应用叠加定理时必须保证各个独立源之间是相互独立的。
如果两个或多个源之间存在相互作用,则不能使用叠加定理进行求解。
3. 负载条件在应用叠加定理时必须注意负载条件。
如果负载存在,那么在计算各个独立源时,必须考虑负载的影响。
五、总结电路的叠加定理是一种基本的电路分析方法。
叠加定理
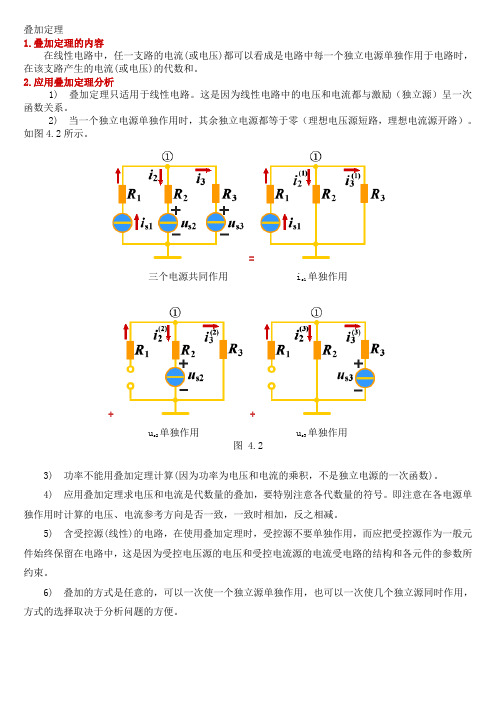
叠加定理1.叠加定理的内容在线性电路中,任一支路的电流(或电压)都可以看成是电路中每一个独立电源单独作用于电路时,在该支路产生的电流(或电压)的代数和。
2.应用叠加定理分析1) 叠加定理只适用于线性电路。
这是因为线性电路中的电压和电流都与激励(独立源)呈一次函数关系。
2) 当一个独立电源单独作用时,其余独立电源都等于零(理想电压源短路,理想电流源开路)。
如图4.2所示。
=三个电源共同作用is1单独作用+ +u s2单独作用us3单独作用图 4.23) 功率不能用叠加定理计算(因为功率为电压和电流的乘积,不是独立电源的一次函数)。
4) 应用叠加定理求电压和电流是代数量的叠加,要特别注意各代数量的符号。
即注意在各电源单独作用时计算的电压、电流参考方向是否一致,一致时相加,反之相减。
5) 含受控源(线性)的电路,在使用叠加定理时,受控源不要单独作用,而应把受控源作为一般元件始终保留在电路中,这是因为受控电压源的电压和受控电流源的电流受电路的结构和各元件的参数所约束。
6) 叠加的方式是任意的,可以一次使一个独立源单独作用,也可以一次使几个独立源同时作用,方式的选择取决于分析问题的方便。
3.叠加定理的应用例4-1 求图示电路的电压U.例4-1图解:应用叠加定理求解。
首先画出分电路图如下图所示当12V电压源作用时,应用分压原理有:当3A电流源作用时,应用分流公式得:则所求电压:例4-2计算图示电路的电压u 。
例4-2图解:应用叠加定理求解。
首先画出分电路图如下图所示当 3A 电流源作用时:其余电源作用时:则所求电压:本例说明:叠加方式是任意的,可以一次一个独立源单独作用,也可以一次几个独立源同时作用,取决于使分析计算简便。
例4-3计算图示电路的电压u 电流i 。
例4-3 图解:应用叠加定理求解。
首先画出分电路图如下图所示当 10V 电源作用时:解得:当5A电源作用时,由左边回路的KVL:解得:所以:注意:受控源始终保留在分电路中。
叠加定理适用范围

叠加定理适用范围一、引言叠加定理(Superposition Theorem)是电路分析中常用的一种方法,通过将电路分解为不同的独立电源进行分析,然后再将结果进行叠加得到最终的解。
这一定理在解决复杂电路问题时具有很大的优势,然而,叠加定理并非适用于所有电路。
本文将探讨叠加定理的适用范围,并提供一些例子来说明其中的限制和局限性。
二、叠加定理的基本原理叠加定理的基本原理可以概括为:在一个线性电路中,如果有多个独立电源作用于电路中,那么最终的电流或电压等可由各个单独电源所产生的效应叠加而成。
如果一个电路中有多个电源,我们可以把每个电源的作用看成是单独进行分析,最后将它们的效应相加得到整个电路的解。
三、叠加定理的适用范围尽管叠加定理对于解决复杂电路问题非常有用,但它并非适用于所有电路。
以下是叠加定理适用范围的一些主要方面:1.仅适用于线性电路:叠加定理只适用于线性电路,即电流与电压之间满足线性关系的电路。
对于非线性电路,叠加定理并不适用,因为非线性元件的电流-电压关系不满足叠加原理。
2.叠加定理不适用于功率和能量:叠加定理可以用于计算电路中特定节点的电压或电流,但它并不能直接计算功率和能量。
功率和能量通常需要通过其他方法进行分析和计算。
3.独立电源:叠加定理只适用于有多个独立电源的电路。
如果电路中的电源相互依赖或由其他因素控制,叠加定理将无法正确应用。
4.线性叠加:叠加定理适用于线性叠加的电路。
线性叠加是指电路响应与输入的线性组合成正比例。
如果电路的响应不满足线性叠加条件,叠加定理将无法得到正确的解。
五、例子和案例分析为了更好地理解叠加定理的适用范围,我们来看几个例子:1.并联电阻:假设有一个由两个电阻 R1 和 R2 并联组成的电路,并且电路中有一个电压源 V。
我们可以使用叠加定理来计算每个电阻上的电流。
关闭电压源 V,只保留 R1,并计算电流 I1。
关闭 R1,只保留 R2,并计算电流 I2。
将这两个电流相加得到总电流 I = I1 + I2。
叠加定理总结

叠加定理总结
叠加定理是电路分析中非常重要的定理之一。
叠加定理表述为:在线性电路中,如果要求某个支路的电流或某个节点的电势,只需要让每个源单独工作,去掉其他源,并把每个影响量的贡献相加在一起即可。
简单来说,叠加定理就是将多个电源按照不同条件分别运行,计算得到的结果再进行叠加,就可以得到最终的结果。
这个定理非常实用,因为在实际电路中,常常存在多个电源互相作用的情况。
总结一下叠加定理的优点:
1. 可以快速地解决复杂电路的问题。
2. 可以在没有手头电路实验条件的情况下进行电路分析。
3. 可以在短时间内得到比较精确的结果,并且可以通过计算来验证分析的正确性。
叠加定理的缺点在于,只适用于线性电路,对于非线性电路则无法使用。
电路叠加定理
电路叠加定理是电路分析中极其重要的一条定理,可以将复杂的电路简化为几个简单电路的叠加,减少计算量,提高了电路分析的效率。
第一段:电路叠加定理的概念
电路叠加定理是指对于线性无源电路,其总电流、总电压、总功率等都可以由各个电源独立作用时的电流、电压、功率之和计算得到。
第二段:电路叠加定理的公式
根据电路叠加定理,可以得到如下公式:对于线性无源电路,其总电流I、总电压U、总功率P均可以表示为各个电源独立作用时的电流、电压、功率之和。
即I=I1+I2+…+In,U=U1+U2+…+Un,
P=P1+P2+…+Pn。
第三段:电路叠加定理的应用
通过电路叠加定理,可以将电路复杂度降低,简化电路分析过程,提高了电路分析的效率。
同时,也可以方便地实现对电路中某一部分进行单独分析。
第四段:电路叠加定理的限制
电路叠加定理只适用于线性无源电路,不能用于非线性电路,也不能用于有源电路。
此外,线性无源电路要满足叠加原因,即各个电源之间不存在相互作用或干扰,此时各个电源之间的作用是线性的。
第五段:电路叠加定理与其它定理的比较
电路叠加定理与其他电路分析定理相比,有其独特的优势。
例如,它比戴维南定理更简单,更能节约时间;比奥姆定律更广义,适用范围更广,具有更大的适应性。
但是,也有其不足,无法用于对有源电路的分析,对于某些特殊情况,其结果也不准确。
总结:电路叠加定理是电路分析中比较重要的一条定理,适用范围广泛,易于实现,但在应用过程中应注意其限制。
叠加定理PPT课件
=
+ Us
+
U
(a )
(b )
(c)
电子发 烧友
' 2 ' 4 ' I ' I1' I 2 (0.9 3) 3.9 A
电子发 烧友
第2章 直流电阻电路的分析计算
THANK
YOU
SUCCESS
2019/5/3
第2章 直流电阻电路的分析计算
THANK
YOU
SUCCESS
2019/5/3
图2.27 例2.12图
第2章 直流电阻电路的分析计算
例 2.12(二)
解 (1) 当电压源单独作用时, 电流源开路, 如图2.27(b)所示, 各支路电流分别为
Us 4.5 I I 0.9 A R1 R3 2 3
' 1 ' 3
Us 4.5 I I 3A R2 R4 1 0.5
例 2.12(三)
电流源支路的端电压U′为
U R I R I (0.5 3 3 0.9) 1.2V
' ' 4 4 ' 3 3
电子发 烧友
第2章 直流电阻电路的分析计算
例 2.12(四)
电子发 烧友
第2章 直流电阻电路的分析计算
教学方法
讲授法
电子发 烧友
第2章 直流电阻电路的分析计算
叠加定理、戴维南定理和诺顿定理
03
诺顿定理
定义与理解
总结词
诺顿定理是电路分析中的一个重要定理,它通过将一个复杂 的线性含源网络等效为一个电流源和电阻的串联组合,简化 了电路的分析和计算。
详细描述
诺顿定理基于电流和电压的基本性质,通过将一个线性含源 网络等效为一个电流源和电阻的串联组合,使得电路的分析 和计算变得更为简单。这个定理在电路分析和设计中具有广 泛的应用。
实例分析
实例1
一个简单的直流电源电路,有两 个电源同时作用于一个电阻上, 通过叠加定理可以计算出电阻上 的电流和电压。
实例2
一个交流电源电路,有三个电源 同时作用于一个电感上,通过叠 加定理可以计算出电感上的电流 和电压。
02
戴维南定理
定义与理解
戴维南定理
任何一个线性有源二端网络,对于外电路而言,都可以用一个等效电源电动势和 内阻串联来表示。
理解
戴维南定理是电路分析中的一个重要定理,它可以将一个复杂的线性有源二端网 络简化为一个等效的电源电动势和内阻串联模型,从而简化电路的分析和计算。
定理的应用
计算等效电源电动势和内阻
01
通过测量网络的开路电压和短路电流,可以计算出等效电源电
动势和内阻。
分析电路性能
02
利用等效电源电动势和内阻,可以分析电路的电压、电流和功
戴维南定理
适用于有源二端网络,将一个有源二端网络等效为一个电压源和 一个电阻的串联。
诺顿定理
适用于有源二端网络,将一个有源二端网络等效为一个电流源和 一个电阻的并联。
定理的互补性及应用场景
叠加定理和戴维南定理、诺顿定理可以相互推导,具有互补性。
在分析和设计线性时不变电路时,可以根据需要选择合适的定理。 如果需要计算电流或电压,可以选择叠加定理;如果需要计算等 效电阻,可以选择戴维南定理或诺顿定理。
叠加定理求电压公式(一)
叠加定理求电压公式(一)叠加定理求电压公式什么是叠加定理?叠加定理是电路分析中常用的一种方法,它可以将复杂的电路分解为简单的部分,通过对每个部分进行独立的分析,最终得到整个电路的电压或电流。
叠加定的思想是将电路中的电源一个个独立地加入,然后求出每个电源作用下的电压,最后将这些电压相加即可得到整个电路的电压。
叠加定理求电压公式叠加定理可以用以下公式来表示:V = V1 + V2 + V3 + … + Vn其中,V表示整个电路的电压,V1、V2、V3等表示每个独立电源作用下的电压。
举例说明假设有一个简单的电路,包含两个电源和两个电阻。
其中电源1为5伏,电源2为3伏,电阻1为20欧姆,电阻2为30欧姆。
我们可以通过叠加定理求出电路中某个节点的电压。
首先,我们将电源1单独加入电路,可以得到电路的电压为5伏。
然后,我们将电源2单独加入电路,得到电路的电压为3伏。
最后,我们将这两个电压相加即可得到整个电路的电压。
所以,根据叠加定理的公式,整个电路的电压为5伏 + 3伏 = 8伏。
通过这个例子,我们可以看到叠加定理的应用是非常方便的,特别是在分析复杂电路时,可以将电路简化为多个简单的部分,然后通过叠加得到整个电路的电压。
总结叠加定理是电路分析中常用的一种方法,可以将复杂的电路分解为简单的部分,然后通过每个部分的电压相加得到整个电路的电压。
在使用叠加定理求电压时,需要注意电压的正负方向问题,以及对于有源元件(如电源)需要根据其正负极性确定电源的电压符号。
通过合理应用叠加定理,可以更好地理解和分析电路的性质和特点。
