测量平差 间接平差典型例题
矿大测量平差模拟试题

二、简述测量观测值中可能存在的偶然误差、系 统误差和粗差的主要特性,并给出针对这些误差 的主要对策。(10分) 三、证明间接平差中,观测值平差值与观测值改 正数不相关 ( Q 0 )。(10分)
ˆ LV
四、若要在两坚强点间布设一条附合水准路线, 已知每公里观测中误差等于 5 . 0 mm ,欲使平差后 线路中点高程中误差不大于 10 . 0 mm ,问该路线 长度最多可达几公里?(10分)
五、有三角网(如图1),其中、B、C为已知点, A、D、E为待定点,观测角(Li=1,2,…,10)。试Байду номын сангаас写条件方程式并对非线性的条件方程进行线性化。 (15分)
图2
《测量平差》作业

《测量平差》作业第1次作业(共2题)(50%)1.测两边及其夹角(3个观测值)刚好可以确定一个三角形的形状和大小。
(表达成诸如:Ω≠∆,如:︒≠++180γβα)(1)如果再观测1个角,会产生什么矛盾? (2)如果再观测2个角,会产生什么矛盾?(3)如果再观测2个角1条边(全部角、全部边均观测),会产生什么矛盾? (50%)2.测两角及其夹边(3个观测值)刚好可以确定一个三角形的形状和大小。
(表达成诸如:Ω≠∆,如:︒≠++180γβα)(1)如果再观测1个角,会产生什么矛盾?(2)如果再观测1个角1条边,会产生什么矛盾?(3)如果再观测1个角2条边(全部角、全部边均观测),会产生什么矛盾?第2次作业(共3题)(20%)1.由已知点A 丈量距离S ,测量坐标方位角α,借于计算P 点的坐标。
观测值及其中误差为: S=127.00m ±0.03m,α=30º00′±2′,设A 点坐标无误差。
求待定点P 的点位中误差。
(40%)2.设有观测值向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⨯32113L L L L ,其协方差阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=212141216LL D 。
求下列函数的方差: (1)321123L L L F -+=。
(2)32212L L L F ++=。
(40%)3.如图所示,令方向观测值i l 的协因数阵为E Q ll =,求角度观测值β的协因数阵ββQ 。
(要点:确定一共有多少个方向观测值并在图中标注;确定一共有多少个水平角并在图中标注)第3次作业(共2题)(10%)1.已知观测值⎥⎦⎤⎢⎣⎡21x x 的协因数阵为:⎥⎦⎤⎢⎣⎡=2112xx Q 。
求向量⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=21211211x x y y Y 的协因数阵YY Q 。
(90%)2.已知观测值⎥⎦⎤⎢⎣⎡=21x x X 的协因数阵为:⎥⎦⎤⎢⎣⎡=1221XX Q 。
测量平差-获奖课件

2 X1
D XX
2 X
2
X1
2 X
n
X1
2 X1X 2
2 X2
2 XnX2
2 X1X n
2 X2Xn
2 Xn
若有X旳t个函数:
z1
Z
t1
z2
KX
K0
zt
k11 k12
K
tn
k21
k22
kt1 kt 2
1n
k2n
ktn
k10
K0
k20
t1 kt0
DZZ
1
xe
(
x)2 2 2
dx
2
数学期望旳传播规律:
常数c旳数学期望为E(c)=c
随机变量X乘以常数c,则有 ECX CEX
随机变量X1, X 2,, X之n 和旳数学期望为
EX1 X2 Xn EX1 EX2 EXn
相互独立旳随机变量 X1, X 2,,X 之n 积旳数学期望为:
二、协因数传播律
Y FX F 0 Z KX K 0
由协方差传播律得:
DYY F DXX F T DZZ K DXX K T DYZ F DXX K T
2 0
DYY
F
2 0
DXX
FT
2 0
DZZ
K
2 0
DXX
KT
2 0
DYZ
F
2 0
DXX
KT
即:
QYY F QXX F T QZZ K QXX K T QYZ F QXX K T
例4:设有函数, Z t ,1
F1
t,n
X
n,1
F1
t,r
测量平差试题

B测量平差基础一、 正误判断(正确“T ”,错误“F ”每题1分,共10 分)。
1.已知两段距离的长度及中误差分别为128.286m ±4.5cm 与218.268m ±4.5cm ,则其真误差与精度均相同( )。
2.如果X 与Y 的协方差0xy σ=,则其不相关( )。
3.水准测量中,按公式i icp s =(i s 为水准路线长)来定权,要求每公里高差精度相同( )。
4.可用误差椭圆来确定待定点与待定点之间的某些精度指标( )。
5.在某一平差问题中,观测数为n ,必要观测数为t ,参数个数u <t 且不独立,则该平差问题可采用附有参数的条件平差的函数模型。
( )。
6.由于同一平差问题采用不同的平差方法得到的结果不同,因此为了得到最佳平差结果,必须谨慎选择平差方法( )。
7.根据公式()222220cos sin 0360E F θσθθθ=+≤≤得到的曲线就是误差椭圆( )。
8.对于特定的平面控制网,如果按间接平差法解算,则误差方程的个数是一定的( )。
9.对于同一个观测值来说,若选定一定权常数0σ,则权愈小,其方差愈小,其精度愈高( )。
10.设观测值向量,1n L 彼此不独立,其权为()1,2,,i P i n = ,12(,,,)n Z f L L L = ,则有22211221111Z n nf f f P L P L P L P ⎛⎫⎛⎫⎛⎫∂∂∂=+++ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ ( )。
二、填空题(每空2分,共24分)。
1、设对某三角网进行同精度观测,得三角形角度闭合差分别为:3秒,-3秒,2秒,4秒,-2秒,-1秒,0秒,-4秒,3秒,-2秒,则测角中误差为 秒。
2、某平差问题函数模型)(I Q =为⎪⎪⎩⎪⎪⎨⎧=-=--=+-+=--0ˆ03060515443121x v v v v v v v v ,则该函数模型为平差方法的模型;=n ,=t ,=r ,=c ,=u 。
测量平差试题一

协因数阵为 QXˆXˆ
0.25 0.15
0.15 0.75
,且单位权方差
ˆ
2 0
3.0cm2
,
(1)计算 P1 点纵、横坐标中误差和点位中误差;
(2)计算 P1 点误差椭圆三要素E、E、 F ; (3)计算 P1 点在方位角为 90 方向上的位差。
(17 分)
一、FFFFT 二、相等 三、aabcd
六. (1)ˆx
3 2
cm,,ˆ y
1.5cm
ˆ p
3cm
(2)E =74. 5或254. 5,E, 1.54cm F 0.79cm
(3)
ˆ
90
1.5cm
9.定权时 0 可任意给定,它仅起比例常数的作用( )。
10.设有两个水平角的测角中误差相等,则角度值大的那个水平角相对精度高( )。
二、 用“相等”或“相同”或“不等”填空(8 分)。
已知两段距离的长度及其中误差为 300.158m±3.5cm; 600.686m±3.5cm。则:
1.这两段距离的中误差(
的测回数 N=( )。
a) 25
b) 20
c) 45
QQYXXX
Q XY QYY
=
0.5 0.25
0.25
0.5
单位权方差 0 2 =±2.0。则 P 点误差椭圆的方位角 T=( )。
a) 90
b) 135
c) 120
4.设 L 的权为 1,则乘积 4L 的权 P=( )。
)。
2.这两段距离的误差的最大限差(
)。
3.它们的精度(
)。
4.它们的相对精度(
)。
三、 选择填空。只选择一个正确答案(25 分)。
误差理论与测量平差基础习题集4
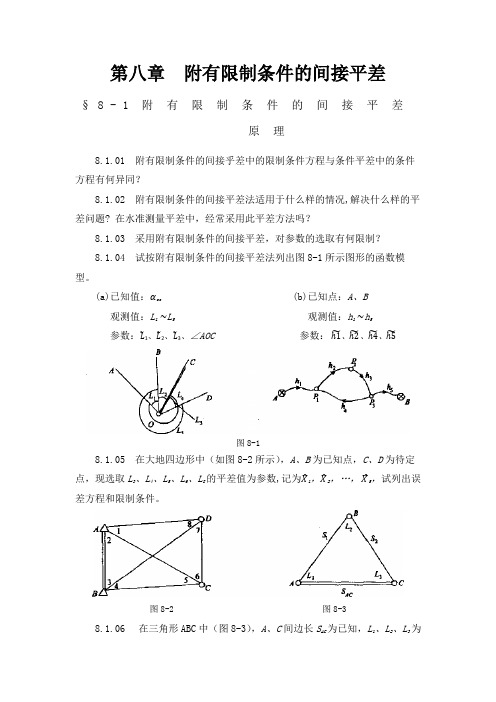
若设参
数
X=[X1X2X3 ]T=[HBh3h4]T,定权时 C=2km。试列出 (1)误差方程式及限制条件; (2)法方程式。 8.1.09 在图 8-6 中,A、B 为已知三角点,C、D 为待定点,观测了 9 个内
角 L1~L9。现选取参数X=[X1X2X3X4X5 ]T =[L1L2L3L4L5 ]T,试列出误差方程 式和限制条件。 8.1.10 在图 8-7 所示的测边网中,A、B 为已知点,1,2 为待定点,观
角度观测精度均为������
= 1″。
������
观测了边长 S1、S2,观测精度均为������ ������
2
= 10mm,
0 ������
������
1
= 148.283m,
= 107.967m。 设 P 点的坐标为未知参数,其近似坐标为������ = 882.270m,
������
0 ������
9.2.04 附有限制条件的条件平差模型在解决实际平差问题中有什么意 义? 9.2.05 某平差问题有 15 个同精度观测值,必要观测数等于 8,现选取 8 个参数,且参数之间有 2 个限制条件。若按附有限制条件的条件平差法进行 平差,应列出多少个条件方程和限制条件方程?由其组成的法方程有几个? 9.2.06 在测站 O 上观测 A、B、C、D 四个方向(如图 9-1 所示) ,得等精 度观测值为: L1=44°03′14.5″, L2=43°14′20.0″, L3=53°33′32.0″, L4=87°17′31.5″,
(a)已知值:矩形的对角边 S 观测值:L1~L4 参数:������1、������2、������3
图 8-4
8.1.08
平差试卷及答案

中南大学考试试卷一-- 学年 学期期末考试试题时间110分钟误差理论与测量平差基础 课程 学时学分 考试形式:卷专业年级: 总分100分,占总评成绩 70 %注:此页不作答题纸,请将答案写在答题纸上一、设有一五边形导线环,等精度观测了各内角,共观测了八组结果,而计算出该导线 环的八组闭合差(即真误差)为-16″、+18″、+22″、-13″、-14″、+16″、 -10″、-12″,试求该导线环之中误差及各角观测中误差。
(本题10分)二、(1)有了误差椭圆为何还要讨论误差曲线?两者有什么关系?(2)已知某平面控制网中有一待定点P ,以其坐标为参数,经间接平差得法方程为:1.2870.4110.53400.411 1.7620.3940x y x y δδδδ++=+-=单位权中误差0ˆ 1.0σ''=,,x y δδ以dm 为单位,试求: 1) 该点误差椭圆参数;2) 该点坐标中误差ˆˆ,x y σσ以及点位中误差ˆp σ; 3) 060ϕ=的位差值。
(本题共20分)三、试证明间接平差中平差值ˆL 与改正数V 的相关性。
(本题10分)四、下图水准网中,P1、P2为待定点,A 、B 、C 、为已知水准点,已测得水准网 中各段高差见下表:且12.000,12.500,14.000A B C H m H m H m ===。
试任选一种平差方法,求:(1)P1、P2点高程平差值;(2)平差后P1、P2点间高差协因数。
(本题共25分)五、下图一平面控制网,试按四种平差方法分别说明: (1)参数的个数?函数模型的个数?(2)函数模型的类型?各种类型的个数?并对不同类型的形式举例说明。
(3)各种平差方法精度评定时有何异同?(本题共25分)六、产生秩亏的原因是什么?水准网、测角网、边角网以及GPS 网的秩亏数各是多少?简述秩亏自由网平差的过程。
(本题10分)试卷一参考答案一、解:导线环中误差为:ˆσ=ˆ43.92σ=;测角中误差为:19.64σ==二、解:由法方程可以得到参数的协因数阵为:1ˆˆ0.83950.19580.19580.6132BBXX Q N --⎛⎫== ⎪-⎝⎭从而得:0.452291()0.95249521()0.5002052ˆ0.97596ˆ0.70725EE XX YY FF XX YY K Q Q Q K Q Q Q K E F σσ===++==+-=====由tan EE XXE XYQ Q Q ϕ-=得: 001500221406E ϕ''=或tan FF XXF XYQ Q Q ϕ-=得:0F 24001ϕ'=或06001'则:ˆ0ˆ0ˆ0ˆ0.91624ˆ0.78307ˆ 1.20518x y p σσσσσσ======将060ϕ=代入 22220(cos sin sin 2)XX yyXY Q Q Q ϕσσϕϕϕ=++中得: 0.71dm ϕσ= 三、证明:基本关系式为:1ˆˆˆT BB L l L x N B Plv Bx l LL V -=+==-=+由协因数传播律得:111ˆˆ11ˆˆ11ˆˆˆˆ1ˆ1111ˆˆˆˆ0T xx BB BB BB T T T xL BB BB Lx vx xx Lx BB BB T T VL xL BBLVT T T T T TVV xx xL Lx BB BB BB BB Q N B PQPBN N Q N B PQ N B Q Q BQ Q BN BN Q BQ Q BNB Q Q Q BQ B BQ Q B Q BN B BN B BN B Q Q BN B------------======-=-==-=-==--+=--+=-所以 ˆ0LV VV LV Q Q Q =+= 即:平差值与各改正数是不相关的。
平差习题2

FILE *fp=fopen(resultfile,"w");
if (fp==NULL)
{
MyBreak("创建结果文件失败!");
return;
}
CLevelingAdjust level;
level.resultfp=fp;
level.Inputdata(datafile);
//粗差探测差算例
void main2()
{
char *datafile ="算例\\粗差探测\\data.txt";
char *resultfile ="算例\\粗差探测\\result.txt";
printf("\n\n粗差探测计算\n");
printf("数据文件:%s\n",datafile);
fclose(fp);
}
void main()
{
printf(" =====第5章水准网平差=====");
printf("\n1.最小二乘平差");
printf("\n2.粗差探测");
printf("\n3.自由网平差");
printf("\n4.拟稳平差");
printf("\n5.闭合差计算\n");
//level.printdata();
level.DataSnooping(0.003);
fprintf(fp,"\n\n在第1、第6号观测值加入模拟粗差之后进行粗差探测:\n");
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6
2
13.000
5
13.005
备 注
教案正文
解:设E、F、G三点高程的最或然值为未知参数 、 、 。因为水准路线长度不同,故为非等精度观测,取权为 ,则得误差方程及相应的权为
设各未知参数的近似值为
m
各改正数以 表示,则将 ( )代入上面的误差方程,取自由项 以mm为单位,可得如下误差方程
观测值及平差值表表(2-5-3)
方向
观测值
角
观测值
V
角度平差值
方向平差值
0°00′00″
30°35′28″
-3"
30°35′25″
0°00′00″
30 35 28
30 35 25
40 05 02
0
40 05 02
70 40 30
70 40 27
58 18 16
-3
58 18 13或然值为未知参数 、 ,并设 , ,观测方向的权阵为单位阵 ,则有
备 注
教案正文
备 注
说明:
检验计算的准确性。
教案正文
角度及方向值的平差值,计算于表(2-5-5)内。
, ,
备 注
点号
已知高程H
(m)
A
35.418
B
45.712
C
25.270
D
24.678
高差观测值及平差值表表(2-5-2)
编号
距离
(km)
高差观测值
(m)
改正数
(mm)
高差平差值
(m)
1
4
8.228
2
8.230
2
4
2.060
4
2.064
3
2
1.515
-1
1.514
4
4
7.477
2
7.479
5
2
12.417
-4
矩阵形式
备 注
教案正文
组成法方程式
法方程式
法方程解算
E、F及G点高程的最或然值
(m)
(m)
(m)
备 注
教案正文
观测高差改正数
高差平差值由 计算,结果列于表(2-5-2)中。
精度估计
计算高差 权倒数的函数式为
(mm)
(mm)
(mm)
(mm)
备 注
教案正文
例2如图(2-5-2),设在测站O独立等精度观测了OA、OB、OC、OD四个水平方向,观测方向值 及 载于表(2-5-3)。又知角AOD的精确值为128°58′40″。试以角度 及 为平差元素,顾及相关性,按参数平差求各角度最或然值,并估计精度。
5参数平差应用举例
例1设有水准网如图(2-5-1)。其中A、B、C、D为已知点,E、F、G为未知点。已知点高程与各点间的观测高差及各水准路线长度如表(2-5-1)及(2-5-2)所示。求各未知点E、F、G高程的最或然值,并解算各点高程的中误差及平差高差 的中误差。(图中箭头指向高端)。
已知高程表表(2-5-1)
