机器人的正运动学
delta型并联机器人运动学正解几何解法

delta型并联机器人运动学正解几何解法
Delta型并联机器人是一种具有优秀运动性能和灵活性的机器人,其运动学正解和逆解是机器人设计中重要的问题。
其中,运动学正解是指已知机器人各个关节的位置和运动学参数,通过正解计算出机器人工具端执行器的位置和姿态。
下面我们介绍一种基于几何解法的Delta型并联机器人运动学正解方法。
首先,我们需要确定Delta型机器人的坐标系。
通常情况下,Delta型机器人的基座为固定坐标系,工具端为可动坐标系。
接着,我们根据机器人的运动学参数和几何关系,计算出机器人的末端执行器位置和姿态。
具体步骤如下:
1. 首先,计算出机器人各个关节的位置和坐标系,并定义各个坐标系之间的变换关系。
2. 根据机器人的末端执行器坐标系,求出工具端姿态矩阵。
其姿态矩阵由工具端坐标系相对于上一级坐标系的旋转矩阵与平移矩阵组成。
3. 根据机器人基座坐标系和关节位置,计算出各个关节相对于机器人基座坐标系的位置,并计算出各个关节的长度。
4. 根据机器人几何结构和运动学参数,求出关节的角度,进而求出工具端末端的位置和姿态。
这种基于几何解法的方法能够较准确地计算出Delta型并联机器人的运动学正解,而且适用于各种复杂的机器人运动学问题。
当然,实际设计中还需根据工程实际情况,综合考虑机器人的性能、精度、可靠性等因素,合理选择机器人的运动学解法,以满足不同的工程需求。
机器人学-第3章_机器人运动学

o
X
由(3-1)式可得运动学约束条件,x&sinq y&cosq 0 平面轮式移动机器人
是所谓的“非完整约束”。物理含义是,机器人不能沿轮轴线方向横移。
设轮距为D,轮半径为r,两轮独立驱动时轮子转速wL,wR 则
v
r 2
wR
wL
,
w
r D
wR
wL
(3-2)
1
v
r 2
wR
wL
,
w
r D
wR
wL
q2 L1
定义参考坐标系{0},它固定在基座上,当第一
个关节变量(q1)为0时坐标系{1}与坐标系{0}重合
,因此建立参考坐标系{0}如图所示,Z0轴与关节1 的轴线重合且垂直于机械臂所在平面。
q1
平面3R机械臂
由于机械臂位于一个平面上,因此所有Z轴相互平
X3
行,且连杆偏距d和连杆转角均为0。该机械臂的DH
动距离分别为lR = rR和lL = rL,
机器人移动距离
l=(lR+lL)/2
方位角变化
q =(lR-lL)/D。
第n步机器人位姿可以按下面公式更新:
qn qn1 q
xn
xn1
l
cos qn1
q
/
2
yn
yn1
l
sin qn1
q
/
2
若已知机器人的初始位姿,根据该递推公式可以确定任意时刻机器
人位姿,比较简单,但因积累误差大,所以长时间不可靠。
相邻连杆间坐标变换公式
建立 {P}、{Q}和{R}3个中间坐标系, 其中{i}和{i-1}是固定在连杆 i 和 i-1 上的固 连坐标系,如图3-13所示。
解释机器人运动学方程的正解和逆解

解释机器人运动学方程的正解和逆解
机器人运动学方程是研究机器人运动规律的一种数学工具。
机器人运动由位置、速度和加速度三部分组成,而机器人运动学方程便是描述这三部分关系的方程。
机器人运动学方程分为正解和逆解。
正解是指根据机器人关节角度、长度等参数,推导出机器人末端执行器的位置、速度和加速度等运动学参数的过程。
在机器人运动学分析中,正解一般使用解析法、几何法和向量法等方法。
通常我们会在正解中借助三角函数和向量函数,对机械臂的运动主体进行数学建模,推导出机器人最终执行器的位置和末端的速度、加速度等参数,完成机器人运动学方程的正解。
而逆解则是指在已知机器人末端执行器的位置、速度和加速度等参数的基础上,求出机器人关节角度,这样机器人才能达到需要执行的动作。
逆解是机器人指令控制中的核心技术之一,一般采用数值计算的方法来求解。
逆解方法有直接法和迭代法两种,直接法一般应用于计算复杂的工业机器人,而迭代法则更适用于机场搬运、医疗康复等关节数较少的应用场景。
机器人运动学方程的正解和逆解都涉及高等数学和工程数学的知识,需要对机器人的运动学规律有一定的理解和掌握。
随着人工智能和机器人技术的不断发展,机器人运动学方程的应用将得到更广泛的推广和应用,成为未来机器人研究和应用的重要工具。
机器人运动学

机器人运动学机器人运动学是研究机器人运动和姿态变化的一门学科。
它通过分析机器人的构造和动力学参数,研究机器人在特定环境下的运动规律和遵循的动力学约束,以实现机器人的准确控制和运动规划。
本文将从机器人运动学的基本概念、运动学模型、运动学正解和逆解等方面进行介绍。
1. 机器人运动学的基本概念机器人运动学是机器人学中的一个重要分支,主要研究机器人在空间中的运动状态、末端执行器的位置和姿态等基本概念。
其中,运动状态包括位置、方向和速度等;末端执行器的位置和姿态是描述机器人末端执行器在空间中的位置和朝向。
通过研究和分析这些基本概念,可以实现对机器人运动的控制和规划。
2. 运动学模型运动学模型是机器人运动学研究的重要工具,通过建立机器人的运动学模型,可以描述机器人在运动过程中的运动状态和姿态变化。
常见的运动学模型包括平面机器人模型、空间机器人模型、连续关节机器人模型等。
每种模型都有其独特的参数和运动学关系,可以根据实际情况选择合适的模型进行分析和研究。
3. 运动学正解运动学正解是指根据机器人的构造和动力学参数,求解机器人末端执行器的位置和姿态。
具体而言,根据机器人的关节角度、关节长度和连杆长度等参数,可以通过连乘法求解机器人末端执行器的位姿。
运动学正解是机器人运动学中的常见问题,解决这个问题可以帮助我们了解机器人在空间中的运动规律和运动范围。
4. 运动学逆解运动学逆解是指根据机器人末端执行器的位置和姿态,求解机器人的关节角度。
反过来,控制机器人的运动状态就需要求解逆运动学问题。
运动学逆解是机器人运动学研究的重要内容之一,它的解决可以帮助我们实现对机器人的准确定位和控制。
总结:机器人运动学是研究机器人运动和姿态变化的学科,通过运动学模型、运动学正解和运动学逆解等方法,可以描述机器人的运动状态、末端执行器的位置和姿态。
深入研究机器人运动学,可以实现对机器人的准确控制和运动规划。
随着机器人技术的不断发展,机器人运动学的研究也得到了越来越广泛的应用和重视。
机器人运动学熊有伦机器人技术基础

s
i 1
dici1
1
3.1.4操作臂运动学方程
T i1 i
{R}
{P}
变换矩阵:i1P i1RT RQT QPT PiT i P
{Q}
化简: 这里:
i 1 P
i1iT i P
T i1 i
i1RT RQT QPT PiT
根据变换 过程:
T i1 i
Rot(
c4c5s6 s4c6
c4 s 5
a3
36T
34T
46T
s5 s6
s4c5c6
c4 s6
s5s6 s4c5s6 c4c6
c5 s4 s5
d4 0
0
0
0 1
c23 s23 0 a2c2
13T
21T
23T
0
s23 0
描述连杆连接的两个参数: 1) link offset 连杆偏距di. 相邻两个连杆之间有一个公
共的关节, 沿着两个相邻连杆公共法线
线的距离可以用一个参数描 述为连杆偏2)距jodini. t angle 关节角θi. 当一i为变移量动. 关节当描时i述为,连两转杆个动偏相关距邻节为连时杆,关绕节公角共为轴一线变旋量转. 的夹角θi.
T i1 i {P}
1.坐标系{i-1}相对于坐标系{i}的变换是由连杆四个参数构成
的函数,其中只有一个变量。
{Q}
2.为求解
T i 1 i
,对每个连杆建立坐标系,分解成4个变换子
问题,每个子变换只包含一个连杆参数。
工业机器人运动系统分析
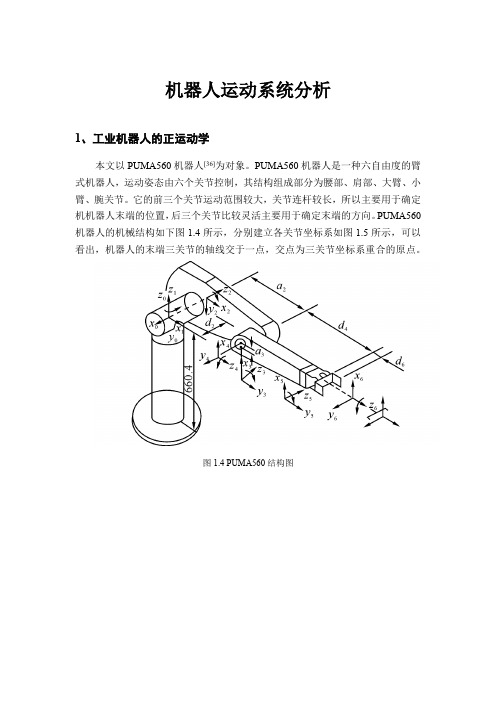
机器人运动系统分析1、工业机器人的正运动学本文以PUMA560机器人[36]为对象。
PUMA560机器人是一种六自由度的臂式机器人,运动姿态由六个关节控制,其结构组成部分为腰部、肩部、大臂、小臂、腕关节。
它的前三个关节运动范围较大,关节连杆较长,所以主要用于确定机机器人末端的位置,后三个关节比较灵活主要用于确定末端的方向。
PUMA560机器人的机械结构如下图1.4所示,分别建立各关节坐标系如图1.5所示,可以看出,机器人的末端三关节的轴线交于一点,交点为三关节坐标系重合的原点。
图1.4 PUMA560结构图图1.5 PUMA560坐标图表1.1为PUMA560机器人的D -H 参数表[37]。
表1.1 PUMA560机器人D -H 参数表表1.1中ιq 列括号里的值为图1.4中机器人关节变量的实际值。
根据齐次坐标变换和表1.1中机器人的参数,得到各连杆的齐次变换矩阵为:112233211233012123224445543445644550000000001000010000010000100010001000001001000000001001;;;;;c s c s c s a s c d s c -s -c c s a c s d -s -c s c ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦T T T T T 66566000010000001c s -s -c -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦T (1.10)其中,ji T 为坐标系{i}相对于坐标系{j}的齐次变换矩阵;sin i i s q =,cos i i c q =。
将以上各齐次变换矩阵依次相乘即可得到机器人末端相对于操作空间的齐次变化矩阵:0123456123456T =T T T T T T(1.11)式(1.11)为关节变量1q ,2q ,……,6q 的函数。
并联机器人正运动学与NURBS轨迹规划

282机械设计与制造Machinery Design&M anufacture第4期2021年4月并联机器人正运动学与NURBS轨迹规划张皓宇\刘晓伟、任川、赵彬w(1.辽宁省气象信息中心,辽宁沈阳110168:2.沈阳新松系统自动化股份有限公司,辽宁沈阳110168;3.东北大学信息科学与工程学院,辽宁沈阳110819)摘要:并联机器人是一种具有高栽荷自重比的封闭式运动结构,针对并联机器人运动控制和N U R B S轨迹问题进行了深入的研究,首先从并联机器人的逆运动学问题进行了解析方法的求解其次,针对正运动学(F KP)在教学上是难以解决问题,提出了一种多层感知器进行反向传播学习的神经网络进行实时求解。
再次,开发了基于N U R B S的通用插补器,它可以处理任何类型的几何图形使得机器人运动轨迹平滑。
最后利用实验验证了运动学和N U R B S曲线求解并联机器人模型的正确性。
该策略在少数迭代和很少执行时间内,位置和方向参数的精度分别接近0.01m m和0.01。
,验证了算法的有效性和正确性。
关键词:并联机器人;N U R B S曲线;运动学;神经网络中图分类号:T H16;TP242.3文献标识码:A文章编号:1001-3997(2021 )04-0282-05Forward Kinematics Control and NURBS Trajectory Planning for Parallel RobotsZHANG Hao-yu1,UU Xiao-wei1,REN Chuan1,ZHAO Bin2.3(1.R e s e a r c h e r L e v e l S e n i o r E n g i n e e r o f M e t e o r o l o g i c a l I n f o r m a t i o n Ce nt er,L i a o n i n g Shenyang110168,China;2.SIASUNRo bot&Aut om at io n Co.,L t d.,L i a o n i n g Shenyang110168,China;3.S c h o o l o f I n f o r m a t i o n S c i e n c e&E n g i n e e r i n g,N o r t h e a s t e r n U n i v e r s i t y,L i a o n i n g Shenyang110819,China)A b s tr a c t:Parallel robot is a closed motion structure with a high load to weight ratio.In this paper^the motion control of parallel robot and NURBS trajectory are studied in depth.Firstly,the inverse kinematics o f parallel robot is solved by analytical method.Secondly,the forward kinematics(FKP)is difficult to solve mathematically9this paper proposes a multilayer perceptron back-propagation learning neural network for real-time solution.Thirdly y a universal interpolator based on NURBS is developedy which can handle any type of geometric shapes to make the robot's trajectory smooth.Finally,the correctness of kinematics and NURBS curves for solving parallel robot model is verified by experiments.The accuracy of position and direction parameters of this strategy is close to O.Q\mm and0.Q\o respectively in few iterations and f ew execution time,which verifies the effectiveness and correctness of the algorithm.Key Words-.Parallel Robot;NURBS Curve;Kinematics;Neural Networkl引言并联机构学理论研究蓬勃发展,并联机器人的运动学理论 也不断得到丰富"-31。
机器人运动控制算法

机器人运动控制算法机器人运动控制是指通过算法和程序对机器人进行控制,使其能够在庞大的自由度空间中完成各种任务。
本文将介绍几种常用的机器人运动控制算法,并探讨其应用和优势。
一、逆运动学算法逆运动学算法是通过已知末端执行器的位置和姿态来计算机器人关节角度的方法。
根据机械结构和运动学原理,可以推导出机器人各个关节的逆运动学方程。
逆运动学算法广泛应用于工业机器人中,能够实现高精度的位置和姿态控制。
其主要优势是计算简单、精确度高,适合用于控制要求较高的场合。
二、正运动学算法正运动学算法是通过已知机器人关节角度来计算末端执行器的位置和姿态的方法。
正运动学算法是逆运动学算法的反向过程,通过关节角度与坐标之间的转换矩阵来实现。
正运动学算法常用于机器人路径规划、碰撞检测和轨迹跟踪等应用。
其主要优势是计算快速、灵活性高,适用于复杂的控制任务。
三、运动规划算法运动规划算法是指根据机器人的初始状态和目标状态,通过路径生成和轨迹规划来实现机器人运动控制的方法。
常用的运动规划算法包括最短路径规划、速度规划和避障规划等。
运动规划算法主要应用于导航系统、物料搬运和自主行驶等场景,能够使机器人安全、高效地完成任务。
四、PID控制算法PID控制算法是一种经典的控制方法,通过不断调整系统的输出来使系统的误差最小化。
PID控制算法根据当前误差、误差变化率和误差累积值来计算控制量,实现对机器人运动的精确控制。
PID控制算法广泛应用于机器人的姿态控制、力控制和位置控制等方面。
其优势是算法简单、稳定性好,适用于各种控制场景。
五、模型预测控制算法模型预测控制算法是一种基于动态模型的先进控制方法,通过对系统未来的状态进行预测来生成最优控制策略。
模型预测控制算法可以考虑系统的约束和目标函数,并进行在线优化,从而实现对机器人运动的预测性和优化性控制。
模型预测控制算法适用于复杂的非线性系统和快速变化的环境,能够实现高度灵活和精准的运动控制。
综上所述,机器人运动控制算法在现代机器人技术中起到了重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机器人的正运动学
机器人正运动学是一种利用对象的运动特性和几何空间的原理来进行模拟的技术,主要是将机器人的空间结构分解,以便使用机械分析法来计算各关节角度,以及末端机器人手臂和机构的位置和姿态。
正运动学技术是机器人运动控制的核心,因此它对机器人在安全和功能上的特性有着重要的影响。
正运动学的起源可以追溯至19世纪末,当时试图描述机器人的基本运动机制。
正运动学首次用于设计机器人在1985年,当时专家利用正运动学计算机模拟机器人自然运动的行为。
随着计算机技术的发展,正运动学变得更加精确和可靠。
正运动学一般涉及一系列矩阵操作,包括齐次变换矩阵,空间重排矩阵,操作矩阵(与物理机器人关节角度相关)以及物理机器人应该跟随的关节角度矩阵等。
正运动学的将各部分分离的特性进行延伸,把连杆系统推广到叫做DH参数的语言中(Denavit-hartenberg),以便描述任意维度的机器人的勾股定理的运动,然后用DH参数可以使用矩阵技术来解决结构化的机器人运动模型。
机器人正运动学已经在机器人技术领域中得到了广泛的应用,其主要使用场景有机器视觉,机器拾取和轨迹控制,几何学规划等。
正运动学正在不断发展,其内置的微调模型也可以更好
地满足复杂任务的要求。
总之,正运动学不仅用于机器人,也广泛应用于模拟和空间运动等领域,可以为机器人技术的进一步发展提供重要的技术支持。
