第2章数据在计算
第2章 数据分析(梅长林)习题题答案
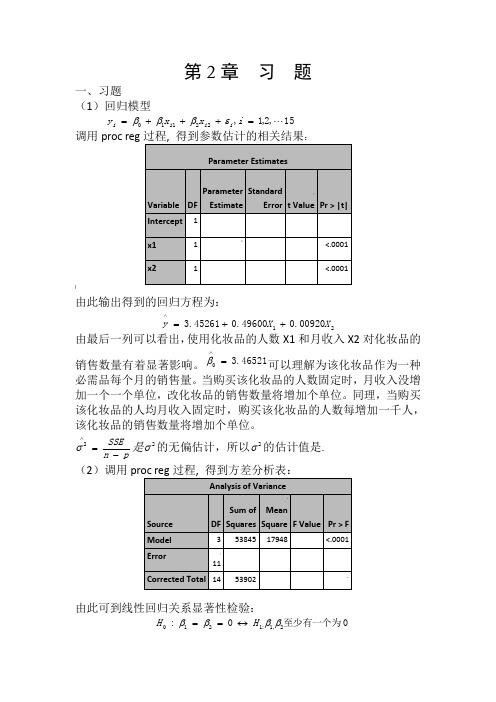
第2章 习 题一、习题(1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用proc reg:]由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是. (2)调用由此可到线性回归关系显著性检验:0至少有一个为0:2,1:1210ββββH H ↔==的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显著。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( )2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显著影响。
数量生态学(第二版)第2章 数据处理

第二章数据的处理数据是数量生态学的基础,我们对数据的类型和特点应该有所了解。
在数量分析之前,根据需要对数据进行一些预处理,也是必要的。
本章将对数据的性质、特点、数据转化和标准化等做简要介绍。
第一节数据的类型根据不同的标准,数据可以分成不同的类型。
下面我们将介绍数据的基本类型,它是从数学的角度,根据数据的性质来划分的;然后叙述生态学数据,它是根据生态意义而定义的,不同的数据含有不同的生态信息。
一、数据的基本类型1、名称属性数据有的属性虽然也可以用数值表示,但是数值只代表属性的不同状态,并不代表其量值,这种数据称为名称属性数据,比如5个土壤类型可以用1、2、3、4、5表示。
这类数据在数量分析中各状态的地位是等同的,而且状态之间没有顺序性,根据状态的数目,名称属性数据可分成两类:二元数据和无序多状态数据。
(1)二元数据:是具有两个状态的名称属性数据。
如植物种在样方中存在与否,雌、雄同株的植物是雌还是雄,植物具刺与否等等,这种数据往往决定于某种性质的有无,因此也叫定性数据(qualitative data)。
对二元数据一般用1和0两个数码表示,1表示某性质的存在,而0表示不存在。
(2)无序多状态数据:是指含有两个以上状态的名称属性数据。
比如4个土壤母质的类型,它可以用数字表示为2、1、4、3,同时这种数据不能反映状态之间在量上的差异,只能表明状态不同,或者说类型不同。
比如不能说1与4之差在量上是1与2之差的3倍,这种数据在数量分析中用得很少,在分析结果表示上有时使用。
2.顺序性数据这类数据也是包含多个状态,不同的是各状态有大小顺序,也就是它一定程度上反映量的大小,比如将植物种覆盖度划为5级,1=0~20%,2=21%~40%,3=41%~60%,4=61%~80%,5=81%~100%。
这里1~5个状态有顺序性,而且表示盖度的大小关系。
比如5级的盖度就是明显大于1级的盖度,但是各级之间的差异又是不等的,比如盖度值分别为80%和81%的两个种,盖度仅差1%,但属于两个等级4和5;而另外两个盖度值分别为41%和60%,相差19%,但属于同一等级。
统计学 第2章 统计数据的收集整理与显示(第二部分)

3.曲线图
当变量数列的组数无限增多时,折线便近似地表现为一条平
滑曲线。
乡 镇 数
12 10 8 15 6 10 4 2 0 700 800 900 5 25
20
频 率 (%)
0 1000 1100 1200 1300 1400 1500 1600 1700
财政收入
11
累计分布(曲线)图
向上累计频数(频率)分布图
直角坐标系下,将各组组距的上限与相应的累 计频数(频率)构成坐标点,依次用折线(光滑曲线) 相连 向下累计频数(频率)分布图 直角坐标系下,将各组组距的下限与相应的累 计频数(频率)构成坐标点,依次用折线(光滑曲线) 相连 以分组变量为横轴,累计频数(频率)为纵轴。 组的次数(频率)越少,曲线越平缓,相反,越陡 峭。
税收按税种分组 工 商 税 税 1999 年总额 8 885.44 562.23 423.50 639.00 172.41 10 682.58 速度(%) 2000 年总额 ( 以 上 年 为 100) 10 366.09 750.48 465.31 827.41 172.22 12 581.51 116.7 纵栏 标题
27
遵循的固定法则。一般而言,数据量大时,分组数 可多些(组距可以小些),数据较少时,分组数应 少些(组距大些)。 经验公式:组数=1+3.3logN 组距=全距/组数
21
注意:所算得的组距可能是一个分数,不方便应用,
此时,须采用它最接近的那个整数。 通常,为了分布列一目了然,人们还要人为的把这 些数字改得更为“整齐”一些。 常见用作组距的形如1,5,10,15,20,25,30等一些“整 5”“整10”的数字。
4
第二章 数据的初步整理

三、数据的统计分类
数据的统计分类是指按照研究对象的本质特征,根据分析研究的目的、任 务,以及统计分析时所用统计方法的可能性,将所获得的数据进行分组归 类。 一)分类时应注意的问题 以研究对象的本质特性为基础 分类标志要包括所有的数据 二)分类标志按形式划分,可分为性质类别和数量类别。 1性质类别——是按事物的不同性质进行分类。如,班级、性别、评定等 级等。 2数量类别——是按数值大小进行分类,并排成顺序。
人 数 初 中 高 中 中 专 大 专 本 科 本 科 以 上
To tal To tal 38 15 6 84 3 41 3 38 1 14 89 14 89
百 分 比
3 10 57 27. 4 2 0. 6 10 0.0
复合表
分组的标志有两个及两个以上的表.如表2.6
地区名 宁波 温州 金华
表2.6 三地区幼儿教师学历 学 历
1
2
3
4
5
6
7
8
9
10
身高 X 135 132 132 129 129 129 127 127 125 120 等级 R 1 2.5 2.5 5 5 5 7.5 7.5 9 10
多余 封口线
多余横线
第二章 数据的初步整理
第二节 统计表
二、统计表的种类
1简单表——只列出观察对象的名称、地点、时序或统计指标 名称的统计表为简单表。 2分组表——只按一个标志分组的统计表为分组表。
3标目——是对统计数据分类的项目。 按其位臵,分横标目和纵标目,可添加总标目。 按其内容,分主语和谓语。主语是对象,在横标目上,谓语 是统计指标,在纵标目上。 设计良好的统计表按“主语——谓语——数字”自左向右的 顺序阅读。
C语言题库(2020版)第2章 数据类型运算符和表达式√

第二章数据类型运算符和表达式一、单项选择1.若有定义语句:int k1=10,k2=20;,执行表达式(k1=k1>k2)&&(k2=k2>k1)后,k1和k2的值分别为( B )2.下面四个选项中,均是不合法的用户标识符的选项是( B )。
3.判断字符型变量c1是否为数字字符的正确表达式为( A )4.在C语言中,要求运算数必须是整型的运算符是( A )5.下面四个选项中,均是合法的用户标识符的选项是(A)。
6.假设所有变量均为整型,则表达式(a=2,b=5,b++,a+b)的值是(B)。
7.若x,i,j和k都是int型变量,则计算表达式x=(i=4,j=16,k=32)后,x的值为(B)。
8.表达式18/4*sqrt(4.0)/8值的数据类型为(B)。
9.若a是数值类型,则逻辑表达式(a==1)||(a!=1)的值是( D )10.判断字符型变量c1是否为小写字母的正确表达式为(B)。
11.在C语言中,char型数据在内存中的存储形式是(C)。
12.以下选项中关于C语言常量的叙述错误的是:( D )13.下面正确的字符常量是(B)14.C语言中的标识符只能由字母、数字和下划线三种字符组成,且第一个字符( D)15.以下选项中,能表示逻辑值"假"的是( B )16.设变量a是整型,f是实型,i是双精度型,则表达式10+'a'+i*f值的数据类型为(C)17.以下选项中非法的字符常量是( B )18.以下关于C语言数据类型使用的叙述中错误的是(B )19.设:int a=1,b=2,c=3,d=4,m=2,n=2;执行(m=a>b) && (n=c>d)后n的值为(C)。
20.若有数学式3aebc,则不正确的C语言表达式是(A)21.下列表达式中,不满足"当x的值为偶数时值为真,为奇数时值为假"的要求的是(C)二、填空1.若s是int型变量,s=6;则表达式s%2+(s+1)%2的值为___1__2.假设所有变量均为整型,则表达式(a=2,b=5,a++,b++,a+b)的值为___9__3.C语言中的标识符只能由三种字符组成,它们是__字母___,_数字____和____下划线_4.若a.b和c均是int型变量,则计算表达式a=(b=4)+(c=2)后,a值为 6,b值为_4,c值为_2_5.在C语言中,不带任何修饰符的浮点常量,是按___double__类型数据存储的。
第2章--试验数据的表图表示

表外附加通常放在表格的下方,主要是一些不便列在表内 的内容,如指标注释、资料来源、不变的试验数据等
注意事项 :
(1) 表格设计应该简明合理、层次清晰,以便于 阅读和使用;
(2) 数据表的表头要列出变量的名称、符号和单 位;
(3) 要注意有效数字位数; (4) 试验数据较大或较小时,要用科学记数法来
2.2 图示法
图表是数字值的可视化表示。用于试验数 据处理的图形种类很多,EXCEL根据图形 的形状可以分为线图、柱形图、条形图、 饼图、环形图、散点图、直方图、面积图、 圆环图、雷达图、气泡图、曲面图等等。 图形的选择取决于试验数据的性质。
图表向导 举例
2.2.1 EXCEL常用图表类型介绍
1.柱形图
公式(函数式):借助于数学方法将实验数据按一 定函数形式整理成方程,即数学模型。
2.1 列表法
将试验数据列成表格,便于随时检查结果是否正 确合理,及时发现问题,利于计算和分析误差, 并在必要时对数据随时查对。通过列表法可有助 于找出有关实验因素之间的规律性,得出定量的 结论或经验公式等。列表法是图示法和公式法的 基础,是工程技术人员经常使用的一种方法。列 表法常分为: ➢ 记录表 ➢ 结果表示表
中反映出关于研究结果的完整概念。 例如:
说明:
三部分组成:表名、表头、数据资料 必要时,在表格的下方加上表外附加
表名应放在表的上方,主要用于说明表的主要内容,为了 引用的方便,还应包含表号
表头通常放在第一行,也可以放在第一列,也可称为行标 题或列标题,它主要是表示所研究问题的类别名称和指标 名称
每个数据标志相关的可能误差量。 所谓趋势线,是用图形的方式显示数据的预测趋
02 第二章 误差与分析数据的处理
1.频数分布
频数是指每组中测量值出现的次数,频数与数据 总数之比为相对频数,即概率密度。
整理上述数据,按组距0.03来分成10组,得频数分布表:
分 组
1.265% 1.295% 1.295% 1.325% 1.325% 1.355% 1.355% 1.385% 1.385% 1.415% 1.415% 1.445% 1.445% 1.475% 1.475% 1.505% 1.505% 1.535% 1.535% 1.565%
因此,应该了解分析过程中误差产生的原因及其出现的 规律,以便采取相应措施,尽可能使误差减小。另一方面 需要对测试数据进行正确的统计处理,以获得最可靠的数 据信息。
2.1 定量分析中的 误差
误差与准确度
准确度(accuracy)是指分析结果(测定平均值)与真值
接近的程度,常用误差大小表示。误差小,准确度高。
两组精密度不同的测量值的正态分布曲线
正态分布规律
(1)x=μ时,y最大。即多数测量值集中在μ附近,或者说
总体平均值是最可信赖值或最佳值。 (2)x=μ时的直线为对称轴。即正负误差出现的概率相等。 (3)x→〒≦时,曲线以x轴为渐近线。即大误差出现的 概率小,出现很大误差的测定值概率趋近零。 (4) ↗, y↘ ,即测量精密度越差,测量值分布越分散, 曲线平坦。
2.正态分布
在分析化学中,测量数据一般符合正态分布规律。正态分 布是德国数学家高斯首先提出的,又称高斯曲线,下图即为正 态分布曲线N(μ,σ2),其数学表达式为
1 y f(x) e 2
(x ) 2 2 2
y表示概率密度;x表示测量值; μ是总体平均值;σ是总体标准偏差 μ决定曲线在x轴的位臵;σ决定 曲线的形状:σ小,数据的精密度好, 曲线瘦高;σ大,数据分散,曲线较扁平。
程序设计基础(人民邮电出版社)答案第2章 数据表示及数据运算
1. 填空题⑴在C语言中,用“\”开头的字符序列称为转义字符。
转义字符“\n”的功能是____换行____;转义字符“\r”的功能是___ 回车_______。
⑵运算符“%”两侧运算对象的数据类型必须都是____整型_______;运算符“++”和“--”运算对象的数据类型必须是______变量______。
⑶表达式8/4*(int)2.5/(int)(1.25*(3.7+2.3))值的数据类型为___整型_________。
⑷表达式(3+10)/2的值为_______6___________。
⑸设x=2.5,a=7,y=4.7,则算术表达式x+a%3*(int)(x+y)%2/4的值是2.5 。
2. 选择题⑴下列4组选项中,均不是C语言关键字的选项是_____A__。
A. define IF typeB. getc char printfC. include case scanfD. while go pow⑵下列4组选项中,均是合法转义字符的选项是___A____。
A. ‘\”’‘\\’‘\n’B. ‘\’‘\017’‘\”’C. ‘\018’‘\f’‘xab’D. ‘\\0’‘\101’‘xlf’⑶已知字母‘b’的ASCII码值为98,如ch为字符型变量,则表达式ch=‘b’+‘5’-‘2’的值为___A____。
A. eB. dC. 102D. 100⑷以下表达式值为3的是____B___。
A. 16-13%10B. 2+3/2C. 14/3-2D. (2+6)/(12-9)⑸以下叙述不正确的是____D___。
A. 在C程序中,逗号运算符的优先级最低B. 在C程序中,MAX和max是两个不同的变量C. 若a和b类型相同,在计算了赋值表达式a=b后,b中的值将放入a中,而b中的值不变D. 当从键盘输入数据时,对于整型变量只能输入整型数值,对于实型变量只能输入实型数值⑹以下非法的赋值语句是 CA. n=(i=2,++i);B. j++; C). ++(i+1); D. x=j>0;⑺以下选项中合法的实型常数是 CA. 5E2.0B. E-3C. .2E0D. 1.3E⑻设a和b均为double型变量,且a=5.5、b=2.5,则表达式(int)a+b/b的值是 DA. 6.500000B. 6C. 5.500000D. 6.000000⑼与数学式子3*x n/(2x-1) 对应的C语言表达式是CA. 3*x^n(2*x-1)B. 3*x**n(2*x-1)C. 3*pow(x,n)*(1/(2*x-1))D. 3*pow(n,x)/(2*x-1)⑽已有定义:int x=3,y=4,z=5;,则表达式!(x+y)+z-1&&y+z/2的值是 DA. 6B. 0C. 2D. 1⑾若有定义:int a=8,b=5,c;,执行语句c=a/b+0.4;后,c的值为 BA. 1.4B. 1C. 2.0D. 2⑿若变量a是int类型,并执行了语句:a='A'+1.6;,则正确的叙述是 DA. a的值是字符CB. a的值是浮点型C. 不允许字符型和浮点型相加D. a的值是字符'A'的ASCII值加上1。
第2章 2误差和分析数据处理
区间内的概率
• 显著性水平():真值落在置信区间 外的概率 =1-P
四、总体均数的区间估计-置信区间
=x u
=x
t(
P、f
)
S x
x t(P、f )
Sx n
• 置信区间分为双侧置信区间和单侧置信区 间。
• 双侧置信区间:指同时存在大于和小于总 体平均值的置信范围,即在一定置信水平 下,μ存在于XL至XU范围内,XL<μ<XU。
0.1000 四位有效数字
pH=3.32 二位有效数字
0.09
二位有效数字
3600
不确定
有效数字 10.05;12.34
;10.20 0.0035020 1.96×10-5 pH=11.20
9.9;8.7
3600;100
位数 4
5 3 2
2或3
不确定
说明
数字中间和未位的“0”为有 效数字,其它数字前面的 “0”只起定位作用,不是 有效数字
• 单侧置信区间:指μ<XU或μ>XL的范围。 • 除了指明求算在一定置信水平时总体平均
值大于或小于某值外,一般都是求算双侧 置信区间。
例题 • 有一组五次测量值的数据如下:
39.10%, 39.12%,39.19%,39.17%, 39.22% 计算置信区间 (置信度为95%)
X=[(39.10+39.12+39.19+39.17+39.22)%]/5
修约
0.0121 1/121= 0.8%
0.0121
25.64 1/2564= 0.04%
25.6
第2章 误差及分析数据统计处理.
Error and Statistical Treatment of Analytical Data
§2.1、定量分析中的误差
§2.2、分析结果的数据处理
§2.3、有效数字及运算规则
2018/10/9
1
本章作业:
P27:思考题:2,5,6 习题:1、2、5(1,2)、6(不求平均值的置信范围) 、10、11(1,4) 有关误差处理方面的参考书: 1、邓勃编,《数理统计方法在化学分析中的应用 》 2、冯师颜,《误差理论与实验数据处理》,科学出版社。 3、陈家鼎,《概率论讲义》,人民教育出版社。 4、姚松年,《信息论在分析化学中的应用》。
2018/10/9
2
§2.1 定量分析中的误差
定量分析的任务是准确测定组分在试样中的含量。但误 差总是存在的,了解分析过程中误差产生的原因及出现的规 律,以便减小误差或正确地处理误差。 定量分析中, 各种原因导致的误差,据其性质,可分为 系统误差或称可测误差 偶然误差或称随机误差
2018/10/9
相对平均偏差 (relative average deviation)
d d r 100% x
(6)
2018/10/9
11
例题1:某测定结果为15.67g, 15.69g 及16.03g, 计算其算术平均偏差及相对
平均偏差。
解:依题意,得: 平均值 :
15.67 15.69 16.03 47.39 x 15.80 3 3
2018/10/9 6
偶然误差的规律性
多次测定的偶然误差遵循正态分布规律。 正态分布曲线的纵坐标代表相对频数,横 坐标代表随机误差的值(x-μ)/σ,这种正 态分布曲线称为标准正态分布曲线。 如图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数 制 间 的 转 换
一. 教学目标
1. 知识技能
(1).了解计算机中数制的表示方法。
(2).掌握十进制、二进制、十六进制数制及相互转换方法。
(3). 掌握十进制、八进制、十六进制数制和二进制的特点
2. 过程方法
(1) 熟悉各种数制的数学表达方式
(2) 掌握二进制的特点
3 情感态度
通过二进制的学习了解二进制优于其它数制,培养学生的逻辑思维能力.
二. 教学重难点
1.重点是二进制数、八进制数、十六进制数的表示方法。
2.难点是二进制数、八进制数、十六进制的相互转换方法。
三. 教学过程
(一.) 数 制
所谓十进制数,是指用 10 个数符即0、1、2、3、4、5、6、7、8、9来表示的数。这种计数的
方法称为十进制计数法。十进制计数法的特点是逢十进一,即数到10时个位回到 0,并向高位进一位,即
表示成“10”,由于这种进位是发生在数到10的时候,故称这种数制为十进制。
在生活中,使用十进制计数法的例子很多,例如人民币,10 分为 1 角,10 角为 1 元;又如10 两
为 1 斤,10 寸为 1 尺等。
其实,人们经常使用的数制也不都为十进制,最典型的例子就是计时制。大家都知道,60 秒为 1 分,
60 分为 1 小时,所以分与小时使用的是六十进制;而 24 个小时为 1 日,所以,日使用的是二十四进制。
还有一个常用的进制就是本节要重点讨论的二进制。因为计算机中所使用的就是二进制。
所谓二进制数(Binary Numbers),仿照本节开头介绍十进制数的说法,是指仅用两个数符即0、1来
表示的数。这种计数的方法称为二进制计数法。二进制计数法的特点就是“逢二进一”,即数到2时个位
回到0,并向高位进一位,即表示成“10”,不过这里的“10”不再读成“十”,而读成“1”“0”。
从 0 开始由小到大地依次写出十个二进制数。
仿照十进制计数法,不难写出:
0 → 1 → 10 → 11 → 100 → 101 → 110 → 111 → 1000 → 1001
如果统一用4位来书写,并将所写的二进制数与十进制数对照起来,可得到一个二进制数与十进制数对照
表,如表 2-1-1 所示。
表 2-1-1 十进制数与二进制数对照表
在计算机中能直接表示和使用的数据,有数值数据和非数值数据两大类。数值数据用于表示数量的
多少,通常都带有表示数值正负的符号位。非数值数据包括英文字母、汉字、数字、运算符号以及其他专
用符号,它们在计算机中也要转换成二进制编码的形式。
所谓数制是指数的制式,是人们利用符号记数的一种科学方法。计算机中常用的数制有十进制、二
进制、八进制和十六进制。
1 十进制数
十进制是一种科学的记数方法,它所能表示的数的范围很大,其特点如下:
(1)它有10个不同的数码(即0~9)。这是构成所有十进制数的基本符号。
(2)它是逢10进位的。十进制数在计数过程中,当它的某位计满10时就要向它邻近的高位进1。
因此,任何一个十进制数不仅和构成它的每个数码本身的值有关,而且还和这些数码在数中的位置有关。
也就是说,任何一个十进制数都可以展开成幂级数形式。
例如:
534.79=5×102 + 3 ×101 + 4× 100 + 7 ×10-1 + 9 ×10-2
一般情况下,对任意一个正的十进制数N,可以表示为:
N=Kn-1(10)n-1+ Kn-2(10)n-2+ … +K0(10)0 + K-1(10)-1 +
K-2(10)-2 + … + K-m(10)-m
式中:Kj可以是0~(P-1)中的任意一个数码;m、n为正整数;P为基数。当P取不同的数值时,N
为不同进制的数。
为了区别不同进制的数,十进制数用后缀D表示,二进制数用后缀B表示,八进制数用后缀Q表示,
十六进制数用后缀H表示。
2 二进制数
二进制数(Binary Number)比十进制数更为简单,它是随着计算机的发展而发展起来的。其主要特
点如下:
(1)它有0和1两个数码,任何一个二进制数都是由这两个数码组成的。
(2)二进制的基数为2。它奉行逢2进1的进位计数原则。
因此,二进制数也可以展开成幂级数的形式。
例如:
1101.11B=1 × 23 + 1 × 22 + 0×21 + 1×20 + 1×2–1 + 1 ×2–2
=8 + 4 + 0 + 1 + 0.5 + 0.25
=13.75D
一般来说,任意一个二进制数N可以表示为:
N=K n–1(2)n–1 + K n–2(2)n–2 + … +K0(2)0 + K–1(2)–1 +
K– 2(2)–2 + … + K –m(2)–m
3 八进制数
八进制数(Octal Number)的主要特点如下:
(1)它有8个不同的数码(即0~7)。任何一个八进制数都是由这8个数码组成的。
(2)八进制的基数为8,它是逢8进1的。
任意一个八进制数N可以表示为:
N=Kn–1(8)n–1 + Kn–2(8)n–2 + „ +K0(8)0 + K–1(8) –1 + K–2(8) –2
+ „ + K –m(8) –m
4 十六进制数
十六进制数(Hexadecimal Number)的主要特点如下:
(1)它有16个不同的数码,即0~9和A~F,任何一个十六进制数都是由这16个数码组成的。
(2)它是逢16进1的。
同样,任意一个十六进制数N可以表示为:
N=Kn–1(16)n–1 + Kn–2(16)n–2 + „ +K0(16)0 + K–1(16) –1 + K–2(16) –2
+ „ + K –m(16) –m
各种数制的对应关系表
(二) 二进制与其他数制的比较
二进制与其他数制相比有以下特点:
1.易于表示
二进制数只有0和1两种状态,这样可以用具有两个稳态的元件来表示,如晶体管导通或截止、脉
冲的有和无、电平的高与低等,都可以用1和0来分别表示。因此,这样的工作状态可靠、抗干扰能力强。
2.运算规则简单
二进制数的运算规则十分简单,可以使计算机中用来实现二进制运算的线路大大简化。
3.节省设备
如果采用十进制表示0~9之间的数,只需要1位,而这1位需要10个设备状态。若采用二进制表
示则需4位,每位只需2个状态,总共8个设备状态。而且这8个设备状态所能表示的数的范围可达
0000~1111,即0~15,这充分说明了二进制的优越性。
4.简化机器结构
用逻辑代数这一数学工具对计算机逻辑线路进行分析和综合,便于简化机器结构 。
(三) 数制间的转换
计算机是采用二进制数操作的,但人们习惯于使用十进制数,这就要求机器能自动对不同数制的数
进行转换。暂不讨论计算机如何进行这种转换的,先来看数学上是如何进行上述3种数制间数的转换的,
如下图所示。
(1) 二进制数与十进制数间的转换
1.二进制数转换为十进制数
将要转换的数按权展开后相加即可。
例2-1:将二进制数10011.01B转换为十进制数。
10011.01B=1 × 24 + 0×23 + 0 ×22 + 1 ×21 + 1× 20 + 0×2-1 + 1 ×2-2
=16+2+1+0.25=19.25D
所以10011.01B=19.25D。
2.十进制数转换为二进制数
要把整数部分和小数部分分别转换,然后再相加即可。
(1)整数转换方法:除2取余法。
注意:第一次得到的余数为二进制数的最低位,最后得到的余数为二进制数的最高位。
例2-2:将十进制数215转换为对应的二进制数。
所以215D=11010111B
(2)小数转换方法:乘2取整法。
注意:最后将每次得到的整数部分(必定是0或1)按先后顺序从左到右排列即得到所对应的二进制小数。
例2-3:将十进制小数0.6879转换为对应的二进制数。
(2) 八进制数和十进制数间的转换
一般来说,任意进制数和十进制数之间的转换原理和方法,同二进制数与十进制数之间的转换相似,区别
在于将基数2换成相应的基数(8或16等)。
1.八进制数转换为十进制数
将八进制数按权展开相加即可。
例2-4:将八进制数42.7Q转换为十进制数。
42.7Q = 4 × 81 + 2×80 + 7 × 8–1
= 32 + 2 + 0.875
= 34.875D
所以42.7Q=34.875D。
2.十进制数转换为八进制数
例2-5:将十进制数91.6875D转换为八进制数。
(3) 十六进制数与十进制数间的转换
1.十六进制数转换为十进制数
将十六进制数按权展开相加即可。
例2-6:将十六进制数B1FH转换为十进制数。
B1FH = 11×162 + 1×161 + 15 × 160
= 2816 + 16 + 15
= 2847
所以B1FH=2847D。
2.十进制数转换为十六进制数
例2-7:将十进制数3901.9032D转换为十六进制数。
(1)整数部分采用除16取余法。
(2)小数部分采用乘16取整法。
教学反思
通过多媒体教学能使直观学习到数制表示形式,各种数制之间直观的演示,使同学更好的掌握各种数制之
间的转换方法,更好的促进了教学效果,达到了预期的教学效果.
公开课教案
课题: 数制间的转换
讲课人: 夏云鹏
