线段和差问题证明
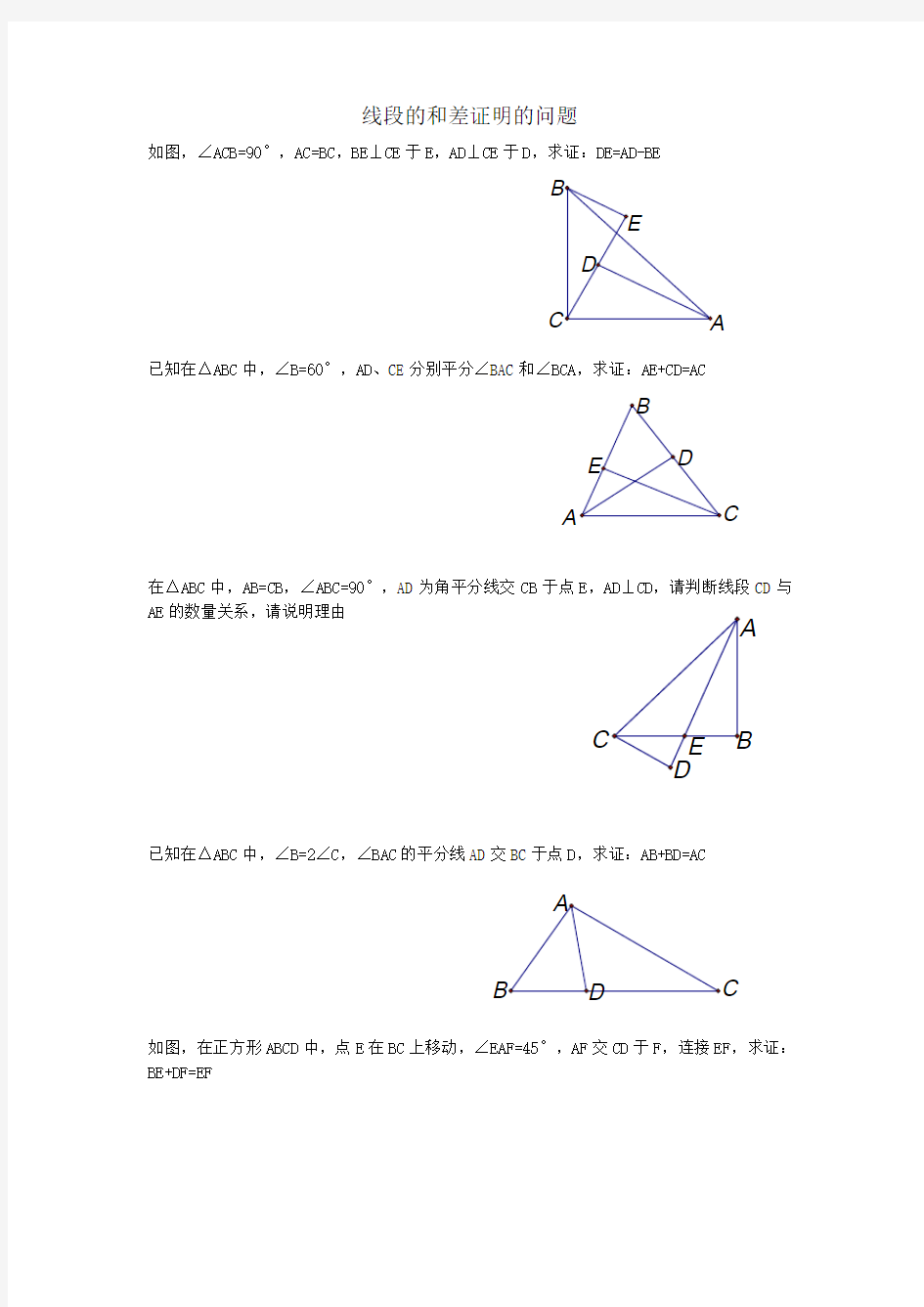

线段的和差证明的问题
如图,∠ACB=90°,AC=BC ,BE ⊥CE 于E ,AD ⊥CE 于D ,求证:DE=AD-BE
已知在△ABC 中,∠B=60°,AD 、CE 分别平分∠BAC 和∠BCA ,求证:AE+CD=AC
在△ABC 中,AB=CB ,∠ABC=90°,AD 为角平分线交CB 于点E ,AD ⊥CD ,请判断线段CD 与AE 的数量关系,请说明理由
已知在△ABC 中,∠B=2∠C ,∠BAC 的平分线AD 交BC 于点D ,求证:AB+BD=AC
如图,在正方形ABCD 中,点E 在BC 上移动,∠EAF=45°,AF 交CD 于F ,连接EF ,求证:BE+DF=EF
A
C
变式:已知AF 平分∠DAE ,求证:AE=BE+DF
变式:已知EF=BE+DF ,求证:∠EAF=45°
如图,点A 、B 、C 、D 顺次在⊙O 上,AB=BD ,BM ⊥AC ,垂足为M ,求证AM=DC+CM
已知在△ABC 的BC 边上取两点D 、F ,使BD=FC ,过D 、F 分别作BA 的平行线,依次交AC 于E 、G ,求证:AB=ED+GF
如图,已知△ABC 和△BED 都是等边三角形,且A 、E 、D 在一条直线上,求证:AB=BD+CD
B
C
如图,在梯形ABCD 中,AD//BC ,∠BAD 和∠ABC 的平分线交于E ,且CD 过点E ,求证:AB=AD+BC
如图,已知在△ABC 中,∠A=108°,AB=AC ,∠B 的平分线交AC 于D ,求证:AC+CD=BC
在四边形ABCD 中,对角线AC 平分∠DAB
1)如图1,当∠DAB=120°时,∠B=∠D=90°时,求证:AB+AD=AC
2)如图2.当∠DAB=120°时,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系?写出你的猜想并证明
3)如图3,当∠DAB=90°时,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系?写出你的猜想并证明
△ABC 为等边三角形,点D 为BC 边上一点,连接AD,以AD 为边作等边△ADE(图1),连接CE,易证:CE+DC=AC.当点D 在BC 延长线(或反向延长线)上时,其他条件不变,如图2、3两种情况下,上述结论是否成立?若成立,给予证明。若不成立,请写出CE 、DC 、AC 之间的关系,并证明
B
证题技巧之三——证明线段或角的和差倍分(推荐文档)
证题技巧之三一一证明线段或角的和差倍分 一、证明线段或角的倍分 1、方法:①长(或大)折半 ②短(或小)加倍 2、判断:两种方法有时对同一个题都能使用,但存在易繁的问 题,因此,究竟是折半还是加倍要以有利于利用已知条件为准。 3、添线:①为折半或加倍而添;②为折半或加倍后创造条件或 利于利用已知条件而添。 4、传递:在加倍或折半后,还不易或不能证明结论,则要找与 被证二量有等量关系的量来传递,或者添加这个量来传递。此时,添 线从两方面考虑:①造等量②为证等量与被证二量相等而添。参考例 4、例 5、例6。 例1 AD 是^ ABC 的中线,ABEF 和ACGH 是分别以AB 和 AC 为边向形外作的正方形。求证:FH=2AD / BAC+ / ACN=180 证明:延长AD 至N 使AD=DN 则ABNC 是平行四边形 CN=AB=FA AC=AH 又/ FAH+ / BAC=180 ???△ FAHY NCA ??? FH=AN 例 2、△ ABC 中,/ B=2 / C , AD 是高,M 是BC 边上的中点。 $ ???
1 求证:DM=2 AB / 2=Z B ???/ 2=2Z 1 ???/ 1 = / DNM 又 AN=DN=ND ? DM=2 A B 1 贝J BFAC ??? BF=AE ???△ AEC 心 BFD ?DF 二CE 二 CD=2CE 作业: 1、在△ABC 中,D 为BC 的中点,E 为AD 的中点,BE 的延长 1 线交AC 于F ,求证:AF=2 FC 2、AB 和AC 分别切? O 于B 和C, BD 是直径。求证/ BAC 二Z CBD 3、圆内接△ ABC 的AB=AC ,过C 作切线交AB 的延长线于D , DE 垂直于AC 的延长线于E 。求证:BD=2CE 例4从平行四边形的钝角顶点 A 向BC 边作垂线,垂足为E , 证明:取AB 的中点N ,连接MN 、DN 贝J MN // AC / 1 = / C ??? DM=DN 例 3 △ ABC 中,AB=AC , E 是 AB 的中点,D 在AB 的延长线上,且 DB=AC 。求证:CD=2CE 证明:过B 作CD 的中线BF V AB=AC , E 是AB 的中点 又 DB=AC
线段和差问题证明
线段的和差证明的问题 已知在△ ABC 中,/ B=60°, AD CE 分别平分/ BAC 和/ BCA 求证:AE+CD=AC 如图,在正方形 ABCD 中,点E 在BC 上移动,/ EAF=45°, AF 交CD 于 F ,连接EF ,求证: BE+DF=EF 在厶ABC 中,AB=CB / ABC=90 , AD 为角平分线交 CB 于点 AE 的数量关系,请说明理由 已知在△ ABC 中,/ B=2/ C,Z BAC 的平分线 AD 交BC 于点D,求证: AB+BD=AC 如图,/ ACB=90 ,
变式:已知 AF 平分/ DAE 求证:AE=BE+DF 变式:已知 EF=BE+DF 求证:/ EAF=45 已知在△ ABC 的BC 边上取两点D F , E 、G,求证: AB=ED+GF 如图,点A B C D 顺次在O O 上 , 如图,已知△ ABC 和△ BED 都是等边三角形,且 A 、E 、D 在一条直线上,求证: AB=BD+CD
如图,在梯形 ABCD 中, AD//BC , / BAD 和/ ABC 的平分线交于 E,且CD 过点E ,求证:AB=AD+BC 在四边形ABCD 中,对角线AC 平分/ DAB 1) 如图 1,当/ DAB=120 时,/ B=Z D=90° 时,求证: AB+AD=AC 2) 如图2.当/ DAB=120时,/ B 与/ D 互补时,线段 AB AD AC 有怎样的数量关系?写 出你的猜想并证明 3) 如图3,当/ DAB=90时,/ B 与/ D 互补时,线段 AB AD AC 有怎样的数量关系?写 △ ABC 为等边三角形,点D 为BC 边上一点,连接AD,以AD 为边作等边△ ADE (图1),连接CE, 易证:CE+DC=AC 当点D 在BC 延长线(或反向延长线)上时,其他条件不变,如图 2、3两 种情况下,上述结论是否成立?若成立,给予证明。若不成立,请写出 CE DC AC 之间的 关系,并证明 如图,已知在厶 ABC 中,/ A=108° 出你的猜想并证明 ,AB=AC
中考几何证明---线段的和差 根号
线段和差根号 1.已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.当三角板绕点C旋转到CD与OA垂直时(如图1),易证:OD+OE=2 OC.当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明. 图1 图2 图3 2.已知等腰△ABC中,AB=AC, ∠ACB=900 ,D为AB的中点,点E为平面内一点,连接DF、BE 。过点D作DE的垂线 交直线BE于点F ,且∠DEF=∠ABC ,连接CF .当点E在△ABC内时,如图1 ,易证:BF=CF+2DF . 当点E在△ABC外时,如图2、3两种情况,线段BF、CF、DF又有怎样的数量关系?请写出你的猜想,并对图3加以证明。 3.在△ABC中,∠ABC=450 , CD⊥AB ,BE⊥AC ,垂足分别为DE ,连接DE . 当点E与点C重合时,此时EC=0 (如图1) ,易证:EB-EC=2DE . 当点E与点C不重合时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,EBECDE又有怎样的数量关系?请写出你的猜想,不需证明。 4.如图,正方形ABCD中,点O是对角线AC的中点,P是直线AC上的一动点,过点P作PF⊥CD ,交直线CD于F . (1)如图1,若点P在线段AO上(不与点A、O重合)时,PE⊥PB ,且PE交CD于点E.求证:DF=EF . (2) 若点P在线段OA上(不与点A、O重合), PE⊥PB ,且PE交直线CD于点E ,求证:PC=PA+2CE . (3) 若点P在直线AC上(不与点A、C重合),PE⊥PB ,且PE交直线CD于点E ,(2)中的结论是否成立?若成立,说明理由。若不成立,请直接写出线段PC、PA、CE间的一个等量关系。 A B C D E F A B C D E F A B C D A B C D E A B C D E
证明线段和差练习题(三角形全等)
证明线段和差练习题 几何中有许多题目要证明一线段等于另两线段的和(或差),解决这类问题常用的方 法大体有五种,即,利用等量线段代换、截短法、接长法、利用面积证明、旋转等五种。下面分别列举几例逐一说明: 一、利用等量线段代换:证一线段等于另两线段的和(或差),只需证这条全线段的两部分,分别等于较短的两条线段,问题就解决了。 例1已知:如图,在△ABC 中,∠B 和∠C 的角平分线BD 、CD 相交于一点D ,过D 点作EF ∥BC 交AB 与点E ,交AC 与点F 。求证:EF=BE+CF 二、截短法或接长法:所谓截短法就是将长线段,截成几条线段,然后分别证明这几条线段等于要证明中的较短的线段,最后代入达到目的。所谓接长法是将较短的两条线段适当的连接起来,然后再证这条线段等于第三条线段,从而达到目的。 例2:如图所示已知 △ABC 中,0 90C ∠=,AC=BC ,AD 是∠BAC 的 角平分线.求证:AB=AC+CD.
三、面积法:利用三角形的面积进行证明。 例3:所示已知△ABC中,AB=AC,P是底边上的任意一点,PE⊥AC, PD⊥AB,BF是腰AC上的高,E、D、F为垂足。 求证:①PE+PD=BF ②当P点在BC的延长线上时,PE、PD、PF之间满足什么关系式? 四、旋转法:通过旋转变换,而得全等三角形是解决正 方形中有关题目类型的一种技巧 例4、如图①,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,则有结论EF=BE+FD成立; (1)如图②,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC、CD上的点,且∠EAF是∠BAD的一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明?若不成立,请说明理由。 (2)若将(1)中的条件改为:在四边形ABCD中,AB=AD,∠B+∠D=180°,延长BC 到点E,延长CD到点F,使得∠EAF仍然是∠BAD的一半,则结论EF=BE+FD是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。 D
怎样证明线段平方的和、差关系
怎样证明线段平方的和、差关系 1.如图所示,在ABC ?中,BC AD ⊥于D ,M 为AD 上任意一点,求证:2 2 2 2 AC AB MC MB -=-. 2.如图所示,已知ABC ?中,?=∠90A ,M 为AC 的中点,BC MD ⊥于D ,求证:2 2 2 CD BD AB -=. 3.已知:如图所示,在ABC ?中,AB=AC ,?=∠90BAC , D 是BC 上一点.求证:2 2 2 2AD CD BD =+. 4.如图所示,已知D 、E 为等腰ABC Rt ?斜边BC 上两点,且?=∠45DAE ,求证:2 22DE BE CD =+. A M B D C A M C D B A D C B A B E D
5.已知:如图所示,在四边形ABCD 中,?=∠+∠90CBA DAB .求证:2 222AB CD BD AC +=+. 6.如图所示,在ABC Rt ?中,?=∠90C ,D 是AB 的中点,E 、F 分别在AC 和BC 上,且DF DE ⊥,求证:222BF AE EF +=. 7.如图所示,在ABC ?中,?=∠90ACB ,D 是AC 上任意一点,连结BD ,求证:2222AC BD AB CD +=+ 8.如图所示,在ABC ?中,AD 是BC 边上的中线,点M 在AB 边上,点N 在AC 边上,且?=∠90MDN .如果2 2 2 2 DN DM CN BM +=+,求证:() 222 4 1 AC AB AD +=. A D B A F E C B C D A A M N C D B
9.已知:如图所示,AD 是ABC ?的中线,AB DE C ⊥?=∠,90于E .求证:2 22AC BE AE =-. 10.已知:如图所示,在ABC ?中,?=∠90C ,D 是AC 的中点.求证:2 2 2 34BC AB BD +=. 11.已知:如图所示,在ABC ?中,AB=AC ,M 是BC 上的点.求证:2 2 AB MC MB MA =?+. 12.已知:如图所示,在P 、Q 分别是ABC Rt ?两直角边AB 、AC 上的点,M 为斜边BC 的中点,且 MQ PM ⊥.求证:2222QM PM QC PB +=+. D E A C A C D B A B C A P Q M B C
线段和差问题证明
线段的和差证明的问题 如图,∠ACB=90°,AC=BC ,BE ⊥CE 于E ,AD ⊥CE 于D ,求证:DE=AD-BE ' 已知在△ABC 中,∠B=60°,AD 、CE 分别平分∠BAC 和∠BCA ,求证:AE+CD=AC 、 在△ABC 中,AB=CB ,∠ABC=90°,AD 为角平分线交CB 于点E ,AD ⊥CD ,请判断线段CD 与AE 的数量关系,请说明理由 ; 已知在△ABC 中,∠B=2∠C ,∠BAC 的平分线AD 交BC 于点D ,求证:AB+BD=AC | 如图,在正方形ABCD 中,点E 在BC 上移动,∠EAF=45°,AF 交CD 于F ,连接EF ,求证: A C
BE+DF=EF — 、 变式:已知AF 平分∠DAE ,求证:AE=BE+DF 变式:已知EF=BE+DF ,求证:∠EAF=45° { 如图,点A 、B 、C 、D 顺次在⊙O 上,AB=BD ,BM ⊥AC ,垂足为M ,求证AM=DC+CM " 已知在△ABC 的BC 边上取两点D 、 F ,使BD=FC ,过D 、F 分别作BA 的平行线,依次交AC 于E 、 G ,求证:AB=ED+GF ~ 如图,已知△ABC 和△BED 都是等边三角形,且A 、E 、D 在一条直线上,求证:AB=BD+CD O B A M D B A G F E D C
\ 如图,在梯形ABCD 中,AD ∠DAB=120°时,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系写出你的猜想并证明 3)如图3,当∠DAB=90°时,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系写出你的猜想并证明 》 △ABC 为等边三角形,点D 为BC 边上一点,连接AD,以AD 为边作等边△ADE(图1),连接CE,易证:CE+DC=AC.当点D 在BC 延长线(或反向延长线)上时,其他条件不变,如图2、3两种情况下,上述结论是否成立若成立,给予证明。若不成立,请写出CE 、DC 、AC 之间的关系,并证明 A D B C E A B C D
几何证明——线段和差模型(中级)
几何证明——线段和差模型(中级) 【知识要点】 在几何证明中,我们经常遇到要求证明两条线段之和等于一条线段(c b a +=),或者两条线段之差等于一条线段(c b a -=)。在处理这类线段和差关系的问题时,我们常用“截长”与“补短”的方法。 截长补短法,是初中数学几何题中一种辅助线的添加方法,也是把几何问题化难为易的一种思想。截长就是在一条线段上截取成两段(一分为二),补短就是在一条边上延长,使其等于一条所求边(合二为一)。 截长法:如果要证明线段等式c b a +=,可以在长的一条线段a 上截取一条线段等于b (或者c ),然后只需证明线段a 上去掉b (或者c )之后剩下的线段等于c (或者b )就行了。 补短法:如果要证明线段等式c b a +=,可以先将短的两条线段b 和c 拼接在一起形成一条长线段d ,然后只需要证明d a =就行了。 截长补短的方法比较灵活,要根据具体的题目条件,作出相应的辅助线。 对于一些经典的截长补短模型,希望同学们能记住并掌握其用法,以便在遇到类似的几何情境时能迅速作出反应。 【经典例题】 例1、(1)正方形ABCD 中,点E 在CD 上,点F 在BC 上,ο 45=∠EAF 。求证:BF DE EF +=。 F (2)正方形ABCD 中,点E 在CD 延长线上,点F 在BC 延长线上,ο 45=∠EAF 。请问现在 BF DE EF 、、又有什么数量关系? E (3)正方形ABCD 中,点E 在DC 延长线上,点F 在CB 延长线上,ο 45=∠EAF 。请问现在 BF DE EF 、、又有什么数量关系? 例2、正三角形ABC 中,E 在AB 上,F 在AC 上ο60=∠EDF 。ο 120=∠=BDC DC DB ,。
线段和差问题证明
线段的和差证明的问题 如图,∠ACB=90°,AC=BC ,BE ⊥CE 于E ,AD ⊥CE 于D ,求证:DE=AD-BE 已知在△ABC 中,∠B=60°,AD 、CE 分别平分∠BAC 和∠BCA ,求证:AE+CD=AC 在△ABC 中,AB=CB ,∠ABC=90°,AD 为角平分线交CB 于点E ,AD ⊥CD ,请判断线段CD 与AE 的数量关系,请说明理由 已知在△ABC 中,∠B=2∠C ,∠BAC 的平分线AD 交BC 于点D ,求证:AB+BD=AC 如图,在正方形ABCD 中,点E 在BC 上移动,∠EAF=45°,AF 交CD 于F ,连接EF ,求证:BE+DF=EF A C
变式:已知AF 平分∠DAE ,求证:AE=BE+DF 变式:已知EF=BE+DF ,求证:∠EAF=45° 如图,点A 、B 、C 、D 顺次在⊙O 上,AB=BD ,BM ⊥AC ,垂足为M ,求证AM=DC+CM 已知在△ABC 的BC 边上取两点D 、F ,使BD=FC ,过D 、F 分别作BA 的平行线,依次交AC 于E 、G ,求证:AB=ED+GF 如图,已知△ABC 和△BED 都是等边三角形,且A 、E 、D 在一条直线上,求证:AB=BD+CD B C
如图,在梯形ABCD 中,AD//BC ,∠BAD 和∠ABC 的平分线交于E ,且CD 过点E ,求证:AB=AD+BC 如图,已知在△ABC 中,∠A=108°,AB=AC ,∠B 的平分线交AC 于D ,求证:AC+CD=BC 在四边形ABCD 中,对角线AC 平分∠DAB 1)如图1,当∠DAB=120°时,∠B=∠D=90°时,求证:AB+AD=AC 2)如图2.当∠DAB=120°时,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系?写出你的猜想并证明 3)如图3,当∠DAB=90°时,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系?写出你的猜想并证明 △ABC 为等边三角形,点D 为BC 边上一点,连接AD,以AD 为边作等边△ADE(图1),连接CE,易证:CE+DC=AC.当点D 在BC 延长线(或反向延长线)上时,其他条件不变,如图2、3两种情况下,上述结论是否成立?若成立,给予证明。若不成立,请写出CE 、DC 、AC 之间的关系,并证明 B
2012中考数学专题复习:证明线段的和差(教案)
专题学习:证明线段的和差 (王成.2012-04-19) 一、中考题回顾: (2011.泸州中考)如图,点P 为等边?ABC 外接圆劣弧BC 上的一点。求证:PA=PB+PC 。 按照这种思路,尝试完成下面这道题。 二、例题分析 例:如图,已知AC ∥BD ,EA 、EB 分别平分∠CAB 和∠DBA ,CD 过点E ,求证:AB=AC+BD 。 评讲:容易得到∠AEB=900 。 法一:在AB 边上取点F ,使AF=AC ,证BF=BD 。→分析:这种方法就是把长线段AB 分割成两段,通过将AC 、BD 转化到AB 上,从而使问题获证。本题是利用什么来转化的?(线段相等)利用什么来证相等的?(三角形全等)在证BED ?≌BEF ?时之所以如此顺利是因为利用好了题目中的哪个条件?(EBF EBD ∠=∠)→可以看作是将ACE ?作了怎样的变换?(关于直线AE 成轴对称) 法二:延长AC 、BE 相交于点D ,证AD=AB 。→分析:这种方法就是把BD 转化到CD ,将两条短线段拼接在一起构成线段AD ,通过证明AD=AB ,从而使问题获证。本题是利用什么来实现转化的?(线段相等)利用什么来证相等的?(三角形全等)在证ABE ?≌ADE ?时之所以如此顺利是因为利用好了哪个条件?(AE 平分CAB ∠)在证BED ?≌DEC ?时之所以如此顺利是因为利用好了哪个条件?(BE DE =)→可以看作是将BED ?作了怎样的变换?(关于点E 成中心对称) 分析:若问题改成“求证:AB —AC=BD ”也可用这样的方法完成。 小结:像这样,证明线段的和或差大都采用转化的方法进行,就是将有关系的线段转化在一条线段上,转化时大都利用相等转化。(板书:证明证明线段的和差的思想:转化。) 证明线段相等时可能用到的定理: ①全等三角形的对应边相等; ②等腰三角形:等角对等边。 ③平行四边形对边相等;
(完整版)证明线段和差练习题(三角形全等)
证明线段和差练习题 一、【方法精讲】常用辅助线添加方法——倍长中线 △ABC 中 方式1: 延长AD 到E , AD 是BC 边中线 使DE=AD , 连接BE 方式2:间接倍长 作CF ⊥AD 于F ,延长MD 到N , 作BE ⊥AD 的延长线于使DN=MD , 连接BE 连接CD 二、利用平行线及等腰三角形性质 例1已知:如图,在△ABC 中,∠B 和∠C 的角平分线BD 、CD 相交于一点D ,过D 点作EF ∥BC 交AB 与点E ,交AC 与点F 。求证:EF=BE+CF 二、截短法或接长法:所谓截短法就是将长线段,等于要证明中的较短的线段,最后代入达到目的。所谓接长法是将较短的两条线段适当的连接起来,然后再证这条线段等于第三条线段,从而达到目的。 例2:如图所示已知 △ABC 中,0 90C ∠=,AC=BC ,AD 是∠BAC 的 角平分线.求证:AB=AC+CD. 三、面积法:利用三角形的面积进行证明。 例3:所示已知 △ABC 中,AB=AC ,P 是底边上的任意一点,PE ⊥AC ,
PD ⊥AB ,BF 是腰AC 上的高,E 、D 、F 为垂足。 求证:①PE+PD=BF ②当P 点在BC 的延长线上时,PE 、PD 、PF 之间满足什么关系式? 例4、如图①,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF=45°,则有结论EF=BE+FD 成立;(1)如图②,在四边形ABCD 中,AB=AD ,∠B=∠D=90°,E 、F 分别是BC 、CD 上的点,且∠EAF 是∠BAD 的一半,那么结论EF=BE+FD 是否仍然成立?若成立,请证明?若不成立,请说明理由。 (2)若将(1)中的条件改为:在四边形ABCD 中,AB=AD ,∠B+∠D=180°,延长BC 到点E ,延长CD 到点F ,使得∠EAF 仍然是∠BAD 的一半,则结论EF=BE+FD 是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。 练习题1. 如图2—1—3所示已知 三角形ABC 中,AD 平分∠BAC ,∠B=2∠C , 求证:AB+BD=AC. 2. 如图2—1—8所示已知△ ABC 中, 090ACB ∠=,AC=BC ,E 是AB 上的一点, BD ⊥CE ,AF ⊥CE ,垂足分别为D 、F ,∠B=2∠C ,求证:DF+AF=CF.
谈线段的和差倍分问题的证明
线段的和差倍分问题的证明 在初中几何中,证明线段的相等关系是一个重要的教学内容,而有关线段的和、差、倍、分问题,则是其中的教学难点。如何搞好线段的和差倍分的教与学?本文通过一些例题,谈谈它的一般证明方法。 一、运用定理法 即直接或间接运用某些涉及线段和差倍分关系的定理或推论进行证明。此类定理和推论有:三角形中位线定理;梯形中位线定理;直角三角形30°的锐角所对的直角边等于斜边的一半;直角三角形斜边上的中线等于斜边的一半。 例1 如图,在△ABC 中,∠B =2∠C ,AD ⊥BC 于D ,M 为BC 中点. 求证:DM = 21AB 分析:如图,因为2 1AB 等于△ABC 的 中位线NM 的长,所以原命题就转化为证明DM =NM 。∵DN 为Rt △ADC 斜边上的中线,∴DN =NC ;∴∠2=∠C ,又∵2∠C =∠B =∠1=∠2+∠3,∴∠2=∠3=∠C ,∴DM =MN ,问题得证。 说明:证明线段的和差倍分问题,大都是采取间接的方法进行,即把线段的和差倍分问题转化为证明两条线段相等的问题。“转化”是证明线段的和差倍分问题的指导思想,它通过对原问题进行变形,促使矛盾的转移,从而达到化未知为已知,化难为易,化繁为简的目的,一般说来,运用定理法证明线段的和差倍分问题,就是根据有关定理将原命题转化后再证明。 二、割补线段法 这是证明线段的和差倍分问题的一种重要方法。即通过“分割”或“添补”的形式,在相关线段或其延长线上构造一线段,使之能够表示几条线段的和差倍
分关系,从而将多线段问题转化为两线段问题。 例2 如图,在△ABC 中,BD =FC ,FG ∥DE ∥BA ,D 、F 在BC 上,E 、G 在AC 上. 求证:FG =AB -DE 分析:本题的关键在于构造一条线段, 使之等于(AB -DE ),如图,在AB 上载取线 段AH =DE ,则AB -DE =BH ,从而把原命题转化 为证明FG =BH 的问题,进而通过证△BHD ≌FGC ,使原命题得证。 例3 如图,P 是正方形ABCD 的边BC 上的任意一点,AQ 平分∠PAD . 求证:AP =BP +DQ . 证明:延长PB 至E ,使BE =DQ , ∵四边形ABCD 是正方形, ∴BA =AD ,∠EBA =∠QDA =90° ∴△ABE ≌△ADQ ,∴∠E =∠4,∠3=∠1, ∵∠1=∠2,∴∠3=∠2,∴∠PAQ =∠BAQ =∠4 ∴∠E =∠PAE ,∴PE =AP ,既BP +BE =AP , ∴BP +DQ =AP 说明:例2通过“分割”的形式构造从两条线段之差,例3通过“添补”的形式构造从两条线段之和,从而将原命题转化为两条线段的问题,值得注意的是:在运用“割补法”证明线段的和差倍分关系时,是运用“添补”的形式构造线段的“和”或“倍”,还是运用“分割”的形式构造线段的“差”或“几分之几”,这不能取决于原命题的和差倍分形式。因为“和”与“差”,“倍”与“分”是可以互相转化的。因此,我们在选择割补的形式时要结合图形和题目的已知条件,即所割补的线段不是“孤立”的,而应能够与原来的图形产生联系。 从以上三个例题可知,在证明线段的和差倍分关系时,往往通过添辅助线,
线段和差问题
5月13日周二数学作业----题型训练 班级学号姓名得分 (离中考还有39天5月13日—6月20日,上课不认真听,作业会费双倍功夫的今天探究线段的和与差的最值问题(作图和论证部分) 1、PA+PB最大最小问题 (1)点A、B落在直线的同侧(P是直线上动点) ①AB∥m 此时,PA+PB最大值不存在; 最小值如图所示的点P即为所求(自己作图)(要求有尺规痕迹)(其实就是 将军饮马)。 ②AB与直线m不平行 此时,PA+PB最大值; 最小值如图所示的点P即为所求(自己作图)(要求有尺规痕迹)(其实就是 将军饮马)。 (2)点A、B落在直线的异侧 此时,PA+PB最大值; 最小值如图所示的点P即为所求(自己作图)(其实就是两点之间线段最短) 本小题(2)的拓展:①如右图,河流的宽度为d,河流的两岸有 A、B两点,求作桥梁PQ(PQ⊥m1),使得从点A到点B 经过桥梁PQ过程中,路程最短(把最短路线画成实线,其余画成虚线) 并利用右下图证明你的结论
②如右图,直线m同侧有两定点A、B,在直线m上求作一条线段PQ(长 度为d),使得AP+PQ+QB最短(在右下图上作图),并证明你的结论 2、∣PA-PB∣最大最小问题 (1)点A、B落在直线的同侧(P是直线上动点) ①AB与直线m不平行 此时,∣PA-PB∣最大值如右下的左图所示的点P即为所求(自己作图),并证明你的结论;最小值如右下的右图所示的点P即为所求(自己作图)(留下尺规痕迹,不证明) ②AB∥m 此时,∣PA-PB∣最大值不存在;∣PA-PB∣最小值如图所示的点P即为所求(要求有尺规 痕迹) 注意:如右图,∣PA-PB∣最小值不存在,因为AB与直线m垂直,AB的垂直平分线与, 产生不了交点P (2)点A、B落在直线的异侧 此时,∣PA-PB∣最大值是如下左图所示的点P即为所求(自己作图);最小值是如下右图所示的点P即为所求(自己作图) 注意:如右图,有无数个点P使得∣PA-PB∣最,因为AB的垂直平分线正好 是m,m上的任何一个点P,PA-PB总是0
线段差的最大值与线段和的最小值问题
线段差的最大值与线段和的最小值问题 有关线段差的最大值与线段和的最小值问题的主要应用原理是:1、两点这间线段最短。2、三角形的任意两边之和大于第三边(找和的最小值)。3、三角形的任意两边之差小于第三边(找差的最大值)。 作图找点的关键:充分利用轴对称,找出对称点,然后,使三点在一条直线上。即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。证明此类问题,可任意另找一点,利用以上原理来证明。 一两条线段差的最大值: (1)两点同侧:如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。 作法:连结AB并延长AB交直线L于点P。点P即为所求。︱PA-PB︱=AB 证明:在直线L上任意取一点P。,连结PA、PB,︱PA-PB︱<AB (2两点异侧:如图,如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。作法:1、作B关于直线L的对称点B。 B 2、连结AB并延长AB交直线L于点P。点P即为所求。︱PA-PB︱=AB 证明:在直线L上任意取一点P。,连结PA、PB、PB。︱PA-PB︱=︱PA-PB︱<AB
(三角形任意两边之差小于第三边) 二、两条线段和的最小值问题: (1))两点同侧:如图,点P在直线L上运动,画出一点P使PA+PB取最小值。 (三角形的任意两边之和大于第三边(找和的最小值),PA+PB=AB (2)两点异侧:如图,点P在直线L上运动,画出一点P使PA+PB取最小值。 (两点之间线段最短) 三、中考考点: 08年林金钟老师的最后一题:如图,在矩形ABCO中,B(3,2),E(3,1),F(1,2)在X轴与Y轴上是否分别存在点M、N,使得四边形EFNM的周长最小若存在,请求出周长的最小值,若不存在,请说明理由。 提示:EF长不变。即求FN+NM+MF的最小值。利用E关于X轴的对称点E,F的对称点F,把这三条线段搬到同一条直线上。
证明线段之间关系的技巧
证明线段之间数量关系的技巧 证明两线段相等 ★1.两全等三角形中对应边相等。 ★2.同一三角形中等角对等边。 3.等腰三角形三线合一。 ★4.直角三角形中斜边上的中点到三个顶点距离相等。 6.中垂线上任意一点到线段两端距离相等。 7.角平分线上任一点到角的两边距离相等。 8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。 ★9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。 证明线段的和差倍分 1.作两条线段的和,证明与第三条线段相等。 2.在第三条线段上截取一段等于第一条线段,证明余下部分等于第二条线段。 3.延长短线段为其二倍,再证明它与较长的线段相等。 4.取长线段的中点,再证其一半等于短线段。 5.利用一些定理(三角形的中位线、含30度的直角三角形、直角三角形斜边上的中线、三角形的重心、相似三角形的性质等)。 2.*证明线段不等 1.同一三角形中,大角对大边。 2.垂线段最短。 3.三角形两边之和大于第三边,两边之差小于第三边。 4.同圆或等圆中,弧大弦大,弦心距小。 5.在两个三角形中有两边分别相等而夹角不等,则夹角大的第三边大。
证明两条线段(直线)之间位置关系的技巧 证明两条直线互相垂直 ★1.等腰三角形的顶角平分线或底边的中线垂直于底边。 2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。 3.在一个三角形中,若有两个角互余,则第三个角是直角。 4.邻补角的平分线互相垂直。 5.一条直线垂直于平行线中的一条,则必垂直于另一条。 6.两条直线相交成直角则两直线垂直。 7.利用到一线段两端的距离相等的点在线段的垂直平分线上。 ★8.利用勾股定理的逆定理。 9.利用菱形的对角线互相垂直。 ★10.在圆中平分弦(或弧)的直径垂直于弦。 ★11.利用半圆上的圆周角是直角。 证明两直线平行 1.垂直于同一直线的各直线平行。 2.同位角相等,内错角相等或同旁内角互补的两直线平行。 3.平行四边形的对边平行。 ★4.三角形的中位线平行于第三边。 ★5.梯形的中位线平行于两底。 6.平行于同一直线的两直线平行。 ★7.一条直线截三角形的两边(或延长线)所得的线段对应成比例,则这条直线平行于第三边。
线段的和差倍分问题的证明2017
线段的和差倍分问题的证明 一、运用定理法 即直接或间接运用某些涉及线段和差倍分关系的定理或推论进行证明。此类定理和推论有:三角形中位线定理;梯形中位线定理;直角三角形30°的锐角所对的直角边等于斜边的一半;直角三角形斜边上的中线等于斜边的一半。 例1 如图,在△ABC 中,∠B =2∠C ,AD ⊥BC 于D ,M 为BC 中点. 求证:DM = 2 1AB 对应练习 1、已知:如图所示,点D 、E 分别是等边ABC ?的边AC 、BC 上的点,AD=CE ,BD 、AE 交于点P ,AE BQ ⊥于Q .求证:PB PQ 2 1 = . 2、如图所示,在ABC ?中,AB=AC ,?=∠90BAC ,BE 平分ABC ∠,交AC 于D ,BE CE ⊥于E 点,求证:BD CE 2 1 =. 3、如图所示,在ABC ?中,BC AB 2 1 =,D 是BC 的中点,M 是BD 的中点.求证:AC=2AM . 4、已知:如图所示,D 是ABC ?的边BC 上一点,且CD=AB ,BAD BDA ∠=∠,AE 是ABD ?的中线.求证:AC=2AE . Q A D P C B E M A D B C A B E D A
5、已知:如图所示,锐角ABC ?中,C B ∠=∠2,BE 是角平分线,BE AD ⊥,垂足是D .求证:AC=2BD . 二、割补线段法 这是证明线段的和差倍分问题的一种重要方法。即通过“分割”或“添补”的形式,在相关线段或其延长线上构造一线段,使之能够表示几条线段的和差倍分关系,从而将多线段问题转化为两线段问题。在证明线段的和差倍分关系时,往往通过添辅助线,构造出能表示线段的和差倍分关系的线段,促使问题的转化。但在添加辅助线之前一定要结合题意和图形深入分析,想一想,图形中是否已经存在能表示有关线段和差倍分关系的线段,否则乱添加辅助线只能把图形复杂化,使思路步人歧途。下面请看一个例子。 例2、P 是正方形ABCD 的边BC 上的任意一点,AQ 平分∠PAD . 求证:AP =BP +DQ . 例3、 如图,△ABC 中,∠BAC =90°,AE 是经过点A 的一条直线,交BC 于F ,且B 、C 在AE 在的异侧,BD ⊥AE 于D ,求证:DB =DE +CE 。 对应练习 1、如图所示,已知ABC ?中,?=∠60A ,BD 、CE 分别平分ABC ∠和ACB ∠,BD 、CE 交于点O .求证:BE+CD=BC . A D E B C A O E B C D
“截长补短法”证明线段的和差问题
“截长补短法”证明线段的和差问题典例分析 河大附中 桑静华 线段的和差问题常常借助于全等三角形的对应边相等,将不在一条直线的两条(或几条)线段转化到同一直线上.实际上是通过翻折构造全等三角形,目的是为了转移的边、角和已知条件中的边、角有机的结合在一起.在无法进行直接证明的情形下,利用“截长补短”作辅助线的方法常可使思路豁然开朗,问题迎刃而解。 例1、如图,已知AC ∥BD 、EA 、EB 分别 平分∠CAB 和∠DBA ,CD 过点E , 则AB 与AC+BD?相等吗?请说明理由. 分析:证明一条线段等于另两条线段之和(差)常见的方法是: (1)在长线段上截取一条线段等于短线段,再证明余下的线段等于另一条短 线段,这种方法叫“截长法” (2)在其中一条短线段的延长线上截取另一条短线段,再证明它们与长线段相等,这种方法叫“补短法”. 34 D C A B 6 5(1) F E 1 2 34 D C A 6 5 (2) E F 12 证法一:如图(1)在AB 上截取AF=AC ,连结EF . 在△ACE 和△AFE 中 D C A B E
12AC AF AE AE =?? ∠=∠??=? ∴△ACE ≌△AFE (SAS ) ∵ ,∴ ,又 ,∴∠6=∠D 在△EFB 和△BDE 中 634D BE BE ∠=∠?? ∠=∠??=? ∴△EFB ≌△EDB (AAS ) ∴FB=DB ∴AC+BD=AF+FB=AB 证法二:如图(2),延长BE ,与AC 的延长线相交于点F ∵ ∴4∠=∠F ,又∵43∠=∠ ∴∠F=∠3 在△AEF 和△AEB 中 312F AE AE ∠=∠?? ∠=∠??=? ∴△AEF ≌△AEB (AAS ), ∴AB=AF ,BE=FE 在△BED 和△FEC 中 564BE FE F ∠=∠?? =??∠=∠? ∴△BED ≌△FEC (ASA ) ∴BD=FC, ∴AB=AF=AC+CF=AC+BD . 例2、如图,在△ABC 中,∠B =2∠C , ∠BAC 的平分线交BC 于D ,求证:AB +BD =AC . 分析1: 因为∠B =2∠C ,所以AC >AB , 可以在AC 上取一点E ,使得AB =AE , 构造△ABD ≌△AED ,把AB 边转移到AE 上, BD 转移到DE 上,要证AB +BD =AC . 即可转化为证AE +BD =AE +EC , 即证明BD =EC . A B C D
谈线段的和差倍分问题
谈线段的和差倍分问题的证明 东方市四更中学董崇雄 在初中几何中,证明线段的相等关系是一个重要的教学内容,而有关线段的和、差、倍、分问题,则是其中的教学难点。如何搞好线段的和差倍分的教与学?本文通过一些例题,谈谈它的一般证明方法。 一、运用定理法 即直接或间接运用某些涉及线段和差倍分关系的定理或推论进行证明。此类定理和推论有:三角形中位线定理;梯形中位线定理;直角三角形30°的锐角所对的直角边等于斜边的一半;直角三角形斜边上的中线等于斜边的一半。 于D,M为BC中点. 1AB 求证:DM = 2 1AB等于△ABC的 分析:如图,因为 2 中位线NM的长,所以原命题就转化为证明DM=NM。∵DN为Rt△ADC斜边上的中线,∴DN=NC;∴∠2=∠C,又∵2∠C=∠B=∠1=∠2+∠3,∴∠2=∠3=∠C ,∴DM=MN,问题得证。 说明:证明线段的和差倍分问题,大都是采取间接的方法进行,即把线段的和差倍分问题转化为证明两条线段相等的问题。“转化”是证明线段的和差倍分问题的指导思想,它通过对原问题进行变形,促使矛盾的转移,从而达到化未知为已知,化难为易,化繁为简的目的,一般说来,运用定理法证明线段的和差倍分问题,就是根据有关定理将原命题转化后再证明。 二、割补线段法 这是证明线段的和差倍分问题的一种重要方法。即通过“分割”或“添补” 的形式,在相关线段或其延长线上构造一线段,使之能够表示几条线段的和差倍
分关系,从而将多线段问题转化为两线段问题。 例2 如图,在△ABC 中,BD =FC ,FG ∥DE ∥BA ,D 、F 在BC 上,E 、G 在AC 上. 求证:FG =AB -DE 分析:本题的关键在于构造一条线段, 使之等于(AB -DE ),如图,在AB 上载取线 段AH =DE ,则AB -DE =BH ,从而把原命题转化 为证明FG =BH 的问题,进而通过证△BHD ≌FGC ,使原命题得证。 例3 如图,P 是正方形ABCD 的边BC 上的任意一点,AQ 平分∠PAD . 求证:AP =BP +DQ . 证明:延长PB 至E ,使BE =DQ , ∵四边形ABCD 是正方形, ∴BA =AD ,∠EBA =∠QDA =90° ∴△ABE ≌△ADQ ,∴∠E =∠4,∠3=∠1, ∵∠1=∠2,∴∠3=∠2,∴∠PAQ =∠BAQ =∠4 ∴∠E =∠PAE ,∴PE =AP ,既BP +BE =AP , ∴BP +DQ =AP 说明:例2通过“分割”的形式构造从两条线段之差,例3通过“添补”的形式构造从两条线段之和,从而将原命题转化为两条线段的问题,值得注意的是:在运用“割补法”证明线段的和差倍分关系时,是运用“添补”的形式构造线段的“和”或“倍”,还是运用“分割”的形式构造线段的“差”或“几分之几”,这不能取决于原命题的和差倍分形式。因为“和”与“差”,“倍”与“分”是可以互相转化的。因此,我们在选择割补的形式时要结合图形和题目的已知条件,即所割补的线段不是“孤立”的,而应能够与原来的图形产生联系。 从以上三个例题可知,在证明线段的和差倍分关系时,往往通过添辅助线,
(完整版)证明线段和差练习题(三角形全等)
证明线段和差练习题、【方法精讲】常用辅助线添加方法一一倍长中线 、利用平行线及等腰三角形性质 例1已知:如图,在△ ABC中,/ B和 / C的角平分线 EF// BC交AB与点E,交AC与点F。求证:EF=BE+CF 二、截短法或接长法:所谓截短法就是将长线段,截成几条线 段,A 等于要证明中的较短的线段,最后代入达到目的。所谓接长法是将较短的两条线段适当的 连接起来,然后再证这条线段等于第三条线段,从而达到目的。 900, AC=BC , AD 是/ BAC的 角平分线.求证:AB=AC+CD. 三、面积法:利用三角形的面积进行证明。 例2:如图所示已知△ ABC中,C 例3:所示已知△ ABC中, A B=AC , P是底边上的任意一点, PE丄AC , A D 方式1:延长AD到E, 使DE=AD,连 接BE 方式2:间接倍长 作CF丄AD于F, 作BE丄AD的延长线于E 连接BE 延长MD到N, 使DN=MD 连 接CD 然后分别证明这几条线段
PDL AB, BF是腰AC上的高,E、D F为垂足。 求证:①PE+PD=BF ②当P点在BC的延长线上时,PE、PD PF之间满足什么关系式? 例4、如图①,在正方形ABCD中,E、F分别是BC、CD上的点,且/ EAF=45 ° , 则有结论EF=BE+FD成立;(1)如图②,在四边形ABCD中,AB=AD,/ B= / D=90 ° , E、F分别是BC、CD上的点,且/ EAF是/ BAD的一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明?若不成立,请说明理由。 (2)若将(1)中的条件改为:在四边形ABCD中,AB=AD,/ B+ / D=180 °,延长BC 到点E,延长CD到点F,使得/ EAF仍然是/ BAD的一半,则结论EF=BE+FD是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。 求证:AB+BD=AC. ACB 90 , AC=BC , E 是AB 上的一点, BD 丄CE, AF L CE 垂足分别为D、F,Z B=2/ C,求证:DF+AF=CF. 练习题1.如图2 — 1 —3所示已知三角形ABC中,AD平分/ BAC / B=2/ C, 2. 如图2 —1 —8所示已知厶ABC中, P
