上海市中考数学压轴题综合复习八(教师版)
2020-2021学年下学期沪教版八年级数学压轴题集第十一讲动点求函数解析式

第十一讲动点求函数解析式【要点导航】函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想.由于某--个点或某图形有条件地运动变化,引起未知量与已知量间的一种变化关系.这种变化关系就是动点问题中的函数关系.这部分压轴题主要是在图形运动变化的过程中探求两个变量之间的函数关系,并根据实际情况确定自变量的取值范围.【典型例题】【例1】在△ABC中,∠C=90°,AC=BC=4,在射线AC、CB上分别有两个动点M、N,且AM= BN,联结MN交AB于点P。
(1)如图1所示,当点M在边AC(与点A、C不重合)上,线段PM与线段PN之间有怎样的大小关系?试证明你得到的结论。
(2)当点M在射线AC上,若设AM=x,BP=y,求y与x的函数关系式及定义域。
(3)过点M作直线AB的垂线,垂足为Q,随着点M、N的移动,线段PQ的长能确定吗?若能确定.请求出PQ的长;若不能确定,请简要说明理由。
图1利用线段和差建立函数关系式.【例2】如图2所示, 在长方形ABCD中,AB= 8,AD= 6,点P、Q分别是AB边和CD 边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP= CQ,设AP= x,BE= y.(1)线段PQ的垂直平分线与BC边相交,设交点为点E,求y与x的函数关系式及x取值范围.(2)在(1)的条件下,是否存在x使△PQE为直角三角形? 若存在,请求出x的值;若不存在,请说明理由.图2方法点晴应用勾股定理建立函数解析式.1. (★★)如图3所示,在△ABC中,已知∠BAC=45°,AD⊥BC交BC边于点D,BD=2,DC=3,求AD的长。
小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题。
请按照小萍的思路,探究并解答下列问题:(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,点D的对称点为E、F 两点,延长EB、FC相交于点G ,证明四边形AEGF是正方形。
2020年中考数学压轴题-专题08 动点产生的平行四边形(解析版)

专题08 动点产生的平行四边形教学重难点1.理解平行四边形的性质和判定;2.能应用平行四边形的性质和判定进行相关计算和证明;3.培养学生能在点的运动过程中寻找平行四边形,继而解决相关问题;4.培养学生分类讨论的能力,能应用分类讨论思想解决相关问题;5.体验运动过程,培养学生动态数学思维能力。
【备注】:1.根据后面两个图让学生回顾平行四边形的性质和判定,为后面的例题讲解做好准备;2.部分地方引导学生填空,让学生自己回顾。
时间大概5分钟。
平行四边形的性质:平行四边形的判定:【备注】:1.以下每题教法建议,请老师根据学生实际情况参考;2.在讲解时:不宜采用灌输的方法,应采用启发、诱导的策略,并在读题时引导学生发现一些题目中的条件(相等的量、不变的量、隐藏的量等等),使学生在复杂的背景下自己发现、领悟题目的意思;3.可以根据各题的“教法指导”引导学生逐步解题,并采用讲练结合;注意边讲解边让学生计算,加强师生之间的互动性,让学生参与到例题的分析中来;4.例题讲解,可以根据“参考教法”中的问题引导学生分析题目,边讲边让学生书写,每个问题后面有答案提示;5.引导的技巧:直接提醒,问题式引导,类比引导等等;6.部分例题可以先让学生自己试一试,之后再结合学生做的情况讲评;7.每个题目的讲解时间根据实际情况处理,建议每题7分钟,选讲例题在时间足够的情况下讲解。
1.(2019·辽宁中考真题)如图1,在平面直角坐标系中,一次函数y =﹣34x +3的图象与x 轴交于点A ,与y 轴交于B 点,抛物线y =﹣x 2+bx +c 经过A ,B 两点,在第一象限的抛物线上取一点D ,过点D 作DC ⊥x 轴于点C ,交直线AB 于点E .(1)求抛物线的函数表达式(2)是否存在点D ,使得⊥BDE 和⊥ACE 相似?若存在,请求出点D 的坐标,若不存在,请说明理由; (3)如图2,F 是第一象限内抛物线上的动点(不与点D 重合),点G 是线段AB 上的动点.连接DF ,FG ,当四边形DEGF 是平行四边形且周长最大时,请直接写出点G 的坐标. 【整体分析】(1)根据334y x =-+,求出A ,B 的坐标,再代入抛物线解析式中即可求得抛物线解析式;(2)⊥BDE 和⊥ACE 相似,要分两种情况进行讨论: ⊥⊥BDE⊥⊥ACE ,求得13(4D ,3);⊥⊥DBE⊥⊥ACE ,求得23(12D ,50)9; (3)由DEGF 是平行四边形,可得DE⊥FG ,DE=FG ,设213(,3)4D m m m -++,3(,3)4E m m -+,213(,3)4F n n n -++,3(,3)4G n n -+,根据平行四边形周长公式可得:DEGF 周长=23892()48m --+,由此可求得点G 的坐标. 【满分解答】(1)在334y x =-+中,令0x =,得3y =,令0y =,得4x =,(4,0)A ∴,(0,3)B ,将(4,0)A ,(0,3)B 分别代入抛物线2y x bx c =-++中,得:24403b c c ⎧-++=⎨=⎩,解得:1343b c ⎧=⎪⎨⎪=⎩,∴抛物线的函数表达式为:21334y x x =-++. (2)存在.如图1,过点B 作BH CD ⊥于H ,设(,0)C t ,则213(,3)4D t t t -++,3(,3)4E t t -+,(,3)H t ;334EC t ∴=-+,4AC t =-,BH t =,2134DH t t =-+,24DE t t =-+BDE ∆∵和ACE ∆相似,BED AEC ∠=∠BDE ACE ∴∆∆∽或DBE ACE ∆∆∽⊥当BDE ACE ∆∆∽时,90BDE ACE ∠=∠=︒,∴BD AC DE CE=,即:BD CE AC DE =g g 23(3)(4)(4)4t t t t t ∴-+=-⨯-+,解得:10t =(舍去),24t =(舍去),3134t =,13(4D ∴,3)⊥当DBE ACE ∆∆∽时,BDE CAE ∠=∠ BH CD ⊥Q90BHD ∴∠=︒,∴tan tan BH CEBDE CAE DH AC=∠=∠=,即:BH AC CE DH =g g 2313(4)(3)()44t t t t t ∴-=-+-+,解得:10t =(舍),24t =(舍),32312t =,23(12D ∴,50)9; 综上所述,点D 的坐标为13(4,3)或23(12,50)9;(3)如图3,Q 四边形DEGF 是平行四边形 //DE FG ∴,DE FG =设213(,3)4D m m m -++,3(,3)4E m m -+,213(,3)4F n n n -++,3(,3)4G n n -+,则:24DE m m =-+,24FG n n =-+,2244m m n n ∴-+=-+,即:()(4)0m n m n -+-=,0m n -≠Q 40m n ∴+-=,即:4m n +=过点G 作GK CD ⊥于K ,则//GK AC EGK BAO ∴∠=∠∴cos cos GK AOEGK BAO EG AB=∠=∠=,即:GK AB AO EG =g g 5()4n m EG ∴-=,即:5()4EG n m =-DEGF ∴周长2253892()2[(4)()]2()448DE EG m m n m m =+=-++-=--+20-<Q ,∴当34m =时,DEGF ∴Y 周长最大值898=, 13(4G ∴,9)16【点睛】此题考查二次函数综合题,综合难度较大,解答关键在于结合函数图形进行计算,再利用待定系数法求解析式,配合辅助线利用相似三角形的性质进行解答.2.如图,在平面直角坐标系中,直线b kx y +=分别与x 轴负半轴交于点A ,与y 轴的正半轴交于点B ,⊙P 经过点A 、点B (圆心P 在x 轴负半轴上),已知AB=10,425=AP 。
沪教版中考数学压轴专题讲义

压轴题训练一1. 已知平面直角坐标系中,点A在抛物线2y上,过点A作AB⊥x轴于点B,AD⊥y轴于点D,将矩形ABOD沿对角线BD折叠后得A的对应点A’,重叠部分为△BDC.(1)求证:△BDC是等腰三角形;(2)如果点A的坐标是(1,m),求△BDC的面积;(3)在(2)的条件下,求直线BC的解析式,并判断点A’是否落在已知的抛物线上?请说明理由。
2. 抛物线21=8y x 如图所示,过y 轴上一点M(0,2)的直线与抛物线交于A 、B 两点,过点A 、B 分别作y 轴的垂线,垂足分别是C 、D 。
(1)当点A 的横坐标为-2时,求点B 的坐标;(2)在(1)的情况下,分别过点A 、B 作AE ⊥x 轴于E ,BF ⊥x 轴于F ,在EF 上是否存在点P ,使∠APB 为直角。
若存在,求点P 的坐标;若不存在,请说明理由;(3)当点A 在抛物线上运动时(点A 与点O 不重合),求AC ·BD 的值。
3. 如图,已知一三角形纸片ABC,面积为25,BC边的长为10,∠B和∠C都为锐角,M为AB边上的一动点(M与点A、B不重合),过点M作MN∥BC,交AC于点N.设MN=x.(1)用x表示△AMN的面积;(2)将△AMN沿MN折叠,使△AMN紧贴四边形BCNM(边AM、AN落在四边形BCNM所在的平面内),设点A落在平面BCNM内的点为A’,△A’MN与四边形BCNM重叠部分的面积为y.求y与x的函数关系式,并写出自变量x的取值范围。
(3)当x为何值时重叠部分的面积y最大,最大为多少?AM NB CAM NB CGHBCEFAD4. 如图,在边长为1的正方形ABCD 中,以点A 为圆心,AB 为半径作BD ,E 是BC 边上的一个动点(与B 、C 点不重合),过点E 作BD 的切线,交CD 于点F ,H 是切点。
过点E 作EG ⊥EF ,交AB 于点G ,联结AE 。
(1)求证:△AGE 是等腰三角形;(2)设BE=x ,△BGE 和△CEF 的面积比为y (即=BGE CEFS y S),求y 关于x 的函数解析式,并写出自变量x 的取值范围;(3)在BC 边上(点B 、C 除外)是否存在点E ,使GE=EF ,若存在,请求出此时BE 的长;若不存在,请说明理由。
(完整)上海八年级数学压轴题.doc

1.已知:如图,在△ABC 中, AD 、 BE 是高, F 是 AB 的中点, FG DE ,点 G 是垂足.求证:点G 是 DE 的中点.2 OBC中,点O为坐标原点,点C坐标为(4 0 B坐标为(2,23 ),.如图,在△,),点AB轴,点A为垂足,OH BC ,点 H 为垂足.动点 P、 Q分别从点O 、A 同时y出发,点 P 沿线段 OH 向点 H 运动,点Q沿线段 AO 向点 O 运动,速度都是每秒 1 个单位长度.设点 P 的运动时间为 t 秒.(1)求证:OB CB;(2)若△OPQ的面积为S,求S与t之间的函数关系式及定义域;(3)当PQ OB (垂足为点M )时,求五边形ABHPQ 的面积的值.yA BQ M HPOC x3.如图,在△ ABC中, AB=AC,点 P是 BC边上的一点, PD⊥AB 于 D,PE⊥ AC于 E,CM⊥AB于M,试探究线段 PD、PE、 CM的数量关系,并说明理由。
AMEDB P C4. 如图, Rt △ ABC中, AB=AC, A 90 ,O为BC中点。
(1)写出点 O到△ ABC三个顶点的距离之间的关系;(2)如果点 M、N分别在边 AB、AC上移动,且保持 AN=BM。
请判断△ OMN的形状,并证明你的结论。
CONA M B5.如图,点 A 的坐标为(3,0 ),点 C 的坐标为( 0,4 ), OABC 为矩形,反比例函数k yx的图像过 AB 的中点 D,且和 BC 相交于点 E, F 为第一象限的点, AF=12, CF =13.k和直线 OE 的函数解析式;(1)求反比例函数yx(2)求四边形 OAFC 的面积.yFC BEDOA x_6.已知:如图,正比例函数的图象与反比例函数的图象交于点(1)试确定上述正比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当取何值时,反比例函数的值大于正比例函数的值?( 3)是反比例函数图象上的一动点,其中过点作直线轴,交轴于点;过点作直线轴交轴于点,交直线于点.当四边形的面积为 6 时,请判断线段与的大小关系,并说明理由.7.已知:如图,在⊿ ABC 中,∠ C= 90°,∠ B= 30°, AC=6,点 D 在边 BC 上, AD 平分∠CAB , E 为 AC 上的一个动点(不与 A、C 重合), EF ⊥ AB,垂足为 F .(1)求证: AD=DB ;(2)设 CE=x ,BF=y ,求 y 关于 x 的函数解析式;(3)当∠ DEF =90°时,求 BF 的长 .AFEC D B第 26题图答案1. 明:EF 、 DF .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分A∵ AD 是高,∴ ADBC ,E FG∴ ADB 90o .⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分又∵ F 是 AB 的中点,BDC∴ DF1AB (直角三角形斜 上的中 等于斜 的一半).⋯⋯ 2 分2同理可得: EF1AB .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分2∴ EF DF .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分 又∵ FG DE ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分 ∴ DGEG .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分即:点 G 是 DE 的中点.2. 解:( 1)∵ OB222 324 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分22CB 2 42 3 4 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分 ∴ OB CB ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分(2)易 :△ OBC 等 三角形.y∵ OHBC ,AB∴ BOHHOC 30o .⋯⋯⋯⋯⋯⋯ 1 分∴ AOB 30 o .Q H点 P 作 PEOA 垂足 点 E .EP在 Rt △ PEO 中, EPO 30o, PO t ,OCx∴ EO1PO t,由勾股定理得: PE3t .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分2 22又∵ OQ AO AQ 2 3 t ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分 ∴ S1OQgPE 1 2 3 t g 3 t 6t 3t 2 .⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分22 2 4即: S3t 23t ( 0t2 3 ).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分42【 明】最后1 分 定 域分数.(3)易 Rt △ OAB ≌Rt △ OHB ≌ Rt △ OHC ,∴ S四边形OABH S VOAB S VOHB S VOHB S VOHC S V OBC 3OC 2 4 3 .1分4易△ OPQ 等三角形,∴OQ OP ,即: 2 3 t t ,解得t 3 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∴SVOPQ 3 OP 2 3 3.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分4 4 ∴S五边形ABHPQ S四边形 OABHSV OPQ4 33 3133 .⋯⋯⋯⋯⋯1分4 43.解: PD+PE=CM ,明:接 AP ,∵ AB=AC ,∴ S△ABC=S △ABP+S △ACP= AB× PD+ AC× PE=× AB×(PD+PE),∵ S△ABC= AB× CM,∴ PD+PE=CM。
沪教版八年级数学期末难题压轴题

四边形综合题1、已知:在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,AE =2.(1)如图①,当四边形EFGH 为正方形时,求△GFC 的面积; (2)如图②,当四边形EFGH 为菱形,且BF = a 时,求△GFC 的面积.(用含a 的代数式)2、已知点E 是正方形ABCD 外的一点,EA=ED ,线段BE 与对角线AC 相交于点F , (1)如图1,当BF=EF 时,线段AF 与DE 之间有怎样的数量关系?并证明;(2)如图2,当△EAD 为等边三角形时,写出线段AF 、BF 、EF 之间的一个数量关系,并证明.D(图1)FD CA BE(图2)FHG图1图23、如图,直线y =+与x 轴相交于点A,与直线y =相交于点P . (1) 求点P 的坐标.(2) 请判断△OPA 的形状并说明理由.(3) 动点E 从原点O 出发,以每秒1个单位的速度沿着O P A →→的路线向点A 匀速运动(E 不与点O 、A 重合),过点E 分别作EF x ⊥轴于F ,EB y ⊥轴于B .设运动t 秒时,矩形EBOF 与△OPA 重叠部分的面积为S .求S 与t 之间的函数关系式.4、如图,在平面直角坐标中,四边形OABC 是等腰梯形,CB ∥OA ,OC=AB=4,BC=6,∠COA=45°,动点P 从点O 出发,在梯形OABC 的边上运动,路径为O →A →B →C ,到达点C 时停止.作直线CP. (1)求梯形OABC 的面积;(2)当直线CP 把梯形OABC 的面积分成相等的两部分时,求直线CP 的解析式; (3)当∆OCP 是等腰三角形时,请写出点P 的坐标(不要求过程,只需写出结果)O ABC Pxy五、27.如图,已知在梯形ABCD 中,AD // BC ,AB = CD ,BC = 8,60B ∠=︒,点M 是边BC 的中点,点E 、F 分别是边AB 、CD 上的两个动点(点E 与点A 、B 不重合,点F 与点C 、D 不重合),且120EMF ∠=︒. (1)求证:ME = MF ;(2)试判断当点E 、F 分别在边AB 、CD 上移动时,五边形AEMFD 的面积的大小是否会改变,请证明你的结论;(3)如果点E 、F 恰好是边AB 、CD 的中点,求边AD的长.A B C DM E F (第27题图) A BCD ME F (备用图)3(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l ∥y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O ﹣C ﹣A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒)0( t .①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?②是否存在以A 、P 、Q 为顶点的三角形是QA=QP 的等腰三角形?若存在,求t 的值;若不存在,请说明理由.3∴y =-x +7,0=x +7,∴x =7,∴B 点坐标为:(7,0),----------------------------1分 ∵y =-x +7=x 34,解得x =3,∴y =4,∴A 点坐标为:(3,4);-------------------1分 (2)①当0<t <4时,PO =t ,PC =4-t ,BR =t ,OR =7-t ,--------------1分 过点A 作AM ⊥x 轴于点M∵当以A 、P 、R 为顶点的三角形的面积为8,∴S 梯形ACOB -S △ACP -S △POR -S △ARB =8, ∴21(AC +BO )×CO -21AC ×CP -21PO ×RO -21AM ×BR =8, ∴(AC +BO )×CO -AC ×CP -PO ×RO -AM ×BR =16,∴(3+7)×4-3×(4-t )-t ×(7-t )-4t =16,∴t 2-8t +12=0. -----------------1分 解得t 1=2,t 2=6(舍去). --------------------------------------------------------------------1分 当4≤t ≤7时,S △APR =21AP ×OC =2(7-t )=8,t=3(舍去);--------------1分 ∴当t =2时,以A 、P 、R 为顶点的三角形的面积为8; ②存在.当0<t ≤4时,直线l 与AB 相交于Q ,∵一次函数y =-x +7与x 轴交于B (7,0)点,与y 轴交于N (0,7)点,∴NO =OB ,∴∠OBN =∠ONB =45°.∵直线l ∥y 轴,∴RQ =RB=t ,AM=BM=4∴QB=t 2,AQ=t 224-----------------1分 ∵RB =OP =QR =t ,∴PQ//OR,PQ=OR=7-t --------------------------------------1分 ∵以A 、P 、Q 为顶点的三角形是等腰三角形,且QP =QA ,∴7-t=t 224-,t=1-32(舍去)--------------------------------------------1分 当4<t ≤7时,直线l 与O A 相交于Q ,若QP =QA ,则t -4+2(t -4)=3,解得t =5;---------------------------------------1分 ∴当t =5,存在以A 、P 、Q 为顶点的三角形是PQ =AQ 的等腰三角形.已知边长为1的正方形ABCD 中, P 是对角线AC 上的一个动点(与点A 、C 不重合), 过点P 作 PE ⊥PB ,PE 交射线DC 于点E ,过点E 作EF ⊥AC ,垂足为点F . (1)当点E 落在线段CD 上时(如图10),① 求证:PB=PE ;② 在点P 的运动过程中,PF 的长度是否发生变化?若不变,试求出这个不变的值, 若变化,试说明理由;(2)当点E 落在线段DC 的延长线上时,在备用图上画出符合要求的大致图形,并判断上述(1)中的结论是否仍然成立(只需写出结论,不需要证明);(3)在点P 的运动过程中,⊿PEC 能否为等腰三角形?如果能,试求出AP 的长,如果不能,试说明理由.D CBAE P 。
上海(沪)八年级第二学期期末数学压轴题及答案(可转为word)
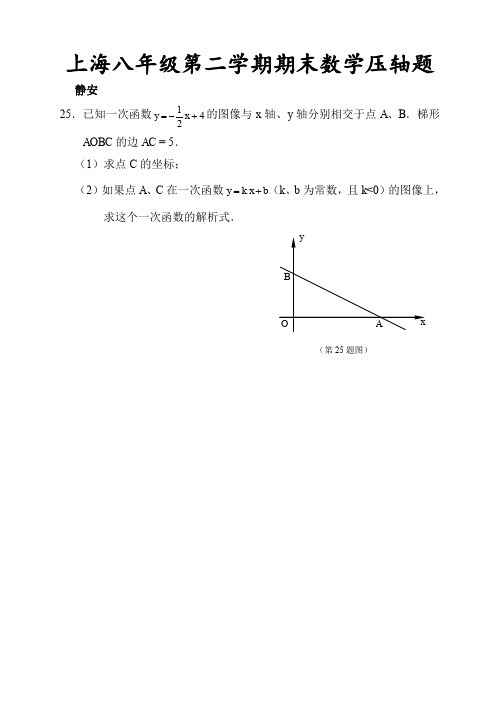
0 8k b, ∴ „„„„„„„„„„„„„„„„„„„„„„„„„(1 分) 4 5k b,
4 k , 3 „„„„„„„„„„„„„„„„„„„„„„„„„(1 分) ∴ 32 b . 3
4 32 .„„„„„„„„„„„„(1 分) x 3 3 26.解: (1)BF +AG= AE.„„„„„„„„„„„„„„„„„„„„„„(1 分) 证明如下:过点 F 作 FH⊥DA,垂足为 H, ∵在正方形 ABCD 中,∠DAE=∠B=90°,∴四边形 ABFH 是矩形.„(1 分) ∴FH=AB=DA.∵BD⊥FG,∴∠G=90°–∠ADE=∠DEA. 又∴∠DAE=∠FHG=90°,∴△FHG≌△DAE. „„„„„„„„„„(1 分) ∴GH=AE,即 HA+AG=AE.∵BF=HA,∴BF+AG=AE.„„„„„„(1 分)
本题满分12分其中第1小题5分第2小题3分第3小题4bcaebcdfdfaeefad四边形aefd是平行四边形efad5aedf?????????????????????????1abcd5rtabertdcfbecfefbccfbecf3在rtabeabaeaebqapaepdcqqcdpabqp当四边形abqp与四边形qcdp的面积相等时3当四边形abqp是平行四边形时pqab当四边形qcdp是平行四边形时可得pqcdcdabpqab此时cqpd11时pqab
FB 3 ,且 AC 10 ,求 FC 的值. BD 5
A
D
F
E
B
C
26. 在梯形 ABCD 中, ∠ABC= 90 , AD∥BC, BC>AD, AB=8cm, BC=18cm, CD=10 cm,点 P 从点 B 开始沿 BC 边向终点 C 以每秒 3cm 的速度移动,点 Q 从点 D 开始沿 DA 边向终点 A 以每秒 2cm 的速度移动,设运动时间为 t 秒. (1)求四边形 ABPQ 为矩形时 t 的值; (2)若题设中的“BC=18cm”改变为“BC= k cm” ,其它条件都不变,要 使四边形 PCDQ 是等腰梯形,求 t 与 k 的函数关系式,并写出 k 的取值范围; (3)在移动的过程中,是否存在 t 使 P、Q 两点 的距离为 10cm ,若存在求 t 的值. 若不存在请说明 理由?
(完整)上海八年级数学压轴题

ABC 中, AD 、 BE 是高, F 是 AB 的中点, FGDE ,点 G 是G 是 DE 的中点.AB y 轴 ,点 A 为垂足, OH BC , 点 H 为垂足 . 动点 P 、 Q 分别从点O 、出发,点P 沿线段 OH 向点 H 运动,点Q 沿线段 AO 向点 O 运动,速度都是每秒 1 个单位长度 . 设点 P 的运动时间为 t 秒 . 1 )求证: OB CB ; 2)若△OPQ 的面积为 S ,求 S 与 t 之间的函数关系式及定义域;3)当 PQ OB (垂足为点M )时,求五边形 ABHPQ 的面积的值 .1 .已知:如图,在△垂足.求证:点 2.如图,在△OBC 中,点 O 为坐标原点,点 C 坐标为( 4, 0) ,点 B 坐标为( 2,2 3), A 同时3.如图,在△ABC中,AB=AC,点P是BC边上的一点,PD⊥AB于D,PE⊥AC于E,CM⊥ AB于M,试探究线段 PD、 PE、 CM的数量关系,并说明理由。
4. 如图, Rt△ ABC中,AB=AC, A 90 , O为 BC中点。
(1 )写出点O 到△ ABC三个顶点的距离之间的关系;52)如果点M、N分别在边AB、 AC上移动,且保持AN=BM。
请判断△OMN的形状,并证明你的结论。
k 5.如图,点A的坐标为(3,0),点 C 的坐标为(0,4 ), OABC 为矩形,反比例函数yxAB 的中点D,且和BC 相交于点E, F 为第一象限的点,AF=12, CF=13.k1 )求反比例函数y 和直线 OE 的函数解析式;x2)求四边形 OAFC 的面积.6.已知:如图,正比例函数的图象与反比例函数的图象交于点( 1 )试确定上述正比例函数和反比例函数的表达式;( 2)根据图象回答,在第一象限内,当取何值时,反比例函数的值大于正比例函数的值?( 3)是反比例函数图象上的一动点,其中过点作直线轴,交轴于点;过点作直线轴交轴于点,交直线于点.当四边形的面积为6 时,请判断线段与的大小关系,并说明理由.7.已知:如图,在⊿ABC 中,∠C= 90°,∠B= 30°,AC=6,点 D 在边 BC 上, AD 平分∠ CAB , E 为 AC 上的一个动点(不与A、 C 重合),EF⊥ AB,垂足为F.1 )求证:AD=DB ;2)设C E=x,BF=y ,求 y 关于 x 的函数解析式;3)当∠DEF =90°时,求BF 的长 .第 26题图1∴ DF AB (直角三角形斜边上的中线等于斜边的一半) .⋯⋯2 分21同理可得:EFAB .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分2∴ EF DF .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1分又∵ FG DE ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∴ DG EG .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分即:点 G 是 DE 的中点.2. 解: ( 1)∵OB 2223 24 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分又∵ OQ AO AQ 2 3 t ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分压轴题答案1 . 证明: 联结 EF 、 DF .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1分AD 是高, ∴ AD BC ,ADB 90o.⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1分又∵ F 是 AB 的中点,A1 1 3 6t 3t2∴ S OQgPE 2 3 t g t .⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1分2 2 24即:S t2t (0 t 2 3 ).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分421 分为定义域分数3)易证Rt△ OAB ≌ Rt△ OHB ≌ Rt△ OHC ,S VOHB S VOHC S VOBC OC 4 3. 1 分 4S VOPQ 4 3 3 3 13 3 .⋯⋯⋯⋯⋯443. 解: PD+PE=CM 证明:连接 AP ,∵ AB=AC , ∴ S △ ABC =S △ ABP +S △ ACP = AB × PD+ AC ×PE= × AB ×( PD+PE ) ,∵ S △ ABC = AB × CM , ∴ PD+PE=CM 。
上海历年中考数学压轴题复习试题附答案

上海历年中考数学压轴题复习试题附答案The document was prepared on January 2, 2021上海历年中考数学压轴题复习2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长(不必写出解题过程). 27.(1)①证明:∵ ∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴ ∠ABP =∠DPC .∵ 在梯形ABCD 中,AD ∥BC ,AB =CD ,∴ ∠A =∠D .∴ △ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252xx -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴DQ AP PD AB =.即yxx +=-252,得225212-+-=x x y ,1<x <4.②AP =2或AP =3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与射线DC 相交于点Q .图5图6图7探究:设A 、P 两点间的距离为x .(1)当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的大小关系试证明你观察得到结论;(2)当点Q 在边CD 上时,设四边形PBCQ 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域;(3)当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形如果可能,指出所有能使△PCQ 成为等腰三角形的点Q 的位置,并求出相应的x 的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用) 五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分) 27.图1 图2 图3(1)解:PQ =PB ……………………(1分) 证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分)∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB . (2)解法一由(1)△QNP ≌△PMB .得NQ =MP . ∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2.得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2(1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分) 解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形. ∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN . S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN …(2分)=CN 2=(1-x 22)2=21x 2-x 2+1 ∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形, 此时x =0 ……………………(1分)②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3) ……………………(1分)解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴ CQ =QN -CN =x 22-(1-x 22)=x 2-1.当2-x =x 2-1时,得x =1. ……………………(1分)解法二 此时∠CPQ =21∠PCN =°,∠APB =90°-°=°, ∠ABP =180°-(45°+°)=°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD 中,AB =1,弧AC 是点B 为圆心,AB 长为半径的圆的一段弧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考压轴题综合复习八
1.培养学生挖掘信息的能力,并能从题目中寻找有利条件;
2.培养学生分析问题解决问题的能力;
3.让学生学会把难题分解,从而分段击破;
4.培养学生动态数学思维能力和综合能力。
知识结构
【备注】引导学生对中考压轴题进行一下概述,为后面讲解铺垫好基础,大概5分钟左右。
一.中考压轴题命题方向:
二.动点产生的分类讨论类型:
例1.已知在梯形ABCD 中,AB ∥DC ,且AB =4,AD =BC =2,∠ABC =120°。
P 、Q 分别为射 线BC 和线段CD 上的动点,且CQ =2BP 。
(★★★★)
(1)如图1,当点P 为BC 的中点时,求证:△CPQ ∽△DAQ ;
(2)如图2,当点P 在BC 的延长线上时,设BP =x ,△APQ 的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域;
(3)以点A 为圆心AQ 为半径作⊙A ,以点B 为圆心BP 为半径作⊙B ,当⊙A 与⊙B 相 切时,求BP 的长。
【参考教法】可参考以下教法引导学生分析问题、解决问题 一.寻找题目中的已知量和特殊条件:
1.哪些边已知?哪些边存在特殊关系? 提示:AB =4,AD =BC =2,AB ∥DC ;
2.哪些角已知?哪些角存在特殊关系? 提示:∠ABC =120°,DAB B ∠=∠;
3.点的运动情况? 提示:P 、Q 分别为射线BC 和线段CD 上的动点。
二.当点P 为BC 的中点时,求证:△CPQ ∽△DAQ :
1.这时,线段BP 、CP 、CQ 、DQ 的长度是否能求解? 提示:让学生计算看看。
2.根据目前已知的条件,怎么证明相似? 提示:因为题中已知的都是边,则利用两边成 比例且夹角相等证明。
三.求解函数关系式:
1.寻找一下x 与y 分别所表示的量? 提示:BP =x ,△APQ 的面积为y
2.三角形面积怎么求解? 提示:因为APQ ∆的每一边都在变化,并且每一条边的长度都 不好求解,则考虑将三角形分成两个三角形;设PA 与DC 的交点为点E ,则: AQE QEP y S S ∆∆=+。
C
D
A
B
备用图
P
C D
Q
A
B
图1
P C
D
Q
A
B
图2
3.计算求解,注意求解函数定义域。
(见后面满分解答部分) 四.两圆相切:
1.回顾两圆相切的三大解题步骤。
提示:求解三个量、分类讨论、计算求解。
2.你能分别求解出两元的半径和圆心距吗? 提示:让学生计算看看。
3.分内切和外切讨论计算。
【满分解答】
(1)过点A 作CD AM ⊥,M 为垂足, 过点A 作CD AN ⊥,N 为垂足
根据题意得:AM =BN ,AB =MN =4,DM =CN 在直角三角形△CBN 中, ∴︒=∠60DCB ,BC =2 CN =1,BN =3 ∴ DM =1,AM =3∴CD =6
∵点P 为BC 的中点,且CQ =2BP ∴CP =1,CQ =2,DA =2,DQ =4
∴
DQ
CQ
DA CP = 又︒=∠=∠60D QCP ∴△CPQ ∽△DAQ (2) ∵AB ∥DC ∴
AB CE PB PC = ∴42CE x x =- ∴x
x CE 8
4-= ∴x
x x x x x QE 8
428422+-=--= 过点P 作CD PH ⊥交DC 的延长线于H
在直角三角形△CBN 中, ∴︒=∠60PCH ,2-=x PC
)2(2
3
-=
x PH ∵AQ P PQ E APQ S S S ∆∆∆+=
∴x
x x x x x x y 842321842)2(232122+-⨯
⨯++-⨯-⨯= ∴)42(2
32
+-=
x x y )32(≤<x (3) ∵x DQ DM 26,1-== ∴x QM 25-= 在直角三角形△AQM 中,
3)25(2+-=x AQ
当⊙A 与⊙B 外切时, AB BP AQ =+
43)25(2=++-x x
221==x x
当⊙A 与⊙B 内切时, AB BP AQ =-
43)25(2=-+-x x
3104141-=
x ,3
10
4142+=x (舍去) ∴当2=BP 时, ⊙A 与⊙B 外切; 当3
10
414-=BP 时, ⊙A 与⊙B 内切时.
1.如图,在四边形ABCD 中,∠B =90°,AD //BC ,AB =4,BC =12,点E 在边BA 的延长线上,AE =2,点F 在BC 边上,EF 与边AD 相交于点G ,DF ⊥EF ,设AG =x , DF =y 。
(1)求y 关于x 的函数解析式,并写出定义域; (2)当AD =11时,求AG 的长;
(3)如果半径为EG 的⊙E 与半径为FD 的⊙F 相切,求这两个圆的半径。
(★★★★)
D
G
B
C
A
E F
【解法点拨】可参考以下方法引导学生分析问题、解决问题 一.寻找题目中的已知量和特殊条件:
1.已知边和特殊关系的边:AB =4,BC =12,AE =2,AD //BC ,DF ⊥EF 。
2.已知角和特殊角度:90B EFD ∠=∠=。
3.相似基本型:AG BF ∥形成相似基本型“A 字型” 二.求解函数关系式:
1.寻找x 与y 所代表的量: AG x =,ADF y =。
2.计算求解:用EAG EBF ∆∆∽、EAG DFG ∆∆∽产生的比例关系式求解。
三.当11AD =:用11AD AG DG =+=求解即可。
四.当⊙E 与⊙F 外切时:
1.分别求解两圆的半径和圆心距:半径E r 、F r ,和圆心距EF ;
2.分内切和外切分类讨论;
3.计算求解。
【满分解答】
(1)∵AD //BC ,∠B =90º,∴∠EAG =∠B =90º,
∴EG =.4222x AG AE +=+
∵,AE
EG AB FG = ∴FG =2242244x x AE EG AB +=+⋅=⋅.
∵∠DFG =∠EAG =90º,∠EGA =∠DGF ,∴△DFG ∽△EAG .
∴
AG AE GF DF =,∴x
x y 2
422=+,
∴y 关于x 的函数解析式为x
x y 2
44+=,定义域为40≤<x .
(2)∵△DFG ∽△EAG ,∴
,AG FG EG GD =∴x x x
GD 22424+=
+,∴GD =x x 228+.
当AD =11时,11282
=++x
x x ,
3
8
,121==x x .
经检验它们都是原方程的根,且符合题意,所以AG 的长为1或
3
8. (3)当⊙E 与⊙F 外切时,EF =EG +FD =EG +FG ,∴FD =FG ,
∵△DFG ∽△EAG ,∴∠E =∠AGE =∠FGD =∠GDF .∴AG =AE =2;
∴⊙E 的半径EG =22,⊙F 的半径FD =24.
当⊙E 与⊙F 内切时,EF = FD –EG ,∴322
2
4444x x
x x +-+=+,
∵042≠+x ,∴3=
14
-x
,∴1=x . ∴⊙E 的半径EG =514=+,⊙F 的半径FD =54.
所以⊙E 的半径为22,⊙F 的半径为42;或⊙E 的半径为5,⊙F 的半径为45。
错误!未指定书签。
错误!未指定书签。
【说明】:本部分为“专题小结”,由“专题知识点或是方法回顾+教师寄语”组成。
先让学生说说本节课的收获,之后是教师寄语。
教师寄语可以是:需要完成的作业、需要总结的知识点、名言名句、提醒学生需要做的事情等等。
