数字信号处理程培青第三版试题及答案
(完整word版)数字信号处理试卷及答案_程培青(第三版),推荐文档

河南工业大学数字信号处理 试卷考试方式:闭卷复查总分 总复查人一、填空题:(本大题共10小题,每空2分,共28分)请在每个空格中填上正确答案。
错填、不填均无分。
1、一线性时不变系统,输入为 x (n )时,输出为y (n ) ;则输入为2x (n )时,输出为;输入为x (n-3)时,输出为 。
2、从奈奎斯特采样定理得出,要使实信号采样后能够不失真还原,采样频率f 与信号最高频率fs 关系为: 。
3、已知一个长度为N 的序列x(n),它的傅立叶变换为X (e jw ),它的N 点离散傅立叶变换X (K )是关于X (e jw )的 点等间隔 。
4、有限长序列x(n)的8点DFT 为X (K ),则X (K )= 。
5、无限长单位冲激响应(IIR )滤波器的结构上有反馈,因此是_ _____型的。
6、若正弦序列x(n)=sin(30n π/120)是周期的,则周期是N= 。
7、已知因果序列x(n)的Z 变换为X(z)=eZ -1,则x(0)=__________。
8、无限长单位冲激响应滤波器的基本结构有直接Ⅰ型,直接Ⅱ型,___ ___和__ _ ___四种。
9、DFT 与DFS 有密切关系,因为有限长序列可以看成周期序列的__________,而周期序列可以看成有限长序列的__________。
10、对长度为N 的序列x(n)圆周移位m 位得到的序列用x m (n)表示,其数学表达式为x m (n)=__________。
《数字信号处理》试卷A 第1页 ( 共 6 页 )二、选择填空题(本大题共6小题,每题2分,共12分)1、δ(n)的z 变换是 。
A. 1B.δ(w)C. 2πδ(w)D. 2π2、序列x 1(n)的长度为4,序列x 2(n)的长度为3,则它们线性卷积的长度是 , 5点圆周卷积的长度是 。
A. 5, 5B. 6, 5C. 6, 6D. 7, 53、在N=32的时间抽取法FFT 运算流图中,从x(n)到X(k)需 级蝶形运算 过程。
数字信号处理(第三版)_课后习题答案全_(原题+答案+图)
第 1 章
时域离散信号和时域离散系统
6. 给定下述系统的差分方程, 试判定系统是否是因果稳定系统, 并说明
理由。
1 N 1 N k 0 (2) y(n)=x(n)+x(n+1)
第 1 章
(2) 令输入为
x(n-n0) 输出为
Байду номын сангаас
时域离散信号和时域离散系统
y′(n)=2x(n-n0)+3
y(n-n0)=2x(n-n0)+3=y′(n)
故该系统是非时变的。 由于 T[ax1(n)+bx2(n)]=2ax1(n)+2bx2(n)+3 T[ax1(n)]=2ax1(n)+3 T[bx2(n)]=2bx2(n)+3 T[ax1(n)+bx2(n)]≠aT[x1(n)]+bT[x2(n)] 故该系统是非线性系统。
m
第 1 章
时域离散信号和时域离散系统
题7图
第 1 章
时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章
解法(二)
时域离散信号和时域离散系统
采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
n n0 k n n0
|x(k)|≤|2n0+1|M, 因
此系统是稳定的; 假设n0>0, 系统是非因果的, 因为输出
数字信号处理-第3版-答案(PDF)

2.1 判断下列序列是否是周期序列。若是,请确定它的最小周期。 (1)x(n)=Acos( (2)x(n)= e (
j
π 5π n+ ) 8 6
n −π) 8 π 3π (3)x(n)=Asin( n+ ) 4 3
(1)对照正弦型序列的一般公式 x(n)=Acos( ωn + ϕ ),得出 ω =
k = −∞
∑ u (k ) a
∞
n−k
u (n − k ) =
k = −∞
∑a
∞
n−k
=
1 − a n +1 u(n) 1− a
2.3 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)= λ
n
u(n)*u(n)
解:(1)
y(n)=
k = −∞ ∞
∑ u(k )u(n − k )
π 2π (n-k)+ ]| 3 6 π 2π =|x(n)|| sin[ (n-k)+ ]| 3 6
≤M|sin[
π 2π (n- k)+ ]|≤M 3 6
故系统是稳定系统。 因 y(n)只取决于现在和过去的输入 x(n),不取决于未来的输入,故该系统是因果系统。 (3)设 y1(n)=
k = −∞
−n
u(-n),0<a<1 用直接计算线性卷积的方法,求
2.6 试证明线性卷积满足交换率、结合率和加法分配率。
证明
(1)交换律 X(n) * y(n) =
k = −∞
∑ x(k ) y (n − k )
∞
令 k=n-t,所以 t=n-k,又- ∞ <k< ∞ ,所以- ∞ <t< ∞ ,因此线性卷积公式变成
数字信号处理试卷及答案_程培青(第三版)

数字信号处理 试卷一、填空题:(本大题共10小题,每空2分,共28分)请在每个空格中填上正确答案。
错填、不填均无分。
1、一线性时不变系统,输入为 x (n )时,输出为y (n ) ;则输入为2x (n )时,输出为 2y(n);输入为x (n-3)时,输出为 y(n-3)。
2、从奈奎斯特采样定理得出,要使实信号采样后能够不失真还原,采样频率f 与信号最高频率fs 关系为: f ≥2fs 。
3、已知一个长度为N 的序列x(n),它的傅立叶变换为X (e jw ),它的N 点离散傅立叶变换X (K )是关于X (e jw )的 N 点等间隔 抽样 。
4、有限长序列x(n)的8点DFT 为X (K ),则X (K )= ()70()nkNn X k x n W==∑ 。
5、无限长单位冲激响应(IIR )滤波器的结构上有反馈,因此是_递归型_的。
6、若正弦序列x(n)=sin(30n π/120)是周期的,则周期是N= 8 。
7、已知因果序列x(n)的Z 变换为X(z)=eZ -1,则x(0)=_ 0_ _。
8、无限长单位冲激响应滤波器的基本结构有直接Ⅰ型,直接Ⅱ型,级联型,并联型四种。
9、DFT 与DFS 有密切关系,因为有限长序列可以看成周期序列的__主值序列 ,,而周期序列可以看成有限长序列的__周期序列__。
10、对长度为N 的序列x(n)圆周移位m 位得到的序列用x m (n)表示,其数学表达式为x m (n)= x((n+m))N R N (n) _。
二、选择填空题(本大题共6小题,每题2分,共12分)1、δ(n)的z 变换是 A 。
A. 1B.δ(w)C. 2πδ(w)D. 2π2、序列x 1(n)的长度为4,序列x 2(n)的长度为3,则它们线性卷积的长度是 B , 5点圆周卷积的长度是 。
A. 5, 5B. 6, 5C. 6, 6D. 7, 53、在N=32的时间抽取法FFT 运算流图中,从x(n)到X(k)需 B 级蝶形运算 过程。
数字信号处理程培青第三版试题及答案

数字信号处理程培青第三版试题及答案It was last revised on January 2, 2021数字信号处理 试卷一、填空题:(本大题共10小题,每空2分,共28分)2、从奈奎斯特采样定理得出,要使实信号采样后能够不失真还原,采样频率f 与信号最高频率fs 关系为:f ≥2fs 。
3、已知一个长度为N 的序列x(n),它的傅立叶变换为X (ejw ),它的N 点离散傅立叶变换X (K )是关于X (ejw )的N 点等间隔抽样。
4、有限长序列x(n)的8点DFT 为X (K ),则X (K )=()70()nk N n X k x n W ==∑ 。
5、无限长单位冲激响应(IIR )滤波器的结构上有反馈,因此是递归型的。
6、若正弦序列x(n)=sin(30n π/120)是周期的,则周期是N= 8 。
7、已知因果序列x(n)的Z 变换为X(z)=eZ-1,则x(0)= 0 。
8、无限长单位冲激响应滤波器的基本结构有直接Ⅰ型,直接Ⅱ型,级联型 和 并联型 四种。
9、DFT 与DFS 有密切关系,因为有限长序列可以看成周期序列的主值序列,而周期序列可以看成有限长序列的 周期序列 。
10、对长度为N 的序列x(n)圆周移位m 位得到的序列用xm(n)表示,其数学表达式为xm(n)=x((n+m))N R N (n)。
二、选择填空题(本大题共6小题,每题2分,共12分) 1、δ(n)的z 变换是 ( A ) 。
A. 1B.δ(w)C. 2πδ(w)D. 2π2、序列x1(n)的长度为4,序列x2(n)的长度为3,则它们线性卷积的长度是 ( B ) , 5点圆周卷积的长度是 。
A. 5, 5B. 6, 5C. 6, 6D. 7, 53、在N=32的时间抽取法FFT 运算流图中,从x(n)到X(k)需 ( B ) 级蝶形运算 过程。
A. 4B. 5C. 6D. 34、下面描述中最适合离散傅立叶变换DFT 的是(B )A .时域为离散序列,频域也为离散序列B .时域为离散有限长序列,频域也为离散有限长序列C .时域为离散无限长序列,频域为连续周期信号D .时域为离散周期序列,频域也为离散周期序列5、设系统的单位抽样响应为h(n),则系统因果的充要条件为(C )A .当n>0时,h(n)=0B .当n>0时,h(n)≠0C .当n<0时,h(n)=0D .当n<0时,h(n)≠06、已知序列Z 变换的收敛域为|z |<1,则该序列为( C )。
数字信号处理(第三版)-课后习题答案全-(原题+答案+图)
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
《数字信号处理》第三版课后习题答案

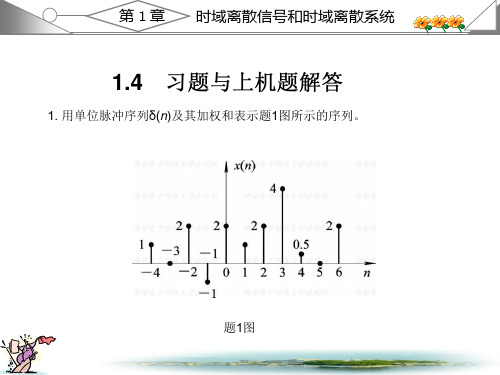
《数字信号处理》第三版课后习题答案数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-??=≤≤其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列;(3)令1()2(2)x n x n =-,试画出1()x n 波形;(4)令2()2(2)x n x n =+,试画出2()x n 波形;(5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理(第三版)_课后习题答案全_(原题+答案+图)

第 1 章
(2) 令输入为
x(n-n0) 输出为
时域离散信号和时域离散系统
y′(n)=2x(n-n0)+3
y(n-n0)=2x(n-n0)+3=y′(n)
故该系统是非时变的。 由于 T[ax1(n)+bx2(n)]=2ax1(n)+2bx2(n)+3 T[ax1(n)]=2ax1(n)+3 T[bx2(n)]=2bx2(n)+3 T[ax1(n)+bx2(n)]≠aT[x1(n)]+bT[x2(n)] 故该系统是非线性系统。
m
第 1 章
时域离散信号和时域离散系统
题7图
第 1 章
时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章
解法(二)
时域离散信号和时域离散系统
采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
第 1 章
(4) y(n)=x(-n)
令输入为 x(n-n0) 输出为 y′(n)=x(-n+n0)
时域离散信号和时域离散系统
y(n-n0)=x(-n+n0)=y′(n) 因此系统是线性系统。 由于
T[ax1(n)+bx2(n)]=ax1(-n)+bx2(-n)
=aT[x1(n)]+bT[x2(n)] 因此系统是非时变系统。
n n0 k n n0
|x(k)|≤|2n0+1|M, 因
此系统是稳定的; 假设n0>0, 系统是非因果的, 因为输出
还和x(n)的将来值有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理 试卷
一、填空题:(本大题共10小题,每空2分,共28分)
2、从奈奎斯特采样定理得出,要使实信号采样后能够不失真还原,采样频率f 与信号最高频率fs 关系为:f ≥2fs 。
3、已知一个长度为N 的序列x(n),它的傅立叶变换为X (ejw ),它的N 点离散傅立叶变换X (K )是关于X (ejw )的N 点等间隔抽样。
4、有限长序列x(n)的8点DFT 为X (K ),则X (K )=()7
0()nk N n X k x n W ==∑ 。
5、无限长单位冲激响应(IIR )滤波器的结构上有反馈,因此是递归型的。
6、若正弦序列x(n)=sin(30n π/120)是周期的,则周期是N= 8 。
7、已知因果序列x(n)的Z 变换为X(z)=eZ-1,则x(0)= 0 。
8、无限长单位冲激响应滤波器的基本结构有直接Ⅰ型,直接Ⅱ型,级联型 和 并联型 四种。
9、DFT 与DFS 有密切关系,因为有限长序列可以看成周期序列的主值序列,而周期序列可以看成有限长序列的 周期序列 。
10、对长度为N 的序列x(n)圆周移位m 位得到的序列用xm(n)表示,其数学表达式为xm(n)=x((n+m))N R N (n)。
二、选择填空题(本大题共6小题,每题2分,共12分) 1、δ(n)的z 变换是 ( A ) 。
A. 1
B.δ(w)
C. 2πδ(w)
D. 2π
2、序列x1(n)的长度为4,序列x2(n)的长度为3,则它们线性卷积的长度是 ( B ) , 5点圆周卷积的长度是 。
A. 5, 5
B. 6, 5
C. 6, 6
D. 7, 5
3、在N=32的时间抽取法FFT 运算流图中,从x(n)到X(k)需 ( B ) 级蝶形运算 过程。
A. 4
B. 5
C. 6
D. 3
4、下面描述中最适合离散傅立叶变换DFT 的是(???B?? ) A .时域为离散序列,频域也为离散序列
B .时域为离散有限长序列,频域也为离散有限长序列
C .时域为离散无限长序列,频域为连续周期信号
D .时域为离散周期序列,频域也为离散周期序列
5、设系统的单位抽样响应为h(n),则系统因果的充要条件为(???C?? ) A .当n>0时,h(n)=0 B .当n>0时,h(n)≠0 C .当n<0时,h(n)=0 D .当n<0时,h(n)≠0
6、已知序列Z 变换的收敛域为|z |<1,则该序列为( C )。
A.有限长序列 B.右边序列 C.左边序列 D.双边序列
三、计算题(本大题共3小题,每题10分,共30分)
1、如果一台计算机的速度为平均每次复乘5µS ,每次复加0.5µS ,用它来计算512点的DFT[x(n)],问直接计算需要多少时间,用FFT 运算需要多少时间。
答: (1)、 直接计算
复乘所需时间 62621510510512 1.31072T N s --=⨯⨯=⨯⨯=
复加所需时间()6610.51010.5105125110.130816T N N s --=⨯⨯⨯-=⨯⨯⨯= 所以12 1.441536T T T s =+= (2)、用FFT 计算 复乘所需时间 66122512510log 510log 5120.0115222
N T N s --=⨯⨯
=⨯⨯= 复加所需时间662220.510log 0.510512log 5120.002304T N N s --=⨯⨯=⨯⨯= 所以120.013824T T T s =+=
2、用长除法、留数定理法、部分分式法分别求以下X(Z)的Z 反变换:
(1)
1
21
112(),12
14
Z X z z Z ---=>
-;
(2)
1
1121(),
14
14
Z X z z Z ---=<
-; (3)
1(),1Z a
X z z aZ
a -=
>
-
解:a. 长除法 1()()2n
x n u n ⎛⎫
=-⋅ ⎪⎝⎭
b .留数法 ()()1()8714n
x n n u n δ⎛⎫
=+-- ⎪⎝⎭
c .部分分式法 ()()111()1n
x n n a u n a a a δ⎛
⎫⎛⎫=-+-- ⎪⎪⎝
⎭⎝⎭
3、设序列x(n)={4,3,2,1} , 另一序列h(n) ={1,1,1,1},n=0,1,2,3
(1)试求线性卷积 y(n)=x(n)*h(n) (2)试求6点圆周卷积。
(3)试求8点圆周卷积。
解:1.y(n)=x(n)*h(n)={4,7,9,10,6,3,1}
2.6点圆周卷积={5,7,9,10,6,3} 3.8点圆周卷积={4,7,9,10,6,3,1,0}
四、证明、画图题(本大题共3小题,每题10分,共30分) 1、设系统差分方程 y(n)=ay(n-1)+x(n)
其中x(n)为输入,y(n)为输出。
当边界条件选为y(-1)=0时,判断系统是否线性的、移不变的。
解:① 令1111()(),()(1)()x n n y n ay n x n δ==-+
则
111111111(0)(1)(0)1
(1)(0)(1)()(1)()n
y ay x y ay x a y n ay n x n a =-+==+==-+
=
同样可求得 1111(1)(2)0,()0n y y y n ≤-=-===即
所以 ()1()n y n a u n =
②令2222()(1),()(1)()x n n y n ay n x n δ=-=-+
则
2222221
222(0)(1)(0)0
(1)(0)(1)1()(1)()n y ay x y ay x y n ay n x n a -=-+==+==-+
=
同样可求得 2221(1)(2)0,()0n y y y n ≤-=-===即
所以 ()12()1n y n a u n -=-
因为1()x n 与2()x n 为移1位关系,而且1()y n 与2()y n 也是移1位关系,所以在y(-1)=0条件下,系统是移不变系统。
③令312333()()()()(1),()(1)()x n x n x n n n y n ay n x n δδ=+=+-=-+ n<0时,3331(2)(3)0,()0n y y y n ≤--=-=
==即
n>=0时,
3333331
333(0)(1)(0)1
(1)(0)(1)1()(1)()n n y ay x y ay x a y n ay n x n a a -=-+==+=+=-+=
+
综上,可得()()1312()()(1)n n y n a u n a u n y n y n -=+-=+
所以系统是线性系统。
2、用级联型结构实现以下系统函数,试问一共能构成几种级联型网络,并画出结构图。
解:
3、请画出8点的按频率抽取的(DIF )基-2 FFT 流图,要求输入自然数顺序,输出倒位序。
解:。
