数字信号处理(姚天任江太辉第三版)课后习题答案
数字信号处理(第三版)_课后习题答案全_(原题+答案+图)
第 1 章
时域离散信号和时域离散系统
6. 给定下述系统的差分方程, 试判定系统是否是因果稳定系统, 并说明
理由。
1 N 1 N k 0 (2) y(n)=x(n)+x(n+1)
第 1 章
(2) 令输入为
x(n-n0) 输出为
Байду номын сангаас
时域离散信号和时域离散系统
y′(n)=2x(n-n0)+3
y(n-n0)=2x(n-n0)+3=y′(n)
故该系统是非时变的。 由于 T[ax1(n)+bx2(n)]=2ax1(n)+2bx2(n)+3 T[ax1(n)]=2ax1(n)+3 T[bx2(n)]=2bx2(n)+3 T[ax1(n)+bx2(n)]≠aT[x1(n)]+bT[x2(n)] 故该系统是非线性系统。
m
第 1 章
时域离散信号和时域离散系统
题7图
第 1 章
时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章
解法(二)
时域离散信号和时域离散系统
采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
n n0 k n n0
|x(k)|≤|2n0+1|M, 因
此系统是稳定的; 假设n0>0, 系统是非因果的, 因为输出
数字信处理课后习题答案
数字信号处理(姚天任江太辉)第三版课后习题答案第二章2.1判断下列序列是否是周期序列。
若是,请确定它的最小周期(1)x(n)二Acos( 5 n86)(2)x(n )= e j(- 8 )(3) x(n )=Asi n(3 n4 3)解(1)对照正弦型序列的-般公式x(n)二 Acos( n ),得出5。
因此82 16是有理数,所以是周期序列。
5 最小周期等于N=^k 16(k取5)。
5(2)对照复指数序列的般公式x(n)二exp[ j ]n,得出1。
因此2168是无理数,所以不是周期序列。
(3)对照正弦型序列的般公式x(n)二 Acos( 3n ),又x(n)二Asin( n ) =Acos(— .门—)=Acos( —n 丄),得出3。
因此2 8是有理数,所以2 434 6 4 3是周期序列。
最小周期等于N=-k38(k 取3)2.2在图2.2中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解利用线性卷积公式y(n )= x(k)h( n k)k按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值(a) y(0)=x(0)h(0)=1y(l)=x(0)h(1)+x(1)h(0)=3y(n)=x(O)h( n)+x(1)h( n-1)+x(2)h( n-2)=4,n (b) x(n )=2 (n)- (n-1)h(n)=- (n)+2 (n-1)+ (n-2)y(n)=-2(n )+5(n-1)= (n-3)(c) y(n )=u(k)kn ka u(n k):n k 1 a n 1/ \=a = . a u(n)k i a2.3计算线性线性卷积(1) y(n )=u( n)*u( n)(2) y(n)= n u(n)*u(n)解:(1) y(n)二u(k)u(n k)ku(k)u(n k)=(n+1),n >0 k 0 即y(n)=(n+1)u(n)(2) y(n )=kku(k)u( n k)2.4图P2.4所示的是单位取样响应分别为 九(n)和h 2(n)的两个线性非移变系统的级联,已知 x(n)=u(n), h ^n)二(n)-(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出 y(n).解(n)=x( n)*h Jn)u(k)[(n-k)- (n-k-4)]k=u( n)-u( n-4)y(n)= (n)*h 2 (n)a k u(k)[u( n-k)-u( n-k-4)]k算线性卷积的方法,求系统的单位阶跃响应即 y(n)二ku(k)u(n1n 1——,n >n 1—u(n)2.5已知一个线性非移变系统的单位取样响应为h(n)二a n u(-n),0<a<1 用直接计2.6 试证明线性卷积满足交换率、结合率和加法分配率。
数字信号处理第三版(姚天任、江太辉) 答案 第三章

3.1 图 P3.1 所示的序列 x(n) 是周期为 4 的周期性序列。请确定其傅里叶级数的系数 X (k) 。
∑ ∑ ∑ 解: X (k)
=
N −1
x(n)WNnk
=
N −1
x(−n)WNnk
=
−( N −1)
x(n)WN−nk
=
X (−k)
解:图 P3.5_1 所示的是计算这两个序列的周期卷积 x3 (n) 的过程,可以看出,x3 (n) 是 x1 (n) 延时 1 的结果, 即 x3(n) = x1(n −1) 。
3.6 计算下列序列的N点DFT:
(1) x(n) = δ (n)
(2) x(n) = δ [(n − n0 )]N * RN (n), 0 < n0 < N
总计需要时间: (105 + 21)s = 126s
用 FFT 计算 DFT:
复数乘法:
N 2
log2
N
=
5120次, 5120 ×100μ s
≈
0.512s
复数加法: N log2 N = 10240次,10240× 20μs ≈ 0.2048s
总计需要时间: (0.512 + 0.2048)s = 0.7168s
(2) x2 (n) = x ⎡⎣(2 − n)⎤⎦4 R4 (n)
解: x1(n) 和 x2 (n) 的图形如图 P3.7_1 所示:
3.8 图 P3.8 表示一个 4 点序列 x(n) 。 (1)绘出 x(n) 与 x(n) 的线性卷积结果的图形。 (2)绘出 x(n) 与 x(n) 的 4 点循环卷积结果的图形。 (3)绘出 x(n) 与 x(n) 的 8 点循环卷积结果的图形,并将结果与(1)比较,说明线性卷积与循环卷
数字信号处理第三版(姚天任、江太辉) 答案 第三章

第三章离散傅里叶变换及其快速算法习题答案参考3.1 图P3.1所示的序列(xn 是周期为4的周期性序列。
请确定其傅里叶级数的系数(X k。
解:(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.2 (1设(xn 为实周期序列,证明(x n 的傅里叶级数(X k 是共轭对称的,即*((X k X k =− 。
(2证明当(xn 为实偶函数时,(X k 也是实偶函数。
证明:(1 111**((([(]((N nk N n N N nk nkNNn n Xk x n W Xk x n W xn W X−−=−−−==−=−===∑∑∑ k(2因(xn 为实函数,故由(1知有 *((Xk X k =− 或*((X k X k −= 又因(xn 为偶函数,即((x n x n =− ,所以有(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.3 图P3.3所示的是一个实数周期信号(xn 。
利用DFS 的特性及3.2题的结果,不直接计算其傅里叶级数的系数(Xk ,确定以下式子是否正确。
(1,对于所有的k; ((10Xk X k =+ (2((Xk X k =− ,对于所有的k; (3; (00X=(425(jkX k eπ,对所有的k是实函数。
解:(1正确。
因为(x n 一个周期为N =10的周期序列,故(X k 也是一个周期为N=10的周期序列。
(2不正确。
因为(xn 一个实数周期序列,由例3.2中的(1知,(X k 是共轭对称的,即应有*((Xk X = k −,这里(X k 不一定是实数序列。
(3正确。
因为(xn (0n ==在一个周期内正取样值的个数与负取样值的个数相等,所以有 10(0N n Xx −=∑ (4不正确。
数字信号处理课后习题答案完整版

数字信号处理课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字信号处理(姚天任江太辉)第三版课后习题答案第二章判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n )(2)x(n)=)8(π-ne j(3)x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =在图中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λn u(n)*u(n)解:(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)图所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联,已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥3已知一个线性非移变系统的单位取样响应为h(n)=a n -u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。
数字信号处理第三版(姚天任、江太辉) 答案 第五章-unprotected

2
N −1 N −1
E[x(i)x( j)]
N n=0
N2 i=0 j=0
N2 i=0 j=0
∑ ∑∑ =
1 N
N −1
E[x2 (n)] −
n=0
1 N2
N −1 N −1
E[x(i)x( j)]
i=0 j=0
∑ ∑ ∑∑ =
1
N −1
E[x2 (n)] −
1
N −1
N −1 N −1
∫ = 1
q
0 −q
xdx
=
1 2q
x2
|0−q =
−
q 2
∞
∫ mx2 = E[x2 ] = −∞ xpx2 (x)dx
∫ = 1
q
q/2 −q/2
xdx
=
1 2q
x2
|−q
/2 q/
2
=
0
∞
∫ mx3 = E[x3 ] = −∞ xpx3 (x)dx
∫ = 1
2π
2π 0
xdx =
1 4π
x2
|02π = π
∞ −∞
(x
−
mx2
)2
px2
( x)dx
∫ = 1 q
q/2 −q / 2
x2dx
=
1 3q
x3
|q / 2
−q/
2
=
q2 12
∫ σ 2 x3
=
E[( x3
− mx3 )2 ] =
∞ −∞
(x
−
mx3
)2
px3
( x)dx
∫ = 1
2π
2π 0
《数字信号处理》第三版课后习题答案

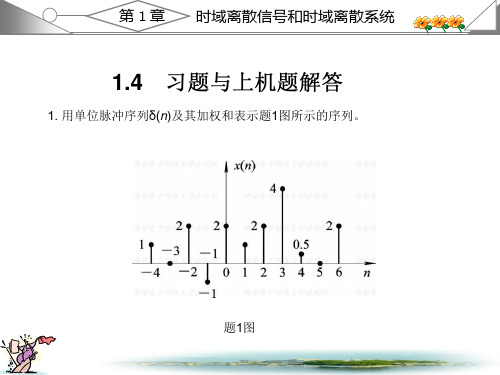
数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理(姚天任江太辉第三版)课后习题答案

第二章2.1 判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n ) (2)x(n)=)8(π-ne j(3)x(n)=Asin(343ππ+n ) 解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =2.2在图2.2中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
(a)1111(b)(c)111110 0-1-1-1-1-1-1-1-1222222 33333444………nnn nnnx(n)x(n)x(n)h(n)h(n)h(n)21u(n)u(n)u(n)a n ===22解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n)2.3 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λnu(n)*u(n)解:(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0 即y(n)=λλ--+111n u(n)2.4 图P2.4所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联,已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a nu(n),|a|<1,求系统的输出y(n).解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥32.5 已知一个线性非移变系统的单位取样响应为h(n)=an-u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章2.1 判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n ) (2)x(n)=)8(π-ne j(3)x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =2.2在图2.2中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
(a)1111(b)(c)111110 0-1-1-1-1-1-1-1-1222222 33333444………nnn nnnx(n)x(n)x(n)h(n)h(n)h(n)21u(n)u(n)u(n)a n ===22解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n)2.3 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λnu(n)*u(n)解:(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)2.4 图P2.4所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联,已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n).解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥32.5 已知一个线性非移变系统的单位取样响应为h(n)=an-u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。
2.6 试证明线性卷积满足交换率、结合率和加法分配率。
证明(1)交换律X(n) * y(n) = ∑∞-∞=-kknykx)()(令k=n-t,所以t=n-k,又-∞<k<∞,所以-∞<t<∞,因此线性卷积公式变成` x(n) * y(n) =∑∞-∞=---ttnnytnx)]([)(=∑∞-∞=-ttytnx)()(=y(n) * x(n)交换律得证.(2)结合律[x(n) * y(n)] * z(n)=[∑∞-∞=-kknykx)()(] * z(n)=∑∞-∞=t [∑∞-∞=-kktykx)()(]z(n-t)=∑∞-∞=k x(k) ∑∞-∞=ty(t-k)z(n-t)=∑∞-∞=k x(k) ∑my(m)z(n-k-m)=∑∞-∞=kx(k)[y(n-k) * z(n-k)]=x(n) * [y(n) * z(n)]结合律得证.(3)加法分配律x(n) * [y(n) + z(n)]= ∑∞-∞=kx(k)[y(n - k) +z(n - k)]=∑∞-∞=k x(k)y(n-k)+ ∑∞-∞=kx(k)z(n - k)=x(n) * y(n) + x(n) *z(n)加法分配律得证.2.7 判断下列系统是否为线性系统、非线性系统、稳定系统、因果系统。
并加以证明(1)y(n)= 2x(n)+3 (2)y(n)= x(n)sin[32πn+6π] (3)y(n)=∑∞-∞=k k x )( (4)y(n)= ∑=nn k k x 0)((5)y(n)= x(n)g(n)解 (1)设y 1(n)=2x 1(n)+3,y 2(n)=2x 2(n)+3,由于 y(n)=2[x 1(n)+x 2(n)]+3 ≠y 1(n)+ y 2(n) =2[x 1(n)+x 2(n)]+6故系统不是线性系统。
由于y(n-k)=2x(n-k)+3,T[x(n-k)]=2x(n-k)+3,因而y(n-k) = T[x(n-k)]故该系统是非移变系统。
故系统是稳定系统。
因y(n)只取决于现在和过去的输入x(n),不取决于未来的输入,故该系统是因果系统。
(3)设 y 1(n)=∑-∞=n k k x )(1,y 2(n)=∑-∞=nk k x )(2,由于y(n)=T[ax 1(n)+ bx 2(n)]=∑-∞=+nk k k )](bx )(ax [21=a∑-∞=nk k x )(1+ b ∑-∞=nk k x )(2=ay 1(n)+by 2(n)故该系统是线性系统。
因 y(n-k)=∑--∞=t n k k x )(= ∑-∞=-nm t m x )(=T[x(n-t)]所以该系统是非移变系统。
设 x(n)=M<∞ y(n)=∑-∞=nk M =∞,所以该系统是不稳定系统。
因y(n)只取决于现在和过去的输入x(n),不取决于未来的输入,故该系统是因果系统。
(4)设 y 1(n)=∑=nn k k x 01)( ,y 2(n)=∑=nn k k x 02)(,由于y(n)=T[ax 1(n)+ bx 2(n)]=∑=+nn k k k 021)](bx )(ax [= a∑=nn k k x 01)(+b ∑=nn k k x 02)(=ay 1(n)+by 2(n)故该系统是线性系统。
因 y(n-k)=∑-=t n n k k x 0)(= ∑+=-ntn m t m x 0)(≠T[x(n-t)]=∑=-nn k t m x 0)(所以该系统是移变系统。
设x(n)=M,则lim n →∞y(n)= lim n →∞(n-n 0)M=∞,所以该系统不是稳定系统。
显而易见,若n ≥n 0。
则该系统是因果系统;若n<n 0。
则该因果系统是非因果系统。
(5)设y 1(n)=x 1(n)g(n),y 2(n)=x 2(n)g(n),由于y(n)=T[ax 1(n)+bx 2(n)]=(ax 1(n)+bx 2(n))g(n) =ax 1(n)g(n)+b 2(n)=ay 1(n)+by 2(n)故系统是线性系统。
因y(n-k)=x(n-k),而T[x(n-k)]=x(n-k)g(n)≠y(n-k) 所以系统是移变系统。
设|x(n)|≤M<∞,则有|y(n)|=|x(n)g(n)|=M|g(n)| 所以当g(n)有限时该系统是稳定系统。
因y(n)只取决于现在和过去的输入x(n),不取决于本来的输入,故该系统是因果系统。
2.8 讨论下列各线性非移变系统的因果性和稳定性 (1)h(n)=2nu(-n) (4) h(n)=(12)nu(n) (2) h(n)=-a n u(-n-1) (5) h(n)=1nu(n) (3) h(n)=δ(n+n 0), n 0≥0 (6) h(n)= 2nR n u(n)解 (1)因为在n<0时,h(n)= 2n≠0,故该系统不是因果系统。
因为S=n ∞=-∞∑|h(n)|=n ∞=∑|2n |=1<∞,故该系统是稳定系统。
(2) 因为在n<O 时,h(n) ≠0,故该系统不是因果系统。
因为S=n ∞=-∞∑|h(n)|=1n -=-∞∑| a n|=n ∞=∞∑an-,故该系统只有在|a|>1时才是稳定系统。
(3) 因为在n<O 时,h(n) ≠0,故该系统不是因果系统。
因为S=n ∞=-∞∑|h(n)|=n ∞=-∞∑|δ(n+n 0)|=1<∞,故该系统是稳定系统。
(4) 因为在n<O 时,h(n)=0,故该系统是因果系统 。
因为S=n ∞=-∞∑|h(n)|=n ∞=∑|(12)n|<∞,故该系统是稳定系统。
(5) 因为在n<O 时,h(n)=1nu(n)=0,故该系统是因果系统 。
因为S=n ∞=-∞∑|h(n)|=n ∞=-∞∑|1n u(n)|= 0n ∞=∑1n =∞,故该系统不是稳定系统。
(6) 因为在n<O 时,h(n)=0,故该系统是因果系统 。
因为S=n ∞=-∞∑|h(n)|=1N n -=∑|2n |=2N-1<∞,故该系统是稳定系统。
2.9 已知y(n)-2cosβy(n-1)+y(n-2)=0,且y(0)=0,y(1)=1,求证y(n)=sin() sinnββ证明题给齐次差分方程的特征方程为α2-2cosβ·α+1=0由特征方程求得特征根α1=cosβ+jsinβ=e jβ,α2=cosβ-jsinβ= e jβ-齐次差分方程的通解为y(n)=c1α1n+c2α2n=c1e j nβ+c2e j nβ-代入初始条件得y(0)=c1+c2=0y(1)= c1e j nβ+c2e j nβ-=1由上两式得到c 1=1j n j ne eββ--=12sinβ,c2=- c1=-12sinβ将c1和c2代入通解公式,最后得到y(n) =c1e j nβ+c2e j nβ-=12sinβ( e j nβ+ e j nβ-)=sin()sinnββ2.10 已知y(n)+2αy(n-1)+β(n-2)=0,且y(0)=0,y(1)=3,y(2)=6,y(3)=36,求y(n) 解首先由初始条件求出方程中得系数a和b由(2)2(1)(0)660(3)2(2)(1)361230 y ay by ay ay by a b ++=+=⎧⎨++=++=⎩可求出a=-1,b=-8 于是原方程为y(n)-2y(n-1)-iy(n-2)=0由特征方程α2-2α-8=0求得特征根α1=4 ,α2=-2齐次差分方程得通解为y(n)=c1α1n+c2α2n= c14n+c2(-2n)代入初始条件得y(n)= c1α1+c2α2= 4α1+2α2=3由上二式得到c 1=12,c 2=-12将c 1和c 2代入通解公式,最后得到y(n)=c 1α1n +c 2α2n =12[4n-(-2) n ]2.11 用特征根法和递推法求解下列差分方程: y(n)-y(n-1)-y(n-2)=0,且y(0)=1,y(1)=1解 由特征方程α2-α-1=0求得特征根α1=12+,α2=12通解为y(n)=c 1α1n +c 2α2n =c 1(12+)n +c 2(12-)n代入初始条件得121211c c c c +=⎧⎪⎨+=⎪⎩ 求出c 1c 2最后得到通解y(n)= c 1()n + c 2)n)1n +)1n +]2.12 一系统的框图如图P2.12所示,试求该系统的单位取样响应h(n)和单位阶跃响应解 由图可知ßy(n)=x(n)+ βy(n-1)为求单位取样响应,令x(n)=δ(n),于是有h(n)= δ(n)+ βh(n-1)由此得到h(n)=()1n Dδβ-=βnu(n)阶跃响应为y(n)=h(n)*u(n)=nk =∑βk y(k)u(n-k)=111n ββ+--u(n)2.13 设序列x(n)的傅立叶变换为X(ejw),求下列各序列的傅立叶变换解 (1)F[ax 1(n)+bx 2(n)]=aX 1(e jw)+bX 2(ejw)(2)F[x(n-k)]=e jwk-X(ejw) (3)F[e0jw nx(n)]=X[e0()j w w -](4)F[x(-n)]=X(ejw-) (5)F[x *(n)]=X *(ejw-) (6)F[x *(-n)]= X *(e jw)(7)(8)jIm[x(n)]=12[X(e jw )-X *(e jw -)] (9)12πX(e j θ)*X(e jw ) (10)j ()jw dx e dw2.14 设一个因果的线性非移变系统由下列差分方程描述y(n)-12y(n-1)=x(n)+ 12x(n-1) (1) 求该系统的单位取样响应h(n) (2) 用(1)得到的结果求输入为x(n)=e jwn时系统的响应(3) 求系统的频率响应 (4) 求系统对输入x(n)=cos(2πn+4π)的响应解 (1)令X (n )=δ(n),得到h(n)-h(n-1)/2=δ(n)+ δ(n-1)/2由于是因果的线性非移变系统,故由上式得出 h(n)=h(n-1)/2+δ(n)+ δ(n-1)/2 ,n ≥0 递推计算出h(-1)=0h(0)=h(-1)/2+δ(0)=1 h(1)=h(0)/2+1/2=1h(2)=h(1)/2=1/2 h(3)=21h(2)=(21)2 h(4)= 21h(2)=(21)3 . ..h(n)=δ(n)+ (21)n-1u(n-1) 或 h(n)= (21)n [u(n)-u(n-1)]也可将差分方程用单位延迟算子表示成(1-D)h(n)=(1+D)δ(n)由此得到h(n)=[(1+21D)/(1-21D)]δ(n) =[1+D+21D 2+ (21)2 D 3+…+(21)k-1 D 3+…] δ(n) =δ(n)+ δ(n-1)+ 21δ(n-2)+21δ(n-3)+... +(21)k-1δ(n-1)+… =δ(n)+ (21)n u(n-1)2)将jwn e n X =)(代入)(*)()(n h n x n y =得到[]()jwjwjwnjwn jw jwnn n jwn jwn e e e e e e D D D D e D D n D De n y ------+=-+=⎥⎥⎦⎤⎢⎢⎣⎡••••+⎪⎭⎫⎝⎛+••••+⎪⎭⎫ ⎝⎛+++=-+=-+=2112112112121211211211)(211211*)(11322δ (3)由(2)得出 ()jw jwjw e e e H ---+=211211 (4)由(3)可知121121121212=-+=⎪⎪⎭⎫ ⎝⎛--wj w j wj e e e H ⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--21arctan 2211arctan 211arctan arg 222ππj j w j e e e H 故:()()()[]⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=⎥⎦⎤⎢⎣⎡++=21arctan 242cos arg 42cos ππππn e H n e H n y jw jw2.15 某一因果线性非移变系统由下列差分方程描述y(n)-ay(n-1)=x(n)-bx(n-1)试确定能使系统成为全通系统的b 值(b ≠a ),所谓全通系统是指其频率响应的模为与频率ω无关的常数的系统。
