高中数学 第一章 立体几何初步 1.3.2 由三视图还原实物图练习 北师大版必修2
2020年高中数学第一章立体几何初步33.1简单组合体的三视图3.2由三视图还原成实物图课件北师大版必修

练一练 已知某物体的三视图如图所示,那么这个物体是 ()
A.长方体 B.圆柱 C.正方体 D.圆锥 答案:B
1.画简单组合体的三视图应注意哪些问题? 答:对于简单组合体的三视图,要先弄清由哪几个基本几何 体组合而成,并注意它们的组成方式,特别是交线位置.能看见 的轮廓线和棱用实线表示,看不见的用虚线表示.
解析:由三视图知,该几何体是一个正方体和一个正四棱锥 的组合体.
答案:正方体和正四棱锥的组合体
5.下面是某个圆锥的三视图,请根据主视图中所标尺寸,求 俯视图中圆的面积及圆锥母线长.
解:由主视图与俯视图长相等得底面圆直径为 20,从而面积 为 100π.由主视图与左视图高相等得圆锥高为 30,而底面圆半径 为 10,则母线长为 302+102=10 10,∴俯视图中圆面积为 100π, 圆锥母线长为 10 10.
【规律总结】 由三视图还原成几何体,通常先根据俯视图 判断几何体是旋转体还是多面体,再结合主视图与左视图确定具 体几何特征,最终确定出几何体.
它的形状.
下图所示是一个几何体的三视图,试画出
解:几何体如图:
画出如图所示几何体的三视图.
【错解】 三视图如图所示:
【错因分析】 画三视图应满足“长对正,高平齐,宽相等”, 错解中主视图与左视图高未相等,左视图与俯视图的宽也未画成 相等,左视图中被遮住的线未画成虚线.
一个长方体去掉一个小长方体,所得几何 体的主视图与左视图分别如图所示,则该几何体的俯视图为 ()
解析:从主视图观察可知去掉的是长方体的左上角,由左视 图观察可知去掉的是右上角,综合这两种情况可知 C 选项正确.
答案:C
下面是一几何体的三视图,想象该几何体的几何结 构特征,画出该几何体的形状.
高中数学 第一章立体几何初步 1.3 三视图练习 北师大版必修2-北师大版高一必修2数学试题
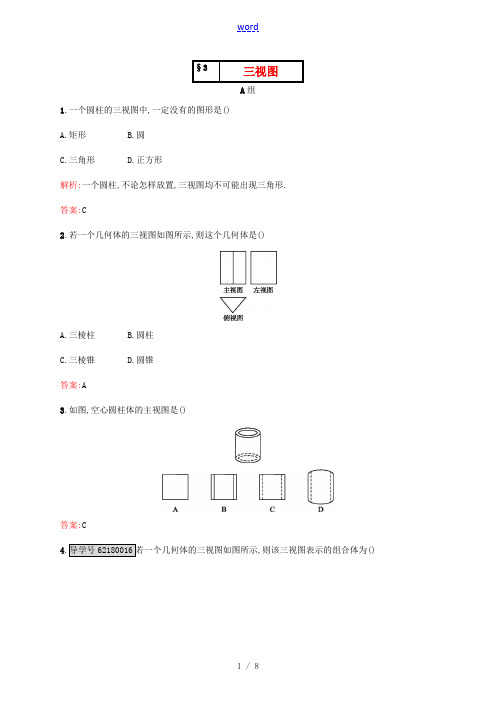
§3三视图A组1.一个圆柱的三视图中,一定没有的图形是()A.矩形B.圆C.三角形D.正方形解析:一个圆柱,不论怎样放置,三视图均不可能出现三角形.答案:C2.若一个几何体的三视图如图所示,则这个几何体是()A.三棱柱B.圆柱C.三棱锥D.圆锥答案:A3.如图,空心圆柱体的主视图是()答案:C4.导学号62180016若一个几何体的三视图如图所示,则该三视图表示的组合体为()A.圆柱与圆锥B.圆柱与三棱锥C.圆柱与四棱锥D.四棱柱与圆锥答案:C5.一个几何体的三视图如图所示,则该几何体的直观图可以是()解析:由俯视图易知,只有选项D符合题意.故选D.答案:D6.如图所示的立体图形,都是由相同的小正方体拼成的.(1)图①的主视图与图②的图相同;(2)图③的主视图与图④的主视图.(填“相同”或“不同”)答案:(1)俯视(2)不同7.如图所示是一个圆锥的三视图,则该圆锥的高为 cm.解析:由三视图知,圆锥的母线长为3 cm,底面圆的直径为3 cm,所以圆锥的轴截面是边长为3 cm 的等边三角形,所以圆锥的高为(cm).答案:8.已知某组合体的主视图与左视图相同(如图1所示,其中AB=AC,四边形BCDE为正方形),则该组合体的俯视图可以是如图2所示的.(把你认为正确的图的序号都填上)图1图2解析:由主视图与左视图可得该几何体可以是由正方体与底面边长相同的四棱锥组合而成的,则其俯视图为图①;可以是由正方体与底面直径与底面正方形边长相同的圆锥组合而成的,则其俯视图为图④;可以是由圆柱与底面相同的圆锥组合而成的,则其俯视图为图③;可以是由圆柱与底面正方形边长等于圆柱底面直径的四棱锥组合而成的,则其俯视图为图②.答案:①②③④9.一个几何体的三视图如图所示,请画出它的实物图.解:由三视图可知,该几何体由正方体和四棱柱组成,如图所示.10.导学号62180017如图所示是一个零件的实物图,画出这个几何体的三视图.解:该零件由一个长方体和一个半圆柱拼接而成,并挖去了一个小圆柱(形成圆孔).主视图反映了长方体的侧面和半圆的底面、小圆柱的底面,左视图反映了长方体的侧面、半圆柱的侧面、小圆柱的侧面,俯视图反映了长方体的底面、半圆柱的侧面和小圆柱的侧面投影后的形状.它的三视图如图所示.B组1.如图①②③分别为三个几何体的三视图,根据三视图可以判断这三个几何体依次分别为()图①图②图③A.三棱台、三棱柱、圆锥B.三棱台、三棱锥、圆锥C.三棱柱、正四棱锥、圆锥D.三棱柱、三棱台、圆锥解析:图①②③对应的原几何体分别是三棱柱、正四棱锥、圆锥,故选C.答案:C2.导学号62180018将正方体(如图1-(1)所示)截去两个三棱锥,得到图1-(2)中的几何体,则该几何体的左视图为(如图2所示)()图1图2解析:左侧被截去的三棱锥的底面三条边中,有两条与正方体的棱重合,另一条应为正方形自左上到右下的对角线,是可见的;右侧被截去的三棱锥的底面的三条边中,有两条与正方体的棱重合,另一条应为正方形自右上到左下(从左面看)的对角线,是不可见的.故选B.答案:B3.如图所示,已知正三棱柱ABC-A1B1C1的底面边长为2,高为3,则其左视图的面积为()A.6B.3C.3D.6解析:由三视图的画法可知,该几何体的左视图是一个矩形,其宽为2sin 60°=,长为3,故面积S=3.答案:C4.已知一几何体的主视图与左视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①②④⑤D.①②③④解析:可以结合实物想象,对于①,可认为该几何体的最下部为棱柱,上部为两个圆柱;对于②,可认为该几何体的上部为两个棱柱,下部为圆柱;对于③,可认为该几何体的上部为圆柱,下部为两个棱柱;对于④,可认为该几何体的上部是底面为等腰直角三角形的棱柱,中间为一圆柱,底部为四棱柱;对于⑤,由原几何体最下部的两个视图可知,其俯视图不可能是一个三角形.答案:D5.如图所示,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为.解析:根据三视图还原成实物图,即四棱锥P-ABCD,所以最长的一条棱的长为PB=2.答案:26.已知三棱锥的直观图及其俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一直角边长为2的直角三角形,则该三棱锥的主视图面积为.解析:三棱锥的主视图如图所示,故主视图的面积为×2×2=2.答案:27.下图是一个几何体的三视图,试画出其实物图.解:由几何体的三视图容易想到该几何体可以由正方体切割而得到,如图所示.俯视图8.导学号62180019一个棱长均为6的正三棱锥,其俯视图如图所示,求其主视图的面积和左视图的面积.解:作出正三棱锥的直观图如图所示,E为BD的中点,AO为三棱锥的高,由三棱锥的放置方式知,其主视图为三角形,底面边长为BD=6,其高等于AO,其左视图为三角形,底面边长等于CE(中线)的长,其高等于AO.在Rt△BCE中,BC=6,BE=3,得CE=3,CO=×CE=2.在Rt△ACO中,AC=6,CO=2,则AO==2,故主视图面积为×6×2=6,左视图的面积为×3×2=9.。
高中数学第一章立体几何初步1.3三视图课时作业含解析北师大版必修2

课时作业3 三视图|基础巩固|(25分钟,60分)一、选择题(每小题5分,共25分)1.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是()解析:本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C,都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.答案:D2.如图所示,甲、乙、丙是三个几何体的三视图,则甲、乙、丙对应的几何体分别为()①长方体;②圆锥;③三棱锥;④圆柱.A.④③②B.①③②C.①②③D.④②③解析:由于甲中的俯视图是圆,则甲对应的几何体是旋转体,又主视图和左视图均是矩形,所以该几何体是圆柱;易知乙对应的几何体是三棱锥;由丙中的俯视图,可知丙对应的几何体是旋转体,又主视图和左视图均是三角形,所以该几何体是圆锥.答案:A3.(2016·河北名师俱乐部3月模拟)某几何体的三视图如图所示,记A为此几何体所有棱的长度构成的集合,则()A.3∈A B.5∈AC.26∈A D.43∈A解析:由三视图可得,该几何体的直观图如图所示,其中底面是边长为4的正方形,AF⊥平面ABCD,AF∥DE,AF=2,DE=4,可求得BE的长为43,BF的长为25,EF的长为25,EC的长为42,故选D.答案:D4.如图为某组合体的三视图,则俯视图中的长和宽分别为()A.10,4 B.10,8C.8,4 D.10,5解析:根据三视图中的“主、俯视图长对正,主、左视图高平齐,俯、左视图宽相等”,可知俯视图的长和主视图的长相等,为2+6+2=10,俯视图的宽与左视图的宽相等,为1+2+1=4,所以选A.答案:A5.(2016·东北四市联考(二))如图,在正方体ABCD-A1B1C1D1中,P是线段CD的中点,则三棱锥P-A1B1A的侧视图为()解析:如图,画出原正方体的侧视图,显然对于三棱锥P-A1B1A,B(C)点均消失了,其余各点均在,从而其侧视图为D.答案:D二、填空题(每小题5分,共15分)6.桌上放着一个半球,如图所示,则在它的三视图及右面看到的图形中,有三个图相同,这个不同的图应该是________.解析:俯视图为圆,主视图与左视图均为半圆.答案:俯视图7.如图,已知正三棱柱ABC-A1B1C1的底面边长为2,高为3,则其左视图的面积为________.解析:由三视图的画法可知,该几何体的左视图是一个矩形,其底面边长为2sin60°=3,高为3,∴面积S=3 3.答案:3 38.(2016·山东安丘市高二上期末)一个几何体的三视图如图所示,其中正视图是边长为2的正三角形,俯视图是正方形,那么该几何体的侧视图的面积是________.解析:根据三视图可知该几何体是一个四棱锥,其底面是正方形,侧棱相等,所以这是一个正四棱锥.其侧视图与正视图是完全一样的正三角形.故其面积为34×22= 3.答案: 3三、解答题(每小题10分,共20分)9.试画出如图所示的正四棱台的三视图.解析:如图.10.根据图中的三视图想象物体原形,并画出物体的实物草图.解析:由俯视图并结合其他两个视图可以看出,这个物体是由上面一个正四棱台和下面一个正方体组合而成的,它的实物草图如图所示.|能力提升|(20分钟,40分)11.(2016·广东省台山市华侨中学高二上期末)定义:底面是正三角形,侧棱与底面垂直的三棱柱叫做正三棱柱.将正三棱柱截去一个角(如图1所示,M,N分别是AB,BC的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图为()解析:N的投影是C,M的投影是AC的中点.对照各图.选D.答案:D12.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.解析:三棱锥、四棱锥和圆锥的正视图都是三角形,当三棱柱的一个侧面平行于水平面,底面对着观测者时其正视图是三角形,四棱柱、圆柱无论怎样放置,其正视图都不可能是三角形.答案:①②③⑤13.如图所示,是一个长方体截去一个角所得多面体的直观图和它的主视图和左视图(单位:cm).请在正视图下面,按照画三视图的要求画出该多面体的俯视图.解析:依据三视图的绘图原则,可作出该几何体的俯视图如图.14.某建筑由相同的若干房间组成,该楼房的三视图如图所示,问:(1)该楼房有几层?从前往后最多要经过几个房间?(2)最高一层的房间在什么位置?请画出此楼房的大致形状.解析:(1)由主视图和左视图可以知道,该楼房有3层;由俯视图知道,从前往后最多要经过3个房间;(2)从主视图和左视图可以知道,最高一层的房间在左侧的最后一排的房间.楼房大致形状如图所示.。
高中数学第一章立体几何初步1.3三视图学案北师大版必修2

1.3 三视图[核心必知]1.三视图中的实虚线在绘制三视图时,分界线和可见轮廓线都用实线画出.不可见边界轮廓线,用虚线画出.2.绘制三视图时的注意事项(1)绘制三视图时,要注意:①主、俯视图长对正;②主、左视图高平齐;③俯、左视图宽相等,前后对应.(2)画简单组合体的三视图的注意事项:①首先,确定主视、俯视、左视的方向.同一物体放置的位置不同,所画的三视图可能不同.②其次,注意简单组合体是由哪几个基本几何体组成的,并注意它们的组成方式,特别是它们的交线位置.3.简单几何体的两种基本组成形式(1)将基本几何体拼接成组合体.(2)从基本几何体中切掉或挖掉部分构成组合体.[问题思考]一个简单几何体的三视图:主视图、左视图和俯视图完全一样,这个几何体是正方体或球,对吗?提示:不一定是正方体.球的主视图、左视图和俯视图是完全一样的圆,而正方体的三视图与观察角度有关,有时三种视图的形状不完全相同.讲一讲1.画出如下图所示的空间几何体的三视图(阴影面为主视面)(尺寸不作严格要求).[尝试解答] 三视图如图所示:1.在画三视图时,要想象几何体的后面、右面、下面各有一个屏幕,一组平行光线分别从前面、左面、上面垂直照射,我们画的是影子的轮廓,再验证几何体的轮廓线,看到的画实线,不能看到的画虚线.2.作三视图时,一般俯视图放在主视图的下面,长度和主视图一样,左视图放在主视图的右面,高度与主视图一样,宽度与俯视图一样.练一练1.画出如图所示的空间几何体的三视图(阴影面为主视面)(尺寸不作严格要求).解:三视图如图.讲一讲2.画出下列几何体的三视图(阴影面为主视面).[尝试解答] 三视图如图所示.对既有拼接,又有切、挖较复杂的组合体,关键是观察清楚轮廓线和分界线,并注意被遮挡部分的轮廓线用虚线表示,在画三视图时,很容易漏画轮廓线,或把虚线画成了实线,要注意检查.练一练2.画出如图所示的组合体的三视图.(阴影部分为主视面,尺寸不作严格要求)解:这个组合体的三视图如图:讲一讲3.如图所示的是一些立体图形的三视图,画出它的实物图.[尝试解答]根据三视图还原几何体实物,要仔细分析和认真观察三视图,进行充分的空间想象,综合三视图的形状,从不同的角度去还原.看图和想图是两个重要的步骤,“想”于“看”中,形体分析的看图方法是解决此类问题的常用方法.练一练3.根据以下三视图想象物体原形,并画出物体实物草图.解:实物草图如图:画出右图的物体的三视图.[错解][错因] 三视图出现多处错误.首先,主视图和左视图的高应该是相同的,而所画的视图没有做到这一点;其次,左视图的宽应该和俯视图的高一致,这一点也没有做到;再次,主视图的长与俯视图的长应对齐,这点还是没有做到;最后,图中有一条看不到的棱应该用虚线表示出来,所以答案存在多处错误.[正解] 如图所示.1.如图所示的一个几何体,它的俯视图是( )解析:选C 根据三视图的画法及特点可知C正确.2.(湖南高考)某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是( )解析:选C A是两个圆柱的组合体,B是一个圆柱和一个四棱柱的组合体,C选项的正视图与侧视图不相同,D可以是一个底面为等腰直角三角形的直三棱柱与一个四棱柱的组合体.3.沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的左视图为( )解析:选B 依题意,侧视图中棱的方向从左上角到右下角,故选B.4.一个几何体的主视图为一个三角形,则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱解析:只要判断正视图是不是三角形就行了,画出图形容易知道三棱锥、四棱锥、圆锥一定可以,对于三棱柱,只需要倒着放就可以了,所以①②③⑤均符合题目要求.答案:①②③⑤5.如图是由小正方体组成的几何图形的三视图,则组成它的小正方体的个数是________.解析:由三视图我们可以得出该几何体的直观图,如图所示.答案:56.画出该组合体的三视图.解:组合体由正六棱柱和圆柱组合而成,其三视图如图所示.一、选择题1.已知某空间几何体的三视图如图所示,则此几何体为( )A.圆台B.四棱锥C.四棱柱 D.四棱台解析:选D 由主视图和左视图可以判断一定为棱台或圆台,又由俯视图可知其一定为棱台且为四棱台.2.(湖南高考)已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为2的矩形,则该正方体的正视图的面积等于( )A.32B.1C.2+12D. 2解析:选D 由已知,正方体的正视图与侧视图都是长为2,宽为1的矩形,所以正视图的面积等于侧视图的面积,为 2.3.三棱柱ABCA1B1C1,如下图所示,以BCC1B1的前面为正前方画出的三视图,正确的是( )解析:选A 正面是BCC1B1的矩形,故主视图为矩形,左侧为△ABC,所以左视图为三角形,俯视图为两个有一条公共边的矩形,公共边为CC 1在面ABB 1A 1内的投影.4.(福建高考)一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( )A .球B .三棱锥C .正方体D .圆柱解析:选D 球的三视图是三个相同的圆;当三棱锥为正三棱锥时其三视图可能是三个全等的三角形;正方体的三视图可能是三个相同的正方形;不论圆柱如何放置,其三视图形状都不会完全相同.5.一个几何体的三视图如图所示,其中主视图中△ABC 是边长为2的正三角形,俯视图为正六边形,那么该几何体的左视图的面积为( )A.32B.23C .12D .6 解析:选A 由主视图、左视图、俯视图之间的关系可以判断该几何体是一个底面为正六边形的正六棱锥.∵主视图中△ABC 是边长为2的正三角形,此三角形的高为3,∴左视图的高为 3.俯视图中正六边形的边长为1,其小正三角形的高为32,∴左视图的底为32×2=3, ∴左视图的面积为12×3×3=32.二、填空题6.如图所示,为一个简单几何体的三视图,它的上部是一个________,下部是一个________.解析:由三视图可知该几何体图示为所以,其上部是一个圆锥,下部是一个圆柱.答案:圆锥圆柱7.用小正方体搭成一个几何体,如图是它的主视图和左视图,搭成这个几何体的小正方体的个数最多为________个.解析:其俯视图如图所示时为小正方体个数最多情况(其中小正方形内的数字表示小正方体的个数)共需7个小正方体.12 111 1答案:78.如图(1),E、F分别为正方体的面ADD1A1和面BCC1B1的中心,则四边形BED1F在该正方体的面上的射影可能是图(2)中的________(要求:把可能的图的序号都填上).解析:根据平行投影的理论,从正方体的上下、前后、左右三个角度分别投影,从上往下投影,选择②,从前往后投影,选择②,从左往右投影,选择③.答案:②③三、解答题9.如图所示,图②是图①中实物的主视图和俯视图,你认为正确吗?如果不正确,请找出错误并改正,然后画出它的左视图.解:图①是由两个长方体组合而成的,主视图正确,俯视图错误.俯视图应该画出不可见轮廓(用虚线表示),左视图轮廓是一个矩形,有一条可视的交线(用实线表示),正确画法如图所示.10.某建筑由若干个面积相同的房间组成,其三视图如下,其中每一个小矩形表示一个房间.(1)该楼有几层?共有多少个房间?(2)画出此楼的大致形状.解:(1)由主视图和左视图可知,该楼共3层,由俯视图可知,该楼一楼有5个房间,结合主视图与左视图,易知二楼和三楼分别有4个,1个房间,故共10个房间.(2)此楼的大致形状如图:。
高中数学第一章立体几何初步1.3.12简单组合体的三视图由三视图还原成实物图课件北师大版必修2

如图所示是两个几何体的三视图,请画出相应的几何体的立 体图形.
解:①为圆柱,②为四棱柱,4】 如图所示的是由几个小正方体所搭成的几何体的 俯视图,小正方形中的数字表示该位置上小正方体的个数.请画 出该几何体的主视图和左视图,并在其上标出小正方体的个数, 求出所有小正方体的个数.
类型三 简单几何体的三视图 【例 1】 画出如图所示的正三棱柱的三视图. 【思路探究】 观察三棱柱的结构,弄清三视图的有关概念, 尝试画图.
【解】 三视图如图所示.
规律方法 画三视图首先要认真观察几何体的特点,根据几 何体的特点,从不同方位找出其主要特点再根据画三视图的步骤 画图即可.
物体三视图的作图步骤是: (1)根据物体的复杂程度及大小,确定图形比例; (2)确定主视图的观察方向(使其主要表面平行或垂直于投射 面,能表达更多的结构形状); (3)布置各视图的位置(画出基准线、对称中心线、轴线); (4)按照“三等规律”画其三视图(可见轮廓线画实线,不可 见轮廓线画虚线); (5)核对有无错漏,擦去多余线条.
(4)注意: 在三视图中,分界线和可见轮廓线用____实_______线画出, 不可见轮廓线用____虚_______线画出.
[答一答] 1.同一物体的三视图的画法相同吗?
提示:不一定.三视图是相对于观察者而言的,相对于不同 的观察者,不同的观察方向,得到的三视图可能不相同.
知识点二 组合体的三视图
【思路探究】 可先根据几何体的俯视图及小正方体个数想 象或画出几何体,再根据几何体的结构特征画出其主视图及左视 图.
【解】 主视图及左视图如下图所示.小正方体的个数为 1 +2+4+3+2=12(个).
规律方法 对于简单几何体的组合体,一定要认真观察,先 认识它的基本结构,再按三视图的定义去观察简单组合体是由哪 几个基本几何体组成的,并注意它们的组成方式,特别是它们的 交线位置.
北师大版必修二数学教材帮目录

北师大版必修二数学教材帮目录第一章立体几何初步(第1页)第一章立体几何初步(第2页)1.1简单旋转体(第3页)1.2简单多面体(第4页)1.2简单多面体(第5页)习题1-1(第6页)2.直观图(第7页)2.直观图(第8页)2.直观图(第9页)2.直观图(第10页)2.直观图(第11页)习题1-2(第12页)3.1简单组合体的三视图(第13页)3.1简单组合体的三视图(第14页)3.1简单组合体的三视图(第15页)3.2由三视图还原成实物图(第16页)3.2由三视图还原成实物图(第17页)习题1-3(第18页)习题1-3(第19页)习题1-3(第20页)习题1-3(第21页)4.1空间图形基本关系的认识(第22页) 4.2空间图形的公理(第23页)4.2空间图形的公理(第24页)4.2空间图形的公理(第25页)习题1-4(第26页)习题1-4(第27页)5.1平行关系的判定(第28页)5.1平行关系的判定(第29页)5.2平行关系的性质(第31页)5.2平行关系的性质(第32页)5.2平行关系的性质(第33页)习题1-5(第34页)6.1垂直关系的判定(第35页)6.1垂直关系的判定(第36页)6.1垂直关系的判定(第37页)6.2垂直关系的性质(第38页)6.2垂直关系的性质(第39页)6.2垂直关系的性质(第40页)习题1-6(第41页)习题1-6(第42页)7.1简单几何体的侧面积(第43页) 7.1简单几何体的侧面积(第44页)7.2棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积(第45页) 7.2棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积(第46页) 7.3球的表面积和体积(第47页)习题1-7(第48页)习题1-7(第49页)阅读材料蜜蜂是对的(第50页)课题学习正方体截面的形状(第51页)本章小结(第52页)本章小结(第53页)复习题一(第54页)复习题一(第55页)复习题一(第56页)第二章解析几何初步(第57页)第二章解析几何初步(第58页)1.1直线的倾斜角和斜率(第59页)1.1直线的倾斜角和斜率(第60页)1.1直线的倾斜角和斜率(第61页)1.1直线的倾斜角和斜率(第62页)1.2直线的方程(第63页)1.2直线的方程(第64页)1.2直线的方程(第65页)1.2直线的方程(第66页)1.2直线的方程(第67页)1.3两条直线的位置关系(第68页)1.3两条直线的位置关系(第69页)1.4两条直线的交点(第70页)1.4两条直线的交点(第71页)1.5平面直角坐标系中的距离公式(第72页) 1.5平面直角坐标系中的距离公式(第73页) 1.5平面直角坐标系中的距离公式(第74页) 1.5平面直角坐标系中的距离公式(第75页) 习题2-1(第76页)习题2-1(第77页)2.1圆的标准方程(第78页)2.2圆的一般方程(第79页)2.2圆的一般方程(第80页)2.3直线与圆、圆与圆的位置关系(第81页) 2.3直线与圆、圆与圆的位置关系(第82页) 2.3直线与圆、圆与圆的位置关系(第83页) 2.3直线与圆、圆与圆的位置关系(第84页) 习题2-2(第85页)习题2-2(第86页)3.1空间直角坐标系的建立(第87页)3.2空间直角坐标系中点的坐标(第88页)3.2空间直角坐标系中点的坐标(第89页)3.3空间两点间的距离公式(第90页)3.3空间两点间的距离公式(第91页)3.3空间两点间的距离公式(第92页)习题2-3(第93页)阅读材料笛卡尔与解析几何(第94页)本章小结(第95页)本章小结(第96页)复习题二(第97页)复习题二(第98页)探究活动1打包问题(第99页)探究活动1打包问题(第100页)探究活动1打包问题(第101页)探究活动2追及问题(第102页)探究活动2追及问题(第103页)附录1部分数学专业词汇中英对照表(第104页)。
新版高中数学北师大版2习题:第一章立体几何初步 1.3.2

3.2由三视图还原成实物图1.若一个几何体的主视图和左视图都是等腰梯形,俯视图是两个同心圆,则这个几何体可能是()A.圆柱B.圆台C.圆锥D.棱台答案:B2.某几何体的三视图如图所示,则该几何体是()A.棱台B.棱柱C.棱锥D.以上均不对解析:由相似比,可知几何体的侧棱相交于一点.答案:A3.如图所示是底面为正方形、一条侧棱垂直于底面的四棱锥的三视图,则该四棱锥的直观图是下列各图中的()解析:由俯视图排除B,C选项;由主视图、左视图可排除A选项,故选D.答案:D4.某几何体的三视图如图所示,则这个几何体是()A.三棱锥B.四棱锥C.四棱台D.三棱台解析:因为主视图和左视图为三角形,可知几何体为锥体.又俯视图为四边形,所以该几何体为四棱锥,故选B.答案:B5.如图所示,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱解析:由题知,该几何体的三视图为一个三角形,两个四边形,经分析可知该几何体为三棱柱,故选B.答案:B6.一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4解析:由三视图画出直观图如图所示,判断这个几何体是底面边长为6,8,10的直角三角形,高为12的躺下的直三棱柱,直角三角形的内切圆的半径为r=-=2,这就是做成的最大球的半径.答案:B7.把边长为的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥C-ABD,其主视图、俯视图均为全等的等腰直角三角形(如图所示),其左视图的面积为.解析:如图所示,根据两个视图可以推知折起后∠CEA=90°,其侧视图是一个两直角边长为1的等腰直角三角形,所以左视图的面积为.答案:8.用n个体积为1的正方体搭成一个几何体,其主视图、左视图都是如图所示的图形,则n的最大值与最小值之差是.解析:由主视图、左视图可知,正方体个数最少时,底层有3个小正方体,上面有2个,共5个;个数最多时,底层有9个小正方体,上面有2个,共11个.故n的最大值与最小值之差是6.答案:69.下图是一个几何体的三视图,想象该几何体的几何结构特征,画出该几何体的形状.解由于俯视图中有一个圆和一个四边形,则该几何体是由旋转体和多面体构成的组合体,结合左视图和主视图,可知该几何体是由上面一个圆柱、下面一个四棱柱拼接成的组合体.该几何体的形状如图所示.★10.已知几何体的三视图如图所示,用斜二测画法画出它的直观图.解由三视图可知其几何体是底面边长为2,高为3的正六棱锥,其直观图如图所示.。
高中数学 1.3.2 由三视图还原成实物图课后训练 北师大版必修2

【志鸿全优设计】2013-2014学年高中数学 1.3.2 由三视图还原成实物图课后训练北师大版必修21.某几何体的三视图如下图所示,那么这个几何体是().A.三棱锥B.四棱锥C.四棱台D.三棱台2.一个圆台的左视图是一个等腰梯形,其上底和下底长分别为2和8,腰长为5,则该圆台的高等于().A34B.4C61D.83.若某几何体的三视图如图所示,则这个几何体的直观图可以是().4.在一个几何体的三视图中,主视图和俯视图如下图所示,则相应的左视图可以为().5.下图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其主视图、俯视图如下图;②存在四棱柱,其主视图、俯视图如下图;③存在圆柱,其主视图、俯视图如下图.其中真命题的个数是().A.3 B.2 C.1 D.06.如图所示的三视图表示的立体图形是________.7.用小立方体搭一个几何体,使得它的三视图如下图,这样的几何体需要__________个小立方体.8.某几何体的三视图如图所示,则该几何体所有侧面的面积之和等于__________.9.根据如图所示的三视图想象物体原形,并画出物体的实物草图.①②10.如图是一个空间几何体的三视图,其中主视图和左视图都是边长为2的正三角形,俯视图是一个正方形.(1)在给定的直角坐标系中作出这个几何体的直观图;(不写作法)(2)求这个几何体的高.参考答案1答案:B解析:由所给三视图可以判定对应的几何体为如下图所示的四棱锥.2答案:B解析:左视图的高就是该圆台的高,设上、下底面半径分别为r,R,则2r =2,2R=8,所以r=1,R=4,又母线长l=5,所以圆台的高22h=--.5(41)=4 3答案:D解析:由主视图中间的虚线可排除A,B,由俯视图可排除C,故选D.4答案:D解析:由题目所给的几何体的主视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示:可知左视图为等腰三角形,且轮廓线为实线,故选D.5答案:A解析:①正确,如下图的直三棱柱,其中四边形BCC1B1与四边形BAA1B1是全等的矩形,且面BCC1B1⊥面BAA1B1,即满足要求.②正确,如下图的正四棱柱ABCD-A1B1C1D1,即满足要求.③正确,横卧的圆柱即可,如图.6答案:正六棱锥7答案:10解析:由三视图知几何体如图所示,正方形上的数字表示有几个小立方体相叠,可知有10个小立方体.8答案:64解析:由三视图可知,该几何体是底面为直角梯形,高为4的直四棱柱.每个侧面均为矩形,其直观图如右:其中底面直角梯形中另一条边的长度为224(52)=5+-,于是所有侧面的面积之和为(2+5+4+5)×4=64.9答案:解:由已知条件中的三视图,可知:①组合体为:上面是一个圆柱,下面是一个圆台,且圆台上底面与圆柱下底面重合,实物草图如图①所示;②组合体为:上面是一个圆锥,下面是一个圆柱,实物草图如图②所示.10答案:解:(1)直观图如图.(2)这个几何体是一个正四棱锥.它的底面边长为2,高在主视图(或左视图)中可求,高h=2sin 60°3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2 由三视图还原实物图
时间:45分钟满分:80分
班级________ 姓名________ 分数________
一、选择题(每小题5分,共5×6=30分)
1.若一个几何体的三视图都是等腰三角形,则这个几何体可能是( )
A.正方体 B.长方体
C.三棱锥 D.圆
答案:C
解析:由三视图的知识,可知答案为C.
2.如图所示,甲、乙、丙是三个几何体的三视图,则甲、乙、丙对应的几何体分别为( )
①长方体;②圆锥;③三棱锥;④圆柱.
A.④③② B.①③②
C.①②③ D.④②③
答案:A
解析:由于甲中的俯视图是圆,则甲对应的几何体是旋转体,又主视图和左视图均是矩形,所以该几何体是圆柱;易知乙对应的几何体是三棱锥;由丙中的俯视图,可知丙对应的几何体是旋转体,又主视图和左视图均是三角形,所以该几何体是圆锥.
3.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )
图1
A
B
C
D
答案:D
解析:本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C,都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.
4.在一个几何体的三视图中,正视图和俯视图如下图所示,则相应的侧视图可以为( )
B
C
D
答案:D
解析:本题考查三视图,可用排除法或特例求答.由正视图知A、B不正确,又由俯视图知C不正确,选D.本题的几何体也可看成是一个圆锥的一半与一个三棱锥的组合体.5.如图是一个物体的三视图,则该物体对应的直观图为( )
答案:C
解析:从俯视图看,A,C,D均符合,再结合主视图看,只有C符合.故选C.
6(主)视图、俯视图如右图②存在四棱柱,其正(主)视图、俯视图如右图③存在圆柱,其正(主)视图、俯视图如右图.其中真命题的个数是( )
A.3 B.2
C.1 D.0
答案:A
解析:主要考查三视图知识.这一知识点近几年都有考查.
①正确,比如一个平放的两底面是等腰直角三角形的直三棱柱.②显然正确,③中可以是一个平放的圆柱.
二、填空题(每小题5分,共5×3=15分)
7.正视图为一个三角形的几何体可以是________(写出三种).
答案:三棱锥、三棱柱、圆锥
解析:正视图是三角形的几何体,最容易想到的是三棱锥,其次是四棱锥、圆锥;对于五棱锥、六棱锥等,正视图也可以是三角形.
8.如图所示为一个简单组合体的主视图和左视图,则该几何体可能是________(填序号).
答案:①
解析:由主视图中左下角至右上角有一实对角线,可知所给的几何体中只有①符合,又根据左视图知①符合,所以选①.
9.给出下列命题:
①如果一个几何体的三个视图是完全相同的,则这个几何体是正方体;②如果一个几何体的主视图和俯视图都是矩形,则这个几何体是长方体;③如果一个几何体的三个视图都是
矩形,则这个几何体是长方体:④如果一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台.
其中正确的是______.(将正确的全都写在横线上)
答案:③
解析:对于①由于球的三个视图也是完全相同的,故①不对;对于④,主视图与左视图
都是等腰梯形的除圆台之外,还有棱台,故④不对;对于②,当圆柱倒置时,如图,其主视图与俯视图均为矩形,故②不正确.
三、解答题(共35分,11+12+12)
10.根据图中的三视图想象物体原形,并画出物体的实物草图.
解:由俯视图并结合其他两个视图可以看出,这个物体是由上面一个正四棱台和下面一个正方体组合而成的,它的实物草图如图所示.
11.某建筑由相同的若干房间组成,该楼房的三视图如图所示,问:
(1)该楼房有几层?从前往后最多要经过几个房间?
(2)最高一层的房间在什么位置?请画出此楼房的大致形状.
解:(1)3层;由俯视图知道,从前往后最多要经过3个房间;
(2)从主视图和左视图可以知道,最高一层的房间在左侧的最后一排的房间.楼房大致形状如图所示.
12.如图是一个空间几何体的三视图,其中主视图和左视图都是边长为2的正三角形,俯视图是一个正方形.
(1)(不写作法)
(2)求这个几何体的高.
解:(1)直观图如图.
(2)这个几何体是一个正四棱锥.
它的底面边长为2,高在主视图(或左视图)中可求,高h=2sin60°= 3.。
