4.5三角形的内切圆课件(青岛版九年级上册)(1)
青岛版数学九年级上册3.5 三角形的内切圆

2S r . B abc 1 S r a b c . 2
A D
●
O
┓
F
E
C
这个结论可叙述为:三角形的面积等于其周 长与内切圆半径乘积的一半.
三角形的内切圆
已知:如图,⊙O是Rt△ABC的内切 圆,∠C是直角,BC=5,r=2. 求△ABC的周长.
A O
1 同理 ∠OCB= ∠OCA= 2 ∠ACB=35 ° B ∴ ∠BOC=180 ° 1(∠ABC+ ∠ACB) 2
C
-
= 180 °-60 °=120 ° (2)若∠A=80 °,则∠BOC=
度。 度。
(3)若∠BOC=100 °,则∠A=
试探讨∠BOC与∠A之间存在怎样的数量关系? 请说明理由.
典型例题
直角三角形的内切圆
已知:如图,⊙O是Rt△ABC的内切 圆,∠C是直角,∠AC=3,BC=4. 求⊙O的半径r.
3 45 r 1. 2
B A D
●
O
┓
┗ F
E
C
直角三角形的内切圆
已知:如图,⊙O是Rt△ABC的内切圆,∠C 是直角,三边长分别是a,b,c. 求⊙O的半径r.
abc r . 2
练 习
1、下列图形中,一定有内切圆的四边形是( ) (A)梯形 (C)矩形 (B)菱形 (D)平行四边形
2、如图,△ABC中,E是内心,∠A的平分线和△ABC的 外接圆相交于点D. 求证:DE=DB
3 、如图,菱形 ABCD 中,周长为 40 ,∠ABC=120°,则 内切圆的半径为( ) 5 2 2 5 2 (D) 3 (A) 3 (B) 2 (C) 2 3 3 2 4 、如图,⊙O 是△ABC 的内切圆, D 、 E 、 F 是切点, ∠A=50°,∠C=60°,则∠DOE=( ) (A)70° (C)120° (B)110° (D)130°
青岛版九年级数学上册《三角形的内切圆》说课稿

青岛版九年级数学上册《三角形的内切圆》说课稿一、教材分析本节课是青岛版九年级数学上册的一节课,涉及到三角形的内切圆的概念和性质。
通过学习本节课,学生将能够了解三角形的内切圆的定义、性质以及相关的定理。
本节课是数学知识的重要环节,对于培养学生的数学思维能力和解题能力具有重要意义。
二、教学目标本节课的教学目标主要有以下几个方面: 1. 了解三角形的内切圆的定义; 2. 掌握三角形内切圆的性质; 3. 掌握相关的定理,能够应用定理解决问题; 4. 培养学生的数学思维和解题能力。
三、教学重难点本节课的教学重点和难点主要集中在以下几个方面: 1.理解三角形的内切圆的概念; 2. 掌握三角形内切圆的性质及其证明; 3. 应用相关的定理解决实际问题。
四、教学准备为了保证本节课的教学顺利进行,我们需要做以下准备工作: 1. 课件和教学演示工具; 2. 相关的教学素材和题目;3. 黑板、粉笔、草稿纸等教学用具; 4. 学生的教材和笔记。
五、教学过程1. 导入与引入首先,我们可以通过提问学生的方式,引入本节课的主题。
例如,可以问学生有关三角形的内切圆的概念,并引导学生思考与内切圆相关的问题。
通过这种方式,可以调动学生的思维,激发学生的学习兴趣。
2. 知识讲解与展示接下来,我们可以通过课件和教学演示工具,向学生详细讲解三角形的内切圆的定义、性质和相关的定理。
在讲解的过程中,可以通过示意图、实例等形式,使学生更好地理解内切圆的概念和性质。
同时,还要强调内切圆与三角形的关系,以及内切圆与三角形边的关系,帮助学生建立相关的联系。
3. 示例分析与练习为了巩固学生的学习成果,我们可以选择一些有代表性的例题进行分析和讲解。
通过演示解题过程,引导学生运用所学到的知识解决实际问题。
在讲解的过程中,要注意引导学生进行思考和讨论,培养他们的解题思路和方法。
4. 深化拓展与实践为了提高学生的综合应用能力,我们可以设计一些拓展性的问题,让学生运用所学知识解决更复杂的问题。
人教九年级数学上册《三角形的内切圆》课件

O
变式2:在△ABC中,点O是内心,
2 1
4 3
∠BOC=120°,求∠BAC的度数。B
C
想想,做做
题2:
求边长为6cm的等边三角形的内切圆半径r与外
接圆半径R。
A
老师提示: 先画草图,由等腰三角形底边上的中垂
线与顶角平分线重合的性质知,等边三角形 的内切圆与外接圆是两个同心圆。
O R
r
B
C
D
变式:
想一想: 你会画三角形的内切圆吗?
老师提示: 看看你刚刚画的图,相信你会有 办法的。
1、定义:和三角形各边都相切的圆叫做三角 形的内切圆,内切圆的圆心叫做三角形的内心, 这个三角形叫做圆的外切三角形。 画三角形的内切圆: 画角平分线→定内心→定半径→画圆→结论
2、内心性质:
内心到三角形三边的距离相等; 内心与顶点连线平分内角。
我 想
---与大家共分享!
说
…
1.定义
2.内心的性质
3.画三角形的内切圆 4.初步应用
考考你自己:
1.你能帮李师傅画出裁剪图吗?
2.以某三角形的内心为圆心, 作一个圆使它与这个三角形 的某一条边(或所在的直线) 相交,那么这个圆与其他两 边(或所在的直线)有怎样 的位置关系?
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年4月21日星期四2022/4/212022/4/212022/4/21 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年4月2022/4/212022/4/212022/4/214/21/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/4/212022/4/21April 21, 2022
九年级数学上册 3.5 三角形的内切圆课件 (新版)青岛版.pptx
ra、=b、ac的关系ab是b c 12
谢谢同学们的 参入配合!
13
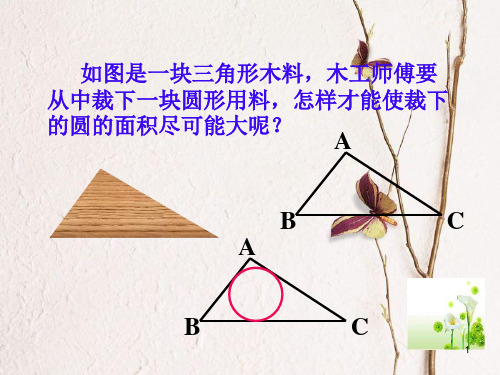
如图是一块三角形木料,木工师傅要 从中裁下一块圆形用料,怎样才能使裁下 的圆的面积尽可能大呢?
A
B
C
A
B
C
1
3.5 三角形的内切圆
2
【学习目标】
1.了解三角形的内切圆相关的概念 2.能利用三角形内心的性质进行证明 和计算 (重点、难点)
【教学重点,难点】
能利用三角形内心的性质进行证明和 计算
3
活动一:思考、操作
∠ABC、∠ACB
C 3.内心在三角形内
部.
8
探讨1: 设△ABC 的内切圆的半径为r,△ABC 的
各边长之和为C,△ABC 的面积S,我们会有什
么结论?
A
D
•
F
1
O
S = rC
B
r
2
(C为三角形周长,r为内切圆半径)
E直角三角形的两直角边分别是a,b,斜边为
c 则其内切圆的半径r为:
A
A
O B
B
C
4
三角形 内切圆 作法:
1、作∠B、∠C的平分线 BM和CN,交点为I。
2.过点I作ID⊥BC,垂足为D。 A
3.以I为圆心,ID为
半径作⊙I. ⊙I就是所求的圆。
NM I
B
D
C
5
定义:和三角形各边都相切的圆叫做三角形的
内切圆,内切圆的圆心叫做三角形的内心,这个 三角形叫做圆的外切三角形。
性质: 1.三角形的内心到三角形各边的距离相等;
2.三角形的内心在三角形的角平分线上;内心
202X秋青岛版数学九上3.5《三角形的内切圆》ppt课件3

历史课件:/kejian/lish i/
C. 三条中线的交点
D. 三边垂直平分线的交点
巩固
2、如图,l1, l2, l3,是三条公路, 要在它们为成三角形内部修建一个加
油站,使加油站到三条公路的距离相
等,加油站应建 在什么位置? 为什么?
l2 l1
A
l3 B
C
范例
例1、△ABC的三边长分别是a、b、c, 它的内切圆的半径为r,求△ABC的 面积。
•
10、阅读一切好书如同和过去最杰出 的人谈 话。14:27:0414:27:0414:275/3/2021 2:27:04 PM
•
11、一个好的教师,是一个懂得心理 学和教 育学的 人。21.5.314:27:0414:27May- 213-M ay-21
•
12、要记住,你不仅是教课的教师, 也是学 生的教 育者, 生活的 导师和 道德的 引路人 。14:27:0414:27:0414:27Monday, May 03, 2021
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成 。21.5.321.5.314:27:0414:27:04May 3, 2021
•
14、谁要是自己还没有发展培养和教 育好, 他就不 能发展 培养和 教育别 人。2021年5月 3日星 期一下 午2时27分4秒14:27:0421.5.3
•
17、儿童是中心,教育的措施便围绕 他们而 组织起 来。下 午2时27分4秒 下午2时 27分14:27:0421.5.3
谢谢观赏
You made my day!
我们,还在路上……
三角形内切圆
最新青岛版九年级数学上册全册完整课件

1.1 相似多边形
最新青岛版九年级数学上册全册完 整课件
1.2 怎样判定三角形相似
最新青岛版九年级数学上册全册完 整课件
1.3 相似三角形的性质
最新青岛版九年级数学上册全册完 整课件
2.2 30°,45°,60°角的三角比
最新青岛版九年级数学上册全册完 整课件
2.3 用计算器求锐角三角比
最新青岛版九年级数学上册全册完 整课件
最新青岛版九年级数学上册全册 完整课件目录
0002页 0035页 0085页 0154页 0190页 0192页 0204页 0206页 0236页 0238页 0280页 0310页 0339页 0373页
第1章 图形的相似 1.2 怎样判定三角形相似 1.4 图形的位似 2.1 锐角三角比 2.3 用计算器求锐角三角比 2.5 解直角三角形的应用 3.1 圆的对称性 3.3 圆周角 3.5 三角形的内切圆 3.7 正多边形与圆 4.1 一元二次方程 4.3 用公式法解一元二次方程 4.5 一元二次方程的应用 4.7 一元二次方程的应用
最新青岛版九年级数学上册全册完 整课件
1.4 图形的位似
最新青岛版九年级数学上册全册完 整课件
第2章 解直角三角形
最新青岛版九年级数学上册全册完 整课件
2.1 锐角三角比
青岛版数学九年级上册3.5三角形的内切圆精讲课件

内部.
巩固训练1
1.如图1,△ABC是⊙O的 内接 三角形。
⊙ O是△ABC的 外接 圆, 点O叫△ABC的 外心 ,
它是三角形 三边垂直平分线
的交点.
2.如图2,△DEF是⊙I的 外切 三角形, ⊙I是△DEF的 内切 圆,
点I是 △DEF的 内 心, 它是三角形 三条角平分线 的交点.
B
做 三角形的内切圆 ,内切圆的圆心叫做三角
.I
形的 内心 ,这个三角形叫
C
A
做 圆的外切三角形 。
三角形的内心是三角形的三条__角__平__分__线_____的交点,它到三角 形___各__边____的距离相等. 任何一个三角形都__有__且__只__有_____一个内心,三角形的内心在三
角形的__内___部___.
3.5 三角形的内切圆
生活中的问题
如图是一块三角形木料,木工师傅要从中 裁下一块圆形用料,怎样才能使裁下的圆的面 积尽可能大呢?
用数学来解决
学习目标: 1、了解三角形的内切圆、三角形的内心、圆的外
切三角形的概念。 2、会利用基本作图作三角形的内切圆。 3、了解三角形内心的性质,并会进行有关的计算。
2
∴ ∠BOC=180 °-(∠1+ ∠3)
O
2 B )1
4 3( C
BOC 90 1 A 2
= 180 °-(20°+ 35 °) =125 °.
(2)若∠A=80 °,则∠BOC = 130 度.
(3)若∠BOC=100 °,则∠A = 20 度.
例题
A
B1
I 2C
4
跟踪训练
1.如图1,⊙O内切于△ABC,切点为D,E,F.已知 ∠B=50°∠C=60°, 连接OE,OF,DE,DF,那么
青岛版数学九年级上册3.5《三角形的内切圆》说课稿

青岛版数学九年级上册3.5《三角形的内切圆》说课稿一. 教材分析青岛版数学九年级上册3.5《三角形的内切圆》是三角形的内切圆相关知识的学习。
本节课主要通过探究三角形的内切圆的性质和公式,让学生理解和掌握三角形的内切圆的相关知识。
在教材中,通过引入三角形的内切圆的概念,引导学生探究内切圆的性质,进而推导出内切圆的半径公式。
整个章节内容环环相扣,逐步深入,让学生在探究中学习,在学习中探究。
二. 学情分析在进入九年级的学生已经具备了一定的几何知识,对三角形的相关性质有一定的了解。
但是,对于三角形的内切圆这一概念和相关性质,学生可能比较陌生。
因此,在教学过程中,需要通过引导学生观察和操作,让学生理解和掌握三角形的内切圆的相关知识。
三. 说教学目标1.知识与技能:理解三角形的内切圆的概念,掌握三角形的内切圆的性质和半径公式。
2.过程与方法:通过观察和操作,培养学生的观察能力和动手能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的合作意识和探究精神。
四. 说教学重难点1.教学重点:三角形的内切圆的概念,内切圆的性质和半径公式。
2.教学难点:内切圆半径公式的推导和应用。
五. 说教学方法与手段在本节课的教学过程中,将采用引导探究法和小组合作法相结合的教学方法。
引导探究法主要用于引导学生观察和操作,培养学生的观察能力和动手能力。
小组合作法主要用于让学生在小组内进行讨论和交流,培养学生的合作意识和探究精神。
此外,还将利用多媒体教学手段,通过展示图片和动画,帮助学生更好地理解和掌握内切圆的相关知识。
六. 说教学过程1.导入:通过展示一些有关三角形内切圆的图片,引导学生思考三角形的内切圆的概念和性质。
2.新课导入:介绍三角形的内切圆的概念,引导学生探究内切圆的性质。
3.案例分析:通过展示一些具体的三角形内切圆的案例,让学生观察和分析,引导学生总结出内切圆的性质。
4.公式推导:引导学生探究内切圆的半径公式,让学生通过小组合作,进行推导和验证。
