第五章相交线与平行线复习导学案
《第五章 相交线与平行线》复习导学案
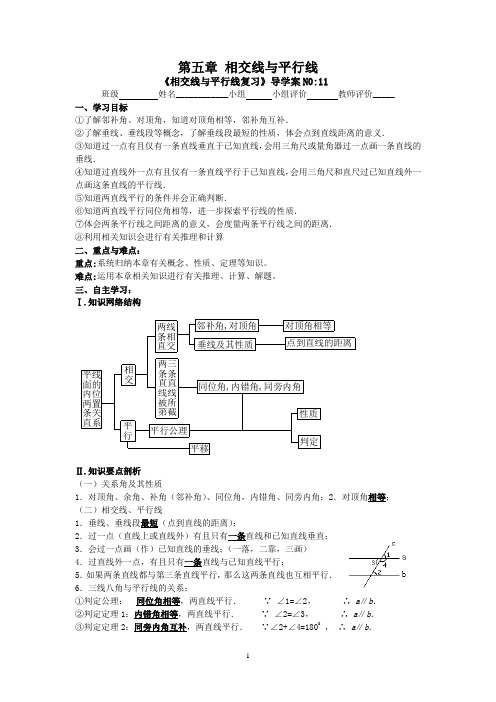
第五章 相交线与平行线《相交线与平行线复习》导学案N0:11班级 姓名____________小组 小组评价 教师评价_____ 一、学习目标①了解邻补角、对顶角,知道对顶角相等,邻补角互补.②了解垂线、垂线段等概念,了解垂线段最短的性质,体会点到直线距离的意义. ③知道过一点有且仅有一条直线垂直于已知直线,会用三角尺或量角器过一点画一条直线的垂线.④知道过直线外一点有且仅有一条直线平行于已知直线,会用三角尺和直尺过已知直线外一点画这条直线的平行线.⑤知道两直线平行的条件并会正确判断.⑥知道两直线平行同位角相等,进一步探索平行线的性质.⑦体会两条平行线之间距离的意义,会度量两条平行线之间的距离. ⑧利用相关知识会进行有关推理和计算 二、重点与难点:重点:系统归纳本章有关概念、性质、定理等知识。
难点:运用本章相关知识进行有关推理、计算、解题。
三、自主学习: Ⅰ.知识网络结构Ⅱ.知识要点剖析(一)关系角及其性质1.对顶角、余角、补角(邻补角)、同位角,内错角、同旁内角;2.对顶角相等; (二)相交线、平行线1.垂线、垂线段最短(点到直线的距离);2.过一点(直线上或直线外)有且只有一条直线和已知直线垂直; 3.会过一点画(作)已知直线的垂线;(一落,二靠,三画) 4.过直线外一点,有且只有一条直线与已知直线平行; 5.如果两条直线都与第三条直线平行,那么这两条直线也互相平行. 6.三线八角与平行线的关系;①判定公理: 同位角相等,两直线平行. ∵ ∠1=∠2, ∴ a ∥b . ②判定定理1:内错角相等,两直线平行. ∵ ∠2=∠3, ∴ a ∥b .③判定定理2:同旁内角互补,两直线平行. ∵∠2+∠4=1800, ∴ a ∥b .平移判定性质同位角,内错角,同旁内角点到直线的距离垂线及其性质对顶角相等邻补角,对顶角平行公理两三条条 直直线线被所第截两线条相直交平行相交平线 面的 内位两置条关直系④性质公理: 两直线平行,同位角相等. ∵ a ∥b , ∴∠1=∠2. ⑤性质定理1:两直线平行,内错角相等. ∵ a ∥b , ∴∠2=∠3.⑥性质定理2:两直线平行,同旁内角互补. ∵ a ∥b , ∴ ∠2+∠4=1800. 7.平行线之间的距离;8.会过直线外一点,画已知直线的平行线. 四.合作探究探索一:基础训练 (一)关系角及性质1.指出图中:对顶角: ,同位角: , 内错角: ,同旁内角: ; 图中哪些角是相等的 .2.若∠A +∠B =90°,则∠A 与∠B 互为 , 若∠α+∠β=180°,则∠α与∠β互为 .3.∵∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3( ); ∵∠1+∠2=180°,∠3+∠4=180°,∠2=∠4,∴∠1=∠3( ). (二)相交线与平行线1.如图,过点P 画直线l 的垂线,这样的垂线有 条. 理由是: .若过点P 画直线l 的平行线,能画 条. 理由是: .在图中试着画一画,你能说出它的画法吗?2.如图,这是小明在体育课上跳远后留下的脚印, 请你谈谈怎样量他的成绩?3.若AB ∥CD ,CD ∥EF ,则 ∥ ,理由: . 4.如图,直线a 、b 被c 所截,(1)∵∠1=∠2 ∴ ∥ ( ); (2)∵∠2=∠3 ∴ ∥ ( ); (3)∵∠2+∠4=180°∴ ∥ ( ). 5.如图,直线AB 、CD 被EF 所截,若AB ∥CD , 则∠EMB = ( );∠AMF = ( ); ∠BMF + =180°( )6.如图直线AB ∥CD ,且被EF 所截,EG ⊥CD ,EF =5,FG =3, 则AB 、CD 之间的距离为 . 探索二:考题回放1.已知∠α=35°19′,则∠α的余角等于 ( )A .144°41′B .144°81′C .54°41′D .54°81′2.已知,如图(1)直线AB 、CD 被直线EF 所截,则∠EMB 的同位角是( ) A .∠AMF B .∠BMF C .∠ENC D .∠END(2),AB ∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于G,若∠EFG=72°,则∠EGF 等于()A.36° B.54° C.72° D.108°4.如图(3),在正方体ABCD—A1B1C1D1中,下列棱中与面CC1D1D垂直的棱()A.A1B1 B.CC1 C.BC D.CD探索三:知识整合1.如图所示,已知∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°.在OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB的度数是()A.60° B.80° C.100° D.120°2.如图,已知∠C=∠AOC,OC平分∠AOD,OC⊥OE,∠D=54°.求∠C、∠BOE的度数.归纳:解答(证明)三条原则:①条理清晰;②言必有据;③因果相应.五、课堂小结1.区分命题的组成;识别命题的真命题、假命题.2.灵活运用学过的定理、定义、性质进行证明简单的题目.六、拓展提高如图所示,已知: AB∥CD,分别探究下面三个图形中∠A、∠C、∠P之间的数量关系,并选一个给予证明.七、课后作业:教材 P35--2、3; P36--6、12、13 .八、达标检测:一.判断题:(1)和为180°的两个角是邻补角.()(2)如果两个角不相等,那么这两个角不是对顶角.()(3)两条直线被第三条直线所截,同位角相等.()(4)邻补角的角平分线所在的两条直线互相垂直.()(5)两条直线相交,所成的四个角中,一定有一个是锐角.()二.选择题:(1)下列命题中,是真命题的是()A.相等的两个角是对顶角 B.有公共顶点的两个角是对顶角C.一条直线只有一条垂线D.过直线外一点有且只有一条直线垂直于已知直线(2)如图,如果AD∥BC,则有①∠A+∠B=180°;②∠B+∠C=180°;③∠C+∠D=180°,上述结论中正确的是()A .只有①;B .只有②;C .只有③;D .只有①和③ (3)如图,如果AB ∥CD ,CD ∥EF ,那么∠BCE 等于 ( ) A .∠1+∠2 B .∠2-∠1 C .180°-∠2 +∠1 D .180°-∠1+∠2 三.填空1.如图1,直线AB 、CD 相交于点O ,∠1=∠2.则∠1的对顶角是_____,∠4的邻补角是______.∠2的补角是_________.2.把命题“直角都相等”改写为“如果…,那么…”的形式是______________________. 3.如图2,要从水渠向水池C 引水,在哪里开沟可使水渠最短,请画出图形.理由是—— —.4.如图3,已知,∠1=35°,AB ⊥CD ,垂足为O ,EF 经过点O .则∠2= 度,∠3= 度,∠4= 度.5.如图4,将一副三角板的直角顶点重合,•摆放在桌面上,• 若∠AOD =145°,则∠BOC =_______度.6.如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐的角∠A是120○,第二次拐的角∠B 是150○,第三次拐的角是∠C ,这时的道路恰好和第一次拐弯之前的道路平行,则∠C 是 . 四.解答题1.如图,已知:AB ∥CD ,∠1=55°∠2=80°, 求∠3的度数.2.如图,已知: AB ∥CD ,BE ∥CF .求证:∠1=∠4.2. 一块边长为8m 的正方形土地,上面修了横竖各两条的 道路,宽都是2m ,空白的部分种上各种花草,请利用平移 的知识求出种花草的面积。
第五章相交线与平行线复习导学案

第五章相交线与平行线复习一、教学目标:1.知识与技能:1.统过对知识的梳理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形。
2.使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行的性质。
2.过程与方法:1.经历把现实物体抽象成几何对象(点、线、面等)的数学化过程.2.经历把文字语言、符号语言和图形语言的相互转化过程.3.通过说理过程,培养逻辑推理和数学表述的能力.4.通过自主知识回顾与整理,经历数学知识系系统化与条理化过程,探索数学复习的方法.3.情感态度与价值观:1.感受数学来源于生活又服务于生活,激发学习数学的乐趣.2.体验用运动变换的观点来揭示知识间内在联系.二、教学重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用。
三、教学难点:垂直、平行的性质和判定的综合应用。
四、教学过程;综合运用一、选择题:(每小题3分,共21分)1.如图1所示,AB∥CD,则与∠1相等的角(∠1除外)共有( )A.5个B.4个C.3个D.2个DCBA1EDCBAOFEDCBA(1) (2) (3)2.如图2所示,已知DE∥BC,CD是∠ACB的平分线,∠B=72°,∠ACB=40°,•那么∠BDC等于( )A.78°B.90°C.88°D.92°3.下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;•③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( )A.①B.②和③C.④D.①和④4.若两条平行线被第三条直线所截,则一组同位角的平分线互相( ) A.垂直 B.平行 C.重合 D.相交5.如图3所示,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,则∠BOF为( )A.35°B.30°C.25°D.20°6.如图4所示,AB∥CD,则∠A+∠E+∠F+∠C等于( )A.180°B.360°C.540°D.720°FEDCBAGFED CBA1F ED CBA(4) (5) (6)7.如图5所示,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角(∠1生:独立解答,相互交流。
()七年级下册数学第五章相交线与平行线导学案

七年级第五章相交线与平行线导学案2.课题:相交线〔一〕学习目标:通过动手、操作、推断、交流等活动,进一步开展空间观念,培养识图能力,推理能力和有条理表达能力在具体情境中了解邻补角、对顶角,能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些简单问题〔二〕学习重点和难点:重点:邻补角与对顶角的概念.对顶角性质与应用难点:理解对顶角相等的性质的探索二、问题导读单:阅读P1—3页答复以下问题:图观察并阅读有关内容体会说明:图中“剪刀〞可以看作:_______________线,画出示图为: __________________阅读“探究〞中有关内容答复相应问题并填写下表。
两条直线相交所形成的分类位置关系数量关系角O如2题图中AB交CD于点O形成四个角,∠1和∠2有一条公共边_____,它们的另一边互为_______________,具有这种关系的两个角,互为邻补角.互为邻补角的还有:___________________________________________________1和∠3有一个_____________,并且∠1的两边分别是∠3的两边的_______________.具有这种位置关系的两个角,互为对顶角.互为对顶角的还有_________________.写出对顶角的性质:___________________.写出性质的推理或说理形式.______________________________________________________________________________________________________________________________例题中求三个角的度数时,应用了哪些“原理〞?分别是:_____________________________________________________________________三、问题训练单:6.如图直线c分别交直线a、b形成如图中8个角,写出图中∠1的邻补角有:∠3的邻补角有:∠5的邻补角有:∠7的邻补角有:所有的对顶角有:__________________________________________________________________________________以下说法对不对〔1〕邻补角可以看成是平角被过它顶点的一条射线分成的两个角〔2〕邻补角是互补的两个角,互补的两个角是邻补角23〔3〕对顶角相等,相等的两个角是对顶角18.如图,填空:4 (1)∠1与∠是邻补角,∠1又与∠是邻补角;(2)∠2与∠是邻补角,∠2又与∠是邻补角;(3)如果∠1=40°,那么∠2=°,∠4=°,∠3=°.9*.如图直线AB、CD、EF相交于点O.1〕写出图中所有对顶角:2〕写出:∠AOC的邻补角有:∠AOE的邻补角有:∠AOF的邻补角有:∠AOD的邻补角有:五、谈本节课收获和体会:课题:〔1〕垂线〔一〕学习目标:1.理解垂线、垂线段的概念,会用三角尺或量角器过一点画直线的垂线。
第五章相交线与平行线复习导学案

EODCB A 第五章 相交线与平行线复习导学案(1)主备 王凤珍 审查 七年级数学备课组 时间2012、6一.知识点回顾1. 两直线相交所成的四个角中,有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为_____________.2. 两直线相交所成的四个角中,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种关系的两个角,互为__________.对顶角的性质:______ _________. 3. 两直线相交所成的四个角中,如果有一个角是直角,那么就称这两条直线相互_______.垂线的性质:⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中,_______________.4. 直线外一点到这条直线的垂线段的长度,叫做________________________.5. 两条直线被第三条直线所截,构成八个角,在那些没有公共顶点的角中,⑴如果两个角分别在两条直线的同一方,并且都在第三条直线的同侧,具有这种关系的一对角叫做___________ ;⑵如果两个角都在两直线之间,并且分别在第三条直线的两侧,具有这种关系的一对角叫做____________ ;⑶如果两个角都在两直线之间,但它们在第三条直线的同一旁,具有这种关系的一对角叫做_______________.6. 在同一平面内,不相交的两条直线互相___________.同一平面内的两条直线的位置关系只有________与_________两种.7. 平行公理:经过直线外一点,有且只有一条直线与这条直线______.推论:如果两条直线都与第三条直线平行,那么_____________________.8. 平行线的判定:⑴两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:_____________________________________.⑵两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:___________________________. ⑶两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:________________________________________.9. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线_______ .10. 平行线的性质:⑴两条平行直线被第三条直线所截,同位角相等.简单说成: _____.⑵两条平行直线被第三条直线所截,内错角相等.简单说成:___________________________⑶两条平行直线被第三条直线所截,同旁内角互补.简单说成_________________________. 11. 判断一件事情的语句,叫做_______.命题由________和_________两部分组成.题设是已知事项,结论是______________________.命题常可以写成“如果……那么……”的形式,这时“如果”后接的部分是_____,“那么”后接的部分是_________.如果题设成立,那么结论一定成立.像这样的命题叫做___________.如果题设成立时,不能保证结论一定成立,像这样的命题叫做___________.定理都是真命题.12. 把一个图形整体沿某一方向移动,会得到一个新图形,图形的这种移动,叫做平移变换,简称_______.图形平移的方向不一定是水平的.平移的性质:⑴把一个图形整体平移得到的新图形与原图形的形状与大小完全______. ⑵新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段_________________.二.典型题集萃(一)、相交线、三线八角1.平面内三条直线交点的个数有 个。
(完整)新人教版七年级数学(下册)第五章导学案及参考答案

新人教版七年级数学(下册)第五章导学案及参考答案第五章 相交线与平行线课题:5.1.1 相交线【学习目标】: 在具体情境中了解邻补角、对顶角, 能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些问题。
【学习重点】:邻补角、对顶角的概念,对顶角性质与应用。
【学习难点】:理解对顶角相等的性质的探索。
【导学指导】 一、知识链接 1.读一读,看一看学生欣赏图片,阅读其中的文字.师生共同总结:我们生活的世界中,蕴涵着大量的相交线和平行线. 本章要研究相交线所成的角和它的特征,相交线的一种特殊形式即垂直,垂线的性质, 研究平行线的性质和平行的判定以及图形的平移问题.2.观察剪刀剪布的过程,引入两条相交直线所成的角教师出示一块布片和一把剪刀,表演剪刀剪布过程,提出问题:剪布时,用力握紧把手,引发了什么变化?进而使什么也发生了变化?学生观察、思考、回答,得出结论: 二、自主探究1.学生画直线AB 、CD 相交于点O,并说出图中4个角,两两相配共能组成几对角? 各对角的位置关系如何?根据不同的位置怎么将它们分类?学生思考并在小组内交流,全班交流.教师再提问:如果改变∠AOC 的大小, 会改变它与其它角的位置关系和数量关系吗?(1)O DCB A3.邻补角、对顶角概念 邻补角的定义是: 对顶角角的定义是: 5.对顶角性质.(1)学生说一说在学习对顶角概念后,结果实际操作获得直观体验发现了什么?并说明理由。
对顶角性质:( 2)学生自学例题例:如图,直线a, b 相交,∠1=40°,求∠2,∠3,∠4的度数.【课堂练习】: 1.课本P3练习2. 课本P8习题1【要点归纳】:邻补角、对顶角的概念及性质:【拓展训练】1. 如图1,直线AB 、CD 、EF 相交于点O,∠BOE 的对顶角是_______,∠COF 的邻补角是________; 若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=_________.(1) (2)2.如图2,直线AB 、CD 相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠EOF=________。
第五章相交线与平行线全章导学案

第五章 相交线与平行线 第一课时:§5.1.1 相交线学习目标1. 了解邻补角、对顶角,2. 能找出图形中的一个角的邻补角和对顶角3. ,理解对顶角相等,并能运用它解决一些问题. 一、自主学习阅读P 1-3课文,回答以下问题:1.探索一:完成课本P 2页的探究,填在课本上.2.你能归纳出“邻补角”的定义吗? . 3.“对顶角”的呢? . 二、合作探究 练习一:1.如图1所示,直线AB 和CD 相交于点O ,OE 是一条射线. (1)写出∠AOC 的邻补角:____ _ ___ __; (2)写出∠COE 的邻补角: __; (3)写出∠BOC 的邻补角:____ _ ___ __;(4)写出∠BOD 的对顶角:____ _.2.如图所示,∠1与∠2是对顶角的是( )探索二:任意画一对对顶角,量一量,算一算,它们相等吗?如果相等,请说明理由. 请归纳“对顶角的性质”: . 练习二:1.如图,直线a ,b 相交,∠1=40°,则∠2=_______∠3=_______∠4=_______ 2.如图直线AB 、CD 、EF 相交于点O ,∠BOE 的对顶角是______,∠COF 的邻补角是____,若∠AOE =30°,那么∠BOE =_______,∠BOF =_______3.如图,直线AB 、CD 相交于点O ,∠COE =90°,∠AOC =30°,∠FOB =90°, 则∠EOF =_____.三、课堂小结1.“对顶角的性质”: . 四、当堂检测1.若两个角互为邻补角,则它们的角平分线所夹的角为 度.2.如图所示,直线a ,b ,c 两两相交,∠1=60°,∠2=23∠4,•求∠3、∠5的度数. b a 4321第1题 F E O D C B A第2题 F EOD C B A 第3题 图13.如图所示,有一个破损的扇形零件,•利用图中的量角器可以量出这个扇形零件的圆心角的度数,你能说出所量的角是多少度吗?你的根据是什么? 4.探索规律:(1)两条直线交于一点,有 对对顶角; (2)三条直线交于一点,有 对对顶角; (3)四条直线交于一点,有 对对顶角; (4)n 条直线交于一点,有 对对顶角. 五、课外作业1、课本:P7习题1、2、8、92、选用课时作业:A 部分基础训练及中考链接;B 基础训练、拓展训练及中考链接。
(完整版)相交线与平行线复习导学案

第五章相交线与平行线复习导学案教学目标1.经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化, 梳理本章的知识结构.2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.3.认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案.重点、难点重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.难点:垂直、平行的性质和判定的综合应用.一.知识点回顾1.两直线相交所成的四个角中,有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为_____________.2.两直线相交所成的四个角中,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种关系的两个角,互为__________.对顶角的性质:______ _________.3.两直线相交所成的四个角中,如果有一个角是直角,那么就称这两条直线相互_______.垂线的性质:⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中,_______________.4.直线外一点到这条直线的垂线段的长度,叫做________________________.5.两条直线被第三条直线所截,构成八个角,在那些没有公共顶点的角中,⑴如果两个角分别在两条直线的同一方,并且都在第三条直线的同侧,具有这种关系的一对角叫做___________ ;⑵如果两个角都在两直线之间,并且分别在第三条直线的两侧,具有这种关系的一对角叫做____________ ;⑶如果两个角都在两直线之间,但它们在第三条直线的同一旁,具有这种关系的一对角叫做_______________.6.在同一平面内,不相交的两条直线互相___________.同一平面内的两条直线的位置关系只有________与_________两种.7.平行公理:经过直线外一点,有且只有一条直线与这条直线______.推论:如果两条直线都与第三条直线平行,那么_____________________.8.平行线的判定:⑴两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:_____________________________________.⑵两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:___________________________.⑶两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:________________________________________. 9.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线_______ .10.平行线的性质:⑴两条平行直线被第三条直线所截,同位角相等.简单说成:_________________.⑵两条平行直线被第三条直线所截,内错角相等.简单说成:__________________________________.⑶两条平行直线被第三条直线所截,同旁内角互补.简单说成:____________________________________ .自我检测1.如果两个角是邻补角,那么一个角是锐角,另一个角是钝角.( )2.平面内,一条直线不可能与两条相交直线都平行.( )3.两条直线被第三条直线所截,内错角的对顶角一定相等.( )4.互为补角的两个角的平行线互相垂直.( )5.两条直线都与同一条直线相交,这两条直线必相交.( )6.如果乙船在甲船的北偏西35°的方向线上, 那么从甲船看乙船的方向角是南偏东规定35°.( )6.如图,,8,6,10,BC AC CB cm AC cm AB cm⊥===那么点A到BC的距离是_____,点B到AC的距离是_______,点A、B两点的距离是_____,点C到AB的距离是________.7.设a、b、c为平面上三条不同直线,a)若//,//a b b c,则a与c的位置关系是_________;b)若,a b b c⊥⊥,则a与c的位置关系是_________;c)若//a b,b c⊥,则a与c的位置关系是________.8.如图,已知AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG的度数.9.如图,AOC∠与BOC∠是邻补角,OD、OE分别是AOC∠与BOC∠的平分线,试判断OD与OE的位置关系,并说明理由.10.如图,AB ∥DE ,试问∠B 、∠E 、∠BCE 有什么关系.解:∠B +∠E =∠BCE 过点C 作CF ∥AB ,则B ∠=∠____( ) 又∵AB ∥DE ,AB ∥CF ,∴____________( ) ∴∠E =∠____( ) ∴∠B +∠E =∠1+∠2即∠B +∠E =∠BCE .11.⑴如图,已知∠1=∠2 求证:a ∥b .⑵直线//a b ,求证:12∠=∠.12.阅读理解并在括号内填注理由:如图,已知AB ∥CD ,∠1=∠2,试说明EP ∥FQ . 证明:∵AB ∥CD ,∴∠MEB =∠MFD ( ) 又∵∠1=∠2,∴∠MEB -∠1=∠MFD -∠2, 即 ∠MEP =∠______∴EP ∥_____.( )11. 已知DB ∥FG ∥EC ,A 是FG 上一点,∠ABD =60°,∠ACE =36°,AP 平分∠BAC ,求:⑴∠BAC 的大小;⑵∠P AG的大小.12. 如图,已知ABC ∆,AD BC ⊥于D ,E 为AB 上一点,EF BC ⊥于F ,//DG BA 交CA 于G .求证12∠=∠.13. 已知:如图∠1=∠2,∠C =∠D ,问∠A 与∠F 相等吗?试说明理由.。
人教版七年级下册第五章 相交线与平行线《复习课》导学案

第五章复习课1.知道对顶角、邻补角、垂线的概念和性质.2.知道平行线的概念、性质,会判断两条直线是否平行,能综合运用平行线的性质和判定解决问题.3.知道平移的概念、性质,在对平移的探索和应用过程中体会数学的美,增强审美意识.4.知道什么是命题,会证明一个命题是真命题,会用举反例的方法说明一个命题是假命题.5.重点:相交线的性质及应用,平行线的性质和判定的综合应用,平移的性质及应用.◆体系构建补全本章知识网络图.◆核心梳理1.对顶角相等.2.两条直线相交所成的四个角中,如果有一个角是直角,那么这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.3.垂线的两条性质:(1)在同一平面内,过一点有且只有一条直线与已知直线垂直;(2)连接直线外一点与直线上各点的所有线段中,垂线段最短.4.平行公理:经过直线外一点,有且只有一条直线与这条直线平行.推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.5.平行线的判定和性质:6. 判断一件事情的语句叫做命题,命题分为真命题和假命题.其中正确性是经过推理证实的,这样的真命题叫做定理.7.平移的两个要素:平移的方向和平移的距离.平移的特征:(1)平移不改变图形的形状和大小;(2)对应点的连线段平行(或在同一条直线上)且相等.专题一邻补角和对顶角的性质及应用1.如图,直线l1,l2,l3相交于一点,则下列答案中,全对的一组是(D)A.∠1=90°,∠2=30°,∠3=∠4=60°B.∠1=∠3=90°,∠2=∠4=30°C.∠1=∠3=90°,∠2=∠4=60°专题二垂线的性质及应用2.如图,直线AB、CD相交于O,OM⊥AB.(1)若∠1=∠2,求∠NOD的度数.∠BOC,求∠BOD的度数.(2)若∠1=14解:(1)∵OM⊥AB,∴∠1+∠AOC=90°,又∵∠1=∠2,∴∠NOC=90°,∴∠NOD=90°.专题三平行线的判定3.如图,AB⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.(1)判断CD与AB的位置关系.(2)BE与DF平行吗?为什么?解: (1)CD与AB平行.(2)平行.因为AB⊥BD,CD⊥MN,所以∠ABM=∠CDM=90°.专题四平行线的性质及应用4.如图,l1∥l2,AB⊥l1 ,∠ABC=130°,那么∠θ的度数为(C)A.60°B.50°C.40°D.30°5.如图,AB∥CD,分别探讨下列四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得四个关系中任意选取一个说明理由.解:(1)∠APC+∠PAB+∠PCD=360°;(2)∠APC=∠PAB+∠PCD;(3)∠APC=∠PCD-∠PAB;(4)∠APC=∠PAB-∠PCD.理由如下:不妨选取(1)加以证明:如图,过P作PF∥AB,所以∠A+∠APE=180°.又因为AB∥CD,AB∥PF,所以CD∥PF.所以∠C+∠FPC=180°.所以∠A+∠APC+∠C=360°.【方法归纳交流】平行线间过转折点作平行线,是一种常用的作辅助线的方法.见《导学测评》P9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章相交线与平行线复习导学案
一.知识点回顾
1、两直线相交所成的四个角中,有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为_____________.
2、两直线相交所成的四个角中,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种关系的两个角,互为__________.对顶角的性质:______ _________.
3、两直线相交所成的四个角中,如果有一个角是直角,那么就称这两条直线相互_______.垂线的性质:⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中,_______________.
4、直线外一点到这条直线的垂线段的长度,叫做________________________.
5、两条直线被第三条直线所截,构成八个角,在那些没有公共顶点的角中,⑴如果两个角分别在两条直线的同一方,并且都在第三条直线的同侧,具有这种关系的一对角叫做___________ ;⑵如果两个角都在两直线之间,并且分别在第三条直线的两侧,具有这种关系的一对角叫做____________ ;⑶如果两个角都在两直线之间,但它们在第三条直线的同一旁,具有这种关系的一对角叫做_______________.
6、在同一平面内,不相交的两条直线互相___________.同一平面内的两条直线的位置关系只有________与_________两种.
7、平行公理:经过直线外一点,有且只有一条直线与这条直线______.
推论:如果两条直线都与第三条直线平行,那么_____________________.
8、平行线的判定:⑴两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:_____________________________________.⑵两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:___________________________.
⑶两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:
________________________________________.
9、在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线_______ .
10、平行线的性质:⑴两条平行直线被第三条直线所截,同位角相等.简单说成:_________________.⑵两条平行直线被第三条直线所截,内错角相等.
简单说成:__________________________________.⑶两条平行直线被第三条直线所截,同旁内角互补.简单说成:____________________________________ .
11、判断一件事情的语句,叫做_______.命题由________和_________两部分组成.题设是已知事项,结论是______________________.命题常可以写成“如果……那么……”的形式,这时“如果”后接的部分是_____,“那么”后接的部分是_________.如果题设成立,那么结论一定成立.像这样的命题叫做___________.如果题设成立时,不能保证结论一定成立,像这样的命题叫做___________.定理都是真命题.
12、把一个图形整体沿某一方向移动,会得到一个新图形,图形的这种移动,叫做平移变换,简称_______.图形平移的方向不一定是水平的.
13、平移的性质:⑴把一个图形整体平移得到的新图形与原图形的形状与大小完全______.
⑵新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段_________________.
自我检测
1.如果两个角是邻补角,那么一个角是锐角,另一个角是钝角.( )
2.平面内,一条直线不可能与两条相交直线都平行.( )
3.两条直线被第三条直线所截,内错角的对顶角一定相等.( )
4.互为补角的两个角的平行线互相垂直.( )
5.两条直线都与同一条直线相交,这两条直线必相交.( )
6.如果乙船在甲船的北偏西35°的方向线上, 那么从甲船看乙船的方向角是南偏东规定35°.( )
6.如图,,8,6,10,
BC AC CB cm AC cm AB cm
⊥===那么点A到BC的距离是_____,点B
到AC的距离是_______,点A、B两点的距离是_____,点C到AB的距离是________.
7.设a、b、c为平面上三条不同直线,
若//,//
a b b c,则a与c的位置关系是_________;
若,
⊥⊥,则a与c的位置关系是_________;
a b b c
若//
⊥,则a与c的位置关系是________.
a b,
b c
8.如图,已知AB 、CD 、EF 相交于点O ,AB ⊥CD ,OG 平分∠AOE ,∠FOD =28°,求∠COE 、
∠AOE 、∠AOG 的度数.
9.如图,AOC ∠与BOC ∠是邻补角,OD 、OE 分别是AOC ∠与BOC ∠的平分线,试判断
OD 与OE 的位置关系,并说明理由.
10.如图,AB ∥DE ,试问∠B 、∠E 、∠BCE 有什么关系.
解:∠B +∠E =∠BCE
过点C 作CF ∥AB ,
则B ∠=∠____( )
又∵AB ∥DE ,AB ∥CF ,
∴____________( )
∴∠E =∠____( )
∴∠B +∠E =∠1+∠2
即∠B +∠E =∠BCE .
11.⑴如图,已知∠1=∠2 求证:a ∥b .⑵直线//a b ,求证:12∠=∠.
12.阅读理解并在括号内填注理由:
如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
证明:∵AB∥CD,
∴∠MEB=∠MFD()
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥_____.()
13、已知DB∥FG∥EC,A是FG上一点,∠ABD=60°,∠ACE=36°,AP平分∠BAC,求:⑴∠BAC的大小;⑵∠P AG的大小.
14、如图,已知ABC
⊥于F,//
DG BA交
⊥于D,E为AB上一点,EF BC
∆,AD BC
CA于G.求证12
∠=∠.
15、已知:如图∠1=∠2,∠C=∠D,问∠A与∠F相等吗?试说明理由.。
