绕对称轴转动的均匀带电圆盘的磁场分布
川师大学物理第十一章-恒定电流的磁场习题解

第十一章 恒定电流的磁场11–1 如图11-1所示,几种载流导线在平面内分布,电流均为I ,求它们在O 点处的磁感应强度B 。
(1)高为h 的等边三角形载流回路在三角形的中心O 处的磁感应强度大小为 ,方向 。
(2)一根无限长的直导线中间弯成圆心角为120°,半径为R 的圆弧形,圆心O 点的磁感应强度大小为 ,方向 。
…解:(1)如图11-2所示,中心O 点到每一边的距离为13OP h =,BC 边上的电流产生的磁场在O 处的磁感应强度的大小为012(cos cos )4πBC I B dμββ=-^IB21图11–2图11–1…B(a )AE(b )0(cos30cos150)4π/3Ih μ︒︒=-=方向垂直于纸面向外。
另外两条边上的电流的磁场在O 处的磁感应强度的大小和方向都与BC B 相同。
因此O 处的磁感应强度是三边电流产生的同向磁场的叠加,即3BC B B ===方向垂直于纸面向外。
(2)图11-1(b )中点O 的磁感强度是由ab ,bcd ,de 三段载流导线在O 点产生的磁感强度B 1,B 2和B 3的矢量叠加。
由载流直导线的磁感强度一般公式012(cos cos )4πIB dμββ=- 可得载流直线段ab ,de 在圆心O 处产生的磁感强度B 1,B 3的大小分别为01(cos0cos30)4cos60)IB R μ︒=︒-︒π(0(12πI R μ=-031(cos150cos180)4πcos60IB B R μ︒==︒-︒0(12πI R μ=-】方向垂直纸面向里。
半径为R ,圆心角α的载流圆弧在圆心处产生的磁感强度的大小为04πI B Rμα=圆弧bcd 占圆的13,所以它在圆心O 处产生的磁感强度B 2的大小为00022π34π4π6II I B R R Rμμαμ===方向垂直纸面向里。
因此整个导线在O 处产生的总磁感强度大小为000012333(1)(1)0.212π22π26I I I I B B B B R R R Rμμμμ=++=-+-+=方向垂直纸面向里。
3.3真空中安培环路定理

dr
dq = σds = 2πσrdr
dI = σω rdr
2π ω 2π
R
q
ω
2r 2r 0dI R 0 σωrdr B = ∫ dB = ∫ = ∫0 2r 2r
0σωR = 2
dB =
0dI
=
0
σωrdr
方向
电场、 电场、磁场中典型结论的比较
电 电
长 直 圆 柱 面 长 直 圆 柱 体 内 内
dl2
B1 dl1 = B2 dl2 =
0 I
2π
dφ
I
r1
r2
l
B1 dl1 + B2 dl2 = 0
∫ B d l = 0
l
多电流情况
B = B1 + B2 + B3
I3
I1
I2
∫ B d l = (I
l 0
2
I3 )
l
以上结果对任意形状 以上结果对任意形状 任意 的闭合电流( 的闭合电流(伸向无限远 的电流)均成立. 的电流)均成立
0 ev 4π×107 ×1.6×1019 × 0.2×106 ∴B = = ≈ 1.14T 2 2 20 4π r 4π× 0.53 ×10
0 qv × r ∵B = 4π r 2
又 v ⊥r
r
∵磁矩 m = ISn p
S = πr 2 I = q = ω q = v e
T 2π 2πr
方向
vLeabharlann 电流均匀分布的长直圆柱导体的磁场 解 1)对称性分析 2)选取回路 ) )
I
r>R
0< r < R
回路包围 的电流为
∫ B dl = ∫ Bdl = 2πrB
均匀带电圆盘转动下的磁场分布

强度越大,离圆,fi,0越远,电磁场强度越小,在无穷远处磁感应强度为0。 3.4结论
.
由(23)式及以上讨论,并结合图2、图3、图4可知,绕均匀带电圆盘对称轴匀速转动时产生的电磁场是一个相当于一个 平面螺线管产生的电磁场,为稳恒磁场,没有辐射的电磁场。
参考文献 【1】郭硕鸿.电动力学【M】.第二版.北京:高等教育出版社.1996,160—177 【2】虞福春,郑春开.电动力擘【M】.北京:北京大学出版社,2003,157—177 【3】孙景李.经典电动力学【M】.北京:高等教育出版社,1987.276—294 【4】李维,田晓岑.电磁辐射问题的简化处理【J】.大学物理,2005,24(4):24—27 【5】谢东,刘庆想.平面螺线外的磁场研究【J】.大学物理,2005,24(9):23—24 【6】林璇英,张之翔.电动力学题解【M】.北京:科学出版社,1999,57—66 【7】陈乃云,魏东北,李一玖.电磁场与电磁波理论基础【M】M.北京:中国铁道出版社,2001,86一103 【8】P.Lorrain and D.R.Corson.Electromagnetic Fields and Waves【M】。1970
(18)
2.2具体求解圆盘矢势jG)
把(10)式代入(18)中得此圆环产生的矢势为:
幽p)=等‘,f2办。r”而雨cos0蒜'd0'面
(19)
jP…oQc。嘭f∥办。r而霄cos丽O'd0' 积分便得圆盘旋转时在尹处的P点所产生的矢势积分表达式为:
’jp)2(20) Nhomakorabea利用幂级数:
6^…=薹(_1)留州<,) 志小!_1-.34 √l—x
m古鲁=。 V c‘Ot
(7)
V2五专等一舻
V2矽专窘一詈
高二物理竞赛利用安培环路定理求磁场的分布PPT(课件)

真空中两无限大的均匀带电平行板?
解: 0 r R, B d l 0 l
B0
r R,
l B d l 0I
B 0I 2 r
例4 在一无限大的导体平板上均匀流有电流密度为 j 的面电流,求平板两侧的磁感应强度。
解:
j
dI
dI’
dB
俯视图
1) 对称性分析:载流平面产生的磁场,其方向与平面 平行,与平面电流成右手螺旋方向。
2) 选回路 L:矩形环路 有对称性分布电流的磁感应强度。
例1 求载流螺绕环的磁场分布
解:1) 对称性分析;B 线为与 螺绕环共轴的圆周。
2) 选回路 L。
L B dl B L dl B2 r
L
0 Iint 0NI
L d
B 0 NI 2 r
(R1 r R2 )
L
r
B 0 (r R1, r R2 )
静电场的高斯定理: (1) 均匀密绕螺线管
E dS q 且与轴线距离相同的各点的磁感强度B值相同.故可以
真空中两无限大的均匀带电平行板?
r
为半径、以轴线为圆心、过P点作一圆形环S路
对均匀密绕螺绕环,磁场几乎全部集中于管内,在环的外部空间,磁感应强度处处为零。
l
为积分路径,利用安培环路定理i求ntB 0
I . dB
dI B
B 的方向与 I 成右螺旋
0 r R,
r R,
B
0 Ir 2 R2
B 0I 2 r
I
R
0I
B
2 R
oR r
例3 无限长载流圆柱面的磁场
L1
(2) 求通过两柱面间长度为L的径向纵截面的磁通量。
r
例3 无限长载流圆柱面的磁场
大学物理(第四版)课后习题及答案磁场
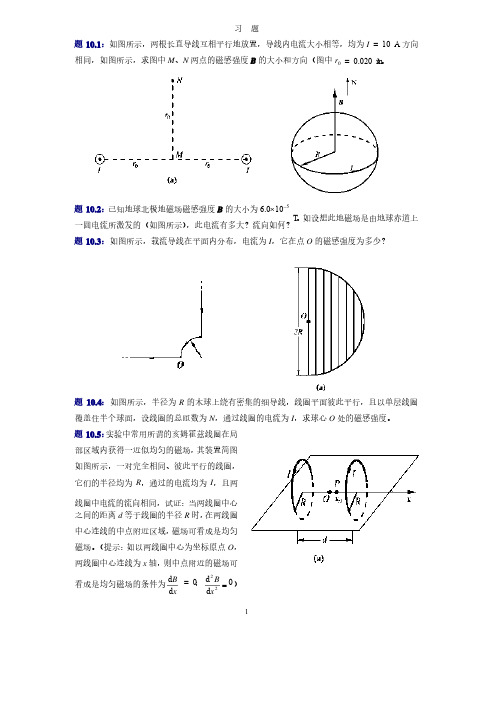
1 习题题10.1:如图所示,两根长直导线互相平行地放置,导线内电流大小相等,均为I = 10 A ,方向,方向相同,如图所示,求图中M 、N 两点的磁感强度B 的大小和方向(图中r 0 = 0.020 m )。
题10.2:已知地球北极地磁场磁感强度B 的大小为6.0´10-5 T 。
如设想此地磁场是由地球赤道上一圆电流所激发的(如图所示),此电流有多大?流向如何?题10.3:如图所示,载流导线在平面内分布,电流为I ,它在点O 的磁感强度为多少?题10.4:如图所示,半径为R 的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈覆盖住半个球面,设线圈的总匝数为N ,通过线圈的电流为I ,求球心O 处的磁感强度。
题10.5:实验中常用所谓的亥姆霍兹线圈在局部区域内获得一近似均匀的磁场,其装置简图如图所示,一对完全相同、彼此平行的线圈,它们的半径均为R ,通过的电流均为I ,且两线圈中电流的流向相同,试证:当两线圈中心之间的距离d 等于线圈的半径R 时,在两线圈中心连线的中点附近区域,磁场可看成是均匀磁场。
(提示:如以两线圈中心为坐标原点O ,两线圈中心连线为x 轴,则中点附近的磁场可看成是均匀磁场的条件为x B d d = 0;0d d 22=x B )题10.6:如图所示,载流长直导线的电流为I ,试求通过矩形面积的磁通量。
,试求通过矩形面积的磁通量。
题10.7:如图所示,在磁感强度为B 的均匀磁场中,有一半径为R 的半球面,B 与半球面轴线的夹角为a ,求通过该半球面的磁通量。
,求通过该半球面的磁通量。
题10.8:已知10 10 mmmm 2裸铜线允许通过50 50 A A 电流而不会使导线过热。
电流在导线横截面上均匀分布。
求:(1)导线内、外磁感强度的分布;(2)导线表面的磁感强度。
)导线表面的磁感强度。
题10.9:有一同轴电缆,其尺寸如图所示,两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑。
电场及磁场的对称性分析

电场及磁场的对称性分析第21卷第3期天津职业技术师范大学2011年9月JOURNALOFTIANJINUNIVERSITY0FTECHN0L0GYANDEDUCATIONV oI.21No.3Sep.2011电场及磁场的对称性分析李凤敏(天津职业技术师范大学理学院,天津300222)摘要:利用对称性的概念和矢量场的对称性分析计算方法,讨论了某些具有对称性的带电体场及载流体场的计算,特别是对其中的重点和难点问题进行了详细的分析和论证.对称性方法可以使具有对称性的场的计算问题的物理图像清晰,简化计算,易于理解.关键词:对称性;极矢量;轴矢量;长直螺线管;感生电场;轴对称载流体中图分类号:0441.4文献标识码:A文章编号:2095—0926(2011)03—0047—03 SymmetryanalysisonelectricfieldandmagneticfieldLIFeng——rain(SchoolofScience,TianjinUniversityofTechnologyandEducation,Tianjin300222,China) Abstract:Thefieldsofsomeofthechargedobjectsandcurrentcarryingobjectswithcertainsy mmetriesarecal—culatedusingthesymmetryconceptandsymmetryanalysismethod,andespecially,thekeypo intsindealingwithsuchproblemsareinvestigatedindetail.Indealingwiththeseproblems,symmetryanalysism ethodcanmakethephysicalpicturesmoreclear,thecalculationsmoresimple,andtheunderstandingmucheasier .Keywords:symmetry;polarvector;axialvector;longandstraightsolenoid;inducedelectricf ield;currentcarrierwithaxialsymmetry对称性又称不变性,在自然界普遍存在.对称性是指体系在某种操作下变成与原状态相同或等价的状态.对称性分析在经典物理及理论物理中都有着广泛的应用.在大学物理电磁学教学中常见的对称操作有平移,转动及镜像反射l11等.根据大学物理教学大纲的基本要求,用高斯定理及安培环路定理进行场的计算是学生必须掌握的内容,而这往往又是教学的难点.比如各类教材中都会有这样的例子:长直螺线管磁场变化时产生的感生电场的计算,电动势的计算,轴对称载流体的磁场分布,轴对称带电体的场强分布等.在以往的教材及教学过程中,对此类问题的处理往往都是根据对称性的特点,定性地解释电场及磁场的大小与方向的分布情况.这种处理问题的方法显然缺乏说服力,因此如果能用比较简单的数学方法来证明,这样不仅使教学内容逻辑性更强,同时也会使学生对所学内容理解更深,概念更清楚.1关于场矢量在电磁学部分,我们遇到的场矢量无非是电场及磁场.但由于电场强度E与磁感应强度在镜像反射下具有不同的变换性质,这导致了电场与磁场许多不同的性质.如图1所示,电场强度E是极矢量,即在镜像反射变换下,与镜面垂直的分量反向,平行分量不变;而磁感应强度为轴矢量,即在镜像反射变换下,『E图1电场强度及磁感应强度镜像反射变化收稿日期:2011-05—17作者简介:李凤敏(1965一),女,副教授,硕士,研究方向为物理教学法?48?天津职业技术师范大学第21卷与镜面垂直的分量不变,平行分量反向嘲.正是由于电场强度E和磁感应强度的这一特性,使得在分析具有某种对称性的带电体场或载流体场时会带来很大的方便.2利用对称性分析具体实例2.1长直螺线管磁场变化引起的感生电场在电磁学教学内容中,通常涉及长直螺线管磁场变化时产生的感生电场的计算,比如大部分教材中都有这样一个例题:通有时变电流的无限长直螺线管内的磁场曰随时间变化,如图2所示.已知的数值,cl求它在管内,外激发的感生电场的分布.,/一,一~,\,/,\,//××x,\『,0\××××××'××:,,×××/,/,\,/,/\~一一一,,一般大学物理教材中给出的解通常如下吲:由磁场分布的轴对称性可知,感生电场的分布也具有轴对称性.即以长直螺线管轴线上任意点为中心的同一闭合回路上各处感生电场的大小相等,方向沿回路的切线方向.因此沿该回路的感生电场的环量由下式求得:.d,:一8.ds(1)Jd当r<R时,由(1)式可得:E2叮『r:一1Tr2Q/7故E:一/-二Ub当>R时,由(1)式可得:E2:一:Q故E:一二,Lib对这样的分析过程并不存在异议,但问题是学生并不清楚为什么在这种情况下产生的感生电场呈上述分布,而其他方向上却不存在.对这一问题的处理, 可以从磁场的对称性分布人手得到解答.设长直螺线管内的磁场变化时产生的感生电场为E,以螺线管轴线上任意点为坐标原点,建立柱坐标系,则空间任意点的感生电场为:E=最+E+E(Z轴与I司向)如图3所示,由于长直螺线管内的磁场具有轴对称性且沿z轴的平移不变性,以该轴为轴线做一闭合圆柱面,由磁场分布的对称性可知,在闭合圆柱面s, 5两个圆面上,对应位置的感生电场的大小,方向均相同,对该闭合面,感生电场的通量为零:即:《Eds=0fEl"(Is=JEi"d$+』El"ds+JEi'ds=0Sls2S▲Z图3以螺线管轴线为轴取闭合面(2)由于只有E及,分量对该闭合面的通量有贡献,因此上式积分结果为:Ezs—EzS+E~2'rrrL:0其中,AS为5,5圆面面积.故E=0即感生电场的径向分量为零.如图4所示,做一闭合回路,则感生电场沿该回路的环量由式(3)给出:fEds:一『『粤.ds(3)L?L丑.,,_—.\,i\一一/图4取一闭合回路由于感生电场在螺线管内,外垂直于轴的方向上的数值并不相等,因此由(3)计算可得:(E岛)z=0,由于E≠,且l#0所以岛=0(其中,分男4为螺线管内外的感生电场)第3期李凤敏:电场及磁场的对称性分析?49?即感生电场沿轴向的分量亦为零,由此证明由长直螺线管磁场变化引起的感生电场的分布只存在E分量,亦即空间各处的感生电场只有切向分量.2.2轴对称载流体的磁场对无限长载流圆柱面(或体),其磁场的分布可由安培环路定理给出[41.一般的求解过程中,只是认为此类载流体由于电流分布的对称性可判断出磁场分布的特点,并未给出严格的证明,此处利用对称性原理给出磁场方向的分析.设电流分布关于平面∑镜像对称,则该电流在∑上激发的的磁场必垂直于∑平面[51(当≠0时),如图5所示图5关于平面对称的电流元在载流圆柱面上任意对称的位置,A:取两个关于平面对称的电流元,ldZ,hall:,分别记为a与b,两电流元到∑平面上任意P点的位矢分别为,和r2,D点为两电流元连线与∑平面的交点,建立图4所示坐标系,由对称性可知:ax=bx,=by,=一bz;/'2x=rh,r=n=0,r五=一rk(4)根据毕奥一萨伐尔定律,任意电流元的磁场为::掣,为此分别计算口Xrl及bXr2onr根据矢量叉乘公式:A×B=(Aysz—A)f+(一A』+(一A)可得:axg1=(k一~zt'ly)f+(rl一kj,+(y—l);b×,=(6,一b.rzy)i+(6,—bxr~)j+(6一byrz~)k;所以(a×,.1+b×r2)=(actk一r1+6,一6.r2v)f+(r1一rk+6一b~r2,)j+(Ctxrl一ayr1+b~rzy—byrz~)k. 利用式(4)的对应关系,可以得到下述结果:(a×,1+b×g2)=(~xl'ly—r上,1+bxr升一byrz~)k= (一ayrk—bT~)k≠0.由此可知,任何关于平面∑呈对称分布的电流元产生的磁场均垂直于对称面.根据上述分析可以断定载流圆柱面(或体)的磁场分布的规律.通过比较直观的数学证明,可以帮助学生深入理解呈轴对称载流体的磁场分布特点.2.3无限长均匀带电圆柱面的电场对无限长均匀带电圆柱面来说,教材中的解均为根据电荷分布的轴对称性认为电场的分布同样也是轴对称的,然后取一同轴的闭合圆柱面直接利用高斯定理解出[31.当然此类问题也可直接积分得出结果,但积分求解过程较麻烦且对大多数学生来说此积分运算困难.在此可以直接利用对称性证明无限长均匀带电圆柱面的场强的方向分布特点.由于此带电体电荷分布为轴对称的,在此不妨设空间的电场分布为:E=Ez+Er+E其中,最,E,为柱坐标系中的3个分量(取对称轴为z轴).过对称轴做一平面,显然带电体关于这一平面是镜像对称的.电场关于此平面同样镜像对称.由于E是极矢量,在镜像反射下应有:=一,另一方面镜像对称要求=,因此只有=0满足条件.同样做一垂直于对称轴的任一平面,显然该平面亦为此带电体的镜像对称面,因此由电场强度是极矢量,可以用同样的方法证明E=0.至此证明了场强的分布只有径向分量E存在.3结束语通过以上几个具体实例,可以看到利用对称性可以很直观地证明电荷及电流分布具有对称性场方向的分布特点.电磁学中关于具有对称分布的带电体及载流体类型较多,因此在解题之前不妨先考虑用对称性分析的方法对场的分布情况进行简要的证明,这样既有利于简化计算,同时又可以帮助学生加深对场概念的理解.参考文献:[1]孙海滨.物理学中的对称性与守恒律[J1.物理与工程, 2006,16(4):49—52.[2]陈熙谋,赵凯华.电磁学教学中对称性分析的积极意义[J].大学物理,2005,24(4):3—5.[3]程守洙,江之永.普通物理学[M].5版.北京:高等教育出版社,1999.[4]张三慧.大学物理学——电磁学[M].2版.北京:清华大学出版社,1999.[5]梁灿斌,秦光戎,梁竹健.电磁学[M].2版,北京:高等教育出版社,2008.。
带电粒子在磁场中的运动 ppt课件

(2)电子从C到D经历的时间是多少?
(电子质量me=
9.1×10-31kg,电量e ppt课件
=
1.6×10-19C)
13
◆带电粒子在单直边界磁场中的运动
①如果垂直磁场边界进入,粒子作半圆运动后 垂直原边界飞出;
O
O1
B
S
ppt课件
14
②如果与磁场边界成夹角θ进入,仍以与磁场 边界夹角θ飞出(有两种轨迹,图中若两轨迹 共弦,则θ1=θ2)。
运动从另一侧面边界飞出。
量变积累到一定程度发生质变,出现临界状态(轨迹与边界相切)
ppt课件
24
【习题】
1、如图所示.长为L的水平极板间,有垂直纸面向内的
匀强磁场,磁感强度为B,板间距离也为L,板不带电,
现有质量为m,电量为q的带正电粒子(不计重力),从左
边极板间中点处垂直磁感线以速度v水平射入磁场,欲
界垂直的直线上
度方向垂直的直线上
①速度较小时,作半圆运动后 从原边界飞出;②速度增加为 某临界值时,粒子作部分圆周 运动其轨迹与另一边界相切; ③速度较大时粒子作部分圆周 运动后从另一边界飞出
①速度较小时,作圆周运动通过射入点; ②速度增加为某临界值时,粒子作圆周 运动其轨迹与另一边界相切;③速度较 大时粒子作部分圆周运动后从另一边界 飞出
圆心
在过
入射
vB
点跟
d
c
速度 方向
o
圆心在磁场原边界上
①速度较小时粒子作半圆 运动后从原边界飞出;② 速度在某一范围内时从侧 面边界飞出;③速度较大 时粒子作部分圆周运动从 对面边界飞出。
垂直
θv
B
的直
线上
①a 速度较小时粒子作部分b 圆周
两个均匀带电同心球面正式版

两个均匀带电同心球面正式版文档资料可直接使用,可编辑,欢迎下载作业31、 两个均匀带电同心球面,半径分别为0.10m 和0.30m ,小球面带电8100.1-⨯库仑,大球面带电8105.1-⨯库仑。
求离球心分别为m 2105-⨯,0.20m ,0.50m 处的电场强度。
2、 有两只电灯,一只是220伏,100瓦,另一只是220伏,40瓦,并联在220伏的电路上。
哪只电灯较亮?若串联时,哪只电灯较亮?为什么?3、 当一直径为0.02m 的10匝圆形线圈通以0.15安培的电流时,其磁矩为多大?若将这个线圈放于磁感应强度大小为1.5特斯拉的匀强磁场中,所受到的最大磁力矩为多少? 4、 有一面积s=6平方厘米的密绕线圈,共50匝,放入B=0.25特斯拉的均匀磁场中,且B的方向与线圈的轴线平行。
若使磁场B 在0.05秒内均匀地下降为零。
求线圈中所产生的感应电动势。
均匀带电圆盘转动下的磁场分布西南交通大学机械工程学院20090994 朱鹏飞[摘要]文章通过麦克斯韦方程导出电磁辐射公式在圆盘上任取一个带电小圆环小圆环转动形成电流电流产生电磁场利用场强叠加原理得整个带电环产生的电磁场再计算整个圆盘绕对称轴匀速转动产生的电磁场并进行适当的讨论,在此基础上增加了数字模拟下的均匀带电圆盘转动下的磁场立体分布,并加以讨论。
[关键词]均匀带电圆盘麦克斯韦方程推迟势磁感应强度引言人们在生活和生产中利用圆盘转动数不胜数,这些圆盘一旦带上电后就成为绕对称轴转动的均匀带电圆盘,由于转动产生电流,电流激电磁场.这种情况可看作若干环形线电荷所激发的电徽场的叠加,这是电磁学中的一个较重要的问题。
本文采用矢势对其进行求解.先通过麦克斯韦方程,达朗贝尔方程和洛伦兹变换条件推导出了载流圆盘周围空间的磁场分布完整的解析表达式。
进而求解转动带电圆盘的磁场,并对结果讲行讨论.1原理和公式的推导1.1波动方程绕对称轴转动在均匀带电圆盘的电磁辐射场应满足麦克斯韦方程组在真空中,取(1)式第一式的旋度并利用第二式及得:同样在(1)中消除电场,可得磁场的偏微分方程:1. 2电磁场的矢势和标势在恒定场中,由的无源性引入矢势使:在变化情况下电场与磁场发生直接关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绕对称轴转动的均匀带电圆盘的磁场分布
机械茅班 杨婧 20091018
摘 要:薄圆盘实现生活中高度对称的一类物体,应用广泛。
摩擦等一些方式使其带电,成为绕对称轴转动的均匀带电圆盘,由于转动产生电磁场,当带电量足够大和变速转动时的角加速度又比较大时,则产生的电磁辐射场将会干扰周围无线电接收机的正常工作,分析绕对称轴转动的均匀带电圆盘具有一定的现实意义。
本文从研究圆环电流出发,在圆盘上任取一个带电小圆环,小圆环转动形成电流,电流产生磁场,利用场强叠加原理得整个带电圆盘的电磁场。
关键词:匀速转动,麦克斯韦方程,推迟势,磁场强度
一.推迟势的推导
绕对称轴转动的均匀带电薄圆盘的电磁辐射场应满足麦克斯韦方程: (1)
220
22022
0221E E-()C 1J
t t
B B J
C t ρμεμ∂∂∇=∇+∂∂∂∇-=∇⨯∂
用矢势和标势为: (2)
B A
A E t ϕ=∇⨯∂=-∇-
∂
矢势和标势满足达朗贝方程和洛伦兹变换条件,于是(1)式得 (3)
22
02222
22021-C 110
A A J
t C t A C t μϕρϕεϕ∂∇=-∂∂∇-=-
∂∂∇+=∂
方程(3)的解为:
(4)
()
()
'0'0,,4,1,4r J r t c A r t dv r
r r t c r t dv r μπρϕπε⎛⎫- ⎪⎝⎭=⎛⎫- ⎪⎝⎭=⎰⎰
二.匀速转动时的磁场
如图1所示,设圆盘在xoy 平面内,对称轴为z 轴,转动的角速度w 不变薄圆盘(厚度不计)均匀带电,电量为Q ,圆盘半径为R ,则电荷密度
2Q R ρπ
=
.
图1 薄圆盘匀速转动时的空间磁场
在圆盘上任取一个细圆环,设圆环的半径为i R ,宽度为i dR ,则由于圆环转动时产生
的电流为
222i i
QwR I dR R ππ=
在圆环上任取一线元dl
,则
(5)
()()3''''2
2[sin cos ]i i
x y nQwR dR
Idl e wt d wt e wt d wt R π=-+
把(5)式代入(4)式得 (6)
()
()()()''2''''1
2'
00
2
20
1
1
,[sin cos ]
,44i x y J r t QwR e wt d wt e wt d wt d A r t dv r R r π
μμ
π
π
π-+==⎰
⎰
由叠加原理,(6)式得 (7)
()
()()2''''2022'
22
[sin cos ]
,2sin cos 4i x y a i i R e wt d wt e wt d wt Qw A r t R r R r wt R
π
μθπ-+=+-⎰⎰
由于1
i r i wR w e e c c <<<< ,得
(8)
'1
i
r R r r t t t t c
c
c -=-
=-≈-
利用幂级数
()()23
021!!11131351...1224246(2)!!1n n n x x x x
n x ∞
=-⋅⋅⋅=++++=-⋅⋅⋅-∑ 1x <
(7)式的分母利用幂级数展开,同时设P 点在中远区,r>>Ri 级数只取二级近似值 (9)
'22'1
11sin cos 2sin cos i i i R wt r r R r R r wt θθ⎛⎫≈+ ⎪
⎝
⎭+-
把(8)式和(9)式代入(7)式积分得
()
()()()()32022
,[sin cos ]1sin cos 4R i i r y Qw
R R A r t e kr wt e kr wt kr wt d kr wt R
r r π
μθπ⎡⎤
=--+-+--⎢⎥⎣⎦⎰⎰
20sin 0sin 221616y QwR QwR e e r r θθ
θ
μμππ== 其中y
e e θ= ,P 点选在Q=0上,由(2)式得,磁感强度为
(10)
()()()
22002223,,sin 2cos sin 1616r QwR QwR B r t A r t Qe e e r r θθ
μμθθππ=∇⨯=∇⨯=+
根据球坐标与直角坐标的关系:
2222r x y z =++
sin cos sin sin cos sin cos cos cos cos sin sin r x y z x y x y z e e e e e e e e e e e ϕθθϕθϕθϕϕθϕθϕθ
=++=-+=+-
可求得均匀带电圆盘在yoz 平面内的磁感强度: ()
()(
)203
222
2
2
2
03222
22222222
3sin cos 162cos sin 16cos sin y y
z z QwR B e y z QwR B e y z z
x y z x y x y z μθθπμθθπθθ=+=
-+=+++=
++
(x=0)
三.结果分析
根据推导所得公式,利用物理数字平台模拟绕对称轴匀速转动的均匀带电圆盘的磁场分布情况,更加直观地得出圆盘周围磁场的变化规律。
由物理数字平台模拟的结果如下图:
由模拟结果可知,调节滑动条1,2分别增大或减小电荷量及圆盘半径,圆盘周围磁感应强度相对应地增大或减小。
调节滑动条3增大或减小角速度,磁感应强度也相应增大或减小。
综合公式(10)及图形可知,绕对称轴匀速转动的均匀带电薄圆盘产生的磁场强度与时间t 无关,为稳恒磁场,没有辐射的电磁场。
带电量Q 越多,磁场越强;半径R 越大,磁场越强;角速度w 越大,磁场越强;离圆心O 越远,磁场强度越小,在无穷远处磁场强度为0。
本文的理论仅适用于圆盘移去负电荷后的带正电体,因为电子在高速转动时电荷重新分布。
参考文献:
【1】郭硕鸿.电动力学【M】.北京:人民教育出版社,1979.160-177
【2】虞福春,郑春开.电动力学【M】.北京:北京大学出版社,2003.157-177
【3】孙景李.经典电动力学【M】.北京:高等教育出版社,1987.276-294
【4】谢东,刘庆想.平面螺线外的磁场研究【J】.大学物理,2005,24(9):23-24
【5】朱平.园电流空间磁场分布.大学物理,200524(9):13-17。
