第三章 水动力学基础
武汉大学水力学教材第三章
第三章 水动力学基础 渐变流与急变流均属非均匀流。
急变流不可能是恒定流。
总水头线沿流向可以上升,也可以下降。
水力坡度就是单位长度流程上的水头损失。
扩散管道中的水流一定是非恒定流。
恒定流一定是均匀流,非恒定流一定是非均匀流。
均匀流流场内的压强分布规律与静水压强分布规律相同。
测管水头线沿程可以上升、可以下降也可不变。
总流连续方程 V1A1 = V2A2对恒定流和非恒定流均适用。
渐变流过水断面上动水压强随水深的变化呈线性关系。
水流总是从单位机械能大的断面流向单位机械能小的断面。
恒定流中总水头线总是沿流程下降的,测压管水头线沿流程则可以上升、下降或水平。
液流流线和迹线总是重合的。
14、 用毕托管测得的点流速是时均流速。
15、 测压管水头线可高于总水头线。
16、 管轴高程沿流向增大的等直径管道中的有压管流,其管轴压强沿流向增大。
17、 理想液体动中,任意点处各个方向的动水压强相等。
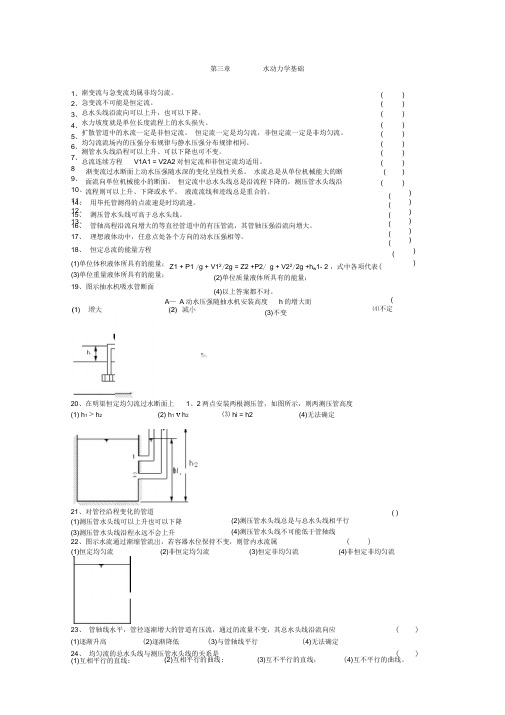
18、 恒定总流的能量方程(1)单位体积液体所具有的能量; (3)单位重量液体所具有的能量; 19、 图示抽水机吸水管断面 1、2、 3、 4、5、6、7、8 9、 10、 11、 12、 13、(( ( ( ( ( ( ( ( ( ( ( ( ( ( ((Z1 + P1 /g + V12/2g = Z2 +P2/ g + V22/2g +h w 1- 2 ,式中各项代表( (2)单位质量液体所具有的能量; (4)以上答案都不对。
A — A 动水压强随抽水机安装高度 h 的增大而 (3)不变( ⑷不定20、在明渠恒定均匀流过水断面上 1、2两点安装两根测压管,如图所示,则两测压管高度 (1) h 1 > h 2 (2) h 1 v h 2 ⑶ hi = h2(4)无法确定 hl 21、对管径沿程变化的管道 (1)测压管水头线可以上升也可以下降(3)测压管水头线沿程永远不会上升) ) ) ) ) ) ) ) ) ) ) ) ) ) ) ) ) )( ) (2)测压管水头线总是与总水头线相平行 (4)测压管水头线不可能低于管轴线 22、图示水流通过渐缩管流岀,若容器水位保持不变,则管内水流属( ) (1)恒定均匀流 (2)非恒定均匀流 (3)恒定非均匀流 (4)非恒定非均匀流 23、 管轴线水平,管径逐渐增大的管道有压流,通过的流量不变,其总水头线沿流向应 ( ) (1)逐渐升高 (2)逐渐降低 (3)与管轴线平行 (4)无法确定 24、 均匀流的总水头线与测压管水头线的关系是()(1)互相平行的直线;(2)互相平行的曲线; (3)互不平行的直线;(4)互不平行的曲线。
长安大学水力学第三章水动力学基本定律

若给定a,b,c,即 可以得到某一质点 的轨迹方程。-迹线
某一液体质点M,在t0时刻占有空间坐
标为(a、b、c),在任意t时刻所占有 的空间坐标为(x、y、z),则(x、y、 z)可表示为时间t与(a、b、c)起始坐 标的函数,即
z t
ux
x t
x(a,b, c,t) t
uy
y t
y(a,b, c,t) t
迹线——是指某个液体质点不同时刻所流经的空
间点所连成的线。流动的轨迹线
流线——是指某一时刻,在流场中,由许多质点
组成的一条光滑曲线,其上所有点的速度方向 都与该曲线相切。
流线能反映瞬时的流动方向 流线图
流线的基本特性
1.恒定流时,流线的形状和位置不随时间而改变。
因为整个流场内各点流速向量均不随
2.恒定流时液体质点运动的迹线与流线相重时合间。而改变,不同时刻的流线的形状
uz
z t
z(a,b, c,t) t
液体质点在任意时刻 的速度。 返回
(x,y,z)
t0
O M (a,b,c) x
y
欧拉法
ux ux (x, y, z,t) uy uy (x, y, z,t) uz uz (x, y, z,t)
ax
dux (x, y, z,t) dt
ay
duy (x, y, z,t) dt
本课程只研究恒定流。
如果流场中任何空间点上有任何一个运动要素是随时间而变化的,这种 水流称为非恒定流。
2.基本概念 Basics of Liquid Flow
• 迹线与流线 • 流管、元流(微小流束)、总流和过水断面 • 流量和断面平均流速 • 水流的分类 • 均匀流、渐变流过水断面的重要特性
第三章 水动力学基础 ppt课件

F y
Q( 2v2z 1v1z )
F z
11
ppt课件
恒定总流动量方程建 立了流出与流进控制体 的动量流量之差与控制 体内流体所受外力之间 的关系,避开了这段流 动内部的细节。对于有 些水力学问题,能量损 失事先难以确定,用动 量方程来进行分析常常 是方便的。
水排
12
ppt课件
水排简介
东汉初(公元31年)杜诗制造的 “水排”,利用溪水流作原动力, 转动鼓风机械供冶炼和铸造铁器农具。这种水平装置的转轮,利 用水流动量原理,是近代水轮机的先驱。水排主体包括装在同 一主轴上的两个水平木轮,将装有叶板的下轮放在河中,水流 冲击叶板即使下轮转动,上轮也同时转动,再带动旁边的绳轮 和连杆、平轴等传动机械,使鼓风的皮囊一开一合地连续运动, 即可把空气送到炼铁炉内。这种利用水流作用力推动轮叶的作 法,是完全和现代水力学的理论相符的,用于冶金、筛面、舂 米、磨面、纺纱和提水扬水工具。
第三章 水动力学基础
本章学习基本要求:
了解描述流体运动的两种方法; 理解流动类型和流束与总流等相关概念; 掌握总流连续性方程、能量方程和动量方程及其应用; 理解量纲分析法。
1
ppt课件
第三章 水动力学基础
3.1 描述液体运动的两种方法
3.2 液体运动的基本概念
3.3 恒定总流的连续性方程
3.4 恒定元流的能量方程
定。 18
ppt课件
弯管内水流对管壁的作用力
管轴竖直放置
1
管轴水平放置
1 2
V1 Rz
R
P1=p1A1 z
Fx V2
G
2
V1
P1=p1A1
x y
x y
P2=p2A·2
水力学第三章水动力学基础PPT课件

斯托克斯定理
总结词
描述流体在重力场中运动时,流速与密 度的关系。
VS
详细描述
斯托克斯定理指出,在不可压缩、理想流 体中,流体的流速与密度之间存在一定的 关系。具体来说,流速大的地方密度小, 流速小的地方密度大。这个定理对于理解 流体运动的基本规律和解决实际问题具有 重要的意义。
06 水动力学中的流动现象与 模拟
设计、预测和控制等领域。
THANKS FOR WATCHING
感谢您的观看
静水压强
静止液体内部压强的分布规律。
液柱压力计
利用静止液体的压强测量压力的方法。
帕斯卡原理
静止液体中任意封闭曲面所受外力之和为零。
浮力原理
浸没在液体中的物体受到一个向上的浮力, 其大小等于物体所排液体的重量。
03 水流运动的基本方程
连续性方程
总结词
描述水流在流场中连续分布的特性
详细描述
连续性方程是水力学中的基本方程之一,它表达了单位时间内流场中某一流体 的质量守恒原理。对于不可压缩流体,连续性方程可以简化为:单位时间内流 出的流量等于该时间内流体的减少量。
湍流
水流呈现不规则状态,流线曲折、交 叉甚至断裂,流速沿程变化大,有强 烈的脉动现象。
均匀流与非均匀流
均匀流
水流在同一条流线上,速度和方向保持一致,过水断面形状和尺寸沿程保持不变 。
非均匀流
水流在同一条流线上,速度和方向发生变化,过水断面形状和尺寸沿程也发生变 化。
一维、二维和三维流动
一维流动
水流只具有一个方向的流动,如 管道中的水流。一维流动的研究 可以通过建立一维数学模型进行。
水力学第三章水动力学基础ppt课 件
目 录
水力学课件

第一章 绪论
§1-2 液体的连续介质模型
一、概念的建立
流体由不连续分布的大量分子组成
10-6 mm3 空气中含有大约2.71010个分子; 10-6 mm3 水中含有大约3.31013个分子。 1、概念:液体是没有空隙的,液体质点完全充满所占的空间。
Px Pn cos(n, x) F x 0 Py Pn cos(n, y) F y 0 Pz Pn cos(n, z) F z 0
Z D Pn Px A Py C
O B Pz X
Y
第一式中
P cos(n, x) p • s •cos(n, x)
n
n
p • 1 y • z
n2
第二章 水静力学
Z D Pn Px A Py C
O B Pz X
Y
第二章 水静力学
四面体的体积 V为
Z D Pn Px A Py
V
1
6
x
•
y
•z
C
O B Pz X
Y
总质量力在三个坐标方向的投影为
Fx
1 6
•
x • y
• z X
Fy
1 6
•
x • y
• z Y
Fz
1 6
•
x • y
• z
Z
第二章 水静力学
按照平衡条件,所有作用于微 小四面体上 的外力在各坐标轴 上投影的代数和应分别为零
p n
第二章 水静力学
这样我们可以得到:
p x
p y
p z
p n
上式表明任一点的静水压强 p是
水力学与桥涵水文

地观察和室内试验,建立实用的经验公式,以解决实际工程
问题。这些成果被总结成以实际液体为对象的重实用的水力 学
代表人物有皮托(H.Pitot)、谢才(A.de Chezy)、达西
(H.Darcy)等
1732年皮托发明了量测流体流速的皮托管
1769年谢才建立了计算均匀流的谢才公式
1856年达西提出了线性渗流的达西定律
理论方法中,流体力学引用的主要定理有: (1)质量守恒定律: (2)动量守恒定律:
(3)牛顿运动第二定律:
(4)机械能转化与守恒定律:动能+压能+位能+能量损失 =const 由于纯理论研究方法在数学上存在一定的困难,因 此亦采用数理分析法求解,即总流分析方法与代数方程为 主的求解方法:理论公式+经验系数,经验公式,二维微分 方程,基础流体力学(应用流体力学)、水力学。
绪
论
主要内容
§1.1 水力学与桥涵水文的性质与任务 §1.2 水力学的任务及其发展简史和研究方法
§1.3 液体的主要物理力学性质
§1.4 作用在流体上的力 §1.5 流体的力学模型
§1.1 水力学与桥涵水文的性质与 任务
《水力学与桥涵水文》是公路与城市道路、桥梁、交通工程 专业的一门技术基础课,侧重介绍有关基础原理与方法,为 专业课作前期理论应用训练及业务素质的培养。桥涵是跨越 河渠、宣泄洪水、沟通两侧灌溉水路及保证道路运行安全的 泄水建筑物,其有关水力水文计算原理与方法则是本学科的 任务。随着我国改革开放的深入,城镇建设日新月异,高等 级立体交叉交通枢纽日益增多,高速公路的里程在迅速增长, 上世纪末,我国已建成贯穿全国的两纵两横国道主干线,这 对路桥工程的等级及设计标准提出了新的要求,合理进行水 力水文计算亦更 具重要意义。
3第三章 水动力学基础

液体运动时的加速度:
du x u x u x dx u x dy u x dz dt t x dt y dt z dt
du x u x u u u ux x u y x uz x dt t x y z 同理可得 du y u y u y u y u y ux uy uz dt t x y z du z u z u u u ux z u y z uz z dt t x y z 即
1 A1 2 A2
Q1 Q2 总流连续性方程适用于连续的不可压缩液体作恒定流的
情况,对理想液体和实际液体的各种流动状态都适用。
第三节
一、理想液体 元流能量方程:
若令 上式即
恒定流元流能量方程
2 u12 p2 u 2 z1 z2 2g 2g
p1
u2 H z 2g p
均匀流具有下列特征:
1)过水断面为平面,且形状和大小沿程不变; 2)同一条流线上各点的流速相同,因此各过水断面上 平均流速 v 相等; 3)同一过水断面上各点的测压管水头为常数(即动水 压强分布与静水压强分布规律相同,具有z p C
的关
系),即在同一过水断面上各点测压管水头为一常数。 3.有压流与无压流(根据过水断面上的周线是否有自由 表面分类)
在管道均匀流中,同一断面上各测压管水面必上升至同一高 度,但不同断面上测压管水面所上升的高程是不相同的。
流动的恒定、非恒定是相对时间而言,均匀、
非均匀是相对空间而言;
恒定流可是均匀流,也可以是非均匀流,
非恒定流也是如此,但是明渠非恒定均匀流是不
可能存在的(为什么?)。
水力学第3章

2 2 u1 p2 u2 Z2 hw 2g 2g
z为单位重量液体的势能(位能)。 u2/2g为单位重量液体的动能。 p/为单位重量液体的压能(压强势能)。
• z+p/=该质点所具有的势能。 • z+p/+ u2/2g=总机械能 • hw'为单位重量的流体从断面1-1流到2-2 过程中由于克服流动的阻力作功而消耗 的机械能。这部分机械能转化为热能而 损失,因此称为水头损失。
0
Δh
h1
h2
动 压 管
A-A
静 压 管
A
1
2
例3 试证明图中所示的具有底坎的矩形断面 渠道中的水流是否有可能发生.
(a) 假设这种水流可以发生 证:
以0-0为基准面,列1-1, 2-2断面能量方程:
p1 1V12 p2 2V22 Z1 Z2 hw12 2g 2g
Q3 Q1 Q2
Q3 Q1 Q2 Q1
Q1 Q2 Q3
Q3 Q2
对于有分叉的恒定总流,连续性方程可以表示为: ∑Q流入=∑Q流出 连续性方程是一个运动学方程,它没有涉及作用 力的关系,通常应用连续方程来计算某一已知过水断 面的面积求断面平均流速或者已知流速求流量,它是 水力学中三个最基本的方程之一。
二、迹线和流线 迹线是液体质点运动的轨迹,它是某一个质 点不同时刻在空间位置的连线。 流线是某一瞬间在流场中画 出的一条曲线,这个时刻位于 曲线上各点的质点的流速方向 与该曲线相切。 对于恒定流,流线的形状不随时间而变化, 这时流线与迹线互相重合;对于非恒定流,流 线形状随时间而改变,这时流线与迹线一般不 重合。
Q dQ udA
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
水力学与桥涵水文
叶镇国 彭文波 编著
3-1 描述液体运动的两种方法
描述液体运动的两种方法
拉格朗日法(迹线法)概述
把液体看成为质点系 流场由质点迹线构成,综合迹线运动状况,求解液 体运动要素(即 p、v 分布) 迹线方程
x=x(a,b,c,t)
y=y(a,b,c,t)
z=z(a,b,c,t)
19
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
液流分类(简化理论研究的方法)
恒定流 运动要素不随时间变化的流动。其特性有:
1.
u u ( x, y , z ) a a ( x, y, z ) (3-15) p p ( x, y , z )
(3-9)
15
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
断面平均流速
udA Q v dA A
A A
(3-10)
v v(s,t )
当Q为常数时
1 v ,v 与 A 成反比例关系 A
应用断面平均流速,欧拉法三无流可简化一元流。这也 是一种科学手段. 公式(3-10)为大中桥孔径计算的理论依据。
水力学与桥涵水文 叶镇国
彭文波 编箸
第三章 水动力学基础
3-1 描述液体运动的两种方法 3-2 欧拉法的基本概念 3-3 恒定流连续性方程 3-4 恒定流元流能量方程(元流伯诺里方程) 3-5 恒定流实际液体总流能量方程(总流伯 诺里方程) 3-6 恒定流总流动量方程
1
水力学与桥涵水文
24
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
过水断面压强分布特性
急变流断面图式(如图3-5)
取 n-n 作过水断面,取隔离体 dl ,在 n-n 断面上无液流 运动。
急变流断面压强分布特性分析
其中外力有:
压力:pdA,(p+dp)dA 重力:G=γdAdl
非恒定流
运动要素随时间变化的流动。特性有:
1.
u u ( x, y, z, t ) p p( x, y, z, t )
u p 0, 0 t t
21
2.
3. 流线与迹线不重合。
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
,过水断面为曲面。(如图3-2c)
3. 流线平行时,过水断面为平面。(如图3-2d)
元流与总流
元流——过水断面无限小的流股,如图3-2,dA1、 dA2 上各点流速压强相等(均匀分布)。
总流
元流总和(断面上各点流速压强不等)
11
水力学与桥涵水文
叶镇国 彭文波 编著
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
流线的性质
光滑曲线(连续介质关系)
流线一般不相交(如图3-1b中的驻点A除外),不成折 线
流线可随时间变化
流线方程
dx dy dz ds ux u y uz u
u——M(x、y、z)点流速
(3-6)
9
水力学与桥涵水文
叶镇国 彭文波 编著
计算动量时的修正系数α′(称动量修正系数)
Ku dm u ρdt u 2 dA
A A
Kv m v ρQdtv ρdtv 2 A Ku (证明见教材) Ku α 1 Kv
'
(3-13)
实验得出:α′=1.02~1.05,常取 α′= 1
由上可知,α、α′与流速分布有关,若知断面流速分布 则可解得α、α′ 。其理论值可有 α 2,α 1.33
u u as u t s p p ( s, t )
(3-5)
12
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
液流计量方法
液体是一种不可数物质,其计量采用如下方法: 流量Q——单位时间内流经过水断面的液体积, 以此作水量计量。 断面平均流速v(断面流速计量)——即断面各点 流速加权均平均值。
3-2 欧拉法的有关概念
三元、二元及一元流动
三元流动——运动要素为三坐标的函数 u=u(x,y,z,t)
二元流动——运动要素为二坐标的函数 u=u(x,y,t) 一元流动——运动要素为一坐标的函数 u=u(s,t)
水力学中常用(又称为流束理论),如管道中的水流。
一元流动有
u u ( s, t )
流线簇彼此呈平行直线的流动。其特性有: 1.过水断面为平面,如图3-2d 2.断面流速分布沿程相同
3. 液流为匀速直线运动,长直管道水流,断面形状一致 的长直渠道水流属此类。
α1 α2 α ;α '1 α '2 α '
非均匀流
定义——流线夹角很大,流线簇弯曲或彼此不呈平行直 线的流动。其特性有:
3.
2.
u p 0, 0 t t (3-16) du as u dt
dx ux dt dy uy dt dz uz dt
(3-17)
20
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
4.流线与迹线重合
17
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
引用断面平均流速计量的误差修正
计算动能时误差修正系数α(称动能修正系数) 动能 E 1 dmu 2 1 ( ρdQdt )u 2 1 ρdt u 3 dA ku A 2 A 2 A 2 1 2 1 1 2 Ekv mv ρQdtv ρdtv 3 A 2 2 2
元流过水断面的液体体积 dV 有: ds udc, dV dsdA udtdA dV dQ udA dt
(3-8)
有: 体积流量
Q udA (m3 / s) A 重量流量 QG γQ (kN / s) 质量流量 Qρ ρQ (kg / s)
du z 等首项称为当地加速度 dt u u x x 等后三项统称为迁移加速度 x
7
(3-4)
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
欧拉法有关概念
流线——同一时刻与流场各点速度矢量相切的 曲线。
流谱——流场中的流线图形(如图3-1)
(图3-1)
8
水力学与桥涵水文
u x u x ( x, y , z , t ) u y u y ( x, y , z , t ) u z u z ( x, y , z , t )
x、y 、z 、t ——欧拉变数
(3-3)
6
水力学与桥涵水文
叶镇国 彭文波 编著
3-1 描述液体运动的两种方法
dux ux ux u x u x ax ux uy uz dt t x y z du y u y u y u y u y ay uy uy uz dt t x y z duz uz uz uz u z az ux uy uz dt t x y z
令 u=v+△u 可证明 (见教材)
3 3
A
u 3dA v3 A,Eku Ekv
2
A u 3dA 1 (3-11) 取 A u dA αv A αv Q (3-12) 则 α 3 v A
18
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
实验得出:α=1.05~1. 10,实际工程中常取α=1
(3-1)
a、b、c——质点初始位置;a、b、c、t——拉格朗日变数
3
水力学与桥涵水文
叶镇国 彭文波 编著
3-1 描述液体运动的两种方法
运动要素描述,见公式(3-2)u x u (a, b, c, t ) x x t 式中:ux、uy、uz——分别为 y 液体质点流速 u 沿三坐标轴 uy u y ( a , b, c , t ) t 的分量; z ax、ay、az——分别为液体质 u u z ( a , b, c , t ) z t 点加速度沿三坐标轴的分量。 (3-2) u x 应用场合 ax a x ( a , b, c , t ) t 研究波浪运动 u y 水文测验,模型试验示踪测 ay a y ( a , b, c , t ) 速 t 因数学关系复杂,水力学 u z 中少用。 az a z ( a , b, c , t ) t
叶镇国 彭文波 编著
3-1 描述液体运动的两种方法
概述
流场——液体的流动空间
动水压强特性:
因水的粘性很小,动水压强与静水压强特性基本相同。 流场中的压强大小受流速影响,各点压强一般情况:
p z C γ
本章理论适用于 v<50 m/s 的低速流体
本章任务——建立三大方程(质量守恒、能量守恒及动 量守恒关系)求解 p、v、R ,即压强、流速及液流对边 壁的作用力
1. p ≠pa,过水断面大小形状固定不变。
2.流量变化,只会引起断面上 p、v 变化。 3.自来水管中的水流运动属此类。
23
水力学与桥涵水文
叶镇国 彭文波 编著
3-2 欧拉法的有关概念
无压流——过水断面部分周界有自由表面的流动。
1.自由表面 pγ=0
2.流量变化,过水断面大小形状可随之变化。而流量不 变也可有多种水深流速的组合变化,如水深大流速小, 水深小流速大。 3.水力计算比有压流复杂(详见第六章)。
