初中教材知识点梳理
八年级书知识点

八年级书知识点八年级是初中阶段的重要学习阶段,也是完善自己知识结构的关键时期,其中涉及了许多重要的知识点和学科。
在八年级的学习生涯中,学生们需要掌握大量知识点,以下是八年级常见的书本知识点。
1.语文八年级语文主要涉及文学鉴赏、作文以及语言应用,要求学生能够深入理解文化内涵,理解诗歌、散文、小说等文学体裁的写作手法和语言运用技巧。
同时,要求学生能够熟练掌握写作规律,进行作文的模仿和创作。
2.数学八年级数学主要包括代数、几何、概率统计等方面的知识点。
其中,代数的学习学生需要掌握一元二次方程、一次不等式等知识点。
几何方面,需要学生掌握勾股定理、正弦、余弦、正切等知识点。
在概率统计方面,需要学生掌握基本概念,如样本空间、事件、概率等。
3.物理八年级物理主要涉及光、声、电等方面的知识点。
在光学方面,主要包括光的反射、折射和光的成像等知识点。
在声学方面,需要学生掌握声音的传播、共鸣和声音的衰减等知识点。
在电学方面,需要学生掌握电流和电压的基本知识以及简单电路的组成和使用。
4.化学八年级化学主要涉及物质与化学反应、化学元素等方面的知识点。
学生需要掌握化学元素的基本概念、元素周期表的特性和规律。
同时要了解化学反应的特性,掌握化学方程式的写法和解题方法。
5.生物八年级生物主要涉及生物分子、细胞、遗传等方面的知识点。
学生需要了解生物分子、细胞的基本组成和功能,掌握遗传规律和基本遗传学的知识。
总之,八年级是学科知识的重要阶段,也是完善学习结构的关键时期。
只有在充分吸收这些基础知识的基础上,才能够更好地应对高中学科知识,同时也为未来的人生发展打下坚实的基础。
2024人教版初中地理知识点概括梳理大全

2024人教版初中地理知识点概括梳理大全2024年人教版初中地理教材主要包括七年级上、七年级下、八年级上、八年级下、九年级上和九年级下共六个册教材。
以下是对每个册教材的知识点进行概括梳理。
7年级上册:本册教材主要介绍了地球与地理位置、地球的运动与昼夜变化、地球的内部结构、地球的外部地貌以及中国的地理位置等内容。
重点知识点包括:1.地球是一个具有自转和公转运动的天体,自转周期为24小时,公转周期为365.25天。
2.地球的内部结构包含地壳、地幔和地核。
3.地球的外部地貌包括平原、高原、山地和盆地等。
7年级下册:本册教材主要介绍了地球的水资源、江河湖泊和地下水等内容。
重点知识点包括:1.地球上的水资源主要包括淡水和咸水,其中淡水占总水量的2.5%。
2.世界上五大洋分别是太平洋、大西洋、印度洋、北冰洋和南冰洋。
3.中国的主要河流有长江、黄河、珠江等,主要湖泊有鄱阳湖、洞庭湖等。
4.地下水是地表水渗漏到地下,形成地下水文特征与地表水密切相关。
本册教材主要介绍了地球的自然地理环境和土地利用问题,以及人口与资源的利用和保护等内容。
重点知识点包括:1.自然地理环境包括气候、土壤和植被等要素,它们相互作用影响着生态系统的形成和发展。
2.土地利用是指人类对土地资源的开发和利用,包括农田、林地、草地和城市用地等。
3.人口与资源利用和保护的关系密切,人口过多或过少都可能造成资源短缺或浪费。
4.可持续发展是指满足当前需求的同时,不破坏自然资源,使子孙后代也能够满足自身需求。
8年级下册:本册教材主要介绍了地球的气候与生物分布、中国的气候和植物资源以及环境保护等内容。
重点知识点包括:1.气候是指长期气象要素的统计值,主要包括温度、降水和风等。
2.中国的气候主要分为北温带、南亚热带、雨林气候、草原气候和温带季风气候等。
3.植物资源是指人类利用的植物物种,包括经济作物、林木和观赏植物等。
4.环境保护是指保护自然环境、减少污染和保护生态系统的行为和活动。
初中数学全册教材知识梳理(表格版)
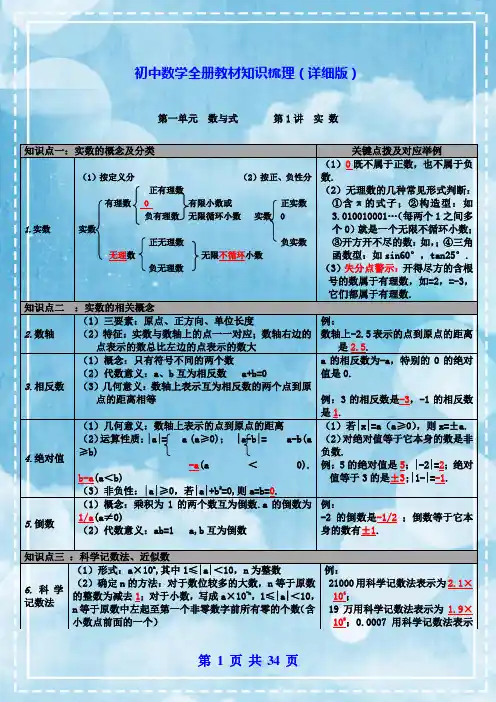
初中数学全册教材知识梳理(详细版)第一单元数与式第1讲实数知识点一:实数的概念及分类关键点拨及对应举例1.实数(1)按定义分(2)按正、负性分正有理数有理数 0 有限小数或正实数负有理数无限循环小数实数 0实数正无理数负实数无理数无限不循环小数负无理数(1)0既不属于正数,也不属于负数.(2)无理数的几种常见形式判断:①含π的式子;②构造型:如3.010010001…(每两个1之间多个0)就是一个无限不循环小数;③开方开不尽的数:如,;④三角函数型:如sin60°,tan25°.(3)失分点警示:开得尽方的含根号的数属于有理数,如=2,=-3,它们都属于有理数.知识点二:实数的相关概念2.数轴(1)三要素:原点、正方向、单位长度(2)特征:实数与数轴上的点一一对应;数轴右边的点表示的数总比左边的点表示的数大例:数轴上-2.5表示的点到原点的距离是2.5.3.相反数(1)概念:只有符号不同的两个数(2)代数意义:a、b互为相反数 a+b=0(3)几何意义:数轴上表示互为相反数的两个点到原点的距离相等a的相反数为-a,特别的0的绝对值是0.例:3的相反数是-3,-1的相反数是1.4.绝对值(1)几何意义:数轴上表示的点到原点的距离(2)运算性质:|a|= a (a≥0); |a-b|= a-b(a≥b)-a(a<0).b-a(a<b)(3)非负性:|a|≥0,若|a|+b2=0,则a=b=0.(1)若|x|=a(a≥0),则x=±a.(2)对绝对值等于它本身的数是非负数.例:5的绝对值是5;|-2|=2;绝对值等于3的是±3;|1-|=-1.5.倒数(1)概念:乘积为1的两个数互为倒数.a的倒数为1/a(a≠0)(2)代数意义:ab=1a,b互为倒数例:-2的倒数是-1/2;倒数等于它本身的数有±1.知识点三:科学记数法、近似数6.科学记数法(1)形式:a×10n,其中1≤|a|<10,n为整数(2)确定n的方法:对于数位较多的大数,n等于原数的整数为减去1;对于小数,写成a×10-n,1≤|a|<10,n等于原数中左起至第一个非零数字前所有零的个数(含小数点前面的一个)例:21000用科学记数法表示为2.1×104;19万用科学记数法表示为1.9×105;0.0007用科学记数法表示知识点一:代数式及相关概念关键点拨及对应举例1.代数式(1)代数式:用运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子,单独的一个数或一个字母也是代数式.(2)求代数式的值:用具体数值代替代数式中的字母,计算得出的结果,叫做求代数式的值.求代数式的值常运用整体代入法计算.例:a-b=3,则3b-3a=-9.为7×10-4.7.近似数(1)定义:一个与实际数值很接近的数.(2)精确度:由四舍五入到哪一位,就说这个近似数精确到哪一位.例:3.14159精确到百分位是3.14;精确到0.001是3.142.知识点四:实数的大小比较8.实数的大小比较(1)数轴比较法:数轴上的两个数,右边的数总比左边的数大.(2)性质比较法:正数>0>负数;两个负数比较大小,绝对值大的反而小.(3)作差比较法:a-b>0a>b;a-b=0a=b;a-b<0a<b.(4)平方法:a>b≥0a2>b2.例:把1,-2,0,-2.3按从大到小的顺序排列结果为___1>0>-2>-2.3_.知识点五:实数的运算9. 常见运算乘方几个相同因数的积; 负数的偶(奇)次方为正(负)例:(1)计算:1-2-6=_-7__;(-2)2=___4__;3-1=_1/3_;π0=__1__;(2)64的平方根是_±8__,算术平方根是__8_,立方根是__4__.失分点警示:类似“的算术平方根”计算错误. 例:相互对比填一填:16的算术平方根是 4___,的算术平方根是___2__.零次幂a0=_1_(a≠0)负指数幂a-p=1/a p(a≠0,p为整数)平方根、算术平方根若x2=a(a≥0),则x=a.其中a是算术平方根.立方根若x3=a,则x=3a.10.混合运算先乘方、开方,再乘除,最后加减;同级运算,从左向右进行;如有括号,先做括号内的运算,按小括号、中括号、大括号一次进行.计算时,可以结合运算律,使问题简单化2.整式(单项式、多项式)(1)单项式:表示数字与字母积的代数式,单独的一个数或一个字母也叫单项式.其中的数字因数叫做单项式的系数,所有字母的指数和叫做单项式的次数.(2)多项式:几个单项式的和.多项式中的每一项叫做多项式的项,次数最高的项的次数叫做多项式的次数.(3)整式:单项式和多项式统称为整式.(4)同类项:所含字母相同并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.例:(1)下列式子:①-2a2;②3a-5b;③x/2;④2/x;⑤7a2;⑥7x2+8x3y;⑦2017.其中属于单项式的是①③⑤⑦;多项式是②⑥;同类项是①和⑤.(2)多项式7m5n-11mn2+1是六次三项式,常数项是__1 .知识点二:整式的运算3.整式的加减运算(1)合并同类项法则:同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.(2)去括号法则: 若括号外是“+”,则括号里的各项都不变号;若括号外是“-”,则括号里的各项都变号.(3)整式的加减运算法则:先去括号,再合并同类项.失分警示:去括号时,如果括号外面是符号,一定要变号,且与括号内每一项相乘,不要有漏项.例:-2(3a-2b-1)=-6a+4b+2.4.幂运算法则(1)同底数幂的乘法:a m·a n=a m+n;(2)幂的乘方:(a m)n=a mn;(3)积的乘方:(ab)n=a n·b n;(4)同底数幂的除法:a m÷a n=a m-n(a≠0).其中m,n都在整数(1)计算时,注意观察,善于运用它们的逆运算解决问题.例:已知2m+n=2,则3×2m×2n=6.(2)在解决幂的运算时,有时需要先化成同底数.例:2m·4m=23m.5.整式的乘除运算(1)单项式×单项式:①系数和同底数幂分别相乘;②只有一个字母的照抄.(2)单项式×多项式: m(a+b)=ma+mb.(3)多项式×多项式: (m+n)(a+b)=ma+mb+na+nb.(4)单项式÷单项式:将系数、同底数幂分别相除.(5)多项式÷单项式:①多项式的每一项除以单项式;②商相加.失分警示:计算多项式乘以多项式时,注意不能漏乘,不能丢项,不能出现变号错.例:(2a-1)(b+2)=2ab+4a-b-2.(6)乘法公式平方差公式:(a+b)(a-b)=a2-b2. 注意乘法公式的逆向运用及其变形公式的运用完全平方公式:(a±b)2=a2±2ab+b2. 变形公式:a2+b2=(a±b)2∓2ab,ab=【(a+b)2-(a2+b2)】 /26.混合运算注意计算顺序,应先算乘除,后算加减;若为化简求值,一般步骤为:化简、代入替换、计算.例:(a-1)2-(a+3)(a-3)-10=_-2a__.知识点五:因式分解7.因式分解(1)定义:把一个多项式化成几个整式的积的形式.(2)常用方法:①提公因式法:ma+mb+mc=m(a+b+c).②公式法:a2-b2=(a+b)(a-b);a2±2ab+b2=(a±b)2.(3)一般步骤:①若有公因式,必先提公因式;②提公因式后,看是否能用公式法分解;③检查各因式能否继续分解.(1) 因式分解要分解到最后结果不能再分解为止,相同因式写成幂的形式;(2) 因式分解与整式的乘法互为逆运算.知识点一:分式的相关概念关键点拨及对应举例1.分式的概念(1)分式:形如BA(A,B是整式,且B中含有字母,B≠0)的式子.(2)最简分式:分子和分母没有公因式的分式.在判断某个式子是否为分式时,应注意:(1)判断化简之间的式子;(2)π是常数,不是字母. 例:下列分式:①;②; ③;④2221xx+-,其中是分式是②③④;最简分式③.2.分式的意义(1)无意义的条件:当B=0时,分式BA无意义;(2)有意义的条件:当B≠0时,分式BA有意义;(3)值为零的条件:当A=0,B≠0时,分式BA=0.失分点警示:在解决分式的值为0,求值的问题时,一定要注意所求得的值满足分母不为0.例:当211xx--的值为0时,则x=-1.3.基本性质( 1 ) 基本性质:A A CB B C⋅=⋅A CB C÷=÷(C≠0).(2)由基本性质可推理出变号法则为:()AA AB B B---==-;A A AB B B--==-.由分式的基本性质可将分式进行化简:例:化简:22121xx x-++=11xx-+.知识点三:分式的运算4.分式的约分和通分(1)约分(可化简分式):把分式的分子和分母中的公因式约去,即babmam=;(2)通分(可化为同分母):根据分式的基本性质,把异分母的分式化为同分母的分式,即bcbdbcacdcba,,⇒分式通分的关键步骤是找出分式的最简公分母,然后根据分式的性质通分.例:分式21x x+和()11x x-的最简公分母为()21x x-.5.分式的加减法(1)同分母:分母不变,分子相加减.即ac±bc=a±bc;(2)异分母:先通分,变为同分母的分式,再加减.即ab±cd=ad±bcbd.例:111xx x+--=-1.2112.111aa a a+=+--6.分式的乘除法(1)乘法:ab·cd=acbd; (2)除法:a cb d÷=adbc;(3)乘方:nab⎛⎫⎪⎝⎭=nnab(n为正整数).例:2a bb a⋅=12;21x xy÷=2y;332x⎛⎫- ⎪⎝⎭=3278x-.7.分式的混合运算(1)仅含有乘除运算:首先观察分子、分母能否分解因式,若能,就要先分解后约分.(2)含有括号的运算:注意运算顺序和运算律的合理应用.一般先算乘方,再算乘除,最后算加减,若有括号,先算括号里面的.失分点警示:分式化简求值问题,要先将分式化简到最简分式或整式的形式,再代入求值.代入数值时注意要使原分式有意义.有时也需运用到整体代入.知识点一:二次根式关键点拨及对应举例1.有关概念(1)二次根式的概念:形如a(a≥0)的式子.(2)二次根式有意义的条件:被开方数大于或等于0.(3)最简二次根式:①被开方数的因数是整数,因式是整式(分母中不含根号);②被开方数中不含能开得尽方的因数或因式失分点警示:当判断分式、二次根式组成的复合代数式有意义的条件时,注意确保各部分都有意义,即分母不为0,被开方数大于等于0等.例:若代数式11x-有意义,则x的取值范围是x>1.2.二次根式的性质(1)双重非负性:①被开方数是非负数,即a≥0;②二次根式的值是非负数,即a≥0.注意:初中阶段学过的非负数有:绝对值、偶幂、算式平方根、二次根式.利用二次根式的双重非负性解题:(1)值非负:当多个非负数的和为0时,可得各个非负数均为0.如1a++1b-=0,则a=-1,b=1.(2)被开方数非负:当互为相反数的两个数同时出现在二次根式的被开方数下时,可得这一对相反数的数均为0.如已知b=1a-+1a-,则a=1,b=0.(2)两个重要性质:①(a)2=a(a≥0);②a2=|a|=()()a aa a⎧≥⎪⎨-<⎪⎩;(3)积的算术平方根:ab=a·b(a≥0,b≥0);(4)商的算术平方根:ab=ab(a≥0,b>0).例:计算:23.14=3.14;()22-=2;24=;=2 ;442939==知识点二:二次根式的运算3.二次根式的加减法先将各根式化为最简二次根式,再合并被开方数相同的二次根式.例:计算:2832-+=32.4.二次根式的乘除法(1)乘法:a·b=ab(a≥0,b≥0);注意:将运算结果化为最简二次根式.例:计算:3223⋅=1;323222==4.(2)除法:ab=ab(a≥0,b>0).5.二次根式的混合运算运算顺序与实数的运算顺序相同,先算乘方,再算乘除,最后算加减,有括号的先算括号里面的(或先去括号).运算时,注意观察,有时运用乘法公式会使运算简便.例:计算:(2+1)(2 -1)= 1 .知识点一:方程及其相关概念关键点拨及对应举例1.等式的基本性质(1)性质1:等式两边加或减同一个数或同一个整式,所得结果仍是等式.即若a=b,则a±c=b±c .(2)性质2:等式两边同乘(或除)同一个数(除数不能为0),所得结果仍是等式.即若a=b,则ac=bc,a bc c=(c≠0).(3)性质3:(对称性)若a=b,则b=a.(4)性质4:(传递性)若a=b,b=c,则a=c.失分点警示:在等式的两边同除以一个数时,这个数必须不为0.例:判断正误.(1)若a=b,则a/c=b/c.(×)(2)若a/c=b/c,则a=b.(√)2.关于方程的基本概念(1)一元一次方程:只含有一个未知数,并且未知数的次数是1,且等式两边都是整式的方程.(2)二元一次方程:含有两个未知数,并且含有未知数的项的次数都是1的整式方程.(3)二元一次方程组:含有两个未知数的两个一次方程所组成的一组方程.(4)二元一次方程组的解:二元一次方程组的两个方程的公共解.在运用一元一次方程的定义解题时,注意一次项系数不等于0.例:若(a-2)|a1|0x a-+=是关于x的一元一次方程,则a的值为0.知识点二:解一元一次方程和二元一次方程组3.解一元一次方程的步骤(1)去分母:方程两边同乘分母的最小公倍数,不要漏乘常数项;(2)去括号:括号外若为负号,去括号后括号内各项均要变号;(3)移项:移项要变号;(4)合并同类项:把方程化成ax=-b(a≠0);(5)系数化为1:方程两边同除以系数a,得到方程的解x=-b/a.失分点警示:方程去分母时,应该将分子用括号括起来,然后再去括号,防止出现变号错误.4.二元一次方程组的解法思路:消元,将二元一次方程转化为一元一次方程. 已知方程组,求相关代数式的值时,需注意观察,有时不需解出方程组,利用整体思想解决解方程组. 例:已知2923x yx y-=⎧⎨-=⎩则x-y的值为x-y=4.方法:(1)代入消元法:从一个方程中求出某一个未知数的表达式,再把“它”代入另一个方程,进行求解;(2) 加减消元法:把两个方程的两边分别相加或相减消去一个未知数的方法.知识点三:一次方程(组)的实际应用5.列方程(组) 解应用题的一般步骤(1)审题:审清题意,分清题中的已知量、未知量;(2)设未知数;(3)列方程(组):找出等量关系,列方程(组);(4)解方程(组);(5)检验:检验所解答案是否正确或是否满足符合题意;(6)作答:规范作答,注意单位名称.(1)设未知数时,一般求什么设什么,但有时为了方便,也可间接设未知数.如题目中涉及到比值,可以设每一份为x.(2)列方程(组)时,注意抓住题目中的关键词语,如共是、等于、大(多)多少、小(少)多少、几倍、几分之几等.6.常见题型及关系式(1)利润问题:售价=标价×折扣,销售额=售价×销量,利润=售价-进价,利润率=利润/进价×100%.(2)利息问题:利息=本金×利率×期数,本息和=本金+利息.(3)工程问题:工作量=工作效率×工作时间.(4)行程问题:路程=速度×时间. ①相遇问题:全路程=甲走的路程+乙走的路程;②追及问题:a.同地不同时出发:前者走的路程=追者走的路程;b.同时不同地出发:前者走的路程+两地间距离=追者走的路程.知识点一:一元二次方程及其解法关键点拨及对应举例1.一元二次方程的相关概念(1)定义:只含有一个未知数,且未知数的最高次数是 2 的整式方程.(2)一般形式:ax2+bx+c=0(a≠0),其中ax2、bx、c分别叫做二次项、一次项、常数项,a、b、c分别称为二次项系数、一次项系数、常数项.例:方程20aax+=是关于x的一元二次方程,则方程的根为-1.2.一元二次方程的解法(1)直接开平方法:形如(x+m)2=n(n≥0)的方程,可直接开平方求解.( 2 )因式分解法:可化为(ax+m)(bx+n)=0的方程,用因式分解法求解.( 3 )公式法:一元二次方程 ax2+bx+c=0的求根公式为x=242b b aca-±-(b2-4ac≥0).(4)配方法:当一元二次方程的二次项系数为1,一次项系数为偶数时,也可以考虑用配方法.解一元二次方程时,注意观察,先特殊后一般,即先考虑能否用直接开平方法和因式分解法,不能用这两种方法解时,再用公式法.例:把方程x2+6x+3=0变形为(x+h)2=k的形式后,h=-3,k=6.知识点二:一元二次方程根的判别式及根与系数的关系3.根的判别式(1)当Δ=24b ac->0时,原方程有两个不相等的实数根.(2)当Δ=24b ac-=0时,原方程有两个相等的实数根.(3)当Δ=24b ac-<0时,原方程没有实数根.例:方程2210x x+-=的判别式等于8,故该方程有两个不相等的实数根;方程2230x x++=的判别式等于-8,故该方程没有实数根.*4.根与系数的关(1)基本关系:若关于x的一元二次方程ax2+bx+c=0(a≠0)与一元二次方程两根相关代数式的常见变形:系有两个根分别为x1、x2,则x1+x2=-b/a,x1x2=c/a.注意运用根与系数关系的前提条件是△≥0.(2)解题策略:已知一元二次方程,求关于方程两根的代数式的值时,先把所求代数式变形为含有x1+x2、x1x2的式子,再运用根与系数的关系求解. (x1+1)(x2+1)=x1x2+(x1+x2)+1,x12+x22=(x1+x2)2-2x1x2,12121211x xx x x x++=等.失分点警示在运用根与系数关系解题时,注意前提条件时△=b2-4ac≥0.知识点三:一元二次方程的应用4.列一元二次方程解应用题(1)解题步骤:①审题;②设未知数;③列一元二次方程;④解一元二次方程;⑤检验根是否有意义;⑥作答.运用一元二次方程解决实际问题时,方程一般有两个实数根,则必须要根据题意检验根是否有意义. (2)应用模型:一元二次方程经常在增长率问题、面积问题等方面应用.①平均增长率(降低率)问题:公式:b=a(1±x)n,a表示基数,x表示平均增长率(降低率),n表示变化的次数,b表示变化n次后的量;②利润问题:利润=售价-成本;利润率=利润/成本×100%;③传播、比赛问题:④面积问题:a.直接利用相应图形的面积公式列方程;b.将不规则图形通过割补或平移形成规则图形,运用面积之间的关系列方程.知识点一:分式方程及其解法关键点拨及对应举例1.定义分母中含有未知数的方程叫做分式方程.例:在下列方程中,①210x+=;②4x y+=-;③11xx=-,其中是分式方程的是③.2.解分式方程基本思路:分式方程整式方程例:将方程12211x x+=--转化为整式方程可得:1-2=2(x-1).解法步骤:(1)去分母,将分式方程化为整式方程;(2)解所得的整式方程;(3) 检验:把所求得的x的值代入最简公分母中,若最简公分母为0,则应舍去.3.增根使分式方程中的分母为0的根即为增根. 例:若分式方程101x=-有增根,则增根为1.知识点二:分式方程的应用方程两边同乘以最简公分母约去分母4.列分式方程解应用题的一般步骤 (1)审题;(2)设未知数;(3) 列分式方程;(4)解分式方程;(5)检验: (6)作答. 在检验这一步中,既要检验所求未知数的值是不是所列分式方程的解,又要检验所求未知数的值是不是符合题目的实际意义.知识点一:不等式及其基本性质 关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子. (2)不等式的解:使不等式成立的未知数的值. (3)不等式的解集:使不等式成立的未知数的取值范围. 例:“a 与b 的差不大于1”用不等式表示为a -b ≤1.2.不等式的基本性质 性质1:若a >b,则 a ±c >b ±c ; 性质2:若a >b,c >0,则ac >bc ,a c >bc ;性质3:若a >b,c <0,则ac <bc ,a c <bc .牢记不等式性质3,注意变号. 如:在不等式-2x >4中,若将不等式两边同时除以-2,可得x <2.知识点二 :一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230m mx ++>是关于x的一元一次不等式,则m 的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x ≥a x >a x ≤a x <a知识点三 :一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x <1-a 的解集是x >-1,则a 的取值范围是a <1.6.解法 先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型 假设a <b 解集 数轴表示 口诀x a x b ≥⎧⎨≥⎩ x ≥b 大大取大 x a x b ≤⎧⎨≤⎩x ≤a 小小取小 x a x b ≥⎧⎨≤⎩ a ≤x ≤b大小,小大中间找 x ax b≤⎧⎨≥⎩ 无解 大大,小小取不了 知识点四 :列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;b.隐含不等关系:如“更省钱”、“更划算”等方案决策问题,一般还需根据整数解,得出最佳方案注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.知识点一:平面直角坐标系关键点拨及对应举例1.相关概念(1)定义:在平面内有公共原点且互相垂直的两条数轴构成平面直角坐标系.(2)几何意义:坐标平面内任意一点M与有序实数对(x,y)的关系是一一对应.点的坐标先读横坐标(x轴),再读纵坐标(y轴).2.点的坐标特征( 1 )各象限内点的坐标的符号特征(如图所示):点P(x,y)在第一象限⇔x>0,y>0;点P(x,y)在第二象限⇔x<0,y>0;点P(x,y)在第三象限⇔x<0,y<0;点P(x,y)在第四象限⇔x>0,y<0.(2)坐标轴上点的坐标特征:①在横轴上⇔y=0;②在纵轴上⇔x=0;③原点⇔x=0,y=0.(3)各象限角平分线上点的坐标①第一、三象限角平分线上的点的横、纵坐标相等;②第二、四象限角平分线上的点的横、纵坐标互为相反数(4)点P(a,b)的对称点的坐标特征:①关于x轴对称的点P1的坐标为(a,-b);②关于y轴对称的点P2的坐标为(-a,b);③关于原点对称的点P3的坐标为(-a,-b).(5)点M(x,y)平移的坐标特征:M(x,y) M1(x+a,y)M2(x+a,y+b)(1)坐标轴上的点不属于任何象限.(2)平面直角坐标系中图形的平移,图形上所有点的坐标变化情况相同.(3)平面直角坐标系中求图形面积时,先观察所求图形是否为规则图形,若是,再进一步寻找求这个图形面积的因素,若找不到,就要借助割补法,割补法的主要秘诀是过点向x轴、y轴作垂线,从而将其割补成可以直接计算面积的图形来解决.3.坐标点的距离问题(1)点M(a,b)到x轴,y轴的距离:到x轴的距离为|b|;)到y轴的距离为|a|.(2)平行于x轴,y轴直线上的两点间的距离:点M1(x1,0),M2(x2,0)之间的距离为|x1-x2|,点M1(x1,y),M2(x2,y)间的距离为|x1-x2|;点M1(0,y1),M2(0,y2)间的距离为|y1-y2|,点M1(x,y1),M2(x,平行于x轴的直线上的点纵坐标相等;平行于y轴的直线上的点的横坐标相等.xy第四象限(+,-)第三象限(-,-)第二象限(-,+)第一象限(+,+)–1–2–3123–1–2–3123Oy 2)间的距离为|y 1-y 2|.知识点二:函 数4.函数的相关概念 (1)常量、变量:在一个变化过程中,数值始终不变的量叫做常量,数值发生变化的量叫做变量.(2)函数:在一个变化过程中,有两个变量x 和y ,对于x 的每一个值,y 都有唯一确定的值与其对应,那么就称x 是自变量,y 是x 的函数.函数的表示方法有:列表法、图像法、解析法.(3)函数自变量的取值范围:一般原则为:整式为全体实数;分式的分母不为零;二次根式的被开方数为非负数;使实际问题有意义. 失分点警示函数解析式,同时有几个代数式,函数自变量的取值范围应是各个代数式中自变量的公共部分. 例:函数y=35x x +-中自变量的取值范围是x ≥-3且x ≠5.5.函数的图象 (1)分析实际问题判断函数图象的方法: ①找起点:结合题干中所给自变量及因变量的取值范围,对应到图象中找对应点;②找特殊点:即交点或转折点,说明图象在此点处将发生变化; ③判断图象趋势:判断出函数的增减性,图象的倾斜方向.(2)以几何图形(动点)为背景判断函数图象的方法: ①设时间为t (或线段长为x ),找因变量与t(或x)之间存在的函数关系,用含t(或x)的式子表示, 再找相应的函数图象.要注意是否需要分类讨论自变量的取值范围.读取函数图象增减性的技巧:①当函数图象从左到右呈“上升”(“下降”)状态时,函数y 随x 的增大而增大(减小);②函数值变化越大,图象越陡峭;③当函数y 值始终是同一个常数,那么在这个区间上的函数图象是一条平行于x 轴的线段.知识点一:一次函数的概念及其图象、性质关键点拨与对应举例1.一次函数的相关概念(1)概念:一般来说,形如y =kx +b (k ≠0)的函数叫做一次函数.特别地,当b =0时,称为正比例函数. (2)图象形状:一次函数y =kx +b 是一条经过点(0,b )和(-b/k ,0)的直线.特别地,正比例函数y =kx 的图象是一条恒经过点(0,0)的直线.例:当k =1时,函数y=kx +k -1是正比例函数,2.一次函数的性质 k ,b 符号 K >0, b >0 K >0, b <0 K >0,b=0 k <0, b >0 k <0, b <0 k <0, b =0 (1)一次函数y=kx+b 中,k 确定了倾斜方向和倾斜程度,b 确定了与y轴交点的位置.(2)比较两个一次函数函数值的大小:性质法,借助函数的图象,也可以运用数值代入法. 例:已知函数y =-2x +b ,大致 图象 经过象限 一、二、三 一、三、四 一、三 一、二、四 二、三、四二、四 图象性质y 随x 的增大而增大 y 随x 的增大而减小函数值y随x的增大而减小(填“增大”或“减小”).3.一次函数与坐标轴交点坐标(1)交点坐标:求一次函数与x轴的交点,只需令y=0,解出x即可;求与y轴的交点,只需令x=0,求出y即可.故一次函数y=kx+b(k≠0)的图象与x轴的交点是⎝⎛⎭⎪⎫-bk,0,与y轴的交点是(0,b);(2)正比例函数y=kx(k≠0)的图象恒过点(0,0).例:一次函数y=x+2与x轴交点的坐标是(-2,0),与y轴交点的坐标是(0,2).知识点二:确定一次函数的表达式4.确定一次函数表达式的条件(1)常用方法:待定系数法,其一般步骤为:①设:设函数表达式为y=kx+b(k≠0);②代:将已知点的坐标代入函数表达式,解方程或方程组;③解:求出k与b的值,得到函数表达式.(2)常见类型:①已知两点确定表达式;②已知两对函数对应值确定表达式;③平移转化型:如已知函数是由y=2x平移所得到的,且经过点(0,1),则可设要求函数的解析式为y=2x+b,再把点(0,1)的坐标代入即可.(1)确定一次函数的表达式需要两组条件,而确定正比例函数的表达式,只需一组条件即可.(2)只要给出一次函数与y轴交点坐标即可得出b的值,b值为其纵坐标,可快速解题. 如:已知一次函数经过点(0,2),则可知b=2.5.一次函数图象的平移规律:①一次函数图象平移前后k不变,或两条直线可以通过平移得到,则可知它们的k值相同.②若向上平移h单位,则b值增大h;若向下平移h单位,则b值减小h.例:将一次函数y=-2x+4的图象向下平移2个单位长度,所得图象的函数关系式为y=-2x+2.知识点三:一次函数与方程(组)、不等式的关系6.一次函数与方程一元一次方程kx+b=0的根就是一次函数y=kx+b(k、b是常数,k≠0)的图象与x轴交点的横坐标. 例:(1)已知关于x的方程ax+b=0的解为x=1,则函数y=ax+b与x轴的交点坐标为(1,0).(2)一次函数y=-3x+12中,当x >4时,y的值为负数.7.一次函数与方程组二元一次方程组的解⇔两个一次函数y=k1x+b 和y=k2x+b图象的交点坐标.8.一次函数与不等式(1)函数y=kx+b的函数值y>0时,自变量x的取值范围就是不等式kx+b>0的解集(2)函数y=kx+b的函数值y<0时,自变量x的取值范围就是不等式kx+b<0的解集知识点四:一次函数的实际应用9.一般步骤(1)设出实际问题中的变量;(2)建立一次函数关系式;(3)利用待定系数法求出一次函数关系式;(4)确定自变量的取值范围;(5)利用一次函数的性质求相应的值,对所求的值进行检验,是否符合实际意义;(6)做答.一次函数本身并没有最值,但在实际问题中,自变量的取值往往有一定的限制,其图象为射线或线段.涉及最值问题的一般思路:确定函数表达式→确定y=k2x+by=k1x+b。
初中各科知识点的系统归纳整理

初中各科知识点的系统归纳整理初中阶段学习的各科知识点涉及多个学科,每个学科都有其特定的内容和要求。
以下是初中各科知识点的系统归纳整理。
一、数学1.整数与有理数:整数的概念,有理数的概念、性质与运算,绝对值与相反数等。
2. 代数:代数ic expressions,代数ic equations和inequalities等。
3.几何:点、线、面、角等基本概念,平行线、相交线、直角、等腰三角形、全等三角形等几何形状和定理。
4.函数:函数概念、函数的表示与性质、函数的应用等。
5.统计与概率:统计基本概念,事件的概率等。
二、物理1.运动学:匀速运动、变速运动等。
2.力学:惯性、力、重力、摩擦力等基本概念,牛顿三定律等。
3.声学:声音的产生、传播、性质等。
4.光学:光的反射、折射、色散等。
三、化学1.物质的基本性质:物质的三态、密度、熔点、沸点等。
2.常见物质的性质:金属、非金属、氧气、水、酸、碱等。
3.反应:化学方程式、化学反应的类型、化学反应速率等。
4.元素、化合物、混合物等基本概念。
5.周期表:元素周期表的排列、元素的周期性规律等。
四、生物1.细胞:植物细胞、动物细胞的结构与功能。
2.生物的基本特征:生长、发育、代谢、运动、感应等。
3.生物的分类:生物的类属、系统演化等。
4.公民的健康:卫生、传染病的预防、饮食、环境污染等。
5.生态学:生态系统的结构、功能、稳定性等。
五、历史1.中国古代史:夏商周时期、秦汉时期、唐宋时期、明清时期等。
2.世界古代史:古埃及文明、希腊罗马文明、印度文明等。
3.近代史:近代中国、世界近代史的发展等。
4.当代史:二战、冷战、世界各国的政治、经济等。
六、地理1.人口与资源:人口的分布、数量、增长、资源的分类、分布等。
2.地球与地理坐标:地球的形状、地球的构造、地理坐标系等。
3.自然环境:气候、水文、地形、植被、动植物资源等。
4.经济地理:工业地理、农业地理、城市地理等。
七、语文1.修辞手法:比喻、拟人等。
人教版初中语文教材的重要知识点总结

人教版初中语文教材的重要知识点总结人教版初中语文教材是我国中小学最常用的教材之一,涵盖了丰富的内容和重要的知识点。
下面将对人教版初中语文教材的重要知识点进行总结,帮助大家更全面地了解和掌握这些知识。
一、古代文学1. 《荀子·劝学》这是荀子的名篇之一,主要谈到学习的重要性以及学习的方法,强调要志存高远,不断努力学习,塑造自己的人生。
2. 《论语》《论语》是孔子及其弟子语录的集成,内容涉及到人性、道德、政治、教育等方面的思想,深刻影响了后世。
3. 诗经《诗经》是我国最早的诗歌总集,包含了风、雅、颂三个部分。
其中,风歌咏自然景物和人民生活,雅是有关礼仪的诗歌,颂是咏赞君主功德的诗歌。
二、近代文学1. 《范进中举》该篇描写了范进冒险中举的故事,借以反映科举制度的不公和范进的坚持追求。
2. 《凤求凰》该篇是梁实秋先生的作品,通过凤凰和皇后的故事,表达了爱情、婚姻的珍贵和人性的美好。
3. 《狼牙山五壮士》这个故事讲述了五个勇敢的小学生为了保护家乡不受日本侵略者的侵犯而英勇献身的故事,是对英雄主义精神的歌颂。
三、写作技巧1. 描写事物的方法描述事物时可以采用具体的形象语言或者借助修辞手法来增强表达的效果,如拟人、比喻、夸张等。
2. 叙事的结构叙事文常采用顺叙、倒叙等不同的叙事结构,以此能够更好地引导读者的阅读情绪,增加文章的吸引力。
3. 议论文的写作技巧议论文需要明确观点、有论据支持、有逻辑严密的论证过程和得出结论,同时应该注意用词准确、语言流畅。
四、修辞手法1. 比喻比喻是通过对两个不同的事物进行比较来传达一种特定的意义或表达一种情感的修辞手法。
2. 拟人拟人是将无生命的事物或抽象的概念赋予人的形象和行为特征,使其更具生动性和形象感。
3. 过渡过渡在文章中起到连接前后内容的作用,可以借助词语、语句、段落等方式进行。
五、阅读方法与技巧1. 阅读理解对于篇章理解,可以先浏览全文,了解文章大意,然后再仔细阅读,划分段落,找到主题句,理解篇章的结构和重点信息。
初中生上学必备知识点总结

初中生上学必备知识点总结一、语文知识点1. 词语的辨析:词义辨析、词性辨析2. 词语的运用:词语搭配、词语活用3. 段落阅读:理解段落、概括段落大意4. 文学常识:古文、现代文学作品的背景和作者5. 写作技巧:写作方法、写作练习6. 审美修养:诗词鉴赏、散文鉴赏、古代文学名句二、数学知识点1. 整数:正数、负数、加减乘除2. 分数:约分、通分、计算3. 小数:四则运算、小数点的运用4. 百分数:百分数的意义、计算方法5. 代数:代数式、整式、分式6. 几何:图形的性质、计算面积、计算周长7. 方程:一元一次方程、解方程的方法8. 消费:消费问题的运算三、英语知识点1. 词汇:常用单词、短语、句型2. 语法:时态、语态、语序、从句3. 阅读:短文阅读、文章阅读、理解文章意思4. 口语:日常口语、交际用语、表达意见5. 写作:作文表达、句子构造、语法使用6. 听力:听力练习、听力理解、听力考试四、科学知识点1. 物理:运动、力、能量2. 化学:物质、化学反应、元素周期表3. 生物:人体、植物、动物、生态系统4. 地理:自然资源、气候、地理环境5. 历史:历史事件、历史人物、历史文化6. 政治:政治制度、国家政务、政治历史五、历史知识点1. 中国古代史:夏商周、春秋战国、秦汉2. 中国中古史:唐宋元明、明清3. 世界历史:古代世界、中世纪世界、现代世界4. 历史文化:历史文化名人、历史文化遗产、历史文化风俗六、地理知识点1. 地球的形状:地球的构造、地球的运动2. 地球的地理位置:地理分区、地理环境3. 地图:地图的绘制、地图的使用4. 世界地理:世界地理概况、世界地理环境5. 国家地理:国家地理概况、国家地理位置6. 地理资源:自然资源、人文资源、地理环境七、生物知识点1. 动物:动物分类、动物习性2. 植物:植物分类、植物生长3. 人体:人体结构、人体功能4. 生态系统:生态概念、生态平衡、保护环境5. 遗传学:遗传基础、遗传变异6. 生物实验:实验方法、实验结果、实验分析以上为初中生上学必备的知识点总结,涵盖了语文、数学、英语、科学、历史、地理和生物等各个方面的知识点。
示例初中各个年级人教版每科知识点总结
示例初中各个年级人教版每科知识点总结语文:初中语文主要以阅读理解、写作能力的培养为重点,包括课文阅读、文言文阅读、写作指导等多个方面。
重点内容包括古代文学作品及其名句、现代文学作品、修辞手法的应用、写作技巧等。
数学:初中数学主要包括数与代数、几何、函数与方程、统计与概率等多个部分。
主要涵盖整数与有理数、多边形与圆、一次函数、二次根式等内容。
其中,应用题的解题方法与思路培养也是数学学习的重点。
英语:初中英语注重培养学生的听、说、读、写四个基本技能,同时也注重语法知识的学习。
主要包括基本的英语语法规则、常用词汇、短语、句型以及听力训练和口语表达等。
物理:初中物理知识主要包括运动、能量、电磁学、光学等各个方面。
学生需要掌握物体的速度、加速度、力、功等基本概念,了解电路、电磁感应、光的传播等基本原理,并能够进行简单的实验操作与分析。
化学:初中化学知识主要包括物质的组成与转化、物质的性质与变化等内容。
学生需要熟悉常见元素及其符号、化学反应的基本类型与特征,并能够运用化学知识解释生活中的现象。
生物:初中生物主要包括生物基本概念、生物遗传与进化、生物生长发育、生物体内环境稳态调节等内容。
学生需要了解细胞、遗传、进化等基本概念,掌握观察、实验、分析和解释生物现象的能力。
历史:初中历史主要包括古代史、近代史和现代史三个板块。
学生需要掌握历史事件的发展脉络、人物的作用和历史文化的内涵,了解历史对现实的启示与影响。
地理:初中地理主要包括自然地理和人文地理两个方面。
学生需要学习地球的形状与运动、自然环境与资源、人类活动与地理环境的关系等内容,了解地理知识在解决实际问题中的应用。
政治:初中政治主要包括人与国家、政治与法律、经济与社会发展、公民与社会等各个方面。
学生需要了解国家的组织与管理、政治制度与政治文化、社会公平与社会责任等内容,并能够进行基本的社会实践与思考。
综合实践活动:初中综合实践活动包括劳动技术、信息技术、美育和健康教育等。
初中人教新目标英语目录及知识点梳理
初中人教新目标英语目录及知识点梳理一、七年级上册1. Unit 1 Hello!重点知识点:问候语、介绍自己、问别人的名字及所在国籍2. Unit 2 This is my sister.重点知识点:指示代词、人称代词、名词所有格、形容词性物主代词3. Unit 3 Is this your pencil?重点知识点:物主代词、一般疑问句、选择疑问句、名词性物主代词4. Unit 4 How old are you?重点知识点:数字、年龄表达、询问年龄、数字词语表达法5. Unit 5 Do you have a soccer ball?重点知识点:物品的拥有、询问人是否有物、常见运动器材的词汇二、七年级下册1. Unit 1 Where did you go on vacation?重点知识点:一般过去式、过去式的构成、问对方去过哪里度假2. Unit 2 How often do you exercise?重点知识点:频率副词、询问人的运动频率、回答频率的方法3. Unit 3 What are you doing for vacation?重点知识点:现在进行时、将来时、练习关于度假活动的对话4. Unit 4 I want to be an actor.重点知识点:职业相关词汇、介绍自己的职业梦想、询问对方的职业梦想5. Unit 5 Do you want to watch a game show?重点知识点:表示愿望和意愿的动词短语、邀请别人做事、回答邀请的方法三、八年级上册1. Unit 1 How do you study for a test?重点知识点:询问他人学习方法、回答他人学习方法、谈论自己的学习方法2. Unit 2 I used to be afraid of the dark.重点知识点:used to句型的用法、谈论过去的变化与习惯3. Unit 3 What were you doing when the UFO arrived?重点知识点:过去进行时、询问过去的情况、谈论过去正在进行的活动4. Unit 4 I wanted to be an actress.重点知识点:过去的愿望与打算、表示过去的动词形式、谈论过去的梦想与打算5. Unit 5 What's the highest mountain in the world?重点知识点:地理相关词汇、谈论地理事物、描述自然地理特征四、八年级下册1. Unit 1 How often do you exercise?重点知识点:谈论自己的健康习惯、询问别人的健康习惯、回答健康习惯的问题2. Unit 2 I think that mooncakes are delicious.重点知识点:表达个人观点的句型、谈论个人观点、询问他人观点3. Unit 3 What were you doing when it started to rain?重点知识点:过去进行时与过去时的区分、谈论过去的活动与情况4. Unit 4 He said I was hard-working.重点知识点:间接引语、直接引语转述、谈论他人的言论5. Unit 5 It must belong to Carla.重点知识点:情态动词must、可能性的推测、推测物的归属五、九年级上册重点知识点:谈论学习方法、提出建议、回应建议2. Unit 2 I think that reading is boring.重点知识点:表达个人观点的句型、谈论个人观点、询问他人观点重点知识点:将来时态的构成、谈论未来事物、预测未来技术4. Unit 4 What would you do?重点知识点:与条件虚拟语气相关的动词短语、假设句型的构成、谈论虚拟情况5. Unit 5 Nelson Mandela-a modern hero重点知识点:人物介绍、描述人物特点、探讨社会问题以上是初中人教新目标英语的目录及部分重要知识点的梳理。
初中学科知识点汇总整理与梳理参考资料目录
初中学科知识点汇总整理与梳理参考资料目录一、数学知识点汇总与梳理1. 数与式1.1 整数的概念与性质1.2 分数的概念与性质1.3 小数的概念与性质1.4 百分数的概念与性质1.5 四则运算的性质与运算规则1.6 代数式的概念与性质2. 图形与几何2.1 点、线、面的概念与性质2.2 直线与直线的关系2.3 角的概念与性质2.4 三角形的性质与分类2.5 四边形的性质与分类2.6 圆的性质与应用3. 同数关系3.1 比例与比例的性质3.2 平均数的概念与性质3.3 相似与相似性质3.4 黄金分割与黄金分割比例4. 函数与方程4.1 函数的概念与性质4.2 一元一次方程的概念与性质4.3 一元一次方程的解法与应用4.4 一元二次方程的概念与性质4.5 一元二次方程的解法与应用二、物理知识点汇总与梳理1. 机械与运动1.1 运动的描述与分析1.2 力的概念与力的作用1.3 动量与能量的概念与计算1.4 机械工作与机械能的转化2. 声与光2.1 声的传播与声音的特性2.2 光的传播与光的特性2.3 镜子与光的反射2.4 透明与不透明物体的特性3. 电与磁3.1 电流与电路的概念与性质3.2 电压与电阻的概念与性质3.3 电磁感应与电磁力的概念与性质3.4 电能的转换与使用三、化学知识点汇总与梳理1. 物质与化学反应1.1 三态物质及物质的变化1.2 元素与化合物的概念与区别1.3 化学反应的基本过程与特点1.4 反应物与生成物的关系2. 物质的组成与性质2.1 原子结构与元素周期表2.2 元素与化合物的化学键2.3 常见离子的形成与性质2.4 物质的酸碱性与氧化性3. 化学计算与实验3.1 摩尔与物质的量3.2 化学方程式的表示与计算3.3 化学反应速率与平衡3.4 化学实验与实验室操作四、生物知识点汇总与梳理1. 细胞组成与结构1.1 细胞的基本结构与功能1.2 细胞的分类与特点1.3 细胞的组成与细胞器的功能2. 物质的运输与代谢2.1 生物的营养需求与摄取2.2 物质的运输与循环2.3 呼吸与燃烧的过程与机制2.4 光合作用与光合产物的运输3. 生物的遗传与进化3.1 遗传与基因的概念与功能3.2 遗传变异与遗传信息的传递3.3 进化与物种的形成与演化3.4 生物分类与生物多样性保护以上是初中学科知识点的汇总与梳理,每个学科都涵盖了多个主题及相关内容。
初中学科知识点重难点总结与梳理
初中学科知识点重难点总结与梳理初中学科知识点的总结与梳理是对学生在初中阶段所学科目的知识进行归纳和整理,以便更好地回顾和复习。
本文将对初中数学、语文、英语和科学四个学科的重难点进行总结与梳理。
1. 数学:(1) 代数知识点:- 一元一次方程与一元一次不等式的解法。
在一元一次方程和不等式中,学生需要了解如何运用加减乘除等运算,解出方程或不等式中的未知数。
- 二次根式。
学生需要掌握二次根式的加减乘除的运算规则,以及简单的二次根式的化简。
- 坐标系与直角坐标系图形的认识与画法。
学生需要了解如何在二维直角坐标系中画出平面图形,并根据坐标系判断图形的性质。
(2) 几何知识点:- 相似三角形与三角形的面积计算。
学生需要掌握相似三角形的判定条件以及根据相似三角形计算其边长比例、面积比例等。
- 平行线与三角形内角和定理。
学生需要了解平行线与三角形内角和定理的定义和证明过程,并能应用于实际问题中。
2. 语文:(1) 文言文知识点:- 古文阅读理解与古文背诵。
学生需要通过不断阅读古代文学作品,理解古文的含义与背景,提高对古文的理解能力。
- 古文病句修改。
学生需要掌握古文语法的规则,对病句进行修改,使之符合语法及语义。
- 古文默写。
学生需要掌握古文的词汇和语法,通过默写的方式提高古文的记忆和理解能力。
(2) 现代文知识点:- 理解与分析文章的结构和逻辑关系。
学生需要通过阅读不同题材和体裁的现代文,理解文章的结构和各个部分之间的逻辑关系。
- 提炼和总结文章的中心思想。
学生需要通过分析文章的论述和推理过程,准确把握文章的主旨和中心思想。
3. 英语:(1) 语法知识点:- 时态与语态的使用。
学生需要掌握各种时态和语态的用法,准确表达不同时期的动作和状态。
- 被动语态。
学生需要了解英语中的被动语态的构成和用法,能够正确地将主动语态转换为被动语态。
(2) 阅读理解知识点:- 理解文章的主旨和细节。
学生需要通过阅读不同题材和难度的文章,抓住文章的主旨和细节信息,理解作者的意图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数备注:红色字体重点记忆人教版七年级上第一章 有理数1.1 正数和负数(一)正数:大于0的数叫正数,为了明确表达意义,正数前面加上符号“+”,这里的“+”通常省略;负数:小于0的数叫负数,在正数的前面加上符号“-”。
(重点看教材例子) (二)0既不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数。
1.2.1 有理数(一)有理数:整数和分数统称有理数。
(二)有理数的分类:① ②1.2.2 数轴(一)数轴:数轴是规定了原点、正方向、单位长度的一条直线。
(二)画数轴的步骤:(1)画直线;(2)在直线上取一点作为原点;(3)确定正方向,并用箭头表示(4)根据需要选取适当单位长度。
(三)一般的,设a 是一个正数,则数轴上表示数a 的点在原点的右边,与原点的距离是a 个单位长度;表示数-a 的点在原点的左边,与原点的距离是a 个单位长度。
1.2.3 相反数(一)相反数:只有符号不同的两个数。
一般地a 和-a 互为相反数,0的相反数还是0。
(二) 相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数。
1.2.4 绝对值(一)绝对值:一般地,数轴上表示数a 的点与远点的距离叫做数a 的绝对值,⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数(二)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.即1.;2.;3.。
4.有理数大小比较(1)正数大于0,0大于负数,正数大于负数;(2)两个负数,绝对值大的反而小。
(3)异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值。
1.3 有理数的加减法(一)有理数的加法法则:1.同号两数相加,取相同的符号,并把绝对值相加;2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加和为0;3.一个数同0相加,仍得这个数。
(二)有理数加法的运算律1.2.(三)有理数的减法法则:减去一个数,等于加上这个数的相反数。
1.4 有理数的乘除法(一)有理数的乘法法则:1.两数相乘,同号为正,异号为负,并把绝对值相乘;2.任何数与0相乘都得0。
(二)几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数。
(三)几个数相乘,如果其中有因数为0,那么积等于0。
(四)乘积是1的两个数互为倒数。
(五)有理数乘法的运算律:1.乘法的交换律:;2.;3.。
(六)有理数的除法法则1.除以一个不等于02.两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不等于0 的数,都得0。
(七)有理数加减乘除混合运算法则:先乘除,后加减。
1.5.1 乘方(一)乘方:求n个相同因数的积的运算,叫做乘方。
乘方的结果叫做幂,在中,叫做底数,n叫做指数。
(二)有理数乘方的法则:1.负数的奇次幂是负数,负数的偶次幂是正数。
2.正数的任何次幂都是正数,0的任何正整数次幂都是0。
(三)有理数的混合运算顺序:(重点看教材例子)1.先乘方,再乘除,最后加减;2.同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
1.5.2 科学计数法科学记数法:把一个大于10的数记成的形式(其中大于或等于1且小于10,n 是正整数),这种记数法叫科学记数法。
1.5.3 近似数近似数的精确位:一个近似数,四舍五入到哪一位,就说这个近似数的精确到哪一位。
第二章整式的加减2.1 整式(一)单项式1.单项式:式子中只含数或字母的积,叫做单项式,单独一个数或一个字母也是单项式。
2.单项式的系数与次数:单项式中的数字因数叫做这个单项式的系数,一个单项式中,所有字母的指数的和叫做这个单项式的次数。
(二)多项式1.多项式:几个单项式的和叫做多项式。
,每个单项式叫做多项式的项,不含字母的项叫常数项。
2.多项式的次数:多项式里,次数最高项的次数,叫做这个多项式的次数。
(三)整式单项式与多项式统称为整式。
2.2 整式的加减(一)同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项。
(二)合并同类项:把多项式中的同类项合并成同一项,叫做合并同类项。
(三)合并同类项法则:合并同类项后,所得项的系数是合并前各同类项系数的和,且字母连同它的指数不变。
(四)去括号法则:1.如果括号外面的因数是正数,去括号后原括号内各项的符号与原来的符号相同;2.如果括号外面的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
(五)整式加减的运算法则:一般的,几个整式相加减,如果有括号就先去括号,然后在合并同类项。
第三章一元一次方程3.1 从算式到方程3.1.1 一元一次方程(一)方程:含有未知数的等式叫方程。
(二)一元一次方程:只含有一个未知数(元),未知数的次数是1,等号两边都是整式,这样的方程叫做一元一次方程。
(三)解方程和方程的解:解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解。
3.1.2 等式的性质,那么(二)等式的性质2 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
即3.2 解一元一次方程(一)——合并同类项与移项移项:把等式一遍的某项变号后移到另一边,叫做移项。
3.3 解一元一次方程(二)——去括号与去分母(一)一元一次方程的标准形式:ax+b=0(x是未知数,a、b是已知数,且a≠0)。
(二)解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1等,通过这些步骤可以使以x为未知数的方程逐步向着x=a的形式转化,这个过程主要依据等式的基本性质和运算律等。
3.4 实际问题与一元一次方程(一)基本过程用一元一次方程解决实际问题的基本过程如本章开头所示。
(二)常用公式1.行程问题:,,2.工程问题:,3.比率问题:,,4.顺逆流问题:顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度;5.利润=售价-成本,6.周长、面积、体积问题:,, ,第四章几何图形初步4.1 几何图形4.1.1 立体图形与平面图形(一)立体图形:几何体的各部分不都在同一平面内的图形叫做几何图形。
(二)平面图形:有些几何图形的各部分都在同一平面内叫做平面图形。
(三)展开图:有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形。
这样的平面图形称为相应立体图形的展开图。
4.1.2 点、线、面、体(一)体:几何体也简称为体。
(二)面:包围体的是面。
(三)线:面和面相交的地方形成线。
(四)点:线和线相交的地方形成点。
4.2 直线、射线、线段(一)事实:经过两点有一条直线,并且只有一条直线。
简单说成:两点确定一条直线。
(二)相交:当两条不同的直线有一个公共点时,称这两条直线相交,这个公共点叫做交点。
(三)中点:点M把线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点。
(四)基本事实:两点的所有连线中,线段最短。
简单说成:两点之间,线段最短。
(五)距离:连接两点间的线段的长度,叫做这两点的距离。
4.3 角4.3.1 角(一)角的单位:度()、分()、秒()。
4.3.2 角的比较与运算角的平分线:一般的,从一个顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。
4.3.4 余角和补角(一)余角:如果两个角的和等于90°(直角),就说这两个角互为余角,其中每一个角是另一个角的余角。
(二)补角:如果两个角的和等于180°(平角),就说这两个角互为补角,其中一个角是另一个角的补角(三)性质:同角(等角)的补角相等。
同角(等角)的余角相等。
第五章相交线与平行线5.1 相交线(一)相交线1.邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
也可以表述为两个角有一条公共边,另一条边互为反向延长线。
2.对顶角:一个角的两边分别是另一个叫的两边的反向延长线,像这样的两个角互为对顶角。
3.性质:对顶角相等。
(二)垂线1.垂直:直线与的夹角为90°时,我们说与2.垂线:两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
3.几何语言:︒=∠∴⊥90,AOC CD AB或者CD AB AOC ⊥∴︒=∠904.垂线的画法:一靠、二过、三画一靠:把三角板的一条直角边靠在已知直线上;二过:让三角板的另一条直角边经过已知的点;三画:沿着直角边经过已知点画直线。
5.性质:(1)在同一平面内,过一点有且只有一条直线与已知直线垂直;(点在线外和点在线上两种情况)(2)连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短。
6.点到直线的距离:直线外一点到这条直线的垂线段的长度叫做点到直线的距离。
7.同位角、内错角、同旁内角(两条直线被第三条直线所截,三线八角)(1)同位角:∠1与∠5像这样具有相同位置关系的一对角叫做同位角。
(F 型)(2)内错角:∠2与∠6像这样的一对角叫做内错角。
(Z型)(3)同旁内角:∠2与∠5像这样的一对角叫做同旁内角。
(U 型)5.2 平行线及其判定(一)平行线1.平行线:在同一平面内,不相交的两条直线叫做平行线。
与互相平行,2.平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
3.推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
即如果,。
(二)平行线的判定1.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行;2.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行;3.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
5.3 平行线的性质(一)平行线的性质1.两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
2.两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。
3.两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。
(二)命题、定理、证明1.命题:判断一件事情的语句叫命题。
命题是由题设和结论两部分组成,命题常可以写成如果…那么…的形式。
即如果+题设,那么+结论。
2.真命题:如果题设成立,那么结论一定成立,这样的命题叫做真命题。
性质和定理都是真命题。
3.假命题:题设成立时,不能保证结论一定成立,这样的命题叫做假命题。
4.定理:经过推理证实得到的命题叫做定理。
5.证明:一个命题的正确性需要经过推理才能做出正确判断,这个推理过程叫做证明。
