一种公交换乘路线智能选择的新方法_陈丽佳
公交乘车最佳线路智能系统

公交乘车最佳线路智能系统薛申芳;程振国【摘要】随着城市化的加速,城市公交也得到了相应的快速发展。
公交车上的智能导航和收费系统设备越来越受到重视,它可以方便乘客,减轻乘务员的劳动等。
就一个简化的城市公交路线情况,利用代数(三维矩阵)方法建立数学模型,并利用MATLAB软件编写智能平台,可以完成当前站点、乘客目的站点的显示和自主选定菜单,智能系统能告诉乘客最佳乘车路线所经过的站次。
这里的数学模型建立方法对复杂的城市公交情况也是适用的。
【期刊名称】《邢台学院学报》【年(卷),期】2011(026)004【总页数】2页(P166-167)【关键词】公交导航;乘车站次;最佳路线;数学模型【作者】薛申芳;程振国【作者单位】邢台学院数学系,河北邢台054001;邢台学院数学系,河北邢台054001【正文语种】中文【中图分类】TP391关于公交乘车路线优选问题,可用优化[1]、遍历搜索[2]方法建立数学模型。
这里针对一个简化的公交路线,确定公交乘车最优路线所经过的站次问题,采用代数方法建立数学模型,并利用MATLAB软件平台去显示当前站点、乘客目的站的显示、自主选择菜单,智能系统能告诉乘客最佳乘车路线所经过的站次。
对城市公交而言,一般来讲,公交车辆较多,线路交叉、错综复杂。
城市公交乘客从某站要乘车到达某目的站时往往有多种乘坐(包括换乘)路线,不同的乘坐路线又致乘坐的站次不同,乘客都需要考虑乘坐最佳路线(这里以乘坐站次最少为原则)以节省时间、费用和公交资源。
为了侧重给出解决问题的数学方法,这里考虑简化的公交线路如图 1所示。
图1中,方向虚线和方向实线给出了不同的两路公交车的两条环路,共有7个站点,S2,S3,S4s,S5,S6为两路车的公共站点。
下面利用MATLAB软件平台编写智能软件,只要乘客在Sj站上车后,再按要达到的目的站Sj,系统就会自动显示出该乘客最佳乘车路线所经过的站次记Si为公交的各站点为方便描述,把上述两路环行公交分别记为:构造三维矩阵(简记为W),这里二维矩阵的第m行第n列元素确定原则为:(1)式中的K为使得矩阵的非对角元素全非0最小整数,利用MATLAB软件可得K=4。
一种公交网络最优路径新算法

计 算 机 应 用 研 究
Ap l a in Re e r h o mp t r p i t s a c fCo u e s c o
Vo . 7 No 3 12 . Ma . 2 0 r 01
一
种 公 交 网络 最优 路径 新 算 法 水
仍然是绝大多数出行者 的首 选方式 。同时 , 高效 、 地使用 合理
公共 交通 系统能够有效地缓 解 日益 严重 的城市道 路交 通紧张 状况 , 因此众多学者提倡 公共交 通 系统优先 理念 , 并得 到 了各 地政府的大力支持 。
1 最优路径算法
1 1 路 径选择 算法 . 根据 公交 线路 的实 际情况 和大众 心理分 析 , 广州 市 内, 在
蔡 念, 蔡彩燕
( 东工业 大 学 信 息工程 学院 , 州 500 ) 广 广 106
摘
要 :从 出行 者的 实际情 况 出发 , 出步 行 愿 望 系数 , 合 考虑 最 小换 乘 次数 、 短 时 间 以及 最 小 费用 等 因 提 综 最
素 , 出 了一种 公 交网络 最优路 径新 算 法 , 用 于广 州市 大学城 内公 交线路 查询 , 提 应 实现相 应 的仿真 系统 。 关 键词 :最优路 径 ; 步行 愿望 系数 ; 交线路 查询 公
最优路径方法对评价和 优化公 交 网络以及公 交线 路查询 具有非常重要的实 际意义 。传统 的最优 路径 问题 往往就
是最短路径 问题 , 只需 找 出两 点 之 间路径 距离 最短 。Dj 即 i k
换乘 次数 小于 等于 两次 是 比较合 理 的 。因此 , 文 不考虑 本 换乘 次数超过两次的方 案 , 样最 多只需进 行三 次搜索 , 这 从而 简化算 法模 型 , 降低程 序运行时间复杂度 , 提高整体查询效率 。
2007 全国赛一等奖公交车路线选择
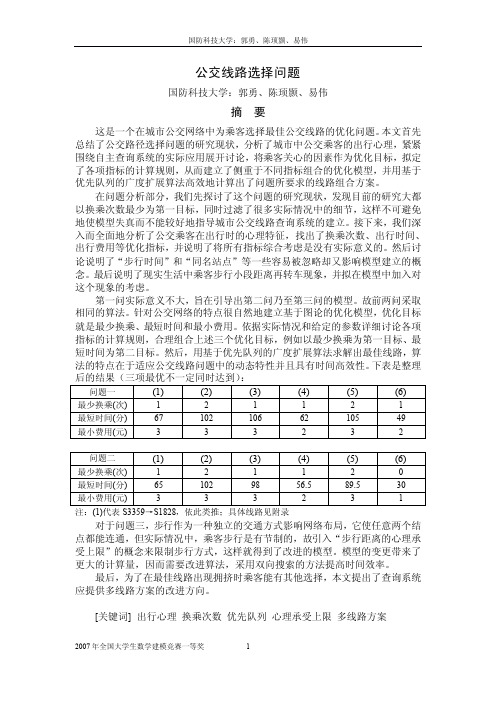
(1)
1 65 3
(2)
2 102 3
(3)
1 98 3
(4)
1 56.5 2
(5)
2 89.5 3
(6)
0 30 1
2007 年全国大学生数学建模竞赛一等奖 3
国防科技大学:郭勇、陈顼颢、易伟
第一,最短线路组合不一定是最佳方案。因为最短路线组合很可能会使乘客 频繁地换乘不同线路的公交车,这是乘客所不愿意的,因此乘客在出行时,总是 希望最好能搭乘一趟车直接到目的地, 除非这趟车确实是绕了个大弯浪费了很多 时间,或者根本没有这种直达的车,乘客才会考虑在中途换乘其他车次。这就是 提出换乘次数这个概念的初衷; 第二,出行距离对应途经站数,即出行距离越长途经站数就越多。本问题中 不考虑从起点到上车站台的距离和从下车站台到终点的距离, 且第一问不考虑中 途换车所步行的距离。这样的话,实际上只要时间上尽量快,乘客是不太会关心 出行距离的,因为整个出行过程中乘客基本都在车上(步行换车在 5.5 中单独考 虑) ,车行驶了多长的距离都不会使他太在意,而一般情况下,要时间尽量快就 得选择途经站数少的即距离较短的车次,这样距离就与时间统一起来了; 第三, 这里讨论的出行时间只包括车行时间、 换乘时间和步行时间。特别 地 , 当不考虑步行方式时,只包括前两者; 第四,在一票制的城市中费用与换乘次数是一致的,但是北京的公交采取单 一票制与分段计价结合,使两个概念有了区别,但是这也不会对二者的一致性产 生太大的影响。 1999 年在南京市 8 个公交站点进行了一次公交乘客出行心理问卷调查 [5] , 共得到有效表格 440 份,图 2 是调查结果。
城市公交换乘最佳路径选择的模型和算法

用线 路 与线路 之 间 的关 系 建立 邻 接 矩 阵 , 样建 立 这
的模 型很容 易在 实际应 用 中实现 .
1 公 交 网络模 型构建 1 1 参数 的定 义 .
站点 序列 为 : 6 S 一 S 2 S 1 S 0 S 一 S 一 S 一 9 1一 1一 1一 7 4
S一 S . 1 L 5 6 L , 2和 L 3分 别 是 三 条公 汽线 路 . 1和 L L 3是两条 上下 行 经过 的站 点一 致 的线 路并 且 两 线 路 经过 的站点有 重合 的部分 , 2是 一条往 返 不一 致 L 的线 路 . 1上行 经过 的 站点 序 列 为 : 1 S 一 S 一 L S一 4 7 S O 下行 经过 的站 点序列 为 :1 一 S 一 S 一 S . 2 I, S 0 7 4 1 L
间 的关 系建 立 邻 接 矩 阵l. , 这 种存 储 方 式 在 实 4 但 6 J 际应 用 中很难 实现 . 比如 , 我们在 实际操 作 中一 般要 将邻 接矩 阵放 到表 中存储 , 但是 表的列 是有 限的 , 最 多 只有 1 2 4列 , 一个 中小 城 市 的 站点 就 可 能 有 0 而 几 千个 . 以 , 所 很多公 交换 乘最佳 路径选 择模型 和算
Li e mar n t x线路关 i
.
系表 : 储 各 条线 路 关 系 的 存
邻接 矩阵 . Trnfrno换 乘 信 息 表 : 储 换 乘 的 详 细 asel f 存
但 是 , 际上人们 出行 路 径 的选 择 是 一个 复 杂 的系 实 统 工程 . 对公共 交通 最佳路 径 的寻求 , 同的出行者 不 追求 的最 优 目标 也 不 尽 相 同 , 换 乘 次 数 、 驶 时 有 行 间、 出行 费用 、 行驶 距 离 、 乘 步行 时间 和距 离 等 多 换
基于多智能体的公交线网动态优化系统

路 过程 ;若发 车频 率高 ,则说 明线 路乘 客需求 大 ,执行新 建
线路 过程 。
三 、结 论
当前 公交 线 网优化周 期较 长 ,线 网优化滞 后于乘 客需 求
单智 能体 和 多智 能体 ( M A S )。单智 能体 系统 的研 究 主要 集 中在 认知 与模 拟人类 的智能行 为 ,它侧 重 于对人类 的智 能行
为进 行研 究和模 拟 。MA S是指 一些 智能体 通过协 同完 成某 些
线 网不 能满 足乘客 需求 时及 时对公 交 网络进行 优化 。优 化过
整。
关键 词 :公 交线 网优 化 ; 多智 能体 ;系统 科 学
引言
公交 线 网优化 ,即在 已有 规划之 下 ,为 了解 决供 需不平
衡 所进行 的优 化 。主要 包括 两方 面 内容 :空 间优 化和 时间优
基于 M A S的单 线公 交 车 运营 控 制 系统 。该 系统 包 含六 种 智 能体 : ( 1 )数据 智 能 体 ; ( 2 )车辆 智 能 体 ; ( 3 ) 用 户 接 口智能体 ; ( 4 ) 增强学 习智能体 ; ( 5 ) 协调智 能体 ; ( 6 ) 智 能体管 理 系统 。 上 述六种 智 能体组 成三层 混合结 构 ,其 中数据 智能 体和 用户接 口智能体 处于 底层 ,将 G P S系统 、A P C系统等采 集到 的车辆 位置 、 速度 和乘 客上下车 数据等处 理后传递 给需求 方 , 同时 为用户提供 可视化 和交互功 能 ; 公交智 能体处 于 中间层 ,
< , < , < 垒 垒 里 里
基于 AVL 与 IC 卡数据的公交换乘判定

基于 AVL 与 IC 卡数据的公交换乘判定丰海宽【摘要】基于成都智能公交数据,以乘客IC刷卡数据、公交GPS数据、公交GIS 数据、上车站点数据及下车站点数据为基础,对连续出行阶段间是否存在换乘提出判定方法.在前人换乘时间阈值、换乘距离阈值、最大等待时间等条件下,进一步细化对同站换乘、异站换乘的判定,完善公交换乘判定模型,为大规模、程序化利用智能公交数据提供支持.最终换乘结果一定程度证实了本文判定模型的有效性与实际意义.【期刊名称】《黑龙江交通科技》【年(卷),期】2018(041)010【总页数】3页(P176-177,180)【关键词】智能公交数据;公交换乘判定;同站换乘;异站换乘【作者】丰海宽【作者单位】西南交通大学,四川成都 611730【正文语种】中文【中图分类】U4921 基础数据预处理1.1 智能公交系统数据说明以成都市智能公交系统为例,提供了三类数据,分别为乘客IC卡数据、车载GPS数据、站点GIS数据。
数据介绍如表1。
表1 三种数据详细信息数据来源名称字段解释数据示例 CardNo卡号130284330 ConsumeDate刷卡时间2014-11-04 07:38:00 IC卡BusNo车号46006 LineNo线路号78 ConsumeType服务类型11BusNo车号46006 LineNo线路号78 GPS Actdatetime触发时间2014-11-04 07:39:00 Stationnum站点编号30463 LineNo线路号20 GISStationnum站点编号30463 StationName站点名称顺城大街南站 Lot站点经度104.02348 Lat站点纬度30.631931.2 上车站点数据获取(1)若IC卡数据对应车辆GPS数据缺失,则无法推算。
(2)若IC刷卡时间晚于对应车辆当日最晚进站时间,则无法推算。
(3)若对应车辆GPS数据存在,且IC刷卡时间早于对应车辆当日最早进站时间,则设15 km的冗余,即如果IC卡刷卡时间早于该车最早进站时间15分钟以内,则推算线路起点为上车站点。
一种改进的公交换乘算法的实现

一种改进的公交换乘算法的实现
许军林;蒋年德
【期刊名称】《电脑知识与技术》
【年(卷),期】2007(003)014
【摘要】针对公交线路中存在往返路线不一致、内外线路等情况,对用改进的邻接矩阵方法实现这一类型的公交换乘进行了研究.最后通过对线路结果集进行筛选、比较实现了最少换乘、最少站点为约束条件的公交换乘查询模块.
【总页数】2页(P517-518)
【作者】许军林;蒋年德
【作者单位】东华理工大学,江西,抚州,344000;东华理工大学,江西,抚州,344000【正文语种】中文
【中图分类】TP301
【相关文献】
1.基于公交智能调度系统的公交换乘算法实现 [J], 刘开元;王中恒
2.基于综合矩阵的城市公交网络模型的公交换乘研究及算法实现 [J], 谭泽芳
3.一种改进的公交换乘算法的实现 [J], 许军林;蒋年德
4.基于改进的DIJKSTRA算法的公交换乘简单实现 [J], 黄忠荣
5.一种基于区域规划换乘点查找的公交换乘方案算法 [J], 王杉
因版权原因,仅展示原文概要,查看原文内容请购买。
城市公交换乘最佳路径选择的模型和算法

城市公交换乘最佳路径选择的模型和算法
陈密芳
【期刊名称】《石家庄职业技术学院学报》
【年(卷),期】2009(21)6
【摘要】换乘是公共交通中常见的问题.为在公交换乘中选择最佳路径,建立了多目标选择的公交换乘最佳路径算法.其核心是通过建立线路关系矩阵,找到起始站点到目的站点3次换乘之内的所有换乘方案,根据优先考虑的目标从所有方案中选出最
佳路径,并同时考虑发车频率、各站间行驶时间和距离、转乘车行走的时间和距离、交通费用等实际因素.最后用一算例验证了该算法的有效性和合理性.
【总页数】4页(P22-25)
【作者】陈密芳
【作者单位】石家庄铁道学院交通工程分院,河北,石家庄,050061
【正文语种】中文
【中图分类】U121;O232
【相关文献】
1.城市公交最优路径选择的数学模型及其算法 [J], 王庆;潘荣英
2.城市公交换乘数据模型研究及算法实现 [J], 扈震;张发勇;刘书良
3.基于综合矩阵的城市公交网络模型的公交换乘研究及算法实现 [J], 谭泽芳
4.城市公交换乘的数学模型及其算法实现 [J], 王庆平;张兴芳;宋颖;于会增
5.基于深度优先遍历算法-回溯算法的公交网络限时免费换乘优化模型求解 [J], 魏金丽;范鑫贺;刘莲莲;刘阳;任杰睦;孙启龙
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第34卷第6期2009年11月测绘科学Science of Surveying and M app ingVol134No16Nov1作者简介:陈丽佳(19842),女,湖北武汉人,中南大学在读硕士研究生,主要从事GI S2T方面的研究。
E2mail:lijia_chen6@1631com收稿日期:2008205213一种公交换乘路线智能选择的新方法陈丽佳,邹峥嵘,李光强(中南大学信息物理工程学院,长沙 410083)【摘 要】公交换乘问题是公共交通信息查询的重要内容,本文首先叙述了经典D ijkstra算法,并分析了其不适合公交网络最优路径选择的原因。
然后提出了一种改进的D ijkstra算法,该算法将求解最短路径获得的站点作为搜索站点,并将这些站点及经过这些站点的线路构成换乘矩阵,结合换乘次数的要求,给出了基于D ijkstra的智能选择换乘线路的实现算法。
最后通过一个实际算例说明改进的D ijkstra算法在公交换乘路线选择中应用的可行性。
【关键词】最优路径;公交网络;公交换乘【中图分类号】P25 【文献标识码】A 【文章编号】100922307(2009)06202732031 引言数字公共交通是“数字城市”的重要组成部分,是城市公共交通网络分析的基础。
随着城市的快速发展,公共交通体系变化迅速,公交半径不断增加,公众出行难、换乘难的问题在大中城市非常突出,所以研究和实现公共交通换乘智能选择系统尤为重要,也是公众化、服务化地理信息系统的功能之一[1]。
目前,影响城市公交换乘方案选择的因素主要有:换乘次数、出行距离、出行耗时以及出行费用等。
通过对公交乘客的出行心理进行研究,其结果表明,“换乘次数”是大部分公交乘客在选择出行路线时首先考虑的因素,其次是出行耗时和距离长短。
而出行耗费的时间与换乘的次数,及等车的时间以及距离的长短密切相关。
因此,对于出行耗时和距离长短,可转化为最短路径基础上换乘次数最少的问题[2]。
本文首先研究了D ijkstra算法在公交网络分析中应用,然后提出了一种改进的D ijkstra算法,并给出详细算法实现步骤,最后通过实例验证了所提方法的可行性。
2 D ijkstra最短路径算法及其在公交网络分析中的应用公交换乘问题的实质就是给出起始点、目标点后,系统根据所定义的公交网络模型,自动搜寻能够通达起始点和目标点的公交线路,并根据用户要求提供出行方案。
公交出行路径的优化方案则是按照换乘次数递增的顺序进行搜索的。
0次换乘即直达线路,搜索每一条公交线路,如果存在既经过起始点又经过目标点的线路,即可入选,如果有多条入选,则按照路径长短进行最优选择,如图1a所示。
如果没有直达线路,就要考虑1次换乘的方案,如图1b所示。
因此,如何确定中转站成为解决问题的关键。
该中转站上的某条线路贯穿了起始点和中转点,另一条线路贯穿了中转点和目标点。
公交网络上的公交站点有若干个,如果对每一个站点都进行测试,寻找可行线路,那么站点和对应线路的换乘矩阵将会很庞大。
考虑到乘客出行的第二约束条件———距离,我们采用基于最短路径的公交换乘方案。
即在公交网络上求出从起始点到目标点的最短路径,将最短路径上的站点作为可能的中转站点,这样就大幅度的减少了中转站的搜索范围,减小了公交站点换乘矩阵,提高了公交路线的搜索速度。
因此公交换乘问题的解决思想可分解为:①求解起始站与目标站之间的最短路径,获得最短路径上的各个站点;②根据最短路径上的各个站点,获得经过站点的路线,构造站点线路对应的换乘矩阵,求解换乘矩阵,获得公交换乘方案。
公交线路换乘方案示意图如图1所示。
图1 公交线路换乘方案示意图D ijkstra算法是经典的最短路径搜索算法之一,因其稳定性和网络拓扑变化的自适应性,在计算机网络通信路径选择以及GI S路径选择中得到广泛的应用。
但是对公交网络来说,D ijkstra不适合公交换乘的查询算法[3],其主要原因如下:1)数据结构复杂:网络在数学和计算机领域中被抽象为图,所以图的存储表示是其基础。
一般而言,无向图可以用邻接矩阵和邻接多重表来表示,而有向图则可以用邻接表和十字链表表示[4]。
由于公交网络在节点与连通性上有一定的特殊性,如果采用现有的最短路径算法分析,所建立的公交线路网络图的数据结构模型将是非常复杂的。
2)算法时间长;在实现D ijkstra算法的过程中,核心步骤就是从未标记的点中选择一个权值最小的弧段,这是一个循环比较的过程,如果不采用任何技巧,未标记点将以无序的形式存放在一个链表或数组中。
那么要选择一个权值最小的弧段就必须把所有的点都扫描一遍,在大数据量的情况下,这无疑是一个制约计算速度的瓶颈,而且传统的D ijkstra算法求解最短路径问题运用了关联矩阵、邻接矩阵和距离矩阵,在存储图形数据和进行运算时,需定义N×N的数组,其中N为网络的结点数,当网络的结点数较大时,将占用大量的计算机内存,同时,大数组运算起来是很浪费时间的[5]。
3)公交换乘的特殊性不一定要求用D ijkstra算法算出一条最短路径。
假设要计算乘客从站点A到站点B的最短距离,将每个公交站点看成网络上的结点,每相邻站点间的路段看作一条边。
如果采用D ijkstra算法,只要网络图中测绘科学 第34卷两个结点之间有边存在,它就会进行搜索,由于忽视了乘客在不同线路上换车所付出了时间和费用代价,所计算出来的结果可能是从站点A 到站点B 的距离是最短的,但需要转乘好几次车才能到达,这样的结果对乘客并不是最佳选择。
因为从前面的公交乘客出行心理研究报告中可以看到,换乘次数少才是乘客出行时考虑的首要因素。
因此,D ijkstra 算法需要改进的方面包括:①选择合适的数据结构实现可降级的优先队列;②采用堆结构来实现优先队列,降低算法的复杂度和减少算法的执行时间;③应考虑换乘次数最少。
3 改进的D ijkstra 最短路径算法在D ijkstra 算法中,为了获得已经计算过的距离中距离值最小的节点,一般采用一个可更新、可排序的优先队列来实现。
因此,如何实现D ijkstra 算法的优先队列结构,就成为提高D ijkstra 算法性能的关键。
标准的优先队列仅支持“插入(insert )”、“删除最小(delete 2m in )”两种元素操作,但使用D ijkstra 算法还需要优先队列具备“降级(decrease 2p ri ority )”操作,以便能动态调整已排序队列中的元素,而选择合适的数据结构实现可降级的优先队列,则可以有效地降低算法的复杂度和减少算法的执行时间,一般可采用堆结构来实现优先队列。
本文描述的D ijkstra 算法采用一种新式堆结构———“配对堆(pairing heap )”来实现优先队列。
配对堆是一种比斐波那契堆简单,但性能却不低于它的数据结构[6]。
配对堆是由配对堆节点组成。
每个堆节点除了用于排序的元素外,还包括前驱节点、左儿子节点、右兄弟节点3个指针。
为了支持“降级”操作,作为最左儿子节点的前驱节点指针将指向其父亲节点;否则这个节点就是一个右兄弟节点,而其前驱节点指针将指向这个节点的左兄弟。
使用堆结构实现优先队列的最大问题是需要知道与已访问的网络节点对应的堆节点指针,由于更改堆的操作都是直接操作堆节点指针完成,因此,需要一种网络节点与堆节点之间的快速访问方式。
如果采用关联表的存储方式,那么每次访问节点的查询时间复杂度就为O (l og V ),这样使D ijkstra 算法的时间复杂度就增加为O ((E +V l og V )l og V );另一种方式是建立网络节点的哈希表,一般采用每个节点具有的唯一整型I D 值作为哈希值。
新的算法在原始D ijkstra 算法的基础上,为每个网络节点增加了一个指向堆节点指针,在算法遍历到新节点时,需要构造配对堆节点,并动态更新配对堆。
新算法流程如图2所示。
图2 改进的D ijkstra 算法流程4 公交换乘线路智能选择算法的实现在最短路径查询后,可通过站点获得所有经过的公交线路。
例如给出起始站点和目标站点S 1,S 5后,从S1到S 5的最短路径上所经过的站点依次是S 1,S 2,……,S 5。
经过这些站点的公交路线有L 1,L 2,……,L 6,经过S 1的公交线路有L 1,L 5,L 6。
将站点与经过路线生成换乘矩阵如下所示,其中列代表从起始站S 1到目标站S 5所经过的所有站点,行代表经过这些站点的公交线路。
1 0 0 1 10 1 1 1 00 1 1 0 10 0 1 0 01 1 1 0 01 0 1 0 1对于公交换乘矩阵(L i ,S j ),其中,L i :表示第i 路公交车;S j :表示第j 个站点;表中元素W ij =1表示L i 路车经过S j 站点,W ij =0则表示L i 路车不经过S j 站点。
从S 1到达S 5的各种方案确定如下[7]:1)直达方案换乘次数ti m e =0从L 1到L 6的所有线路中,如果存在L i ∈[L 1,L 6],使得W i,1=W i,5=1,则说明S 1到S 5可以直达。
所乘的线路是L i 路公交车。
2)一次换乘方案换乘次数ti m e =1如果存在L i ,L j ∈[L 1,L 6],及S x ∈(S 1,S 5),使得W i,x =W i,1=1,且W j,x =W j,5=1,则说明,从S 1到S 5可乘坐L i 路车在S x 站点下车,换乘L j 路公交车到达站点S 5。
3)二次换乘方案ti m e =2如果存在L i ,L j ,L k ∈L 1,L 6],及S x ,S y ∈(S 1,S 5),使得W i,x =W j,x =1,且W j,y =W k,y =1。
则说明从S 1到S 5,可在S 1站点乘坐L i 路公交车,在S x 站点下车,换乘L j 路公交车,在S y 站点下车,换乘L k 路公交车到达S 5。
4)多次换乘ti m e >2的情况以上过程实质是一个递归的过程[8,9]。
如要获得换乘次数为1的方案,就要满足条件:起始站到中转站存在直达线路,同时该中转站到目标站也存在直达线路。
同样,要获得换乘次数为2的方案,就要满足条件:起始站到中转站存在直达线路,同时该中转站到目标站能够一次换乘到达;或者,起始站到中转站可一次换乘到达,同时中转站到目标站存在直达线路。
依此类推。
对于复杂的公交线路来讲,公交换乘矩阵可能会比较庞大。
矩阵中可能存在大量0元素,采用数组存储会浪费大量空间。
公交换乘矩阵表也可以作些改进。
方法如下:如果某条线路所经过的站点恰是最短路径上的站点,则将该最短路径上站点的序号,即该站点在矩阵中的位置号,存入该条线路的关联站点数组中。
