3.4整式的加减.4整式的加减
整式的加减课件北师大版数学七年级上册

nⅠ
Ⅱ
8n 5n 8 5n 13n
乘法分配律
像这样把同类项合并成一项叫做合并同类项.
二、新知探索
例1.根据乘法分配律合并同类项.
1 xy2 3xy2
24m2n2 7m2n2
解:原式 1 3xy2 解:原式 4 7m2n2
2xy2
11m2n2
5mn 3mn 6mn
13x 3y 6xy
27x 5x 2x2
3 y2 y2 0
=2x
419a2b 9ab2 10 Nhomakorabea= 2y2
=10ab2
五、反馈练习
3.求代数式 8 p2 7q 6q 7 p2 7的值,其中 p 3, q 4.
解:原式= 8p2 7 p2 7q 6q 7
所含字母相同 相同字母的指数相同
合并同类项 法则
系数相加做为结果的系数 字母与字母的指数不变
五、反馈练习
1.合并同类项.
13 f 2 f 7 f
解:原式=3+2 7 f
=2f
23pq 7 pq 4 pq pq
解:原式=3+7+4+1 pq
=15 pq
2.下列各题的结果是否正确?指出错误的地方.
你能总结出整式加减运算的步骤吗?
整式加减运算的步骤:先去括号,再合并同类项。
单三击、此例处题编解辑析母版标题样式
例2. 先化简再求值:-3(2x2-xy)+2(x2+xy),其中x=1,y=3.
解:原式 6x2 3xy 2x2 2xy 4x2 5xy
当x=1,y=3时, 原式 412 51 3
=p2 q 7 当p 3, q 4时 原式=32 4 7
整式的加减(教案)
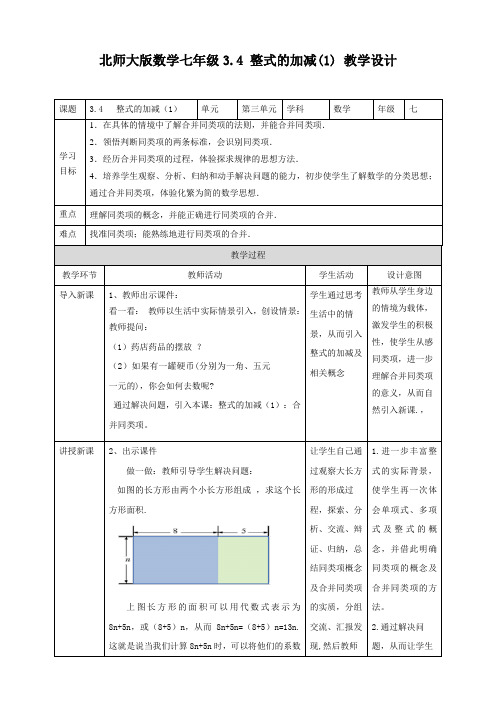
北师大版数学七年级3.4 整式的加减(1) 教学设计课题 3.4 整式的加减(1)单元第三单元学科数学年级七学习目标1.在具体的情境中了解合并同类项的法则,并能合并同类项.2.领悟判断同类项的两条标准,会识别同类项.3.经历合并同类项的过程,体验探求规律的思想方法.4.培养学生观察、分析、归纳和动手解决问题的能力,初步使学生了解数学的分类思想;通过合并同类项,体验化繁为简的数学思想.重点理解同类项的概念,并能正确进行同类项的合并.难点找准同类项;能熟练地进行同类项的合并.教学过程教学环节教师活动学生活动设计意图导入新课1、教师出示课件:看一看:教师以生活中实际情景引入,创设情景:教师提问:(1)药店药品的摆放?(2)如果有一罐硬币(分别为一角、五元一元的),你会如何去数呢?通过解决问题,引入本课:整式的加减(1):合并同类项。
学生通过思考生活中的情景,从而引入整式的加减及相关概念教师从学生身边的情境为载体,激发学生的积极性,使学生从感同类项,进一步理解合并同类项的意义,从而自然引入新课.,讲授新课2、出示课件做一做:教师引导学生解决问题:如图的长方形由两个小长方形组成,求这个长方形面积.上图长方形的面积可以用代数式表示为8n+5n,或(8+5)n,从而8n+5n=(8+5)n=13n.这就是说当我们计算8n+5n时,可以将他们的系数让学生自己通过观察大长方形的形成过程,探索、分析、交流、辩证、归纳,总结同类项概念及合并同类项的实质,分组交流、汇报发现,然后教师1.进一步丰富整式的实际背景,使学生再一次体会单项式、多项式及整式的概念,并借此明确同类项的概念及合并同类项的方法。
2.通过解决问题,从而让学生合并同类项时,把同类项的系数相加,字母和字母的指数不变. 例3 合并同类项:归纳总结“合并同类项”的方法:一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;三合,将同一括号内的同类项相加即可. 3.出示课件 试一试 :鼓励学生尝试用第二种方法解得出方法一,先化简再求值会更简便例3. 求代数式-3x ²y+1.5x-1.5x ²y+3.5x ²y-7的值, 其中x=1,y=0师:试试用两种方法去解该题,你又发现了什么?总结提高学生对同类项及合并同类项的认知。
2022秋七年级数学上册第3章整式及其加减3.4整式的加减第2课时去括号课件新版北师大版

【点拨】由题意得,当每条棱上的小球数为m时,正方体 上的所有小球数为12m-8×2=12m-16. 而12(m-1)=12m-12≠12m-16,4m+8(m-2)=12m -16,12(m-2)+8=12m-16, 所以A选项表达错误,符合题意; B,C,D选项表达正确,不符合题意.
【答案】C
16.先化简,再求值: (1)12x-2x-13y2+-32x+13y2,其中 x=-2,y=23;
B.2n+9 D.6n+3
【点拨】另外两个奇数分别为2n+3和2n+5, 故所求和为(2n+1)+(2n+3)+(2n+5) =2n+1+2n+3+2n+5=6n+9.
【答案】C
*15.(2020·达州)如图,正方体的每条棱上放置相同数目的 小球,设每条棱上的小球数为m,下列代数式表示正 方体上小球总数,则表达错误的是( ) A.12(m-1) B.4m+8(m-2) C.12(m-2)+8 D.12m-16
13.一个长方形的周长为一边长为( C )
A.5a+b
B.4a+2b
C.a+b
D.a+2b
*14.(2021·大连第九中学月考)三个连续的奇数,最小的一 个 是 2n + 1(n 为 自 然 数 ) , 则 这 三 个 连 续 奇 数 的 和 为
() A.6n+6 C.6n+9
21.已知有理数a,b,c,d在数轴上对应点的位置如图所示.
化简:|a-b|+3|c-a|-|b-c|+|a+d|. 【思路点拨】先判断绝对值符号内各个式子的正负,再用 绝对值的性质化简.各个式子的正负可用特殊值法验证, 如a+d,当a=-1,d=-2时,a+d=-1-2=-3<0.
【点拨】除了用数轴判断式子的正负外,还可以用特殊 值法判断,一般利用此法验证判断的结果是否正确.
3_4整式的加减(一)

第三章整式及其加减4.整式的加减(一)(一)教学目标知识与技能目标1.在具体情境中感受合并同类项的必要性,理解合并同类项法则所依据的运算律;2.理解合并同类项的法则,能实行同类项的合并;过程与方法目标1、通过具体情境导入同类项以及合并同类项的概念,经历合并同类项的过程,培养学生的观察、归纳等水平。
2、通过大量练习巩固,培养学生计算水平,协助学生形成解题经验。
情感态度与价值观目标。
在学习中培养学生分类、化繁为简等数学思想、方法,鼓励学生敢于发表自己的观点,从交流中获益。
(二)教学重点准确合并同类项(三)教学难点找出同类项并准确合并(四)教学准备见配套PPt(五)教学方法探究性学习等教学过程一、情境引入,导出定义。
教材【图3---6的长方形由两个小长方形组成……,议一议……a2与a3是不是同类项?】注意:本局部内容以学生自己探究为主;1、同类项的识别是重点,在合并上这里不要过度展开,因为后面第二环节有详细的研究;2、可用PPt分别展示教材中的“矩形图”,“合并同类项”,“同类项”等;如:同类项要点:①字母相同;②所含字母的指数也相同。
这样一方面提升学生学习的兴趣,另一方面帮学生理解概念实质,为后续学习扫清障碍。
二、领悟法则,准确合并。
活动内容:教材【例1……,做一做……说说你是怎么做的。
】注意:1、本局部内容以师生合作共同探究为主,尤其方法、步骤应以教师引导归纳为主;2、强化法则要点:①同类项系数相加;②字母和字母指数不变3、强化解题方法:记号分类(用不同的下划线或不同字体颜色等),括号分组(这里括号前统一为正号);4、强化解题一般步骤:①观察记号;②括号分组;③准确合并;④处理结论(按某字母的升幂或降幂排列)。
如:例1(2)7a+3a+2a-a+3;观察记号=(7a+2a)+(3a2-a2)+3;括号分组=9a+2a2+3;准确合并=2a2+9a+3。
处理结论三、小结归纳,随堂练习。
教材【随堂练习……】活动目的:旨在学会归纳、梳理、掌握学习要点,如:定义、法则、方法、步骤等,考查所学知识掌握情况。
3.4 整式的加减 同步辅导

4 整式的加减1.同类项 定义所含字母相同,并且相同字母的指数也相同的项,叫做同类项. 谈重点 同类项的理解“两个相同”:①所含字母相同; ②相同字母的指数也相同.“两个无关”:①同类项只与项中的字母有关,与系数无关; ②同类项与项中字母的排列顺序无关.“一个特别”:特别地,几个常数项也是同类项.如5与-8是同类项.为便于记忆,我们将其总结为:“同类项、同类项,两个条件不能忘,字母要相同,指数要一样.”【例1】 下列各组代数式中,属于同类项的有( )组.①0.5a 2b 3与0.5a 3b 2;②xy 与xz ;③mn 与0.3mn ;④xy 2与12xy 2;⑤3与-6.A .5B .4C .3D .1解析:答案:C2.合并同类项及法则 (1)合并同类项把同类项合并成一项叫做合并同类项.如:2a -a 中,2a 与-a 是同类项,可以合并为a .(2)合并同类项的法则把同类项的系数相加,字母和字母的指数不变.如:2xy+3xy=(2+3)xy=5xy.谈重点合并同类项合并同类项时,只把同类项的系数相加,字母及其指数都不变.为便于记忆,我们将其总结为:“合并同类项,法则不能忘;只求系数和,字母、指数不变样.”【例2】下列合并同类项,正确的是( ).A.3a+2b=5ab B.7ab-7ba=0C.3x2+2x3=5x5 D.4x2y-5y2x=-xy解析:只有同类项才可以合并,而选项A,C,D中前后两项都不是同类项,不可以合并.答案:B3.去括号法则法则:括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号都不改变;括号前是“-”号,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.谈重点去括号的技巧①去括号时应将括号前的符号连同括号一起去掉;②要注意括号前的符号,它是去括号后括号内各项是否变号的依据;③要注意括号前面是“-”号时,不管括号前是否有系数,去掉括号后,括号内的各项都要改变符号,不能只改变括号内第一项或前几项的符号,而忘记改变其余项的符号;④当括号里的第一项是省略“+”号的正数时,去掉括号和它前面的“+”号后要补上原先省略的“+”号;⑤括号内原有几项,去括号后仍有几项,不能丢项.去括号口诀:去括号,看符号;是“+”号,不变号;是“-”号,全变号.【例3】下列去括号正确的是( ).A.3a+(2b-c)=3a+2b+c B.3a-(2b+c)=3a-2b+cC.3a-(2b+c)=3a+2b+c D.3a-(2b+c)=3a-2b-c解析:根据去括号法则判断.选项A中去括号时,-c变成了+c,所以是错误的;选项B中去括号时,括号内c未变号;选项C中去括号时,括号内各项都没有变号;只有选项D符合去括号法则,故应选D.答案:D4.根据同类项的概念求字母的值同类项具备两个条件:①含有相同的字母;②相同字母的指数相同.根据上面的条件可以求出同类项中字母的指数.其方法是:①找出同类项中的相同字母;②根据相同字母的指数相同列出等式;③求出字母指数.【例4】若25a4b n与5m a m b3是同类项,则m=__________,n=__________.解析:此题中5m a m b3中5的指数,a 的指数都是m,而5又在前,很容易让人认为5m=25,从而m=2.实际上,在5m a m b3中,5m只是这个代数式的系数,不管m等于几(m等于4除外),都和5m a m b3与25a4b n是同类项无关.答案:4 35.合并同类项的步骤(1)合并同类项的依据是逆用乘法分配律,根据合并同类项的法则进行合并.(2)合并同类项的一般步骤可以简单归纳为:找→移→并.找:找出多项式中的同类项;移:将多项式中的同类项通过移动位置,将同类项集中在一起;并:将系数相加,完成合并同类项.辨误区合并同类项的注意事项(1)只有同类项才能合并,合并时应注意不要漏项.(2)多项式中含有两种以上的同类项时,为防止漏项或混淆,可先在各项的下边用不同的记号标示出各种同类项,然后再分别进行合并.【例5】合并同类项:(1)2x2-7-x-3x-4x2;(2)-3a2+2a-1+a2-5a+7;(3)4(a+b)-5(a-b)-6(a-b)+7(a+b).分析:先找出各代数式中的同类项,再进行合并.解:(1)2x2-7-x-3x-4x2找=(2x2-4x2)+(-x-3x)-7 移=(2-4)x2+(-1-3)x-7 并=-2x2-4x-7;(2)-3a2+2a-1+a2-5a+7 找=(-3a2+a2)+(2a-5a)+(-1+7) 移=(-3+1)a2+(2-5)a+(-1+7) 并=-2a2+(-3)a+6=-2a2-3a+6;(3)4(a+b)-5(a-b)-6(a-b)+7(a+b) 找=[4(a+b)+7(a+b)]+[-5(a-b)-6(a-b)]…移=11(a+b)-11(a-b)=22b. 并6.去括号的技巧当代数式中含有多重括号时,即有大括号、中括号、小括号时,可以由内向外逐层去括号,也可以由外向内逐层去括号,主要有以下几种方法:①按常规顺序去括号,先去小括号,再去大括号.②改变常规先去大括号,再去小括号.③先局部合并再去括号.④大小括号同时去掉.⑤先整体合并再去括号.⑥运用乘法分配律去括号.若代数式括号前有系数,可先进行乘法分配律,再去括号;也可以用乘法分配律直接将括号前面的系数乘以括号内的各项.【例6】计算:4xy2-3x2y-{3x2y+xy2-[2xy2-4x2y+(x2y-2xy2)]}.分析:看清题,去多重括号可以由内向外逐层进行,也可以由外向内逐层进行,如果去括号法则掌握得较熟练,也可以内外同时去括号.解:方法一:(由内向外逐层去括号)原式=4xy2-3x2y-[3x2y+xy2-(2xy2-4x2y+x2y-2xy2)]=4xy2-3x2y-(3x2y+xy2-2xy2+4x2y-x2y+2xy2)=4xy2-3x2y-(6x2y+xy2)=4xy2-3x2y-6x2y-xy2=3xy2-9x2y.方法二:(由外向内去括号)原式=4xy2-3x2y-3x2y-xy2+[2xy2-4x2y+(x2y-2xy2)]=3xy2-6x2y+2xy2-4x2y+(x2y-2xy 2)=5xy 2-10x 2y +x 2y -2xy 2=3xy 2-9x 2y .方法三:(内外同时去括号)原式=4xy 2-3x 2y -3x 2y -xy 2+(2xy 2-4x 2y +x 2y -2xy 2)=3xy 2-6x 2y -3x 2y =3xy 2-9x 2y .7.去括号的应用以下几种应用中都会用到去括号: (1)代数式化简及求值化简有括号的代数式或求代数式的值时,要用到去括号法则.解决此类题的一般步骤: ①去括号:按照去括号法则进行去括号;②合并同类项:将代数式中的同类项合并,化简代数式;③代入计算:用具体的数值代替代数式中的字母,按照代数式中指明的运算计算出结果. (2)实际问题中的去括号在列代数式表示实际问题中的数量关系时,有时会用到括号,因此,实际问题的解决中也会用到去括号法则.解决时主要的步骤:①认真审题,根据题意列出表示问题中数量关系的代数式; ②去括号,合并同类项,化简代数式; ③写出答案.【例7】 数学课上,李老师给同学们出了一道整式的化简求值的练习题: (xyz 2+7xy -2)+(-3xy +xyz 2-5)-(2xyz 2+4xy ).李老师看着题目对同学们说:“大家任意给出x ,y ,z 的一组值,我能马上说出答案.”同学们不相信,小刚同学立刻站起来,但他刚说完“x =2 013,y =-277,z =193”后,李老师就说出了答案是-7.同学们都感到不可思议,计算速度也太快了吧,何况是这么复杂的一组数值呢!但李老师却信心十足地说:“这个答案准确无误.”同学们,你知道李老师为什么算得这么快吗?分析:要知道李老师算得快的原因,可以先化简整式,看看化简后的结果,你就知道李老师算得快的奥妙了.解:(xyz 2+7xy -2)+(-3xy +xyz 2-5)-(2xyz 2+4xy ) =xyz 2+7xy -2-3xy +xyz 2-5-2xyz 2-4xy =(1+1-2)xyz 2+(7-3-4)xy +(-2-5) =0+0+(-7)=-7.原来化简后的结果不含有字母x,y,z,也就是说整式的值与x,y,z的取值无关.所以李老师的答案是正确的.。
3.4整式的加减

③ 13-(7-5)= 13-7+5
④ 9a-(6a-a)= 9a - 6a+a
1、以上练习中的括号怎么了? 2、去括号后,括号内各项的符号有何变化?
去括号法则 1、括号前是 “+”号,把 括号和它前面的“+”号 去掉, 括号里各项都不改变符号。
2、括号前是 “ - ”号,把 括号和它前面的“-”号 去掉,
二、自主探究,明晰法则
小明:4+3(X-1)=4+3X-3; 小颖:4X-(X-1)=4X-X+1;
你能总结去括号的法则吗?
括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各 项的符号都不改变;
括号前是“-”号,把括号和它前面的“-”号去掉后,原括号 里各项的符号都要改变;
三、法则应用,归纳步骤
(6)81M-11M=70
-4a
不是同类项不可以合并 不是同类项不可以合并
×
字母及字母的次数 该写下来
随堂练习: 1.下列各对不是同类项的是( ) A ,-3x2y与2x2y B, -2xy2与 3x2y C, -5x2y与3yx2 D, 3mn2与2mn2 2.合并同类项正确的是( ) A 4a+b=5ab B 6xy2-6y2x=0 C 6x2-4x2=2 D 3x2+2x3=5x5
1、什么是同类项?
说一说: 下面这组 单项式 有什么相同点。
3 2
相同字母的指数相同
指数3
指数2
2 3 2 3 2 2 3 2 5x y 和 x y 5 x y , x y 3 3
1.所含的字母相同
含有相同字母x, y
同类项
2.相同字母的指数也相同
同类项的定义: 所含字母相同,并且相同字母的指数也相 同的单项式叫做同类项。
七年级数学上册第3章整式的加减3.4整式的加减3.4.3去括号与添括号去括号(1)导学案(新版)华东师大版

(2)括号内的项的变与不变是 统一的;
(3)如果括号前有数字,那么 这个数字必须乘以括号内的每 一项。
【自学检测】:
1、去括号:
(1) a (b c)
(2) a (b c)
(3) a (b c)
(4) a (b c)
【巩固训练】: 先去括号,再合并同类项:
(1) (x y z) (x y z) (x y z)
去括号
年级
七
人
学习目标
1、熟练掌握去括号法则; 2、能够通过对去括号法则的掌握,从而熟练地解决有括号的多项式的同类项合 并。
学习重点 去括号法则的应用;
学习难点 去括号法则的形成。 导学过程
【温故互查】:
1、(1)某时,市 2 路某趟公交车上有乘客 a 名,后来第一个停靠站上来了 b 名乘客,在第二个停靠站又上来了 c 名乘客,则(1)此时,此公交车上有乘
a (b c) a b c 及 x ( y z) x y z
观察两个式子的左右两边,你发现了什么规律?
概括:去括号法则:
(1)括号前面 是“+”号,把
去掉,括号里各项
符号;
(2)括号前面是“-”号,把
去掉,括号里各项
符号;
1
注:(1)去括号是去掉了两部分:括号与括号前的符号。
客
名。
(2)还可以理解为:后来一共上来了乘客
名,因而此时公交车上共有
乘客
名。
由于以上的两个式子:
与
都表示同一个量,所有我们
有:
。
2、若图书馆要离开,第一批走了 y 位同学,第二批又走了 z 位同学,试用
复备栏
华师大版七年级数学上册课件:3.4.4整式的加减3

8.已知有理数a 、b 、c在数轴上的位 置如图所示,试化简: a b b c c a
2 2 2 2 2
5.李华老师给学生们出了一道这样的题: “当m=0.3572,n=-0,289时,求多项式
7m3 6m3n 3m2n 3m3 6m3n 3m2n 10m3
的值.”题目出完后,张晓同学说: “题 目给岀的条件m=0.3572,n=-0,289是多余 的.”胡伟同学说: “不给这个条件,就 不能求岀结果,所以不是多余的.”你认 为他俩谁说得有道理?为什么?
1 2 2 a 1 5 a 1 4a 2a 2
2
其中
a 2.
学科网
3.由于看错了运算符号,某学生把一个整式减 去多项式ab-2bc+3ac误认为加上这个多项式, 结果得出答案是2bc-3ac+2ab,求原题的正确 答案.
解: ﹝(2bc-3ac+2ab)-(ab-2bc+3ac) ﹞ - (ab-2bc+3ac) = 2bc-3ac+2ab-ab+2bc-3ac-ab+2bc-3ac =6bc-9ac
Zx.xk
2012.11.6
1. 化简;
x 1 3 2 x 3x 5 x x 2 2 2
2.先化简,再求值:
2 2 2m 3m 5 4m 3m m 1 3 5 2
Hale Waihona Puke 其中1 m 1 . 2
3.小明在实践课中做了一个长方形的模 型,模型一边长是 3a 5b, 另一边长是 2a b, 则这个长方形模型的周长是多少?
4.已知 2 x 2 mn y 2 n3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.4整式的加减
4.整式的加减
解:n (n 1) (n 2) (n 3) …列代数式 n n 1 n 2 n 3 ……….去括号 (n n n n) (1 2 3) …找同类项 4n 6 ……….合并同类项
其中a 243 ,b 3
例 代数式(x2+ax-2y+7)-(bx2-2x+9y-1)
的值与字母x的取值无关,求a、b的值
2 2 解:(x +ax-2y+7)-(bx -2x+9y-1) =x2+ax-2y+7-bx2+2x-9y+1 2 =(1-b)x +(a+2)x-11y+8 ∵代数式(x2+ax-2y+7)-(bx2-2x+9y-1)
注意:如果括号前面有系数,可按 乘法分配律和去括号法则去括号, 不要漏乘,也不要弄错各项的符号.
练一练(1) (2)
2 3 2 3 2 3 2x y +(-4x y )-(-3x y )
2 2 (8xy-3y )-5xy-2(3xy-2x )
例11 化简求值:2x2y-3xy2+4x2y-5xy2 其中x=1,y=-1
例在多项式ax5+bx3+cx-5中,当x=-3时, 它的值为7;当x=3时,它的值是多少?
解三:巧用方程 5 3 当x=-3时,原式=-3 a-3 b-3c-5=7 ① 当x=3时, 原式=35a+33b+3c-5 设35a+33b+3c-5=m ② ; ①+ ②得:-10=7+m,∴m=-17 即当x=3时,原式=-17
例在多项式ax5+bx3+cx-5中,当x=-3时, 它的值为7;当x=3时,它的值是多少? 解二:(巧用相反数) 当x=-3时, 原式=a(-3)5+b(-3)3+c(-3)-5 =-35a-33b-3c-5=7, ∴ -35a-33b-3c=12, ∵ (-35a-33b-3c)+(35a+33b+3c)=0, ∴35a+33b+3c=-12, 当x=3时, 原式=35a+33b+3c-5 =-12-5=-17
2 2 例9.求整式x -7x-2与-2x +4x-1的差.
解:由题意得 (x2-7x-2)-(-2x2+4x-1) = x2-7x-2+2x2-4x+1 2 = 3x -11x-1 注:几个整式相加减,通常用括号 把每一个整式括起来,再用加减号 连接。
例10.计算:-2y3+(3xy2-x2y)-2(xy2-y3).
的值与字母x的取值无关.
评析:这是一个利用整式加减解答的综 思考:若代数式(2x2+ax-5y+b)-(2bx2合问题,先通过去括号,合并同类项将 3x+5y-1)的值与字母x的取值无关,求代 所给的代数式化简,然后根据题意列出 2-ab-b2)-(4a2+ab+b2)的值。 数式 3(a 方程,从而求出a、b的值。
例在多项式ax5+bx3+cx-5中,当x=-3时, 它的值为7;当x=3时,它的值是多少? 解一:巧添括号 当x=-3时, 原式=a(-3)5+b(-3)3+c(-3)-5 =-35a-33b-3c-5 =7 ∴-35a-33b-3c=12 当x=3时, 原式=35a+33b+3c-5 =-(-35a-33b-3c)-5 =-12-5 =-17
例在多项式ax5+bx3+cx-5中,当x=-3时, 它的值为7;当x=3时,它的值是多少? 解四:巧用特殊值 当x=-3时,原式=-35a-33b-3c-5=7. 由于a、b、c的值不确定,因此可 用取特殊值法来解. 考虑到a、b的系数较大, 不妨取a=b=0,则c=-4。 ∴当x=3时, 原式=35a+33b+3c-5 =0+0+3×(-4)-5 =-17
∴1-b=0,a+2=0,∴a=-2
,b=1.
[例] 计算3x2-2x+1-(3+x+3x2) 易错 错解:原式=3x2-2x+1-3+x+3x2 精讲 =3x2+3x2-2x+x+1-3 =6x2-x-2 正解:原式=3x2-2x+1-3-x-3x2 =3x2-3x2-2x-x+1-3 =-3x-2 评析:去括号时,括号前是“ -”号的, 思考:计算(3a2+2a+1)-(2a2+3a-5) 的结 去括号后,里面各项的符号都要改变。 果是( ) A.a2-5a+6 B.a2-5a-4 C.a2-a-4 D.a2-a+6
解: 2x2y-3xy2+4x2y-5xy2 =(2x2y+4x2y)-(3xy² +5xy2) =6x2y-8xy² . 当x=1,y=-1时, 原式=6×12×(-1)-8×1×(-1)2 =-14
1、填空: -2x (1)3x与-5x的和是_____; 8x 3x与-5x的差是_____. (2)a-b,b-c,c-a三个多项式的和是 0 . x+y+z (3) 化简:(x+y-z)+(z-y+x)-(x-y-z)=______. 2、将代数式先化简,再求值: 2 2 2 2 2 2 2a b (2b a ) (a 2b )
整式的加减
整式的加减就是求几个整式的 和或者差的代数运算。 注意பைடு நூலகம்整式的加减包括,单项式的加减、 多项式的加减、单项式与多项式之 间的加减。
例求单项式2x2y3、-4x2y3与-3x2y3的和.
解:2x2y3+(-4x2y3)+(-3x2y3) = 2x2y3-4x2y3-3x2y3 = (2-4-3)x2y3 2 3 = -5x y 评析:直接从“和”的意义出发, 练习 :计算(8xy-3y2)-5xy-2(3xy-2x2) 列出算式,注意后两项要带上括号。 因为单项式包括它前面的符号,然 后再按去括号法则去括号后合并同 类项就是结果。
整式的加减的一般步骤: (1)如果有括号,那么先去括号; (2)如果有同类项,再合并同类项
教室里原有a位同学,后来有 (b+2)位同学去打篮球,有(b+3)位 同学去参加兴趣小组,问最后教室里 还有多少人? 解 a-(b+2): =a-b-2-b-3 (去括号) (b+3) =a-2b-5 (合并同类项)
评析:在上述四种解法的解题过程中, 始终没有求出35和33的值,这是因为35 和33是非必须要求的成分,这样做可以 省时省力,提高解题效率。
