2016-2017学年河南省周口市商水县八年级(下)期末数学试卷

合集下载

河南省商水县2024届数学八年级第二学期期末学业质量监测试题含解析

河南省商水县2024届数学八年级第二学期期末学业质量监测试题注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（每题4分，共48分）1．如图，四边形ABCD 为菱形，AB=5，BD=8，AE ⊥CD 于E ，则AE 的长为（）A ．165B ．325C ．245D ．1252．若1(A x ，1)y ，2(B x ，2)y 是直线(1)2y m x =-+上的两点，当12x x <时，有12y y >，则m 的取值范围是( ) A ．1m B ．1m < C ．1m ≠ D ．0m <3．如图，直线y mx =与双曲线k y x=交于A 、B 两点，过点A 作AM x ⊥轴，垂足为M ，连接BM ，若2ABM S ∆=，则k 的值是（）A ．2B ．4C ．-2D ．-44．下列命题中正确的是（）A ．一组对边相等，另一组对边平行的四边形是平行四边形B ．对角线相等的四边形是矩形C ．对角线互相垂直的四边形是菱形D ．对角线互相垂直平分且相等的四边形是正方形5．已知，矩形OABC 按如图所示的方式建立在平面直角坐标系总，AB ＝4，BC ＝2，则点B 的坐标为（）A．（4，2）B．（﹣2，4）C．（4，﹣2）D．（﹣4，2）6．如图，平行四边形ABCD中，E是BC边的中点，连接DE并延长交AB的延长线于点F，则在题中条件下，下列结论不能成立的是（）A．BE＝CE B．AB＝BF C．DE＝BE D．AB＝DC7．下列图形既是中心对称图形又是轴对称图形的是（）A ．B ．C ．D ．8．P1（x1，y1），P2（x2，y2）是正比例函数1y x2=-图象上的两点，下列判断中，正确的是A．y1＞y2B．y1＜y2C．当x1＜x2时，y1＜y2D．当x1＜x2时，y1＞y29．甲、乙、丙、丁四名射击运动员在选拔赛中，每人射击了10次、甲、乙两人的成绩如表所示，丙、丁两人的成绩如图所示.欲选一名运动员参赛，从平均数和方差两个因素分析，应选（）.甲乙平均数9 8方差 1 1A．甲B．乙C．丙D．丁10．如图，∠1＝∠2，DE∥AC，则图中的相似三角形有（）A．2对B．3对C．4对D．5对11．如图，在中，分别以点A，C 为圆心，大于长为半径画弧，两弧相交于点M，N，作直线MN交BC于点D，连接AD ．若，，则的周长是( )A．7 B．8 C．9 D．1012．已知反比例函数y＝21kx+的图上象有三个点（2，y1），（3，y2），（﹣1，y3），则y1，y2，y3的大小关系是（）A．y1＞y2＞y3B．y2＞y1＞y3C．y3＞y1＞y2D．y3＞y2＞y1二、填空题（每题4分，共24分）13．如图，利用函数图象可知方程组32x kyy x+⎧⎨⎩＝＝的解为______．14．用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”时第一步先假设所求证的结论不成立，即问题表述为______．15．如图，若点P(﹣2，4)关于y轴的对称点在一次函数y＝x+b的图象上，则b的值为____．16．小军旅行箱的密码是一个六位数，由于他忘记了密码的末位数字，则小军能一次打开该旅行箱的概率是________．17．计算：33＝_____；|﹣12|＝_____．18．函数y=12-+1xx中自变量x的取值范围是______．三、解答题（共78分）19．（8分）如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．（1）在图1 中，画一个三角形，使它的三边长都是有理数；（2）在图2 中，画一个直角三角形，使它们的直角边都是无理数；（3）在图3 中，画一个正方形，使它的面积是1．20．（8分）如图，在平面直角坐标系中，已知点A（3，4），B（﹣3，0）．（1）只用直尺（没有刻度）和圆规按下列要求作图．（要求：保留作图痕迹，不必写出作法）Ⅰ）AC⊥y轴，垂足为C；Ⅱ）连结AO，AB，设边AB，CO交点E．（2）在（1）作出图形后，直接判断△AOE与△BOE的面积大小关系．21．（8分）已知反比例函数y =m x 的图象经过点A （x 1，y 1）和B （x 2，y 2）（x 1＜x 2）（1）若A （4，n ）和B （n +13，3），求反比例函数的表达式；（2）若m =1， ①当x 2=1时，直接写出y 1的取值范围；②当x 1＜x 2＜0，p =122y y +，q =122x x +，试判断p ，q 的大小关系，并说明理由；（3）若过A 、B 两点的直线y =x +2与y 轴交于点C ，连接BO ，记△COB 的面积为S ，当13＜S ＜1，求m 的取值范围． 22．（10分）关于x 的方程（2m +1）x 2+4mx +2m ﹣3＝0有两个不相等的实数根．（1）求m 的取值范围；（2）是否存在实数m ，使方程的两个实数根的倒数之和等于﹣1？若存在，求出m 的值；若不存在，说明理由．23．（10分）如图，已知四边形ABCD 和四边形DEFG 为正方形，点E 在线段DC 上，点,,A D G 在同一直线上，连接,,AC CG AE ，并延长AE 交CG 于点H ．（1）求证：AH GC ⊥．（2）若3AD =，1DE =，求线段AH 的长．（3）设AD y =，DE x =，当点H 是线段GC 的中点时，则y 与x 满足什么样的关系式.24．（10分）如图，ABC ∆是边长为x 的等边三角形.（1）求BC 边上的高h 与x 之间的函数关系式。

河南省周口市商水县2023-2024学年八年级下学期期末数学试题

河南省周口市商水县2023-2024学年八年级下学期期末数学试题一、单选题1．在平面直角坐标系中，若点P 的坐标为()4,3-，则点P 所在的象限是（） A ．第四象限 B ．第三象限 C ．第二象限 D ．第一象限 2．勿忘草是多年生草本植物，它拥有世界上最小的花粉勿忘草的花粉直径为0．000004米，数据0.000004用科学记数法表示为（）A ．4⨯105B ．4⨯106C ．4⨯10-5D ．4⨯10-63．如图，一次函数y ax b =+和反比例函数k y x =的图象相交于()12,A y -，()21,B y 两点，则通过图象可求不等式k ax b x+>的解集，其所用到的数学思想方法是（）A ．转化思想B ．类比思想C ．方程思想D ．数形结合思想 4．如图，在▱ABCD 中，∠A ＝125°，则∠1＝（）A ．65°B ．50°C ．55°D ．45°5．化简2326a b ab 的结果是（） A ．13 B ．23a b C ．22a b D ．3a ab6．如图，在矩形ABCD 中，对角线AC ，BD 交于点O ，添加下列一个条件，能使矩形ABCD 成为正方形的是（）A ．OD CD =B ．60AOB ∠=︒C ．DC AD = D ．BD AC =7．光从空气进入水中，入水前与入水后的光路图如图所示，若建立坐标系，并设入水前与入水后光线所在直线的表达式分别为11y k x =，22y k x =，则下列关于1k 与2k 的大小关系中，正确的是（）A ．10k >，20k <B ．10k >，20k >C ．12k k >D ．12k k <8．已知在菱形ABCD 中，10AB =，16BD =，则菱形ABCD 的面积为（）A ．160B ．80C ．40D ．969．我校为推荐一项作品参加人工智能比赛，对甲、乙、丙、丁四项候选作品进行量化评分，具体成绩（满分100分）如表所示，如果按照创新性占60%，实用性占40%计算总成绩，并根据总成绩择优推荐，那么应推荐的作品是（）A ．甲B ．乙C ．丙D ．丁10．如图，在正方形ABCD 内作45EAF ∠=︒，AE 交BC 于点E ，AF 交CD 于点F ，连接EF ．若5AB =，2DF =，则BE 的长为（）A ．157B ．53C ．115D ．2二、填空题11．计算：015⎛⎫-= ⎪⎝⎭． 12．如图，已知一次函数y kx b =+和正比例函数y mx =的图象交于点()2,6P ，则关于x 的一元一次方程kx b mx +=的解是．13．王大伯前几年承包了甲、乙两片荒山，两山各栽种了100棵枣树，现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了四棵枣树上的枣，每棵的产量如图所示，由统计图提供的信息可知，枣产量较稳定的是．14．如图，点A 在反比例函数m y x=的图象上，AB x ⊥轴于点B ，点C 在x 轴上，且CO OB =，若ABC V 的面积为3，则m 的值为．15．如图在矩形ABCD 中，8cm AB =，6cm BC =，E 为CD 的中点，动点P 从点A 出发，以每秒1cm 的速度沿A B C →→运动，最终到达点C ，若点P 运动的时间为x 秒，则当APE V 的面积为218cm 时，x 值为．三、解答题16．（110120222023-⎛⎫-- ⎪⎝⎭．（2）下面是小明同学进行化简分式22121244x x x x x x +-⎛⎫-÷ ⎪--+⎝⎭的过程，请认真阅读并完成相应任务．解：原式()()2212222x x x x x x x ⎛-+-=-÷--⎪⎝⎭-⎫ ……第一步()()221222x x x x x x -+--=⋅--……第二步 1x =-……第三步 ①任务一：第_________步开始出现错误．②任务二：请写出本题的正确化简过程．17．如图，在ABCD Y 中，BD 是对角线．(1)实践与操作：利用尺规过点C 作CE AB ⊥，垂足为E ．（要求尺规作图并保留作图痕迹，不写作法，标明字母）(2)在（1）的条件下，若12ABD S =V ，6AB =，求CE 的长．18．新郑红枣又名鸡心大枣，是河南省郑州市新郑市的特产，素有“灵宝苹果潼关梨，新郑大枣甜似蜜”的盛赞．某商店用1400元购进一批新郑红枣，销售发现供不应求，于是，又用6300元再购进一批红枣，第二批红枣的数量是第一批红枣数量的4倍，但第二批红枣的进货单价比第一批每箱贵10元．问第一批新郑红枣的进货单价为每箱多少元？19．2024年4月25日20时59分，神舟十八号载人飞船准时顺利点火发射成功．为弘扬载人航天精神，某校组织开展了“光耀星空”航天知识竞赛，现从该校七年级和八年级参与竞赛的学生中各随机抽取20名同学的成绩进行分析，将学生竞赛成绩分为A B C D ，，，四个等级，分别是A ．70x <，B ．7080x ≤<，C ．8090x ≤<，D ．90100x ≤≤．抽取的七年级学生的竞赛成绩：66，75，76，78，79，81，82，83，84，86，86，88，88，88，91，92，94，95，96，96．八年级等级C 的学生成绩：87，81，86，83，88，82，89．根据以上信息，解答下列问题：(1)填空：=a __________，b =__________，m =__________．(2)统计图中，B 等级所对应的扇形圆心角的度数是多少？(3)根据以上数据，你认为在此次知识竞赛中，哪个年级的成绩更好？请说明理由．（写出一条理由即可）20．如图，在平行四边形ABCD 中，过点D 作DE AB ⊥于点E ，点F 在CD 边上，CF AE =，连接AF ，BF ．(1)求证：四边形BFDE 是矩形．(2)若AF 平分DAB ∠，5CF =，13DF =，求四边形BFDE 的面积．21．紫外线杀菌灯的电阻(k Ω)y 随温度C ()x ︒的变化的大致图象如图所示．通电后温度由室温10C ︒上升到30C ︒时，电阻与温度成反比的函数关系．且在温度达到30C ︒时，电阻下降到最小值，随后电阻随温度升高而增加，温度每上升1C ︒，电阻增加4k Ω15．(1)当时1030x ≤≤时，求y 与x 之间的关系式．(2)紫外线杀菌灯在使用过程中，温度x 在什么范围内时，电阻不超过6k Ω．22．如图1，四边形ABCD 为正方形，E 为对角线AC 上一点，连接DE ，BE ．(1)求证：BE DE =．(2)如图2，过点E 作EF DE ⊥，交边BC 于点F ，以DE ，EF 为邻边作矩形DEFG ． ①求证：矩形DEFG 是正方形．②若正方形ABCD 1AE =，直接写出正方形DEFG 的边长． 23．综合与实践如图，直线y kx b =+与x 轴，y 轴分别交于点A 和点B ，点C 在线段AO 上，将ABC V 沿BC 所在直线翻折后，点A 恰好落在y 轴上的点D 处，已知4OA =，3OB =．(1)求直线AB 的解析式．(2)求:ABC OCD S S △△的值．(3)直线CD 上是否存在点P 使得45PBC ∠=︒？若存在，请直接写出点P 的坐标；若不存在，请说明理由．。

河南省周口市八年级下学期数学期末试卷

河南省周口市八年级下学期数学期末试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）下面调查中，适合采用全面调查的事件是（）．A . 对全国中学生心理健康现状的调查．B . 对我市食品合格情况的调查．C . 对桂林电视台《桂林板路》收视率的调查．D . 对你所在的班级同学的身高情况的调查．2. （2分） (2019七下·乌兰浩特期中) 下列条件不能判定AB//CD的是（）A . ∠3=∠4B . ∠1=∠5C . ∠1+∠2=180°D . ∠3=∠53. （2分） (2017七下·东莞期末) 将点P（2，1）向左平移2个单位后得到P’，则P’的坐标是（）A . （2，3）B . （2，-1）C . （4，1）D . （0，1）4. （2分） (2017七下·汇川期中) 在﹣1.732，，π，2+ ，3.212212221…（按照规律，两个1之间增加一个2）这些数中，无理数的个数为（）A . 5B . 2C . 3D . 45. （2分）在同一平面内，两条不重合直线的位置关系可能是（）A . 平行或相交B . 垂直或相交C . 垂直或平行D . 平行、垂直或相交6. （2分） (2019八上·驿城期中) 在直角坐标系中，将点（﹣2，3）关于原点的对称点向左平移2个单位长度得到的点的坐标是（）A . （4，﹣3）B . （﹣4，3）C . （0，﹣3）D . （0，3）7. （2分）如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=1，FD=2，则BC的长为（）A .B .C .D .8. （2分）已知x=2是不等式（x﹣5）（ax﹣3a+2）≤0的解，且x=1不是这个不等式的解，则实数a的取值范围是（）A . a＞1B . a≤2C . 1＜a≤2D . 1≤a≤29. （2分）若是5x2ym与4xn+m+1y2n-2同类项，则m2-n的值为（）A . 1B . －1C . －3D . 以上答案都不对10. （2分） (2017七下·无棣期末) 如图为某餐厅的价目表，今日每份餐点价格均为价目表价格的九折．若李心通同学在此餐厅点了橙汁鸡丁饭后想再点第二份餐点，且两份餐点的总花费不超过20元，则他的第二份餐点最多有几种选择（）A . 5B . 7C . 9D . 1111. （2分）方程组的解是（）A .B .C .D .12. （2分）如果点P(m ， 1-2m)在第四象限，那么m的取值范围是（）A .B .C .D .二、填空题 (共8题；共10分)13. （2分）绝对值不大于的非负整数是________．14. （1分）在一个不透明的布袋中装有红色、白色玻璃球共50个，除颜色外其他完全相同．小明通过多次摸球试验后发现，其中摸到红色球的频率稳定在16%左右，则口袋中红色球可能有________个．15. （1分） (2017八上·宁波期中) 将点P(－2，y)先向下平移4个单位，再向左平移2个单位后得到点Q(x，－1)，则x＋y＝________．16. （1分） (2016七下·莒县期中) 已知c的立方根为3，且（a﹣4）2+ =0，则a+6b+c的平方根是________．17. （1分）如图，点B是AD延长线上的一点，DE∥AC，AE平分∠CAB，∠C=50°，∠E=30°，则∠CDA的度数等于________ ．18. （2分）根据题意结合图形填空：已知：如图，AD⊥BC于D，EG⊥BC与G，∠E=∠3，试问：AD是∠BAC 的平分线吗？若是，请说明理由．答：是，理由如下：∵AD⊥BC，EG⊥BC（已知）∴∠4=∠5=90°（________ ）∴AD∥EG（________ ）∴∠1=∠E（________ ）∠2=∠3（________ ）∵∠E=∠3（已知）∴（∠1）=（∠2）（等量代换）∴AD是∠BAC的平分线（________ ）19. （1分） (2017九上·渭滨期末) 如图，在△ABC中，点D，E，F分别在AB，AC，BC上，DE∥B C，EF∥AB．若AB=8，BD=3，BF=4，则FC的长为________．20. （1分） (2018七上·秀洲月考) 观察下列各式：┉┉ 请你将猜想到的规律用含自然数n(n≥1)的代数式表示出来是___ __ ________.三、解答题 (共6题；共75分)21. （10分） (2017八上·丹东期末) 解方程组：．22. （10分）(2018·阜宁模拟) 解不等式组23. （15分） (2013八下·茂名竞赛) “最美女教师”张丽莉，为抢救两名学生，以致双腿高位截肢，社会各界纷纷为她捐款，我市某中学九年级一班全体同学参加了捐款活动，该班同学捐款情况的部分统计图如图所示：（1）求该班的总人数；（2）将条形图补充完整，并写出捐款总额的众数；（3）该班平均每人捐款多少元？24. （15分）如图，描出A（﹣3，﹣2）、B（2，﹣2）、C（﹣2，1）、D（3，1）四个点，线段AB、CD有什么关系？顺次连接A、B、C、D四点组成的图形是什么图形？25. （10分） (2017七下·濮阳期中) 问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．（1）按小明的思路，易求得∠APC的度数为________度；（2）问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；（3）在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC 与α、β之间的数量关系．26. （15分）(2016·荆门) A城有某种农机30台，B城有该农机40台，现要将这些农机全部运往C，D两乡，调运任务承包给某运输公司．已知C乡需要农机34台，D乡需要农机36天，从A城往C，D两乡运送农机的费用分别为250元/台和200元/台，从B城往C，D两乡运送农机的费用分别为150元/台和240元/台．（1）设A城运往C乡该农机x台，运送全部农机的总费用为W元，求W关于x的函数关系式，并写出自变量x的取值范围；（2）现该运输公司要求运送全部农机的总费用不低于16460元，则有多少种不同的调运方案？将这些方案设计出来；（3）现该运输公司决定对A城运往C乡的农机，从运输费中每台减免a元（a≤200）作为优惠，其它费用不变，如何调运，使总费用最少？参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共8题；共10分)13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共6题；共75分) 21-1、22-1、23-1、23-2、23-3、24-1、25-1、25-2、25-3、26-1、26-2、26-3、第11 页共11 页。

河南省周口市八年级下学期数学期末考试试卷

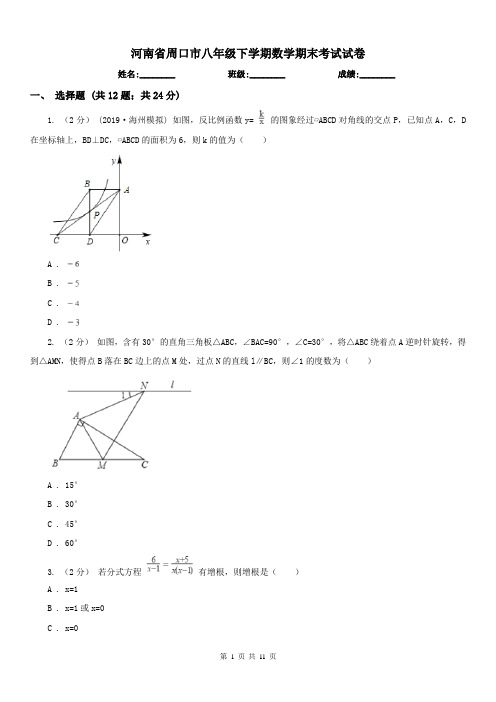
河南省周口市八年级下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）(2019·海州模拟) 如图，反比例函数y= 的图象经过▱ABCD对角线的交点P，已知点A，C，D 在坐标轴上，BD⊥DC，▱ABCD的面积为6，则k的值为（）A .B .C .D .2. （2分）如图，含有30°的直角三角板△ABC，∠BAC=90°，∠C=30°，将△ABC绕着点A逆时针旋转，得到△AMN，使得点B落在BC边上的点M处，过点N的直线l∥BC，则∠1的度数为（）A . 15°B . 30°C . 45°D . 60°3. （2分）若分式方程有增根，则增根是（）A . x=1B . x=1或x=0C . x=0D . 不确定4. （2分）分以下各组数为三角形的三条边长，其中能作成直角三角形的是（）A . 2，3，4B . 4，5，6C . 1，，D . 2，，45. （2分）若直线y=x-2与直线y=-x+a相交于x轴上，则直线y=-x+a不经过（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限6. （2分）数据8，0，2，﹣4，4的标准差等于（）A .B . 4C .D .7. （2分） (2019八下·嘉陵期中) 化简的值为（）A .B .C .D .8. （2分） (2017八下·山西期末) 四边形ABCD的四个角∠A∶∠B∶∠C∶∠D满足下列哪一条件时，四边形ABCD是平行四边形（）A . 1∶2∶2∶1B . 2∶1∶1∶1C . 1∶2∶3∶4D . 2∶1∶2∶19. （2分）函数y=x+的图象如图所示，下列对该函数性质的论述正确的是（）A . 该函数的图象是轴对称图形B . 在每个象限内，y的值随x值的增大而减小C . 当x＞0时，该函数在x=1时取得最小值2D . y的值可能为110. （2分） (2017八上·西安期末) 如图，把RI△ABC放在直角坐标系内，其中∠CAB=90°， BC=5．点A，B的坐标分别为（1，0）、（4，0）．将△ABC沿x轴向右平移，当点C落在直线上时，线段BC扫过的面积为（）A . 4B . 8C . 16D .11. （2分）某村引进甲乙两种水稻良种，各选6块条件相同的实验田，同时播种并核定亩产，结果甲、乙两种水稻的平均产量均为550kg/亩，方差分别为S甲2=141.7，S乙2=433.3，则产量稳定，适合推广的品种为（）A . 甲、乙均可B . 甲C . 乙D . 无法确定12. （2分）某同学参加射击训练，共射击了六发子弹，击中的环数分别为3,4,5,7,7,10．则下列说法错误的是（）A . 其平均数为6B . 其众数为7C . 其中位数为7D . 其中位数为6二、填空题： (共3题；共9分)13. （5分） (2018八上·辽宁期末) 若关于x的方程有增根，则a的值为__．14. （3分）把一个三角形进行平移或翻折或旋转后，其________和________ 都不变，但________ 发生了变化．15. （1分）(2016·长沙模拟) 如图，在▱ABCD中，BE平分∠ABC，BC=6，DE=2，则▱ABCD的周长等于________．三、解答题 (共6题；共50分)16. （5分）如图的斜边AB=5，cosA=（1）用尺规作图作线段AC的垂直平分线（保留作图痕迹，不要求写作法、证明）；（2）若直线与AB，AC分别相交于D,E两点，求DE的长17. （15分） (2019八下·番禺期末) 在▱ABCD中，∠ADC的平分线交直线BC于点E ，交直线AB于点F ．（1）如图①，证明：BE＝BF．（2）如图②，若∠ADC＝90°，O为AC的中点，G为EF的中点，试探究OG与AC的位置关系，并说明理由．（3）如图③，若∠ADC＝60°，过点E作DC的平行线，并在其上取一点K（与点F位于直线BC的同侧），使EK＝BF，连接CK，H为CK的中点，试探究线段OH与HA之间的数量关系，并对结论给予证明．18. （5分） (2017八下·江海期末) 已知一次函数的图象过点（3，5）与点（﹣4，﹣9），求这个一次函数的解析式．19. （10分）综合题。

河南省商水县2024届八年级数学第二学期期末学业质量监测试题含解析

河南省商水县2024届八年级数学第二学期期末学业质量监测试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。

用2B 铅笔将试卷类型（B ）填涂在答题卡相应位置上。

将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)1．下列命题是假命题的是( )A ．四个角相等的四边形是矩形B ．对角线相等的平行四边形是矩形C ．对角线垂直的四边形是菱形D ．对角线垂直的平行四边形是菱形2．要使分式12x x +-有意义，则x 的取值应满足（） A ．2x ≠ B ．1x ≠- C ．2x = D ．1x =-3．如图，EF 为△ABC 的中位线，若AB=6，则EF 的长为（）A ．2B ．3C ．4D ．54．某校规定学生的平时作业，期中考试，期末考试三项成绩分别是按30%、30%、40%计人学期总评成绩，小明的平时作业，期中考试，期末考试的英语成绩分别是93分、90分、96分，则小明这学期的总评成绩是（） A ．92 B ．90 C ．93 D ．93.35．若234a b c ==，则2222232a bc c a ab c-+--的值是( ) A ．13 B ．13- C ．12 D ．12- 6．赵强同学借了一本书，共280页，要在两周借期内读完．当他读了一半时，发现平均每天要多读21页才能在借期内读完．他读前一半时，平均每天读多少页？如果设读前一半时，平均每天读x 页，则下面所列方程中，正确的是（）A．1401401421x x+=-B．2802801421x x+=+C．1401401421x x+=+D．1010121x x+=+7．巫溪某中学组织初一初二学生举行“四城同创”宣传活动，从学校坐车出发，先上坡到达A地后，宣传8分钟；然后下坡到B地宣传8分钟返回，行程情况如图．若返回时，上、下坡速度仍保持不变，在A地仍要宣传8分钟，那么他们从B地返回学校用的时间是( )A．45.2分钟B．48分钟C．46分钟D．33分钟8．下列特征中，平行四边形不一定具有的是（）A．邻角互补B．对角互补C．对角相等D．内角和为360°9．如果，则a的取值范围是（）A．B．C．D．10．小明骑自行车到公园游玩，匀速行驶一段路程后,开始休息，休息了一段时间后，为了尽快赶到目的地，便提高了，车速度,很快到达了公园．下面能反映小明离公园的距离y(千米)与时间x(小时)之间的函数关系的大致图象是（）A．B．C．D．二、填空题(每小题3分,共24分)11．设甲、乙两车在同一直线公路上匀速行驶，开始甲车在乙车的前面，当乙车追上甲车后，两车停下来，把乙车的货物转给甲车，然后甲车继续前行，乙车向原地返回．设秒后两车间的距离为千米，关于的函数关系如图所示，则甲车的速度是______米/秒．12．已知一次函数y 2x 6=-与y x 3=-+的图象交于点P ，则点P 的坐标为______．13．某书定价25元，如果一次购买20本以上，超过20本的部分打八折，未超过20本的不打折，试写出付款金额y （单位：元）与购买数量x （单位：本）之间的函数关系_______．14．当x =__________时，分式242x x --的值等于零. 15．如图，已知函数y=2x 和函数y=k x的图象交于A 、B 两点，过点A 作AE ⊥x 轴于点E ，若△AOE 的面积为4，P 是坐标平面上的点，且以点B 、O 、E 、P 为顶点的四边形是平行四边形，则k=_____，满足条件的P 点坐标是_________________．16．已知一组数据6、4、a 、3、2的平均数是5，则a 的值为_____．17．如图，已知P 是正方形ABCD 对角线BD 上一点，且BP ＝BC ，则∠ACP 度数是_____度．18．某天工作人员在一个观测站测得：空气中PM2.5含量为每立方米0.0000023g ，则将0.0000023用科学记数法表示为_____．三、解答题(共66分)19．（10分）解不等式.20．（6分）如图，直线l 1交x 轴于A （3，0），交y 轴于B （0，﹣2）（1）求直线l 1的表达式；（2）将l 1向上平移到C （0，3），得到直线l 2，写出l 2的表达式；（3）过点A 作直线l 3⊥x 轴，交l 2于点D ，求四边形ABCD 的面积．21．（6分）计算与化简：()1计算：()1011813π-⎛⎫--- ⎪⎝⎭ ()2化简：221111x x x -⎛⎫-÷ ⎪++⎝⎭ ()3已知2,1a b ==-，求：22211a b a ab a-+÷-的值 22．（8分）随着新能源汽车推广力度加大，产业快速发展，越来越多的消费者接受并购买新能源汽车。

2015-2016学年河南省周口市商水县八年级(下)期末数学试卷(解析版)

2015-2016学年河南省周口市商水县八年级（下）期末数学试卷一、选择题（共8小题，每小题3分，满分24分.每小题只有一个正确答案）1．（3分）计算（﹣3）0的结果为（）A．0B．1C．﹣3D．32．（3分）若一次函数y＝（m﹣3）x+5的函数值，y随x的增大而增大，则（）A．m＜0B．m＞0C．m＜3D．m＞33．（3分）一个菱形的两条对角线长分别为6cm和10cm，则这个菱形的面积是（）A．60cm2B．30cm2C．32cm2D．15cm24．（3分）某校有21名同学参加比赛，预赛成绩各不相同，要取前11名参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需再知道这21名同学成绩的（）A．中位数B．众数C．平均数D．最高分5．（3分）如果分式方程＝无解，则m的值为（）A．﹣2B．﹣1C．0D．16．（3分）给出下列命题，其中，真命题的个数是（）①平行四边形的对角线互相平分②对角线相等的四边形是矩形③菱形的对角线互相垂直平分④对角线互相垂直且相等的四边形是正方形．A．4个B．3个C．2个D．1个7．（3分）在“大家跳起来”的乡村学校舞蹈比赛中，某校10名学生参赛成绩统计如图所示．对于这10名学生的参赛成绩，下列说法中错误的是（）A．众数是90B．中位数是90C．平均数是90D．极差是15 8．（3分）如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x＝9时，点R应运动到（）A．N处B．P处C．Q处D．M处二、填空题（共7小题，每小题3分，满分21分）9．（3分）在▱ABCD中，已知∠A＝70°，则∠C＝°．10．（3分）某红外线遥控器发出的红外线波长为0.00000094m，用科学记数法表示这个数是m．11．（3分）如图，点P是x轴上的一个点，过点P作x轴的垂线PQ交双曲线于点Q，△OPQ的面积是4，则双曲线的表达式是．12．（3分）已知一组数据：1，a，3，6，7，它的平均数是4，这组数据的众数是．13．（3分）直线y＝kx可以看成是将直线y＝kx+b沿y轴向上平移3个单位得到的，则b ＝．14．（3分）如图，E、F是▱ABCD对角线BD上的两点，请你添加一个适当的条件：，使四边形AECF是平行四边形．15．（3分）如图，在正方形ABCD中，AC为对角线，E为AC上一点，连接EB，ED，BE 的延长线交AD于点F，∠BED＝120°，则∠EFD的度数为．三、解答题（共8小题，满分75分）16．（8分）先化简，然后﹣1、0、2中选取一个合适的数作为x的值代入求值．17．（8分）已知双曲线y＝﹣上一点P的横坐标为﹣，P点关于y轴的对称点是Q，双曲线y＝经过点Q．（1）求y＝的表达式；（2）说出双曲线y＝所在的象限以及在每个象限内y随x值的增大而变化的情况．18．（8分）一家公司打算招聘一名部门经理，现对甲、乙两名应试者从笔试、面试、实习成绩三个方面的表现进行评价，笔试占总成绩的20%、面试占30%、实习成绩占50%，各项成绩如表所示．试判断谁会被公司录取，为什么？19．（9分）如图，正比例函数y＝2x的图象与一次函数y＝kx+b的图象交于点A（m，2），一次函数图象经过点B（﹣2，﹣1）与x轴的交点为C．（1）求一次函数的解析式；（2）求△AOC的面积．20．（10分）如图，在平行四边形ABCD中，E为BC边上的一点，连结AE、BD且AE＝AB．（1）求证：∠ABE＝∠EAD；（2）若∠AEB＝2∠ADB，求证：四边形ABCD是菱形．21．（10分）甲、乙两同学学习计算机打字，甲打一篇3000字的文章与乙打一篇2400字的文章所用的时间相同．已知甲每分钟比乙每分钟多打12个字，问甲、乙两人每分钟各打多少个字？李明同学是这样解答的：设甲同学打印一篇3 000字的文章需要x分钟，根据题意，得（1）解得：x＝50．经检验x＝50是原方程的解．（2）答：甲同学每分钟打字50个，乙同学每分钟打字38个．（3）（1）请从（1）、（2）、（3）三个步骤说明李明同学的解答过程是否正确，若有不正确的步骤改正过来．（2）请你用直接设未知数列方程的方法解决这个问题．22．（10分）甲、乙两种水稻试验田连续5年的平均单位面积产量如下：（单位：吨/公顷）（1）哪种水稻的平均单位面积产量比较高？（2）哪种水稻的产量比较稳定．23．（12分）阅读下列材料：问题：如图所示，在正方形ABCD和▱BEFG中，点A，B，E在同一直线上，P是线段DF 中点，连接PG，PC．探究：当PG与PC的夹角为90°时，平行四边形BEFG是正方形．小聪同学的思路是：首先可以证明四边形BEFG是矩形，然后延长GP交DC于点H，构造全等三角形，经过推理可以探索出问题答案．请你参考小聪同学的思路，探究并解决这个问题．（1）求证：四边形BEFG是矩形；（2）求证：PG与PC的夹角为90°时，四边形BEFG是正方形．2015-2016学年河南省周口市商水县八年级（下）期末数学试卷参考答案与试题解析一、选择题（共8小题，每小题3分，满分24分.每小题只有一个正确答案）1．【解答】解：（﹣3）0＝1．故选：B．2．【解答】解：∵一次函数y＝（m﹣3）x+5中，y随着x的增大而增大，∴m﹣3＞0，解得：m＞3．故选：D．3．【解答】解：根据菱形面积等于对角线乘积的一半可得：S＝×10×6＝30cm2．故选：B．4．【解答】解：共有21名学生参加预赛，取前11名，所以小颖需要知道自己的成绩是否进入前11．我们把所有同学的成绩按大小顺序排列，第11名的成绩是这组数据的中位数，所以小颖知道这组数据的中位数，才能知道自己是否进入决赛．故选：A．5．【解答】解：方程去分母得：x＝m，当x＝﹣1时，分母为0，方程无解．即m＝﹣1方程无解，故选：B．6．【解答】解：①∵平行四边形的对角线互相平分，∴①是真命题；②∵对角线互相平分且相等的四边形是矩形，∴②是假命题；③∵菱形的对角线互相垂直平分，∴③是真命题；④∵对角线互相垂直平分且相等的四边形是正方形，∴④是假命题；真命题的个数有2个，故选：C．7．【解答】解：∵90出现了5次，出现的次数最多，∴众数是90；故A正确；∵共有10个数，∴中位数是第5、6个数的平均数，∴中位数是（90+90）÷2＝90；故B正确；∵平均数是（80×1+85×2+90×5+95×2）÷10＝89；故C错误；极差是：95﹣80＝15；故D正确．综上所述，C选项符合题意，故选：C．8．【解答】解：当点R运动到PQ上时，△MNR的面积y达到最大，且保持一段时间不变；到Q点以后，面积y开始减小；故当x＝9时，点R应运动到Q处．故选：C．二、填空题（共7小题，每小题3分，满分21分）9．【解答】解：∵四边形ABCD是平行四边形，∴∠C＝∠A＝36°．故答案为：70．10．【解答】解：0.00000094＝9.4×10﹣7；故答案为：9.4×10﹣7．11．【解答】解：由S△OPQ＝xy＝4，得k＝xy＝8．所以，反比例函数的表达式为y＝，故答案为：y＝．12．【解答】解：据题意得：（1+a+3+6+7）÷5＝4，得a＝3，所以这组数据的众数是3．故填3．13．【解答】解：根据上加下减的原则可得：b+3＝0，解得b＝﹣3．故答案为：﹣3．14．【解答】解：添加的条件是BE＝DF，理由是：连接AC交BD于O，∵平行四边形ABCD，∴OA＝OC，OB＝OD，∵BE＝DF，∴OE＝OF，∴四边形AECF是平行四边形．故答案为：BE＝DF．15．【解答】解：∵四边形ABCD是正方形，∴BC＝CD，∠ECB＝∠ECD＝45°．∴在△BEC与△DEC中，，∴△BEC≌△DEC（SAS），∴∠BEC＝∠DEC＝∠BED，∵∠BED＝120°，∴∠BEC＝60°＝∠AEF，∴∠EFD＝∠CAD+∠AEF＝60°+45°＝105°．故答案为：105°．三、解答题（共8小题，满分75分）16．【解答】解：原式＝•＝，∵x≠0，x≠1，∴当选x＝﹣1时，原式＝＝﹣．17．【解答】解：（1）∵点P在双曲线y＝﹣上，∴把x＝﹣代入得：y＝6，即P（﹣，6），∵P与Q关于y轴对称，∴Q（，6），代入y＝中得：k＝4，则反比例解析式为y＝；（2）∵y＝，且k＝4＞0，∴此函数的图象在第一、三象限，在每个象限内y随x的增大而减小．18．【解答】解：甲的平均成绩为：85×20%+83×30%+90×50%＝17+24.9+45＝86.9乙的平均成绩为：80×20%+85×30%+92×50%＝16+25.5+46＝87.5∵87.5＞86.9，∴乙的平均成绩较高，∴乙会被公司录取．19．【解答】解：（1）∵正比例函数y＝2x的图象与一次函数y＝kx+b的图象交于点A（m，2），∴2m＝2，m＝1．把（1，2）和（﹣2，﹣1）代入y＝kx+b，得，解得，则一次函数解析式是y＝x+1；（2）令y＝0，则x+1＝0，x＝﹣1．所以点C的坐标为（﹣1，0），则△AOC的面积＝×1×2＝1．20．【解答】证明：（1）在平行四边形ABCD中，AD∥BC，∴∠AEB＝∠EAD，∵AE＝AB，∴∠ABE＝∠AEB，∴∠ABE＝∠EAD；（2）∵AD∥BC，∴∠ADB＝∠DBE，∵∠ABE＝∠AEB，∠AEB＝2∠ADB，∴∠ABE＝2∠ADB，∴∠ABD＝∠ABE﹣∠DBE＝2∠ADB﹣∠ADB＝∠ADB，∴AB＝AD，又∵四边形ABCD是平行四边形，∴四边形ABCD是菱形．21．【解答】解：（1）李明同学的解答过程中第（3）步不正确．应为：甲每分钟打字（个）．乙每分钟打字60﹣12＝48（个）．答：甲每分钟打字为60个，乙每分钟打字为48个．（2）设乙每分钟打字x个，则甲每分钟打字（x+12）个．根据题意得：．解得：x＝48．经检验：x＝48是原方程的解．∴甲每分钟打字x+12＝48+12＝60（个）．答：甲每分钟打字为60个，乙每分钟打字为48个．22．【解答】解：（1），，所以甲、乙两种水稻的平均产量一样高；（2）甲中水稻产量的方差是：[（9.8﹣10）2+（9.9﹣10）2+（10.1﹣10）2+（10﹣10）2+（10.2﹣10）2]＝0.02，乙种水稻产量的方差是：[（9.4﹣10）2+（10.3﹣10）2+（10.8﹣10）2+（9.7﹣10）2+（9.8﹣10）2]＝0.244．∴0.02＜0.244，∴产量比较稳定的水稻品种是甲．23．【解答】证明：（1）在正方形ABCD中，∠ABC＝90°，∴∠EBG＝90°，∵四边形BEFG是平行四边形，∴平行四边形BEFG是矩形，（2）如图，延长GP交DC于点H，∵在正方形ABCD和▱BEFG中，∴AB∥DC，RE∥GF，∴DC∥GF，∴∠HDP＝∠GFP，∠DHP＝∠FGP，∵点P是线段DF中点，∴DP＝FP，∴△DHP≌△FGP，∴DH＝FG，HP＝GP，∵∠CPG＝90°，∴CH＝CG，在正方形ABCD中，DC＝BC，∴DH＝BG，∴BG＝GF，由（1）知，四边形BEFG是矩形，∴四边形BEFG是正方形．。

河南省商水县_八年级数学下学期质量调研试题(精选资料)

2015—2016学年度下学期质量调研试卷八年级数学总分1．本试卷共6页，三个大题，满分120分，考试时间100分钟，请用蓝、黑色钢笔或圆珠笔直接答在试卷上．2．答卷前将密封线内的项目填写清楚．一、选择题（每小题3分，共24分。

下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内。

）1.若分式11x x -+的值为0，则x 的值为( )A.-1B. 1C. ±1D. 02.长度单位1纳米=910m -，目前发现一种新型病毒直径为25100纳米，用科学记数法表示该病毒直径为( )A. 625.110m -⨯B. 40.25110m -⨯C. 52.5110m ⨯D. 52.5110m -⨯3.平面直角坐标系中有一点P ，点P 到y 轴的距离为2，点P 的纵坐标为-3，则点P 的坐标是( )A.（-3，-2）B.（-2，-3）C.（2，-3）D. （2，-3）或（-2，-3）4.已知一组数据3,,45a ，的众数为4，则这组数据的平均数为 ( ) A. 3 B. 4 C. 5 D. 65.如图，在周长为20cm 的ABCD 中，AB ≠AD ，AC 、BD 相交于点O ，OE ⊥BD 交AD于E ，则△ABE 的周长为( )A. 10cmB. 8cmC. 6cmD. 4cm6. 如图，把一张矩形纸片对折两次，然后剪下一个角，为了得到一个锐角为60°的菱形，剪口与折痕所成的角α的度数应为( )A. 15°或30°B. 30°或45°C. 30°或60°D. 45°或60°7.如图，直线y x m =-+与4(0)y nx n n =+≠的交点的横坐标为-2，则关于x 的不等式40x m nx n -+>+>的整数解为 ( )A. -1B. -3C. -4D. -5 8. 已知120k k >> ，则函数1y k x =和2k y x=的图象在同一平面直角坐标系中大致是下图中的 ( )A. B. C. D. 二、填空题（每小题3分，共21分）9. 计算：011()102016-⨯=_________. 10. 如下图，在ABCD 中，已知点A （-1,0），B （2,0），D （0,1）.则点C 的坐标为_________.11. 如下图，正方形ABCD 中，以对角线AC 为一边作菱形AEFC,则FAB ∠=_________. 12. 已知关于x 的方程232x mx +=-的解是非负数，则m 的取值范围是_________. 13. 如下图，在矩形ABCD 中，AB=1，E 、F 分别为AD 、CD 的中点，沿BE 将△ABE 折叠，若点A 恰好落在BF 上，则AD=_________.14．如下图，在平面直角坐标系中，正方形的中心在原点O ，且正方形的一组对边与x 轴平行，点(2,)P a a 是反比例函数2y x=的图象与正方形的一个交点，则图中阴影部分的面积是_________．第10题图第11题图第13题图第14题图 15.过点（-1,7）的一条直线与x 轴，y 轴分别相交于点A 、B ，且与直线312y x =-+平行.则在线段AB 上，横、纵坐标都是整数的点的坐标是 . 三、解答题（本大题共8个小题，满分75分）16. (8分)先化简2222(2)m n n m n m mn m-÷++-，再求值，其中21(2)0m n -+-=17.(9分) 如图，在△ABC 中，AB=AC ，D 是BC 的中点，连接AD ，在AD 的延长线上取一点E ，连接BE ，C E 。

2016----2017学年第二学期八年级数学期末试卷

2016----2017学年第二学期八年级数学期末试卷试卷分值：100 分考试时间： 120分钟一、选择题：(本大题共10个小题，每小题3分，共30分) 1．若m ＞－1，则下列各式中错误的．．．是（） A ．6m ＞－6 B ．－5m ＜－5 C ．m+1＞0 D ．1－m ＜2 2.下列各式中,正确的是( )A.16=±4B.±16=4C.327-=-3 D.2(4)-=-43．已知a ＞b ＞0，那么下列不等式组中无解．．的是（） A ．⎩⎨⎧-><b x a x B ．⎩⎨⎧-<->b x a x C ．⎩⎨⎧-<>b x a x D ．⎩⎨⎧<->b x ax4．一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度可能为（）(A) 先右转50°，后右转40° (B) 先右转50°，后左转40° (C) 先右转50°，后左转130° (D) 先右转50°，后左转50° 5．解为12x y =⎧⎨=⎩的方程组是（） A.135x y x y -=⎧⎨+=⎩ B.135x y x y -=-⎧⎨+=-⎩ C.331x y x y -=⎧⎨-=⎩ D.2335x y x y -=-⎧⎨+=⎩6．如图，在△ABC 中，∠ABC=500，∠ACB=800，BP 平分∠ABC ，CP 平分∠ACB ，则∠BPC 的大小是（） A ．100B ．110C ．115D ．1200PCA 小刚小军小华(1) (2) (3)7．四条线段的长分别为3，4，5，7，则它们首尾相连可以组成不同的三角形的个数是（）A ．4B ．3C ．2D ．18．各个内角都相等多边形中，一个外角等于一个内角的12，这个多边形的边数是（）A ．5B ．6C ．7D ．89．如图，△A 1B 1C 1是由△ABC 沿BC 方向平移了BC 长度的一半得到的，若△ABC 的面积为20 cm 2，则四边形A 1DCC 1的面积为（）A ．10 cm 2B ．12 cm 2C ．15 cm 2D ．17 cm 210.课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(•0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )A.(5,4)B.(4,5)C.(3,4)D.(4,3)二、填空题：（每小题3分，共24分，把答案直接填在答题卷的横线上．） 11.49的平方根是________,算术平方根是______,-8的立方根是_____. 12.不等式5x-9≤3(x+1)的解集是________.13.如果点P(a,2)在第二象限,那么点Q(-3,a)在_______. 14.如图3所示,在铁路旁边有一李庄,现要建一火车站,•为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由:____________. 15.从A 沿北偏东60°的方向行驶到B,再从B 沿南偏西20°的方向行驶到C,•则∠ABC=_______度.16.如图,AD ∥BC,∠D=100°,CA 平分∠BCD,则∠DAC=_______. 17．给出下列正多边形：① 正三角形；② 正方形；③ 正六边形；④ 正八边形．用上述正多边形中的一种能够辅满地面的是_____________．(将所有答案的序号都填上) 18.若│x 2-25│3y -则x=_______,y=_______.三、解答题：（本大题共7个小题，共46分）19．解不等式组：⎪⎩⎪⎨⎧+<-≥--.21512,4)2(3x x x x ,并把解集在数轴上表示出来．县学校姓名考号班级…………………………………………………..密……………………………………….封……………………………………………….线………………………………………………….CBAD火车站李庄C 1A 1ABB 1 CD20．解方程组：2313424()3(2)17x y x y x y ⎧-=⎪⎨⎪--+=⎩21.如图, AD ∥BC , AD 平分∠EAC,你能确定∠B 与∠C 的数量关系吗?请说明理由。

河南省周口市商水县2018-2019学年八年级下学期数学期末考试试卷及参考答案

河南省周口市商水县2018-2019学年八年级下学期数学期末考试试卷
一、单选题
1. 不论x取何值，下列分式中总有意义的是（）
A.
B.
C.
D.
2. 在一次手工制作比赛中，某小组八件作品的成绩分别是7，10，9，8，7，9，9，8（单位：分），对这组数据，下
列说法正确的是（）
A . 中位数是8 B . 众数是9 C . 平均数是8 D . 极差是7
的路径匀速前进到D为止.在这个过程中，
A.
B.
C.
D.
8. 如图所示，、、是双曲线的一支上的三点，过这三点分别作y轴的垂线，得到
、
、
，设它们的面积分P别是、、，则（）
A.
B.
C.D.9Fra bibliotek 一次函数和反比例函数
的图象如图所示，若
，则x的取值范围是（）
A.
或 B.
C.
或 D.
或
10. 如图，在矩形ABCD中，E，F，G，H分别为边AB，BC，CD，DA的中点.若
3. 某红外线遥控器发出的红外线波长为0.000 000 94m，用科学记数法表示这个数为（）
A.
mB.
mC.
mD.
m
4. 在平面直角坐标系中，点A（2,3）与点B关于轴对称，则点B的坐标为（）
A . （3,2） B . （－2，－3） C . （－2,3） D . (2,－3)
5. 关于正比例函数
18. 如图，四边形ABCD中，
，E是边CD的中点，连接BE并延长求证：四边形BDFC是平行四边
形。
19. 如图，在形.
中，AE平分∠BAD且与BC相交于点E，

河南省周口市八年级下学期数学期末考试试卷

河南省周口市八年级下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、填空题 (共6题；共7分)1. （1分） (2019七下·监利期末) 使式子有意义的m的取值范围是________2. （1分） (2019八上·嘉定期中) 已知y与x成正比例，当x=8时，y=﹣12，则y与x的函数的解析式为________．3. （1分）极差、________、________都是用来描述一组数据的________情况的特征数据．4. （1分）如图，EF是△ABC的中位线，将△AEF沿AB方向平移到△EBO的位置，点D在BC上，已知△AEF 的面积为5，则图中阴影部分的面积为________.5. （1分） (2020九上·香坊月考) 在直角坐标系中，点P(2，3)到原点的距离是________。

6. （2分） (2019八下·大庆期中) 在平行四边形ABCD中，AB=10，AD=6，E是AD的中点，在直线AB上取一点F，使△CBF与△CDE相似，则BF的长为________二、单选题 (共8题；共16分)7. （2分） (2020八下·南宁期中) 下列计算正确的是（）A .B .C .D .8. （2分） (2016八上·锡山期末) 以下列线段长为边，能构成直角三角形的是（）A . 2，3，5B . 2，3，4C . 3，，4D . 2，4，59. （2分）某班6名同学参加体能测试的成绩如下（单位：分）：75，95，75，75，80，80．关于这组数据的表述错误的是（）A . 众数是75B . 平均数是80C . 中位数是75D . 极差是2010. （2分）(2013·南宁) 如图，直线y= 与双曲线y= （k＞0，x＞0）交于点A，将直线y= 向上平移4个单位长度后，与y轴交于点C，与双曲线y= （k＞0，x＞0）交于点B，若OA=3BC，则k的值为（）A . 3B . 6C .D .11. （2分）⊙O的弦AB的长为8cm，弦AB的弦心距为3 cm，则⊙O的直径为（）A . 4 cmB . 5 cmC . 8 cmD . 10 cm12. （2分）无论实数m取什么值，直线y=x+m与y=－x+5的交点都不能在（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限13. （2分）(2020·昆山模拟) 如图，矩形ABCD中，对角线AC的垂直平分线EF分别交BC，AD于点E，F，若BE＝4，AF＝6，则AC的长为（）A . 4B . 6C . 2D .14. （2分） (2019八下·端州期中) 如图，在矩形中，对角线，相交于点，如果，，那么的长为（）A .B .C .D .三、解答题 (共9题；共92分)15. （10分） (2020八下·许昌期末)（1）计算：（2）当，时，求代数式的值16. （10分） (2020八下·重庆期末) 一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发.设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系式.根据题中所给信息解答以下问题：（1）甲、乙两地之间的距离为________km；图中点C的实际意义为：________；慢车的速度为________，快车的速度为________；（2）求线段BC所表示的y与x之间的函数关系式，以及自变量x的取值范围；（3）若在第一列快车与慢车相遇时，第二列车从乙地出发驶往甲地，速度与第一列快车相同，请直接写出第二列快车出发多长时间，与慢车相距200km.17. （10分） (2020九下·丹阳开学考) 如图，在中，，的平分线交于点，点是上一点，过、两点，且分别交、于点、 .（1）求证：是的切线；（2）已知，，求的半径 .18. （12分）(2018·新乡模拟) 2018年3月，某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动，活动结束后，随机抽取了部分同学的成绩（x均为整数，总分100分），绘制了如下尚不完整的统计图表．调查结果统计表组别成绩分组（单位：分）频数频率A80≤x＜85500.1B85≤x＜9075C90≤x＜95150cD95≤x≤100a合计b1根据以上信息解答下列问题：（1）统计表中，a=________，b=________，c=________；（2）扇形统计图中，m的值为________，“C”所对应的圆心角的度数是________；（3）若参加本次竞赛的同学共有5000人，请你估计成绩在95分及以上的学生大约有多少人？19. （10分） (2017七上·宁波期中) 小聪是个数学爱好者，他发现从1开始，连续几个奇数相加，和的变化规律如右表所示：加数个数连续奇数的和S11=21+3=2231+3+5=3241+3+5+7=4251+3+5+7+9=52n…（1）如果n=7，则S的值为________；（2）求1+3+5+7+…+199的值；（3）求13+15+17+…+79的值．20. （5分）如图，已知：在中，，AC=70，AB=30. 求：BC的长.21. （10分） (2020八下·安阳期末) 某学校要进行校园绿化，计划购进A，B两种树苗共30棵，已知A种种树苗每棵80元，B种树苗每颗50元，设购买A种树苗x棵，购买两种树苗所需的费用是y元，（1）求y与x的函数关系式；（2）若购买A种树苗的数量不少于B种树苗的数量的2倍，请给出一种费用最少的购买方案，并求出该方案所需的费用.22. （10分）(2019·景县模拟) 如图，在平行四边形ABCD中，E、F为BC上的两点，且BE-CF，AF=DE．求证：（1）△ABF≌△DCE:（2）四边形ABCD是矩形。

2017-2018学年河南省周口市商水县八年级(下)期末数学试卷

2017-2018学年河南省周口市商水县八年级（下）期末数学试卷（考试时间：100分满分：120分）一、选择题（每小题3分，共30分．下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内）1．（3分）分式的值为0，则（）A．x＝﹣2 B．x＝±2 C．x＝2 D．x＝02．（3分）函数：中自变量x的取值范围是（）A．x≥﹣1 B．x≠3 C．x≥﹣1且x≠3 D．x＜﹣13．（3分）国家质检总局出台了国内销售的纤维制品甲醛含量标准，从2003年1月1日起正式实施．该标准规定：针织内衣．床上用品等直接接触皮肤的制品，甲醛含量应在百万分之七十五以下．百万分之七十五用科学记数法表示应写成（）A．75×10﹣7B．75×10﹣6C．7.5×10﹣6D．7.5×10﹣54．（3分）解分式方程的结果为（）A．1 B．﹣1 C．﹣2 D．无解5．（3分）五个整数从小到大排列，中位数是4，如果这组数据唯一的众数是6，则这五个整数的和的最大值可能是（）A．17 B．19 C．21 D．226．（3分）已知四边形ABCD，有以下四个条件：①AB∥CD；②AB＝CD；③BC∥AD；④BC＝AD．从这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法种数共有（）A．6种B．5种C．4种D．3种7．（3分）已知点（﹣1，y1），（﹣2，y2），（﹣，y3）都在反比例函数y＝的图象上，则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y3＜y1＜y2C．y2＜y1＜y3D．y3＜y2＜y18．（3分）函数与y＝kx+1（k≠0）在同一坐标系内的图象大致为图中的（）A．B．C．D．9．（3分）某同学5次上学途中所花的时间（单位：分钟）分别为x，y，10，11，9，已知这组数据的平均数为10，方差为2，则|x﹣y|的值为（）A．1 B．2 C．3 D．410．（3分）如图，正方形ABCD的边长为1cm，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分面积是（）cm2．A．B．C．D．二、填空题（每小题3分，共15分）11．（3分）计算：（﹣1）0+（）﹣1＝．12．（3分）已知：如图，平行四边形ABCD中，BE平分∠ABC交AD于E，CF平分∠BCD交AD于F，若AB＝3，BC＝5，则EF＝．13．（3分）正方形ABCD在平面直角坐标系中的位置如图所示，已知A点坐标（0，4），B点坐标（﹣3，0），则C点坐标．14．（3分）如图所示，在菱形ABCD中，∠B＝∠EAF＝60°，∠BAE＝20°，则∠AEF的大小是．15．（3分）如图，已知点P（6，3），过点P作PM⊥x轴于点M，PN⊥y轴于点N，反比例函数y＝的图象交PM于点A，交PN于点B．若四边形OAPB的面积为12，则k＝．三、解答题（本大题共8个小题，满分75分）16．（8分）先化简，再求值：1﹣•[（﹣1）÷（﹣）]，其中x＝﹣3．17．（9分）今年端午节，某乡镇成立一支龙舟队，共30名队员，他们的身高情况如下表：身高（cm）165 166 169 170 172 174人数 3 2 6 7 8 4根据表中的信息回答以下问题：（1）龙舟队员身高的众数是（172），中位数是（170）；（2）这30名队员平均身高是多少cm？身高大于平均身高的队员占全的百分之几？18．（9分）如图，在▱ABCD中，E、F分别为边AD、BC的中点，对角线AC分别交BE，DF于点G、H．求证：AG＝CH．19．（9分）如图，一次函数y＝kx+b的图象与反比例函数y＝的图象相交于点A（﹣1，3）和点B（3，n）．（1）求这两个函数的解析式；（2）直接写出不等﹣kx﹣b＞0式的解集．20．（9分）在▱ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF＝BE，连接AF，BF．（1）求证：四边形BFDE是矩形；（2）若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB．21．（10分）某服装厂设计了一款新式夏装，想尽快制作8800件投入市场，服装厂有AB两个制衣间，A车间每天加工的数量是B车间的1.2倍，A、B两车间共完成一半后，A车间出现故障停产，剩下全部由B车间单独完成，结果前后共用了20天完成，求A、B两车间每天分别能加工多少件．22．（10分）如图，在四边形ABCD中，AB＝AD，CB＝CD，E是CD上一点，BE交AC于F，连接DF．（1）证明：∠BAC＝∠DAC，∠AFD＝∠CFE．（2）若AB∥CD，试证明四边形ABCD是菱形．23．（11分）在体育局的策划下，市体育馆将组织明星篮球赛，为此体育局推出两种购票方案（设购票张数为x，购票总价为y）：方案一：提供8000元赞助后，每张票的票价为50元；方案二：票价按图中的折线OAB所表示的函数关系确定．（1）若购买120张票时，按方案一和方案二分别应付的购票款是多少？（2）求方案二中y与x的函数关系式；（3）至少买多少张票时选择方案一比较合算？2017-2018学年河南省周口市商水县八年级（下）期末数学试卷参考答案与试题解析一、选择题（每小题3分，共30分．下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内）1．（3分）分式的值为0，则（）A．x＝﹣2 B．x＝±2 C．x＝2 D．x＝0【分析】分式的值为零：分子等于零，且分母不等于零．【解答】解：由题意，得x2﹣4＝0，且x+2≠0，解得x＝2．故选：C．【点评】本题考查了分式的值为零的条件．若分式的值为零，需同时具备两个条件：（1）分子为0；（2）分母不为0．这两个条件缺一不可．2．（3分）函数：中自变量x的取值范围是（）A．x≥﹣1 B．x≠3 C．x≥﹣1且x≠3 D．x＜﹣1【分析】根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，可以求出x的范围．【解答】解：根据题意得：x+1≥0且x﹣3≠0，解得：x≥﹣1且x≠3．故选：C．【点评】函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．3．（3分）国家质检总局出台了国内销售的纤维制品甲醛含量标准，从2003年1月1日起正式实施．该标准规定：针织内衣．床上用品等直接接触皮肤的制品，甲醛含量应在百万分之七十五以下．百万分之七十五用科学记数法表示应写成（）A．75×10﹣7B．75×10﹣6C．7.5×10﹣6D．7.5×10﹣5【分析】科学记数法表示为a×10n（1≤|a|＜10，n是整数）．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．直接套用即可．【解答】解：＝0.000 075＝7.5×10﹣5．故选：D．【点评】本题考查用科学记数法表示较小的数．一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．注意先将分数化为小数．4．（3分）解分式方程的结果为（）A．1 B．﹣1 C．﹣2 D．无解【分析】观察可得最简公分母是（x﹣1）（x+2），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．【解答】解：方程的两边同乘（x﹣1）（x+2），得：x+2＝3解得：x＝1．检验：把x＝1代入（x﹣1）（x+2）＝0，即x＝1不是原分式方程的解．则原分式方程无解．故选：D．【点评】此题考查了分式方程的求解方法．此题比较简单，注意掌握转化思想的应用，注意解分式方程一定要验根．5．（3分）五个整数从小到大排列，中位数是4，如果这组数据唯一的众数是6，则这五个整数的和的最大值可能是（）A．17 B．19 C．21 D．22【分析】根据中位数和众数的定义分析可得答案．【解答】解：因为五个整数从小到大排列后，其中位数是4，这组数据的唯一众数是6．所以这5个数据分别是x，y，4，6，6，且x＜y＜4，当这5个数的和最大时，整数x，y取最大值，此时x＝2，y＝3，所以这组数据可能的最大的和是2+3+4+6+6＝21．故选：C．【点评】主要考查了根据一组数据的中位数来确定数据的能力．将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．注意：找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求．如果是偶数个则找中间两位数的平均数．6．（3分）已知四边形ABCD，有以下四个条件：①AB∥CD；②AB＝CD；③BC∥AD；④BC＝AD．从这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法种数共有（）A．6种B．5种C．4种D．3种【分析】根据平行四边形的判定方法即可找到所有组合方式：（1）两组对边平行①③；（2）两组对边相等②④；（3）一组对边平行且相等①②或③④，所以有四种组合．【解答】解：依题意得有四种组合方式：（1）①③，利用两组对边平行的四边形是平行四边形判定；（2）②④，利用两组对边相等的四边形是平行四边形判定；（3）①②或③④，利用一组对边平行且相等的四边形是平行四边形判定．故选：C．【点评】此题主要考查了平行四边形的判定方法，熟练掌握平行四边形的判定方法是解题的关键．7．（3分）已知点（﹣1，y1），（﹣2，y2），（﹣，y3）都在反比例函数y＝的图象上，则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y3＜y1＜y2C．y2＜y1＜y3D．y3＜y2＜y1【分析】由条件知该反比例函数在第二、四象限，且所给的三个点都在第二象限，y随x的增大而增大，可得出答案．【解答】解：∵在y＝中k＝﹣2＜0，∴其函数图象在第二、四象限内，且在每个象限内y随x的增大而增大，∵﹣2＜﹣1＜﹣，∴y2＜y1＜y3，故选：C．【点评】本题主要考查反比例函数的图象和性质，掌握当k＜0时反比例函数的图象在第二、四象限，在每个象限内y随x的增大而增大是解题的关键．8．（3分）函数与y＝kx+1（k≠0）在同一坐标系内的图象大致为图中的（）A．B．C．D．【分析】根据反比例函数及一次函数的性质对四个选项进行逐一分析即可．【解答】解：A、由此反比例函数的图象在二、四象限可知，k＜0；而一次函数的图象经过一、三象限k＞0，相矛盾，故本选项错误；B、由此反比例函数的图象在一、三象限可知，k＞0；而一次函数的图象经过二、四象限，k＜0，相矛盾，故本选项错误；C、由此反比例函数的图象在二、四象限可知，k＜0；而一次函数的图象经过一、三象限，k＜0，两结论一致，故本选项正确；D、由此反比例函数的图象在一、三象限可知，k＞0；而一次函数的图象经过一、三象限，k＜0，因为1＞0，所以此一次函数的图象应经过一、二、三象限，故本选项错误．故选：C．【点评】本题考查的是反比例函数的图象与一次函数的图象，熟知反比例函数的图象与一次函数的图象的特点是解答此题的关键，9．（3分）某同学5次上学途中所花的时间（单位：分钟）分别为x，y，10，11，9，已知这组数据的平均数为10，方差为2，则|x﹣y|的值为（）A．1 B．2 C．3 D．4【分析】由平均数和方差的公式列出方程组，解方程组求得x，y的值，再求代数式的值．【解答】解：由题意知：＝10，[（x﹣10）2+（y﹣10）2+1+1]＝2，化简可得：x+y＝20，即（x﹣10）+（y﹣10）＝0，（x﹣10）2+（y﹣10）2＝8，解得：（x﹣10）＝（y﹣10）＝2或﹣2，∴x＝12时y＝8或y＝12时x＝8即x﹣y＝±4，∴|x﹣y|的值为4．故选：D．【点评】本题考查了平均数和方差的计算公式．关键是要记清公式．10．（3分）如图，正方形ABCD的边长为1cm，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分面积是（）cm2．A．B．C．D．【分析】连接CG，根据同底等高的三角形面积相等，得出四个三角形：△BEG、△EGC、△GCF、△GFD的面积相等，再求出△BFC的面积，即可求出一个三角形的面积，进而求出空白部分的面积，再利用正方形的面积减去空白部分的面积即可．【解答】解：如图，连接CG．∵正方形ABCD的边长为1cm，E、F分别是BC、CD的中点，∴△CDE≌△CBF，易得，△BGE≌△DGF，所以S△BGE＝S△EGC，S△DGF＝S△CGF，于是S△BGE＝S△EGC＝S△DGF＝S△CGF，又因为S△BFC＝1××＝cm2，所以S△BGE＝×＝cm2，则空白部分的面积为4×＝cm2，于是阴影部分的面积为1×1﹣＝cm2．故选：B．【点评】此题将阴影部分的面积和正方形的性质相结合，有一定的难度．解题的关键是利用同底等高的三角形的面积相等．二、填空题（每小题3分，共15分）11．（3分）计算：（﹣1）0+（）﹣1＝ 4 ．【分析】根据零指数幂、负指数幂的运算法则解答即可．【解答】解：（﹣1）0+（）﹣1＝1+3＝4．故答案为：4．【点评】主要考查了零指数幂，负指数幂的运算，负指数为正指数的倒数；任何非0数的0次幂等于1．12．（3分）已知：如图，平行四边形ABCD中，BE平分∠ABC交AD于E，CF平分∠BCD交AD于F，若AB＝3，BC＝5，则EF＝ 1 ．【分析】先证明AB＝AE＝3，DC＝DF＝3，再根据EF＝AE+DF﹣AD即可计算．【解答】解：∵四边形ABCD是平行四边形，∴AB＝CD＝3，BC＝AD＝5，AD∥BC，∵BE平分∠ABC交AD于E，CF平分∠BCD交AD于F，∴∠ABF＝∠CBE＝∠AEB，∠BCF＝∠DCF＝∠CFD，∴AB＝AE＝3，DC＝DF＝3，∴EF＝AE+DF﹣AD＝3+3﹣5＝1．故答案为1．【点评】本题考查平行四边形的性质，等腰三角形的判定和性质等知识，解题的关键是熟练掌握这些知识的应用，属于常见题，中考常考题型．13．（3分）正方形ABCD在平面直角坐标系中的位置如图所示，已知A点坐标（0，4），B点坐标（﹣3，0），则C点坐标（1，﹣3）．【分析】根据正方形的性质，过C点作CE⊥x轴于E，可证△ABO≌△BCE，求出CE，BE的长，从而求解．【解答】解：过C点作CE⊥x轴于E．∵四边形ABCD为正方形，∴AB＝BC，∠ABC＝90°，∴∠ABO+∠CBE＝90°，又∠ABO+∠BAO＝90°，∴∠BAO＝∠CBE，又∠AOB＝∠BEC＝90°，∴△ABO≌△BCE，∴CE＝OB＝3，BE＝OA＝4，∴C点坐标为（4﹣3，﹣3），即（1，﹣3）．故答案为：（1，﹣3）．【点评】本题充分运用正方形的性质，先证△ABO≌△BCE，把已知坐标转化为相关线段的长，再求与点C 的坐标有关的长度，从而确定C点坐标．14．（3分）如图所示，在菱形ABCD中，∠B＝∠EAF＝60°，∠BAE＝20°，则∠AEF的大小是60°．【分析】由菱形的性质可证△ABC，△ACD都是等边三角形，可得∠B＝∠ACF＝∠BAC＝60°，则可证△ABE ≌△ACF，可得AE＝AF，即可证△AEF是等边三角形，即可求∠AEF的大小．【解答】解：连接AC∵四边形ABCD是菱形∴AB＝BC＝CD＝AD，∠B＝∠D＝60°∴△ABC，△ACD都是等边三角形∴AC＝AB，∠B＝∠ACD＝60°＝∠BAC∵∠BAC＝60°＝∠EAF∴∠BAE＝∠CAF又∵AC＝AB，∠B＝∠ACD＝60°∴△ABE≌△ACF′∴AE＝AF且∠EAF＝60°∴△AEF是等边三角形∴∠AEF＝60°故答案为60°【点评】本题考查了菱形的性质，全等三角形的判定，等边三角形的性质，证明△ABE≌△ACF是本题的关键．15．（3分）如图，已知点P（6，3），过点P作PM⊥x轴于点M，PN⊥y轴于点N，反比例函数y＝的图象交PM于点A，交PN于点B．若四边形OAPB的面积为12，则k＝ 6 ．【分析】根据点P（6，3），可得点A的横坐标为6，点B的纵坐标为3，代入函数解析式分别求出点A的纵坐标和点B的横坐标，然后根据四边形OAPB的面积为12，列出方程求出k的值．【解答】解：∵点P（6，3），∴点A的横坐标为6，点B的纵坐标为3，代入反比例函数y＝得，点A的纵坐标为，点B的横坐标为，即AM＝，NB＝，∵S四边形OAPB＝12，即S矩形OMPN﹣S△OAM﹣S△NBO＝12，6×3﹣×6×﹣×3×＝12，解得：k＝6．解法二：△OAM的面积＝△OBN的面积＝k，∴k＝四边形OMPN的面积﹣四边形OAPB的面积＝6×3﹣12＝6故答案为：6．【点评】本题考查了反比例函数系数k的几何意义，解答本题的关键是根据点A、B的纵横坐标，代入解析式表示出其坐标，然后根据面积公式求解．三、解答题（本大题共8个小题，满分75分）16．（8分）先化简，再求值：1﹣•[（﹣1）÷（﹣）]，其中x＝﹣3．【分析】根据分式的乘除法和减法可以化简题目中的式子，然后将x＝﹣3代入化简后的式子即可解答本题．【解答】解：1﹣•[（﹣1）÷（﹣）]＝1﹣＝1﹣＝1﹣＝＝，当x＝﹣3时，原式＝＝2．【点评】本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．17．（9分）今年端午节，某乡镇成立一支龙舟队，共30名队员，他们的身高情况如下表：身高（cm）165 166 169 170 172 174人数 3 2 6 7 8 4根据表中的信息回答以下问题：（1）龙舟队员身高的众数是（172），中位数是（170）；（2）这30名队员平均身高是多少cm？身高大于平均身高的队员占全的百分之几？【分析】（1）根据众数和中位数的定义解答；（2）平均数是指在一组数据中所有数据之和再除以数据的个数．【解答】解：（1）172出现了6次，出现的次数最多，故众数是172（cm）；这组数据共30个，正中间两个是第15，16个，∴中位数为（170+170）÷2＝170（cm）．故填172；170．（2）＝170.1（cm），由表可知，身高大于平均身高的队员共有12人，占全队的百分比为＝40%．【点评】主要考查了平均数，众数，中位数的概念．要掌握这些基本概念才能熟练解题．18．（9分）如图，在▱ABCD中，E、F分别为边AD、BC的中点，对角线AC分别交BE，DF于点G、H．求证：AG＝CH．【分析】根据平行四边形的性质得到AD∥BC，得出∠ADF＝∠CFH，∠EAG＝∠FCH，证出四边形BFDE是平行四边形，得出BE∥DF，证出∠AEG＝∠CFH，由ASA证明△AEG≌△CFH，得出对应边相等即可．【解答】证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADF＝∠CFH，∠EAG＝∠FCH，∵E、F分别为AD、BC边的中点，∴AE＝DE＝AD，CF＝BF＝BC，∴DE∥BF，DE＝BF，∴四边形BFDE是平行四边形，∴BE∥DF，∴∠AEG＝∠ADF，∴∠AEG＝∠CFH，在△AEG和△CFH中，，∴△AEG≌△CFH（ASA），∴AG＝CH．【点评】本题考查了平行四边形的性质和判定，全等三角形的判定与性质；熟练掌握平行四边形的判定与性质，证明三角形全等是解决问题的关键．19．（9分）如图，一次函数y＝kx+b的图象与反比例函数y＝的图象相交于点A（﹣1，3）和点B（3，n）．（1）求这两个函数的解析式；（2）直接写出不等﹣kx﹣b＞0式的解集．【分析】（1）先把A点坐标代入y＝求出m，从而得到反比例函数解析式为y＝﹣，再利用反比例函数解析式确定B点坐标，然后利用待定系数法求一次函数解析式；（2）观察函数图象得到当﹣1＜x＜0或x＞3时，反比例函数图象都在一次函数图象上方，即有＞kx+b．【解答】解：（1）把A（﹣1，3）代入y＝得m＝﹣1×3＝﹣3，所以反比例函数解析式为y＝﹣，把B（3，n）代入y＝﹣得3n＝3，解得n＝﹣1，所以B点坐标为（3，﹣1），把A（﹣1，3）、B（3，﹣1）代入y＝kx+b得，解得，所以一次函数解析式为y＝﹣x+2；（2）﹣1＜x＜0或x＞3．【点评】本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了待定系数法求函数解析式以及观察函数图象的能力．20．（9分）在▱ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF＝BE，连接AF，BF．（1）求证：四边形BFDE是矩形；（2）若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB．【分析】（1）根据平行四边形的性质，可得AB与CD的关系，根据平行四边形的判定，可得BFDE是平行四边形，再根据矩形的判定，可得答案；（2）根据平行线的性质，可得∠DFA＝∠FAB，根据等腰三角形的判定与性质，可得∠DAF＝∠DFA，根据角平分线的判定，可得答案．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AB∥CD．∵BE∥DF，BE＝DF，∴四边形BFDE是平行四边形．∵DE⊥AB，∴∠DEB＝90°，∴四边形BFDE是矩形；（2）∵四边形ABCD是平行四边形，∴AB∥DC，∴∠DFA＝∠FAB．在Rt△BCF中，由勾股定理，得BC＝＝5，∴AD＝BC＝DF＝5，∴∠DAF＝∠DFA，∴∠DAF＝∠FAB，即AF平分∠DAB．【点评】本题考查了平行四边形的性质，利用了平行四边形的性质，矩形的判定，等腰三角形的判定与性质，利用等腰三角形的判定与性质得出∠DAF＝∠DFA是解题关键．21．（10分）某服装厂设计了一款新式夏装，想尽快制作8800件投入市场，服装厂有AB两个制衣间，A车间每天加工的数量是B车间的1.2倍，A、B两车间共完成一半后，A车间出现故障停产，剩下全部由B车间单独完成，结果前后共用了20天完成，求A、B两车间每天分别能加工多少件．【分析】首先设B车间每天能加工x件，则A车间每天能加工1.2x件，由题意可得等量关系：A、B两车间生产4400件所用的时间+B两车间生产4400件所用的时间＝20天，有等量关系可列出方程+＝20，解方程可得答案，注意不要忘记检验．【解答】解：设B车间每天能加工x件，则A车间每天能加工1.2x件，由题意得：＝20，解得：x＝320，经检验：x＝320是原分式方程的解，且符合题意．1.2×320＝384（件）．答：A车间每天能加工384件，B车间每天能加工320件．【点评】此题主要考查了分式方程的应用，关键是正确理解题意，找出题目中的等量关系，再列出方程．列分式方程解应用题的一般步骤：设、列、解、验、答，必须严格按照这5步进行做题，规范解题步骤，另外还要注意完整性．22．（10分）如图，在四边形ABCD中，AB＝AD，CB＝CD，E是CD上一点，BE交AC于F，连接DF．（1）证明：∠BAC＝∠DAC，∠AFD＝∠CFE．（2）若AB∥CD，试证明四边形ABCD是菱形．【分析】（1）要证明∠BAC＝∠DAC，只需证明利用SSS证明△ABC≌△ADC即可；要证明∠AFD＝∠CFE先证明△ABF≌△ADF得到∠AFD＝∠AFB，再结合∠AFB＝∠AFD即可得到结论；（2）要证明四边形ABCD是菱形需要证明四条边相等，证明出∠CAD＝∠ACD，即可得到AD＝CD，结合题干条件即可得到结论．【解答】（1）证明：在△ABC和△ADC中，，∴△ABC≌△ADC（SSS），∴∠BAC＝∠DAC，在△ABF和△ADF中，，∴△ABF≌△ADF，∴∠AFD＝∠AFB，∵∠AFB＝∠AFD，∴∠AFD＝∠CFE；（2）证明：∵AB∥CD，∴∠BAC＝∠ACD，又∵∠BAC＝∠DAC，∴∠CAD＝∠ACD，∴AD＝CD，∵AB＝AD，CB＝CD，∴AB＝BC＝CD＝AD，∴四边形ABCD是菱形．【点评】本题主要考查了菱形的判定与全等三角形的判定与性质的知识，解答（1）问的关键是利用全等三角形的性质求出∠AFD＝∠AFB，解答（2）问的关键是掌握四边相等的四边形是菱形，此题难度一般．23．（11分）在体育局的策划下，市体育馆将组织明星篮球赛，为此体育局推出两种购票方案（设购票张数为x，购票总价为y）：方案一：提供8000元赞助后，每张票的票价为50元；方案二：票价按图中的折线OAB所表示的函数关系确定．（1）若购买120张票时，按方案一和方案二分别应付的购票款是多少？（2）求方案二中y与x的函数关系式；（3）至少买多少张票时选择方案一比较合算？【分析】（1）方案一中，总费用y＝8000+50x，代入x＝120求得答案；由图可知方案二中，当x＝120时，对应的购票总价为13200元；（2）分段考虑当x≤100时，当x≥100时，设出一次函数解析式，把其中两点的坐标代入即可求得相应的函数解析式；（3）由（1）（2）的解析式建立不等式，求得答案即可．【解答】解：（1）若购买120张票时，方案一购票总价：y＝8000+50x＝14000元，方案二购票总价：y＝13200元．（2）当0≤x≤100时，设y＝kx，代入（100，12000）得12000＝100k，解得k＝120，∴y＝120x；当x＞100时，设y＝kx+b，代入（100，12000）、（120，13200）得，解得，∴y＝60x+6000．（3）由（1）可知，要选择方案一比较合算，必须超过120张，由此得8000+50x＜60x+6000，解得x＞200，所以至少买201张票时选择方案一比较合算．【点评】此题考查了一次函数的应用，一元一次不等式的运用；根据自变量不同的取值分情况进行探讨是解决本题的关键．。

河南省周口市商水县八年级(下)期末数学试卷(无答案)

河南省周口市商水县八年级（下）期末数学试卷（无答案）（1）龙舟队员身高的众数是（172），中位数是（170）；（2）这30名队员平均身高是多少cm？身高大于平均身高的队员占全的百分之几？18．（9分）如图，在▱ABCD中，E、F分别为边AD、BC的中点，对角线AC分别交BE，DF于点G、H．求证：AG=CH．19．（9分）如图，一次函数y=kx+b的图象与反比例函数y=的图象相交于点A （﹣1，3）和点B（3，n）．（1）求这两个函数的解析式；（2）直接写出不等﹣kx﹣b＞0式的解集．20．（9分）在▱ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．（1）求证：四边形BFDE是矩形；（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．21．（10分）某服装厂设计了一款新式夏装，想尽快制作8800件投入市场，服装厂有AB两个制衣间，A车间每天加工的数量是B车间的1.2倍，A、B两车间共完成一半后，A车间出现故障停产，剩下全部由B车间单独完成，结果前后共用了20天完成，求A、B两车间每天分别能加工多少件．22．（10分）如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．（1）证明：∠BAC=∠DAC，∠AFD=∠CFE．（2）若AB∥CD，试证明四边形ABCD是菱形．23．（11分）在××局的策划下，市体育馆将组织明星篮球赛，为此××局推出两种购票方案（设购票张数为x，购票总价为y）：方案一：提供8000元赞助后，每张票的票价为50元；方案二：票价按图中的折线OAB所表示的函数关系确定．（1）若购买120张票时，按方案一和方案二分别应付的购票款是多少？（2）求方案二中y与x的函数关系式；（3）至少买多少张票时选择方案一比较合算？。

2017-2018学年河南省周口市商水县八年级(下)期末数学试卷

2017-2018学年河南省周口市商水县八年级（下）期末数学试卷一、选择题（每小题3分，共30分．下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内） 1．（3分）分式242x x -+的值为0，则( )A ．2x=-B ．2x=± C ．2x=D ．0x=2．（3分）函数：3yx =-中自变量x 的取值范围是()A ．1x -…B ．3x ≠ C ．1x -…且3x ≠ D ．1x<-3．（3分）国家质检总局出台了国内销售的纤维制品甲醛含量标准，从2003年1月1日起正式实施．该标准规定：针织内衣．床上用品等直接接触皮肤的制品，甲醛含量应在百万分之七十五以下．百万分之七十五用科学记数法表示应写成( )A ．77510-⨯B ．67510-⨯C ．67.510-⨯D ．57.510-⨯4．（3分）解分式方程131(1)(2)x x x =--+的结果为()A ．1B ．1-C ．2-D ．无解5．（3分）五个整数从小到大排列，中位数是4，如果这组数据唯一的众数是6，则这五个整数的和的最大值可能是( )A ．17B ．19C ．21D ．226．（3分）已知四边形A B C D ，有以下四个条件：①//A BC D；②A BC D=；③//B CA D；④B CA D=．从这四个条件中任选两个，能使四边形A B C D 成为平行四边形的选法种数共有( )A ．6种B ．5种C ．4种D ．3种7．（3分）已知点1(1,)y -，2(2,)y -，1(2-，3)y 都在反比例函数2yx-=的图象上，则1y 、2y 、3y 的大小关系是()A ．123y y y <<B ．312y y y <<C ．213y y y <<D ．321y y y <<8．（3分）函数k yx=与1(0)ykx k =+≠在同一坐标系内的图象大致为图中的()A ．B ．C ．D ．9．（3分）某同学5次上学途中所花的时间（单位：分钟）分别为x ，y ，10，11，9，已知这组数据的平均数为10，方差为2，则||x y -的值为()A ．1B ．2C ．3D ．410．（3分）如图，正方形A B C D 的边长为1cm ，E 、F 分别是B C 、C D 的中点，连接B F 、D E，则图中阴影部分面积是(2)c m．A ．45B ．23C ．56D ．34二、填空题（每小题3分，共15分） 11．（3分）计算：011(1)()3--+=．12．（3分）已知：如图，平行四边形A B C D 中，B E 平分A B C ∠交A D 于E ，C F 平分B C D∠交A D 于F ，若3A B=，5B C=，则E F=．13．（3分）正方形A B C D 在平面直角坐标系中的位置如图所示，已知A 点坐标(0,4)，B 点坐标(3,0)-，则C 点坐标．14．（3分）如图所示，在菱形A B C D中，60B E A F∠=∠=︒，20B A E∠=︒，则AEF∠的大小是．15．（3分）如图，已知点(6,3)P，过点P作P M x⊥轴于点M，P N y⊥轴于点N，反比例函数kyx=的图象交P M于点A，交P N于点B．若四边形O A P B的面积为12，则k=．三、解答题（本大题共8个小题，满分75分）16．（8分）先化简，再求值：2224111[(1)()]442xx x x+--÷--，其中3x=-．17．（9分）今年端午节，某乡镇成立一支龙舟队，共30名队员，他们的身高情况如下表：根据表中的信息回答以下问题：（1）龙舟队员身高的众数是(172)，中位数是(170)；（2）这30名队员平均身高是多少c m？身高大于平均身高的队员占全的百分之几？18．（9分）如图，在A B C D中，E 、F 分别为边A D 、B C 的中点，对角线A C分别交B E ，D F 于点G 、H ．求证：A G C H=．19．（9分）如图，一次函数ykx b=+的图象与反比例函数m yx=的图象相交于点(1,3)A -和点(3,)B n ．（1）求这两个函数的解析式；（2）直接写出不等m kx b x-->式的解集．20．（9分）在A B C D中，过点D 作D EAB⊥于点E ，点F 在边C D 上，D FBE=，连接A F，B F ．（1）求证：四边形B F D E 是矩形；（2）若3C F=，4BF =，5D F=，求证：A F 平分D AB ∠．21．（10分）某服装厂设计了一款新式夏装，想尽快制作8800件投入市场，服装厂有A B 两个制衣间，A 车间每天加工的数量是B 车间的1.2倍，A 、B 两车间共完成一半后，A 车间出现故障停产，剩下全部由B 车间单独完成，结果前后共用了20天完成，求A 、B 两车间每天分别能加工多少件．22．（10分）如图，在四边形A B C D 中，A BA D=，C BC D=，E 是C D 上一点，B E 交A C于F ，连接D F ．（1）证明：B A CD A C∠=∠，A F DC F E∠=∠．。

河南省周口市商水县八年级数学下学期期中考试试卷(含解析)

河南省周口市商水县八年级数学〔下〕期中试卷一、选择题1.式子中，分式共〔〕A. 1个B. 2个C. 3个D. 4个【答案】C【解析】【分析】判断分式的依据是看分母中是否含有字母，如果含有字母那么是分式，如果不含有字母那么不是分式．【详解】在所列代数式中，分式有、、这3个．应选C．【点睛】此题考查了分式的定义，熟知分式的定义是解答此题的关键．2. 以下运算正确的选项是〔〕A. 〔2a2〕3=6a6B. -a2b2•3ab3=-3a2b5C.D.【答案】D【解析】试题解析：A.原式=8a6，错误；B.原式=-3a3b5，错误；C.原式=，错误；D.原式=，正确；应选D．考点：1.分式的乘除法；2.幂的乘方与积的乘方；.3.单项式乘单项式；4.分式的加减法．3.如图，在□ABCD中，AD=8cm，AB=6cm，DE平分∠ADC交BC边于点E，那么BE等于〔〕A. 2cmB. 4cmC. 6cmD. 8cm【答案】A【解析】试题分析：由平行四边形对边平行根据两直线平行，内错角相等可得∠EDA=∠DEC，而DE平分∠ADC，进一步推出∠EDC=∠DEC，在同一三角形中，根据等角对等边得CE=CD=6，那么BE可求BE=BC-EC=8-6=2．应选：A．考点：1.平行四边形的性质；2.等腰三角形的性质4.氢原子的半径约为0.000 000 000 05m，用科学记数法表示为〔〕A. 5×10﹣10mB. 5×10﹣11mC. 0.5×10﹣10mD. ﹣5×10﹣11m【答案】B【解析】【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【详解】0.00000000005=5×10﹣11．应选B．【点睛】此题考查了用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．5.假设点P〔﹣1﹣2a，2a﹣4〕关于原点对称的点在第一象限内，那么a的整数解有〔〕A. 1个B. 2个C. 3个D. 4个【答案】B【解析】【分析】根据题意可得出点P在第三象限，从而列出不等式组求解即可．【详解】∵点P〔﹣1﹣2a，2a﹣4〕关于原点对称的点在第一象限内，∴，由①得：a，由②得：a＜2，∴＜a＜2．∵a为整数，∴a=1或0．应选B．【点睛】此题考查了关于原点对称的点的坐标，以及一元一次不等式组的整数解，是根底知识要熟练掌握．6.如图，在周长为20cm的▱ABCD中，AB≠AD，对角线AC.BD相交于点O，OE⊥BD交AD于E，那么△ABE的周长为〔〕A. 4cmB. 6cmC. 8cmD. 10cm【答案】D【解析】试题解析：根据平行四边形的性质得：OB=OD，∵EO⊥BD，∴EO为BD的垂直平分线，根据线段的垂直平分线上的点到两个端点的距离相等得：BE=DE，∴△ABE的周长=AB+AE+DE=AB+AD=×20=10cm．应选：D．考点：1．线段垂直平分线的性质；2．平行四边形的性质．7.假设关于x的分式方程有增根，那么m的值为〔〕A. ﹣1或﹣2B. ﹣1或2C. 1或2D. 0或﹣2【答案】D【解析】【分析】增根是化为整式方程后产生的不适合分式方程的根．所以应先确定增根的可能值，让最简公分母x〔x+1〕=0，得到x=0或﹣1，然后代入化为整式方程的方程算出m的值．【详解】方程两边都乘x〔x+1〕，得：x2﹣〔m+1〕=〔x+1〕2．∵原方程有增根，∴最简公分母x〔x+1〕=0，解得：x=0或﹣1，当x=0时，m=﹣2，当x=﹣1时，m=0．故m的值可能是﹣2或0．应选D．【点睛】此题考查了分式方程的增根，增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．8.如图，在▱ABCD中，AC，BD为对角线，BC＝6，BC边上的高为4，那么阴影局部的面积为( )A. 3B. 6C. 12D. 24【答案】C【解析】∵四边形ABCD为平行四边形，∴OA=OC，OB=OD，∴△OBE≌△ODH，△OAQ≌△OCG，△OPD≌△OFB，∴S阴影=S△BCD，∴S△BCD=S平行四边形ABCD=×6×4=12．应选C.9.某航空公司规定，旅客乘机所携带行李的质量x〔kg〕与其运费y〔元〕由如下列图的一次函数图象确定，那么旅客可携带的免费行李的最大质量为〔〕A. 20kgB. 25kgC. 28kgD. 30kg【答案】A【解析】根据图中数据，用待定系数法求出直线解析式，然后求y=0时，x对应的值即可．解：设y与x的函数关系式为y=kx+b，由题意可知，所以k=30，b=﹣600，所以函数关系式为y=30x﹣600，当y=0时，即30x﹣600=0，所以x=20．应选A．“点睛〞此题考查的是与一次函数图象结合用一次函数解决实际问题，此题关键是理解一次函数图象的意义以及与实际问题的结合．10.如图，反比例函数y1＝和一次函数y2＝k2x+b的图象交于A.B两点．A.B两点的横坐标分别为2，﹣3．通过观察图象，假设y1＞y2，那么x的取值范围是〔〕A. 0＜x＜2B. ﹣3＜x＜0或x＞2C. 0＜x＜2或x＜﹣3D. ﹣3＜x＜0【答案】C【解析】【分析】根据两函数的交点A.B的横坐标和图象得出答案即可．【详解】∵反比例函数y1和一次函数y2=k2x+b的图象交于A.B两点，A.B两点的横坐标分别为2，﹣3，∴通过观察图象，当y1＞y2时x的取值范围是0＜x＜2或x＜﹣3．应选C．【点睛】此题考查了一次函数和反比例函数的交点问题的应用，主要考查学生的理解能力和观察图形的能力，用了数形结合思想．二、填空题11.计算〔〕﹣1+〔〕0＝_____【答案】3【解析】【分析】根据负整数指数幂和零指数幂的意义计算即可．【详解】原式=2+1=3．故答案为：3．【点睛】此题考查了负整数指数幂和零指数幂．掌握负整数指数幂和零指数幂的意义是解题的关键．12.如图，在□ABCD中，CE⊥AB于E，如果∠A=125°，那么∠BCE=______．【答案】35【解析】试题分析：∵四边形平ABCD是平行四边形，∴AD∥BC，∴∠B=180°﹣∠A=55°，又∵CE⊥AB，∴∠BCE=35°．考点：1.平行四边形的性质；2.直角三角形的两个锐角互余13.如图，函数y=ax+b和y=kx的图象交于点P，那么根据图象可得，关于x，y的二元一次方程组的解是_______．【答案】【解析】解：如图，点P的坐标为〔-4，-2〕，所以二元一次方程组的解是。

河南省周口市商水县八年级数学下学期期末试卷(含解析)新人教版

河南省周口市商水县八年级数学下学期期末试卷（含解析）新人教版一、选择题（共8小题，每小题3分，满分24分.每小题只有一个正确答案）1．计算（﹣3）0的结果为（）A．0 B．1 C．﹣3 D．32．若一次函数y=（m﹣3）x+5的函数值，y随x的增大而增大，则（）A．m＜0 B．m＞0 C．m＜3 D．m＞33．一个菱形的两条对角线长分别为6cm和10cm，则这个菱形的面积是（）A．60cm2B．30cm2C．32cm2D．15cm24．某校有21名同学参加比赛，预赛成绩各不相同，要取前11名参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需再知道这21名同学成绩的（）A．中位数B．众数 C．平均数D．最高分5．如果分式方程=无解，则m的值为（）A．﹣2 B．﹣1 C．0 D．16．给出下列命题，其中，真命题的个数是（）①平行四边形的对角线互相平分②对角线相等的四边形是矩形③菱形的对角线互相垂直平分④对角线互相垂直且相等的四边形是正方形．A．4个B．3个C．2个D．1个7．在“大家跳起来”的乡村学校舞蹈比赛中，某校10名学生参赛成绩统计如图所示．对于这10名学生的参赛成绩，下列说法中错误的是（）A．众数是90 B．中位数是90 C．平均数是90 D．极差是158．如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x=9时，点R应运动到（）A．N处B．P处C．Q处D．M处二、填空题（共7小题，每小题3分，满分21分）9．在□ABCD中，已知∠A=70°，则∠C= °．10．某红外线遥控器发出的红外线波长为0.00000094m，用科学记数法表示这个数是m．11．如图，点P是x轴上的一个点，过点P作x轴的垂线PQ交双曲线于点Q，△OPQ的面积是4，则双曲线的表达式是．12．已知一组数据：1，a，3，6，7，它的平均数是4，这组数据的众数是．13．直线y=kx可以看成是将直线y=kx+b沿y轴向上平移3个单位得到的，则b= ．14．如图，E、F是□ABCD对角线BD上的两点，请你添加一个适当的条件：，使四边形AECF 是平行四边形．15．如图，在正方形ABCD中，AC为对角线，E为AC上一点，连接EB，ED，BE的延长线交AD于点F，∠BED=120°，则∠EFD的度数为．三、解答题（共8小题，满分75分）16．先化简，然后﹣1、0、2中选取一个合适的数作为x的值代入求值．17．已知双曲线y=﹣上一点P的横坐标为﹣，P点关于y轴的对称点是Q，双曲线y=经过点Q．（1）求y=的表达式；（2）说出双曲线y=所在的象限以及在每个象限内y随x值的增大而变化的情况．18．一家公司打算招聘一名部门经理，现对甲、乙两名应试者从笔试、面试、实习成绩三个方面的表现进行评价，笔试占总成绩的20%、面试占30%、实习成绩占50%，各项成绩如表所示．试判断谁会被公司录取，为什么？应聘者笔试面试实习甲85 83 90乙80 85 9219．如图，正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A（m，2），一次函数图象经过点B（﹣2，﹣1）与x轴的交点为C．（1）求一次函数的解析式；（2）求△AOC的面积．20．如图，在平行四边形ABCD中，E为BC边上的一点，连结AE、BD且AE=AB．（1）求证：∠ABE=∠EAD；（2）若∠AEB=2∠ADB，求证：四边形ABCD是菱形．21．甲、乙两同学学习计算机打字，甲打一篇3000字的文章与乙打一篇2400字的文章所用的时间相同．已知甲每分钟比乙每分钟多打12个字，问甲、乙两人每分钟各打多少个字？李明同学是这样解答的：设甲同学打印一篇3 000字的文章需要x分钟，根据题意，得（1）解得：x=50．经检验x=50是原方程的解．（2）答：甲同学每分钟打字50个，乙同学每分钟打字38个．（3）（1）请从（1）、（2）、（3）三个步骤说明李明同学的解答过程是否正确，若有不正确的步骤改正过来．（2）请你用直接设未知数列方程的方法解决这个问题．22．甲、乙两种水稻试验田连续5年的平均单位面积产量如下：（单位：吨/公顷）品种第1年第2年第3年第4年第5 年甲9.8 9.9 10.1 10 10.2乙9.4 10.3 10.8 9.7 9.8（1）哪种水稻的平均单位面积产量比较高？（2）哪种水稻的产量比较稳定．23．阅读下列材料：问题：如图所示，在正方形ABCD和▱BEFG中，点A，B，E在同一直线上，P是线段DF中点，连接PG，PC．探究：当PG与PC的夹角为90°时，平行四边形BEFG是正方形．小聪同学的思路是：首先可以证明四边形BEFG是矩形，然后延长GP交DC于点H，构造全等三角形，经过推理可以探索出问题答案．请你参考小聪同学的思路，探究并解决这个问题．（1）求证：四边形BEFG是矩形；（2）求证：PG与PC的夹角为90°时，四边形BEFG是正方形．2015-2016学年河南省周口市商水县八年级（下）期末数学试卷参考答案与试题解析一、选择题（共8小题，每小题3分，满分24分.每小题只有一个正确答案）1．计算（﹣3）0的结果为（）A．0 B．1 C．﹣3 D．3【考点】零指数幂．【分析】直接利用零指数幂的性质化简求出答案．【解答】解：（﹣3）0=1．故选：B．【点评】此题主要考查了零指数幂的性质，正确把握定义是解题关键．2．若一次函数y=（m﹣3）x+5的函数值，y随x的增大而增大，则（）A．m＜0 B．m＞0 C．m＜3 D．m＞3【考点】一次函数图象与系数的关系．【分析】直接根据一次函数的性质可得m﹣3＞0，解不等式即可确定答案．【解答】解：∵一次函数y=（m﹣3）x+5中，y随着x的增大而增大，∴m﹣3＞0，解得：m＞3．故选：D【点评】本题考查的是一次函数的性质，熟知一次函数y=kx+b（k≠0）中，当k＜0时，y随x的增大而减小是解答此题的关键．3．一个菱形的两条对角线长分别为6cm和10cm，则这个菱形的面积是（）A．60cm2B．30cm2C．32cm2D．15cm2【考点】菱形的性质．【分析】根据菱形面积等于对角线乘积的一半进行计算即可．【解答】解：根据菱形面积等于对角线乘积的一半可得：S=×10×6=30cm2．故选B．【点评】本题考查了菱形的性质，解答本题的关键是掌握菱形面积等于对角线乘积的一半．4．某校有21名同学参加比赛，预赛成绩各不相同，要取前11名参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需再知道这21名同学成绩的（）A．中位数B．众数 C．平均数D．最高分【考点】统计量的选择．【分析】由于有21名同学参加比赛，要取前11名参加决赛，故应考虑中位数的大小．【解答】解：共有21名学生参加预赛，取前11名，所以小颖需要知道自己的成绩是否进入前11．我们把所有同学的成绩按大小顺序排列，第11名的成绩是这组数据的中位数，所以小颖知道这组数据的中位数，才能知道自己是否进入决赛．故选：A．【点评】本题考查了用中位数的意义解决实际问题．将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．5．如果分式方程=无解，则m的值为（）A．﹣2 B．﹣1 C．0 D．1【考点】分式方程的解．【分析】分式方程无解的条件是：去分母后所得整式方程无解，或解这个整式方程得到的解使原方程的分母等于0．【解答】解：方程去分母得：x=m，当x=﹣1时，分母为0，方程无解．即m=﹣1方程无解，故选B．【点评】本题考查了分式方程无解的条件，是需要识记的内容，解分式方程一定要验根．6．给出下列命题，其中，真命题的个数是（）①平行四边形的对角线互相平分②对角线相等的四边形是矩形③菱形的对角线互相垂直平分④对角线互相垂直且相等的四边形是正方形．A．4个B．3个C．2个D．1个【考点】命题与定理．【分析】由平行四边形的性质、矩形的判定、菱形的性质、正方形的判定分别对各个选项判断即可．【解答】解：①∵平行四边形的对角线互相平分，∴①是真命题；②∵对角线互相平分且相等的四边形是矩形，∴②是假命题；③∵菱形的对角线互相垂直平分，∴③是真命题；④∵对角线互相垂直平分且相等的四边形是正方形，∴④是假命题；真命题的个数有2个，故选：C．【点评】本题主要考查了命题与定理、平行四边形和菱形的性质以及矩形和正方形的判定；熟记各种四边形的性质和判定是解决问题的关键．7．在“大家跳起来”的乡村学校舞蹈比赛中，某校10名学生参赛成绩统计如图所示．对于这10名学生的参赛成绩，下列说法中错误的是（）A．众数是90 B．中位数是90 C．平均数是90 D．极差是15【考点】折线统计图；算术平均数；中位数；众数；极差．【分析】根据众数、中位数、平均数、极差的定义和统计图中提供的数据分别列出算式，求出答案．【解答】解：∵90出现了5次，出现的次数最多，∴众数是90；故A正确；∵共有10个数，∴中位数是第5、6个数的平均数，∴中位数是（90+90）÷2=90；故B正确；∵平均数是（80×1+85×2+90×5+95×2）÷10=89；故C错误；极差是：95﹣80=15；故D正确．综上所述，C选项符合题意，故选：C．【点评】此题考查了折线统计图，用到的知识点是众数、中位数、平均数、极差，关键是能从统计图中获得有关数据，求出众数、中位数、平均数、极差．8．如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则当x=9时，点R应运动到（）A．N处B．P处C．Q处D．M处【考点】动点问题的函数图象．【专题】压轴题；动点型．【分析】注意分析y随x的变化而变化的趋势，而不一定要通过求解析式来解决．【解答】解：当点R运动到PQ上时，△MNR的面积y达到最大，且保持一段时间不变；到Q点以后，面积y开始减小；故当x=9时，点R应运动到Q处．故选C．【点评】本题考查动点问题的函数图象问题，有一定难度，注意要仔细分析．二、填空题（共7小题，每小题3分，满分21分）9．在□ABCD中，已知∠A=70°，则∠C=70°．【考点】平行四边形的性质．【分析】由平行四边形的性质：对角相等，得出∠C=∠A=70°即可．【解答】解：∵四边形ABCD是平行四边形，∴∠C=∠A=36°．故答案为：70．【点评】此题考查的是平行四边形的性质；熟记平行四边形的对角相等是解决问题的关键．10．某红外线遥控器发出的红外线波长为0.00000094m，用科学记数法表示这个数是9.4×10﹣7m．【考点】科学记数法—表示较小的数．【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：0.00000094=9.4×10﹣7；故答案为：9.4×10﹣7．【点评】本题考查了用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．11．如图，点P是x轴上的一个点，过点P作x轴的垂线PQ交双曲线于点Q，△OPQ的面积是4，则双曲线的表达式是y=．【考点】待定系数法求反比例函数解析式；反比例函数系数k的几何意义．【分析】因为Q点在反比例函数图象上，根据△OPQ的面积直接可求出k的值．【解答】解：由S△OPQ=xy=4，得k=xy=8．所以，反比例函数的表达式为y=，故答案为：y=．【点评】本题考查反比例函数的综合应用，根据反比例函数上的点构成的面积可确定k的值，以及根据点确定函数式．12．已知一组数据：1，a，3，6，7，它的平均数是4，这组数据的众数是3．【考点】众数；算术平均数．【分析】首先根据平均数的计算公式，可以算出a的值，再根据众数的定义解答．【解答】解：据题意得：（1+a+3+6+7）÷5=4，得a=3，所以这组数据的众数是3．故填3．【点评】本题为统计题，考查众数与平均数的意义．众数是一组数据中出现次数最多的数．13．直线y=kx可以看成是将直线y=kx+b沿y轴向上平移3个单位得到的，则b=﹣3．【考点】一次函数图象与几何变换．【分析】根据上加下减的原则可知，将直线y=kx+b沿y轴向上平移3个单位得到直线y=kx+b+3，即直线y=kx，那么b+3=0，即可求出b的值．【解答】解：根据上加下减的原则可得：b+3=0，解得b=﹣3．故答案为：﹣3．【点评】本题考查图形的平移变换和函数解析式之间的关系．在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．平移后解析式有这样一个规律“左加右减，上加下减”．关键是要搞清楚平移前后的解析式有什么关系．14．如图，E、F是□ABCD对角线BD上的两点，请你添加一个适当的条件：BE=DF，使四边形AECF 是平行四边形．【考点】平行四边形的判定与性质．【分析】连接AC交BD于O，根据平行四边形性质推出OA=OC，OB=OD，求出OE=OF，根据平行四边形的判定推出即可．【解答】解：添加的条件是BE=DF，理由是：连接AC交BD于O，∵平行四边形ABCD，∴OA=OC，OB=OD，∵BE=DF，∴OE=OF，∴四边形AECF是平行四边形．故答案为：BE=DF．【点评】本题考查了对平行四边形的性质和判定的应用，此题是一个开放性的题目，关键是添加一个适合的条件，能推出平行四边形AECF，答案不唯一，题型不错，难度也不大．15．如图，在正方形ABCD中，AC为对角线，E为AC上一点，连接EB，ED，BE的延长线交AD于点F，∠BED=120°，则∠EFD的度数为105°．【考点】正方形的性质．【分析】由四边形ABCD是正方形，易得证得△BEC≌△DEC，然后根据全等三角形的性质知对应角相等，即∠BEC=∠DEC=∠BED，又由对顶角相等、三角形的一个内角的补角是另外两个内角的和求得∠EFD=∠BEC+∠CAD，问题得解．【解答】解：∵四边形ABCD是正方形，∴BC=CD，∠ECB=∠ECD=45°．∴在△BEC与△DEC中，，∴△BEC≌△DEC（SAS），∴∠BEC=∠DEC=∠BED，∵∠BED=120°，∴∠BEC=60°=∠AEF，∴∠EFD=∠CAD+∠AEF=60°+45°=105°．故答案为：105°．【点评】此题考查了正方形的性质、全等三角形的判定与性质以及三角形外角的性质．此题难度不大，熟练掌握各种特殊几何图形的性质是解题关键．三、解答题（共8小题，满分75分）16．先化简，然后﹣1、0、2中选取一个合适的数作为x的值代入求值．【考点】分式的化简求值．【专题】探究型．【分析】先根据分式混合运算的法则把原式进行化简，再选取一个合适的数作为x的值代入进行计算即可．【解答】解：原式=•=，∵x≠0，x≠1，∴当选x=﹣1时，原式==﹣．【点评】本题考查的是分式的化简求值，解答此题时要注意x≠0，这是此题的易错点．17．已知双曲线y=﹣上一点P的横坐标为﹣，P点关于y轴的对称点是Q，双曲线y=经过点Q．（1）求y=的表达式；（2）说出双曲线y=所在的象限以及在每个象限内y随x值的增大而变化的情况．【考点】待定系数法求反比例函数解析式；反比例函数图象上点的坐标特征．【专题】计算题；反比例函数及其应用．【分析】（1）把P横坐标代入已知双曲线解析式求出纵坐标，确定出P坐标，进而求出Q坐标，代入反比例解析式求出k的值，即可求出反比例解析式；（2）利用反比例函数性质判断即可．【解答】解：（1）∵点P在双曲线y=﹣上，∴把x=﹣代入得：y=6，即P（﹣，6），∵P与Q关于y轴对称，∴Q（，6），代入y=中得：k=4，则反比例解析式为y=；（2）∵y=，且k=4＞0，∴此函数的图象在第一、三象限，在每个象限内y随x的增大而减小．【点评】此题考查了待定系数法求反比例函数解析式，以及反比例函数图象上点的坐标特征．18．一家公司打算招聘一名部门经理，现对甲、乙两名应试者从笔试、面试、实习成绩三个方面的表现进行评价，笔试占总成绩的20%、面试占30%、实习成绩占50%，各项成绩如表所示．试判断谁会被公司录取，为什么？应聘者笔试面试实习甲85 83 90乙80 85 92【考点】加权平均数．【专题】计算题．【分析】首先根据加权平均数的计算方法，分别求出甲、乙的平均成绩各是多少；然后比较大小，判断出谁会被公司录取即可．【解答】解：甲的平均成绩为：85×20%+83×30%+90×50%=17+24.9+45=86.9乙的平均成绩为：80×20%+85×30%+92×50%=16+25.5+46=87.5∵87.5＞86.9，∴乙的平均成绩较高，∴乙会被公司录取．【点评】此题主要考查了加权平均数的求法，要熟练掌握，解答此题的关键是：笔试占总成绩的20%、面试占30%、实习成绩占50%．19．如图，正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A（m，2），一次函数图象经过点B（﹣2，﹣1）与x轴的交点为C．（1）求一次函数的解析式；（2）求△AOC的面积．【考点】两条直线相交或平行问题．【分析】（1）首先根据正比例函数解析式求得m的值，再进一步运用待定系数法求得一次函数的解析式；（2）根据（1）中的解析式，令y=0求得点C的坐标，从而求得三角形的面积．【解答】解：（1）∵正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A（m，2），∴2m=2，m=1．把（1，2）和（﹣2，﹣1）代入y=kx+b，得，解得，则一次函数解析式是y=x+1；（2）令y=0，则x+1=0，x=﹣1．所以点C的坐标为（﹣1，0），则△AOC的面积=×1×2=1．【点评】此题综合考查了待定系数法求函数解析式、直线与坐标轴的交点的求法，关键是根据正比例函数解析式求得m的值．20．如图，在平行四边形ABCD中，E为BC边上的一点，连结AE、BD且AE=AB．（1）求证：∠ABE=∠EAD；（2）若∠AEB=2∠ADB，求证：四边形ABCD是菱形．【考点】菱形的判定；平行四边形的性质．【专题】证明题．【分析】（1）根据平行四边形的对边互相平行可得AD∥BC，再根据两直线平行，内错角相等可得∠AEB=∠EAD，根据等边对等角可得∠ABE=∠AEB，即可得证；（2）根据两直线平行，内错角相等可得∠ADB=∠DBE，然后求出∠ABD=∠ADB，再根据等角对等边求出AB=AD，然后利用邻边相等的平行四边形是菱形证明即可．【解答】证明：（1）在平行四边形ABCD中，AD∥BC，∴∠AEB=∠EAD，∵AE=AB，∴∠ABE=∠AEB，∴∠ABE=∠EAD；（2）∵AD∥BC，∴∠ADB=∠DBE，∵∠ABE=∠AEB，∠AEB=2∠ADB，∴∠ABE=2∠ADB，∴∠ABD=∠ABE﹣∠DBE=2∠ADB﹣∠ADB=∠ADB，∴AB=AD，又∵四边形ABCD是平行四边形，∴四边形ABCD是菱形．【点评】本题考查了菱形的判定，平行四边形的性质，平行线的性质，等边对等角的性质，等角对等边的性质，熟练掌握平行四边形与菱形的关系是解题的关键．21．甲、乙两同学学习计算机打字，甲打一篇3000字的文章与乙打一篇2400字的文章所用的时间相同．已知甲每分钟比乙每分钟多打12个字，问甲、乙两人每分钟各打多少个字？李明同学是这样解答的：设甲同学打印一篇3 000字的文章需要x分钟，根据题意，得（1）解得：x=50．经检验x=50是原方程的解．（2）答：甲同学每分钟打字50个，乙同学每分钟打字38个．（3）（1）请从（1）、（2）、（3）三个步骤说明李明同学的解答过程是否正确，若有不正确的步骤改正过来．（2）请你用直接设未知数列方程的方法解决这个问题．【考点】分式方程的应用．【专题】应用题．【分析】若设直接未知数的话，应根据所用时间相同来列等量关系．等量关系为：甲打一篇3000字的文章时间=乙打﹣篇2400字的文章所用的时间．【解答】解：（1）李明同学的解答过程中第（3）步不正确．应为：甲每分钟打字（个）．乙每分钟打字60﹣12=48（个）．答：甲每分钟打字为60个，乙每分钟打字为48个．（2）设乙每分钟打字x个，则甲每分钟打字（x+12）个．根据题意得：．解得：x=48．经检验：x=48是原方程的解．∴甲每分钟打字x+12=48+12=60（个）．答：甲每分钟打字为60个，乙每分钟打字为48个．【点评】应用题中一般有三个量，求一个量，明显的有一个量，一定是根据另一量来列等量关系的．在一般情况下，设直接未知数步骤少，也少出差错．本题考查分式方程的应用，分析题意，找到合适的等量关系是解决问题的关键．本题应用的等量关系为：工作时间=工作总量÷工效．22．甲、乙两种水稻试验田连续5年的平均单位面积产量如下：（单位：吨/公顷）品种第1年第2年第3年第4年第5 年甲9.8 9.9 10.1 10 10.2乙9.4 10.3 10.8 9.7 9.8（1）哪种水稻的平均单位面积产量比较高？（2）哪种水稻的产量比较稳定．【考点】方差．【分析】首先求得平均产量，然后求得方差，比较方差，越小越稳定．【解答】解：（1），，所以甲、乙两种水稻的平均产量一样高；（2）甲中水稻产量的方差是：[（9.8﹣10）2+（9.9﹣10）2+（10.1﹣10）2+（10﹣10）2+（10.2﹣10）2]=0.02，乙种水稻产量的方差是：[（9.4﹣10）2+（10.3﹣10）2+（10.8﹣10）2+（9.7﹣10）2+（9.8﹣10）2]=0.244．∴0.02＜0.244，∴产量比较稳定的水稻品种是甲．【点评】此题考查了方差，用到的知识点是方差和平均数的计算公式，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．23．阅读下列材料：问题：如图所示，在正方形ABCD和▱BEFG中，点A，B，E在同一直线上，P是线段DF中点，连接PG，PC．探究：当PG与PC的夹角为90°时，平行四边形BEFG是正方形．小聪同学的思路是：首先可以证明四边形BEFG是矩形，然后延长GP交DC于点H，构造全等三角形，经过推理可以探索出问题答案．请你参考小聪同学的思路，探究并解决这个问题．（1）求证：四边形BEFG是矩形；（2）求证：PG与PC的夹角为90°时，四边形BEFG是正方形．【考点】三角形综合题．【分析】（1）先有正方形ABCD得出∠EBG=90°，即可得出结论；（2）先由正方形得出∠HDP=∠GFP，∠DHP=∠FGP，从而判断出△DHP≌△FGP，再由正方形的性质即可【解答】证明：（1）在正方形ABCD中，∠ABC=90°，∴∠EBG=90°，∵四边形BEFG是平行四边形，∴平行四边形BEFG是矩形，（2）如图，延长GP交DC于点H，∵在正方形ABCD和▱BEFG中，∴AB∥DC，RE∥GF，∴DC∥GF，∴∠HDP=∠GFP，∠DHP=∠FGP，∵点P是线段DF中点，∴DP=FP，∴△DHP≌△FGP，∴DH=FG，HP=GP，∵∠CPG=90°，∴CH=CG，在正方形ABCD中，DC=BC，∴DH=BG，∴BG=GF，由（1）知，四边形BEFG是矩形，∴四边形BEFG是正方形．【点评】此题是三角形综合题，主要考查了矩形的判定，正方形的性质和判定和平行四边形的性质，全等三角形的判定和性质，解本题的关键是判断出△DHP≌△FGP．。

河南省周口市八年级下学期数学期末试卷

河南省周口市八年级下学期数学期末试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）下列各式：、、、、其中分式共有（）个。

A . 1B . 2C . 3D . 42. （2分） (2017九上·萝北期中) 在下列四个图案中，不是中心对称图形的是（）A .B .C .D .3. （2分）若代数式有意义，则x应满足（）A . x=0B . x≠1C . x≥﹣5D . x≥﹣5且x≠14. （2分）把一个图形先沿着一条直线进行轴对称变换，再沿着与这条直线平行的方向平移，我们把这样的图形变换叫做滑动对称变换．在自然界和日常生活中，大量地存在这种图形变换（如图1）．结合轴对称变换和平移变换的有关性质，你认为在滑动对称变换过程中，两个对应三角形（如图2）的对应点所具有的性质是（）A . 对应点连线与对称轴垂直B . 对应点连线被对称轴平分C . 对应点连线被对称轴垂直平分D . 对应点连线互相平行5. （2分） (2019八上·南岗月考) 若分式中，x、y都扩大4倍，则该分式的值（）A . 不变B . 扩大到原来的4倍C . 扩大到原来的16倍D . 缩小到原来的6. （2分） (2019八下·抚顺月考) 如图，在四边形ABCD中，AB∥CD，要使得四边形ABCD是平行四边形，可添加的条件不正确的是（）A . AB=CDB . BC∥ADC . BC=ADD . ∠A=∠C7. （2分）去分母解关于x的方程时会产生增根，那么m的值为（）A . 1B . ﹣1C . 2D . 无法确定8. （2分）直线l1：y＝k1x＋b与直线l2：y＝k2x＋c在同一平面直角坐标系中的图象如图所示，则关于x 的不等式k1x＋b＜k2x＋c的解集为（）A . x＞1B . x＜1C . x＞－2D . x＜－29. （2分） (2019八下·湖南期中) 如图，直线y= x+ 与x轴、y轴分别交于点A、B，在坐标轴上找点 P，使△ABP为等腰三角形，则点P的个数为（）A . 2B . 4C . 6D . 810. （2分） (2020八下·天府新期末) 据中央气象台报道,某日我市最高气温是33℃,最低气温是25℃,则当天气温t（℃）的变化范围是（）A . t＞25B . t≤25C . 25＜t＜33D . 25≤t≤33二、填空题 (共9题；共10分)11. （1分）正五边形每个内角的度数为________12. （2分）当x=________时，分式的值等于2.13. （1分）(2017·潮安模拟) 在菱形ABCD中，E，F分别是AD，BD的中点，若EF=2，则菱形ABCD的周长是________．14. （1分） (2017八下·南通期末) 如图，在Rt△ABC中，∠C＝90° ，将△ABC绕点C顺时针旋转90°得到△A′B′C，M、M′分别是AB、A′B′的中点，若AC＝4，BC＝2，则线段MM′的长为________．15. （1分） (2019七上·新吴期末) 若a2﹣3b＝4，则3b﹣a2+2018＝________.16. （1分） (2019七下·监利期末) 如果不等式组的整数解仅为2，且a、b均为整数，则代数式2a2+b的最大值＝________.17. （1分）(2019·永昌模拟) 方程﹣＝3的解是________.18. （1分） (2019七下·梅江月考) 火车匀速通过隧道时，火车在隧道内的长度（米）与火车行驶时间（秒）之间的关系用图象描述如图所示，有下列结论：①火车的长度为120米；②火车的速度为30米/秒；③火车整体都在隧道内的时间为25秒；④隧道长度为750米．其中正确的结论是________．（把你认为符合题意结论的序号都填上）19. （1分）(2020·广西) 如图，在边长为的菱形中，，点分别是上的动点，且与交于点 .当点从点运动到点时，则点的运动路径长为________.三、解答题 (共9题；共84分)20. （10分） (2019·港南模拟)（1）计算： .（2）解不等式组： .21. （5分）(2017·深圳模拟) 综合题（1）计算（2）先化简，再求值 ,其中22. （2分）如图，已知单位长度为1的方格中有个△ABC．（1）请画出△ABC向上平移3格再向右平移2格所得△ ．（2）请以点A为坐标原点建立平面直角坐标系（在图中画出），然后写出点B、点的坐标：B（，）；（，）．23. （2分） (2017八下·海安期中) 在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A 作AF∥BC交BE的延长线于点F．（1）求证：△AEF≌△DEB；（2）证明四边形ADCF是菱形；（3）若AC=3，AB=4，求菱形ADCF的面积．24. （10分） (2017九上·商水期末) 九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：时间x（天）1≤x＜5050≤x≤90售价（元/件）x+4090每天销量（件）200﹣2x已知该商品的进价为每件30元，设销售该商品的每天利润为y元．（1）求出y与x的函数关系式；（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．25. （15分）(2020·鄂尔多斯) 如图1，抛物线y＝x2+bx+c交x轴于A，B两点，其中点A的坐标为(1，0)，与y轴交于点C（(0，﹣3)．（1）求抛物线的函数解析式；（2）点D为y轴上一点，如果直线BD与直线BC的夹角为15°，求线段CD的长度；（3）如图2，连接AC，点P在抛物线上，且满足∠PAB＝2∠ACO，求点P的坐标．26. （10分）某商店购进45件A商品和20件B商品共用了800元，购进60件A商品和35件B商品共用了1100元.（1） A、B两种商品的单价分别是多少元？（2）已知该商店购进B商品的件数比购进A商品件数的2倍少4件，如果需要购进A、B两种商品的总件数不少于32件，且该商店购进A、B两种商品的总费用不超过296元，那么该商店有几种购进方案？并写出所有可能的购进方案.27. （15分） (2019八上·海安期中) 如图，△ABC是边长为5cm的等边三角形，点P，Q分别从顶点A，B 同时出发，沿线段AB，BC运动，且它们的速度都为1cm/s.当点P到达点B时，P，Q两点停止运动，设点P的运动时间为t（s）.（1）当t为何值时，△PBQ是直角三角形？（2）连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数.28. （15分） (2017八下·扬州期中) 如图，正方形AOCB的边长为4，反比例函数的图象过点E（3，4）．（1）求反比例函数的解析式；（2）反比例函数的图象与线段BC交于点D，直线y=﹣ x+b过点D，与线段AB相交于点F，求点F的坐标；（3）连接OF，OE，探究∠AOF与∠EOC的数量关系，并证明．参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共9题；共10分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、三、解答题 (共9题；共84分)20-1、20-2、21-1、21-2、22-1、22-2、23-1、23-2、23-3、24-1、24-2、24-3、25-1、25-2、26-1、26-2、27-1、27-2、28-1、28-2、28-3、。

河南省周口市商水县八年级数学下学期期中试卷(含解析)

河南省周口市商水县八年级数学（下）期中试卷一、选择题（每小题3分，共30分．下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内．）1．式子、﹣、、、﹣a+ B.﹣中，分式共（）A．1个B．2个C．3个D．4个2．下列运算正确的是（）A．（2a2）3＝6a6 B．﹣a2b2•3ab3＝﹣3a2b5C．•＝﹣1 D． +＝﹣13．如图，在▱ABCD中，已知AD＝8cm，AB＝6cm，DE平分∠ADC交BC边于点E，则BE等于（）A．2cm B．4cm C．6cm D．8cm4．氢原子的半径约为0.000 000 000 05m，用科学记数法表示为（）A．5×10﹣10m B．5×10﹣11m C．0.5×10﹣10m D．﹣5×10﹣11m5．若点P（﹣1﹣2a，2a﹣4）关于原点对称的点在第一象限内，则a的整数解有（）A．1个B．2个C．3个D．4个6．如图，在周长为20cm的▱ABCD中，AB≠AD，对角线AC.BD相交于点O，OE⊥BD交AD于E，则△ABE的周长为（）A．4cm B．6cm C．8cm D．10cm7．若关于x的分式方程有增根，则m的值为（）A．﹣1或﹣2 B．﹣1或2 C．1或2 D．0或﹣28．如图，在平行四边形ABCD中，AC，BD为对角线，BC＝6，BC边上的高为4，则图中阴影部分的面积为（）A．3 B．6 C．12 D．249．某航空公司规定，旅客乘机所携带行李的质量x（kg）与其运费y（元）由如图所示的一次函数图象确定，那么旅客可携带的免费行李的最大质量（）A．20kg B．25kg C．28kg D．30kg10．如图，反比例函数y1＝和一次函数y2＝k2x+b的图象交于A.B两点．A.B两点的横坐标分别为2，﹣3．通过观察图象，若y1＞y2，则x的取值范围是（）A．0＜x＜2 B．﹣3＜x＜0或x＞2C．0＜x＜2或x＜﹣3 D．﹣3＜x＜0二、填空题（每小题3分，共15分）11．计算（）﹣1+（）0＝_________12．如图，在▱ABCD中，CE⊥AB于E，如果∠A＝125°，那么∠BCE＝__________．13．如图，已知函数y＝ax+b和y＝kx的图象交于点P，则根据图象可得，关于x，y的二元一次方程组的解是_________．14．已知关于x的方程﹣2＝有一个正数解，则m的取值范围_______．15．如图，△OAC和△BAD都是等腰直角三角形，∠ACO＝∠ADB＝90°，反比例函数y＝在第一象限的图象经过点B．若OA2﹣AB2＝12，则k的值为________．三、解答题（本大题共8个小题，满分75分16．（8分）先化简，再求值：1﹣，其中x、y满足|x﹣2|+（3﹣y）2＝0．17．（8分）计算与化简（1）a﹣2b2•（﹣2a2b﹣2）﹣2÷（a﹣4b2）（2）18．（9分）如图，已知：平行四边形ABCD中，∠BCD的平分线CE交边AD于E，∠ABC的平分线BG 交CE于F，交AD于G．求证：AE＝DG．19．（9分）已知反比例函数y＝的图象的一支位于第一象限．（1）判断该函数图象的另一支所在的象限，并求m的取值范围；（2）如图，O为坐标原点，点A在该反比例函数位于第一象限的图象上，点B与点A关于x轴对称，若△OAB的面积为6，求m的值．20．（10分）如图，直线y＝2x+3与x轴交于点A，与y轴于点B．（1）求A，B两点的坐标；（2）过点B过直线BP与x轴交于点P，且OP＝2OA，求△ABP的面积．21．（10分）在我市某一城市美化工程招标时，有甲、乙两个工程队投标，经测算：甲队单独完成这项工程需要60天，若由甲队先做20天，剩下的工程由甲、乙合作24天可完成．（1）乙队单独完成这项工程需要多少天？（2）甲队施工一天，需付工程款3.5万元，乙队施工一天需付工程款2万元．若该工程计划在70天内完成，在不超过计划天数的前提下，是由甲队或乙队单独完成工程省钱？还是由甲乙两队全程合作完成该工程省钱？22．（10分）昨天早晨7点，小明乘车从家出发，去西安参加中学生科技创新大赛，赛后，他当天按原路返回，如图，是小明昨天出行的过程中，他距西安的距离y（千米）与他离家的时间x（时）之间的函数图象．根据下面图象，回答下列问题：（1）求线段AB所表示的函数关系式；（2）已知昨天下午3点时，小明距西安112千米，求他何时到家？23．（11分）已知反比例函数y1＝的图象与一次函数y2＝ax+b的图象交于点A（1，4）和点B（m，﹣2）（1）求这两个函数的表达式；（2）观察图象，当x＞0时，直接写出y1＞y2时自变量x的取值范围；（3）如果点C与点A关于x轴对称，求△ABC的面积．参考答案与试题解析一、选择题（每小题3分，共30分．下列各小题均有四个答案，其中只有一个是正确的，将正确答案的代号字母填入题后括号内．）1．式子、﹣、、、﹣a+ B.﹣中，分式共（）A．1个B．2个C．3个D．4个【分析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．【解答】解：在所列代数式中，分式有、、﹣这3个，故选：C．【点评】本题考查的是分式的定义，熟知一般地，如果A，B表示两个整式，并且B中含有字母，那么式子A/B叫做分式是解答此题的关键．2．下列运算正确的是（）A．（2a2）3＝6a6 B．﹣a2b2•3ab3＝﹣3a2b5C．•＝﹣1 D． +＝﹣1【分析】A.原式利用幂的乘方与积的乘方运算法则计算得到结果，即可做出判断；B.原式利用单项式乘以单项式法则计算得到结果，即可做出判断；C.原式约分得到结果，即可做出判断；D.原式变形后，利用同分母分式的减法法则计算，约分即可得到结果．【解答】解：A.原式＝8a6，错误；B.原式＝﹣3a3b5，错误；C.原式＝，错误；D.原式＝＝＝﹣1，正确；故选：D．【点评】此题考查了分式的乘除法，幂的乘方与积的乘方，单项式乘单项式，以及分式的加减法，熟练掌握运算法则是解本题的关键．3．如图，在▱ABCD中，已知AD＝8cm，AB＝6cm，DE平分∠ADC交BC边于点E，则BE等于（）A．2cm B．4cm C．6cm D．8cm【分析】由平行四边形对边平行根据两直线平行，内错角相等可得∠EDA＝∠DEC，而DE平分∠ADC，进一步推出∠EDC＝∠DEC，在同一三角形中，根据等角对等边得CE＝CD，则BE可求解．【解答】解：根据平行四边形的性质得AD∥BC，∴∠EDA＝∠DEC，又∵DE平分∠ADC，∴∠EDC＝∠ADE，∴∠EDC＝∠DEC，∴CD＝CE＝AB＝6，即BE＝BC﹣EC＝8﹣6＝2．故选：A．【点评】本题直接通过平行四边形性质的应用，及等腰三角形的判定，属于基础题．4．氢原子的半径约为0.000 000 000 05m，用科学记数法表示为（）A．5×10﹣10m B．5×10﹣11m C．0.5×10﹣10m D．﹣5×10﹣11m【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：0.000 000 000 05＝5×10﹣11，故选：B．【点评】本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．5．若点P（﹣1﹣2a，2a﹣4）关于原点对称的点在第一象限内，则a的整数解有（）A．1个B．2个C．3个D．4个【分析】根据题意可得出点P在第三象限，从而列出不等式组求解即可．【解答】解：∵点P（﹣1﹣2a，2a﹣4）关于原点对称的点在第一象限内，∴，由①得，a＞﹣，由②得，a＜2，∴a＝1或0．故选：B．【点评】本题考查了关于原点对称的点的坐标，以及一元一次不等式组的整数解，是基础知识要熟练掌握．6．如图，在周长为20cm的▱ABCD中，AB≠AD，对角线AC.BD相交于点O，OE⊥BD交AD于E，则△ABE的周长为（）A．4cm B．6cm C．8cm D．10cm【分析】根据线段垂直平分线的性质可知BE＝DE，再结合平行四边形的性质即可计算△ABE的周长．【解答】解：根据平行四边形的性质得：OB＝OD，∵EO⊥BD，∴EO为BD的垂直平分线，根据线段的垂直平分线上的点到两个端点的距离相等得：BE＝DE，∴△ABE的周长＝AB+AE+DE＝AB+AD＝×20＝10cm．故选：D．【点评】此题主要考查了平行四边形的性质及全等三角形的判定及性质，还利用了中垂线的判定及性质等，考查面积较广，有一定的综合性．7．若关于x的分式方程有增根，则m的值为（）A．﹣1或﹣2 B．﹣1或2 C．1或2 D．0或﹣2【分析】增根是化为整式方程后产生的不适合分式方程的根．所以应先确定增根的可能值，让最简公分母x（x+1）＝0，得到x＝0或﹣1，然后代入化为整式方程的方程算出m的值．【解答】解：方程两边都乘x（x+1），得x2﹣（m+1）＝（x+1）2∵原方程有增根，∴最简公分母x（x+1）＝0，解得x＝0或﹣1，当x＝0时，m＝﹣2，当x＝﹣1时，m＝0，故m的值可能是﹣2或0．故选：D．【点评】本题考查了分式方程的增根，增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．8．如图，在平行四边形ABCD中，AC，BD为对角线，BC＝6，BC边上的高为4，则图中阴影部分的面积为（）A．3 B．6 C．12 D．24【分析】由于在平行四边形中，对边分别平行且相等，对角线相互平分，图中的线条把平行四边形分成5组全等三角形，通过仔细观察分析图中阴影部分，可得出每组全等三角形中有一个带阴影，所以阴影部分的面积是平行四边形的面积的一半．【解答】解：通过观察结合平行四边形性质得：S阴影＝×6×4＝12．故选：C．【点评】本题考查的是平行四边形的性质，平行四边形的对角线相互平分．9．某航空公司规定，旅客乘机所携带行李的质量x（kg）与其运费y（元）由如图所示的一次函数图象确定，那么旅客可携带的免费行李的最大质量（）A．20kg B．25kg C．28kg D．30kg【分析】根据图中数据，用待定系数法求出直线解析式，然后求y＝0时，x对应的值即可．【解答】解：设y与x的函数关系式为y＝kx+b，由题意可知，所以k＝30，b＝﹣600，所以函数关系式为y＝30x﹣600，当y＝0时，即30x﹣600＝0，所以x＝20．故选：A．【点评】本题重点考查了一次函数的图象及一次函数的应用，是一道难度中等的题目．10．如图，反比例函数y1＝和一次函数y2＝k2x+b的图象交于A.B两点．A.B两点的横坐标分别为2，﹣3．通过观察图象，若y1＞y2，则x的取值范围是（）A．0＜x＜2 B．﹣3＜x＜0或x＞2C．0＜x＜2或x＜﹣3 D．﹣3＜x＜0【分析】根据两函数的交点A.B的横坐标和图象得出答案即可．【解答】解：∵反比例函数y1＝和一次函数y2＝k2x+b的图象交于A.B两点，A.B两点的横坐标分别为2，﹣3，∴通过观察图象，当y1＞y2时x的取值范围是0＜x＜2或x＜﹣3，故选：C．【点评】本题考查了一次函数和反比例函数的交点问题的应用，主要考查学生的理解能力和观察图形的能力，用了数形结合思想．二、填空题（每小题3分，共15分）11．计算（）﹣1+（）0＝ 3【分析】根据负整数指数幂和零指数幂的意义计算．【解答】解：原式＝2+1＝3．故答案为3．【点评】本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．12．如图，在▱ABCD中，CE⊥AB于E，如果∠A＝125°，那么∠BCE＝35 °．【分析】根据平行四边形性质及直角三角形的角的关系，即可求解．【解答】解：∵四边形平ABCD是平行四边形，∴AD∥BC，∴∠B＝180°﹣∠A＝55°，又∵CE⊥AB，∴∠BCE＝35°．故答案为：35．【点评】本题考查了平行四边形的性质，用的知识点有：平行四边形的对边互相平行、平行线的性质以及直角三角形的两个锐角互余．13．如图，已知函数y＝ax+b和y＝kx的图象交于点P，则根据图象可得，关于x，y的二元一次方程组的解是．【分析】由图可知：两个一次函数的交点坐标为（﹣4，﹣2）；那么交点坐标同时满足两个函数的解析式，而所求的方程组正好是由两个函数的解析式所构成，因此两函数的交点坐标即为方程组的解．【解答】解：函数y＝ax+b和y＝kx的图象交于点P（﹣4，﹣2），即x＝﹣4，y＝﹣2同时满足两个一次函数的解析式．所以关于x，y的方程组的解是．故答案为：．【点评】方程组的解就是使方程组中两个方程同时成立的一对未知数的值，而这一对未知数的值也同时满足两个相应的一次函数式，因此方程组的解就是两个相应的一次函数图象的交点坐标．14．已知关于x的方程﹣2＝有一个正数解，则m的取值范围m＜6且m≠3 ．【分析】分式方程去分母转化为整式方程，由分式方程有正数解，确定出m的范围即可．【解答】解：去分母得：x﹣2x+6＝m，解得：x＝6﹣m，由分式方程有一个正数解，得到6﹣m＞0，且6﹣m≠3，解得：m＜6且m≠3，故答案为：m＜6且m≠3【点评】此题考查了分式方程的解，始终注意分母不为0这个条件．15．如图，△OAC和△BAD都是等腰直角三角形，∠ACO＝∠ADB＝90°，反比例函数y＝在第一象限的图象经过点B．若OA2﹣AB2＝12，则k的值为 6 ．【分析】设B点坐标为（a，b），根据等腰直角三角形的性质得OA＝AC，AB＝AD，OC＝AC，AD ＝BD，则OA2﹣AB2＝12变形为AC2﹣AD2＝6，利用平方差公式得到（AC+AD）（AC﹣AD）＝6，所以（OC+BD）•CD＝6，则有a•b＝6，根据反比例函数图象上点的坐标特征易得k＝6．【解答】解：设B点坐标为（a，b），∵△OAC和△BAD都是等腰直角三角形，∴OA＝AC，AB＝AD，OC＝AC，AD＝BD，∵OA2﹣AB2＝12，∴2AC2﹣2AD2＝12，即AC2﹣AD2＝6，∴（AC+AD）（AC﹣AD）＝6，∴（OC+BD）•CD＝6，∴a•b＝6，∴k＝6．故答案为：6．【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数y＝（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy＝k．三、解答题（本大题共8个小题，满分75分16．（8分）先化简，再求值：1﹣，其中x、y满足|x﹣2|+（3﹣y）2＝0．【分析】根据分式的除法和减法可以化简题目中的式子，再根据|x﹣2|+（3﹣y）2＝0可以求得x、y的值，然后代入化简后的式子即可解答本题．【解答】解：1﹣＝1﹣＝1﹣＝＝，∵|x﹣2|+（3﹣y）2＝0，∴x﹣2＝0，3﹣y＝0，解得，x＝2，y＝3，∴原式＝﹣＝﹣3．【点评】本题考查分式的化简求值、非负数的性质，解答本题的关键是明确分式化简求值的方法．17．（8分）计算与化简（1）a﹣2b2•（﹣2a2b﹣2）﹣2÷（a﹣4b2）（2）【分析】（1）根据积的乘方、同底数幂的乘除法可以解答本题；（2）根据分式除法和减法可以解答本题．【解答】解：（1）a﹣2b2•（﹣2a2b﹣2）﹣2÷（a﹣4b2）＝a﹣2b2•2﹣2a﹣4b4÷（a﹣4b2）＝；（2）＝＝＝0．【点评】本题考查分式的混合运算、整式的混合运算、负整数指数幂，解答本题的关键是明确它们各自的计算方法．18．（9分）如图，已知：平行四边形ABCD中，∠BCD的平分线CE交边AD于E，∠ABC的平分线BG 交CE于F，交AD于G．求证：AE＝DG．【分析】由角的等量关系可分别得出△ABG和△DCE是等腰三角形，得出AB＝AG，DC＝DE，则有AG ＝DE，从而证得AE＝DG．【解答】证明：∵四边形ABCD是平行四边形（已知），∴AD∥BC，AB＝CD（平行四边形的对边平行，对边相等）∴∠GBC＝∠BGA，∠BCE＝∠CED（两直线平行，内错角相等）又∵BG平分∠ABC，CE平分∠BCD（已知），∴∠ABG＝∠GBC，∠BCE＝∠ECD（角平分线定义）∴∠ABG＝∠AGB，∠ECD＝∠CED．∴AB＝AG，CD＝DE（在同一个三角形中，等角对等边）∴AG＝DE，∴AG﹣EG＝DE﹣EG，即AE＝DG．【点评】本题考查平行四边形的性质、等腰三角形判定等知识．由等腰三角形的判定和等量代换推出AG＝DE是关键．运用平行四边形的性质和等腰三角形的知识解答．19．（9分）已知反比例函数y＝的图象的一支位于第一象限．（1）判断该函数图象的另一支所在的象限，并求m的取值范围；（2）如图，O为坐标原点，点A在该反比例函数位于第一象限的图象上，点B与点A关于x轴对称，若△OAB的面积为6，求m的值．【分析】（1）根据反比例函数的图象是双曲线．当k＞0时，则图象在一、三象限，且双曲线是关于原点对称的；（2）由对称性得到△OAC的面积为3．设A（x、），则利用三角形的面积公式得到关于m的方程，借助于方程来求m的值．【解答】解：（1）根据反比例函数的图象关于原点对称知，该函数图象的另一支在第三象限，且m ﹣7＞0，则m＞7；（2）∵点B与点A关于x轴对称，若△OAB的面积为6，∴△OAC的面积为3．设A（x，），则x•＝3，解得m＝13．【点评】本题考查了反比例函数的性质、图象，反比例函数图象上点的坐标特征等知识点．根据题意得到△OAC的面积是解题的关键．20．（10分）如图，直线y＝2x+3与x轴交于点A，与y轴于点B．（1）求A，B两点的坐标；（2）过点B过直线BP与x轴交于点P，且OP＝2OA，求△ABP的面积．【分析】（1）由函数解析式y＝2x+3，令y＝0求得A点坐标，x＝0求得B点坐标；（2）有两种情况，若BP与x轴正方向相交于P点，则AP＝3OA；若BP与x轴负方向相交于P点，则AP＝OA，由此求得△ABP的面积．【解答】解：（1）令y＝0，得x＝﹣1.5，∴A点坐标为（﹣1.5，0），令x＝0，得y＝3，∴B点坐标为（0，3）；（2）设P点坐标为（x，0），∵OP＝2OA，A（﹣1.5，0），∴x＝±3，∴P点坐标分别为P1（3，0）或P2（﹣3，0）．∴S△ABP1＝×（1.5+3）×3＝6.75，S△ABP2＝×（3﹣1.5）×3＝2.25，∴△ABP的面积为6.75或2.25．【点评】本题考查了一次函数图象上点的坐标特征，三角形的面积，关键是能求出符合条件的两种情况．21．（10分）在我市某一城市美化工程招标时，有甲、乙两个工程队投标，经测算：甲队单独完成这项工程需要60天，若由甲队先做20天，剩下的工程由甲、乙合作24天可完成．（1）乙队单独完成这项工程需要多少天？（2）甲队施工一天，需付工程款3.5万元，乙队施工一天需付工程款2万元．若该工程计划在70天内完成，在不超过计划天数的前提下，是由甲队或乙队单独完成工程省钱？还是由甲乙两队全程合作完成该工程省钱？【分析】（1）求的是乙的工效，工作时间明显．一定是根据工作总量来列等量关系．等量关系为：甲20天的工作量+甲乙合作24天的工作总量＝1．（2）把在工期内的情况进行比较．【解答】解：（1）设乙队单独完成需x天．根据题意，得：×20+（+）×24＝1．解这个方程得：x＝90．经检验，x＝90是原方程的解．∴乙队单独完成需90天．答：乙队单独完成需90天．（2）设甲、乙合作完成需y天，则有（+）×y＝1．解得，y＝36，①甲单独完成需付工程款为60×3.5＝210（万元）．②乙单独完成超过计划天数不符题意，③甲、乙合作完成需付工程款为36×（3.5+2）＝198（万元）．答：在不超过计划天数的前提下，由甲、乙合作完成最省钱．【点评】本题考查分式方程的应用，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．22．（10分）昨天早晨7点，小明乘车从家出发，去西安参加中学生科技创新大赛，赛后，他当天按原路返回，如图，是小明昨天出行的过程中，他距西安的距离y（千米）与他离家的时间x（时）之间的函数图象．根据下面图象，回答下列问题：（1）求线段AB所表示的函数关系式；（2）已知昨天下午3点时，小明距西安112千米，求他何时到家？【分析】（1）可设线段AB所表示的函数关系式为：y＝kx+b，根据待定系数法列方程组求解即可；（2）先根据速度＝路程÷时间求出小明回家的速度，再根据时间＝路程÷速度，列出算式计算即可求解．【解答】解：（1）设线段AB所表示的函数关系式为：y＝kx+b，依题意有，解得．故线段AB所表示的函数关系式为：y＝﹣96x+192（0≤x≤2）；（2）12+3﹣（7+6.6）＝15﹣13.6＝1.4（小时），112÷1.4＝80（千米/时），（192﹣112）÷80＝80÷80＝1（小时），3+1＝4（时）．答：他下午4时到家．【点评】本题主要考查一次函数的应用，解决本题的关键是利用待定系数法求一次函数的解析式．同时考查了速度、路程和时间之间的关系．23．（11分）已知反比例函数y1＝的图象与一次函数y2＝ax+b的图象交于点A（1，4）和点B（m，﹣2）（1）求这两个函数的表达式；（2）观察图象，当x＞0时，直接写出y1＞y2时自变量x的取值范围；（3）如果点C与点A关于x轴对称，求△ABC的面积．【分析】（1）由A在反比例函数图象上，把A的坐标代入反比例解析式，确定出k的值，从而得出反比例函数解析式，又B也在反比例函数图象上，把B的坐标代入确定出的反比例解析式即可确定出m的值，从而得到B的坐标，由A和B都在一次函数图象上，故把A和B都代入到一次函数解析式中，得到关于a与b的方程组，求出方程组的解得到a与b的值，从而确定出一次函数解析式；（2）根据图象结合交点坐标即可求得；（3）由点C与点A关于x轴对称可得AC，AC边上的高为A，B两点横坐标绝对值的和，代入三角形的面积公式即可．【解答】解：（1）∵函数y＝的图象过点A（1，4），即4＝，∴k＝4，即y1＝，又∵点B（m，﹣2）在y1＝上，∴m＝﹣2，∴B（﹣2，﹣2），又∵一次函数y2＝ax+b过A.B两点，即，解得．∴y2＝2x+2，综上可得y1＝，y2＝2x+2；（2）要使y1＞y2，即函数y1的图象总在函数y2的图象上方，∴0＜x＜1；（3）过B作BD⊥AC于D，由图形及题意可得：AC＝4+4＝8，BD＝|﹣2|+1＝3，∴s△ABC＝AC•BD＝×8×3＝12．【点评】本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了待定系数法求函数解析式以及观察函数图象的能力．。

河南省周口市八年级下学期期末质量检测数学试题

河南省周口市八年级下学期期末质量检测数学试题姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）计算的结果是（）A . 2B . -2C . ±2D . ±42. （2分） (2017八下·洛阳期末) 若式子在实数范围内有意义，则x的取值范围是（）A . x≥B . x＞C . x≥D . x＞3. （2分）如图，射线L甲、L乙分别表示甲、乙两名运动员在自行车比赛中所行路程S（米）与时间t（分）的函数图象．则他们行进的速度关系是（）A . 甲、乙同速B . 甲比乙快C . 乙比甲快D . 无法确定4. （2分） (2018八上·互助期末) “两条直线相交只有一个交点”的题设是（）A . 两条直线B . 相交C . 只有一个交点D . 两条直线相交5. （2分）我们学习了数据收集，下列正确的是（）A . 折线图易于显示数据的变化趋势B . 条形图能够显示每组中的百分比的大小C . 扇形图显示部分在总体中的具体数据D . 直方图能够显示数据的大小6. （2分）如图，将两块全等的直角三角板拼接在一起．这个图形可以看作是由一块直角三角板绕着直角顶点经过一次旋转后得到的，那么旋转的角度是（）．A . 30°B . 60°C . 90°D . 180°7. （2分）(2019·株洲) 对于任意的矩形，下列说法一定正确的是（）A . 对角线垂直且相等B . 四边都互相垂直C . 四个角都相等D . 是轴对称图形，但不是中心对称图形8. （2分） (2017八下·钦州港期中) 下列运算错误的是（）A .B .C .D .9. （2分）(2017·诸城模拟) 如图所示，边长为1的小正方形构成的网格中，半径为1的⊙O的圆心O在格点上，则∠AED的正切值等于（）A .B .C . 2D .10. （2分）若一次函数y=(2-m)x-2的函数值y随x的增大而减小，则m的取值范围是（）A . m＜0B . m＞0C . m＜2D . m＞211. （2分）(2017·平顶山模拟) 如图，已知直线y1=x+m与y2=kx﹣1相交于点P（﹣1，1），则关于x的不等式x+m＜kx﹣1的解集在数轴上表示正确的是（）A .B .C .D .12. （2分）π、，﹣，，3.1416，0. 中，无理数的个数是（）A . 1个B . 2个C . 3个D . 4个二、填空题 (共6题；共11分)13. （3分）已知直线ln：y=-（n是不为零的自然数）．当n=1时，直线l1： y=-2x+1与x轴和y 轴分别交于点A1和B1 ，设△A1OB1（其中O是平面直角坐标系的原点）的面积为S1；当n=2时，直线l2：与x轴和y轴分别交于点A2和B2 ，设△A2OB2的面积为S2；…依此类推，直线ln与x轴和y轴分别交于点An和Bn ，设△AnOBn的面积为Sn.则S1＝________ ．S1+S2+S3+……+Sn=________ S1+S2+S3+……+S2001＝________14. （1分）在直径为10cm的圆中，弦的长为8cm，则它的弦心距为________cm.15. （1分）如图，已知钝角三角形ABC，∠A=35°，OC为边AB上的中线，将△AOC绕着点O顺时针旋转，点C落在BC边上的点C′处，点A落在点A′处，联结BA′，如果点A、C、A′在同一直线上，那么∠BA′C′的度数为________16. （1分） (2019九上·珠海开学考) 直线y＝kx﹣1与y＝2x平行，则y＝kx﹣1的图象不经过第________象限．17. （4分）中考体育测试前，某区教育局为了了解选报引体向上的初三男生的成绩情况，随机抽测了本区部分选报引体向上项目的初三男生的成绩，并将测试得到的成绩绘成了下面两幅不完整的统计图：请你根据图中的信息，解答下列问题：（1）写出扇形图中a=________ %，并补全条形图；（2）在这次抽测中，测试成绩的众数和中位数分别是________ 个、________ 个．（3）该区体育中考选报引体向上的男生共有1800人，如果体育中考引体向上达6个以上（含6个）得满分，请你估计该区体育中考中选报引体向上的男生能获得满分的有________ 名18. （1分）(2018·道外模拟) 不等式组的解集为________．三、解答题 (共7题；共78分)19. （10分） (2018九下·江阴期中) 计算（1）计算－2cos 30°＋－|1－ |（2）化简：(a＋2b)(a－2b)＋(a＋2b)2－4ab．20. （15分） (2018九上·孝感月考) 如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，的三个顶点的坐标分别（1）画出关于轴的对称图形；（2）画出将绕原点逆时针方向旋转得到的；（3）求（2）中线段扫过的图形面积．21. （12分）(2017·西华模拟) 在甲、乙两名同学中选拔一人参加“中华好诗词”大赛，在相同的测试条件下，两人5次测试成绩（单位：分）如下：甲：79，86，82，85，83乙：88，79，90，81，72．回答下列问题：（1）甲成绩的平均数是________，乙成绩的平均数是________；（2）经计算知S甲2=6，S乙2=42．你认为选拔谁参加比赛更合适，说明理由；（3）如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析，求抽到的两个人的成绩都大于80分的概率．22. （6分） (2019七下·思明期中) 在同一平面内，若一个点到一条直线的距离不大于1，则称这个点是该直线的“邻点”.在平面直角坐标系中，已知点，，，过点作直线平行于轴，并将进行平移，平移后点分别对应点．（1）点 ________ (填写是或不是)直线的“邻点”，请说明理由；（2）若点刚好落在直线上，点的横坐标为，点落在轴上，且的面积为，求点的坐标，判断点是否是直线的“邻点”，并说明理由．23. （15分） (2018九上·沙洋期中) 如图，在ΔABC中，AB=AC,若将ΔABC绕点C顺时针180º得到ΔFEC。

河南省周口市商水县2022-2023学年八年级下学期期末数学试题

A．60︒B．5．如图所示的是根据河南某商场该商场5天的用水量的中位数为（A ．+9.3分B ．9.49．如图，在四边形ABCD 中，周长为（）A ．14cmB ．20cm 10．正方形ABCD 的顶点A ，B 分别在点D 在第二象限内，若3AO BO =，则正方形A ．10B ．3二、填空题（本大题共5个小题，每小题11．写出一个函数值y 随x 的值增大而减小的正比例函数，其表达式为15．如图，在矩形ABCD 中，AB =段AD 以1cm /s 的速度运动，同时点时间为(0 4.5)s t t ≤≤，若当以A ，P 长为cm ．三、解答题（本大题共8个小题，共75分，解答应写出必要的文字说明，证明过程或演算步骤）16．（1）计算：101(19)|4|3-⎛⎫---+- ⎪⎝⎭．（2）解方程：762x x =+．(1)补全条形统计图．(2)不同工种的员工每月的工资如下表：工种起重工电工木工瓦工月工资/万元 2.00.70.60.5①求该工程队员工月工资的平均数、中位数．②选择________（填“平均数”或“中位数”）来描述该工程队员工月工资收入的集中趋势更合适．18．已知ABC ．(1)按下列步骤利用尺规作图（保留作图痕迹，标明字母）①作边BC 的垂直平分线MN ，MN 交边BC ②连接AO 并延长；③以O 为圆心，OA 为半径画弧，交AO 的延长线于点④连接BD ，CD ，得四边形ABDC ．(2)在（1）的条件下，若90BAC ∠=︒，AB =19．如图，在四边形ABCD 中，AB DC ，AB (1)求证：四边形ABCD 是菱形．(2)若5AB =，2BD =，求AC 的长．(1)分别求反比例函数和一次函数的表达式．(2)直接写出不等式kmx nx+<的解集：________(3)若点A与点C关于x轴对称，连接AC21．如图，在正方形ABCD中，BD是对角线，于点F．(1)求证：四边形OECF是正方形．(2)若4=AD，求正方形OECF的面积．22．毛笔书法是我国传统文化中极具代表性的一种艺术形式．毛笔，已知每支A种毛笔的价格比每支的数量与用800元购买B种毛笔的数量同样多．(1)问A，B两种毛笔每支各多少元？(2)若要求购进A，B两种毛笔共50支，且买这两种毛笔总费用的最小值．23．综合与实践问题背景：已知在等边ABC 中，D 是直线BC 上一点，以AD 为边向右作菱形ADEF ，且120ADE ∠=︒，连接CF ．猜想验证：(1)如图1，若D 是线段BC 上一点，则DB 与FC 之间的数量关系为________．(2)如图2，若D 是射线BC 上一点，试猜想AFC ∠，FCG ∠，DAC ∠之间的数量关系，并给出证明．(3)如图3，若D 是射线CB 上一点，2AB =，3AD =，请直接写出CF 的长．设OB m =，则3OA m =．∵90ABO CBE ∠+∠=︒，CBE ∠∴ABO BCE Ð=Ð．∵AB BC =，∴ABO BCE ≌，∴CE OB m ==，3BE AO ==∵四边形APEQ 是平行四边形，∴32t t =-，解得1s t =，∴1cm AP EQ ==，312cm BQ =-=，∴22223213cm PE AQ AB BQ ==+=+=．②当点Q 在点E 的右边时，则23QE BQ BE t =-=-．∵四边形APQE 是平行四边形，∴23t t =-，∴3s t =，∴3cm AP EQ ==，6cm BQ =，∴633cm BE BQ QE =-=-=，∴AP BE =，∵90B Ð=°，AP BE ∥，∴四边形ABEP 是矩形，∴3cm PE AB ==，∴当13cm PE =或3cm 时，以A ，P ，E ，Q 为顶点的四边形为平行四边形．【点睛】本题考查矩形的判定和性质，平行四边形的性质．解题的关键是掌握矩形和平行四边形的性质，利用分类讨论的思想进行求解．16．（1）6；（2）14x =-（2）①该工程队员工的月平均工资为120⨯中位数为6060.2.60.=+．②选择中位数来描述该工程队员工月工资收入的集中趋势更合适．故答案为：中位数．【点睛】本题考查统计图及有关统计量的知识．根据条形统计图得出必要的信息和数据，掌握加权平均数，中位数的概念和意义是解题关键．18．(1)见解析(2)5（2）由作图可知，BO =∴四边形ABDC 是平行四边形．∵90BAC ∠=︒，∴四边形ABDC 是矩形，∴AD BC =．∵4AB =，3AC =，∴22435BC =+=，∴5AD BC ==．【点睛】本题考查作图—正确的画出四边形．19．(1)见解析(2)4【分析】（1）由平行线的性质及角平分线可证AB CD =，证得四边形ABCD （2）利用菱形的性质，结合勾股定理即可求解．∵ABC 是等边三角形，∴AB BC AC ==，∴112BO CO BC ===，∴2222AO AB BO =-=∵3AD =，∴在Rt ADO △中，根据勾股定理，得DO AD =∴61DB DO BO =-=-．由（2）知ABD ACF △≌△，∴61CF DB ==-，∴CF 的长为61-．【点睛】此题是四边形综合题，考查了等边三角形的性质、菱形的性质、全等三角形的判定与性质、勾股定理等知识，熟练运用有关定理并作出合理的辅助线是解题的关键。