中考数学每日一练:反比例函数与一次函数的交点问题练习题及答案_2020年压轴题版
中考数学总复习《反比例函数与一次函数交点问题》专题训练-附答案

中考数学总复习《反比例函数与一次函数交点问题》专题训练-附答案学校:___________班级:___________姓名:___________考号:___________ 1.如图,一次函数11y kx =+与反比例函数2(0)m y m x =≠相交于A 、B 两点,与x 轴,y 轴分别交于D 、C 两点,已知5sin 5CDO ∠=,BOD 的面积为1.(1)求一次函数和反比例函数的表达式;(2)请直接写出使12y y >的x 的取值范围.2.如图,一次函数y nx b =+(0n ≠,n ,b 为常数)的图象与反比例函数k y x=(0k ≠,k 为常数)的图象交于点()3,1A 和()3B a -,.(1)求一次函数和反比例函数的解析式;(2)直接写出不等式k nx b x+<的解集. 3.如图,一次函数11y x =-的图象与反比例函数2(0)k y k x =≠的图交于点(,1)A m 和(1,)B n -.(1)求反比例函数2(0)k y k x=≠的解析式. (2)当12y y >时,请直接写出x 的取值范围.4.如图,在平面直角坐标系xOy 中,一次函数11y x =--与反比例函数2m y x=的图象交于点(2,1)A -和(1,)B n .(1)求反比例函数的表达式;(2)连接OA OB ,,求AOB 的面积;(3)根据图象,请直接写出满足不等式1m x x--<的x 取值范围. 5.如图,在平面直角坐标系中,一次函数1y kx b =+的图象上与反比例函数2m y x =的图象交于A 、B 两点,与y 轴交于点C ,已知点()4,1A ,点B 的横坐标为2-.(1)求一次函数与反比例函数的解析式;(2)若点D 是y 轴上一点,且9ABD S =△,求点D 坐标.6.如图,一次函数y x b =+的图像与反比例函数k y x =的图像交于(2,3)A ,(,2)B n -两点.(1)求一次函数与反比例函数的表达式.(2)过点B 作BC y ⊥轴,垂足为C ,连接AC ,求点B 的坐标,并直接写出ABC 的面积.7.如图,直线OA 与反比例函数()0m y m x=≠的图像在第一象限交于点A ,已知4OA =,直线OA 与y 轴的夹角为30︒.(1)求反比例函数的解析式;(2)若点P 是坐标轴上的一点,当AOP 是直角三角形时,直接写出点P 的坐标.8.如图,一次函数y kx b =+的图象与反比例函数m y x=的图象交于点()13A ,和()3B n ,.(1)直接写出m =_______;n = _______;(2)请结合图象直接写出不等式m kx b x+>的解集是_______;(3)在y 轴上是否存在一点P ,使PAB 是等腰三角形,若存在,请求出点P 的坐标;若不存在,请说明理由. 9.如图,已知直线2y x =与双曲线(0)k y k x=≠交第一象限于点(,4)A m .(1)求点A 的坐标和反比例函数的解析式;(2)将点O 绕点A 逆时针旋转90︒至点B ,求直线OB 的函数解析式;(3)在(2)的条件下,若点C 是射线OB 上的一个动点,过点C 作y 轴的平行线,交双曲线(0)k y k x=≠的图像于点D ,交x 轴于点E ,且:2:3DCO DEO S S =△△,求点C 的坐标.10.如图,一次函数22y x =-的图象与反比例函数k y x=的图象交于,M N 两点.(1)求反比例函数的表达式;(2)求OMN 的面积;(3)根据图象,直接写出使反比例函数值大于一次函数值时x 的取值范围.11.如图,一次函数1y kx =-的图象与反比例函数m y x=的图象相交于A 、B 两点,已知点A 的坐标是()2,1-,AOB 的面积为32.(1)求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值小于反比例函数的值的x 的取值范围.12.如图,一次函数4y x =+的图象与反比例函数k y x=(k 为常数且0k ≠)的图象交于A ,B 两点,其中()1,3A -,直线4y x =+与y 轴、x 轴分别交于C ,D 两点.(1)求反比例函数的表达式;(2)在x 轴上找一点P ,使PA PB +的值最小,并求满足条件的点P 的坐标;(3)在坐标平面中是否存在点Q ,使得以Q ,A ,B 为顶点的三角形与COD △相似?如果存在,请直接写出所有满足条件的点Q 的坐标.13.如图,点A 是反比例函数k y x=的图象上一点,延长AO 交该图象于点B ,AC x ⊥轴,BC y ⊥轴,若()3,4C -.(1)求Rt ACB △的面积.(2)求经过AB 两点的直线y k x '=,并直接写出k k x x '>时x 的取值范围.14.如图,在平面直角坐标系中,一次函数32y x =+的图象与y 轴交于点A ,与反比例函数(0)k y k x=≠在第一象限内的图象交于点B ,且点B 的横坐标为1,过A 作AC y ⊥轴交反比例函数的图象于点C ,连接BC .(1)求反比例函数表达式;(2)求ABC 面积.15.如图,一次函数4y x =-+的图象与反比例函数k y x=(k 为常数,且0k ≠)的图象交于()1,A a ,B 两点.(1)求反比例函数的表达式及点B 的坐标;(2)直接写出一次函数4y x =-+的值大于反比例函数k y x=的值自变量x 的范围; (3)在y 轴上找一点P ,使PA PB +的值最小,求点P 的坐标.参考答案:1.(1)1112y x =+ 24y x= (2)40x -<<或 2x >2.(1)2y x =- 3y x=(2)1x <-或03x <<3.(1)反比例函数为22y x=; (2)10x -<<或2x >. 4.(1)反比例函数的表达式为:22y x=- (2)32AOB S = (3)20x -<<或1x >5.(1)24y x = 1112y x =-; (2)()0,2D 或()0,4-.6.(1)1y x =+ 6y x =(2)1527.(1)43y x =; (2)()0,23或()2,0或830,3⎛⎫ ⎪ ⎪⎝⎭或()8,0.8.(1)3,1;(2)0x <或13x <<;(3)存在,点P 的坐标为()0,37+或()0,37-或()0,0.9.(1)()8A 2,4y x=, (2)13y x = (3)2222,3⎛⎫ ⎪ ⎪⎝⎭或 (210, 210)310.(1)4y x= (2)3OMN S =△(3)02x <<或1x <-11.(1)2y x=- =1y x -- (2)20x -<<或1x >12.(1)3y x =-(2)5,02⎛⎫- ⎪⎝⎭(3)()1,1- ()3,3- ()1,1 ()3,5- ()1,1-- ()5,3-13.(1)24(2)30x -<<或3x >14.(1)5y x =(2)15415.(1)3y x = ()3,1 (2)0x <13x <<或(3)502⎛⎫⎪⎝⎭,。
中考数学反比例函数-经典压轴题附答案

中考数学反比例函数-经典压轴题附答案一、反比例函数1.如图,反比例函数y= 的图象与一次函数y=kx+b的图象交于A、B两点,点A的坐标为(2,3n),点B的坐标为(5n+2,1).(1)求反比例函数与一次函数的表达式;(2)将一次函数y=kx+b的图象沿y轴向下平移a个单位,使平移后的图象与反比例函数y= 的图象有且只有一个交点,求a的值;(3)点E为y轴上一个动点,若S△AEB=5,则点E的坐标为________.【答案】(1)解:∵A、B在反比例函数的图象上,∴2×3n=(5n+2)×1=m,∴n=2,m=12,∴A(2,6),B(12,1),∵一次函数y=kx+b的图象经过A、B两点,∴,解得,∴反比例函数与一次函数的表达式分别为y= ,y=﹣ x+7.(2)解:设平移后的一次函数的解析式为y=﹣ x+7﹣a,由,消去y得到x2+(2a﹣14)x+24=0,由题意,△=0,(21a﹣14)2﹣4×24=0,解得a=7±2 .(3)(0,6)或(0,8)【解析】【解答】(3)设直线AB交y轴于K,则K(0,7),设E(0,m),由题意,PE=|m﹣7|.∵S△AEB=S△BEP﹣S△AEP=5,∴ ×|m﹣7|×(12﹣2)=5.∴|m﹣7|=1.∴m1=6,m2=8.∴点E的坐标为(0,6)或(0,8).故答案为(0,6)或(0,8).【分析】(1)由A、B在反比例函数的图象上,得到n,m的值和A、B的坐标,用待定系数法求出反比例函数与一次函数的表达式;(2)由将一次函数y=kx+b的图象沿y轴向下平移a个单位,得到平移后的一次函数的解析式,由平移后的图象与反比例函数的图象有且只有一个交点,得到方程组求出a的值;(3)由点E为y轴上一个动点和S△AEB=5,求出点E的坐标.2.如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y= 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.(1)求双曲线和抛物线的解析式;(2)计算△ABC的面积;(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.【答案】(1)解:把点A的坐标代入双曲线的解析式得:k=﹣1×4=﹣4.所以双曲线的解析式为y=﹣.设点B的坐标为(m,﹣m).∵点B在双曲线上,∴﹣m2=﹣4,解得m=2或m=﹣2.∵点B在第四象限,∴m=2.∴B(2,﹣2).将点A、B、C的坐标代入得:,解得:.∴抛物线的解析式为y=x2﹣3x.(2)解:如图1,连接AC、BC.令y=0,则x2﹣3x=0,∴x=0或x=3,∴C(3,0),∵A(﹣1,4),B(2,﹣2),∴直线AB的解析式为y=﹣2x+2,∵点D是直线AB与x轴的交点,∴D(1,0),∴S△ABC=S△ADC+S△BDC= ×2×4+ ×2×2=6;(3)解:存在,理由:如图2,由原抛物线的解析式为y=x2﹣3x=(x﹣)2﹣,∴原抛物线的顶点坐标为(,﹣),∴抛物线向左平移个单位,再向上平移个单位,而平移前A(﹣1,4),B(2,﹣2),∴平移后点A(﹣,),B(,),∴点A关于y轴的对称点A'(,),连接A'B并延长交y轴于点P,连接AP,由对称性知,∠APE=∠BPE,∴△APB的内切圆的圆心在y轴上,∵B(,),A'(,),∴直线A'B的解析式为y=3x﹣,∴P(0,﹣).【解析】【分析】(1)首先将点A的坐标代入反比例函数的解析式求得k的值,然后再求得B的值,最后根据点A的坐标求出双曲线的解析式,进而得出点B的坐标,最后,将点A、B、O三点的坐标代入抛物线的解析式,求得a、b、c的值即可;(2)由点A和点B的坐标可求得直线AB的解析式,然后将y=0可求得点D的横坐标,最后用三角形的面积和求解即可;(3)先确定出平移后点A,B的坐标,进而求出点A关于y轴的对称点的坐标,求出直线BA'的解析式即可得出点P的坐标.3.如图,在平面直角坐标系中,平行四边形的边,顶点坐标为,点坐标为 .(1)点的坐标是________,点的坐标是________(用表示);(2)若双曲线过平行四边形的顶点和,求该双曲线的表达式;(3)若平行四边形与双曲线总有公共点,求的取值范围.【答案】(1);(2)解:∵双曲线过点和点,∴,解得,∴点的坐标为,点的坐标为,把点的坐标代入,解得,∴双曲线表达式为(3)解:∵平行四边形与双曲线总有公共点,∴当点在双曲线,得到,当点在双曲线,得到,∴的取值范围 .【解析】【分析】(1)由四边形ABCD为平行四边形,得到A与B纵坐标相同,C与D纵坐标相同,横坐标相差2,得出B、C坐标即可;(2)根据B与D在反比例图象上,得到C与D横纵坐标乘积相等,求出b的值确定出B坐标,进而求出k的值,确定出双曲线解析式;(3)抓住两个关键点,将A坐标代入双曲线解析式求出b的值;将C坐标代入双曲线解析式求出b的值,即可确定出平行四边形与双曲线总有公共点时b的范围.4.如图,过原点O的直线与双曲线交于上A(m,n)、B,过点A的直线交x轴正半轴于点D,交y轴负半轴于点E,交双曲线于点P.(1)当m=2时,求n的值;(2)当OD:OE=1:2,且m=3时,求点P的坐标;(3)若AD=DE,连接BE,BP,求△PBE的面积.【答案】(1)解:∵点A(m,n)在双曲线y=上,∴mn=6,∵m=2,∴n=3;(2)解:由(1)知,mn=6,∵m=3,∴n=2,∴A(3,2),∵OD:OE=1:2,设OD=a,则OE=2a,∵点D在x轴坐标轴上,点E在y轴负半轴上,∴D(a,0),E(0,﹣2a),∴直线DE的解析式为y=2x﹣2a,∵点A(3,2)在直线y=2x﹣2a上,∴6﹣2a=2,∴a=2,∴直线DE的解析式为y=2x﹣4①,∵双曲线的解析式为y=②,联立①②解得,(点A的横纵坐标,所以舍去)或,∴P(﹣2,﹣3);(3)解:∵AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,A(m,n),∴E(0,﹣n),D( m,0),∴直线DE的解析式为y= x﹣n,∵mn=6,∴m=,∴y= x﹣n③,∵双曲线的解析式为y=④,联立③④解得,∴(点A的横纵坐标,所以舍去)或,∴P(﹣2m,﹣2n),∵A(m,n),∴直线AB的解析式为y=x⑤.联立④⑤解得,(点A的横纵坐标,所以舍去)或∴B(﹣m,﹣n),∵E(0,﹣n),∴BE∥x轴,∴S△PBE= BE×|y E﹣y P|= ×m×|﹣n﹣(﹣2n)|= mn=3.【解析】【分析】(1)把A(2,n)代入解析式即可求出n;(2)先求出A点坐标,设OD=a,则OE=2a,得D(a,0),E(0,﹣2a),直线DE的解析式为y=2x﹣2a,把点A(3,2)代入求出a,再联立两函数即可求出交点P;(3)由AD=DE,点D在x轴坐标轴上,点E在y轴负半轴上,故A(m,n),E(0,﹣n),D( m,0),求得直线DE 的解析式为y= x﹣n,又mn=6,得y= x﹣n,与y=联立得,即为P点坐标,由直线AB的解析式为y= x与双曲线联立解得B (﹣m,﹣n),再根据S△PBE= BE×|y E﹣y P|= ×m×|﹣n﹣(﹣2n)|求出等于3.5.如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.(1)求直线AB和反比例函数的解析式;(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.【答案】(1)解:设反比例函数解析式为y= ,把B(﹣2,﹣3)代入,可得k=﹣2×(﹣3)=6,∴反比例函数解析式为y= ;把A(3,m)代入y= ,可得3m=6,即m=2,∴A(3,2),设直线AB 的解析式为y=ax+b,把A(3,2),B(﹣2,﹣3)代入,可得,解得,∴直线AB 的解析式为y=x﹣1(2)解:由题可得,当x满足:x<﹣2或0<x<3时,直线AB在双曲线的下方(3)解:存在点C.如图所示,延长AO交双曲线于点C1,∵点A与点C1关于原点对称,∴AO=C1O,∴△OBC1的面积等于△OAB的面积,此时,点C1的坐标为(﹣3,﹣2);如图,过点C1作BO的平行线,交双曲线于点C2,则△OBC2的面积等于△OBC1的面积,∴△OBC2的面积等于△OAB的面积,由B(﹣2,﹣3)可得OB的解析式为y= x,可设直线C1C2的解析式为y= x+b',把C1(﹣3,﹣2)代入,可得﹣2= ×(﹣3)+b',解得b'= ,∴直线C1C2的解析式为y= x+ ,解方程组,可得C2();如图,过A作OB的平行线,交双曲线于点C3,则△OBC3的面积等于△OBA的面积,设直线AC3的解析式为y= x+ ,把A(3,2)代入,可得2= ×3+ ,解得 =﹣,∴直线AC3的解析式为y= x﹣,解方程组,可得C3();综上所述,点C的坐标为(﹣3,﹣2),(()).【解析】【分析】(1)用待定系数法求出反比例函数解析式,一次函数解析式,将已知的点A,B的坐标代入设的函数解析式列出关于待定系数的方程(组)求出系数,再回代到解析式(2)结合图像判断直线AB在双曲线的交点坐标为A,B,X取值范围为双曲线所在象限交点的横坐标,第一象限为为小于横坐标大于零,第三象限为小于横坐标(3)结合已知条件根据同底等高、等底同高作出与原三角形面积相等的三角形,再结合已知条件用待定系数法求出与双曲线有交点的直线的解析式,得出点的坐标,注意要考虑满足条件的所有点C的坐标。
中考数学与反比例函数有关的压轴题附答案解析

中考数学与反比例函数有关的压轴题附答案解析一、反比例函数1.如图,在平面直角坐标系中,反比例函数y= 的图象与一次函数y=ax+b的图象交于点A(﹣2,3)和点B(m,﹣2).(1)求反比例函数和一次函数的解析式;(2)直线x=1上有一点P,反比例函数图象上有一点Q,若以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,直接写出点Q的坐标.【答案】(1)解:∵点A(﹣2,3)在反比例函数y= 的图形上,∴k=﹣2×3=﹣6,∴反比例函数的解析式为y=﹣,∵点B在反比例函数y=﹣的图形上,∴﹣2m=﹣6,∴m=3,∴B(3,﹣2),∵点A,B在直线y=ax+b的图象上,∴,∴,∴一次函数的解析式为y=﹣x+1(2)解:∵以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,∴AB=PQ,AB∥PQ,设直线PQ的解析式为y=﹣x+c,设点Q(n,﹣),∴﹣ =﹣n+c,∴c=n﹣,∴直线PQ的解析式为y=﹣x+n﹣,∴P(1,n﹣﹣1),∴PQ2=(n﹣1)2+(n﹣﹣1+ )2=2(n﹣1)2,∵A(﹣2,3).B(3,﹣2),∴AB2=50,∵AB=PQ,∴50=2(n﹣1)2,∴n=﹣4或6,∴Q(﹣4. )或(6,﹣1)【解析】【分析】(1)先利用待定系数法求出反比例函数解析式,进而求出点B的坐标,再用待定系数法求出直线解析式;(2)先判断出AB=PQ,AB∥PQ,设出点Q的坐标,进而得出点P的坐标,即可求出PQ,最后用PQ=AB建立方程即可得出结论.2.抛物线y= +x+m的顶点在直线y=x+3上,过点F(﹣2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.(1)先通过配方求抛物线的顶点坐标(坐标可用含m的代数式表示),再求m的值;(2)设点N的横坐标为a,试用含a的代数式表示点N的纵坐标,并说明NF=NB;(3)若射线NM交x轴于点P,且PA•PB= ,求点M的坐标.【答案】(1)解:y= x2+x+m= (x+2)2+(m﹣1)∴顶点坐标为(﹣2,m﹣1)∵顶点在直线y=x+3上,∴﹣2+3=m﹣1,得m=2;(2)解:过点F作FC⊥NB于点C,∵点N在抛物线上,∴点N的纵坐标为: a2+a+2,即点N(a, a2+a+2)在Rt△FCN中,FC=a+2,NC=NB﹣CB= a2+a,∴NF2=NC2+FC2=( a2+a)2+(a+2)2,=( a2+a)2+(a2+4a)+4,而NB2=( a2+a+2)2,=( a2+a)2+(a2+4a)+4∴NF2=NB2,NF=NB(3)解:连接AF、BF,由NF=NB,得∠NFB=∠NBF,由(2)的思路知,MF=MA,∴∠MAF=∠MFA,∵MA⊥x轴,NB⊥x轴,∴MA∥NB,∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°,∴2∠MAF+2∠NBF=180°,∠MAF+∠NBF=90°,∵∠MAB+∠NBA=180°,∴∠FBA+∠FAB=90°,又∵∠FAB+∠MAF=90°,∴∠FBA=∠MAF=∠MFA,又∵∠FPA=∠BPF,∴△PFA∽△PBF,∴ = ,PF2=PA×PB= ,过点F作FG⊥x轴于点G,在Rt△PFG中,PG= = ,∴PO=PG+GO= ,∴P(﹣,0)设直线PF:y=kx+b,把点F(﹣2,2)、点P(﹣,0)代入y=kx+b,解得k= ,b= ,∴直线PF:y= x+ ,解方程 x2+x+2= x+ ,得x=﹣3或x=2(不合题意,舍去),当x=﹣3时,y= ,∴M(﹣3,).【解析】【分析】(1)利用配方法将二次函数化成顶点式,写出顶点坐标,由顶点再直线y=x+3上,建立方程求出m的值。
中考数学每日一练:反比例函数与一次函数的交点问题练习题及答案_2020年解答题版

中考数学每日一练:反比例函数与一次函数的交点问题练习题及答案_2020年解答题版答案答案2020年中考数学:函数_反比例函数_反比例函数与一次函数的交点问题练习题~~第1题~~(2019.中考模拟) 如图,一次函数y =kx+b (k 、b 为常数,k≠0)的图象与x 轴、y轴分别交于A 、B 两点,且与反比例函数y = (n 为常数,且n≠0)的图象在第二象限交于点C.CD ⊥x 轴,垂足为D ,若OB =2OA =3OD =12.(1) 求一次函数与反比例函数的解析式;(2) 记两函数图象的另一个交点为E ,求△CDE 的面积;(3) 直接写出不等式kx+b≤ 的解集.考点: 待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;相似三角形的判定与性质;~~第2题~~(2019滨州.中考模拟) 如图,一次函数y =kx +b 的图象与反比例函数y= 的图象交于点A 、B 两点,与x 轴、y 轴交于C 、D 两点,且点C 、D 刚好是线段AB 的三等分点,OD =2,tan ∠DCO =(1) 求一次函数与反比例函数的解析式;(2) 求△AOB 的面积;(3) 若y ≤y ,请直接写出相应自变量x 的取值范围考点: 待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;~~第3题~~(2019中山.中考模拟) 如图,一次函数y=ax+b 的图象与反比例函数y=的图象交于C ,D 两点,与x ,y 轴交于B ,A 两点,过点C 作CE 垂直x 轴交于点E 。
且tan ∠ABO=,OB=4,OE=2.(1) 求一次函数的解析式和反比例函数的解析式;(2) 求△OCD 的面积;1212答案答案答案(3) 根据图象直接写出一次函数的值大于反比例函数的值时,自变量x 的取值范围.考点: 一次函数图象、性质与系数的关系;反比例函数与一次函数的交点问题;~~第4题~~(2019中山.中考模拟) 如图,一次函数y=kx+b 与反比例函数y= (x>0)的图象交于点A(a ,3)和B(3,1).(1) 求一次函数的解析式.(2) 观察图象,写出反比例函数值小于一次函数值时x 的取值范围.(3) 点P 是线段AB 上一点,过点P 作PD ⊥x 轴于点D ,交反比例函数图象于点Q ,连接OP 、OQ ,若△POQ 的面积为,求P 点的坐标。
2020年中考数学压轴题每日一练(含答案)
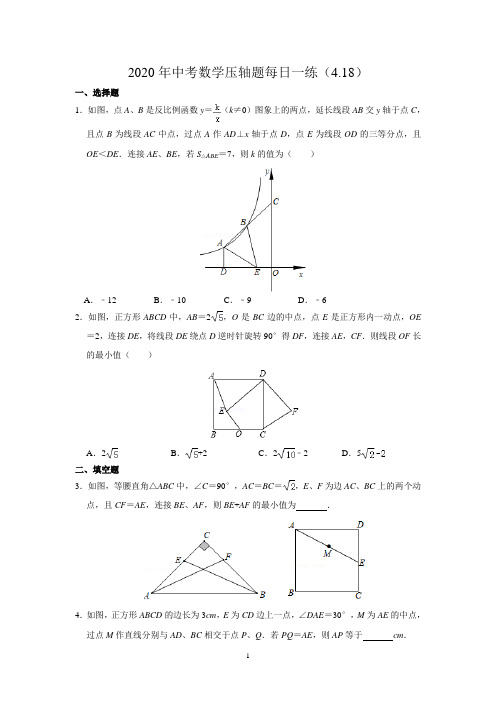
2020年中考数学压轴题每日一练(4.18)一、选择题1.如图,点A、B是反比例函数y=(k≠0)图象上的两点,延长线段AB交y轴于点C,且点B为线段AC中点,过点A作AD⊥x轴于点D,点E为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为()A.﹣12 B.﹣10 C.﹣9 D.﹣62.如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE =2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.则线段OF长的最小值()A.2B.+2 C.2﹣2 D.5二、填空题3.如图,等腰直角△ABC中,∠C=90°,AC=BC=,E、F为边AC、BC上的两个动点,且CF=AE,连接BE、AF,则BE+AF的最小值为.4.如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于cm.三、解答题5.如图,矩形ABCD中,AB=a,BC=b,动点P从A点出发,按A→B→C的方向在AB 和BC上移动,记P A=x,点D到直线P A的距离为y,且y关于x的函数图象大致如图:(1)a=,b=;(2)求y关于x的函数关系式,并直接写出x的取值范围;(3)当△PCD的面积是△ABP的面积的时,求y的值.6.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于点A,B(3,0),交y轴于点C(0,3).(1)求抛物线的解析式;(2)在直线BC上有一点P,使PO+P A的值最小,求点P的坐标;(3)在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.【答案与解析】一、选择题1.【分析】设A(m,),C(0,n),则D(m,0),E(m,0),由AB=BC,推出B(,),根据点B在y=上,推出•=k,可得mn=3k,连接EC,OA.因为AB=BC,推出S△AEC=2•S△AEB=14,根据S△AEC=S△AEO+S△ACO﹣S△ECO,构建方程即可解决问题;【解答】解:设A(m,),C(0,n),则D(m,0),E(m,0),∵AB=BC,∴B(,),∵点B在y=上,∴•=k,∴k+mn=4k,∴mn=3k,连接EC,OA.∵AB=BC,∴S△AEC=2•S△AEB=14,∵S△AEC=S△AEO+S△ACO﹣S△ECO,∴14=•(﹣m)•+•n•(﹣m)﹣•(﹣m)•n,∴14=﹣k﹣+,∴k=﹣12.故选:A.2.【分析】连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,证明△EDO≌△FDM,可得FM=OE=2,由条件可得OM=5,根据OF+MF≥OM,即可得出OF的最小值.【解答】解:如图,连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,∵∠EDF=∠ODM=90°,∴∠EDO=∠FDM,∵DE=DF,DO=DM,∴△EDO≌△FDM(SAS),∴FM=OE=2,∵正方形ABCD中,AB=2,O是BC边的中点,∴OC=,∴OD=,∴OM=,∵OF+MF≥OM,∴OF≥.故选:D.二、填空题3.如图,等腰直角△ABC中,∠C=90°,AC=BC=,E、F为边AC、BC上的两个动点,且CF=AE,连接BE、AF,则BE+AF的最小值为.【分析】如图,作点C关于直线AB的对称点D,连接AD,BD,延长DA到H,使得AH=AD,连接EH,BH,DE.想办法证明AF=DE=EH,BE+AF的最小值转化为EH+EB 的最小值.【解答】解:如图,作点C关于直线AB的对称点D,连接AD,BD,延长DA到H,使得AH=AD,连接EH,BH,DE.∵CA=CB,∠C=90°,∴∠CAB=∠CBA=45°,∵C,D关于AB对称,∴DA=DB,∠DAB=∠CAB=45°,∠ABD=∠ABC=45°,∴∠CAD=∠CBD=∠ADC=∠C=90°,∴四边形ACBD是矩形,∵CA=CB,∴四边形ACBD是正方形,∵CF=AE,CA=DA,∠C=∠EAD=90°,∴△ACF≌△DAE(SAS),∴AF=DE,∴AF+BE=ED+EB,∵CA垂直平分线段DH,∴ED=EH,∴AF+BE=EB+EH,∵EB+EH≥BH,∴AF+BE的最小值为线段BH的长,BH==,∴AF+BE的最小值为,故答案为.4.如图,正方形ABCD的边长为3cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于2或1cm.【分析】根据题意画出图形,过P作PN⊥BC,交BC于点N,由ABCD为正方形,得到AD=DC=PN,在直角三角形ADE中,利用锐角三角函数定义求出DE的长,进而利用勾股定理求出AE的长,根据M为AE中点求出AM的长,利用HL得到三角形ADE与三角形PQN全等,利用全等三角形对应边,对应角相等得到DE=NQ,∠DAE=∠NPQ =30°,再由PN与DC平行,得到∠PF A=∠DEA=60°,进而得到PM垂直于AE,在直角三角形APM中,根据AM的长,利用锐角三角函数定义求出AP的长,再利用对称性确定出AP′的长即可.【解答】解:根据题意画出图形,过P作PN⊥BC,交BC于点N,∵四边形ABCD为正方形,∴AD=DC=PN,在Rt△ADE中,∠DAE=30°,AD=3cm,∴tan30°=,即DE=cm,根据勾股定理得:AE=2cm,∵M为AE的中点,∴AM=AE=cm,在Rt△ADE和Rt△PNQ中,,∴Rt△ADE≌Rt△PNQ(HL),∴DE=NQ,∠DAE=∠NPQ=30°,∵PN∥DC,∴∠PF A=∠DEA=60°,∴∠PMF=90°,即PM⊥AF,在Rt△AMP中,∠MAP=30°,cos30°=,∴AP===2cm;由对称性得到AP′=DP=AD﹣AP=3﹣2=1cm,综上,AP等于1cm或2cm.故答案为:1或2.三、解答题5.如图,矩形ABCD中,AB=a,BC=b,动点P从A点出发,按A→B→C的方向在AB 和BC上移动,记P A=x,点D到直线P A的距离为y,且y关于x的函数图象大致如图:(1)a=3,b=4;(2)求y关于x的函数关系式,并直接写出x的取值范围;(3)当△PCD的面积是△ABP的面积的时,求y的值.【分析】(1)根据函数的图象,即可得出a、b的值;(2)分点P在线段AB上跟点P在线段BC上讨论,依据相似三角形的性质,即可得出y与x之间的关系;(3)由等高三角形的面积比等于底边长之比,可得出BP的长,根据勾股定理得出x的值,代入到(2)中的关系式中即可求出y的值.【解答】解:(1)当点P在线段AB上时,D到AB的距离为AD,由函数图象可看出,AD=4,即BC=b=4,当点P运动到线段BC上时,D到AB的距离出现变化,由函数图象可看出,AB=3=a.故答案为:3;4.(2)①当点P在线段AB上时,有0≤AP≤AB,即0≤x≤3,此时y=4.②当点P在线段BC上时,连接AC,过点D作DE⊥AP于点E,如图,由勾股定理可得:AC==5.∵此时P点过B点向C点运动,∴AB<AP≤AC,即3<x≤5.∵AD∥BC,∴∠DAE=∠APB,又∵∠ABP=∠DEA=90°,∴△DAE∽△APB,∴=,即=,∴y=.综合①②得:y=.(3)∵△PCD的面积是△ABP的面积的,且两三角形等高,∴BP=3PC,∵BP+PC=BC=4,∴BP=3,由勾股定理可得:x==3,将x=3代入,得y==2.故当△PCD的面积是△ABP的面积的时,y的值为2.6.如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于点A,B(3,0),交y轴于点C(0,3).(1)求抛物线的解析式;(2)在直线BC上有一点P,使PO+P A的值最小,求点P的坐标;(3)在x轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.【分析】(1)根据点B,C的坐标,利用待定系数法可求出抛物线的解析式;(2)利用二次函数图象上点的坐标特征可得出点A的坐标,由点B,C的坐标可得出直线BC的解析式,作O关于BC的对称点O′,则点O′的坐标为(3,3),由两地之间线段最短可得出当A,P,O′共线时,PO+P A取最小值,由点O′,A的坐标可求出该最小值,由点A,O′的坐标,利用待定系数法可求出直线AO′的解析式,联立直线AO′和直线BC的解析式成方程组,通过解方程组可求出点P的坐标;(3)由点B,C,D的坐标可得出BC,BD,CD的长,由CD2+BC2=BD2可得出∠BCD=90°,由点A,C的坐标可得出OA,OC的长度,进而可得出=,结合∠AOC=∠DCB=90°可得出△AOC∽△DCB,进而可得出点Q与点O重合时△AQC∽△DCB;连接AC,过点C作CQ⊥AC,交x轴与点Q,则△ACQ∽△AOC∽△DCB,由相似三角形的性质可求出AQ的长度,进而可得出点Q的坐标.综上,此题得解.【解答】解:(1)将B(3,0),C(0,3)代入y=﹣x2+bx+c,得:,解得:,∴抛物线的解析式为y=﹣x2+2x+3.(2)当y=0时,﹣x2+2x+3=0,解得:x1=﹣1,x2=3,∴点A的坐标为(﹣1,0).∵点B的坐标为(3,0),点C的坐标为(0,3),∴直线BC的解析式为y=﹣x+3.如图1,作O关于BC的对称点O′,则点O′的坐标为(3,3).∵O与O′关于直线BC对称,∴PO=PO′,∴PO+P A的最小值=PO′+P A=AO′==5.设直线AO′的解析式为y=kx+m,将A(﹣1,0),Q′(3,3)代入y=kx+m,得:,解得:,∴直线AO′的解析式为y=x+.联立直线AO′和直线BC的解析式成方程组,得:,解得:,∴点P的坐标为(,).(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴点D的坐标为(1,4).又∵点C的坐标为(0,3),点B的坐标为(3,0),∴CD==,BC==3,BD==2,∴CD2+BC2=BD2,∴∠BCD=90°.∵点A的坐标(﹣1,0),点C的坐标为(0,3),∴OA=1,OC=3,∴==.又∵∠AOC=∠DCB=90°,∴△AOC∽△DCB,∴当Q的坐标为(0,0)时,△AQC∽△DCB.如图2,连接AC,过点C作CQ⊥AC,交x轴与点Q.∵△ACQ为直角三角形,CO⊥AQ,∴△ACQ∽△AOC.又∵△AOC∽△DCB,∴△ACQ∽DCB,∴=,即=,∴AQ=10,∴点Q的坐标为(9,0).综上所述:当Q的坐标为(0,0)或(9,0)时,以A,C,Q为顶点的三角形与△BCD相似.。
2020年九年级数学中考压轴每日一练:《反比例函数综合》(解析版)

三轮压轴每日一练:《反比例函数综合》1.如图,直线y =mx +6与反比例函数y =(x >0)的图象交于点A (,n )与x 轴交于点B (﹣3,0),M 为该图象上任意一点,过M 点作x 轴的平行线交y 轴于点P ,交AB 于点N .(1)求m 、n 的值和反比例函数的表达式;(2)若点P 为MN 中点时,求△AMN 的面积.2.如图直线y 1=﹣x +4,y 2=x +b 都与双曲线y =交于点A (1,3),这两条直线分别与x 轴交于B ,C 两点.(1)求k 的值;(2)直接写出当x >0时,不等式x +b >的解集;(3)若点P 在x 轴上,连接AP ,且AP 把△ABC 的面积分成1:2两部分,则此时点P 的坐标是 .3.如图,直线l1:y=kx+b与双曲线y=(x>0)交于A,B两点,与x轴交于点C,与y 轴交于点E,已知点A(1,3),点C(4,0).(1)求直线l1和双曲线的解析式;(2)将△OCE沿直线l1翻折,点O落在第一象限内的点H处,求点H的坐标;(3)如图,过点E作直线l2:y=3x+4交x轴的负半轴于点F,在直线l2上是否存在点P,使得S△PBC =S△OBC?若存在,请直接写出所有符合条件的点P的坐标;如果不存在,请说明理由.4.如图,在平面直角坐标系中,菱形ABCD的对角线AC与BD交于点P(﹣2,3),AB⊥x 轴于点E,正比例函数y=(m﹣1)x的图象与反比例函数y=的图象相交于A,P两点.(1)求m,n的值与点A的坐标;(2)求cos∠ABP的值.5.如图,已知一次函数y=kx+b的图象交反比例函数的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.(1)求这两个函数的表达式;(2)求△AOB的面积;(3)请直接写出不等式的解集.6.如图,反比例函数y=经过点A,且点A的坐标为(1,2).(1)求反比例函数的解析式;(2)点C在y轴的正半轴上,点D在x轴的正半轴上,直线CD经过点A,直线CD交反比例函数图象于另一点B,若OC=OD,求点B的坐标.7.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m ≠0)的图象交于第二、四象限内的A、B两点,与y轴交于点C,过点A作AM⊥x轴,垂足为M,OA=4,cos∠AOM=,点B的横坐标为.(1)求该反比例函数和一次函数的解析式;(2)连接MC,在x轴上找一点P,使△PMC的面积与四边形AMCO的面积相等,求P的坐标.8.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m ≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点.点D为x轴负半轴上一点,连接AO,延长AO交反比例函数于点E,连接BE.已知AO=4,tan∠AOD=2,∠ACO=45°.(1)求反比例函数和直线AB的解析式;(2)求△ABE的面积.9.已知:在矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=(k>0)的图象与AC边交于点E.(1)记S=S△OEF ﹣S△ECF,当S取得最大值时,求k的值;(2)在(1)的条件下,若直线EF与x轴、y轴分别交于点M,N,求EM•FN的值.10.如图,在平面直角坐标系xOy中,次函数y=﹣x+5的图象与反比例函数y=(k>0)的图象相交于A,B两点,与x轴相交于点C,连接OB,且△BOC的面积为.(1)求反比例函数的表达式;(2)将直线AB向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线AB向下平移了几个单位长度?11.如图,一次函数y=kx+b的图象分别交x轴、y轴于C,D两点,交反比例函数y=图象于A(,4),B(3,m)两点.(1)求直线CD的表达式;(2)点E是线段OD上一点,若S△AEB=,求E点的坐标;(3)请你根据图象直接写出不等式kx+b≤的解集.12.九年级数学兴趣小组组织了以“等积变形”为主题的课题研究.第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2,则S△ABC=S△ABD;反之亦成立.第二学习小组发现:如图(2),点P是反比例函数y=上任意一点,过点P作x轴、y 轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.请利用上述结论解决下列问题:(1)如图(3),四边形ABCD、与四边形CEFG都是正方形点E在CD上,正方形ABCD边长为2,则S△BDF=.(2)如图(4),点P、Q在反比例函数y=图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG =8,则S△POH=,k=.(3)如图(5)点P、Q是第一象限的点,且在反比例函数y=图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.13.如图,在平面直角坐标系中,菱形ABOD的顶点O与坐标原点重合,点B在y轴的正半轴上,点A在反比例函数的图象上,点D的坐标为(8,6).(1)求反比例函数的表达式;(2)E是x轴正半轴上的动点,过点E作x轴的垂线交线段OA于点M,交双曲线于点P,在E点运动过程中,M点正好是线段EP中点时,求点E的坐标.14.小明在课外研究中,设计如下题目:直线y=kx+b过点A(6,0),B(0,3),直线y =kx+b与曲线y=交于点C(4,n).(1)求直线和曲线的关系式.(2)小明发现曲线y=关于直线y=x对称,他把曲线y=与直线y =x的交点P叫做曲线的顶点(图2),①直接写出P点的坐标.②若点D从P点出发向上运动,运动到PD=PC时停止,求此时△PCD的面积.15.如图,定义:若双曲线y=(k>0)与它的其中一条对称轴y=x相交于M,N两点,则线段MN的长度为双曲线y=(k>0)的对径.(1)双曲线y=的对径是.(2)若双曲线y=(k>0)的对径是4,求k的值.(3)正方形AOCB的边长为4,(2)中双曲线与线段BC交于点D,与线段AB相交于点E,直线y=﹣x+b过点D与线段AB相交于点F,连接OF、OE,探究∠AOF与∠EOC的数量关系,并证明.16.如图,在平面直角坐标系中,点A的坐标为(a,6),AB⊥x轴于点,反比例函数的图象的一支分别交AO,AB于点C,D,延长AO交反比例函数的图象的另一支于点E,已知D的纵坐标为.(1)求反比例函数的解析式及直线OA的解析式;(2)连接BC,已知E(﹣4,﹣3),求S△CEB(3)若在x轴上有两点M(m,0),N(﹣m,0),将直线OA绕点O旋转,仍与交于C,E,能否构成以E,M,C,N为顶点的四边形为菱形,如果能请求出m的值,如果不能说明理由.参考答案1.解:(1)将点B的坐标代入y=mx+6并解得:m=2;故直线的表达式为y=2x+6;将点A的坐标代入上式得:n=2×+6=+3,则点A(,)代入y=得,k=×(+3)=4,故反比例函数表达式为y=;(2)设点M在y=上,则点M(t,),点P为MN中点,点N在直线y=2x+6上,则点N(﹣t,6﹣2t),∵MN∥x轴,故=6﹣2t,解得:t=1或2,当t=1时,点M、N的坐标分别为(1,4)、(﹣1,4),则点P(0,4),则MN=1+1=2,△AMN的面积=×MN×(y A﹣y P)=×2×(+3﹣4)=﹣1,当t=2时,同理可得:△AMN的面积=2+2,故△AMN的面积为﹣1或2+2.2.解:(1)将点A的坐标代入y=得,k=xy=1×3=3;(2)从图象看,x>0,当不等式x+b>时,x>1;(3)将点A的坐标代入y2=x+b得,3=+b,解得:b=,y 2=x+,令y2=0,则x=﹣3,即点C(﹣3,0),y 1=﹣x+4,令y1=0,则x=4,即点B(4,0),则BC=7,AP把△ABC的面积分成1:2两部分,则点P把BC分成1:2两部分,即PB=BC或BC,即BP=或,设点P的横坐标为x,则4﹣x=或,解得:x=或﹣故点P的坐标为:(﹣,0)或(,0);故答案为:(﹣,0)或(,0).3.解:(1)将A(1,3),C(4,0)代入y=kx+b,得,解得:,∴直线l的解析式为y=﹣x+4.1将A(1,3)代入y=(x>0),得m=3,∴双曲线的解析式为y=(x>0);(2)将x=0代入y=﹣x+4,得y=4,∴E(0,4).∴△COE是等腰直角三角形.∴∠OCE=∠OEC=45°,OC=OE=4.由翻折得△CEH≌△CEO,∴∠COE=∠CHE=∠OCH=90°.∴四边形OCHE是正方形.∴H(4,4);(3)存在,理由:如图,过点O作直线m∥BC交直线l于点P′,2于点P,在x轴取点H,使OC=CH(即等间隔),过点H作直线n∥BC交直线l2S△PBC =S△OBC,根据同底等高的两个三角形面积相等,则点P(P′)为所求点.直线BC表达式中的k值为﹣1,则直线m、n表达式中的k值也为﹣1,故直线m的表达式为:y=﹣x①,直线l2的表达式为:y=3x+4②,联立①②并解得:x=﹣1,y=1,故点P′(﹣1,1);设直线n的表达式为:y=﹣x+s,而点H(8,0),将点H的坐标代入上式并解得:s=8,故直线n的表达式为:y=﹣x+8③,联立②③并解得:x=1,y=7,故点P的坐标为(1,7);综上,点P的坐标为(﹣1,1)或(1,7).4.解:(1)将点P的坐标代入正比例函数y=(m﹣1)x表达式得,3=﹣2(m﹣1),解得:m=﹣;将点P的坐标代入反比例函数y=得,n+1=﹣6,解得:n=﹣7;则正比例函数的表达式为:y=﹣x①,反比例函数表达式为:y=﹣②,联立①②并解得:x=±2(舍去2),故点A(2,﹣3);(2)∵点A(2,﹣3),∴OE=2,AE=3,则OA==,在△AOE中,sin∠EAO===,在Rt△ABP中,cos∠ABP=sin∠BAP=sin∠EAO=.5.解:(1)把A(2,﹣4)的坐标代入得:4﹣2m=﹣8,反比例函数的表达式是y=﹣;把B(n,﹣2)的坐标代入y=﹣得:﹣2=﹣,解得:n=4,∴B点坐标为(4,﹣2),把A(2,﹣4)、B(4,﹣2)的坐标代入y=kx+b并解得:k=1,b=﹣6,∴一次函数表达式为y=x﹣6;(2)当y=0时,x=0+6=6,∴OC=6,∴△AOB的面积=×6×4﹣×6×2=6;(3)由图象知,0<x<2或x>4.6.解:(1)将点A的坐标代入函数表达式得:2=,解得:k=2,故反比例函数的解析式为:y=;(2)设直线CD的表达式为:y=ax+b,设OD=OC=m,则点C、D的坐标分别为:(0,m)、(m,0),将点C、D的坐标代入一次函数表达式得:,解得:,故直线CD的表达式为:y=﹣x+m,将点A的坐标代入上式得:2=﹣1+m,解得:m=3,故直线CD的表达式为:y=﹣x+3,联立直线CD和反比例函数表达式得:,解得:,,故点B(2,1).7.解:(1)cos∠AOM=,则∠AOM=30°,则点A(﹣2,2),则m=﹣4,故反比例函数的表达式为:y=﹣,点B的横坐标为,则点B(,﹣4),将点A、B的坐标代入一次函数表达式y=kx+b并解得:k=﹣,b=﹣2,故点C(0,﹣2),则一次函数的表达式为:y=﹣x﹣2;(2)AM=2=OC,且AM∥OC,则四边形AMCO为平行四边形,①当点P在x轴右侧时,OP=OM时,△PMC的面积与四边形AMCO的面积相等,故点P(2,0);②当点P在x轴左侧时,OP=2OM时,△PMC的面积与四边形AMCO的面积相等,故点P(﹣4,0);综上,点P(2,0)或(﹣4,0).8.解:(1)tan∠AOD=2,则sin∠AOD=,则AH =AO sin ∠AOD =×=8,同理OH =4,故点A (﹣4,8),则点E (4,﹣8) 故反比例函数表达式为:y =﹣…①;∵∠ACO =45°,则一次函数表达式为:y =﹣x +b , 将点A 的坐标代入上式并解得:b =4, 故直线AB 的表达式为:y =﹣x +4…②;(2)联立①②并解得:x =﹣4或8,故点B (8,﹣4), 令y =﹣x +4=0,则x =4,故点C (4,0),而点E (4,﹣8), 故CE ⊥x 轴,故△ABE 的面积=×CE ×(x B ﹣x A )=×8×(8+4)=48. 9.解:(1)∵OB =4,OA =3,且E 、F 为反比例函数图象上的两点, ∴E ,F 两点坐标分别为E (,3),F (4,), 如图,连接OE 、OF ,∴S △ECF =(3﹣),∴S △EOF =S 矩形AOBC ﹣S △AOE ﹣S △BOF ﹣S △ECF =3×4﹣××3﹣4×﹣S △ECF ,∴S △ECF =12﹣k ﹣S △ECF ,∴S =S △OEF ﹣S △ECF =12﹣k ﹣2S △ECF =12﹣k ﹣2×(3﹣),∴S =﹣k 2+k .当k =﹣=6时,S 有最大值,即S 取得最大值时k =6.(2)∵k=6,∴E(2,3),F(4,),∴EC=2,FC=,EF=,设∠CEF=α,则sinα==,cosα==,∴EM•FN=•=25.10.解:(1)一次函数y=﹣x+5中,令y=0,解得x=5,∴C(5,0),∴OC=5,作BD⊥OC于D,∵△BOC的面积为,∴OC•BD=,即BD=,∴BD=1,∴点B的纵坐标为1,代入y=﹣x+5中,求得x=4,∴B(4,1),∵反比例函数y=(k>0)的图象经过B点,∴k=4×1=4,∴反比例函数的解析式为y=;(2)将直线AB向下平移m(m>0)个单位长度得直线解析式为y=﹣x+5﹣m,∵直线AB向下平移m(m>0)个单位长度后与反比例函数的图象只有一个公共交点,∴=﹣x+5﹣m,整理得x2+(m﹣5)x+4=0,△=(m﹣5)2﹣4×1×4=0,解得m=9或m=1,即m的值为1或9.11.(1)把点A(,4)代入中,得:,解得n=6∴反比例函数的解析式为,将点B(3,m)代入得m=2,∴B(3,2)设直线AB的表达式为y=kx+b,则有,解得∴直线CD的表达式为;(2)设E点的坐标为(0,b)令x=0,则y=6∴D点的坐标为(0,6)DE=6﹣b∵S△DEB ﹣S△DEA=S△AEB∴,解得:b=1,∴E点的坐标为(0,1);(3)不等式kx+b≤的解集是.12.解:(1)连接CF,∵四边形ABCD与四边形CEFG都是正方形,∴CF∥BD,△CBD与△FBD同底等高,∴S△BDF =S△BDC=S正方形ABCD=2;(2)设P(x,y),则k=xy,根据题意,得GQ=﹣2x,PG=2y,∴S△PQG=×GQ×PG=8,即•(﹣2x)•2y=8,解得xy=﹣4,即k=﹣4,S △POH =×OH ×PH =﹣xy =2;(3)PQ ∥MN .理由:作PA ⊥y 轴,QB ⊥x 轴,垂足为A ,B ,连接PN ,MQ , 根据双曲线的性质可知,S 矩形AOMP =S 矩形BONQ =k , ∴S 矩形ANCP =S 矩形BMCQ ,可知S △NCP =S △MCQ , ∴S △NPQ =S △MPQ , ∴PQ ∥MN .故本题答案为:(1)2,(2)2,﹣4. 13.解:(1)过点D 作x 轴的垂线,垂足为F , ∵点D 的坐标为(8,6), ∴OF =8,DF =6, ∴OD =10, ∴AD =10,∴点A 坐标为(8,16), ∴k =xy =8×16=128, ∴反比例函数表达式为;(2)∵点A 坐标为(8,16), ∴OA 的表达式为y =2x ,设E 点坐标为(m ,0),则M 点坐标(m ,2m ),F 点坐标,∵M 点正好是线段EP 中点, ∴P (m ,4m ), ∴,解得:,∴.14.解:(1)将点A、B的坐标代入直线表达式得:,解得:,故直线表达式为:y=﹣x+3,当x=4时,y=﹣x+3=﹣2+3=1=n,故点C(4,1);将点C的坐标代入曲线的表达式得:1=,解得:m=4,故曲线的表达式为:y=;(2)①联立曲线和直线y=x表达式得:解得:,(舍去),故点P(2,2);②设直线CD与y=x交于点H,如下图,曲线y=关于直线y=x对称,且PD=PC,则点C、D关于直线y=x对称,故CD⊥PH,∵直线y=x的倾斜角为45°,则直线CD与直线AO的夹角为45°,故设直线CD的表达式为:y=﹣x+t,将点C的坐标代入上式并解得:t=5,故直线CD的表达式为:y=﹣x+5,联立y=x和y=﹣x+5并解得:x=,y=,故点H(,),则PH==,同理可得:CH=,点C、D关于y=x对称,则CD=2CH=2DH,△PCD的面积=CD×PH=CH×PH=×=.15.解:(1)过A点作AC⊥x轴于C,如图1,解方程组,得:,,∴A点坐标为(1,1),B点坐标为(﹣1,﹣1),∴OC=AC=1,∴OA=OC=,∴AB=2OA=2,∴双曲线y=的对径是2;故答案为:;(2)∵双曲线与对称轴由y=x均关于原点对称,设点M坐标为M(a,a)(a>0),则点N坐标为N(﹣a,﹣a),∴MN=2OM=2a=4,∴a=2,∴点M坐标为.代入得,即k=12.(3)∵正方形ABCD,边长为4,∴A(0,4),C(4,0),B(4,4),∵双曲线与BC交于D,∴D(4,3),∵双曲线与AB交于E点,∴E(3,4),∴,BE=1,∵直线过点D(4,3),∴b=5,∴,∴F(2,4),取BC中点H,连接EH,并延长交x轴于G点,连接OH,在△EBH与△GCH中,∴△EHB≌△GHC(ASA),∴BE=CG=1,∴OE=OG=5,EH=HG,∴∠EOH=∠HOC,∵A(0,4),F(2,4),∴,∵HC=2,OC=4,∴,∴tan∠AOF=tan∠HOC,∴,即.16.解:(1)∵点A的坐标为(a,6),AB⊥x轴于B,∴AB=6,∵,∴OB=8,∴点D在反比例函数的图象上,∴,∴反比例函数的解析式为设直线OA的解析式y=bx,∴8b=6解得:;∴直线OA的解析式为;(2)由(1)知C(4,3),E(﹣4,﹣3),B(8,0)∴=;(3)因为CE所在直线OA不可能与x轴垂直,即CE不能与MN垂直所以E,M,N,C为顶点的四边形不能是菱形;。
2023年中考九年级数学高频考点 专题训练--反比例函数与一次函数交点问题

2023年中考九年级数学高频考点专题训练--反比例函数与一次函数交点问题一、综合题1.如图,直线y1=3x﹣5与反比例函数y2= k−1x的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.(1)求k和n的值;(2)求△AOB的面积;(3)直接写出y1>y2时自变量x的取值范围.2.如图,在平面直角坐标系中,双曲线L:y= k x(x>0)过点A(a,b)(0<a<2)、B(2,1)。
过点A作AC△x轴,垂足为C。
(1)求L的解析式;(2)当△ABC的面积为2时,求点A的坐标;(3)点P为双曲线L上A,B之间(包括A,B两点)的动点,直线l1:y=mx+1过点P。
在(2)的条件下,若y=mx+1具有y随x的增大而增大的性质,请直接写出m的取值范围(不必说明理由)。
3.如图,已知正比例函数y=k1x的图象与反比例函数y=k2x的图象都经过点P(2,3),点D是正比例函数图象上的一点,过点D作y轴的垂线,垂足为Q,DQ交反比例函数的图象于点A,过点A作x轴的垂线,垂足为B,AB交正比例函数的图于点E.(1)求正比例函数解析式、反比例函数解析式.(2)当点D的纵坐标为9时,求ΔAEP的面积.(3)若直线OD上存在一点M,点M的横坐标为m,ΔAEM的面积为S,直接写出S关于m的解析式,并写出定义域.4.在平面直角坐标系中,过点P(0,a)作直线l分别交y=mx(m>0、x>0)、y=n x(n<0、x<0)于点M、N,(1)若m=4,MN△x轴,S△MON=6,求n的值;(2)若a=5,PM=PN,点M的横坐标为3,求m-n的值;(3)如图,若m=4,n=-6,点A(d,0)为x轴的负半轴上一点,B为x轴上点A右侧一点,AB=4,以AB为一边向上作正方形ABCD,若正方形ABCD与y=mx(m>0、x>0)、y=nx(n<0、x<0)都有交点,求d的范围.5.如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=mx(m≠0,x<0)的图象交于点A(-3,1)和点C,与y轴交于点B,△AOB的面积是6.(1)求一次函数与反比例函数的解析式;(2)求sin△ABO的值;(3)当x<0时,比较y1与y2的大小.6.如图,已知反比例函数y1=k x的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).(1)求这两个函数的关系式;(2)如果在x轴上找一点C使△ABC的面积为18,求点C坐标.7.如图,一次函数y=ax+b与反比例函数y=k x的图象交于A(2,2),B(4,1)两点.(1)求这两个函数的表达式;(2)在反比例函数y=k x第三象限的图象上有一点P,且点P到直线AB的距离最短,求点P的坐标.8.已知一次函数y=kx+b的图象与反比例函数y=-8x的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:(1)一次函数的解析式;(2)△AOB的面积;(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.9.如图,在平面直角坐标系中,反比例函数y =k x(x>0)的图象经过点A(2,6),将点A向右平移2个单位,再向下平移a个单位得到点B,点B恰好落在反比例函数y =k x(x>0)的图象上,过A,B两点的直线与y轴交于点C.(1)求k的值及点C的坐标;(2)在y轴上有一点D(0,5),连接AD,BD,求△ABD的面积.10.如图,已知直线y=mx+b(m≠0)与双曲线y= k x(k≠0)交于A(﹣3,﹣1)与B(n,6)两点,连接OA、OB.(1)求直线与双曲线的表达式;(2)求△AOB的面积.11.如图,在平面直角坐标系中,O为坐标原点,已知△ACB=90°,A(0,2),C(6,2).D为等腰直角三角形ABC的边BC上一点,且S△ABC=3S△ADC.反比例函数y1=k x(k≠0)的图象经过点D.(1)求反比例函数的解析式;(2)若AB所在直线解析式为y2=ax+b(a≠0),当y1>y2时,求x的取值范围.12.若反比例函数y=k x与一次函数y=2x-4的图象都经过点A(a,2).(1)求反比例函数y=kx的表达式;(2)当反比例函数y=kx的值大于一次函数y=2x-4的值时,求自变量x的取值范围.13.如图,已知直线y=ax+b与双曲线y=k x(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).14.如图,直线y1=mx与双曲线y2=k x交于点A、B,过点A作AP△x轴,垂足P点的坐标是(−2,0),连接BP,且S△ABP=4.(1)求正比例函数y1=mx和反比例函数y2=k x的解析式.(2)当y1<y2时,求x的取值范围.15.如图,一次函数y=kx+b与反比例函数y=4x(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M,N两点.(1)求一次函数的表达式;(2)根据图象直接写出kx+b-4x>0中x的取值范围;(3)求△AOB的面积.16.如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=k x(k≠0)的图象交于A(﹣3,2),B(2,n).(1)求反比例函数y=k x的解析式;(2)求一次函数y=ax+b的解析式;(3)观察图象,直接写出不等式ax+b<kx的解集.答案解析部分1.【答案】(1)解:∵点B(n,﹣6)在直线y=3x﹣5上.∴-6=3n-5,解得:n= −1 3.∴B(−13,-6);∵反比例函数y=k−1x的图象也经过点B(−13,-6),∴k-1=-6×( −13)=2,解得:k=3;(2)解:设直线y=3x﹣5分别与x轴,y轴相交于点C,点D,当y=0时,即3x﹣5=0,x= 5 3,∴OC= 5 3,当x=0时,y=3×0-5=-5,∴OD=5,∵点A(2,m)在直线y=3x﹣5上,∴m=3×2-5=1,即A(2,1).∴S△AOB=S△AOC+S△COD+S△BOD=12×(53×1+53×5+13×5)=356(3)解:由图象可知y1>y2时自变量x的取值范围为:−13<x<0或x>2.2.【答案】(1)解:将B(2,1)代入y= k x,得k=2,∴L的解析式为y= 2 x(2)解:∵点A(a,b)在反比例函数上,∴b= 2 a,∵S△ABC= 12b(2-a)=2,即12b(2−2b)=2,∴b=3,点A的坐标为( 23,3)(3)解:m的取值范围为0<m≤3提示:当点P与点A重合时,把( 23、3)代入y=mx+1,解得m=3∵y=mx+1具有y随x的增大而增大的性质,∴m>0,∴m的取值范围为0<m≤33.【答案】(1)解:∵正比例函数y=k1x的图象与反比例函数y=k2x的图象都经过点P(2,3),∴3=2k1,3=k22,∴k1=32,k2=6,∴正比例函数解析式为y=32x ,反比例函数解析式为y=6x;(2)解:当y=9=6x时,x=23,∴A(23,9),把x=23代入y=32x,得y=1,∴E(23,1),∴AE=9−1=8,∴S△AEP=12⋅AE⋅|x P−x A|=12×8×|2−23|=163;(3)解:由题意得,S△AEM=12⋅AE⋅|x M−x E|=12×8×|m−23|,∴S关于m的解析式为S={4m−83(m>23)−4m+83(m<23).4.【答案】(1)解:点P(0,a),则点M、N的坐标分别为(ma,a)、(na,a),则S△MON=6= 12×MN×OP= 12×(4a- na)×a解得:n=-8(2)解:点M、N的坐标分别为(ma,a)、(na,a),∵PM=PN,则ma=-na,解得:m=-n,若a=5,点M的横坐标为3,则点M(3,5),故m=3×5=15=-n,故m-n=30(3)解:点A(d,0),则点B(d+4,0),点D、C的坐标分别为(d,4)、(d+4,4),设正方形交两个反比例函数于点G、H,则点G、H的坐标分别为(d,- 6d)、(d+4,4d+4),若正方形ABCD与y= mx(m>0、x>0),y=nx(n<0,x<0)都有交点,则HD≥0且CG≥0,即{4+6d≥04−4d+4≥0,且d<0,d+4>0,解得:-3≤d≤ −3 2,故d的范围为:-3≤d≤ −3 2 .5.【答案】(1)解:把A(-3,1)代入y2=mx得m=xy=-3×1=-3,∴反比例函数的解析式为y=−3x.过点A做AD△y轴于D,∵A(-3,1),∴AD=3.∵S△AOB=12OB•AD,∴12OB•3=6,OB=4.∴B(0,4).把A(-3,1).B(0,4)代入y1=kx+b得{−3k+b=1b=4,∴{k=1b=4,.∴一次函数的解析式为y=x+4(2)解:∵在Rt△ABD中,AD=3,BD=BO-OD=4-1=3∴△ABO=45°∴sin△ABO=sin45°=√22(3)解:由{y=−3xy=x+4得{x1=−1y1=3,{x2=−3y2=1.∴C(-1,3).∴当x<-3或-1<x<0时,y2> y1当-3<x<-1时, y 2 > y 16.【答案】(1)解:∵函数y 1=k x的图象过点A(1,4), ∴4=k 1, ∴k=4,即y 1=4x, 又∵点B(m ,-2)在y 1=4x的图象上, ∴m=-2,∴B(-2,-2),又∵一次函数y 2=ax+b 的图象过A ,B 两点,∴{−2a +b =−2a +b =4,解之得{a =2b =2, ∴y 2=2x+2.综上可得y 1=4x,y 2=2x+2. (2)解:设直线AB 交x 轴于点D ,易求D (-1 ,0)设C(x ,0),∵s ΔABC =s ΔADC +s ΔBCD ,∴12y A |x +1|+12|y B ||x +1|=18, 12×4×|x +1|+12×2×|x +1|=18 3|x+1|=18,解得:x=5或x=-7,∴C(5,0)或(-7,0).7.【答案】(1)解:设反比例函数的表达式为 y =k x, 将点 A(2,2) 代入 y =k x中,得 k =4 , ∴反比例函数的表达式为 y =4x;设一次函数的表达式为 y =kx +b ,将点 A(2,2) , B(4,1) 代入 y =kx +b 中,得 {2k +b =24k +b =1, 解得 {k =−12b =3, ∴一次函数的表达式为 y =−12x +3 (2)解:如图,作直线 AB 的平行线,当其与反比例函数的图象只有一个交点 P 时,此时点 P 到直线 AB 的距离最短,设直线 PM 的解析式为 y =−12x +n ,则 4x =−12x +n , 去分母,得 x 2−2nx +8=0 ,由题意得, Δ=0 ,∴4n 2−32=0 ,解得 n 1=−2√2 , n 2=2√2 (不合题意,舍去).∴x 2+4√2x +8=0 ,解得 x 1=x 2=−2√2 ,∴在 y =4x中,当 x =−2√2 时, y =−√2 . ∴点 P 的坐标为 (−2√2,−√2) .8.【答案】(1)解:令反比例函数y=- 8x中x=-2,则y=4, ∴点A 的坐标为(-2,4); 反比例函数y=- 8x 中y=-2,则-2=- 8x,解得:x=4, ∴点B 的坐标为(4,-2). ∵一次函数过A 、B 两点, ∴{4=−2k +b −2=4k +b ,解得: {k =−1b =2, ∴一次函数的解析式为y=-x+2 (2)解:设直线AB 与y 轴交于C , 令为y=-x+2中x=0,则y=2, ∴点C 的坐标为(0,2),∴S △AOB = 12 OC•(x B -x A )= 12×2×[4-(-2)]=6 (3)解:观察函数图象发现: 当x <-2或0<x <4时,一次函数图象在反比例函数图象上方, ∴一次函数的函数值大于反比例函数的函数值时x 的取值范围为x <-2或0<x <4.9.【答案】(1)解:把点 A(2,6) 代入 y =k x, k =2×6=12 , ∴ 反比例函数的解析式为 y =12x, ∵ 将点 A 向右平移2个单位,∴x =4 ,当 x =4 时, y =124=3 , ∴B(4,3) ,设直线 AB 的解析式为 y =mx +n ,由题意可得 {6=2m +n 3=4m +n, 解得 {m =−32n =9, ∴y =−32x +9 ,当 x =0 时, y =9 ,∴C(0,9) ;(2)解:由(1)知 CD =9−5=4 ,∴S ΔABD =S ΔBCD −S ΔACD =12CD ⋅|x B |−12CD ⋅|x A |=12×4×4−12×4×2=4 .10.【答案】(1)解:把(﹣3,﹣1)代入y= k x 得k=3, 则反比例函数的解析式是y= 3x; 把(n ,6)代入y= 3x 得n= 12. 根据题意得: {−3m +b =−112m +b =6 , 解得: {m =2b =5, 则一次函数的解析式是y=2x+5(2)解:在y=2x+5中,令x=0,解得y=5,则S △AOB = 12 ×5×( 12 +3)= 35411.【答案】(1)解:∵A (0,2),C (6,2),∴AC=6,∵△ABC 是等腰直角三角形,∴AC=BC=6,∵S △ABC =3S △ADC ,∴BC=3DC ,∴DC=2,∴D (6,4),∵反比例函数y 1=k x(k≠0)的图象经过点D , ∴k=6×4=24,∴反比例函数的解析式为y 1=24x; (2)解:∵C (6,2),BC=6,∴B (6,8),把点B 、A 的坐标分别代入y 2=ax +b 中,得{6a +b =8b =2, 解得:{a =1b =2, ∴直线AB 的解析式为y 2=x +2,解方程x+2=24x, 整理得:x 2+2x-24=0,解得:x=4或x=-6,∴直线y 2= x+2与反比例函数y 1=24x的图象的交点为(4,6)和(-6,-4), ∴当y 1>y 2时,0<x<4或x<-6.12.【答案】(1)解:将A (a ,2)代入一次函数y=2x-4中得:2=2a-4,即a=3, ∴A (3,2),将x=3,y=2代入反比例解析式得:k=6,则反比例解析式为y= 6x; (2)解:联立两函数解析式得: {y =6x y =2x −4,解得: {x =3y =2 或 {x =−1y =−6 ,即两函数的两交点分别为(3,2),(-1,-6),作出两函数图象,如图所示:则由函数图象得:反比例函数y= 6x的值大于一次函数y=2x-4的值时,自变量x 的取值范围为x <-1或0<x <3.13.【答案】(1)解:∵直线y=ax+b 与双曲线y=k x(x >0)交于A (1,3), ∴k=1×3=3,∴y=3x, ∵B (3,y 2)在反比例函数的图象上,∴y 2=33=1, ∴B (3,1),∵直线y=ax+b 经过A 、B 两点,∴{a +b =33a +b =1解得{a =−1b =4, ∴直线为y=﹣x+4,令y=0,则x=4,∴P (4,0)(2)解:如图,作AD△y 轴于D ,AE△x 轴于E ,BF△x 轴于F ,BG△y 轴于G ,AE 、BG 交于H ,则AD△BG△x 轴,AE△BF△y 轴,∴CD OC =AD OP ,PF PE =BF AE =PB PA, ∵b=y 1+1,AB=BP ,∴1y 1+1=x 16, PF PE =BF AE =12, ∴B (6+x 12,12y 1) ∵A ,B 两点都是反比例函数图象上的点,∴x 1•y 1=6+x 12•12y 1, 解得y 1=2,代入1y 1+1=x 16,解得x 1=2, ∴A (2,2),B (4,1).(3)解:根据(1),(2)中的结果,猜想:x 1,x 2,x 0之间的关系为x 1+x 2=x 0.14.【答案】(1)解:过点B 作BD△AP 于点D ,交y 轴于E ,∵点P 的坐标为(-2,0),∴OP=2,根据题意得点A 、B 关于原点对称,∴BE=DE=OP=2,∴BD=4,又S △ABP =4,∴12AP ⋅4=4, ∴AP=2,∴点A 的坐标为(-2,-2),代入y 1=mx ,得m=1;代入y 2=k x,得k=4,∴正比例函数的解析式为y 1=x ,反比例函数y 2=k x的解析式为y 2=4x ; (2)解:由(1)可知点B 的坐标为(2,2),由图象可知,当x<-2或0<x<2时y 1<y 2.15.【答案】(1)解:∵点A 在反比例函数y = 4x 上,∴4m=4.解得m =1,∴点A 的坐标为(1,4).又∵点B 也在反比例函数y = 4x 上,∴42=n ,解得n =2,∴点B 的坐标为(2,2).又∵点A ,B 在y =kx +b 的图象上,∴{k +b =42k +b =2 解得 {k =−2b =6∴一次函数的表达式为y =-2x +6 (2)解:由图象可得,当 1<x<2 时,直线在双曲线的上方,∴这时 kx +b> 4x,即kx +b - 4x>0 ,∴ x 的取值范围为1<x<2 . (3)解:∵直线y =-2x +6与x 轴的交点为N ,∴点N 的坐标为(3,0).∴S △AOB =S △AON -S △BON = 12 ×3×4- 12×3×2=3. 16.【答案】(1)解:把A (﹣3,2)代入反比例解析式得:k=﹣6,则反比例解析式为 y =−6x(2)解:把B (2,n )代入反比例解析式得:n=﹣3,即B (2,﹣3),把A (﹣3,2)与B (2,﹣3)代入y=ax+b 中得: {−3a +b =22a +b =−3,解得:a=﹣1,b=﹣1,则一次函数解析式为y=﹣x+1 (3)解:∵A (﹣3,2),B (2,﹣3),∴结合图象得:不等式ax+b < k x的解集为﹣3<x <0或x >2。
中考数学每日一练:反比例函数与一次函数的交点问题练习题及答案_2020年综合题版

中考数学每日一练:反比例函数与一次函数的交点问题练习题及答案_2020年综合题版答案答案2020年中考数学:函数_反比例函数_反比例函数与一次函数的交点问题练习题~~第1题~~(2019天水.中考真卷) 如图,一次函数与反比例函数的图象交于、两点,与坐标轴分别交于、 两点.(1) 求一次函数的解析式;(2) 根据图象直接写出中 的取值范围;(3) 求 的面积.考点: 反比例函数与一次函数的交点问题;~~第2题~~(2020郑州.中考模拟) 如图,在平面直角坐标系中,O 为坐标原点,△ABO 的边AB 垂直于x 轴,垂足为点B ,反比例函数y= (x <0)的图象经过AO 的中点C ,交AB 于点D .若点D 的坐标为(﹣4,n ),且AD=3.(1) 求反比例函数y= 的表达式;(2) 求经过C 、D 两点的直线所对应的函数解析式;(3) 设点E 是线段CD 上的动点(不与点C 、D 重合),过点E 且平行y 轴的直线l 与反比例函数的图象交于点F ,求△O EF面积的最大值.考点: 反比例函数与一次函数的交点问题;~~第3题~~(2020余干.中考模拟) 如图,直线y =﹣x+1与反比例函数y =的图象相交于点A 、B ,过点A 作AC ⊥x 轴,垂足为点C (﹣2,0),连接AC 、BC .(1) 求反比例函数的解析式;答案答案答案(2) 求S ;(3) 利用函数图象直接写出关于x 的不等式﹣x+1< 的解集.考点: 反比例函数与一次函数的交点问题;~~第4题~~(2020宁波.中考模拟) 如图,在平面直角坐标系中,直线y=kx+b 与反比例函数y= 的图象交于A (2,m )、B (n ,-1)两点,与y 轴交于点C ,与x 轴交点D ,P 为x 轴负半轴上的一点,连结PB 、PC 。
(1) 求直线AB 的解析式;(2) 若△PBD 的面积为7,求△PDC 的面积。
考点: 反比例函数与一次函数的交点问题;相似三角形的判定与性质;~~第5题~~(2020广西壮族自治区.中考模拟) 如图,一次函数y =kx +b 与反比例函数y = (x>0)的图象交于A (m ,4),B (2,n )两点,与坐标轴分别交于M ,N 两点.(1) 求一次函数的表达式;(2) 根据图象直接写出kx +b - >0中x 的取值范围;(3) 求△AOB 的面积.考点: 反比例函数与一次函数的交点问题;三角形的面积;2020年中考数学:函数_反比例函数_反比例函数与一次函数的交点问题练习题答案1.答案:△A BC2.答案:3.答案:4.答案:5.答案:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案
~~第4题~~ (2019湖州.中考模拟) Rt△ABC在直角坐标系内的位置如图所示,反比例函数 交于点D(4,m),与AB边交于点E(2,n),△BDE的面积为2.
在第一象限内的图象与BC边
(1) 求m与n的数量关系;
(2) 当
时,求反比例函数的解析式和直线AB的解析式;
(3) 设P是线段AB边上的点,在(2)的条件下,是否存在点P,以B、C、P为顶点的三角形与△EDB相似?若存在
与点 、 间的距离之和 始终是一个定值.求此时 的值及定值 .
考点: 反比例函数图象的对称性;反比例函数图象上点的坐标特征;反比例函数与一次函数的交点问题;
答案
~~第3题~~ (2019新华.中考模拟) 如图,直线y=2x+2与x轴,y轴分别交于A,B两点,与反比例函数y= 过M作MH⊥x轴于点H,且AB=BM,点N(a,1)在反比例函数y= (x>0)的图象上。
中考数学每日一练:反比例函数与一次函数的交点问题练习题及答案_2020年
压轴题版
2020年 中 考 数 学 : 函 数 _反 比 例 函 数 _反 比 例 函 数 与 一 次 函 数 的 交 点 问 题 练 习 题
~~第1题~~ (2019兰州.中考模拟) 如图,已知反比例函数y= 的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).
2020年 中 考 数 学 : 函 数 _反 比 例 函 数 _反 比 例 函 数 与 一 次 函 数 的 交 点 问 题 练 习 题 答 案
1.答案:
.
答案
2.答案:
3.答案:
4.答案:
5.答案:
,求出此时点P的坐标;若不存在,请说明理由.
考点: 反比例函数与一次函数的交点问题;相似三角形的判定与性质;
答案
~~第5题~~ (2019吴兴.中考模拟) 如图1,已知A,B两点分别在x轴和y轴的正半轴上,连接AB与反比例函数 两点.
的图象交于C、D
(1) 当OA=6,OB=3,点D的横坐标为2时,则k=, =.
(1) 求n和b的值;
(2) 求△OAB的面积;
(3) 直接写出一次函数值大于反比例函数值的自变量x的取值范围.
考点: 待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;三角形的面积;
答案
~~第2题~~
(2019泰州.中考真卷) 已知一次函数
和反比例函数.ຫໍສະໝຸດ (1) 如图1,若,且函数 、 的图象都经过点
(x>0)的图象交于点M,
(1) 求k的值;
(2) 在x轴的正半轴上存在一点P,使得PM+PN的值最小,求点P的坐标;
(3) 点N关于x轴的对称点为N',把△ABO向右平移m个单位到△A'B'O'的位置,当N'A'+N'B'取得最小值时,请你在横
线上直接写出m的值,m=.
考点: 反比例函数与一次函数的交点问题;
.
①求 , 的值;
②直接写出当
时 的范围;
(2) 如图2,过点
作 轴的平行线 与函数 的图象相交于点 ,与反比例函数
的图象相交于
点.
①若 ;
,直线 与函数 的图象相交点 .当点 、 、 中的一点到另外两点的距离相等时,求
的值
②过点 作 轴的平行线与函数 的图象相交于点 .当
的值取不大于1的任意实数时,点 、 间的距离
(2) 当OA=a,OB=b时,请猜测AC与BD之间的数量关系,并说明理由.
(3) 如图2,以D为顶点且过点O的抛物线分别交函数
的图像和 轴于点E、F,连接CF,设
①若∠AFC=90°,则 的值为多少?
②若∠ACF=90°,且
时,请用含 的代数式表示tan∠BAO的值.
考点: 反比例函数与一次函数的交点问题;二次函数的实际应用-几何问题;锐角三角函数的定义;
