第十一讲 练习题
第十一讲 指数函数(一)
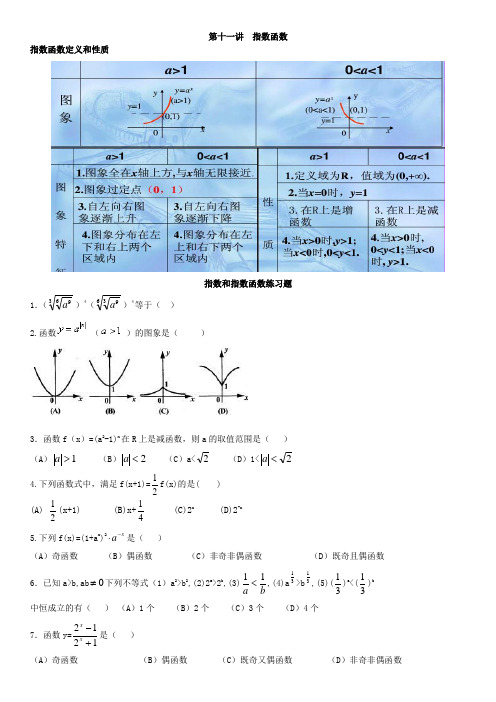
第十一讲 指数函数指数函数定义和性质指数和指数函数练习题1.(369a )4(639a )4等于( ) 2.函数( )的图象是( )3.函数f (x )=(a 2-1)x 在R 上是减函数,则a 的取值范围是( )(A )1>a (B )2<a (C )a<2 (D )1<2<a 4.下列函数式中,满足f(x+1)=21f(x)的是( ) (A) 21(x+1) (B)x+41 (C)2x (D)2-x 5.下列f(x)=(1+a x )2x a -⋅是( )(A )奇函数 (B )偶函数 (C )非奇非偶函数 (D )既奇且偶函数6.已知a>b,ab 0≠下列不等式(1)a 2>b 2,(2)2a >2b ,(3)b a 11<,(4)a 31>b 31,(5)(31)a <(31)b 中恒成立的有( ) (A )1个 (B )2个 (C )3个 (D )4个7.函数y=1212+-x x 是( ) (A )奇函数 (B )偶函数 (C )既奇又偶函数 (D )非奇非偶函数8.函数y=121-x 的值域是( ) (A )(-1,∞) (B )(-,∞0)⋃(0,+∞) (C )(-1,+∞) (D )(-∞,-1)⋃(0,+∞)9.下列关系中正确的是( )(A )(21)32<(51)32<(21)31 (B )(21)31<(21)32<(51)32(C )(51)32<(21)31<(21)32 (D )(51)32<(21)32<(21)3110. 函数()x f x a =(0a >,且1a ≠)对于任意的实数x ,y 都有( ) A.()()()f xy f x f y =B.()()()f xy f x f y =+ C.()()()f x y f x f y += D.()()()f x y f x f y +=+11.下列各式中,正确的是___.(填序号)①12()a -;②13a -=(0)a a =-<;④34())a a b =≠、b 0. 12.当[]1,1-∈x 时函数23)(-=x x f 的值域是( ) [][]55A.,1 B.1,1 C.1, D.0,133⎡⎤⎡⎤--⎢⎥⎢⎥⎣⎦⎣⎦13.函数x a y =在[]1,0上的最大值与最小值的和为3,则a =( ) A.21 B.2 C.4 D.4114.15.设0<a<1,解关于x 的不等式a1322+-x x >a 522-+x x 。
小学语文修辞手法(二)练习题

:第十一讲:修辞手法(二)一、修辞手法——设问和反问【知识简介】【练习】1、看到那数不尽的青松白桦,怎能不马上向四面八方望一望呢?疑问句()反问句()设问句()2、小立又在悄悄地为集体做什么好事呢?疑问句()反问句()设问句()3、老师傅问:“一件手艺,有的三个月就能学会,有的人得三年才能学会。
学三个月和学三年,有什么不同?”“学三个月的,手艺扎根在眼里;学三年的,手艺扎根在心里。
”鲁班回答。
疑问句()反问句()设问句()4、春风又绿江南岸,明月何时照我还?疑问句()反问句()设问句()5、为什么瓜秧开了花不结瓜?原来是岛上没有昆虫,西瓜开了花没授成粉。
疑问句()反问句()设问句()6、你知道我今天为什么这么高兴吗?告诉你吧,我接到了重点中学的录取通知!疑问句()反问句()设问句()7、怎样才是一个合格的小学生毕业生呢?疑问句()反问句()设问句()8、我们怎么能不遵守交通规则呢?疑问句()反问句()设问句()9、是谁创造了人类历史?是我们劳动群众。
疑问句()反问句()设问句()二、修辞手法——反复【知识简介】【练习】抄写下面诗词寻寻觅觅,冷冷清清,凄凄惨惨戚戚。
乍暖还寒时候,最难将息。
三杯两盏淡酒,怎敌他,晚来风急?雁过也,正伤心,却是旧时相识。
满地黄花堆积,憔悴损,如今有谁堪摘?守着窗儿,独自怎生得黑?梧桐更兼细雨,到黄昏,点点滴滴。
这次第,怎一个愁字了得!三、修辞手法——借代【知识简介】【练习】判断下列借代的内容:1、枪杆子里面出政权。
“”借代“”2、我们的时代需要千千万万个雷锋。
“”借代“”3、一队红领巾唱着山歌走下山来。
“”借代“”4、你怎么不把龙井沏上。
“”借代“”5、他一天抽一盒“黄鹤楼”。
“”借代“”四、综合练习1.按要求改写句子。
①难道不是我们劳动群众创造了人类世界吗?改为设问句:_______________________________________________________②前面不远处走来了一队少先队员。
人教版四年级语文下册第十一课蝙蝠和雷达练习题

人教版四年级语文下册第十一课蝙蝠和雷达练习题人教版四年级语文下册第十一课《蝙蝠和雷达》是一篇讲科学知识的课文,介绍了仿生学的应用——人们从蝙蝠身上受到启发,使飞机能安全地夜航。
店铺在此整理了人教版四年级语文下册第十一课《蝙蝠和雷达》练习题,供大家参阅,希望大家在阅读过程中有所收获!人教版四年级语文下册第十一课《蝙蝠和雷达》练习题1一、看拼音,字词语。
fēi élínɡ dānɡ sāi zhù jiē kāi( )( )( )( )yínɡ pínɡ duǒ bì biān fú zhànɡ ài( )( )( )( )二、写出下列词语的近义词。
模仿( )研究( )启示( )敏锐( )灵巧( )避开( )揭开( )障碍( )显示( )反复( )秘密( )配合( )三、选择关联词语填空。
因为……所以…… 不仅……还……不是……而是…… 即使……也……1、蝙蝠( )能在夜里飞行,( )能捕捉飞蛾和蚊子。
2、( )一根极细的电线,它( )能灵巧地避开。
3、蝙蝠在夜里飞行,靠的( )眼睛,( )嘴和耳朵。
4、( )驾驶员从雷达的荧光屏中,能够看清楚前方有没有障碍物,( )飞机在夜里飞行也十分安全。
四、判断下列句子,意思对的打“√”,错的打“×”。
1、“在漆黑的夜里,飞机怎么能安全飞行呢?原来是人们从蝙蝠身上得到了启示。
”这是一个反问句。
( )2、“难道它的眼睛特别敏锐,能在漆黑的夜里看清楚所有的东西吗?”这是一个设问句。
( )3、“你知道蝙蝠在夜里飞行是怎样用嘴巴和耳朵配合起来探路的吗?”这是一个疑问句。
( )五、指出下列各句所用的修辞手法。
1、在漆黑的夜里,飞机怎么能安全飞行呢?原来是人们从蝙蝠身上得到的启示。
( )2、超声波像波浪一样向前推进。
( )3、蝙蝠就像没头苍蝇似的到处乱撞,挂在绳子上的铃铛响个不停。
2020版高考生物大一轮人教习题:第11讲 细胞的有丝分裂及相关实验(Word版含解析)

第11讲细胞的有丝分裂及相关实验课后·分层训练(时间:25分钟满分:100分)1.在一个细胞周期中,以下变化可能发生于同一时期的是()A.DNA分子的复制和染色体数目加倍B.染色单体形成和细胞板的出现C.着丝点的分裂和同源染色体的分离D.核膜的消失和纺锤体的形成解析DNA的复制发生在细胞分裂间期,染色体数目加倍发生在分裂后期,A 错误。
染色单体形成在间期,细胞板出现在末期,B错误。
着丝点分裂在后期,同源染色体分离在减Ⅰ后期,有丝分裂中不发生同源染色体的分离,C错误。
核膜消失和纺锤体形成都在前期,D正确。
答案 D2.下列关于细胞有丝分裂各阶段的描述,正确的是()A.蛋白质合成较旺盛的时期,纺锤体可由中心体发出的星射线或细胞两极发出的纺锤丝形成B.染色体的螺旋化程度达到最高的时期,细胞内不一定有同源染色体但一定有染色单体C.着丝点数目加倍的时期,细胞内全部染色体数与全部DNA数之比为1∶1D.有核膜和核仁的时期,细胞内的DNA聚合酶较为活跃,而RNA聚合酶不活跃解析蛋白质合成较旺盛的时期为间期,而纺锤体形成于前期,A错误;染色体的螺旋化程度达到最高的时期为中期,细胞内一定有染色单体,对于只含有一个染色体组的单倍体生物而言,其细胞的有丝分裂过程无同源染色体,B正确;着丝点数目加倍的时期为后期,细胞核内全部染色体数与全部核DNA数之比为1∶1,但线粒体内还有质DNA,C错误;有核膜和核仁的时期可能是间期或末期,DNA聚合酶较为活跃的时期是间期,D错误。
答案 B3.(2016·四川名校联盟检测)下列关于细胞周期的叙述,正确的是()A.机体内所有的体细胞都处于细胞周期中B.受抗原刺激后的淋巴细胞细胞周期变长C.细胞种类不同,细胞周期持续时间不同D.成熟的生殖细胞产生后立即进入下一个细胞周期解析只有连续进行有丝分裂的细胞才具有细胞周期,已经分化的细胞无细胞周期,A错误;受抗原刺激后的淋巴细胞分裂增殖,细胞周期变短,B错误;细胞种类不同,细胞周期持续时间不同,C正确;成熟的生殖细胞不再分裂,无细胞周期,D错误。
小学二年级奥数下册第十一讲找规律法习题+答案

仔细观察,可发现该数列的第6项同第1项,第7项同第2项,第8项同第3项,…也就是说该数列各项的出现具有周期性,…也就是说该数列各项的出现具有周期性,他们是循环出现他们是循环出现的,一个循环节包含5项.100100÷÷5=20.可见第100项与第5项、第10项一样(项数都能被5整除),即第100项是51234.例2 2 把写上把写上1到100这100个号码的牌子,像下面那样依次分发给四个人,你知道第73号牌子会落到谁的手里?号牌子会落到谁的手里?解:仔细观察,你会发现:解:仔细观察,你会发现:分给小明的牌子号码是1,5,9,1313,…,号码除以,…,号码除以4余1; 分给小英的牌子号码是2,6,1010,,1414,…,号码除以,…,号码除以4余2; 第十一讲 找规律法观察、观察、搜集已知事实,搜集已知事实,搜集已知事实,从中发现具有规律性的线索,从中发现具有规律性的线索,从中发现具有规律性的线索,用以探索未知事用以探索未知事件的奥秘,是人类智力活动的主要内容件的奥秘,是人类智力活动的主要内容. .数学上有很多材料可用以来模拟这种活动、培养学生这方面的能力数学上有很多材料可用以来模拟这种活动、培养学生这方面的能力. . 例1 1 观察数列的前面几项,找出规律,写出该数列的第观察数列的前面几项,找出规律,写出该数列的第100项来?项来? 1234512345,,2345123451,,3451234512,,4512345123,…,…,…解:为了寻找规律,再多写出几项出来,并给以编号:分给小方的牌子号码是3,7,1111,…,号码除以,…,号码除以4余3; 分给小军的牌子号码是4,8,1212,…,号码除以,…,号码除以4余0(整除)(整除). . 因此,试用4除73看看余几?看看余几?7373÷÷4=184=18…余…余…余 1 1可见73号牌会落到小明的手里号牌会落到小明的手里. .这就是运用了如下的规律:这就是运用了如下的规律:用这种规律预测第几号牌子发给谁,用这种规律预测第几号牌子发给谁,是很容易的,是很容易的,请同学们自己再试一试一试. .例3 3 四个小动物换位,开始小鼠、小猴、小兔和小猫分别坐在四个小动物换位,开始小鼠、小猴、小兔和小猫分别坐在1、2、3、4号位子上(如下图所示)号位子上(如下图所示)..第一次它们上下两排换位,第二次左右换位,第三次又上下交换,第四次左右交换位,第三次又上下交换,第四次左右交换..这样一直交换下去,问十次换位后,小兔坐在第几号座位上?位后,小兔坐在第几号座位上?解:为了能找出变化规律,再接着写出几次换位情况,见下图解:为了能找出变化规律,再接着写出几次换位情况,见下图. .盯住小兔的位置进行观察:盯住小兔的位置进行观察:第一次换位后,它到了第1号位;号位;第二次换位后,它到了第2号位;号位;第三次换位后,它到了第4号位;号位;第四次换位后,它到了第3号位;号位;第五次换位后,它又到了第1号位;号位;…可以发现,可以发现,每经过四次换位后,每经过四次换位后,每经过四次换位后,小兔又回到了原来的位置,小兔又回到了原来的位置,小兔又回到了原来的位置,利用这个利用这个规律以及1010÷÷4=24=2…余…余2,可知:,可知:第十次换位后,小兔的座位同第二次换位后的位置一样,小兔的座位同第二次换位后的位置一样,即在第二号即在第二号位.如果再仔细地把换位图连续起来研究研究,如果再仔细地把换位图连续起来研究研究,可以发现,可以发现,随着一次次地交换,交换,小兔的座位按顺时针旋转,小兔的座位按顺时针旋转,小鼠的座位按逆时针旋转,小鼠的座位按逆时针旋转,小猴的座位按顺时针旋转,小猴的座位按顺时针旋转,小猫的座位按逆时针旋转,小猫的座位按逆时针旋转,按这个规律也可以预测任何小动物在交换几次后的座位按这个规律也可以预测任何小动物在交换几次后的座位. .例4 4 从从1开始,每隔两个数写出一个数,得到一列数,求这列数的第100个数是多少?个数是多少?1,4,7,1010,,1313,…,…,…解:解:不难看出,不难看出,不难看出,这是一个等差数列,这是一个等差数列,这是一个等差数列,它的后一项都比相邻的前一项大它的后一项都比相邻的前一项大3,即公差,即公差=3=3=3,还可以发现:,还可以发现:,还可以发现:第2项等于第1项加1个公差即个公差即4=1+14=1+1××3.第3项等于第1项加2个公差即个公差即7=1+27=1+2××3.第4项等于第1项加3个公差即个公差即10=1+310=1+3××3.第5项等于第1项加4个公差即个公差即13=1+413=1+4××3.…可见第n 项等于第1项加(项加(n-1n-1n-1)个公差,即)个公差,即)个公差,即按这个规律,可求出:按这个规律,可求出: 第100项=1+=1+((100-1100-1)×)×)×3=1+993=1+993=1+99××3=298.例5 5 画图游戏先画第一代,一个△,再画第二代,在△下面画出两画图游戏先画第一代,一个△,再画第二代,在△下面画出两条线段,条线段,在一条线段的末端又画一个△,在一条线段的末端又画一个△,在一条线段的末端又画一个△,在另一条的末端画一个○;在另一条的末端画一个○;在另一条的末端画一个○;画第画第三代,三代,在第二代的△下面又画出两条线段,在第二代的△下面又画出两条线段,在第二代的△下面又画出两条线段,一条末端画△,一条末端画△,一条末端画△,另一条末端画另一条末端画○;○;而在第二代的○的下面画一条线,而在第二代的○的下面画一条线,而在第二代的○的下面画一条线,线的末端再画一个△;线的末端再画一个△;线的末端再画一个△;…一直照此…一直照此画下去(见下图),问第十次的△和○共有多少个?解:解:按着画图规则继续画出几代,按着画图规则继续画出几代,按着画图规则继续画出几代,以便于观察,以便于观察,以便于观察,以期从中找出图形的以期从中找出图形的生成规律,见下图生成规律,见下图. .数一数,各代的图形(包括△和○)的个数列成下表:可以发现各代图形个数组成一个数列,可以发现各代图形个数组成一个数列,这个数列的生成规律是,这个数列的生成规律是,从第三项起每一项都是前面两项之和三项起每一项都是前面两项之和..按此规律接着把数列写下去,可得出第十代的△和○共有89个(见下表):个(见下表):这就是著名的裴波那契数列这就是著名的裴波那契数列..裴波那契是意大利的数学家,他生活在距今大约七百多年以前的时代距今大约七百多年以前的时代. .例6 6 如下图所示,如下图所示,如下图所示,55个大小不等的中心有孔的圆盘,个大小不等的中心有孔的圆盘,按大的在下、按大的在下、按大的在下、小小的在上的次序套在木桩上构成了一座圆盘塔的在上的次序套在木桩上构成了一座圆盘塔..现在要把这座圆盘塔移到另一个木桩上一个木桩上..规定移动时要遵守一个条件,每搬一次只许拿一个圆盘而且任何时候大圆盘都不能压住小圆盘任何时候大圆盘都不能压住小圆盘..假如还有第三个木桩可作临时存放圆盘之用盘之用..问把这5个圆盘全部移到另一个木桩上至少需要搬动多少次?(下图所示)(下图所示)解:先从最简单情形试起解:先从最简单情形试起. .① 仅有一个圆盘时,显然只需搬动一次(见下页图)仅有一个圆盘时,显然只需搬动一次(见下页图). .②当有两个圆盘时,只需搬动3次(见下图)次(见下图). .③当有三个圆盘时,需要搬动7次(见下页图)次(见下页图). .对于有更多圆盘的情况可由这个公式算出来对于有更多圆盘的情况可由这个公式算出来. .进一步进行考察,并联想到另一个数列:若把n 个圆盘搬动的次数写成an an,把两个表对照后,,把两个表对照后,,把两个表对照后, 总结,总结,找规律找规律:①当仅有一个圆盘时,只需搬1次.②当有两个圆盘,上面的小圆盘先要搬到临时桩上,上面的小圆盘先要搬到临时桩上,等大圆盘搬到中等大圆盘搬到中间桩后,小圆盘还得再搬回来到大圆盘上间桩后,小圆盘还得再搬回来到大圆盘上..所以小的要搬两次,下面的大盘要搬1次.这样搬到两个圆盘需3次.③当有三个圆盘时,必须先要把上面的两个小的圆盘搬到临时桩上,见上图中的(见上图中的(11)~()~(33).由前面可知,这需要搬动3次.然后把最下层的最大圆盘搬一次到中间桩上,见图(最大圆盘搬一次到中间桩上,见图(44),之后再把上面的两个搬到中间桩上,这又需搬3次,见图中(次,见图中(55)~()~(77).所以共搬动2×3+1=7次.④推论,当有4个圆盘时,就需要先把上面的3个圆盘搬到临时桩上,需要7次,然后把下面的大圆盘搬到中间桩上(1次),之后再把临时桩上的3个圆盘搬到中间桩上,这又需要7次,所以共需搬动2×7+1=15次.⑤可见当有5个圆盘时,要把它按规定搬到中间桩上去共需要:2×15+1=31次.这样也可以写出一个一般的公式(叫递推公式)可得出可得出有了这个公式后直接把圆盘数代入计算就行了,不必再像前一个公式那样进行递推了那样进行递推了. .习题十一1.1.先计算下面的前几个算式,找出规律,再继续往下写出一些算式:先计算下面的前几个算式,找出规律,再继续往下写出一些算式: ①1×9+2= 9+2= ②②9×9+7=1212××9+3= 989+3= 98××9+6=123123××9+4= 9879+4= 987××9+5=12341234××9+59+5== 9876 9876××9+4=… …2.2.先计算下面的奇妙算式,找出规律,再继续写出一些算式:先计算下面的奇妙算式,找出规律,再继续写出一些算式:19+919+9××9=118+98118+98××9=1117+9871117+987××9=11116+987611116+9876××9=111115+98765111115+98765××9=…3.3.先计算下面的前几个算式,找出规律,再继续写出一些算式:先计算下面的前几个算式,找出规律,再继续写出一些算式:1×1=1111××11=111111××111=11111111××1111=1111111111××11111=…4.4.有一列数是有一列数是2、9、8、2、…,从第三个数起,每一个数都是它前面的两个数相乘积的个位数字(比如第三个数8就是2×9=18的个位数字).问这一列数的第100个数是几?个数是几?5.5.如果全体自然数按下表进行排列,那么数如果全体自然数按下表进行排列,那么数1000应在哪个字母下面?面?6.6.如果自然数如下图所示排成四列,问如果自然数如下图所示排成四列,问101在哪个字母下面?在哪个字母下面?7.37.3××3的末位数字是9,3×3×3的末位数是7,3×3×3×3的末位数字是1.1.求求35个3相乘的结果的末位数字是几?相乘的结果的末位数字是几?习题十一解答1.1.①①1×9+2=111212××9+3=111123123××9+4=111112341234××9+5=111111234512345××9+6=111111 123456123456××9+7=1111111 12345671234567××9+8=11111111 1234567812345678××9+9=111111111. ②9×9+7=889898××9+6=888987987××9+5=8888 98769876××9+4=88888 9876598765××9+3=888888 987654987654××9+2=8888888 98765439876543××9+1=88888888.2.19+92.19+9××9=100 118+98118+98××9=1000 1117+9871117+987××9=10000 11116+987611116+9876××9=100000 111115+98765111115+98765××9=1000000 1111114+9876541111114+987654××9=10000000 11111113+987654311111113+9876543××9=100000000 111111112+98765432111111112+98765432××9=1000000000 1111111111+9876543211111111111+987654321××9= 10000000000.3.1×1=11111××11=121111111××111=1232111111111××1111=12343211111111111××11111=123454321111111111111××111111=1234565432111111111111111××1111111=12345676543211111111111111111××11111111=123456787654321111111111111111111××111111111=123456789876543214.4.解:解:按数列的生成规律再多写出一些数来,再仔细观察,找出规律: 2、9、8、2、6、2、2、4、8、2、6、2、2、4、8、2、6、2、2、4、…、… 可见,除最前面的两个数2和9以外,以外,88、2、6、2、2、4这六个数依次重复出现因此,可利用这个规律,按下面的方法找出第100个数出来:来:100-2=98100-2=98,,9898÷÷6=166=16……2.即第100个数与这六个数的第2个数相同,即第100个数是2.5.5.解:不难发现,每个字母下面的数除以解:不难发现,每个字母下面的数除以7的余数都是相同的的余数都是相同的..如第1列的三个数1、8和1515,除以,除以7时的余数都是1;第2列的三个数2、9和1616,除以,除以7时的余数都是2;第3列的三个数3、10和1717,除以,除以7的余数都是3;….利用这个规律,可求出第1000个自然数在哪个字母下面:10001000÷÷7=142142 (6)所以1000在字母F 的下面的下面. .6.6.解:可以这样找出排列的规律性:全体自然数依次循环排列在解:可以这样找出排列的规律性:全体自然数依次循环排列在A 、B 、C 、D 、D 、C 、B 、A 八个字母的下面,即八个字母的下面,即。
语法第十一讲名代数冠练习(III)
21.-Who is singing in the classroom, Linda?
-I think
may be Susan.
A.she
B. it
C. this
D. he
Thank you!
感谢观看
单击此处添加文本
A. nine-thousand-words
B. nine-thousands-words
C. nine-thousand-word
D. nine-thousands-word
4.They saw a lot of _____ on the farm.
A. deers and sheeps
B. deer and sheeps
A. a friend of my father
B. a friend of my father’s
C. my father friend
D. my father friend’s
9.They are not _____ but _____.
10.You can’t reach my hometown by plane, but there are plenty of
— is OK. I'm free today and tomorrow.
A.Either
B. Neither C. Both are D. None
19.I like playing _____ football and my sister likes playing _____ guitar.
A. /; the D. the; the
B. a; a
C. the; /
20.-This skirt is much too large for me. Could you show me one?
人教版五年级数学下册第11讲通分、分数与小数的互化专题精讲练习试题及答案

【专题讲义】人教版五年级数学下册第11讲通分、分数与小数的互化专题精讲(学生版)知识要点梳理页1考点11.最小公倍数:几个数公有的倍数叫做这几个数的公倍数。
其中最小的一个叫做这几个数的最小公倍数。
2.求最小公倍数的方法:(1)列举法:分别写出两个数各自的倍数,再从中找出最小公倍数。
(2)筛选法:先写出两个数中较大数的倍数,然后从这些数中从小到大圈出较小数的倍数,第一个圈出的数就是它们的最小公倍数。
(3)分解质因数法:分别把两个数分解质因数,公有的质因数对齐写,特有的质因数单独写,然后,公有的质因数取一个,特有的全部取出来,把它们连乘,所得的积就是最小公倍数。
(4)短除法:用两个数公有的质因数按从小到大的顺序依次作为除数连续取除这两个数,一直除到所得的商只有公因数1为止,然后把所有的除数和最后所得的商相乘,所得的积就是最小公倍数。
3.求最大公倍数的特殊情况4.两个数公倍数与最小公倍数的关系:两个数的公倍数一定是它们最小公倍数的倍数。
页2考点2 求两个数最小公倍数的实际应用考点3 通分:把异分母分数分别化成和原来分数相等的同分母分数。
通分的方法:通分时用原分数的最小公倍数做公分母,然后把每个分数都化成用这个最小公倍数做分母的分数。
分数大小的比较方法:(1)分母相同的两个分数相比较,分子大的分数大。
(2)分子相同的两个分数相比较,分母小的分数大。
考点4 分数和小数的互化:1.小数化分数,原来是几位小数,就在1的后面写几个0作为分母,把原来的小数去掉小数点作为分子,化成分数后,能约分的要约分。
2.分数化小数(1)分母是10,100,1000 ,…的分数化小数,可以直接去掉分母,看1后面有几个0,就在分子中从后一位起向左数出几位,点上小数点。
(2)分母是其它的数,用分子除以分母,如果分子除分母除不尽,要根据需要按四舍五入法保留几位小数。
页3页 4(一)最小公倍数 例1.(1)最小的合数与最大的一位数的最小公倍数是( )。
(生物)第11讲 种群、群落与生态系统—2021届九年级中考科学(华东师大版)复习习题训练

第11讲种群、群落与生态系统1.地球上所有大熊猫共同组成了一个(B)A.个体B.种群C.群落D.生态系统2.(2020,开封)下列说法中,能够被看做一个生态系统的是(D)A.一个池塘中的植物、动物和微生物B.一片麦地里的空气、土壤、阳光等环境因素C.一片树林中的树木、小草及空气D.一片草地上的所有生物和环境因素3.(2019,天水)生物既能影响环境,又能适应环境。
下列属于生物适应环境的实例是(D)A.大树底下好乘凉B.绿色植物能够更新空气C.森林可保持水土D.仙人掌的叶特化为刺4.(2020,开封)某生物兴趣小组的同学用河水、池泥、水藻、植食性小鱼、广口瓶、凡士林等材料制作了一个生态瓶(如图所示)。
下列对生态瓶的分析错误的是(B)A.该生态瓶就是一个微型生态系统B.该生态瓶中有一条食物链:水草→小鱼→细菌C.若河水被污染,一段时间后小鱼体内污染物含量最多D.该生态瓶中的能量转变顺序是:光能→化学能→热能第4题图第5题图5.对如图食物网的分析,错误的是(B)A.要构成一个完整的生态系统,除了图中所示成分外,还需加入的成分是分解者和非生物环境B.该食物网共有4条食物链C.在“农作物→鼠→蛇”这条食物链中,若大量捕捉蛇,鼠的数量会先增多后减少D.该食物网中最长的食物链是:农作物→昆虫→蜘蛛→青蛙→蛇6.(2020,长沙)《齐民要术》是我国古代的农业百科全书,对世界农业科学史产生了重要的影响。
其中对菜地的管理有“有草锄之”的论述。
种菜要锄草,因为杂草与蔬菜之间的关系是(A) A.竞争B.合作C.寄生D.共生7.(2019,咸阳)如图是某生态系统示意图,据图分析下列说法错误的是(A)A.图中的生物构成了食物链和食物网B.②→③→④构成一条食物链C.③、④是消费者,④体内毒素富集最多D.该生态系统的自动调节能力是有限的8.(2020,郴州)在一生态系统中,能构成食物链的4种生物的相对数量大致如图。
下列说法正确的是(B)A.该食物链能量的最终来源是②B.“②→①→④→③”可以表示一条食物链C.当①的数量大量减少时,短期内对④没有直接影响D.如果有难以分解的有毒物质进入该食物链,那么③体内有毒物质积累最少9.下列关于人类活动对生物圈影响的说法中,正确的是(D)A.资源和环境问题就是指环境污染问题B.人类活动对环境造成的破坏都是可以修复的C.生物圈中的资源是取之不尽,用之不竭的D.为了人类和生物圈的可持续发展,必须控制人口的增长10.(2020,荆门)生物圈中,生物与环境的关系主要有:生物影响环境,生物适应环境,环境影响生物等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一讲练习题一、概念解释1.学习 2.接受学习 3.发现学习 4.陈述性知识 5.程序性知识 6.学习策略1.学习:目前教育心理学界对于学习概念的理解主要有这样三种:一种是广义的学习概念。
认为学习是人和动物共有的一种心理现象,它集中表现为通过实践或者练习而获得,由经验而引起的比较持久的心理和行为变化的过程。
另一种是次广义的学习概念,专指人类的学习。
其这定义为“在社会生活实践中,以语言为中介,自觉地、积极主动地掌握社会和个体经验的过程。
”第三种是狭义的学习概念。
即指在校学生的学习。
学生的学习是在教师的指导下,有目的、有计划、有组织、有系统地进行的,是在较短的时间内接受前人所积累的文化科学知识,并以此来充实自己的过程。
2.接受学习:指人类个体经验的获得,来源于学习活动中,主体对他人经验的接受,把别人发现的经验经过其掌握、占有或吸收,转化成自己的经验。
3.发现学习:就是通过学习者的独立学习,独立思考,自行发现知识,掌握原理原则。
发现,并不局限于寻求人类尚未知晓的事物。
4.陈述性知识:也叫“描述性知识”它是指个人具有有意识的提取线索,而能直接加以回忆和陈述的知识。
5.程序性知识:是个人没有有意识提取线索,只能借助某种作业形式间接推论其存在的知识。
6.学习策略:就是学习者为了提高学习的效果和效率,有目的、有意识地制定的有关学习过程的复杂方案。
二、单项选择题(在每小题给出的四个选项中,选出一项最符合题目要求的选项)1.小学生认知发展的特点之外的现象是(D )A.注意的稳定性较差 B.注意的范围小 C.注意的分配能力不强 D.机械记忆仍不占主要地位2.梅耶则提出了对学习的三种类型的分类办法,下列哪项没有涉及(D)A.语义性学习B.程序性学习C.策略性学习D.意义学习3.反映中学生个性发展特点的主要品质是(C)A.自我为中心的性格倾向逐步减弱B.缺乏适当的自控能力C.自我意识的发展从具体的、片面的向抽象的、较为全面的认识过渡D.独立批判性思维增强三、填空题1.奥苏伯尔将学习分为__机械学习_______和___意义学习______。
2.陈述性知识的学习可以分为__习得阶段_______、_巩固与转化阶段________和___提取应用阶段______ 三个阶段。
3.动作技能的构成包括_动作或动作组________、__体能_______和___认知能力______ 三种成分。
四、判断正误1.接受学习是儿童青少年的主要学习方式。
(错误)2.复述是短时记忆的信息进入长时记忆的必要条件。
(错误)3.进入青春期后,中学生自我意识迅速发展,性心理的影响日益增强,出现创造力的高峰,情感丰富、充满活力。
(正确)五、简答题1.简述学习的实质和主要类型。
答:传统的行为主义学习理论强调学习的本质是刺激与反应之间的联系,学习重在强化训练。
当代认知理论认为,学习的实质就是获得符号性的表征或结构、并应用这些表征或结构的过程。
学习更多的是发生在学习者个人内部的一种活动。
建构主义者强调,学习活动本质是主体的建构活动,需要个体的积极参与实践,与他人、环境等相互作用的过程,是形成参与实践活动的能力、提高社会化水平的过程。
学习更多的是发生在社会环境中的一种活动。
哲学界认为,哲学界提出,学习的本质是人类个体的自我意识与自我超越活动。
伽德默尔说过:教育哲学:学习是人类在认识与实践过程中获取经验和知识,掌握客观规律,使身心获得发展的社会活动(桑新民,2005)总的来讲,目前学术界对学习实质的认识,普遍强调学习中个体的自觉能动作用,注重学习者的主动建构。
越来越逼近对学习实质问题的深层理解。
当前国外学习理论各派别的共同倾向是,心理学家们始终不懈地在寻找探析学习这种现象的新方式。
由于各学者的观点、视野和研究方法各不相同,因而形成了各种学习理论的流派。
目前国外学者对学习的分类。
美国心理学家索里(1983)把学习类型分为五种:1、联想性学习(经典性条件作用);2、(尝试学习)工具性条件作用;3、模仿性学习;4、顿悟性学习;5、含有推理的学习。
认知心理学家加涅则将学习划分为:言语信息、智慧技能、动作技能、态度。
其中智慧技能的学习中分别为:1、连锁学习;2、辨别学习;3、具体概念的学习;4、定义概念的学习;5、规则的学习;6、高级规则的学习(相当于解决问题)。
奥苏伯尔将学习分为机械学习、意义学习,而后者又分为接受学习和发现学习。
安德森(1983)将知识学习划分为两种:陈述性知识和程序性知识学习。
梅耶则提出了语义性学习、程序性学习、策略性学习这样三种类型的分类办法。
斯皮罗将知识划分“结构良好的知识”与“结构不良的知识”这样两种类型。
2.试述布鲁纳的认知学习理论要点及意义。
答:布鲁纳主要研究有机体在知觉与思维方面的认知学习,他把认知结构称为有机体感知和概括外部世界的一般方式。
布鲁纳始终认为,学校教育与实验室研究猫、狗、小白鼠受刺激后作出的行为反应是截然不同的两回事,他强调学校教学的主要任务就是要主动地把学习者旧的认知结构置换成新的,促成个体能够用新的认知方式来感知周围世界。
(1)重视学科基本结构的掌握。
布鲁纳强调“不论我们选教什么学科,务必使学生理解该学科的基本结构”。
所谓“基本”,就是“具有既广泛而又有强有力的适用性”,学科的基本结构包括基本概念、原理和规律,也就是每科教学要着重教给学生这“三基”。
布鲁纳的认知结构教学理论深受皮亚杰发生认识论的影响,他认为认知结构是通过同化和顺应及其相互间的平衡而形成的。
但他也不完全同意皮亚杰的观点,皮亚杰认为认知结构是在其他外界作用下形成发展起来的,而布鲁纳则反复强调认知结构对外的张力,认为认知结构是个体拿来认识周围世界的工具,它可以在不断的使用中自发地完善起来,学校的教学工作主要是帮助学生掌握基础学科的知识,并以此为同化点来完成对知识结构的更新,促使他们运用新的认知结构来完成对周围世界的感知,这就是有机体智慧生长的过程。
因此,布鲁纳主张教给学科的基本结构,主要是让学生掌握概括性程度更高的概念或一般原理,以有利于后继新知识的同化和顺应。
(2)提倡有效学习方法的形成。
在布鲁纳看来,人类具有对于不同事物进行分类的能力,人的学习其实就是按照知识的不同类别把刚学习的内容纳入到以前学习所形成的心理框架(或现实的模式)中,有效地形成学习者知识体系的过程。
布鲁纳认为,人类的知觉过程也就是对客观事物不断进行归类的过程,所以,他提倡教师在帮助学习者学习的过程中,不仅要提供必要的信息,而且要教会学生掌握并综合运用对客观事物归类的方法。
他认为,学习者的探究实际上并不是发现对世界上各种事件分类的方式,而是创建分类的方式,而在具体的学习过程中,这些相关的类别就构成了编码系统。
编码系统是人们对所学知识加以分组和组合的方式,它在人类的不断的学习中进行着持续的变化和重组。
在布鲁纳看来,知识迁移实际上就是学习者将已经掌握的编码系统应用于其他新的信息,从而有效地掌握新信息的过程。
因此,教育工作者在教授新知识时,客观地了解学习者已有的编码系统是非常重要的。
(3)强调基础学科的早期教学。
布鲁纳有句名言──“任何学科的基础知识都可以用某种形式教给任何年龄的任何人”,因此主张将基础知识下放到较低的年级教学,他认为任何学科的最基本的观念是既简单又强有力的,教师如果能够根据各门学科的基本概念按照儿童能够接受的方式开展教学的话,就能够帮助学生缩小“初级”知识和“高级”知识之间的距离,有效地促进知识之间的迁移,引导学生早期智慧的开发。
他认为,加强基础学科的早期教学,让学生理解基础学科的原理,向儿童提供挑战性但是适合的机会使其步步向前,有助于儿童在学习的早期就形成以后进一步学习更高级知识的同化点。
布鲁纳列举了物理学和数学学习中的例子来进一步说明如果儿童能早一点儿懂得学科学习的基本原理的话,就能帮助他们更容易地完成学科知识的学习,他把这种对学科基本原理的领会和掌握称为通向“训练迁移”的大道,其意义在于不仅能够帮助儿童理解当前学习所指向的特定事物,而且“能促使他们理解可能遇见的其他类似的事物”。
(4)主张学生的发现学习。
所谓发现是指学习者独自遵循他自己特有的认识程序亲自获取知识的一切方式。
布鲁纳反复强调教学是要促进学生智慧或认知的生长,他认为,“教育工作者的任务是要把知识转换成一种适应正在发展着的学生的形式,以表征系统发展的顺序,作为教学设计的模式”。
由此,他提倡教师在教学中要使用发现学习的方法。
使用发现法应遵循六个步骤:提出和明确学生感兴趣的问题;使学生体验到对问题的某种程度的不确定性;提供解决问题的多种可能的假设;协助学生收集可供下断语的资料;组织学生审查有关资料,得出应有的结论;引导学生用分析思维去证实结论。
布鲁纳之所以强调在教学中要重视学生的发现学习,原因在于他通过比较研究发现学习和接受学习,看到发现学习有以下几个比较明显的优点。
第一,发现学习不仅强调对学习结果的存储,而且它还重视学习者在学习中以有意义的方式组织知识,因而学习者对知识掌握的牢固程度要高。
第二,发现学习强调学习者内部学习动机的激发,要求学习者在教师所提供的教学信息面前,自己探索解决问题的模型,所以实践表明发现学习更加容易激发学习者的智慧潜能。
第三,发现学习强调培养学生的直觉思维能力,注重在学习的过程中让学习者运用假设去推测关系,应用自己的能力去解决问题或发现新事物,因而发现学习在一定程度上可以有效提升学习者发现问题、解决问题的能力。
第四,在发现学习的过程中,教师与学生处于合作状态,此时的学生就不再是静坐的听众或观众了,他们主动合作,投入教与学的互动中,在不断的探究中获得新的信息,从而大大提高学生学习的主动性。
3.简述陈述性与程序性知识的表征及类型?答:(一)陈述性知识的表征命题表征:命题是表达判断的语言形式。
具体由一个简单的句子来表达。
例如:大学一年级的学生在军训。
命题网络表征:若干命题彼此联系组成命题网络。
例如:平时严肃的张老师表扬了在学习中取得进步的李华(二)程序性知识的表征1、产生式:IF……THEN……IF 是条件项,THEN是反应项。
一个产生式就是一个IF-THEN语句。
2、产生式系统:前一产生式的反应为后一产生式的发生提供了条件时,互相联系的产生式构成产生式系统。
六、论述与案例解析题1.目前“中考”和高考命题中出现“偏、难、怪”趋势,用学习理论分析评价其合理性与应对策略。
近几年中考数学命题规律实数是以一些容易混淆,容易出错,概念性的知识点为考点(如:相反数、绝对值、倒数、科学记数法、实数的简单计算)。
而科学记数法、实数的简单计算是历年考试的热点。
以容易题的身份出现,有时作为数式探索性试题出现(如:08年的第16题--数字规律探究)。
方程与方程组体现它是数学的基础工具。
