Matlab与统计分析
Matlab第十一讲--数据的统计分析
输入：name——概率分布类型、P（概率）——数据向 量、A——分布参数 输出：Y——逆累积分布向量
name同前
计算均值为0，方差为1的正态分布， x = icdf(‘norm',0.1:0.2:0.9,0,1)
Matlab相关命令介绍
Matlab相关命令介绍
mle 系列函数：参数估计
[phat,pci]=mle(‘name’,X,alpha)
load 从matlab数据文件中载入数据
S=load('数据文件名') 如果数据格式是XXXX.mat ，可以直接 load XXXX; 如果文本格式XXXX.txt，也可以用load载入，load 'XXXX.txt'; 另外文本格式也可以通过Import data转换成.mat格式， matlab默认处理.mat格式数据！
name+stat 系列函数：均值与方差函数
数字特征的相关函数
var 方差
1 n 2 2 var( X ) s ( xi X ) n 1 i 1
%若X为向量，则返回向量的样本方差。A为矩阵，返回A的列向 量的样本方差构成的行向量。 std 标准差
n n
1 1 2 2 ( xi X ) 或者 n ( xi X ) n 1 i 1 i 1
Matlab相关命令介绍
name+rnd 系列函数：随机数发生函数 random(‘name’,A1,A2,A3,m,n) %(通用函数）
normrnd(1:6,1./(1:6)) normrnd([1 2 3;4 5 6],0.1,2,3) %mu为均值矩阵 normrnd(10,0.5,[2,3]) %mu为10，sigma为0.5的2 行3列个正态随机数 y=random('norm',2,0.3,3,4) %产生12（3行4列） 个均值为2，标准差为0.3的正态分布随机数
matlab 统计浮点运算
在MATLAB中进行浮点运算统计，可以使用MATLAB内置的函数和工具。
以下是一些常用的函数和工具：
1. `flops`函数：用于计算一个操作所需的浮点运算次数。
例如，`flops(A*B)`将计算矩阵A和B相乘所需的浮点运算次数。
2. `profile`函数：用于分析MATLAB代码的执行时间，包括浮点运算次数。
使用`profile on`开启分析，然后运行代码，最后使用`profile off`关闭分析。
在分析结果中，可以查看每个函数的执行时间和浮点运算次数。
3. `timeit`函数：用于测量MATLAB代码的执行时间。
使用`timeit(func)`测量函数func的执行时间，包括浮点运算次数。
4. `tic`和`toc`函数：用于测量代码段的执行时间。
使用`tic`开始计时，然后在代码段结束后使用`toc`结束计时。
计时结果包括浮点运算次数。
这些函数和工具可以帮助您分析和优化MATLAB代码中的浮点运算性能。
matlab统计种类
matlab统计种类Matlab是一种用于数值计算和数据可视化的高级编程语言和环境。
它在科学研究、数据分析和工程设计方面都有广泛的应用。
在数据统计方面，Matlab提供了多种用于统计分析、数据处理和模型建立的函数和工具箱。
下面将介绍一些常用的Matlab统计函数和工具箱。
1. 基本统计功能：Matlab提供了一系列基本的统计计算函数，如平均数、标准差、方差、中位数等。
这些函数可以直接应用于数据向量或矩阵。
2. 概率分布函数：Matlab提供了多种概率分布函数，如正态分布、二项分布、泊松分布等。
这些函数可用于生成服从指定分布的随机数，或计算概率密度函数和累积分布函数。
3. 统计图表：Matlab内置的绘图函数可以用于创建各种统计图表，如直方图、散点图、箱线图等。
这些图表可用于数据的可视化和分析。
4. 回归分析：Matlab提供了回归分析函数和工具箱，可用于拟合线性或非线性回归模型。
这些函数可用于评估变量之间的关系，并预测未来的观测值。
5. 方差分析：Matlab提供了方差分析函数和工具箱，可用于比较多个组别之间的均值差异。
方差分析可用于检验因素对观测值之间差异的显著性。
6. 非参数统计：Matlab提供了多种非参数统计函数和工具箱，如Mann-Whitney U检验、Wilcoxon符号秩检验等。
非参数统计方法可应用于不满足正态分布假设的数据。
7. 时间序列分析：Matlab提供了时间序列分析函数和工具箱，可用于模型拟合、趋势分析、季节性调整等。
时间序列分析可用于预测未来的观测值或分析时间序列数据的波动性。
8. 多元分析：Matlab提供了多元分析函数和工具箱，如主成分分析、因子分析、聚类分析等。
多元分析可用于降维、数据压缩和数据分类。
9. 假设检验：Matlab提供了多种假设检验函数和工具箱，可用于验证统计推断的显著性。
常见的假设检验方法包括t检验、卡方检验、F检验等。
10. 贝叶斯统计：Matlab提供了贝叶斯统计函数和工具箱，可用于贝叶斯推断和模型选择。
MATLAB数据分析方法
MATLAB数据分析方法
MATLAB是一种强大的数据分析工具，它提供了丰富的函数和工具箱，可以帮助用户进行各种数据处理和分析。
在本文中，我们将介绍一些常用的MATLAB 数据分析方法，包括数据可视化、统计分析、机器学习等内容。
首先，数据可视化是数据分析的重要环节之一。
MATLAB提供了丰富的绘图函数，可以用来绘制各种类型的图表，如折线图、散点图、柱状图等。
通过可视化数据，我们可以更直观地了解数据的分布规律、趋势变化和异常情况，从而为后续的分析工作提供重要参考。
其次，统计分析是数据分析的核心内容之一。
MATLAB中有许多统计分析的函数和工具箱，可以用来进行描述性统计、假设检验、方差分析等分析。
通过统计分析，我们可以对数据的分布特征、相关性、差异性等进行深入分析，从而揭示数据背后的规律和规律。
此外，机器学习在数据分析中也扮演着重要的角色。
MATLAB提供了丰富的机器学习工具箱，包括分类、回归、聚类、降维等算法，可以帮助用户构建和训练机器学习模型，从而实现对数据的自动化分析和预测。
机器学习的应用领域非常广泛，包括金融、医疗、电商等领域，可以帮助用户挖掘数据中的潜在价值，为决策提供支持。
总之，MATLAB是一种非常强大的数据分析工具，它提供了丰富的函数和工具箱，可以帮助用户进行各种数据处理和分析。
通过数据可视化、统计分析、机器学习等方法，我们可以更好地理解数据，揭示数据背后的规律和规律，为决策提供支持。
希望本文介绍的MATLAB数据分析方法对您有所帮助，谢谢阅读！。
Matlab在概率与数理统计分析中的运用
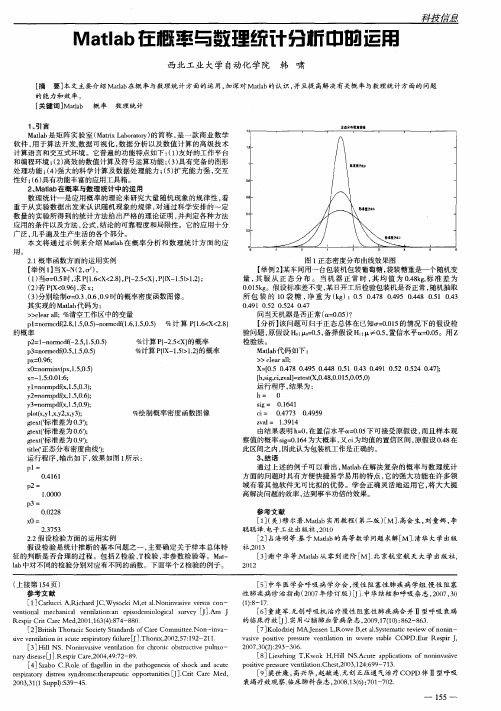
ｘ ０ ＝ ｎ ｏ ｒ ｍｉ ｎ ｖ （ ｐ ｘ ， １ ． ５ ， ０ ． ５ ）
ｘ ＝一１ ． ５ ： ０． ０１ ： ６ ：
科技信息
Ｍａ ｔ ｌ ａ ｂ在概 率与数理 Nhomakorabea计 分析 【 ｌ 】 明 运用
西北 工业 大 学 自动 化 学院 韩 啸
［ 摘 要］ 本文主要介绍 Ｍａ ｔ ｌ ａ ｂ 在概 率与数 理统计方 面的运 用 ， 加 深对 Ｍａ ｔ ｌ ａ ｂ 的认识 ， 并且提 高解决有 关概率 与数理 统计方面的 问题 的能力和效率 。 ［ 关键词］ Ｍａ ｔ ｌ ａ ｂ 概率 数理统计
１ 、 引言
Ｍａ ｔ ｌ ａ ｂ 是 矩 阵实验 室 （ Ｍａ ｔ ｉ ｒ ｘ Ｌ ａ ｂ ｏ ｒ ａ ｔ ｏ ｒ ｙ ） 的简称 ， 是 一款 商业数 学 软件， 用 于算法 开发， 数据 可视化 ， 数据分 析 以及数 值计算 的高级技 术 计算语 言和交互式环境 。它普遍 的功能特点如下 ： （ １ ） 友好 的工作平台 和编程环 境 ； （ ２ ） 高效 的数值计算及符号 运算功能 ； （ ３ ） 具有完备 的图形 处理 功能 ； （ ４ ） 强大 的科学 计算及数据 处理能力 ； （ ５ ） 扩充 能力强 ， 交 互 性好 ； （ ６ ） 具有 功能丰富的应用工具箱。 ２ 、 Ｍａ ｔ ｌ ａ ｂ 在概率与数理统计 中的运用 数 理统计一 是应用概 率的理论来 研究大量 随机现象 的规律性 ， 着 重 于从 实验数 据出发来认 识随机现象 的规律 ， 对 通过科学安 排 的一定 数量 的实验所 得到 的统计 方法给 出严 格的理论证 明 ， 并判定 各种方法 应用 的条 件以及方法 ， 公式 ， 结论 的可靠程 度和局限性 。它 的应用 十分 广泛 ， 几乎遍及 生产生活的各个 部分。 本 文将 通过示 例来 介绍 Ｍ ａ ｔ ｌ ａ ｂ 在概 率分 析和数 理统 计方 面的应 用。 ２ ． １ 概率 函数方 面的运用实例
使用MATLAB进行数据分析的基本步骤
使用MATLAB进行数据分析的基本步骤数据分析是现代科学研究和工程实践中不可或缺的一环。
随着大数据时代的到来，对于海量数据的分析和处理变得尤为重要。
MATLAB作为一种强大的数据分析工具，能够帮助研究人员和工程师高效地进行数据分析。
本文将介绍使用MATLAB进行数据分析的基本步骤。
一、数据准备在进行数据分析之前，首先需要准备好待分析的数据。
数据可以来自于各种渠道，如实验采集、传感器监测、数据库等。
在导入数据之前，需要对数据进行预处理，包括数据清洗、缺失值处理、异常值检测等。
MATLAB提供了丰富的数据处理函数和工具箱，可以方便地完成这些任务。
二、数据导入在MATLAB中，可以使用多种方式导入数据，如直接读取文本文件、Excel文件、数据库查询等。
对于文本文件，可以使用readtable函数进行导入，对于Excel文件，可以使用xlsread函数进行导入。
对于大型数据库，可以使用Database Toolbox进行连接和查询操作。
导入数据后，可以使用MATLAB的数据结构进行存储和处理。
三、数据可视化数据可视化是数据分析的重要环节，能够直观地展示数据的分布和趋势。
MATLAB提供了丰富的绘图函数和工具箱，可以绘制各种类型的图形，如折线图、散点图、柱状图等。
通过调整绘图参数和添加标签，可以使图形更加美观和易于理解。
数据可视化可以帮助研究人员和工程师更好地理解数据，发现潜在的规律和关联。
四、数据分析在数据可视化的基础上，可以进行更深入的数据分析。
MATLAB提供了丰富的统计分析函数和工具箱，包括描述统计分析、假设检验、方差分析、回归分析等。
可以根据具体的问题选择合适的分析方法，并使用MATLAB进行计算和结果展示。
数据分析的目的是从数据中提取有用的信息和知识，为进一步的决策和优化提供依据。
五、模型建立与预测在某些情况下，可以通过建立数学模型对数据进行预测和优化。
MATLAB提供了强大的建模和仿真工具，如曲线拟合、回归分析、神经网络等。
MATLAB在金融统计分析中的应用
基 本 功 能 ，相 对 比较 “业 余 ”，往 往 无 法 满
足 专 业 化 了 需求 【Ｉ】。
ＳＰＳＳ，全 称 “统 计 产 品 与 服 务 解 决 方
案 ” 软 件 （Ｓｔａｔｉｓｔｉｃａｌ Ｐｒｏｄｕｃｔ ａｎｄ Ｓｅｒｖｉｃｅ Ｓｏｌｕｔｉｏｎｓ），是世界上最早 的统计软件 ，也是
当今运用最广泛的专业统计软件， 目前被
随着世界经济的不断发展 ，金融体制 的不断深化，全球 经济一体化的进程逐步 加 快 ，使 得 金 融 市场 的 范 围 不 断 扩 大 。面 对复杂的 国际 国内金融活动 ，各类金融数 据数不胜数 。要获得高效的金融管理 ，就 必 须全面准确地 分析 大量 的金融数据 ，无 论 是从微观层面 ～ 为了精 确分析 市场 行 情 、把 握 时 机 赚 取 利 润 ，还 是 宏 观 角 度 … 为 了引 导 市 场 健 康 发 展 、有 效 抑 制 泡 沫 的 产 生 ，都 对 金 融 业 的 统 计 分 析 和 数 值 计 算 提 出 了更 高 的要 求 ，统 计 工 具 与 金 融 业 的 结 合 成 了必 然 的 发 展 趋 势 。在 我 国 国 内 ， 随着金融业在 中国的迅猛发展 ，人们逐渐
Ｍｉｃｒｏｓｏｔｌ ｏｆｆ ｉｃｃ的组 件 之 一 。是 目前 运 用
的 最 广 泛 的 数 据 处 理 工 具 。 它 与
ＭＡＴＬＡＢ 在 金 融 统 计 分 析 中 的 应 用 Ｍｉｃｒｏｓｏｔｔ ｏｆｆ ｉｃｅ的 其 他 组 件 如 ＷＯＲＤ、 Ｐ０ｗ ＥＲＰ０ＩＮＴ 等 的 功 能 瓦补 ， 他 们 的 配
有 可 靠 的 依 据 也 是 现 代 设 备 健 全 的 重 要
证 明 。 ◆
．
参 考 文 献 ： ［１】王灵芝 ．加 强医院 内部控 制制度 建设 的 思 考 【Ｊ】．当代经济，２００７（９）． 【２】王 玉．浅析如何 加 强 医院财务 管理 【Ｊ】．中 国 科 技 信 息 ，２００５（１８）． 【３】郭泽光 主编．财 务管 理．中国市 场 出版 社 ，
常用统计分析软件
常用统计分析软件常用的统计分析软件有很多，下面我将介绍一些常见的统计分析软件及其特点。
1. SPSS（Statistical Package for the Social Sciences）：是一款统计分析软件，具有强大的数据处理、数据分析和报告生成功能。
它可进行描述性统计、假设检验、方差分析、回归分析、聚类分析、因子分析等常用统计分析。
2. SAS（Statistical Analysis System）：是一种完整的统计分析解决方案，包含数据管理、数据分析、统计建模和数据可视化等功能。
它适用于大规模数据的处理和分析，具有高效、稳定和灵活的特点。
3.R：是一种免费的开源统计分析软件，拥有丰富的统计分析函数和高级绘图功能。
R语言具有强大的数据处理能力和灵活的编程特点，适用于各种统计分析及数据可视化的需求。
4. Python：是一种通用的编程语言，也可以进行统计分析。
配合一些科学计算库（如NumPy、SciPy、Pandas等），Python可以进行各种统计分析任务，包括数据处理、数据分析、机器学习等。
5. Excel：是一种常用的电子表格软件，也可以进行一些简单的统计分析。
Excel提供了一些常用的统计函数和图表功能，对于小规模数据的分析和可视化比较便捷。
6.MATLAB：是一种功能强大的数学计算软件，也可以用于统计分析。
MATLAB提供了丰富的数学和统计函数，可以进行各种统计分析任务，包括回归分析、方差分析、时间序列分析等。
7. Stata：是一种统计分析软件，广泛应用于社会科学研究。
Stata 具有易用的用户界面和灵活的命令语言，提供了丰富的统计分析函数和专门的模块，满足各种统计分析需求。
8. Minitab：是一种易学易用的统计分析软件，广泛应用于工业和质量管理等领域。
Minitab提供了丰富的统计分析和质量管理工具，方便用户进行数据处理和分析，能够生成报告和图表。
9. Gretl：是一种专门用于计量经济学研究的统计分析软件。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Matlab与统计分析 一、 回归分析 1、多元线性回归 1.1 命令 regress( )， 实现多元线性回归，调用格式为 [b,bint,r,rint,stats]=regress(y,x,alpha) 其中因变量数据向量Y和自变量数据矩阵x按以下排列方式输人
nnknnkkyyyyxxxxxxxxxx21212222111211,1
1
1
对一元线性回归，取k=1即可。alpha为显著性水平(缺省时设定为0.05)，输出向量b，bint为回归系数估计值和它们的置信区间，r，rint为残差及其置信区间，stats是用于检验回归
模型的统计量，有三个数值，第一个是2R， 其中R是相关系数，第二个是F统计量值，第三个是与统计量F对应的概率P，当P 时拒绝0H，回归模型成立. 注：1、两组数据的相关系数在概率论的标准定义是： R= E{(x - E{x}) * (y - E{y})} / (sqrt({(x - E{x})^2) * sqrt({(y - E{y})^2)) E{}求取期望值。也就是两组数据协方差与两者标准差乘积的商。如果|R|=1说明两者相关，R=0说明两者不相关.
1、F是方差分析中的一个指标，一般方差分析是比较组间差异的。F值越大，P值越小，表示结果越可靠.
1.2 命令 rcoplot(r，rint)，画出残差及其置信区间. 1.3 实例 1 已知某胡八年来湖水中COD浓度实测值(v)与影响因素湖区工业产值(x1)、总人口数(x2 )、捕鱼量(x3 )、降水量( x4)资料，建立污染物Y的水质分析模型.
Step 1 输入数据 x1=[1.376, 1.375, 1.387, 1.401, 1.412, 1.428, 1.445, 1.477]; x2=[0.450，0.475，0.485，0.500，0.535，0.545，0.550，0.575]; x3=[2.170，2.554，2.676，2.713，2.823，3.088，3.122，3.262]; x4=[0.8922, 1.1610，0.5346，0.9589, 1.0239, 1．0499,1.1065, 1.1387]; Y=[5.19, 5.30，5.60，5.82，6.00，6.06，6.45，6.95];
Step 2 保存数据（以数据文件.mat 形式保存，便于以后调用） save data x1 x2 x3 x4 y load data %取出数据
Step 3 执行回归命令 x=[ones(8,1),x1,x2,x3,x4]； [b,bint,r,rint,stats]=regress(y,x)
得到结果： b=(-16.5283, 15.7206， 2.0327．-0.2106，-0.1991)' stats=(0.9908,80.9530，0.0022)' 即 Y= -16.5283+15.7206x1+2.0327x2-0.2106xl+0.1991x4
2R
=0.9908, F=80.9530,P=0.0022
2、非线性回归 2.1 命令 nlinfit( ) 实现非线性回归，调用格式为 [beta,r,J]=nlinfit(x,y,‘model’,beta0) 其中，输入数据x，y分别为n×m矩阵和n维列向量，对一元非线性回归，x为n维列向量；model是事先用m-文件定义的非线性函数，beta0是回归系数的初值．beta是估计出的回归系数，r是残差，J是Jacobian矩阵，它们是估计预测误差需要的数据.
2.2 命令 nlpredci( ) 预测和预测误差的估计，调用格式为 [y,delta]=npredci('model',x,beta,r,j) 2.3 实例 2 对实例1中COD浓度实测值(Y)，建立时序预测模型，这里选用logistic模型，即 ktbeay1 Step 1 建立非线性函数 对所要拟合的非线性模型建立m-文件model.m如下 function yhat=model(beta,t) yhat=beta(1).／(1+beta(2)*exp(-beta(3)*t))
Step 2 输入数据 t= 1:8 load data y(在data．mat中取出数据y) beta0=[50，10，1]’
Step 3 求回归系数 [beta，r，J]=nlinfit(t，Y，‘model’, beta0) 得结果： beta=(56.1157，10.4006，0.0445)’ 即
0445.04006.1011157.56e
y
Step 4 预测及作图 [YY,delta]=nlpredci(‘model’,x',beta,r ,J)； plot(x,y,'k+',x,YY,'r')
3、逐步回归 逐步回归的命令是stepwise， 它提供了一个交互式画面．通过此工具可自由地选择变量，进行统计分析.调用格式为：
stepwise（x，y，inmodel，alpha） 其中x是自变量数据,是mn阶矩阵，y是因变量数据，1n阶矩阵，inmodel是矩阵的列数指标（给出初始模型中包括的子集（缺省时设定为全部自变量），alpha是显著性水平（缺省时为0.5）. 运行stepwise命令时产生三个图形窗口：Stepwise Plot，Stepwise Table，Stepwise History.在Stepwise Plot窗口，显示出各项的回归系数及其置信区间.Stepwise Table 窗口中列出了一个统计表，包括回归系数及其置信区间，以及模型的统计量剩余标准差（RMSE）、相关系数（R-square）、F值、与F对应的概率P.
二、 主成分分析 这里给出江苏省生态城市主成份分析实例。 我们对江苏省十个城市的生态环境状况进行了调查，得到生态环境指标的指数值，见表 1。现对生态环境水平进行分析和评价。
我们利用Matlab6．5中的princomp命令实现。具体程序如下 x= [0．7883 0．7391 0．8111 0．6587 0．6543 0．8259 0．8486 0．6834 0．8495 0．7846 0．7633 0．7287 0．7629 0．8552 0．7564 0．7455 0．7800 0．9490 0．8918 0．8954 0．4745 0．5126 0．8810 0．8903 0．8288 0．7850 0．8032 0．8862 0．3987 0．3970 0．8246 0．7603 0．6888 0．8977 0．7926 0．7856 0．6509 0．8902 0．6799 0．9877 0．8791 0．8736 0．8183 0．9446 0．9202 0．9263 0．9185 0．9505 0．8620 0．8873 0．9538 0．9257 0．9285 0．9434 0．9154 0．8871 0．9357 0．8760 0．9579 0．9741 0．8785 0．8542 0．8537 0．9027 0．8729 0．8485 0．8473 0．9044 0．8866 0．9035 0．6305 0．6187 0．6313 0．7415 0．6398 0．6142 0．5734 0．8980 0．6186 0．7382 0．8928 0．7831 0．5608 0．8419 0．8464 0．7616 0．8234 0．6384 0．9604 0．8514]
x=x'; stdr=std(x)； ％求各变量标准差 [n,m]=size(x)； sddata= x.／stdr(ones(n,1),:)； ％标准化变换 [p，princ，egenvalue]=princomp(sddata) ％调用主成分分析程序 p3=p(：，1:3) ％输出前三个主成分系数 sc=princ(：，1:3) ％输出前三个主成分得分 egenvalue ％输出特征根 per=100*egenvalue／sum(egenvalue) ％ 输出各个主成分贡献率
执行后得到所要结果，这里是前三个主成分、主成分得分、特征根。即
egenvalue=[3．8811，2．6407，1．0597]' ， per=[43．12，29．34，11．971]' ． 这样，前三个主成分为 Zl = -0．3677xl+ 0．3702x2+ 0．1364x3+ 0．4048x4+ 0．3355x5-0．1318x6+0．4236x7+ 0．4815x8-0．0643x9
Z2 = 0．1442xl+ 0．2313x2-0．5299x3+ 0．1812x4-0．1601x5+ 0．5273x6+0．3116x7-0．0267x8+ 0．4589x9
Z3 = -0．3282xl-0．3535x2+ 0．0498x3+ 0．0582x4+ 0．5664x5-0．0270x6-0．0958x7-0．2804x8+ 0．5933x9
第一主成分贡献率为43.12％，第二主成分贡献率为29.34％，第三主成分贡献率为11.97％，前三个主成分累计贡献率达84．24％。
如果按80％ 以上的信息量选取新因子，则可以选取前三个新因子。第一新因子Z1包含的 信息量最大为43.12％％，它的主要代表变量为x8(城市文明)、x7(生产效率)、 x4(城市绿 化)，其权重系数分别为0．4815、0．4236、0．4048，反映了这三个变量与生态环境水平密切相关，第二新因子Z2包含的信息量次之为29．34％，它的主要代表变量为x3(地理结构)、x6(资源配置)、 x9(可持续性)，其权重系数分别为0．5299、0．5273、0．4589，第三新因子 Z3包含的信息量为11．97％，代表总量为 x9(可持续性)、 x5(物质还原)，权重系数分别为0．5933、0．5664。
这些代表变量反映了各自对该新因子作用的大小，它们是生态环境系统中最重要的影响因