(完整版)一次函数与等腰三角形的存在性问题
一次函数综合—线段和差、存在性问题
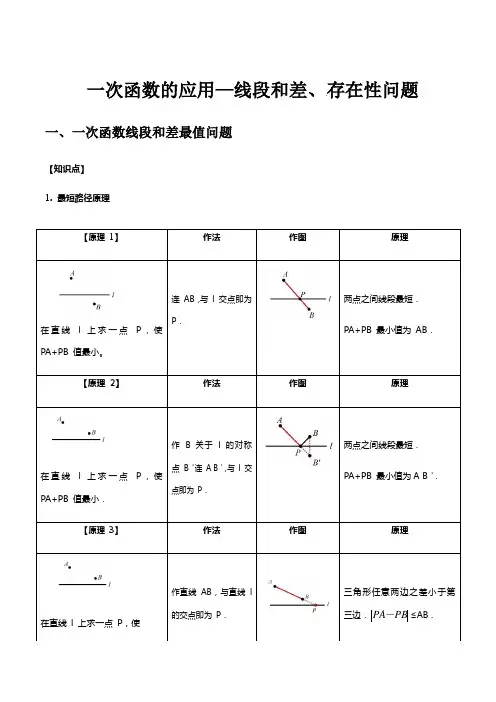
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。
连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式；（2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。
3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy中，y轴上有一点P，它到点(4,3)A，(3,1)B 的距离之和最小，则点P的坐标是()A．(0,0)B．4(0,)7C．5(0,)7D．4(0,)5的值最大 .【原理4】作法作图原理在直线l 上求一点P，使的值最大 .作B 关于l 的对称点B＇作直线A B＇，与l交点即为P．三角形任意两边之差小于第三边．≤A B＇ .PB PA－PB PA－PB PA－★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)B-，在x轴上存在点P到A，B两点的A，点(2,1)距离之和最小，则P点的坐标是．★★☆练习2．如图，直线34120+-=与x轴、y轴分别交于点B、A两点，以线段AB为边在第一象限x y内作正方形ABCD．若点P为x轴上的一个动点，求当PC PD+的长最小时点P的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3∆的周长最小时，求点E OB=，D为边OB的中点，若E为x轴上的一个动点，当CDEOA=，4的坐标()A ．(3,0)-B ．(1,0)C ．(0,0)D ．(3,0)★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为 ．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边 在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A，(2,3)B-，点P为x轴上一点，当||PA PB-最大时，点P 的坐标为()A．1(,0)2B．5(,0)4C．1(,0)2-D．(1,0)★★☆练习1．平面直角坐标系中，已知(4,3)A、(2,1)B，x轴上有一点P，要使PA PB-最大，则P点坐标为★★☆练习2．如图，在平面直角坐标系中，点A的坐标为(0,4)，点B的坐标为(6,0)，点P在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。
一次函数特殊三角形存在性
特殊三角形存在性知识点睛1.存在性问题：通常是在变化的过程中，根据已知条件，探索某种状态是否存在的题目，主要考查运动的结果．2.存在性问题处理框架：①研究背景图形．②分析不变特征，确定分类标准．③分析特殊状态的形成因素，画出符合题意的图形并求解．④结果验证．3.不变特征举例：①等腰三角形以定线段作为底边或者腰确定分类标准，利用两圆一线确定点的位置．②等腰直角三角形根据直角顶点确定分类标准，然后借助两腰相等或者45°角确定点的位置．精讲精练1.如图，在平面直角坐标系中，已知点A的坐标为(-3，4)，P是x轴上的一个动点，则当△AOP是等腰三角形时，点P的坐标为____________．2.如图，在平面直角坐标系中，一次函数y x =+与x 轴交于点A ，与y 轴交于点B ．将△AOB 沿过点B 的直线折叠，使点O 落在AB 上的点D 处，折痕交x 轴于点E ． （1）求点D 的坐标．（2）x 轴上是否存在点P ，使得△PAD 是等腰三角形？若存在，求出点P 的坐标；若不存在，请说明理由．3. 直线y =kx -4与x 轴、y 轴分别交于点A ，B ，且43OB OA =．点C 在第一象限，是直线y =kx -4上的一个动点，当△AOC 的面积为6时，x 轴上是否存在点P ，使△ACP 是等腰三角形？若存在，求出点P 的坐标；若不存在，请说明理由．4.如图，直线334y x=-+与x轴、y轴分别交于点A，B，在第一象限内是否存在点P，使以A，B，P为顶点的三角形是等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．5.如图，直线y=x轴、y轴分别交于点A，B，点C在点A左侧，是x轴上一点，且满足AC=OA，过点C作x轴的垂线交直线AB于点D，在第二象限内是否存在点P，使得△PAD是等腰直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由．6.如图，在平面直角坐标系中，点A的坐标为(2，0)，Q是直线x=3上的一个动点，y轴正半轴上是否存在点P，使△APQ为等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．【参考答案】 知识点睛1.运动的结果2.坐标或表达式 精讲精练1.(5,0)，(-5,0)，(-6，0)，(256-，0)2.（1）(-3（2）存在 (，0)，(-6-0)， (0，0)，(-4，0)3.存在(8，0)，(-2，0)，(9，0)，(436，0)4.存在(7，4)，(3，7)，(72，72)5.存在3，3)，6，3+)，6.存在(0，1)，(0，3)，(0，4)。
第4章一次函数-一次函数之等腰直角三角形的存在性(教案)
五、教学反思
今天我们在课堂上探讨了《一次函数之等腰直角三角形的存在性》，整体来看，学生的学习效果还是不错的。但在教学过程中，我也发现了一些值得思考的问题。
首先，我发现有些学生对一次函数图像与等腰直角三角形之间的关系理解不够深入。在讲解过程中，我尽量用生动的例子和形象的比喻来帮助他们理解，但显然，这部分内容对于他们来说还是有一定难度的。在今后的教学中，我需要更加关注这部分学生的需求，尽可能用简单易懂的方式讲解难点，让他们能够真正消化吸收。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解一次函数和等腰直角三角形的基本概念。一次函数是形如y=kx+b的函数，其中k是斜率，b是y轴截距。等腰直角三角形是一种特殊的三角形，它的两条腰相等且与底边成直角。在一次函数图像中，等腰直角三角形的存在性与函数的斜率有关。
2.案例分析：接下来，我们来看一个具体的案例。这个案例将展示如何在一次函数图像中找出等腰直角三角形，以及它如何帮助我们解决实际问题。
-运用逻辑推理和分析数据的能力，解决一次函数图像中等腰直角三角形的定位问题。
举例解释：
-解释斜率为1或-1时，图像上的点与原点的连线和x轴或y轴形成的特殊角度题时，指导学生如何从问题描述中提取关键信息，构建一次函数模型，并利用等腰直角三角形的性质进行解答。
其次，在实践活动环节，学生们的参与度很高，但部分小组在讨论时显得有些拘谨，可能是因为对等腰直角三角形在实际生活中的应用不够了解。在今后的教学中，我会多设计一些与实际生活紧密相关的案例，让学生在实践中更好地理解理论知识。
【八年级压轴精选】一次函数背景下的存在性问题与最值问题，一题通关！
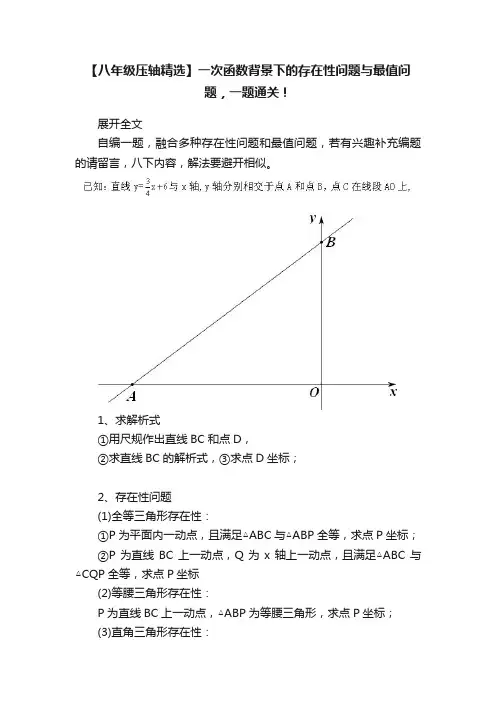
【八年级压轴精选】一次函数背景下的存在性问题与最值问题，一题通关！展开全文自编一题，融合多种存在性问题和最值问题，若有兴趣补充编题的请留言，八下内容，解法要避开相似。
1、求解析式①用尺规作出直线BC和点D，②求直线BC的解析式，③求点D坐标；2、存在性问题(1)全等三角形存在性：①P为平面内一动点，且满足△ABC与△ABP全等，求点P坐标；②P为直线BC上一动点，Q为x轴上一动点，且满足△ABC与△CQP全等，求点P坐标(2)等腰三角形存在性：P为直线BC上一动点，△ABP为等腰三角形，求点P坐标；(3)直角三角形存在性：直线l过原点，且与BC平行，P为直线l上一动点，△ABP为直角三角形，求点P坐标；(4)等腰直角三角形存在性：P为第二象限内上一动点，△ABP为等腰直角三角形，求点P坐标；(5)等边三角形存在性（九年级用）P为第二象限内上一动点，△ABP为等边三角形，求点P坐标；(7)平行四边形存在性：①三定一动：P为平面内一动点，且以A、B、C、P为顶点的四边形为平行四边形，求点P坐标；②两定两动：P为直线AB上一动点，Q为y轴上一动点，且以B、C、P、Q为顶点的四边形为平行四边形，求点P、Q的坐标；(8)菱形存在性：P为直线BC上一动点，Q为平面内一动点，且以A、B、P、Q为顶点的四边形为菱形，求点P、Q的坐标；(9)矩形存在性：直线l过原点，且与BC平行，P为直线l上一动点，Q为平面内一动点，且以A、B、P、Q为顶点的四边形为矩形，求点P、Q的坐标；本讲先来解析部分小题：1、求解析式①用尺规作出直线BC和点D，②求直线BC的解析式，③求点D坐标；（考查内容：尺规作图、图形折叠、待定系数法求解析式，勾股定理或等积法求线段长）①折叠想到重合，全等，可得BC为∠ABO平分线，完成基本作图作已知角的角平分线即可，由D、O重合，可知BD=BO，CD=CO，CD⊥AB，所以在AB上截取BD=BO或CD=CO，或过C作CD⊥AB 于D(此法较繁)②待定系数法求直线解析式，需知两点，已知B（0，6）只要知道点C坐标，算OC长，八年级求线段长两种方法：勾股和等积，如下：再来解析2（7），考查平行四边形存在性，解法参考我之前文章：“平四”存在性问题探究2(7)平行四边形存在性：①三定一动：P为平面内一动点，且以A、B、C、P为顶点的四边形为平行四边形，求点P坐标；②两定两动：P为直线AB上一动点，Q为y轴上一动点，且以B、C、P、Q为顶点的四边形为平行四边形，求点P、Q的坐标；②码字太累，手写版本：上面方法优点：1、不会漏解，2、无需画图(5)等边三角形存在性（九年级用）P为第二象限内上一动点，△ABP为等边三角形，求点P坐标；解法参考我之前文章：一题5解。
一次函数背景下等腰三角形存在性问题分析与策略
解题技巧与方法JIETI JIQIAO YU FANGFA员猿源 数学学习与研究 2022.12◎肖 杜1 罗 丽2∗ (1.重庆市南开两江中学校,重庆 401135;2.西南大学银翔实验中学,重庆 401533)【摘要】等腰三角形的存在性问题一直是中学数学的重点、难点,对学生的数学能力要求很高,又往往出现在压轴题中,让许多学生望而却步.本文从等腰三角形产生的原理上归类分析,先从常规的两圆一线说起,再到平移、旋转.特别是旋转过程中产生的等腰三角形,利用圆这个工具,能有效解决找不到、找不全的问题.【关键词】等腰三角形;存在性;两圆一线;平移;旋转在中考数学的压轴题中,等腰三角形的存在性问题是一个热门考点,也一直是教学中的重点、难点内容,对学生分析问题和解决问题的能力要求较高,让许多学生望而却步.本文从等腰三角形产生的原理上进行归类分析,谈谈解决此类问题的常用方法和策略.类型一 两圆一线产生等腰三角形1.如图1-1,点A 的坐标为(1,1),点B 的坐标为(4,3),在x 轴上存在一点C ,使△ABC 是等腰三角形,求出点C 的坐标.解析 分三种情况讨论△ABC :①AB =AC ②BA =BC ③CA =CB图1-1①当AB =AC 时,即以点A 为圆心,AB 长为半径画圆,与x 轴的交点即为此时的C 点(如图1-2),由图可知,此时的C 点有两个,分别记为C 1,C 2.过点A 作AH ⊥x 轴于点H ,AB =13,所以AC 1=AC 2=13,图1-2所以H (1,0),HC 1=HC 2=23,所以C 1(1-23,0),C 2(1+23,0).②当BA =BC 时,即以点B 为圆心,AB 长为半径画圆,与x 轴的交点即为此时的C 点(如图1-3),由图可知,此时的C 点有两个,分别记为C 3,C 4.图1-3过点B 作BH ⊥x 轴于点H ,所以BC 3=BC 4=AB =13,H (4,0),所以HC 3=HC 4=2,所以C 3(2,0),C 4(6,0).③当CA =CB 时,此时点C在AB 的垂直平分线上,所以AB 的垂直平分线与x 轴的交点即为此时的C 点(如图1-4),记为C 5.设点C 5的坐标为(x ,0),图1-4所以C 5A =(x -1)2+1,C 5B =(x -4)2+9,则(x -1)2+1=(x -4)2+9解得x =236,所以C 5236,0().综上,点C 的坐标为(1-23,0)或(1+23,0)或(2,0)或(6,0)或236,0().类型二 平移变换中的等腰三角形2.如图2-1,直线AB :y =-33x -1交x 轴于点A ,交y 轴于点B ,将直线AB 沿x 轴翻折交y 轴于点C.将直线BA 沿射线AC 平移分别交AC 于点H ,交x 轴于点K ,当△OKH 为等腰三角形时,请写出OK 的长,并说明理由.图2-1解析 由题中给出的直线AB 的解析式可知,∠CAO =∠BAO =30°,从这个特殊的角度出发,通过平移、讨论,大致确定K ,H 的位置,通过几何计算,解决问题.JIETI JIQIAO YU FANGFA解题技巧与方法员猿缘数学学习与研究 2022.12①当KO =KH 时,根据平移,先大致确定两个位置,如图2-2,2-3所示,在图2-2中,过点H 作HM ⊥x 轴于点M ,因为∠HAK =∠HKA =30°,图2-2所以HA =HK ,AK =2MK =23HM ,KO =KH =2HM ,所以AO =23+2HM =3所以OK =2HM =3-32.在图2-3中,过点H 作HM ⊥x 轴于点M ,因为∠HAK =∠HKA =30°,图2-3所以HA =KH =KO ,AK =2MK =23HM.因为AK =AO +KO =AO +HK =3+2HM ,所以23=3+2HM ,所以HM =3+34,所以OK =2HM =3+32.②当OK =OH 时,如图2-4所示,过点H 作HM ⊥x 轴于点M ,图2-4因为∠HAK =∠HKA =30°,所以HA =HK =2HM ,OH =OK =2OM ,AM =KM =3OM ,所以AO =4OM =3,所以OM =34,所以OK =32.综上,OK 的长为3-32或3+32或32.为什么没有讨论HO =HK 呢?实际上若HO =HK ,则∠HOK =∠HKO =30°,而∠HAO =30°,显然矛盾,因此舍去了.类型三 旋转变换中的等腰三角形3.如图3-1,在平面直角坐标y =-2x -2与x轴交于点A ,与y 轴交于点C ,直线y -2与x 轴交于点B ,点E 是点A 关于y 轴的对称点,连接CE ,将△BCE 绕点E 旋转,旋转后点B ,C 的对应点分别为点B′,C′,在旋转过程中,直线B′C′与x 轴交于点M 、与直线BC 交于点N.当△BMN 是以MN 为腰的等腰三角形时,求BM 的长度.图3-1解析 在直线BC 绕点E 旋转的过程中,点E 到直线BC 的距离保持不变,过点E 作EH ⊥BC 于点H ,以点E 为圆心,EH 的长为半径作圆,记r =EH =3-12,则直线B′C′始终保持与☉E 相切,而∠MBN =30°不变.在旋转过程中,利用∠MNB 与∠NMB 的变化趋势确定所在位置.利用这个方法,不容易漏掉某些存在的情况,能帮助我们找出所有的解.①如图3-2,记此时的M ,N 为M 1,N 1,∠M 1N 1B =∠M 1BN 1=30°,所以∠EM 1N 1=60°,图3-2所以r EM 1=32,EM 1=2-33,所以BM 1=231-2-33=733-3.②如图3-3,记此时的M ,N 为M 2,N 2,∠M 2N 2B =∠M 2BN 2=30°,图3-3解题技巧与方法JIETI JIQIAO YU FANGFA员猿远 数学学习与研究 2022.12所以r EM 2=32,EM 2=2-33,所以BM 2=23-1+2-33=533+1.③如图3-4,记此时的M ,N 为M 3,N 3,∠N 3M 3B =∠M 3BN 3=30°,图3-4所以EM 3=2r =23-1,所以BM 3=23-1+23-1=43-2.综上,BM 的长为733-3或533+1或43-2.4.如图4-1,四边形OABC 是边长为6的正方形,点P为OA 边上任意一点(与点O ,A 不重合),连接CP ,若OP =23,把△OCP 绕点O 顺时针旋转一周的过程中,设旋转后的三角形为△OC′P′,直线C′P′与直线OB 的交点为Q ,当△OP′Q 为等腰三角形时,写出点Q 的坐标,并说明理由.图4-1解析由题可知,∠PCO =30°,∠COP =90°,在Rt △OCP 旋转的过程中,角度和边长均不发生变化,又OP =23,OC =6,从而点O 到线段CP 的距离不变,设点O 到线段CP 的距离为r ,则r =3.以点O 为圆心,r 为半径作圆,则在旋转过程中,CP 始终与☉O 相切,利用旋转过程中OQ 的长度变化趋势以及Q 点位置变化确定Q 点大致位置,再利用△OP′Q 为等腰三角形及∠AOB =45°,计算出Q 点的坐标.①如图4-2,记此时的P′,C′,Q 为P′1,C′1,Q 1,因为OP′1=OQ 1=23,∠AOB =45°,所以x Q1=y Q 1=232=6,所以Q 1(6,6).图4-2②如图4-3,记此时的P′,C′,Q 为P′2,C′2,Q 2,因为∠OP′2C′2=60°,所以∠Q 2P′2O =120°.图4-3又P′2O =P′2Q 2=23,所以OQ 2=OC′2=23×3=6,x Q 2=y Q 2=-62=-32,所以Q 2(-32,-32.③如图4-4,记此时的P′,C′,Q 为P′3,C′3,Q 3,因为OP′3=OQ 3=23∠Q 3P′3O =60°,所以此时的△Q 3P′3O 为等边三角形,当然,不难算出x Q 3=y Q3=-232=-6,所以Q 3(-6,-6).图4-4图4-5④如图4-5,记此时的P′,C′,Q 为P′4,C′4,Q 4,因为∠OP′4C′4=60°,所以∠Q 4P′4O =120°.又P′4O =P′4Q 4=23,所以OQ 4=OC′4=23×3=6,x Q 4=y Q 4=62=32,所以Q 4(32,32).综上,点Q 的坐标为(6,6)或(-32,-32)或(-6,-6)或(32,32).通过上面的例题,我们总结经验,发现等腰三角形的存在性问题找对、找全并不是太难,关键在于找到其中不变的量以及变化的量的变化趋势,同时要有克服困难的勇气,不断尝试突破,找到一些规律,也就慢慢熟练解题了.【参考文献】[1]刘正荣,董建功.关于等腰三角形存在性问题的解题策略初探[J ].中小学数学(初中版),2012(5):34-36.[2]于芸.等腰三角形存在性问题的解题策略[J ].中学数学研究(华南师范大学版),2013(20):34-35.[3]左效平.例析一次函数图像截出的等腰三角形问题[J ].初中数学教与学,2016(15):33-35.。
一次函数中特殊三角形的存在性问题(上课)
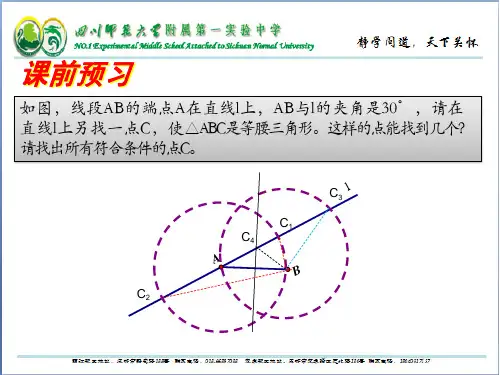
如图，线段AB的端点A在直线l上，AB与l的夹角是30°，请在 直线l上另找一点C，使△ABC是等腰三角形。这样的点能找到几个？ 请找出所有符合条件的点C。
C3 l
C1 C4 A
B C2
合作交流，探索新知
如图，直线 y 3 x 3与x轴、y轴分别交于A、B两点.
4
（1）直接写出A、B两点的坐标; （2）在x轴上是否存在点P，使以A，B，P为顶点的三角形是
y
B
O
A
x
2、本节课涉及了哪些数学思想或方法？
（1）.数形结合思想
（2）.分类讨论思想
（3）.方程思想
课后练习，巩固提高
1、如图，在平面直角坐标系xOy中，四边形OABC的边OC，OA
分别与x轴、y轴重合，AB∥OC，∠AOC=90°，∠BCO=45°，
BC= ，点C的坐标为(-9，0)．
（1）求点B的坐标．
件的点；
存（2象．在的2为）交点底在点P：，就x做轴是使已上符以知合是线A条否、段件的的垂点直．平分线，中垂线y与所要求的图
B、P为顶点的三角
形是等腰三角形？
若存在，求出点P的
B 3 4-m
坐标；若不存在， 请说明理由；
P3
P1 O m P4 4-mA
P2
x
合作解交决存流在，性问探题小索策新略：知 如图假若，设能直存导线在出合→y 理推 的理3结论x 果证3与，→就得x轴做出、出结“论y轴存。分在别”的交判于断A；、B两点. 导出矛盾，就做4出不存在的判断。
B
么问题？你能解决它吗？
O
A
x
合作交流，探索新知
如图，直线 y 3 x 3与x轴、y轴分别交于A、B两点.
2019-2020学年度北师大版八年级上册一次函数与等腰三角形存在性专题( 解析版)
2019-2020一次函数与等腰三角形存在性专题（含解析）一、单选题1．一次函数分别交轴、轴于，两点，在轴上取一点，使为等腰三角形，则这样的点最多有几个（）A.5B.4C.3D.22．如图，直线y=x+与x轴、y轴分别交于点A、B，在坐标轴上找点P，使△ABP为等腰三角形，则点P的个数为（）A.2B.4C.6D.83．如图，在平面直角坐标系xOy中，A（0，2），B（0，6），动点C在直线y＝x上．若以A、B、C 三点为顶点的三角形是等腰三角形，则点C的个数是（）A．6 B．5 C．4 D．34．在平面直角坐标系中，已知点A(－4，0)，点B(4，0)，若点C在一次函数122y x=-+的图象上，且△ABC为等腰三角形，则满足条件的点C有（）A.5个B.4个C.3个D.2个二、填空题5．如图，一次函数1y x =-+的图象与x 轴、y 轴分别交于点A B 、，点M 在x 轴上，要使ABM ∆是以AB 为腰的等腰三角形，那么点M 的坐标是_____．6．如图，已知直线334y x =-+与坐标轴相交于A 、B 两点，动点P 从原点O 出发，以每秒1个单位长度的速度沿x 轴正方向运动，当点P 的运动时间是__________秒时，PAB ∆是等腰三角形．三、解答题7．已知正比例函数y ＝kx 经过点A ，点A 在第四象限，过点A 作AH ⊥x 轴，垂足为点H ，点A 的横坐标为3，且△AOH 的面积为3．（1）求正比例函数的表达式；（2）在x 轴上能否找到一点M ，使△AOM 是等腰三角形？若存在，求点M 的坐标；若不存在，请说明理由．8．如图，在平面直角坐标系xOy 中，直线24y x =-+ 与x 轴，y 轴分别交于点A ，点B 。
（1）求点A 和点B 的坐标；（2）若点P 在x 轴上，且BOP 1S AOB 2∆=∆ 求点P 的坐标。
（3）在y 轴是否存在点M ，使三角形MAB 是等腰三角形，若存在。
一次函数与三角形存在性问题
一次函数与三角形的存在性问题1．如图，直线y=2x+m（m＞0）与x轴交于点A（﹣2，0），直线y=﹣x+n（n＞0）与x轴、y轴分别交于B、C两点，并与直线y=2x+m（m＞0）相交于点D，若AB=4．（1）求点D的坐标；（2）求出四边形AOCD的面积；（3）若E为x轴上一点，且△ACE为等腰三角形，求点E的坐标．2．已知：如图，在平面直角坐标系xOy中，直线y=x+4与x轴交于A、与y轴交于B，点C（a，b），其中a＜b，且a、b是方程x2﹣7x+12=0的两根．（1）求直线AC的解析式；（2）点D为直线AC与y轴的交点，请求出△ABD和△BCD的周长差；（3）点E是线段AC上一动点，是否存在点E，使△COE为直角三角形？若存在，请求出点E的坐标；若不存在，请说明理由．3、如图：直线y=kx+3与x轴、y轴分别交于A、B两点，34OBOA，点C(x,y)是直线y＝kx＋3上与A、B不重合的动点。
（1）求直线y=kx+3的解析式；（2）当点C运动到什么位置时，△AOC的面积是6；（3）过点C的另一直线CD与y轴相交于D点，是否存在点C使△BCD与△AOB全等？若存在，请求出点C的坐标；若不存在，请说明理由。
4、如图，在平面直角坐标系中，O为坐标原点．△ABC的边BC在x轴上，A、C两点的坐标分别为A （0，m）、C（n，0），B（﹣5，0），且（n﹣3）2+=0，点P从B出发，以每秒2个单位的速度沿射线BO匀速运动，设点P运动时间为t秒．（1）求A、C两点的坐标；（2）连接PA，用含t的代数式表示△POA的面积；（3）当P在线段BO上运动时，是否存在一点P，使△PAC是等腰三角形？若存在，请写出满足条件的所有P点的坐标并求t的值；若不存在，请说明理由．5、如图，在平面直角坐标系中，A（18，0），B（12，8），C（0，8），动点P、Q分别从原点O、点B 同时出发，动点P沿x轴正方向以每秒2个单位长度的速度运动，动点Q在线段BC上以每秒1的单位长度的速度向C运动，当点Q到达C点时，点P随之停止运动，设运动时间为t（秒），直线PQ与直线AB交于点D．（1）直接写出线段AB的长为；（2）求直线AB的函数表达式；（3）当t=2时，求直线PQ的表达式以及点D的坐标；（4）直接写出所有t的值，使得此时△ADP是等腰三角形．6．在平面直角坐标系xOy中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒，当t为多少时，△PQB为直角三角形．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第1页（共5页）
一次函数与等腰三角形的存在性问题
一．选择题（共3小题）
1．在平面直角坐标系中有两点：A（﹣2，3），B（4，3），C是坐标轴x轴上
一点，若△ABC是直角三角形，则满足条件的点C共有（ ）
A．2个 B．3个 C．4个 D．6个
2．（2008•天津）在平面直角坐标系中，已知点A（﹣4，0），B（2，0），若
点C在一次函数y=﹣x+2的图象上，且△ABC为直角三角形，则满足条件
的点C有（ ）
A．1个 B．2个 C．3个 D．4个
3．（2016•江宁区一模）已知点A，B的坐标分别为（﹣4，0）和（2，0），
在直线y=﹣x+2上取一点C，若△ABC是直角三角形，则满足条件的点C
有（ ）
A．1个 B．2个 C．3个 D．4个
二．填空题（共4小题）
4．（2015•杭州模拟）在平面直角坐标系xOy中，点A（﹣4，0），B（2，0），
设点C是函数y=﹣（x+1）图象上的一个动点，若△ABC是直角三角形，
则点C的坐标是 ．
5．（2009秋•南昌校级期末）在直角坐标系中，点A、B、C的坐标分别为（1，
2）、（0，0）、（3，0），若以点A、B、C、D为顶点构成平行四边形，则点D
的坐标应为 ．
6．（2009秋•扬州校级期中）在平面直角坐标系中若△ABC的顶点坐标分别
为：A（3，0）、B（﹣1，0）、C（2，3）、若以点A、B、C、D为顶点的四边
形是平行四边形，则点D的坐标为 ．
7．（2010春•江岸区期中）一个平行四边形在平面直角坐标系中三个顶点的
坐标分别是（﹣1，﹣1），（﹣2，3），（3，﹣1），则第四个顶点的坐标
为 ．
三．解答题（共14小题）
8．四边形ABCD中，BD，AC相交于O，且BD⊥AC，求证：AB2+CD2=AD2+BC2．
9．如图，直线y=﹣x+3与x轴、y轴分别交于点A，点B，在第一象限是
否存在点P，使以A，B，P为顶点的三角形是等腰直角三角形？若存在，求
出点P的坐标；若不存在，请说明理由．
第2页（共5页）
10．（2012秋•中山区期末）已知，如图，在平面直角坐标系中，A、B两点
坐标分别为A（4，0），B（0，8），直线y=2与直线AB交于点C，与y轴交
于点D；
（1）求直线AB的解析式；
（2）点E是直线AB上的一个动点，问：在y轴上是否存在点F，使得△DEF
为等腰直角三角形？若存在，请求出点E及对应的点F的坐标；若不存在，
请说明理由．
11．（2011秋•东城区期末）如图，四边形OABC的顶点A（0，4），B（﹣2，
4），C（﹣4，0）．过作B、C直线l，将直线l平移，平移后的直线l与x轴
交于D，与y轴交于点E．
探究：当直线l向左或向右平移时（包括直线l与BC直线重合），在直线AB
上是否存在P，使△PDE为等腰直角三角形？若存在，请求出所有满足条件
的P点的坐标；若不存在，请说明理由．
第3页（共5页）
12．（2005•大连）如图，P是y轴上一动点，是否存在平行于y轴的直线x=t，
使它与直线y=x和直线y=﹣x+2分别交于点D、E（E在D的上方），且△PDE
为等腰直角三角形？若存在，求t的值及点P的坐标；若不存在，请说明原
因．
13．（2014春•曲靖期末）如图，直线y=﹣x+6与坐标轴分别相交于点A、B．
（1）求A、B两点坐标；
（2）以AB为边在第一象限内作等边三角形ABC，求△ABC的面积；
（3）在坐标系中是否存在点M，使得以M、O、A、B为顶点的四边形为平
行四边形？若存在，请直接写出M的坐标；若不存在，请说明理由．
17．（2014秋•长兴县期末）如图，在平面平面直角坐标系中，直线y=﹣2x+4
交x轴于点A，交y轴与点B，点C是AB的中点，过点C作直线CD⊥x轴
于点D，点P是直线CD上的动点．
（1）填空：线段OA的长为 ；线段OB的长为 ；
（2）求点C的坐标；
（3）是否存在这样的点P，使△POB为等腰三角形？若存在，请求出点P的
坐标；若不存在，请说明理由．
第4页（共5页）
20．（2012秋•淮安校级期末）在直角坐标系中，有A（﹣1，1），B（3，1），
C（2，4）三点，另有一点D与点A、B、C构成平行四边形的顶点，求点D
的坐标．
21．（2013秋•丽水期末）如图，在平面直角坐标系中，直线l经过点A（，
0），点B（0，）．
（1）求直线l的函数解析式；
（2）若给定点M（5，0），存在直线l上的两点P，Q，使得以O，P，Q为
顶点的三角形与△OMP全等，请求出所有符合条件的点P的坐标．
第5页（共5页）
参考答案
一．选择题（共3小题）
1．B； 2．D； 3．D；
二．填空题（共4小题）
4．（-4，3），（2，-3），（-，），（，-）； 5．（4，2）或（-2，
2）或（2，-2）； 6．（-2，3）或（6，3）或（0，-3）； 7．（2，3）或（-6，
3）或（4，-5）；