物理光学-光的电磁理论
郁道银 工程光学-物理光学答案整理

第一章 光的电磁理论基础1.一平面电磁波可表示为 x E = 0 ,y E = 2cos[2π×1014(c z-t )+2π] ,z E = 0,求: (1)该电磁波的频率、波长、振幅和原点的初相位? (2)波的传播方向和电矢量的振动方向? (3)相应的磁场B 的表达式?解:(1)由y E = 2cos[2π×1014(c z-t )+2π]知: 频率:f=1014(Hz )λ=ct=c/f =ss m 114810103⨯=6103⨯(m) )(3m μ= A=2(m v ) 0ϕ=2π (2)传播方向Z , 振动方向Y 。
(3)相应磁矢量B 的大小εμ1=B E C = 881067.01032-⨯=⨯=B ()⎪⎪⎪⎩⎪⎪⎪⎨⎧==⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-⨯⨯-=-002102cos 1067.0148z y x B B T t c z B ππ2.在玻璃中传播的一个线偏振光可以表示为21510cos 10(),0,00.65x y z zE t E E cπ=-==,求:(1)光的频率、波长、振幅;(2)玻璃的折射率;(3)光波的传播方向和电矢量的振动方向。
解:(1)由21510cos 10()0.65x zE t cπ=-可知: 15141051022f ωπππ===⨯15220.39100.65um kcππλπ=== A=2(m v )xz(v)0Z H E =⨯y(E)(H)(2) 1.53c c n v fλ=== (3)传播方向Z , 振动方向X 。
3. 已知:h=0.01mm 5.1=μnm 500=λ 插入前后所引起的光程位相变化求光程的位相变化 解:)(10501.05.001.0101.05.13mm l -⨯=⨯=⨯-⨯=∆ )(202rad lππλϕ=⨯∆=∆4.已知: ()t a E ωα-=111cos ,()t a E ωα-=222cosHz 15102⨯=πω ,m v a 61= ,m v a 82= ,01=α,22πα=求:合成波表达式解:()()t a t a E E E ωαωα-+-=+=221121cos cos()t A ωα-=cos)cos(2212122212αα-++=a a a a Am v 100c o s 86264362=⨯⨯++=π3406806cos cos sin sin 22112211=++⨯=++=αααααa a a a tg)(927.01801.531.53)34(rad arctg o =⨯===πα ())(102927.0cos 105m v t E ⨯-=π5. 已知:()t A x E c zx -=ωcos 0 ,()[]450cos πωω+-=t A y E c z y求:所成正交分量的光波的偏振态 解:由已知得 A a a ==21,454512πωπωαα=⋅-+⋅=-c z c z 代入椭圆方程:()()1221221222212sin cos 2αααα-=--+a a E E a E a E y x y x2122222222=-+A E E A E A E y x y x ()2245sinsin 12-==-παα <0 ∴右旋椭圆光1λ椭圆长轴与x 轴夹角ψ ∞=-=ψδcos 22222121a a a a tg oo 902702==ψ∴或 又2345ππδπ<=< 的解舍去o 902=ψ∴o 2702=ψ∴ o135=ψ 第二章光的干涉和干涉系统1。
物理光学

3.4.2光源非单色性的影响 3.4.3两相干光波振幅比的影响
3.5.1互相干函数和复相干度 3.5.2时间相干度 3.5.3空间相干度
3.6.1条纹的定域 3.6.2等倾条纹 3.6.3圆形等倾条纹 3.6.4透射光条纹
3.7.1定域面的位置及定域深度 3.7.2楔形平板产生的等厚条纹 3.7.3等厚条纹的应用
5.1惠更斯-菲 涅耳原理
2
*5.2基尔霍夫 衍射理论
3 5.3菲涅耳衍
射和夫琅禾费 衍射
4 5.4矩孔和单
缝的夫琅禾费 衍射
5
5.5圆孔的夫 琅禾费衍射
5.6光学成像系统的 衍射和分辨本领
*5.7双缝夫琅禾费 衍射
5.8多缝夫琅禾费衍 射
5.9衍射光栅
*5.11直边的菲涅 耳衍射
5.10圆孔和圆屏的 菲涅耳衍射
5.10.1菲涅耳衍射 5.10.2菲涅耳波带法 5.10.3圆孔衍射图样 5.10.4圆屏的菲涅耳衍射 5.10.5菲涅耳波带片
5.11.1菲涅耳积分及其图解 5.11.2半平面屏的菲涅耳衍射 5.11.3单缝菲涅耳衍射 5.11.4矩孔菲涅耳衍射
5.12.1什么是全息照相 5.12.2全息照相原理 5.12.3全息照相的特点和要求 5.12.4全息照相应用举例
2.1两个频率 1
相同、振动方 向相同的单色 光波的叠加
2
2.2驻波
3 2.3两个频率
相同、振动方 向互相垂直的 光波的叠加
4 2.4不同频率
的两个单色光 波的叠加
5
2.5光波的分 析
2.1.1代数加法 2.1.2复数方法 2.1.3相幅矢量加法
2.2.1驻波的形成 2.2.2驻波实验
2.3.1椭圆偏振光 2.3.2几种特殊情况 2.3.3左旋和右旋 2.3.4椭圆偏振光的强度 2.3.5利用全反射产生椭圆和圆偏振光
光的电磁理论基础

10-18 ~ 19
求解方程,有
z E f ( t)
v
z B f ( t)
v
10-20 ~ 21
这正是行波的表示形式。表示源点的振动经过一定时间才传播到场点,电磁波是逐点传播的。
(二)平面简谐电磁波的波动形式
以上是波动方程的通解,具体的波动形式取决于源的波动形式。取最简单的简谐振动作为波动方程
的特解,因为这种振动形式简单,更重要的是可以从傅里叶分析方法可知,任何形式的波动都可以分解
为许多不同频率的简谐振动的和。于是有
z E Acos[ ( t)]
v
z B A`cos[ ( t)]
v
10-22 ~ 23
就是平面简谐电磁波的波动公式,对于光波就是平面单色光波的波动公式。式中,A 和 A`分别是
5
E~ A1 exp(ikr) r
10-38
当考察平面离波源很远,并且只注意考察平面上一个小范围时,r 的变化对球面波振幅的影响可以
忽略,这时的球面波可以视为球面波。
柱面波是具有无限长圆柱型波面(等位相面)的波。在光学实验中,用一平面波照射一细长狭缝,
可以获得接近圆柱面型的柱面波。柱面波的场强分布只与离开光源(狭缝)的距离 r 和时间 t 有关,可
χ射线 γ射线
表 10-1 电磁波谱
频率范围 Hz <10 9
10 9 ~ 10 12 10 12 ~ 4.3×10 14 4.3×10 14 ~ 7.5×10 14 7.5×10 14 ~ 10 16
10 16 ~ 10 18 >10 18
波长范围 >300nm 300 ~ 0.3nm 300 ~ 0.7μm 0.7 ~ 0.4μm 0.4 ~ 0.03μm 30 ~ 0.03 nm <0.03 nm
《物理光学》课后解答

第四章 光的电磁理论4-1计算由8(2)exp 610)i y t ⎡⎤=-+++⨯⎢⎥⎣⎦E i 表示的平面波电矢量的振动方向、传播方向、相位速度、振幅、频率、波长。
解:由题意:)81063(2t y x i eE x ⨯++-= )81063(32t y x i e E y ⨯++=∴3-=xy E E ∴振动方向为:j i3+-由平面波电矢量的表达式: 3=x k 1=y k∴传播方向为: j i+3平面电磁波的相位速度为光速: 8103⨯=c m/s;振幅:4)32()2(222200=+-=+=oy x E E E V/m频率:8810321062⨯=⨯==πππωf Hz 波长:πλ==fcm 4-2 一列平面光波从A 点传到B 点,今在AB 之间插入一透明薄片,薄片的厚度mm h 2.0=,折射率n =。
假定光波的波长为5500=λnm ,试计算插入薄片前后B 点光程和相位的变化。
解:设AB 两点间的距离为d ,未插入薄片时光束经过的光程为:d d n l ==01 插入薄片后光束经过的光程为:h n d nh h d n l )1()(02-+=+-= ∴光程差为:mm h n l l 1.02.05.0)1(12=⨯=-=-=∆ 则相位差为:ππλπδ6.3631.010550226=⨯⨯=∆=- (4-3 试确定下列各组光波表示式所代表的偏振态:(1))sin(0kz t E E x -=ω,)cos(0kz t E E y -=ω (2))cos(0kz t E E x -=ω,)4/cos(0πω+-=kz t E E y (3))sin(0kz t E E x -=ω,)sin(0kz t E E x --=ω 解:(1)∵)2cos()sin(00πωω--=-=kz t E kz t E E x∴2πϕϕϕ=-=x y∴ 为右旋圆偏振光。
·(2)4πϕϕϕ=-=x y∴ 为右旋椭圆偏振光,椭圆长轴沿y =x (3)0=-=x y ϕϕϕ∴ 为线偏振光,振动方向沿y =-x4-4 光束以30°角入射到空气和火石玻璃(n 2=)界面,试求电矢量垂直于入射面和平行于入射面分量的反射系数s r 和p r 。
物理光学简明教程

小结
振幅反射率
rs
E1s E1s
n1 cos1 n2 cos2 n1 cos1 + n2 cos2
s波
振幅透射率
ts
E2s E1s
2n1 cos1 n1 cos1 + n2 cos2
振幅反射率
rp
E1p E1 p
n2 cos1 n1 cos2 n2 cos1 + n1 cos2
p波
振幅透射率
tp
某一时刻位相相同的空间点的轨迹构成光波的等相面或波面
因子
cos[ 2
(z
t)
0 ]决定电场和磁场随空间和时间的变化关系
沿z方向传播的单色平面波
各物理量之间的关系
2 2 T T (介质中) 0 cT (真空中) 0 n
(1.2-5) (1.2-4)
是振动频率,T为振动周期,为光波波长
1.3.3 辐射能
辐射强度矢量 ---- 坡印亭矢量 (S描述电磁能量的传播)
S EH
(1.3-5)
对于光波,电场、磁场变化迅速,变化频率在1015赫兹左右,
的值也s 迅速变化,无法接收 的瞬时s值,只能接收其平均值。
称辐射强度矢量的时间平均值为光强,记为I。
对于平面波的情况,有
I s 1 T sdt v A2 1 T cos2 (kr t)dt
3、折射率
电磁波在真空中的速度与介质中速度之比称为介质绝对折射率
n c / rr
其中,相对介电常数:
r
0
相对磁导率: r 0
1.2 单色平面波和球面波
1.2.1 单色平面波的表示
1.余弦函数表示
假设平面波沿z方向以速度 v传播,平面简谐电磁波的波动公式为
第一章光的电磁理论基础详解

卷积的规则
g*h = h*g f *(g *h) = ( f * g)*h f *(g + h) = f * g + f *h
时间信号的傅立叶分析 一个一维时间函数的傅立叶变换定义为
∫ F(ν ) = F.T.{ f (t)} = ∞ f (t) exp(−i2πν t)dt −∞
逆变换
∫ f (t) = F.T.−1{F(ν )} = ∞ F(ν ) exp(i2πν t)dν −∞
平面波可以表示为
U (x, y, z) = Aexp(ik ir ) = Aexp[ik(x cosα + y cos β + z cosγ )]
= Aexp[i2π ( fx x + fy y + fz z)]
fx
=
cosα λ
fy
=
cos β λ
fz
=
cos γ λ
等相位面
k ir −ωt = constant
=
0
⎨
⎪⎪⎩∇2 B
−
1 c2
∂2B ∂t 2
=
0
无源波动方程
介质中波动方程
⎧ ⎪⎪∇2 E ⎨
− με
∂2E ∂t 2
=
0
⎪⎩⎪∇2 H
− με
∂2H ∂t 2
=0
或写成
⎧ ⎪⎪∇2 E ⎨
−
1 v2
∂2E ∂t 2
=
0
⎪⎪⎩∇2 H
−
1 v2
∂2H ∂t 2
=0
在无限大均匀介质中没有自由电荷和传导电流,场矢量的每一个 分量都满足齐次波动方程
dreeeerrrrrr5强场作用下的非线性介质边界条件在两种介质界面上电场强度矢量的切向分量连续21rtrtee210neer磁感应矢量的法向分量在界面上连续2r1nnbbr210nbbrg边界条件界面上磁场强度切向分量21ttshhjr21snhhjrr界面上电位移矢量的法向分量21nnrsdrgd21snddrsj自由电流线密度s自由电荷面密度边界条件21nnbdebde21nn21tt21tthh在无损介质的界面上0s0sj无源波动方程22002r2200200eertbbtrr介质中的麦克斯韦方程组0btedthrrjdbrrrrrgg真空中无自由电荷及传导电流00e00dbjehrrrrrr真空中波动方程2222r22221c01c0eertbbtrr或写成无源波动方程22222200eeththrrrr介质中波动方程或写成222222221v01v0eeththrrrr在无限大均匀介质中没有自由电荷和传导电流场矢量的每一个分量都满足齐次波动方程222222221v01v0iiiiethteixyzhixyz这个方程可以有多种形式的解其中最常见的是在直角坐标系中的平面波解在球坐标下的球面波解及在柱坐标系中的高斯光束解
大学物理光学
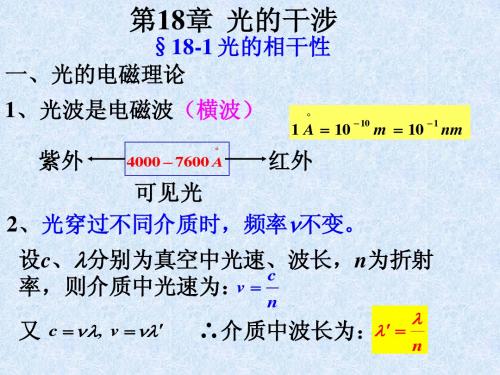
3、普通光源获得相干光的途径 思路: 同出一源,分开再合
同一发光 原子的同 一次发光
单缝 双缝 屏
三、光程与光程差
1、光程 定义 L=nr为光程。 2、光程差( )与相差( △ )的关系 P n r n r n1 r1 S1 易知:两光波传至P点 同相相 r2 干光源 的相差为 2 n2 S2
可将缝分为两个半波带。 时,
1 2 1′ 2′
f2
光线1(2…)与1 ′(2 ′…)在P点 的光程差为/2,
/2
∴两半波带发的光在P处 干涉相消形成暗纹中心。
▲当 a sin
B a A
3 2
/2
时,可将缝分成三个半波带。 其中两个相邻的半波带发的 光在P处干涉相消,剩一个半 波带发的光在P处合成。 ∴P处为明纹中心。
0 0 0 0
合振动:
E E 0 cos( t 0 )
令 2 1
0
0
合振幅
E0
E 1 E 2 2 E 1 E 2 cos
2 2
0 0 0 0
又:光的强度
I E0
2
定义: 相对光强 I E0 对相干光的叠加: ▲ 相长干涉(明) ▲相消干涉(暗)
e=0(中心)为零级暗纹(暗斑)。
r R (R e) 2R e e
2 2 2 2
R e e 2 Re
2
r
2 Re
⊥入射
R>>e
r
(k
1 2
) R / n 2 , k 1,2 明
kR / n 2 , k 0 ,1 暗
《物理光学》课件

过一定时间以后,电磁振动所到达的各点将构成一个以O点为中
心的球面,如图所示。这时的波阵面是球面,这种波就称为球
面波。
光线
波面
O
R
设图中的球面波为单色光波。由于球面波波面上各点的位相相 同,因此只需研究从O点发出的任一方向上各点的电磁场变化规 律,即可知道整个空间的情况。 取沿OR方向传播的光波为对象。设O点的初相为0,则距O点为r 的某点P的位相为
nc v
代入c、v各自的表达式,有
n c v
00
rr
r为相对介电常数,r为相对磁导率。
对除磁性物质以外的大 多数物质而言, r 1,故 n r
这个表达式称麦克斯韦 关系。
§3 平面电磁波 本节根据波动的两个偏微分方程,结合边界条件、初始条件,
得出其中的平面波解-平面波的波函数。
对积分得
2E z 2
1 v2
2E t 2
2E 4
0
即
E
0
E g
g 是的任意矢量函数
再对 积分得
E
g
d
f2
f1
f2
f1z vt f2 z vt
vt
取周期为2的余弦函数作为波动方 程的特解:
E
A cos
2
z
vt
3
B
A
cos
2
z
vt
4
二 平面简谐波
(3)(4)式是平面简谐波的波函数,即我们认定研究的电磁 波为平面简谐波。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E=A cos
2
(z
vt
)
B=A ' cos
2
(z
vt
)
A: 电场振幅矢量
A ':磁场振幅矢量
: 波长
2
z
vt
称为位相
位相是时间和
空间坐标的函
=2 2 / T
:振动频率
数,表示平面
vT , 0 cT 0 / n
:波长
波在不同时刻 空间各点的振 动状态。
k 2 / / v
P(x,y,z)
k
复振幅:
r
E=Aexp(ik r )
o
z
复振幅:只关心光波在 y
s=r k
空间的分布。
四 平面电磁波的性质
1、电磁波是横波:电矢量和磁矢量的方向均垂直波的
传播方向。
k E 0, k B 0
2、E、B、k互成右手螺旋系。
B
1 v
(k0
E)
(k0 E)
3、E和B同相
B
和空间角频率k。
v or c
vT 0 cT
三 一般坐标系下的波函数
E=Acos(k r t)
k k cosi cos j cos k
r xi yj zk
E=Acos k x cos y cos z cos t
平面波的复数形式:
E=Aexp[i(k r t)] x
物理光学
第一章 光的电磁理论
本章教学目的:
1. 光的电磁理论、电磁场的波动性; 2. 光波在介质中的传播速率、介质折射率的物理意
义及其表达式;
3. 平面简谐光波场的时间、空间特性,平面简谐光 波的数学表达式中各项参数的物理意义;
4. 光强的概念,计算相对光强的方法; 5. 菲涅耳公式的表达式,利用菲涅耳公式来计算光
电感强度(D):辅助物理量, D E P 。单位c/m2。
磁感强度(B ):单位T,1T=1N․s/c․m。速度为1m/s电 量为1c的电荷受到的磁力为1N时的磁感应强度。 磁场强度(H):辅助物理量, H B M 。单
位A/m。
静电场和稳恒磁场的基本规律
高斯定理:
D ds Q
S
k:波数 / 空间角频率
k0 2 / 0 / c
波矢量(沿等相面法线方向)
波动公式: E=Acos2 ( z t )
T E=Acos(kz t)
上式是一个具有单一频率、在时间和空间上 无限延伸的波。
空间周期性:
时间周期性:
在空间域中(时间轴为某
在时间域中(空间某点)
一时刻),参量:、 1/ 、 参量:T、、及角频率
3、麦克斯韦方程组的微分形式
微分形式:
D
B 0
E B t H j D
揭示了电流、电场、磁 场相互激励的性质
t
:封闭曲面内的自由电荷密度;
j:积分闭合回路上的传导电流密度; D :位移电流密度。 t
(1) (2) (3)
(4)
二、物质方程 (描述物质在场作用下特性的方程)
j E D E B H
波在介质界面上的折射、反射,反射时的半波损失 现象;
6. 全反射规律;光的色散、吸收、散射现象。
教学重点:
1.波动的描述,平面波、球面波; 2.菲涅耳公式及其应用。
1.1 光的电磁波性质
一、麦克斯韦方程组 (Maxwell’s equation) 1、静电场和稳恒磁场的基本规律
电场强度( E ):电场中某点在数量和方向上等于单 位正电荷在该点所受的电场力。单位N/c或V/m。
S B ds 0
安培定则: E dl 0 l
l H dl I
2、麦克斯韦方程组的积分形式
S D ds Q
S B ds 0
l E dl
d dt
B t
ds
l H dl
I
D ds t
D:电感强度 E:电场强度 B:磁感强度 H:磁场强度 :磁通量
后两个公式反映了磁场和电场之间的相互作用。
E B t
B E
t
正比
E
=-
t
B
2E t 2
E E 2E
结果:2 E
2E t 2
0
2 B 2 B 0
t 2
(1.8) (1.9)
E 0
四、电磁波
结果: 2 E
2E t 2
0
2B 2B 0
t 2
2E 1 2E 0 v2 t 2
2B
1 v2
2B t 2
k0 E
E
1
v
B
1.3 球面波和柱面波
除平面波外,球面波和柱面波也是两种 常见的波。在光学中他们分别由点光源和 线光源产生。 一 、球面波的波函数: 二、球面波的复振幅: 三、柱面波的波函数:
:电导率; :介电常数; :磁导率。
在真空中: =0, =0=8.854210-12C 2 / N • m(2 库2 / 牛 • 米2) =0=4 10-7 N • S 2 / C(2 牛• 秒2 / 库2)
三、电磁场的波动性(波动方程)
对于电磁场远离辐射源:=0,j=0
E 0 B 0 点积为零,叉积与时间偏导成
0
电磁波的传播速度:v 1 =1 0r 0r 真空中的光速:c 1 00 2.99794 108 m / s
引入相对介电常数r和相对磁导率r r 0 ; r 0
电磁波的速度:v c r r 电磁波的折射率:n c v r r r
The electromagnetic spectrum
short
Wave length
Gamma X- Ultra V Infra
Rays Rays violet
-red
long
Micro Radio -waves -waves
380nm 780nm
violet-blue deep-red
1.2 平面电磁波
一 波f1和f2是以(z vt)和(z vt) 为变量的任意函数。
f1(z vt)表示沿z轴正向传播的平面波, f2 (z vt)表示沿z轴负向传播的平面波。
取正向传播:
E=f1(z vt) B=f1(z vt)
这是行波的表示式,表 示源点的振动经过一定 的时间推迟才传播到场 点。
二 平面简谐波 (Simple Harmonic Wave)
y
=x0
x
y0
y
z0
z
z0
z
x
v
z
结果:2E 1 2E 0 v2 t 2
2E 1 2E 0 z2 v2 t 2
令 =z vt, z vt,代入上式则有
E=f1(z vt) f2 (z vt)
同理可求 B=f1(z vt) f2 (z vt)
2、解的意义:
E=f1(z vt) f2 (z vt) B=f1(z vt) f2 (z vt)
